High dimensional robust M-estimation: asymptotic variance via approximate message passing

Abstract

In a recent article, El Karoui et al. (Proc Natl Acad Sci 110(36):14557–14562, 2013) study the distribution of robust regression estimators in the regime in which the number of parameters p is of the same order as the number of samples n. Using numerical simulations and ‘highly plausible’ heuristic arguments, they unveil a striking new phenomenon. Namely, the regression coefficients contain an extra Gaussian noise component that is not explained by classical concepts such as the Fisher information matrix. We show here that that this phenomenon can be characterized rigorously using techniques that were developed by the authors for analyzing the Lasso estimator under high-dimensional asymptotics. We introduce an approximate message passing (AMP) algorithm to compute M-estimators and deploy state evolution to evaluate the operating characteristics of AMP and so also M-estimates. Our analysis clarifies that the ‘extra Gaussian noise’ encountered in this problem is fundamentally similar to phenomena already studied for regularized least squares in the setting $n<p$.

1 M-estimation under high dimensional asymptotics

Consider the traditional linear regression model

$$\begin{aligned} Y\, =\, {\mathbf {X}}\,\theta _0+ W, \end{aligned}$$

(1)

with $Y = (Y_1,\cdots ,Y_n)^\mathsf{T}\in {\mathbb {R}}^n$ a vector of responses, ${\mathbf {X}}\in {\mathbb {R}}^{n\times p}$ a known design matrix, $\theta _0\in {\mathbb {R}}^p$ a vector of parameters, and $W\in {\mathbb {R}}^n$ random noise having zero-mean components $W = (W_1,\cdots ,W_n)^{\mathsf{T}}$ i.i.d. with distribution $F = F_{W}$ having finite second moment.¹

We are interested in estimating $\theta _0$ from observed data² $(Y,{\mathbf {X}})$ using a traditional M-estimator, defined by a non-negative convex function $\rho : {\mathbb {R}}\rightarrow {\mathbb {R}}_{\ge 0}$:

$$\begin{aligned} \widehat{\theta }(Y;{\mathbf {X}}) \equiv \arg \min _{\theta \in {\mathbb {R}}^p}{\mathcal {L}}(\theta ;Y,{\mathbf {X}}),\;\;\;\;\;\;\;\;\; {\mathcal {L}}(\theta ;Y,{\mathbf {X}}) \equiv \sum _{i=1}^n \rho \big (Y_i-\langle X_i,\theta \rangle \big ), \end{aligned}$$

(2)

where $\langle u,v\rangle =\sum _{i=1}^mu_iv_i$ is the standard scalar product in ${\mathbb {R}}^m$, and $\widehat{\theta }$ is chosen arbitrarily if there is multiple minimizers.

Although this is a completely traditional problem, we consider it under high-dimensional asymptotics where the number of parameters p and the number of observations n are both tending to infinity, at the same rate. This is becoming a popular asymptotic model owing to the modern awareness of ‘big data’ and ‘data deluge’; but also because it leads to entirely new phenomena.

1.1 Extra Gaussian noise due to high-dimensional asymptotics

Classical statistical theory considered the situation where the number of regression parameters p is fixed and the number of samples n is tending to infinity. The asymptotic distribution was found by Huber [2, 18] to be normal $\mathsf{N}(0,{\mathbf {V}})$ where the asymptotic variance matrix ${\mathbf {V}}$ is given by

$$\begin{aligned} {\mathbf {V}}= V(\psi ,F_W) ({\mathbf {X}}^{\mathsf{T}}{\mathbf {X}})^{-1} \end{aligned}$$

(3)

here $\psi = \rho '$ is the score function of the M-estimator and $V(\psi ,F) = (\int \psi ^2 \mathrm{d}F)/(\int \psi ' \mathrm{d}F)^2$ the asymptotic variance functional of [17], and $({\mathbf {X}}^{\mathsf{T}}{\mathbf {X}})$ the usual Gram matrix associated with the least-squares problem. Importantly, it was found that for efficient estimation—i.e. the smallest possible asymptotic variance—the optimal M-estimator depended on the probability distribution $F_W$ of the errors W. Choosing $\psi (x)= (\log f_W(x))'$ (with $f_W$ the density of W), the asymptotic variance functional yields $V(\psi ,F_W) = 1/I(F_W)$, with I(F) denoting the Fisher information. This achieves the fundamental limit on the accuracy of M-estimators [18].

In modern statistical practice there is increasing interest in applications where the number of explanatory variables p is very large, and comparable to n. Examples of this new regime can be given, spanning bioinformatics, machine learning, imaging, and signal processing (a few research areas in the last domains include [8, 23, 28, 29]).

This paper considers the properties of M-estimators in the high-dimensional asymptotic $n \rightarrow \infty$, $n/p(n) \rightarrow \delta \in (1,\infty )$. In this regime, the asymptotic distribution of M-estimators no longer needs to obey the classical formula (3) in widespread use. We make a random-design assumption on the ${\mathbf {X}}$’s detailed below. We show that the asymptotic covariance matrix of the parameters is now of the form

$$\begin{aligned} {\mathbf {V}}= V(\tilde{\Psi },\tilde{F}_W) \left( {\mathbb {E}}\{{\mathbf {X}}^{\mathsf{T}}{\mathbf {X}}\}\right) ^{-1}, \end{aligned}$$

(4)

where V is still Huber’s asymptotic variance functional, but $\tilde{\Psi }$ is the effective score function, which is different from $\psi$ under high-dimensional asymptotics and $\tilde{F}_W$ is the effective error distribution, which is different from $F_W$ under high-dimensional asymptotics. In the limit $\delta \rightarrow \infty$, the effective score and the effective error distribution both tend to their classical counterparts, and one recovers $V(\psi ,F_W)$.

The effective error distribution $\tilde{F}_W$ is a convolution of the noise distribution with an extra Gaussian noise component, not seen in the classical setting (here $\star$ denotes convolution):

$$\begin{aligned} \widetilde{F}_W\equiv F_W \star \mathsf{N}(0,\tau _*^2(\psi ,F_W,\delta )). \end{aligned}$$

(5)

The extra Gaussian noise depends in a complex way on $\psi$, $F_W$, $\delta$, which we characterize fully below in Theorem 4.2.

Several important insights follow immediately:

• 1. Existing formulas are inadequate for confidence statements about M-estimates under high dimensional asymptotics, and will need to be systematically broadened.

• 2. Classical maximum likelihood estimates are inefficient under high-dimensional asymptotics. The idea dominating theoretical statistics since R.A. Fisher to use $\psi = (- \log f_W)'$ as a scoring rule, does not yield the efficient estimator.

• 3. The usual Fisher Information bound is not necessarily attainable in the high-dimensional asymptotic, as $I(\widetilde{F}_W) < I(F_W)$.

M-estimation in this high-dimensional asymptotic setting was considered in a recent article by El Karoui et al. [15], who studied the distribution of $\widehat{\theta }$ for Gaussian design matrices ${\mathbf {X}}$. In short they observed empirically the basic phenomenon of extra Gaussian noise appearing in high-dimensional asymptotics and rendering classical inference incorrect. The dependence of the additional variance $\tau _*^2$ on $\delta$, $\psi$ and F was characterized by [15] through a non-rigorous heuristics.³ that the authors describe as ‘highly plausible and buttressed by simulations.⁴

1.2 Asymptotic variance: a formal statement

In order to provide a preview of our rigorous results, we state here formally our asymptotic variance result. As explained below, this follows as a corollary of our technical results, and—for the reader’s convenience—will be restated and proved as Theorem 4.2. We will work with random Gaussian designs, defined as follows. (We refer to Sect. 5.)

Definition 1.1

We say that a sequence of random design matrices $\{{\mathbf {X}}(n)\}_n$, with $n\rightarrow \infty$ is a Gaussian design if each ${\mathbf {X}}={\mathbf {X}}(n)$ has dimensions $n\times p$, and entries $(X_{ij})_{i\in [n],j\in [p]}$ that are i.i.d. $\mathsf{N}(0,1/n)$. Further, $p = p(n)$ is such that $\lim _{n\rightarrow \infty } n/p(n) = \delta \in (0,\infty )$.

Associated to $\rho$, we introduce the family $\rho _b$ of regularizations of $\rho$:

$$\begin{aligned} \rho _b(z) \equiv \min _{x\in {\mathbb {R}}} \Big \{b\rho (x) + \frac{1}{2}(x-z)^2\Big \} , \end{aligned}$$

(6)

in words, this is the min-convolution of the original loss with a square loss. Each $\rho _b$ has a corresponding score function

$$\begin{aligned} \Psi (z;b) = \rho '_b(z). \end{aligned}$$

(7)

We are now in position to state formally our asymptotic variance result.

Theorem 1.2

Assume that the loss function $\rho$ is strongly convex and smooth, that the sequence of matrices $\{{\mathbf {X}}(n)\}_{n}$ is a standard Gaussian design with $\delta >1$. Further assume that $F_W$ has finite second moment.

Then, the asymptotic variance of $~\widehat{\theta }$ obeys

$$\begin{aligned} \lim _{n,p \rightarrow \infty } \mathrm{Ave}_{i\in [p]}{\mathrm{Var}}(\widehat{\theta }_i) =_{\mathrm{a.s}} V(\tilde{\Psi },\tilde{F}), \end{aligned}$$

(8)

where $\mathrm{Ave}_{i\in [p]}$ denotes the average across indices i, $V(\psi ,F)$ denotes the usual Huber asymptotic variance formula for M-estimates—$V(\psi ,F) = (\int \psi ^2 \mathrm{d}F)/(\int \psi ' \mathrm{d}F)^2$—and the effective score $\tilde{\Psi }$ is

$$\begin{aligned} \tilde{\Psi }(\cdot ) = \Psi (\cdot ; b_*) , \end{aligned}$$

while the effective noise distribution $\tilde{F}$ is

$$\begin{aligned} \tilde{F} = F_W \star \mathsf{N}(0,{\tau }_*^2). \end{aligned}$$

Here $(\tau _*,b_*)$ is defined to be the solution of the two equations below (which is proved to exist and be unique):

$$\begin{aligned} \tau ^2&= \delta \; {\mathbb {E}}\Big \{\Psi (W+\tau \, Z;b)^2\Big \}, \end{aligned}$$

(9)

$$\begin{aligned} \frac{1}{\delta }&= {\mathbb {E}}\Big \{\Psi '(W+\tau \,Z;b)\Big \}. \end{aligned}$$

(10)

As mentioned above, this is proved as Theorem 4.2 below.

1.3 Proof strategy: approximate message passing

In the present paper, we show that this important statistical phenomenon can be characterized rigorously, in a way that we think fully explains the main new concepts of extra Gaussian noise, effective noise and the effective score. Our proof strategy has three steps

• Introduce an Approximate Message Passing (AMP) algorithm for M-estimation; an iterative procedure with the M-estimator as a fixed point, and having the effective score function $\tilde{\Psi }$ as its score function at algorithm convergence.

• Introduce state evolution for calculating properties of the AMP algorithm iteration by iteration. We show that these calculations are exact at each iteration in the large-n limit where we freeze the iteration number and let $n \rightarrow \infty$.

  At the center of the state evolution calculation is precisely an extra Gaussian noise term that is tracked from iteration to iteration, and which is shown to converge to a nonzero noise level. In this way, state evolution makes very explicit that AMP faces at each iteration and even in the limit, an effective noise that differs from the noise W by addition of an appreciable extra independent Gaussian noise.

• Show that the AMP algorithm converges to the solution of the M-estimation problem in mean square, from which it follows that the asymptotic variance of the M-estimator is identical to the asymptotic variance of the AMP algorithm. More specifically, the asymptotic variance of the M-estimator is given by a formula involving the effective score function and the effective noise.

As it turns out, our formula for the asymptotic variance coincides with the one derived heuristically in [15, Corollary 1] although our technique is remarkably different, and our proof provides a very clear understanding of the operational significance of the terms appearing in the asymptotic variance. It also allows explicit calculation of many other operating characteristics of the M-estimator, for example when used as an outlier detector.⁵

1.4 Underlying tools

At the heart of our analysis, we are simply applying an approach developed [4, 5] for rigorous analysis of solutions to convex optimization problems under high-dimensional asymptotics.

That approach grew out of a series of earlier papers studying the compressed sensing problem [5, 9, 11, 13]. From the perspective of this paper, those papers considered the same regression model (1) as here; however, they emphasized the challenging asymptotic regime where there are fewer observations than predictors, (i.e. $n/p(n)\rightarrow \delta \in (0,1)$) so that even in the noiseless case, the equations $Y = {\mathbf {X}}\theta$ would be underdetermined. In the $p > n$ setting, it became popular to use $\ell _1$-penalized least squares (Lasso [7, 34]). That series of papers considered the Lasso convex optimization problem in the case of ${\mathbf {X}}$ with iid $\mathsf{N}(0,1/n)$ entries (just as here) and followed the same 3-step strategy we use here; namely, (1) Introducing an AMP algorithm; (2) Obtaining the asymptotic distribution of AMP by state evolution; and (3) Showing that AMP agrees with the Lasso solution in the large-n limit. This procedure proved that the Lasso solution has the asymptotic distribution

$$\begin{aligned} \widehat{\theta }^u\sim \mathsf{N}\left( \theta _0, (\sigma ^2+\tau _\mathrm{Lasso}^2)\mathrm{I}_{p\times p}\right) \end{aligned}$$

(11)

where $\sigma ^2$ is the variance of the noise in the measurements, and $\tau _\mathrm{Lasso}^2$ is the variance of an extra Gaussian noise, not appearing in the classical setting where $p(n)/n \rightarrow 0$. The variance of this extra Gaussian noise was obtained by state evolution and shown to depend on the distribution of the coefficients being recovered, and on the noise level in a seemingly complicated way that can be characterized by a fixed-point relation, see [5, 13]. At the center of the rigorous analysis stand the papers [4, 5] which analyze recurrences of the type used by AMP and establish the validity of State Evolution in considerable generality. Those same papers stand at the center of our analysis in this paper.

Apart from allowing a simple treatment, this provides a unified understanding of the phenomenon of high-dimensional extra Gaussian noise.

1.5 The role of AMP

This paper introduces a new first-order algorithm for computing the M-estimator $\widehat{\theta }$ which is uniquely appropriate for the random-design case. This algorithm fits within the class of approximate message passing (AMP) algorithms introduced in [4, 11] (see also [27] for extensions). This algorithm is of independent interest because of its low computational complexity.

AMP has a deceptive simplicity. As an iterative procedure for convex optimization, it looks almost the same as the ‘standard’ application of simple fixed-stepsize gradient descent. However, it is intended for use in the random-design setting, and it has an extra memory term (aka reaction term) that modifies the iteration in a profound and beneficial way. In the Lasso setting, AMP algorithms have been shown to have remarkable fast convergence properties [11], far outperforming more complex-looking iterations like Nesterov and FISTA.

In the present paper, AMP has an second important wrinkle—it solves a convex optimization problem associated to minimizing $\rho$ with iterations based on gradient descent with an objective $\rho _{b_t}$ which varies from one iteration to the next, as $b_t$ changes, but which does not tend to $\rho$ in the limit.

In the present paper, AMP is mainly used as a proof device, one component of the three-part strategy outlined earlier. However, a key benefit produced by the curious features of AMP is strong heuristic insight, which would not be available for a ‘standard’ gradient-descent algorithm.

The AMP proof strategy makes visible the extra Gaussian noise appearing in the M-estimator $\widehat{\theta }$. Elementary considerations show that such extra noise is present at iteration zero of AMP. state evolution faithfully tracks the dynamics of this extra noise across iterations. State evolution proves that the extra noise level does not go to zero asymptotically with increasing iterations, but instead that the extra noise level tends to a fixed nonzero value. Because AMP is solving the M-estimation problem, the M-estimator must be infected by this extra noise.

The AMP algorithm and its state evolution analysis shows that the extra noise in parameter $\widehat{\theta }_i^t$ at iteration t is due to cross-parameter estimation noise leakage, where errors in the estimation of all other parameters at the previous iteration $(t-1)$ cause extra noise to appear in $\widehat{\theta }_i^t$. In the classical setting no such effect is visible. One could say that the central fact about the high-dimensional setting revealed here as well as in our earlier work [5, 9, 11, 13], is that when there are so many parameters to estimate, one cannot really insulate the estimation of any one parameter from the errors in estimation of all the other parameters.

2 Approximate message passing (AMP)

This section introduces the Approximate Message Passing algorithm relevant to the general M-estimation problem (2). Its analysis through state evolution is discussed in the next section.

The interested reader can find relevant background on AMP [4, 12], and in the tutorial papers [25, 35]. In particular, the techniques used here have been already applied to a large number of problems. An list of simple examples includes:

• 1. Bolthausen [6] considers the Sherrington–Kirkpatrick model of mean-field spin glasses. It develops an iterative scheme to construct a solution of the celebrated TAP (Thouless–Anderson–Palmer) equations. This scheme and its analysis can be regarded as special cases of AMP and State Evolution.

• 2. Our early work [4] develops the general state evolution techniques on a rigorous basis, building on ideas from [6]. It illustrates it in a few examples: (1) Linear estimation (Sect. 2.1); (2) Compressed sensing via soft-thresholding (Sect. 2.2); (3) Multi-user detection (Sect. 2.3).

  A different proof technique, and a universality result are proved in [3].

• 3. The tutorial chapter [35] contains an expository presentation of a simple AMP algorithm for the hidden clique problem, alongside its state evolution analysis (Sect. 6). More details on the same problem can be found in [10].

2.1 A family of score functions

For the rest of the paper, we make the following smoothness assumption on $\rho$:

Definition 2.1

We call the loss function $\rho :{\mathbb {R}}\rightarrow {\mathbb {R}}$ smooth if it is continuously differentiable, with absolutely continuous derivative $\psi = \rho '$ having an a.e. derivative $\psi '$ that is bounded: $\sup _{u\in {\mathbb {R}}}\psi '(u)<\infty$.

Our assumption excludes some interesting cases, such as $\rho (u) = |u|$, but includes for instance the Huber loss⁶

$$\begin{aligned} \rho _{\mathrm{H}}(z; \lambda ) = {\left\{ \begin{array}{ll} z^2/2 &{} \text{ if } \,\,|z|\le \lambda ,\\ \lambda |z| - \lambda ^2/2 &{} \text{ otherwise. } \end{array}\right. } \end{aligned}$$

(12)

Recall the definition of regularized loss $\rho _b$, and corresponding score function $\Psi (z;b)$, given in Eqs. (6) and (7). The effective score of the M-estimator belongs to this family, for a particular choice of b, explained below.

In the classical M-estimation literature [16], monotonicity and differentiability of the score function $\psi$ is frequently useful; our assumptions on $\rho$ guarantee these properties for the nominal score function $\psi$. The score family $\Psi (\,\cdot \, ; b)$ has such properties as well: for any b, $\Psi (\,\cdot \,;b)$ is a strictly monotone increasing function; second, for any $b>0$, $\Psi (\,\cdot \,;b)$ is a contraction. With $\Psi '$ denoting differentiation with respect to the first variable, we have $\Psi '(z;b) \in (0,1)$. For proof and further discussion, see Appendix 1.

Before proceeding, we give an example. Consider the Huber loss $\rho _{\mathrm{H}}(z; \lambda )$, with score function $\psi (z;\lambda ) = \min (\max (-\lambda ,z),\lambda )$. We have

$$\begin{aligned} \Psi ( z ; b) = b \psi \Big ( \frac{z}{1+b} ; \lambda \Big ). \end{aligned}$$

In particular the shape of each $\Psi$ is similar to $\psi$, but the slope of the central part is now $\Vert \Psi '( \,\cdot \,;b) \Vert _\infty = \frac{b}{1+b} < 1$.

2.2 AMP algorithm

Our proposed approximate message passing (AMP) algorithm for the optimization problem (2) is iterative, starting at iteration 0 with an initial estimate $\widehat{\theta }^0\in {\mathbb {R}}^p$. At iteration $t=0,1,2,\dots$ it applies a simple procedure to update its estimate $\widehat{\theta }^{t}\in {\mathbb {R}}^p$, producing $\widehat{\theta }^{t+1}$. The procedure involves three steps.

Adjusted residuals Using the current estimate $\widehat{\theta }^t$, we compute the vector of adjusted residuals $R^t\in {\mathbb {R}}^n$,

$$\begin{aligned} R^t&= Y -{\mathbf {X}}\widehat{\theta }^t+\Psi \left( R^{t-1};b_{t-1}\right) ; \end{aligned}$$

(13)

where to the ordinary residuals $Y - {\mathbf {X}}\widehat{\theta }^t$ we here add the extra term⁷ $\Psi (R^{t-1};b_{t-1})$.

Effective score We choose a scalar $b_t > 0$, so that the effective score $\Psi (\,\cdot \,; b_t)$ has empirical average slope $p/n \in (0,1)$. Setting $\delta =\delta (n) = n/p>1$, we take any solution⁸ (for instance the smallest solution) to⁹:

$$\begin{aligned} \frac{1}{\delta } = \frac{1}{n}\sum _{i=1}^n\Psi '(R^t_i;b). \end{aligned}$$

(14)

Scoring We apply the effective score function $\Psi (R^t; b_t)$:

$$\begin{aligned} \widehat{\theta }^{t+1}&= \widehat{\theta }^t+\delta {\mathbf {X}}^{\mathsf{T}}\Psi (R^t;b_t). \end{aligned}$$

(15)

The Scoring step of the AMP iteration (15) is similar to traditional iterative methods for M-estimation, compare [2]. Indeed, using the traditional residual $z^t = Y - {\mathbf {X}}\theta ^t$, the traditional method of scoring at iteration t would read

$$\begin{aligned} \widehat{\theta }^{t+1} = \widehat{\theta }^t + \frac{1}{\frac{1}{n}\sum _{i=1}^n\psi '(z^t_i)} ({\mathbf {X}}^{\mathsf{T}}{\mathbf {X}})^{-1} {\mathbf {X}}^{\mathsf{T}} \psi (z^t), \end{aligned}$$

(16)

and one can see correspondences of individual terms to the method of scoring used in AMP. Of course the traditional term $[\sum _{i=1}^n\psi '(z^t_i)/n]^{-1}$ corresponds to AMP’s $[\sum _{i=1}^n\Psi '(R^t_i; b_t)/n]^{-1} \equiv \delta$ (because of step 14), while the traditional term $({\mathbf {X}}^{\mathsf{T}}{\mathbf {X}})^{-1}$ corresponds to AMP’s implicit $\mathrm{I}_{p\times p}$—which is appropriate in the present context because our random-design assumption below makes ${\mathbf {X}}^{\mathsf{T}}{\mathbf {X}}$ behave approximately like the identity matrix.

2.3 Relation to M-estimation

The next lemma explains the reason for using the effective score $\Psi (\cdot ; b_t)$ in the AMP algorithm: this is what connects the AMP iteration to M-estimation (2).

Lemma 2.2

Let $(\widehat{\theta }_*,R_*,b_*)$ be a fixed point of the AMP iteration (13), (14), (15) having $b_*>0$. Then $\widehat{\theta }_*$ is a minimizer of the problem (2). Viceversa, any minimizer $\widehat{\theta }_*$ of the problem (2) corresponds to one (or more) AMP fixed points of the form $(\widehat{\theta }_*,R_*,b_*)$.

Proof

By differentiating Eq. (2), and omitting the arguments $Y,{\mathbf {X}}$ for simplicity from ${\mathcal {L}}(\theta ;Y,{\mathbf {X}})$, we get

$$\begin{aligned} \nabla _{\theta }{\mathcal {L}}(\theta ) = -\sum _{i=1}^n \rho '\big (Y_i-\langle X_i,\theta \rangle \big )\, X_i = - {\mathbf {X}}^{\mathsf{T}} \rho '(Y-{\mathbf {X}}\theta ), \end{aligned}$$

(17)

where as usual $\rho '$ is applied component-wise to vector arguments. The minimizers of ${\mathcal {L}}(\theta )$ are all the vectors $\theta$ for which the right hand side vanishes.

Consider then a fixed point $(\widehat{\theta }_*,R_*,b_*)$, of the AMP iteration (13), (15). This satisfies the equations

$$\begin{aligned} R_*&= Y -{\mathbf {X}}\widehat{\theta }_*+\Psi (R_*;b_*),\end{aligned}$$

(18)

$$\begin{aligned} 0&= \delta {\mathbf {X}}^{\mathsf{T}}\Psi (R_*;b_*). \end{aligned}$$

(19)

The first equation can be written as

$$\begin{aligned} Y-{\mathbf {X}}\theta _* = R_* - \Psi (R_*;b_*), \end{aligned}$$

(20)

Using Proposition 6.4 below, (20) implies that $\Psi (R_*;b_*) = b_* \rho '(Y-{\mathbf {X}}\widehat{\theta }_*)$. Hence the second equation reads

$$\begin{aligned} 0&= \delta b_*{\mathbf {X}}^{\mathsf{T}}\rho '(Y-{\mathbf {X}}\widehat{\theta }_*), \end{aligned}$$

(21)

which coincides with the stationarity condition (17) for $b_*>0$. This concludes the proof. $\square$

2.4 Example

To make the AMP algorithm concrete, we consider an example with $n=1000$, $p=200$, so $\delta =5$. For design matrix we let $X_{i,j} \sim \mathsf{N}(0,\frac{1}{n})$, and we draw $\theta _0$ a random vector of norm $\Vert \theta _0 \Vert _2 = 6 \sqrt{p}$. For the distribution $F = F_W$ of errors, we use Huber’s contaminated normal distribution $\mathsf{CN}(0.05,10)$, so that $F = 0.95 \Phi \,+\, 0.05 H_{10}$, where $H_x$ denotes a unit atom at x. For the loss function, we use the Huber’s $\rho _{\mathrm{H}}(z;\lambda )$ with $\lambda = 3$. Starting the AMP algorithm with $\widehat{\theta }^0 = 0$, we run 20 iterations.

Separately, we solved the M-estimation problem using CVX, obtaining $\widehat{\theta }$.

Figure 1 (left panel) shows the progress of the AMP algorithm across iterations, presenting

$$\begin{aligned} \mathrm{RMSE}(\widehat{\theta }^t;\theta _0) \equiv \frac{1}{\sqrt{p}}\,\Vert \widehat{\theta }^t-\theta _0\Vert _2, \end{aligned}$$

while Fig. 1 (right panel) shows the progress of AMP in approaching the M-estimate $\widehat{\theta }$, as measured by

$$\begin{aligned} \mathrm{RMSE}(\widehat{\theta }^t; \widehat{\theta }) \equiv \frac{1}{\sqrt{p}}\,\Vert \widehat{\theta }^t-\widehat{\theta }\Vert _2. \end{aligned}$$

As is evident, the iterations converge rapidly, and they converge to the M-estimator, both in the sense of convergence of risks—measured here by $\mathrm{RMSE}(\widehat{\theta }^t;\theta _0) \rightarrow \mathrm{RMSE}(\widehat{\theta }; \theta _0) \approx 1.6182$—and, more directly, in convergence of the estimates themselves: $\mathrm{RMSE}(\widehat{\theta }^t; \widehat{\theta }) \rightarrow 0$.

Fig. 1

Left panel RMSE of AMP versus iteration (black curve), and its convergence to RMSE of M-estimation (constant green curve). Right panel discrepancy of AMP from M-estimate, versus iteration

Figure 2 (left panel) shows the process by which the effective score parameter $\hat{b}_t$ is obtained at iteration $t=3$, while the right panel shows how $\hat{b}_t$ behaves across iterations. In fact it converges quickly towards a limit $b_\infty \approx 0.2710$.

Fig. 2

Left panel determining the regularization parameter at iteration 3. Blue curve average slope (vertical) versus regularization parameter b (horizontal). The blue curve intersects desired level $0.2 =1/\delta$ near 0.3. Right panel regularization parameter $b_t$ versus iteration; it converges rapidly to roughly 0.2710

2.5 Contrast to iterative M-estimation

Earlier we pointed to resemblances between AMP (15) and the traditional method of scoring for obtaining M-estimators (16). In reality the two approaches are very different:

• The precise form of various terms in (13), (14) (15) is dictated by the statistical assumptions that we are making on the design ${\mathbf {X}}$. In particular the memory terms are crucial for the state evolution analysis to hold. Several papers document this point [22, 25, 27, 30, 31].

• Under classical asymptotics, where p is fixed and $n \rightarrow \infty$, it is sufficient to run a single step of such an algorithm [2], in the high-dimensional setting it is necessary to iterate numerous times. The resulting analysis is considerably more complex because of correlations arising as the algorithm evolves.

3 State evolution description of AMP

State evolution is a method for computing the operating characteristics of the AMP iterates $\widehat{\theta }^t$ and $R^t$ for arbitrary fixed t, under the high-dimensional asymptotic limit $n,p\rightarrow \infty$, $n/p \rightarrow \delta$.

In this section we initially describe a purely formal procedure which assumes that the AMP adjusted residuals $R^t = Y - {\mathbf {X}}\widehat{\theta }^t + \Psi (R^t;b_t)$ really behave as $W + \tau _t Z$, with W the error distribution and Z an independent standard normal, for $t=0,1,2,\dots$. The variable $\tau _t^2$ thus quantifies the extra Gaussian noise supposedly present in the adjusted residuals of AMP; we show how this ansatz allows one to calculate $\tau _t^2$ for each $t=0,1,2,3, \dots$, and to calculate the limit of $\tau _t$ as $t \rightarrow \infty$. Later in the section we present a rigorous result validating the method under the random Gaussian design assumption.

3.1 Initialization of the extra variance

Under the Gaussian design assumption, suppose that $\mathbf{u}$ is a vector in ${\mathbb {R}}^p$ with norm $\Vert u \Vert _2$. Then $\{{\mathbb {E}}\Vert {\mathbf {X}}u \Vert _2^2\} = \Vert u\Vert _2^2$. Moreover, $X\mathbf{u}$ is a Gaussian random vector with entries iid $\mathsf{N}(0,\Vert u\Vert _2^2/n)$.

It will be convenient to introduce for any estimator $\tilde{\theta }$ the notation

$$\begin{aligned} \mathrm{MSE}(\tilde{\theta },\theta _0) = \frac{1}{p}\, m \Vert \tilde{\theta } - \theta _0 \Vert _2^2. \end{aligned}$$

(22)

So initialize AMP with a deterministic estimate $\widehat{\theta }^0$, and take $R^{-1}=0$. Then the initial residual is $R^1 = Y - {\mathbf {X}}\widehat{\theta }^0 = W + {\mathbf {X}}( \theta _0 - \widehat{\theta }^0)$. The terms W and ${\mathbf {X}}( \theta _0 - \widehat{\theta }^0)$ are independent, and ${\mathbf {X}}( \theta _0 - \widehat{\theta }^0)$ is Gaussian with variance $\tau _0^2 = \Vert \widehat{\theta }^0 - \theta _0\Vert _2^2/n = \mathrm{MSE}(\widehat{\theta }^0, \theta _0)/\delta$. Consider some fixed coordinate $R^1(i)$ of $R^1$. Then

$$\begin{aligned} {\mathrm{Var}}(R^1_i) = {\mathrm{Var}}(W) + {\mathrm{Var}}({\mathbf {X}}(\theta _0 - \widehat{\theta }^0)) = {\mathrm{Var}}(W) + \mathrm{MSE}(\theta ^0, \theta _0)/\delta . \end{aligned}$$

Hence, when AMP is started this way, we see that the adjusted residuals initially contain an extra Gaussian noise of variance $\tau _0^2 = \mathrm{MSE}(\widehat{\theta }^0,\theta _0)/\delta$.

3.2 Evolution of the extra Gaussian variance to its ultimate limit

Assuming the adjusted residuals continue, at later iterations, to behave as $W + \tau _t\, Z$ with Z an independent standard normal, we now calculate $\tau _t^2$ for each $t=1,2,3, \dots$, and eventually identify the limit of $\tau _t$ as $t \rightarrow \infty$.

For a given $\tau > 0$, $\delta = n/p$ and noise distribution $F_W$, define the variance map

$$\begin{aligned} {\mathcal {V}}(\tau ^2 , b; \delta , F_W)= \delta \, {\mathbb {E}}\Big \{\Psi (W+\tau \, Z;b)^2\Big \}, \end{aligned}$$

where $W\sim F_W$, and, independently, $Z\sim \mathsf{N}(0,1)$. In this display, the reader can see that extra Gaussian noise of variance $\tau ^2$ is being added to the underlying noise W, and ${\mathcal {V}}$ measures the $\delta$-scaled variance of the resulting output. Evidently for $b > 0$, $0 \le {\mathcal {V}}(\tau ^2, b) \cdot \delta \le ({\mathrm{Var}}(W)+\tau ^2) \cdot \delta$.

Under our assumptions for $\Psi$, for each given specification $(\tau ;\delta ,F_W)$ of the ingredients besides b that go into ${\mathcal {V}}$, there is (as clarified by Lemma 6.5) a well-defined value $b = b(\tau ;\delta ,F_W)$ giving the smallest solution $b \ge 0$ to

$$\begin{aligned} \frac{1}{\delta } = {\mathbb {E}}\Big \{\Psi '(W+\tau \cdot \,Z;b)\Big \}\, . \end{aligned}$$

(23)

Definition 3.1

State evolution is an iterative process for computing the scalars $\{\tau ^2_t\}_{t\ge 0}$, starting from an initial condition $\tau _0^2\in {\mathbb {R}}_{\ge 0}$ following

$$\begin{aligned} \tau _{t+1}^2 = {\mathcal {V}}(\tau _t^2 , b(\tau _t) ) = {\mathcal {V}}(\tau _t , b(\tau _t; \delta ,F_W) ; \delta , F_W). \end{aligned}$$

(24)

Defining $\tilde{\mathcal {V}}(\tau ^2)= {\mathcal {V}}(\tau ^2 , b(\tau ) )$, we see that the evolution of $\tau _t$ follows the iterations of the map $\tilde{\mathcal {V}}$. In particular, we make these observations:

• $\tilde{\mathcal {V}}(0) > 0$,

• $\tilde{\mathcal {V}}(\tau ^2)$ is a continuous, nondecreasing function of $\tau$.

• $\tilde{\mathcal {V}}(\tau ^2) < \tau ^2$ as $\tau \rightarrow \infty$.

Figure 3, left panel, considers the case where W again follows the Huber’s contaminated normal distribution $\mathsf{CN}(0.05,10)$ and $\psi$ is the standard Huber estimator with parameter $\lambda =3$. The ratio $n/p = \delta = 2$, and the parameter vector has $\Vert \theta _0 \Vert _2^2/p = 6^2$. It displays the function $\tilde{V}(\tau ^2)$ as a function of $\tau$.

Fig. 3

The state evolution variance mapping. Left panel Blue curve $\tilde{\mathcal {V}}$ versus $\tau ^2$, Red curve: diagonal; unique fixed point at about 0.472. Right panel the iteration history of state evolution, starting from $\tau _0^2 = 2.0556$

Evidently, there is a stable fixed point $\tau _* = \tau _*(\delta ,F_W)$, i.e. a point obeying $\tilde{\mathcal {V}}(\tau _*^2) = \tau _*^2$, such that $\tau ^2 \mapsto \tilde{\mathcal {V}}(\tau ^2)$ has a derivative less than 1 at $\tau _*^2$. We conclude that $\tau _t$ evolves under state evolution to a nonzero limit. Figure 3, right panel, shows how $\tau _t^2$ evolves to the fixed point near 0.472 starting from $\tau _0^2 = 2.056$.

3.3 Predicting operating characteristics from state evolution

State Evolution offers a formal¹⁰ procedure for predicting operating characteristics of the AMP iteration at any fixed iteration t or in the limit $t \rightarrow \infty$. Later in this section, we will provide rigorous validation of these predictions.

Call the tuple $S = (\tau ; b, \delta , F)$ a state; in running the AMP algorithm we assume that the algorithm is initialized with $\widehat{\theta }^0$ so that $\tau _0^2 = \mathrm{MSE}(\widehat{\theta }^0,\theta _0)/\delta$, so that AMP starts in state $S = (\tau _0; b^0,\delta ,F)$, and visits $S_1 = (\tau _1;b^1,\delta ,F)$, $S_ 2 = (\tau _2;b^2,\delta ,F)$, ...; eventually AMP visits states arbitrarily close to the equilibrium state $S_*= (\tau _*; b^*, \delta , F)$.

SE predictions of operating characteristics are provided by two rules assigning predictions to certain classes of observables, based on the state that AMP is in.

Definition 3.2

The state evolution formalism assigns predictions ${\mathcal {E}}$ to two types of observables under specific states.x

Observables involving $\widehat{\theta }-\theta _0$ Given a univariate test function ${\xi }: {\mathbb {R}}\mapsto {\mathbb {R}}$, assign the predicted value for $p^{-1}\sum _{i\in p}{\xi }( \widehat{\theta }_i - \theta _{0,i})$ under state S by the rule

$$\begin{aligned} {\mathcal {E}}({\xi }(\widehat{\theta }- \vartheta ) | S) \equiv {\mathbb {E}}\Big \{{\xi }(\sqrt{\delta }\,\tau \, Z)\Big \} , \end{aligned}$$

where expectation on the right hand side is with respect to $Z \sim \mathsf{N}(0,1)$.

Observables involving residual, error Let R denote some coordinate of the adjusted residual for AMP in state S and W the same coordinate of the underlying error. Given a bivariate test function ${\xi }_2 : {\mathbb {R}}^2 \mapsto {\mathbb {R}}$, assign the prediction of $n^{-1}\sum _{i=1}^{n}{\xi }_2(R_i,W_i)$ in state S by

$$\begin{aligned} {\mathcal {E}}({\xi }_2(R,W) | S) \equiv {\mathbb {E}}{\xi }_2(W+\tau \, Z,W) \end{aligned}$$

where $Z \sim \mathsf{N}(0,1)$ and $W \sim F_W$ is independent of Z.

The two most important predictions of operating characteristics are undoubtedly:

• $\mathrm{MSE}$ at iteration t. We let $S_t = (\tau _t, b(\tau _t), \delta , F_W)$ denote the state of AMP at iteration t, and predict

  $$\begin{aligned} \mathrm{MSE}(\widehat{\theta }^t, \theta _0) \approx {\mathcal {E}}((\hat{\vartheta } - \vartheta )^2 | S_t) = {\mathbb {E}}\Big \{(\sqrt{\delta }\,\tau _t\, Z)^2 \Big \} = \delta \tau _t^2. \end{aligned}$$

• $\mathrm{MSE}$ at convergence. With $\tau _* > 0$ the limit of $\tau _t$, let $S_* = (\tau _*, b(\tau _*), \delta , F_W)$ denote the state of AMP at convergence. and predict

  $$\begin{aligned} \mathrm{MSE}(\widehat{\theta }_*, \theta _0) \approx {\mathcal {E}}((\hat{\vartheta } - \vartheta )^2 | S_*) = {\mathbb {E}}\Big \{(\sqrt{\delta }\,\tau _*\, Z)^2 \Big \}= \delta \tau _*^2. \end{aligned}$$

Other predictions might also be of interest. Thus, concerning the mean absolute error $MAE(\widehat{\theta }^t,\theta _0) = \Vert \widehat{\theta }^t - \theta _0 \Vert _1/p$, state evolution predicts $MAE \approx \sqrt{2 \delta \tau _t^2/\pi }$. Concerning functions of (R, W), consider the ordinary residuals $Y - X \widehat{\theta }^*$ at AMP convergence. These residuals will of course in general not have the distribution of the errors W. Setting $\eta ( z ; b) = z - \Psi ( z; b)$, we have $Y - X \widehat{\theta }^* = \eta (R; b_*)$. State evolution predicts that the ordinary residuals will have the same distribution as $\eta ( W + \tau _* Z ; b_*)$.

3.4 Example of state evolution predictions

Continuing with our running example, we again consider the case of contaminated normal data $W \sim \mathsf{CN}(0.05,10)$ and Huber $\rho$ with $\lambda =3$. If we start AMP with the all-zero estimate $\widehat{\theta }^0 = 0$, then since $\Vert \theta _0 \Vert _2 = 6 \sqrt{p}$ we start SE with $\tau _0 = 2.056$. Figure 4 presents predictions by state evolution for the MSE (left panel) and for the mean absolute error MAE.

Fig. 4

State evolution predictions for $\mathsf{CN}(0.05,10)$, with Huber $\psi$, $\lambda =3$. Predicted evolutions of two observables of $\widehat{\theta }^t-\theta _0$: Left MSE, mean squared error. Right MAE mean absolute error

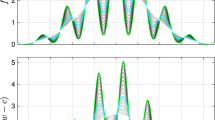
Again in our running example, these predictions can be tested empirically. For illustration, we conducted a very small experiment, generating 10 independent realizations of the running model at $n=1000$ and $p=200$, and comparing the actual evolutions of observables during AMP iterations with the predicted evolutions. Figure 5 shows that the predictions from SE are very close to the averages across realizations.

Fig. 5

Experimental means from 10 simulations compared with state evolution predictions under $\mathsf{CN}(0.05,10)$, with Huber $\psi$, $\lambda =3$. Upper left $\hat{\tau }_t = \Vert \widehat{\theta }^t - \theta _0 \Vert _2/\sqrt{n}$. Upper right $\hat{b}_t$. Lower left MSE mean squared error. Lower right MAE mean absolute error. Blue ‘+’ symbols empirical peans of AMP observables. Green curve theoretical predictions by SE

3.5 Correctness of state evolution predictions

The predictions of state evolution can be validated in the large-system limit $n,p \rightarrow \infty$, under the random Gaussian design assumption of Definition 1.1. We impose regularity conditions on the observables whose behavior we attempt to predict:

Definition 3.3

A function $\xi :{\mathbb {R}}^k\rightarrow {\mathbb {R}}$ is pseudo-Lipschitz if there exists $L<\infty$ such that, for all $x,y\in {\mathbb {R}}^k$, $|\xi (x)-\xi (y)|\le L(1+\Vert x\Vert _2+\Vert y\Vert _2)\,\Vert x-y\Vert _2$.

In particular, $\xi (x) = x^2$ is pseudo-Lipschitz.

Recall also the definition of MSE in Eq. (22). For a sequence of estimators $\tilde{\theta }$, define the per-coordinate asymptotic mean squared error (AMSE) as the following large-system limit:

$$\begin{aligned} \mathrm{AMSE}(\tilde{\theta };\theta _0) =_{\mathrm{a.s.}} \lim _{n,p_n \rightarrow \infty } \mathrm{MSE}(\tilde{\theta };\theta _0), \end{aligned}$$

(25)

when the indicated limit exists.

The following result validates the predictions of state evolution for pseudo-Lipschitz observables. Our proof is deferred to Appendix 2.

Theorem 3.4

Assume that the loss function $\rho$ is convex and smooth, that the sequence of matrices $\{{\mathbf {X}}(n)\}_{n}$ is a standard Gaussian design, and that $\theta _{0}$, $\widehat{\theta }^0$ are deterministic sequences such that $\mathrm{AMSE}(\theta _{0}$, $\widehat{\theta }^0) = \delta \tau _0^2$. Further assume that $F_W$ has finite second moment and let $\{\tau _t^2\}_{t\ge 0}$ be the state evolution sequence with initial condition $\tau _0^2$. Let $\{\widehat{\theta }^t,R^t\}_{t\ge 0}$ be the AMP trajectory with parameters $b_t$ as per Eq. (23).

Let ${\xi }:{\mathbb {R}}\rightarrow {\mathbb {R}}$, ${\xi }_2:{\mathbb {R}}\times {\mathbb {R}}\rightarrow {\mathbb {R}}$ be pseudo-Lipschitz functions. Then, for any $t>0$, we have, for $Z\sim \mathsf{N}(0,1)$ independent of $W\sim F_W$

$$\begin{aligned} \lim _{n\rightarrow \infty }\frac{1}{p}\sum _{i=1}^p{\xi }(\widehat{\theta }_i^t-\theta _{0,i}) =_{a.s.} \,&{\mathbb {E}}\Big \{{\xi }(\sqrt{\delta }\,\tau _t\, Z)\Big \} ,\end{aligned}$$

(26)

$$\begin{aligned} \lim _{n\rightarrow \infty }\frac{1}{n}\sum _{i=1}^n{\xi }_2(R^t_i,W_i) =_{a.s.} \,&{\mathbb {E}}\Big \{{\xi }_2(W+\tau _t\, Z,W)\Big \}. \end{aligned}$$

(27)

In particular, we may take $\xi (x) = x^2$ and obtain for the AMP iteration

$$\begin{aligned} \mathrm{AMSE}(\widehat{\theta }^t,\theta _0) = \delta \tau _t^2, \end{aligned}$$

in full agreement with the predictions of state evolution in Definition 3.2.

4 Convergence and characterization of M-estimators

The key step for characterizing the distribution of the M-estimator $\widehat{\theta }$, cf. Eq. (2), is to prove that the AMP iterates $\widehat{\theta }^t$ converge to $\widehat{\theta }$. We will prove that this is indeed the case, at least in the limit $n,p\rightarrow \infty$, and for suitable initial conditions.¹¹

Throughout this section, we shall assume that $\rho$ is strongly convex, i.e. that $\inf _{x\in {\mathbb {R}}}\rho ''(x)>0$. This corresponds to assuming $\inf _{x\in {\mathbb {R}}}\psi '(x)>0$, which is rather natural from the point of view of robust statistics since it ensures uniqueness of the M estimator.¹²

The key step is to establish the following high-dimensional convergence result.

Theorem 4.1

(Convergence of AMP to the M-Estimator) Assume the same setting as in Theorem 3.4, and further assume that $\rho$ is strongly convex and that $\delta >1$.

Let $(\tau _*,b_*)$ be a solution of the two equations

$$\begin{aligned} \tau ^2&= \delta \; {\mathbb {E}}\Big \{\Psi (W+\tau \, Z;b)^2\Big \}\, , \end{aligned}$$

(28)

$$\begin{aligned} \frac{1}{\delta }&= {\mathbb {E}}\Big \{\Psi '(W+\tau \,Z;b)\Big \}. \end{aligned}$$

(29)

and assume that $\mathrm{AMSE}(\widehat{\theta }^0,\theta _0)= \delta \tau _*^2$. Then

$$\begin{aligned} \lim _{t\rightarrow \infty } \mathrm{AMSE}(\widehat{\theta }^t,\widehat{\theta }) = 0. \end{aligned}$$

(30)

From this and Theorem 3.4, the desired characterization of $\widehat{\theta }$ immediately follows.

To tie back to the introduction, we prove formula (4), that we restate here for the reader’s convenience.

Theorem 4.2

(Asymptotic Variance Formula under High-Dimensional Asymptotics) Assume the setting of Theorem 3.4, and further assume that $\rho$ is strongly convex and $\delta >1$. The asymptotic variance of $\widehat{\theta }$ obeys

$$\begin{aligned} \lim _{n,p \rightarrow \infty } \mathrm{Ave}_{i\in [p]}{\mathrm{Var}}(\widehat{\theta }_i) =_{\mathrm{a.s}} V(\tilde{\Psi },\tilde{F}), \end{aligned}$$

(31)

where $\mathrm{Ave}_{i\in [p]}$ denotes the average across indices i, $V(\psi ,F)$ denotes the usual Huber asymptotic variance formula for M-estimates – $V(\psi ,F) = (\int \psi ^2 \mathrm{d}F)/(\int \psi ' \mathrm{d}F)^2$ – and the effective score $\tilde{\Psi }$ is

$$\begin{aligned} \tilde{\Psi }(\cdot ) = \Psi (\cdot ; b_*) , \end{aligned}$$

while the effective noise distribution $\tilde{F}$ is

$$\begin{aligned} \tilde{F} = F_W \star \mathsf{N}(0,{\tau }_*^2). \end{aligned}$$

Here $(\tau _*,b_*)$ are the unique solutions of the Eqs. (28), (29).

Proof

By symmetry, $\mathrm{Ave}_{i\in [p]} {\mathrm{Var}}(\widehat{\theta }_i) = {\mathbb {E}}\mathrm{MSE}(\widehat{\theta },\theta _0)$. Theorem 4.1 and state evolution show that $\mathrm{AMSE}(\widehat{\theta },\theta _0) = \delta \tau _*^2$. By (28) and (29)

$$\begin{aligned} V(\tilde{\Psi },\tilde{F}) = \frac{{\mathbb {E}}\Psi ^2(W + \tau _*Z;b_*)}{[{\mathbb {E}}\Psi '(W + \tau _* Z; b_*)]^2} = \frac{ \tau _*^2/\delta }{\delta ^{-2}} = \delta \tau _*^2. \end{aligned}$$

$\square$

Corollary 4.3

Assume the setting of Theorem 3.4, and further assume that $\rho$ is strongly convex and $\delta >1$. Then for any pseudo-Lipschitz function ${\xi }:{\mathbb {R}}\rightarrow {\mathbb {R}}$, we have, for $Z\sim \mathsf{N}(0,1)$

$$\begin{aligned} \lim _{n\rightarrow \infty }\frac{1}{p}\sum _{i=1}^p{\xi }(\widehat{\theta }_i^t-\theta _{0,i}) =_{a.s.} \, {\mathbb {E}}\Big \{{\xi }(\sqrt{\delta }\; \tau _*\, Z)\Big \}. \end{aligned}$$

(32)

In particular, the solution of Eqs. (28) and (29) is necessarily unique.

Among other applications, this result can be used to bound the suboptimality of AMP after a fixed number of iterations. Combining Theorems 3.4 and 4.1 gives:

Corollary 4.4

Assume the same setting as in Theorem 3.4, and further assume that $\rho$ is strongly convex and $\delta >1$. Then the almost sure limits $\mathrm{AMSE}(\widehat{\theta }^t;\theta _0)$ and $\mathrm{AMSE}(\widehat{\theta };\theta _0)$ exist, and obey

$$\begin{aligned} \mathrm{AMSE}(\widehat{\theta }^t;\theta _0)-\mathrm{AMSE}(\widehat{\theta };\theta _0) =\delta (\tau _t^2-\tau _*^2). \end{aligned}$$

(33)

Theorem 4.1 extends to cover general Gaussian matrices ${\mathbf {X}}$ with i.i.d. rows.

Definition 4.5

We say that a sequence of random design matrices $\{{\mathbf {X}}(n)\}_n$, with $n\rightarrow \infty$, is a general Gaussian design if each ${\mathbf {X}}={\mathbf {X}}(n)$ has dimensions $n\times p$, and rows $(X_{i})_{i\in [n]}$ that are i.i.d. $\mathsf{N}(0,\Sigma /n)$, where $\Sigma =\Sigma (n)\in {\mathbb {R}}^{p\times p}$ is a strictly positive definite matrix. Further, $p = p(n)$ is such that $\lim _{n\rightarrow \infty }n/p(n) = \delta \in (0,\infty )$.

Notice that, if ${\mathbf {X}}$ is a general Gaussian design, then ${\mathbf {X}}\Sigma ^{-1/2}$ is a standard Gaussian design. The following then follows from Corollary 4.6 together with a simple change of variables argument, cf. [15, Lemma 1].

Corollary 4.6

Assume the same setting as in Theorem 3.4, but with $\{{\mathbf {X}}(n)\}_{n\ge 0}$ being a general Gaussian design with covariance $\Sigma$, and further assume that $\rho$ is strongly convex and $\delta >1$. There is a scalar random variable $T_n$ so that

$$\begin{aligned} \widehat{\theta }= \theta _0 + \sqrt{\delta }\, T_n \Sigma ^{-1/2}{\mathbf {Z}}\, , \end{aligned}$$

(34)

where ${\mathbf {Z}}\sim \mathsf{N}(0,\mathrm{I}_{p\times p})$ and we have the almost-sure limit $\lim _{n\rightarrow \infty }\ T_n =_{a.s.} \tau _*$, where $\tau _*$ solves Eqs. (28), (29).

This result coincides with Corollary 1 in [15] apart from a factor $\sqrt{n}$ in the random part of Eq. (34) that arises because of a difference in the normalization of ${\mathbf {X}}$.

5 Discussion

The asymptotic variance formula proven in Theorem 1.2 establishes rigorously the main conjecture of [15]: the two formulae for asymptotic variance coincide. As mentioned above, [15] derived this formula exclusively on the basis of heuristic arguments.¹³

Apart from providing a rigorous proof of the asymptotic variance formula, we belief that our treatment is of independent interest. In particular, we develop an efficient algorithm (AMP) that converges exponentially fast to the M-estimator, at least for random designs. This can be regarded as a iterative version of classical ‘one-step’ estimators [2] and its risk can be analyzed sharply after any number of iterations. In contrast, [15] resorted to generic convex optimization algorithms.

Several generalizations of the present proof technique should be possible, and would be of interest. We list a few in order of increasing difficulty:

• 1. Generalize the i.i.d. Gaussian rows model for ${\mathbf {X}}$ by allowing different rows to be randomly scaled copies of a common $X\sim \mathsf{N}(0,\Sigma /n)$. This is the setting of [15, Result 1].

• 2. Remove the smoothness and strong convexity assumptions on $\rho$.

• 3. Add a regularization term to the objective function ${\mathcal {L}}(\theta )$ cf. Eq. (2), of the form $\sum _{i=1}^p J(\theta _i)$, with $J:{\mathbb {R}}\rightarrow {\mathbb {R}}$ a convex penalty. For $\ell _1$ penalty and $\ell _2$ loss, this reduces to the Lasso, studied [5].

• 4. Generalize the present results to non-Gaussian designs. We expect—for instance —that they should hold universally across matrices ${\mathbf {X}}$ with i.i.d. entries (under suitable moment conditions). A similar universality result was established in [3] for compressed sensing.

  A possible approach would be to use the Lindeberg principle following the route traced in [21].

Let us mention that alternative proof techniques would be worth exploring as well. In particular, Shcherbina and Tirozzi [32] define a statistical mechanics model with energy function that is analogous to the loss ${\mathcal {L}}(\theta )$, cf. Eq. (2), and Talagrand [33, Chapter 3] proves further results on the same model. While this treatment focuses on estimating a certain partition function, in the case of strongly convex $\rho$ it should be possible to extract properties of the minimizer from a ‘zero-temperature’ limit.

Rangan [27] considers a similar regression model to the one studied here using approximate message passing algorithms, albeit from a Bayesian point of view.

Shortly after the present paper appeared as preprint and was submitted for publication, El Karoui [20] independently proved a result analogous to our Theorem 1.2. The proof technique is very different from ours, and of independent interest.

6 Duality between robust regression and regularized least squares

The reader might have noticed many analogies between the analysis in the last pages and earlier work on estimation in the underdetermined regime $n<p$ using the Lasso [5, 9, 11, 13]. Most specifically, the central tool in our proof of the correctness of State Evolution is a set of lemmas and theorems about analysis of recursive systems that were developed to understand the Lasso. That the same machinery directly gives results in robust regression—see for example our proof of correctness of state evolution in Appendix 2 below—might seem particularly unexpected. In this section we briefly point out that the two problems are so closely linked that phenomena which appear in one situation are bound to appear in the other.

6.1 Duality of optimization problems

In a very strong sense, solving an M-estimation problem with $p < n$ is the very same thing as solving a related penalized regression problem in $\tilde{p}> \tilde{n}$. Given a convex function $J:{\mathbb {R}}\rightarrow {\mathbb {R}}$, define the $\rho$ function

$$\begin{aligned} \rho _J(z) \equiv \min _{x\in {\mathbb {R}}}\Big \{\frac{1}{2}(z-x)^2+J(x)\Big \} \end{aligned}$$

(35)

We then have the M-Estimation problem

$$\begin{aligned} (M_J) \qquad \qquad \min _{\theta \in {\mathbb {R}}^p} \;\; \sum _{i=1}^n \rho _J(Y_i - \langle X_i , \theta \rangle ) \end{aligned}$$

(36)

This problem has $p < n$ and is generically a determined problem. We now construct a corresponding underdetermined problem with the ‘same’ solution. Set $\tilde{n}= n-p$, $\tilde{p}=n$. We soon will construct a vector/matrix pair $(\widetilde{Y}\in {\mathbb {R}}^{\tilde{n}},\widetilde{\mathbf {X}}\in {\mathbb {R}}^{\tilde{n}\times \tilde{p}})$ obeying $\tilde{n}< \tilde{p}$, where $\widetilde{Y}$ and $\widetilde{\mathbf {X}}$ are related to Y and $\widetilde{\mathbf {X}}$ in a specific way. With this pair we pose the J-penalized least squares problem

$$\begin{aligned} (L_{J}) \qquad \qquad \min _{\beta \in {\mathbb {R}}^{\tilde{p}}} \;\;\frac{1}{2}\Vert \widetilde{Y}-\widetilde{\mathbf {X}}\beta \Vert _2^2+\sum _{i=1}^{\tilde{p}}J(\beta _i). \end{aligned}$$

(37)

with solution $\widehat{\beta }(\widetilde{Y};\widetilde{\mathbf {X}})$, say.

Here is the specific pair that links $(M_J)$ with $(L_J)$. We let $\widetilde{\mathbf {X}}$ be a matrix with orthonormal rows such that $\widetilde{\mathbf {X}}{\mathbf {X}}= 0$, i.e.

$$\begin{aligned} \mathrm{null}(\widetilde{\mathbf {X}}) = \mathrm{image}( {\mathbf {X}}), \end{aligned}$$

(38)

finally, we set $\widetilde{Y}= \widetilde{\mathbf {X}}Y$.

6.1.1 The Lasso-Huber connection

Of special interest is the case $J(x) = \lambda \,|x|$ in which case $(L_J)$ of (37) defines the Lasso estimator. Then $\rho _J(x) = \rho _{\mathrm{H}}(x;\lambda )$ is the Huber loss and $(M_J)$ of (36) defines the Huber M-estimate. Indeed, in that case $(L_J)$ is more classically presented as

$$\begin{aligned} (\hbox {Lasso}_\lambda ) \qquad \min _{\beta \in {\mathbb {R}}^{\tilde{p}}} \frac{1}{2}\Vert \widetilde{Y}-\widetilde{\mathbf {X}}\beta \Vert _2^2+ \lambda \sum _{i=1}^{\tilde{p}}| \beta _i| , \end{aligned}$$

(39)

while $(M_J)$ is more classically presented as

$$\begin{aligned} (\hbox {Huber}_\lambda ) \qquad \min _{\beta \in {\mathbb {R}}^p} \sum _{i=1}^n \rho _{\mathrm{H}}(Y_i - \langle X_i , \beta \rangle ;\lambda ) \end{aligned}$$

(40)

In this special case, our general result from the next section implies the following:

Proposition 6.1

With problem instances (Y, X) and $(\widetilde{Y},\widetilde{\mathbf {X}})$ related as above, the optimal values of the Lasso problem $(\text{ Lasso }_\lambda )$ and the Huber problem $(\text{ Huber }_\lambda )$ are identical. The solutions of the two problems are in one-one-relation. In particular, we have

$$\begin{aligned} \widehat{\theta }= ({\mathbf {X}}^{\mathsf{T}}{\mathbf {X}})^{-1}{\mathbf {X}}^{\mathsf{T}}(Y-\widehat{\beta }). \end{aligned}$$

(41)

In a sense the Lasso problem solution $\widehat{\beta }$ is finding the outliers in Y; once the solution is known, the solution of the M-estimation problem is simply a least squares regression on adjusted data $Y_\mathrm{adj} \equiv (Y-\hat{\beta })$ with outliers removed.

6.1.2 General duality result

We will now show that the problem (36) is dual to (37) under or special choice of $(\widetilde{Y},\widetilde{\mathbf {X}})$, via (38).

Notation. For $x\in {\mathbb {R}}^n$, we denote by $\partial \rho (x)$ the subgradient of the convex function $\sum _{i=1}^n\rho (x_i)$, at x. Analogously, for $z\in {\mathbb {R}}^{\tilde{p}}$, we denote by $\partial J(z)$ the subgradient of the convex function $\sum _{i=1}^{\tilde{p}} J(z_i)$, at z.

Proposition 6.2

Assume that $\rho (\,\cdot \,) = \rho _J(\,\cdot \,)$, that $\widetilde{\mathbf {X}}$ has orthonormal rows with $\mathrm{null}(\widetilde{\mathbf {X}}) = \mathrm{image}( {\mathbf {X}})$, and finally that $\widetilde{Y}= \widetilde{\mathbf {X}}\, Y$. Then the solutions of the regularized least squares problem (37) are in one-to-one correspondence with the solutions of the robust regression problem (2), via the mappings

$$\begin{aligned} \widehat{\beta }&= Y-{\mathbf {X}}\widehat{\theta }- u ,\;\;\;\;\;\;\;\; u\in \mathrm{null}({\mathbf {X}}^{\mathsf{T}})\cap \partial \rho (y-{\mathbf {X}}\widehat{\theta }), \end{aligned}$$

(42)

$$\begin{aligned} \widehat{\theta }&= ({\mathbf {X}}^{\mathsf{T}}{\mathbf {X}})^{-1}{\mathbf {X}}^{\mathsf{T}}(Y-\widehat{\beta }). \end{aligned}$$

(43)

Proof

‘Differentiating’ Eq. (35) it is easy to see that

$$\begin{aligned} u \in \partial \rho (x) \;\;\; \text{ if } \text{ and } \text{ only } \text{ if } \;\;\; u \in \partial J(x-u). \end{aligned}$$

(44)

First assume $\widehat{\theta }$ is a minimizer of problem (36). This happens if and only if there exists $u\in {\mathbb {R}}^n$ such that

$$\begin{aligned} {\mathbf {X}}^{\mathsf{T}} u =0,\quad u\in \partial \rho (Y-{\mathbf {X}}\widehat{\theta })\,. \end{aligned}$$

(45)

We then claim that $\widehat{\beta }\equiv Y-{\mathbf {X}}\widehat{\theta }- u$ is a minimizer of Eq. (37). Indeed

$$\begin{aligned} \widetilde{\mathbf {X}}^{\mathsf{T}}(\widetilde{Y}-\widetilde{\mathbf {X}}\widehat{\beta })&=\widetilde{\mathbf {X}}^{\mathsf{T}}\widetilde{\mathbf {X}}(Y-\widehat{\beta }) \end{aligned}$$

(46)

$$\begin{aligned}&= \widetilde{\mathbf {X}}^{\mathsf{T}}\widetilde{\mathbf {X}}\big ({\mathbf {X}}\widehat{\theta }+u \big ) = u, \end{aligned}$$

(47)

where the last identity follows since, by Eq. (38), $\mathrm{null}({\mathbf {X}}^{\mathsf{T}}) = \mathrm{image}( \widetilde{\mathbf {X}}^{\mathsf{T}})$, and hence $u\in \mathrm{image}( \widetilde{\mathbf {X}}^{\mathsf{T}})$ by Eq. (45). Using again Eqs. (45) and (44), we deduce that $u\in \partial J(\widehat{\beta })$, i.e.

$$\begin{aligned} \widetilde{\mathbf {X}}^{\mathsf{T}}(\widetilde{Y}-\widetilde{\mathbf {X}}\widehat{\beta }) \in \partial J(\widehat{\beta }), \end{aligned}$$

(48)

which is the stationarity condition for the problem (37).

Viceversa a similar argument shows that, given $\widehat{\beta }$ that minimizes Eq. (37), and $\widehat{\theta }\equiv ({\mathbf {X}}^{\mathsf{T}}{\mathbf {X}})^{-1}{\mathbf {X}}^{\mathsf{T}}(Y-\widehat{\beta })$ is a minimizer of the robust regression problem (36). $\square$

6.2 Comparison to AMP in the $p > n$ case

The last section raises the possibility that the phenomena found in this paper for M-estimation in the $p < n$ case are actually isomorphic to those found in our previous work on penalized regression in the $p > n$ case; [5, 9, 11, 13]. Here we merely content ourselves with sketching a few similarities.

To be definite, consider robust regression using the Huber loss [16, 17] $\rho (x) = x^2/2$ for $|x|\le \lambda$ and $\rho (x) = \lambda |x|-\lambda ^2/2$ otherwise. In this case it is easy to see that

$$\begin{aligned} \Psi (z;b) = {\left\{ \begin{array}{ll} \lambda b &{} \hbox { if }\,\, z>\lambda (1+b),\\ b\, z/(1+b) &{} \hbox { if }\,\, |z|\le \lambda (1+b),\\ -\lambda b &{} \hbox { if }\,\, z<-\lambda (1+b). \end{array}\right. } \end{aligned}$$

(49)

In order to make contact with the Lasso, recall the definition of soft thresholding operator $\eta (x;\alpha ) = \mathrm{sign}(x)\,(|x|-\alpha )_+$. We have the relationship

$$\begin{aligned} \Psi (z;b) = \frac{b\,z}{1+b}-\eta \Big (\frac{b\,z }{1+b};\lambda b\Big ). \end{aligned}$$

(50)

Letting $c_t\equiv b_t/(1+b_t)$, the state evolution Eq. (24), then reads

$$\begin{aligned} \tau _{t+1}^2 = \delta c_t^2 \; {\mathbb {E}}\Big \{\Big [\eta \Big (W+\tau _t\, Z;\lambda (1+b_t)\Big )-W-\tau _t\, Z\Big ]^2\Big \}. \end{aligned}$$

(51)

This is very close to the state evolution equation in compressed sensing for reconstructing a sparse signal whose entries have distribution $F_W$, from an underdetermined number of linear measurements; indeed in that setting we have the state evolution recursion

$$\begin{aligned} \tau _{t+1}^2 = \delta \; {\mathbb {E}}\Big \{\Big [\eta \Big (W+\tau _t\, Z;\lambda \tau _t\Big )-W ]^2\Big \}; \end{aligned}$$

(52)

[5, 9, 11, 13]. The connection is quite suggestive: while in compressed sensing we look for the few non-zero coefficients in the signal, in robust regression we try to identify the few outliers contaminating the linear relation. A similar duality was already pointed out in [14], although in a specific setting.

Appendices

Appendix 1: Properties of the functions $\mathsf{Prox}$, $\Psi$

Throughout this section $\rho :{\mathbb {R}}\rightarrow {\mathbb {R}}$ is convex bounded below and smooth (i.e. with bounded second derivative). Recall the definition of $\mathsf{Prox}:{\mathbb {R}}\times {\mathbb {R}}_{>0}\rightarrow {\mathbb {R}}$ and $\Psi :{\mathbb {R}}\times {\mathbb {R}}_{>0}\rightarrow {\mathbb {R}}$, given by

$$\begin{aligned} \mathsf{Prox}(z;b)&\equiv \arg \min _{x\in {\mathbb {R}}} \Big \{\rho (x) + \frac{1}{2b}(x-z)^2\Big \}, \end{aligned}$$

(53)

$$\begin{aligned} \Psi (z;b)&\equiv b\, \rho '\big (\mathsf{Prox}(z;b)\big ). \end{aligned}$$

(54)

Proposition 6.3

The function $\mathsf{Prox}:{\mathbb {R}}\times {\mathbb {R}}_{>0}\rightarrow {\mathbb {R}}$ is differentiable in its domain, with partial derivatives

$$\begin{aligned} \frac{\partial \mathsf{Prox}}{\partial z}(z;b) =\left. \frac{1}{1+b\rho ''(x)}\right| _{x = \mathsf{Prox}(z;b)} ,\quad \frac{\partial \mathsf{Prox}}{\partial b}(z;b) =\left. -\frac{\rho '(x)}{1+b\rho ''(x)}\right| _{x = \mathsf{Prox}(z;b)}. \end{aligned}$$

(55)

In particular, letting $\Vert \rho ''\Vert _{\infty } \equiv \sup _{x\in {\mathbb {R}}}\rho ''(x)$, and for any fixed b, $z\mapsto \mathsf{Prox}(z;b)$ is strictly increasing and Lipschitz continuous, with

$$\begin{aligned} \frac{1}{1+b\Vert \rho ''\Vert _{\infty }}\le \frac{\partial \mathsf{Prox}}{\partial z}(z;b) \le 1 \end{aligned}$$

(56)

Proof

Since, for $b>0$, $x\mapsto \rho (x) + (x-z)^2/(2b)$ is differentiable and strongly convex, $x= \mathsf{Prox}(z;b)$ is uniquely determined by setting to zero the first derivative:

$$\begin{aligned} x+b\rho '(x) -z = 0. \end{aligned}$$

(57)

The claim then follows from the implicit function theorem. $\square$

Proposition 6.4

For $(z,b)\in {\mathbb {R}}\times {\mathbb {R}}_+$, we have

$$\begin{aligned} \Psi (z;b) = z-\mathsf{Prox}(z,b), \end{aligned}$$

(58)

and hence $\Psi$ is differentiable, with partial derivatives

$$\begin{aligned} \frac{\partial \Psi }{\partial z}(z;b) =\left. \frac{b\rho ''(x)}{1+b\rho ''(x)}\right| _{x = \mathsf{Prox}(z;b)}\, ,\;\;\;\;\; \frac{\partial \Psi }{\partial b}(z;b) =\left. \frac{\rho '(x)}{1+b\rho ''(x)}\right| _{x = \mathsf{Prox}(z;b)}. \end{aligned}$$

(59)

In particular, for any fixed b, $z\mapsto \Psi (z;b)$ is strictly increasing and Lipschitz continuous, with

$$\begin{aligned} \frac{b\inf _{x\in {\mathbb {R}}}\rho ''(x)}{1+b\inf _{x\in {\mathbb {R}}}\rho ''(x)}\le \frac{\partial \Psi }{\partial z}(z;b) \le \frac{b\Vert \rho ''\Vert _{\infty }}{1+b\Vert \rho ''\Vert _{\infty }}. \end{aligned}$$

(60)

Proof

Using again the stationarity condition (57) that holds for $x=\mathsf{Prox}(z;b)$, we have

$$\begin{aligned} \mathsf{Prox}(z;b)+b\rho '(\mathsf{Prox}(z;b)) -z = 0, \end{aligned}$$

(61)

which is our first claim. The other claims immediately follow by calculus. $\square$

Finally, we prove that Eq. (23) that defines $b_t$ as a function of $\tau _t$ always has at least one solution.

Lemma 6.5

For $\tau >0$ fixed, let $G:{\mathbb {R}}_{>0}\rightarrow {\mathbb {R}}$ be defined by

$$\begin{aligned} G(b) \equiv {\mathbb {E}}\Big \{\Psi '(W+\tau \,Z;b)\Big \}. \end{aligned}$$

(62)

Then for any $a\in (0,1)$, the set of solutions

$$\begin{aligned} \mathcal{S}_a \equiv \big \{b\in {\mathbb {R}}_{>0}:\; G(b)= a\big \}, \end{aligned}$$

(63)

is closed and non-empty.

Proof

It follows immediately from the continuity properties of $\Psi$ that $b\mapsto G(b)$ is continuous. The claim follows by proving that $\lim _{b\rightarrow 0}G(b) = 0$ and $\lim _{b\rightarrow \infty }G(b) = 1$.

By Proposition 6.4 Eq. (60) $0\le \Psi '(z;b)\le 1$. The limit $b\rightarrow 0$ follows from dominated convergence since, by the upper bound in (60) $\lim _{b\rightarrow 0}\Psi '(z;b) = 0$ for each z.

In order to obtain the limit as $b\rightarrow \infty$, note that by Stein Lemma:

$$\begin{aligned} G(b) =\frac{1}{\tau }{\mathbb {E}}\Big \{Z\, \Psi (W+\tau \,Z;b)\Big \}. \end{aligned}$$

(64)

Since $0\le \Psi '(z,b)\le 1$, the integrand is bounded in modulus by an integrable quantity. We can therefore use again dominated convergence. Now $\lim _{b\rightarrow \infty } \mathsf{Prox}(z;b) = \arg \min _{x\in {\mathbb {R}}}\rho (x)\equiv c_0$ and hence $\lim _{b\rightarrow \infty } \Psi (z;b) = z-c_0$. By dominated convergence we obtain

$$\begin{aligned} \lim _{b\rightarrow \infty }G(b) =\frac{1}{\tau }{\mathbb {E}}\Big \{Z\, (W+\tau Z-c_0)\Big \} = 1. \end{aligned}$$

(65)

$\square$

Appendix 2: Proof of correctness of state evolution (Theorem 3.4)

We will show correctness of state evolution for the AMP algorithm using analytically defined $b_t$. Namely, we suppose that with $b_t$ defined recursively as the smallest positive solution of the second equation in this system:

$$\begin{aligned} \tau _{t+1}^2&= \delta \; {\mathbb {E}}\Big \{\Psi (W+\tau _t\, Z;b_t)^2\Big \}, \end{aligned}$$

(66)

$$\begin{aligned} \frac{1}{\delta }&= {\mathbb {E}}\Big \{\Psi '(W+\tau _t\,Z;b_t)\Big \}. \end{aligned}$$

(67)

For analysis purposes, we consider a recursion equivalent to the AMP recursion, in which the data are recentered and the recursion is recast around recentered variables. We change the initial condition of the AMP iteration by letting $\widehat{\theta }^{\mathrm{cen},0} = \widehat{\theta }^0-\theta _0$, and change data by letting $Y^{\mathrm{cen}} = Y-{\mathbf {X}}\theta _0\equiv W$. Applying the AMP recursion in these new coordinates gives the new trajectory $\widehat{\theta }^{\mathrm{cen},t} = \widehat{\theta }^t-\theta _0$ for all t, and $R^{\mathrm{cen},t} = R^t$ for all t.

The new trajectory follows the recursion

$$\begin{aligned} R^{\mathrm{cen},t}&= W-{\mathbf {X}}\widehat{\theta }^{\mathrm{cen},t}+\Psi (R^{\mathrm{cen},t-1};b_{t-1}), \end{aligned}$$

(68)

$$\begin{aligned} \widehat{\theta }^{\mathrm{cen},t+1}&= \widehat{\theta }^{\mathrm{cen},t}+\delta {\mathbf {X}}^{\mathsf{T}}\Psi (R^{\mathrm{cen},t};b_t), \end{aligned}$$

(69)

In this form, the recursion can be reduced to a recursion studied [4], for which state evolution has been proven correct. The reduction is to introduce a recursion generating iterates $\{{\vartheta }^t,S^t\}$ that approximates closely the iterates $\{\widehat{\theta }^{\mathrm{cen},t},R^{\mathrm{cen},t}\}$ defined by (68), (69). The new sequence is defined by letting ${\vartheta }^0 = \widehat{\theta }^0-\theta _0$ and, for all $t \ge 0$

$$\begin{aligned} S^t&= -{\mathbf {X}}{\vartheta }^t+\Psi \left( W+S^{t-1};b_{t-1}\right) , \end{aligned}$$

(70)

$$\begin{aligned} {\vartheta }^{t+1}&= \delta {\mathbf {X}}^{\mathsf{T}}\Psi (W+S^t;b_t)+q_t{\vartheta }^t, \end{aligned}$$

(71)

where

$$\begin{aligned} q_t = \delta \left\{ \frac{1}{n}\sum _{i=1}^n\Psi '(W_i+S^t_i;b_t)\right\} . \end{aligned}$$

(72)

The only difference between this recursion and the previous one cf. Eqs. (68) and (69), lies in the new coefficient $q_t$, which was identically equal to 1 in the previous recursion. The benefit of this specific recursion is that we already know that state evolution is correct.

Lemma 6.6

Under the assumptions of Theorem 3.4, we have, for any fixed $t\ge 0$,

$$\begin{aligned} \lim _{n\rightarrow \infty } \frac{1}{p}\sum _{i=1}^p{\xi }({\vartheta }^t_i)=_{\mathrm{a.s.}} \,&{\mathbb {E}}\{{\xi }(\sqrt{\delta }\, \tau _t\, Z)\}\, \end{aligned}$$

(73)

$$\begin{aligned} \lim _{n\rightarrow \infty }\frac{1}{n}\sum _{i=1}^n{\xi }_2(S^t_i,W_i) =_{\mathrm{a.s.}} \,&{\mathbb {E}}\Big \{{\xi }_2(\tau _t\, Z,W)\Big \}. \end{aligned}$$

(74)

Proof

This is an immediate application of Theorem 2 in [4]. $\square$

Theorem 3.4 now follows from the equivalence of the last two recursions.

Lemma 6.7

Under the assumptions of Theorem 3.4, we have, for any fixed $t\ge 0$,

$$\begin{aligned} \lim _{n\rightarrow \infty } \frac{1}{p}\Vert \widehat{\theta }^{\mathrm{cen},t}-{\vartheta }^t\Vert _2^2 =_{\mathrm{a.s}} \, 0, \;\;\;\;\;\;\;\;\;\; \lim _{n\rightarrow \infty } \frac{1}{n}\Vert R^{\mathrm{cen},t}-S^t-W\Vert _2^2 =_{\mathrm{a.s.}} \, 0. \end{aligned}$$

(75)

1.1 Appendix 2.1: Proof of Lemma 6.7 (Equivalence of recursions)

Throughout this proof, we will drop the superscript ‘cen’ from $R^{\mathrm{cen},t}$ and $\widehat{\theta }^{\mathrm{cen},t}$. Define $S^t_+\equiv W+S^t$, whence

$$\begin{aligned} S^t_+&= W-{\mathbf {X}}{\vartheta }^t+\Psi (S_+^{t-1};b_{t-1}), \end{aligned}$$

(76)

$$\begin{aligned} {\vartheta }^{t+1}&= \delta {\mathbf {X}}^{\mathsf{T}}\Psi (S^t_+;b_t)+q_t{\vartheta }^t\, , \end{aligned}$$

(77)

Comparing the first of these equations with Eq. (68), and using triangular inequality, we get

$$\begin{aligned} \Vert R^{t}-S^t_+\Vert _2&\le \Vert {\mathbf {X}}\Vert _2\Vert \widehat{\theta }^t-{\vartheta }^t\Vert _2 + \Vert \Psi (R^{t-1};b_{t-1}) - \Psi (S_+^{t-1};b_{t-1}) \Vert _2\, \end{aligned}$$

(78)

$$\begin{aligned}&\le \Vert {\mathbf {X}}\Vert _2\Vert \widehat{\theta }^t-{\vartheta }^t\Vert _2 + \Vert R^{t-1}- S_+^{t-1}\Vert _2, \end{aligned}$$

(79)

where the last inequality follows since $\Psi (\,\cdot \,;b):{\mathbb {R}}\rightarrow {\mathbb {R}}$ is Lipschitz continuous with Lipschitz constant at most 1, cf Proposition 6.4.

Comparing analogously Eqs. (69) and (77), we obtain

$$\begin{aligned} \Vert \widehat{\theta }^{t+1}-{\vartheta }^{t+1}\Vert _2&\le \delta \Vert {\mathbf {X}}\Vert _2\, \Vert \Psi (R^t;b_t) -\Psi (S^t_+;b_t)\Vert _2+\Vert \widehat{\theta }^t-{\vartheta }^t\Vert _2+|q_t-1|\,\Vert {\vartheta }^t\Vert _2 \end{aligned}$$

(80)

$$\begin{aligned}&\le \delta \Vert {\mathbf {X}}\Vert _2\, \Vert R^t-S^t_+\Vert _2+\Vert \widehat{\theta }^t-{\vartheta }^t\Vert _2+|q_t-1|\,\Vert {\vartheta }^t\Vert _2. \end{aligned}$$

(81)

Iterating the upper bounds (79) and (81), and using the fact that ${\vartheta }^0=\widehat{\theta }^0$, we conclude that there exists a constant $A=A(\delta )<\infty$ such that

$$\begin{aligned} \Vert \widehat{\theta }^{t}-{\vartheta }^{t}\Vert _2\le (A\Vert {\mathbf {X}}\Vert _2)^{2t}\sum _{\ell =0}^{t-1}|q_{\ell }-1|\,\Vert {\vartheta }^{\ell }\Vert _2 \end{aligned}$$

(82)

By Lemma 6.6, we have, almost surely

$$\begin{aligned} \lim _{n\rightarrow \infty }\frac{1}{\sqrt{p}}\Vert {\vartheta }^{\ell }\Vert _2 = \tau _{\ell }<\infty , \end{aligned}$$

(83)

and

$$\begin{aligned} \lim _{n\rightarrow \infty }q_{t}&= \delta \lim _{n\rightarrow \infty }\frac{1}{n}\sum _{i=1}^n\Psi '(W_i+S^t_i;b_t) \end{aligned}$$

(84)

$$\begin{aligned}&= \delta {\mathbb {E}}\{\Psi '(W+\tau _t Z;b_t) \}= 1, \end{aligned}$$

(85)

where the second identity follows from Lemma 6.6 and, in the third, we used the definition of $b_t$. (Note that we are applying here Lemma 6.6 to ${\xi }(\,\cdot \,)=\Psi '(\,\cdot \,;b_t)$ which is bounded and non-negative but not necessarily continuous. However, since $W+\tau _t Z$ has a density for every $\tau _t>0$, the limit holds by a standard weak convergence argument, approximating ${\xi }$ by simple functions. Namely, we construct a sequence of simple functions $\xi _\ell$ such that $\xi _{\ell }(t)\le \xi (t)\le \xi _{\ell }(t) +(1/\ell )$ for all t, and apply Lemma 6.6—which implies weak convergence of the empirical distribution of $\{W_i+S^t_i\}$– to $\xi _{\ell }$.)

Finally, it is a standard result in random matrix theory [1] that $\lim _{n\rightarrow \infty }\Vert {\mathbf {X}}\Vert _2 = C(\delta )<\infty$. Hence, by taking the limit of Eq. (82) we get, almost surely,

$$\begin{aligned} \lim _{n\rightarrow \infty }\frac{1}{\sqrt{p}}\Vert \widehat{\theta }^{t}-{\vartheta }^{t}\Vert _2 = 0. \end{aligned}$$

(86)

The norm $\Vert R^{t}-S^t_+\Vert _2$ is then controlled using Eq. (79).

Appendix 3: Proof that AMP converges to the M-estimator (Theorem 4.1)

Notice first of all that, by construction, $\tau _t^2=\tau _*^2$, $b_t = b_*$ for all t.

Given $\delta$, $\rho$ as in the statement of the theorem and $\tau _*$, $b_*$ a solution of the fixed point Eqs. (28) and (29), we define the doubly infinite matrix ${\Gamma }= ({\Gamma }_{t,s})_{t,s\ge 0}$ by letting, recursively for $t,s\ge 0$

$$\begin{aligned} {\Gamma }_{t+1,s+1} = \delta {\mathbb {E}}\{\Psi (W+Z_t;b_*) \Psi (W+Z_s;b_*)\}, \end{aligned}$$

(87)

where the expectation is with respect to $(Z_t,Z_s)$ jointly Gaussian, with zero means and covariance ${\mathbb {E}}\{Z_t^2\} = {\Gamma }_{t,t}$, ${\mathbb {E}}\{Z_s^2\} = {\Gamma }_{s,s}$, ${\mathbb {E}}\{Z_tZ_s\} = {\Gamma }_{t,s}$, independent of $W\sim F_W$. This is supplemented with the boundary condition ${\Gamma }_{0,0} = \tau _*^2$ and ${\Gamma }_{0,t} = {\Gamma }_{t,0}= 0$ for $t>0$.

Notice that, in particular, ${\Gamma }_{s,t}= {\Gamma }_{t,s}$ for all $s,t\ge 0$ and ${\Gamma }_{t,t}=\tau _*^2$ for all t.

The significance of these quantities is clarified by the following result.

Lemma 6.8

Under the hypotheses of Theorem 3.4, further assume that $\tau _*^2$ and ${\Gamma }$ are defined as above. Then, for any $t,s\ge 0$,

$$\begin{aligned} \lim _{n\rightarrow \infty }\frac{1}{p}\sum _{i=1}^p{\xi }_2(\widehat{\theta }^t_{i}-\theta _{0,i}, \widehat{\theta }_i^s-\theta _{0,i})&=_{\mathrm{a.s.}} \, {\mathbb {E}}{\xi }_2(\sqrt{\delta }\, Z_t,\sqrt{\delta }\, Z_s), \end{aligned}$$

(88)

$$\begin{aligned} \lim _{n\rightarrow \infty }\frac{1}{n}\sum _{i=1}^n{\xi }_2(R^t_{i}-W_i,R_i^s-W_i)&=_{\mathrm{a.s.}} \, {\mathbb {E}}{\xi }_2( Z_t, Z_s), \end{aligned}$$

(89)

where the expectation is with respect to $(Z_t,Z_s)$ jointly Gaussian, with zero means and covariance ${\mathbb {E}}\{Z_t^2\} = {\Gamma }_{t,t}$, ${\mathbb {E}}\{Z_s^2\} = {\Gamma }_{s,s}$, ${\mathbb {E}}\{Z_tZ_s\} = {\Gamma }_{t,s}$, independent of $W\sim F_W$.

The proof is deferred to Sect. 1.

As a special case of the latter result, we have

$$\begin{aligned} \lim _{n\rightarrow \infty }\frac{1}{p}\Vert \widehat{\theta }^{t}-\widehat{\theta }^s\Vert _2^2&\, =_{a.s.} \, 2\delta \,\big (\tau _*^2-{\Gamma }_{t,s}\big ),\end{aligned}$$

(90)

$$\begin{aligned} \lim _{n\rightarrow \infty }\frac{1}{n}\Vert R^{t}-R^s\Vert _2^2&\, =_{a.s.} \, 2\,\big (\tau _*^2-{\Gamma }_{t,s}\big ). \end{aligned}$$

(91)

The following lemma provides information about the asymptotic behavior of ${\Gamma }_{t,s}$. Its proof is deferred to Sect. 1.

Lemma 6.9

Let $\tau _*$, ${\Gamma }$ be defined as above for $\delta >1$. Then

$$\begin{aligned} \lim _{t\rightarrow \infty } {\Gamma }_{t,t+1} = \tau _*^2 \end{aligned}$$

(92)

Applying this result to Eqs. (90) and (91) we get, for any fixed $h\in {\mathbb {N}}$,

$$\begin{aligned} \lim _{t\rightarrow \infty }\lim _{n\rightarrow \infty }\frac{1}{p}\Vert \widehat{\theta }^{t+h}-\widehat{\theta }^t\Vert _2^2&\, =_{a.s.} \, 0,\end{aligned}$$

(93)

$$\begin{aligned} \lim _{t\rightarrow \infty }\lim _{n\rightarrow \infty }\frac{1}{p}\Vert R^{t+h}-R^t\Vert _2^2&\, =_{a.s.} \, 0. \end{aligned}$$

(94)

(The case $h>1$ follows from $h=1$ by the triangle inequality.)

We are now ready to prove Theorem 4.1. Recall that ${\mathcal {L}}(\theta ) = {\mathcal {L}}(\theta ;Y,{\mathbf {X}})$ denotes the loss function defined in Eq. (2), and that its gradient and Hessian are given by

$$\begin{aligned} \nabla _{\theta }{\mathcal {L}}(\theta )&= -\sum _{i=1}^n\rho '(Y_i-\langle X_i,\theta \rangle )\, X_i,\end{aligned}$$

(95)

$$\begin{aligned} \nabla ^2_{\theta }{\mathcal {L}}(\theta )&= \sum _{i=1}^n\rho ''(Y_i-\langle X_i,\theta \rangle )\, X_iX_i^{\mathsf{T}}. \end{aligned}$$

(96)

In particular, letting $\sigma _\mathrm{min}({\mathbf {X}})$ denote the minimum non-zero singular value of ${\mathbf {X}}$, we have

$$\begin{aligned} \lambda _\mathrm{min} (\nabla ^2_{\theta }{\mathcal {L}}(\theta )) \ge \inf _{x\in {\mathbb {R}}}\rho ''(x)\, \cdot \sigma _\mathrm{min}({\mathbf {X}})^2. \end{aligned}$$

(97)

Using the hypothesis of strong convexity and standard concentration of measure for the singular values of Wishart matrices [36], these exists constants $c_0,c_1, n_0>0$ for $\delta >1$ such that for any $n\ge n_0$,

$$\begin{aligned} {\mathbb {P}}\Big (\nabla ^2_{\theta }{\mathcal {L}}(\theta )\succeq c_0\, \mathrm{I}\;\;\;\; \forall \theta \in {\mathbb {R}}^p\Big ) \ge \, 1-e^{-c_1\, n}. \end{aligned}$$

(98)

As a consequence, with probability at least $1-e^{-c_1n}$, we have

$$\begin{aligned} {\mathcal {L}}(\widehat{\theta }^t) \ge {\mathcal {L}}(\widehat{\theta })\ge {\mathcal {L}}(\widehat{\theta }^t) +\langle \nabla _{\theta }{\mathcal {L}}(\widehat{\theta }^t),\widehat{\theta }-\widehat{\theta }^t\rangle +\frac{1}{2}\, c_0\, \Vert \widehat{\theta }-\widehat{\theta }^t\Vert _2^2. \end{aligned}$$

(99)

Hence using Cauchy–Schwartz

$$\begin{aligned} \Vert \widehat{\theta }-\widehat{\theta }^t\Vert _2\le \frac{2}{c_0}\, \Vert \nabla _{\theta }{\mathcal {L}}(\widehat{\theta }^t)\Vert _2. \end{aligned}$$

(100)

The last step of the proof consists in showing that, almost surely

$$\begin{aligned} \lim _{t\rightarrow \infty }\lim _{n\rightarrow \infty }\frac{1}{p}\Vert \nabla _{\theta }{\mathcal {L}}(\widehat{\theta }^t)\Vert _2^2 = 0. \end{aligned}$$

(101)

In order to prove this claim, reconsider Eq. (13), for time $t+1$, with $b_t=b_*$. Using the fact that $\Psi (z;b_*) = z-\mathsf{Prox}(z;b_*)$, this can be rewritten as

$$\begin{aligned} \mathsf{Prox}(R^{t};b_*) = Y-{\mathbf {X}}\widehat{\theta }^{t+1}+R^t-R^{t+1}\, . \end{aligned}$$

(102)

By Eq. (15), and recalling that $\Psi (z;b) = b\,\rho '(\mathsf{Prox}(z;b))$, we have

$$\begin{aligned} \frac{1}{b_*\delta }\, \big (\widehat{\theta }^{t+1}-\widehat{\theta }^t\big )&= {\mathbf {X}}^{\mathsf{T}} \rho '(\mathsf{Prox}(R^t;b_*)) \end{aligned}$$

(103)

$$\begin{aligned}&={\mathbf {X}}^{\mathsf{T}} \rho '\Big ( Y-{\mathbf {X}}\widehat{\theta }^{t+1}+R^t-R^{t+1}\Big ) , \end{aligned}$$

(104)

where the last identity followed by Eq. (102). Using the triangle inequality and noting that, by the smoothness assumption $C\equiv \sup _{z\in {\mathbb {R}}}\rho ''(z)<\infty$, we get

$$\begin{aligned} \Vert {\mathbf {X}}^{\mathsf{T}} \rho '\left( Y-{\mathbf {X}}\widehat{\theta }^{t+1}\right) \Vert _2 \le \frac{1}{b_*\delta }\, \Vert \widehat{\theta }^{t+1}-\widehat{\theta }^t\Vert _2+ C\Vert {\mathbf {X}}\Vert _2\Vert R^t-R^{t+1}\Vert _2. \end{aligned}$$

(105)

Hence, using Eqs. (93) and (93), and recalling that $\lim _{n\rightarrow \infty }\Vert {\mathbf {X}}\Vert _2<\infty$ almost surely [1], we get

$$\begin{aligned} \lim _{t\rightarrow \infty }\lim _{n\rightarrow \infty }\frac{1}{p}\Vert {\mathbf {X}}^{\mathsf{T}} \rho '\left( Y-{\mathbf {X}}\widehat{\theta }^{t+1}\right) \Vert _2^2 = 0. \end{aligned}$$

(106)

This is equivalent to the claim (101) since $\nabla _{\theta }{\mathcal {L}}(\theta ) = -{\mathbf {X}}\rho '(Y-{\mathbf {X}}\theta )$.

1.1 Appendix 3.1: Proof of Lemma 6.8

First of all note that, due to Lemma 6.7, it is sufficient to prove that

$$\begin{aligned} \lim _{n\rightarrow \infty }\frac{1}{p}\sum _{i=1}^p{\xi }_2({\vartheta }^t_{i},{\vartheta }_i^s)&=_{a.s.} \, {\mathbb {E}}{\xi }_2(\sqrt{\delta }\, Z_t,\sqrt{\delta }\, Z_s),\end{aligned}$$

(107)

$$\begin{aligned} \lim _{n\rightarrow \infty }\frac{1}{n}\sum _{i=1}^n{\xi }_2(s^t_{i},S_i^s)&=_{a.s.} \, {\mathbb {E}}{\xi }_2( Z_t, Z_s). \end{aligned}$$

(108)

Note that a similar statement is proved in [5, Theorem 4.2] for characterizing the Lasso estimator. While the same argument can be followed here, we outline an alternative argument that is based on a reduction to the setting of [19].

We fix an even number $q\in {\mathbb {N}}$, and will prove the claim for all $t,s\le T\equiv (q/2)-1$. Let $N \equiv n+p$. For $t\in \{ 0,\dots , T\}$, we introduce a vector $z^t\in ({\mathbb {R}}^q)^N$, which we think of as a vector with entries in ${\mathbb {R}}^q$: $z^{t}=({\mathbf {z}}^t_1,\dots ,{\mathbf {z}}^t_N)$ ${\mathbf {z}}^t_i\in {\mathbb {R}}^q$. Its entries are defined as follows:

$$\begin{aligned} {\mathbf {z}}^t_i&= (S^0_i,0,S^{1}_i,0,S^{2}_i,0,\dots \;,S^t_i,0,0,0,\dots , 0) \quad \text{ if } \quad 1\le i\le n,\end{aligned}$$

(109)

$$\begin{aligned} {\mathbf {z}}^{t+1}_i&= (0,{\vartheta }^1_j,0,{\vartheta }^{2}_j,0,{\vartheta }^{3}_j,\dots ,0, {\vartheta }^{t+1}_i,0,0,0,\dots , 0)\nonumber \\&\quad \text{ if } \quad n+1\le i=j+n\le n+p. \end{aligned}$$

(110)

Further, we let $A\in {\mathbb {R}}^{N\times N}$ be a symmetric matrix with $A_{ii} = 0$, $A_{ij} = \sqrt{n/N}\, X_{i,j-n}$ for $1\le i\le n$ and $n+1\le j\le n+p$, and all the other entries $A_{ij}$ $i<j$ i.i.d. $\mathsf{N}(0,1/N)$. It is then easy to see that the iteration in Eqs. (70) and (71) is equivalent to the following

$$\begin{aligned} z^{t+1} = A\, f(z^t;t) -\mathsf{B}_t\, f(z^{t-1};t-1). \end{aligned}$$

(111)

Here, for each t, $f(\,\cdot \,;t):({\mathbb {R}}^q)^N\rightarrow ({\mathbb {R}}^q)^N$ is separable in the following sense

$$\begin{aligned} f(z;t) = (f_1({\mathbf {z}}_1;t);f_2({\mathbf {z}}_2;t);\dots ;f_N({\mathbf {z}}_N;t)), \end{aligned}$$

(112)

with $f_i(\,\cdot \,;t):{\mathbb {R}}^q\rightarrow {\mathbb {R}}^q$. These are defined as follows (letting $\Psi _{t,i}(x) = \Psi (W_i+x;b_t)$ and $h = \sqrt{(1+\delta )/\delta }$)

$$\begin{aligned} f_i({\mathbf {z}}_i;t)&= (0,\delta h\,\Psi _{0,i}({\mathbf {z}}_{i,1}),0,\delta h\,\Psi _{1,i} ({\mathbf {z}}_{i,3}),0, \dots ,0,\delta h\,\Psi _{t,i}({\mathbf {z}}_{i,2t-1}),0,0,0,\dots ,0) \nonumber \\&\quad \text{ if } 1\le i\le n,\end{aligned}$$

(113)

$$\begin{aligned} f_i({\mathbf {z}}_i;t)&= (0,0,-h\,{\mathbf {z}}_{i,2},0,-h\,{\mathbf {z}}_{i,4},0, \dots , - h\,{\mathbf {z}}_{i,2t},0,0,0,0,\dots ,0) \nonumber \\&\quad \text{ if } n+1\le i\le n+p. \end{aligned}$$

(114)

The matrix multiplication in Eq. (111) operates in the natural way over $({\mathbb {R}}^{q})^N$, namely we identified A with the Kronecker product $A\otimes \mathrm{I}_{q\times q}$. Explicitly, Eq. (111) reads

$$\begin{aligned} {\mathbf {z}}^{t+1}_i = \sum _{j\in [N]}A_{ij}\, f_j({\mathbf {z}}_j^t;t) -\mathsf{B}_t\, f_i({\mathbf {z}}_i^{t-1};t-1). \end{aligned}$$

(115)

Finally $\mathsf{B}_t\in {\mathbb {R}}^{q\times q}$ is given by

$$\begin{aligned} \mathsf{B}_t = \frac{1}{N}\sum _{i=1}^N\frac{\partial f_i}{\partial {\mathbf {z}}}({\mathbf {z}}^t_i;t). \end{aligned}$$

(116)

The recursion (111) is characterized in [19, Theorem 1], which establishes—for instance—that, for ${\xi }:{\mathbb {R}}^q\rightarrow {\mathbb {R}}$ pseudo-Lipschitz, we have, almost surely,

$$\begin{aligned} \lim _{N\rightarrow \infty }\frac{1}{p}\sum _{i=n+1}^{n+p} {\xi }({\mathbf {z}}_i^t) = {\mathbb {E}}\{{\xi }({\mathbf Z}_t)\}. \end{aligned}$$

(117)

Here ${\mathbf Z}_t$ is a Gaussian random vector whose covariance is fully specified in [19]. The proof of the lemma is finished by comparing the expressions in [19] for the covariance wit the ones in the statement of the lemma.

1.2 Appendix 3.2: Proof of Lemma 6.9

First of all we introduce the notation $q_t \equiv {\Gamma }_{t,t+1}/\tau _*^2$. We then have the recursion

$$\begin{aligned} q_{t+1}&= \mathsf{H}(q_t), \end{aligned}$$

(118)

$$\begin{aligned} \mathsf{H}(q)&= \frac{\delta }{\tau _*^2}\, {\mathbb {E}}_q\{\Psi (W+\tau _*\, Z_1;b_*) \Psi (W+\tau _*\,Z_2;b_*)\}, \end{aligned}$$

(119)

where expectation ${\mathbb {E}}_q$ is with respect to the centered Gaussian vector $(Z_1,Z_2)$ with ${\mathbb {E}}_q\{Z_1^2\}={\mathbb {E}}_q\{Z_2^2\} = 1$ and ${\mathbb {E}}_q\{Z_1Z_2\}= q$, independent of $W\sim F_W$. We claim that:

• (i) $\mathsf{H}(1) = 1$;

• (ii) $\mathsf{H}(q)$ is increasing for $q\in [0,1]$;

• (iii) $\mathsf{H}(q)$ is strictly convex for $q\in [0,1]$.

In order to prove (i), note that, for $q=1$, $Z_1=Z_2\equiv Z\sim \mathsf{N}(0,1)$ and hence

$$\begin{aligned} \mathsf{H}(1) = \frac{\delta }{\tau _*^2}\, {\mathbb {E}}_q\{\Psi (W+\tau _*\, Z;b_*)^2\}, \end{aligned}$$

(120)

which is equal to 1 since $b_*$, $\tau _*$ satisfy Eq. (28).

In order to prove (ii), (iii), define

$$\begin{aligned} h_W(z)&\equiv \Psi (W+\tau _*\, z ; b_*), \end{aligned}$$

(121)

$$\begin{aligned} {\mathcal {H}}(q)&\equiv {\mathbb {E}}_q\{h_W(Z_1) h_W(Z_2)|W\}, \end{aligned}$$

(122)

We will prove that ${\mathcal {H}}$ is strictly increasing and convex for any W, whence claims (ii) and (iii) follow by linearity. The argument is the same as in [5, Lemma C.1] Let $\{X_t\}_{t\ge 0}$ be the stationary Ornstein–Uhlenbeck process with covariance ${\mathbb {E}}(X_0X_t) = e^{-t}$, and denote by $\mathsf{E}$ expectation with respect to X. Then

$$\begin{aligned} {\mathcal {H}}(q) = \mathsf{E}\{h_W(X_0) h_W(X_t)\}\Big |_{t= \log (1/q)}, \end{aligned}$$

(123)

Then we have the spectral representation (for $t= \log (1/q)$)

$$\begin{aligned} {\mathcal {H}}(q) = \sum _{\ell = 0}^{\infty }c_{\ell }^2\, e^{-\ell \, t} = \sum _{\ell = 0}^{\infty }c_{\ell }^2\, q^{\ell }, \end{aligned}$$

(124)

whence the claim follows since $c_{\ell }\ne 0$ for some $\ell \ge 2$ as long as $h_W(x)$ is non-linear.

Because of the remarks (i)–(iii) just proven, it follows that $\lim _{t\rightarrow \infty }q_t= 1$ (and hence $\lim _{t\rightarrow \infty }{\Gamma }_{t,t+1} = \tau _*^2$) if and only if $\mathsf{H}'(1)\le 1$. A simple calculation yields

$$\begin{aligned} \mathsf{H}'(1) = \delta \, {\mathbb {E}}\big \{\Psi '(W+\tau _*\, Z;b_*)^2\big \}, \end{aligned}$$

(125)

where $Z\sim \mathsf{N}(0,1)$. Recalling that $\Psi '(z;b)\in (0,1)$, we have $(\Psi ')^2 \le \Psi '$ and so

$$\begin{aligned} \mathsf{H}'(1) \le \delta \, {\mathbb {E}}\big \{\Psi '(W+\tau _*\, Z;b_*)\big \}=1, \end{aligned}$$

(126)

where the last identity follows because $(\tau _*,b_*)$ solve Eq. (29). This finishes the proof.