Polarization Optimality of Equally Spaced Points on the Circle for Discrete Potentials

Abstract

We prove a conjecture of Ambrus, Ball and Erdélyi that equally spaced points maximize the minimum of discrete potentials on the unit circle whenever the potential is of the form

$$\begin{aligned} \sum _{k=1}^n f(d(z,z_k)), \end{aligned}$$

where $f:[0,\pi ]\rightarrow [0,\infty ]$ is non-increasing and convex and $d(z,w)$ denotes the geodesic distance between z and w on the circle.

1 Introduction and Main Results

Let $\mathbb{S }^1:=\{z=x+{\text{ i }}y \mid x,y \in \mathbb{R },\,\,x^2+y^2 =1\}$ denote the unit circle in the complex plane $\mathbb{C }$. For $z,w\in \mathbb{S }^1$, we denote by $d(z,w)$ the geodesic (shortest arclength) distance between z and w. Let $f:[0,\pi ]\rightarrow [0,\infty ]$ be non-increasing and convex on $(0,\pi ]$ with $f(0)=\lim _{\theta \rightarrow 0^+}f(\theta )$. It then follows that f is a continuous extended real-valued function on $[0,\pi ]$.

For a list of n points (not necessarily distinct) $\omega _n=(z_1 ,\ldots , z_n)\in (\mathbb{S }^1)^n$, we consider the f-potential of $\omega _n$,

$$\begin{aligned} U^f(\omega _n;z):=\sum _{k=1}^n f(d(z,z_k)) \quad (z\in \mathbb{S }^1), \end{aligned}$$

(1)

and the f-polarization of $\omega _n$,

$$\begin{aligned} M^f(\omega _n;\mathbb{S }^1):=\min _{z\in \mathbb{S }^1}U^f(\omega _n;z). \end{aligned}$$

(2)

In this note, we are chiefly concerned with the n-point f-polarization of $\mathbb{S }^1$ (also called the nth f-Chebyshev constant of $\mathbb{S }^1$),

$$\begin{aligned} M^f_n(\mathbb{S }^1):=\sup _{\omega _n\in (\mathbb{S }^1)^n}M^f(\omega _n;\mathbb{S }^1), \end{aligned}$$

(3)

which has been the subject of several recent papers (e.g., [1, 2, 5, 6]).

In the case (relating to Euclidean distance) when

$$\begin{aligned} f(\theta )=f_s(\theta ):= |{\text{ e }}^{{\text{ i }}\theta }-1|^{-s}=(2 \sin |\theta /2|)^{-s},\quad s>0, \end{aligned}$$

(4)

we abbreviate the notation for the above quantities by writing

$$\begin{aligned} U^s(\omega _n;z)&:= \sum _{k=1}^n f_s(d(z,z_k))=\sum _{k=1}^n \frac{1}{|z-z_k|^s}, \nonumber \\ M^s(\omega _n;\mathbb{S }^1)&:= \min _{z\in \mathbb{S }^1} \sum _{k=1}^n \frac{1}{|z-z_k|^s},\\ M^s_n(\mathbb{S }^1)&:= \sup _{\omega _n \in (\mathbb{S }^1)^n} M^s(\omega _n;\mathbb{S }^1). \nonumber \end{aligned}$$

(5)

The main result of this note is the following theorem conjectured by Ambrus et al. [2]. Its proof is given in the next section.

Theorem 1

Let $f:[0,\pi ]\rightarrow [0,\infty ]$ be non-increasing and convex on $(0,\pi ]$ with $f(0)=\lim _{\theta \rightarrow 0^+}f(\theta )$. If $\omega _n$ is any configuration of n distinct equally spaced points on $\mathbb{S }^1$, then $M^f(\omega _n;\mathbb{S }^1)=M^f_n(\mathbb{S }^1)$. Moreover, if the convexity condition is replaced by strict convexity, then such configurations are the only ones that achieve this equality.

Applying this theorem to the case of $f_s$ given in (4) we immediately obtain the following.

Corollary 2

Let $s>0$ and $\omega _n^*:=\{\mathrm{{e}}^{\mathrm{{i}}2\pi k/n}\,: k=1,2,\ldots ,n\}$. If $(z_1,\ldots , z_n)\in (\mathbb{S }^1)^n$, then

$$\begin{aligned} \min _{z\in \mathbb{S }^1}\sum _{k=1}^n \frac{1}{|z-z_k|^s}\le M^s(\omega _n^*;\mathbb{S }^1)= M^s_n(\mathbb{S }^1), \end{aligned}$$

(6)

with equality if and only if $(z_1,\ldots , z_n)$ consists of distinct equally spaced points.

The following representation of $M^s(\omega _n^*;\mathbb{S }^1)$ in terms of Riesz s-energy was observed in [2]:

$$\begin{aligned} M^s(\omega _n^*;\mathbb{S }^1) = \frac{\mathcal{E }_s(\mathbb{S }^1;2n)}{2n} - \frac{\mathcal{E }_s(\mathbb{S }^1;n)}{n}, \end{aligned}$$

where

$$\begin{aligned} \mathcal{E }_s(\mathbb{S }^1;n):=\inf _{\omega _n\in (\mathbb{S }^1)^n} \sum _{j=1}^n\sum _{\begin{array}{c} k=1\\ k\ne j \end{array}}^n\frac{1}{|z_j-z_k|^s}. \end{aligned}$$

Thus, applying the asymptotic formulas for $\mathcal{E }_s(\mathbb{S }^1;n)$ given in [3], we obtain the dominant term of $M^s_n(\mathbb{S }^1)$ as $n\rightarrow \infty$:

$$\begin{aligned} M^s_n(\mathbb{S }^1) \sim \left\{ \begin{array}{ll} \displaystyle {\frac{2 \zeta (s)}{(2\pi )^s} \, (2^s - 1)n^s}, &{} s> 1\,, \\ \displaystyle { ({1}/{\pi }) \, n\log n}, &{} s = 1\,, \\ \displaystyle {\frac{2^{-s}}{\sqrt{\pi }} \, \frac{\Gamma \big ( \frac{1-s}{2}\big )}{\Gamma \big (1-\frac{s}{2} \big )}}\, n, &{} s \in [0,1), \end{array}\right. \end{aligned}$$

where $\zeta (s)$ denotes the classical Riemann zeta function and $a_n \sim b_n$ means that $\lim _{n \rightarrow \infty }{a_n/b_n} = 1$. These asymptotics, but for $M^s (\omega _n^*;\mathbb{S }^1)$, were stated in [2]¹.

For s an even integer, say $s=2m$, the precise value of $M^{2m}_n(\mathbb{S }^1)=M^{2m}(\omega _n^*;\mathbb{S }^1)$ can be expressed in finite terms, as can be seen from formula (1.20) in [3].

Corollary 3

We have

$$\begin{aligned} M_n^{2m}(\mathbb{S }^1)= \frac{2}{(2\pi )^{2m}} \sum _{k=1}^m n^{2k}\zeta (2k)\alpha _{m-k}(2m)(2^{2k}-1),\quad m \in \mathbb{N }, \end{aligned}$$

where $\alpha _j(s)$ is defined via the power series for $\mathrm{sinc\,} z = (\sin \pi z)/(\pi z)$:

$$\begin{aligned} (\mathrm{sinc\,} z)^{-s} = \sum _{j=0}^\infty \alpha _j(s) z^{2j}\,, \quad \alpha _0(s)=1. \end{aligned}$$

In particular,

$$\begin{aligned} M^2_n(\mathbb{S }^1)&= \frac{2}{(2\pi )^2}n^2\zeta (2)=\frac{n^2}{4},\\ M_n^4(\mathbb{S }^1)&= \frac{2}{(2\pi )^4}[n^2\zeta (2)\alpha _1(4)(2^2-1)+n^4\zeta (4)(2^4-1)]= \frac{n^2}{24}+\frac{n^4}{48} ,\\ M_n^6(\mathbb{S }^1)&= \frac{2}{(2\pi )^6}[n^2\zeta (2)\alpha _2(6)(2^2-1)+n^4\zeta (4)\alpha _1(6)(2^4-1)+n^6\zeta (6)(2^6-1)]\\&= \frac{n^2}{120} + \frac{n^4}{192} + \frac{n^6}{480}, \end{aligned}$$

The case $s=2$ of the above corollary was first proved in [1, 2] and the case $s=4$ was first proved in [5]. We remark that an alternative formula for $\alpha _j(s)$ is

$$\begin{aligned} \alpha _j(s) = \frac{(-1)^j B_{2j}^{(s)}(s/2)}{(2j)!}(2\pi )^{2j}, \quad j = 0,1,2,\dots , \end{aligned}$$

where $B_j^{(\alpha )}(x)$ denotes the generalized Bernoulli polynomial. Asymptotic formulas for $M^f_n(\mathbb{S }^1)$ for certain other functions f can be obtained from the asymptotic formulas given in [4].

As other consequences of Theorem 1, we immediately deduce that equally spaced points are optimal for the following problems:

$$\begin{aligned} \min _{\omega _n\in (\mathbb{S }^1)^n} \max _{z\in \mathbb{S }^1} \sum _{k=1}^n {|z-z_k|^\alpha }\quad (0<\alpha \le 1), \end{aligned}$$

(7)

and

$$\begin{aligned} \max _{\omega _n\in (\mathbb{S }^1)^n} \min _{z\in \mathbb{S }^1} \sum _{k=1}^n \log \frac{1}{|z-z_k|}, \end{aligned}$$

(8)

with the solution to (8) being well-known. Furthermore, various generalizations of the polarization problem for Riesz potentials for configurations on $\mathbb{S }^1$ are worthy of consideration, such as minimizing the potential on circles concentric with $\mathbb{S }^1$.

2 Proof of Theorem 1

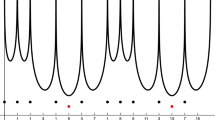
For distinct points $z_1,z_2\in \mathbb{S }^1$, we let $\widehat{z_1z_2}$ denote the closed subarc of $\mathbb{S }^1$ from $z_1$ to $z_2$ traversed in the counterclockwise direction. We further let $\gamma (\widehat{z_1z_2})$ denote the length of $\widehat{z_1z_2}$ (thus, $\gamma (\widehat{z_1z_2})$ equals either $d(z_1,z_2)$ or $2\pi -d(z_1,z_2)$). Observe that the points $z_1$ and $z_2$ partition $\mathbb{S }^1$ into two subarcs: $\widehat{z_1z_2}$ and $\widehat{z_2z_1}$. The following lemma (see proof of Lemma 1 in [2]) is a simple consequence of the convexity and monotonicity of the function f and is used to show that any n-point configuration $\omega _n\subset \mathbb{S }^1$ such that $M^f(\omega _n; \mathbb{S }^1)=M_n^f(\mathbb{S }^1)$ must have the property that any local minimum of $U^f(\omega _n; \cdot )$ is a global minimum of this function (Fig. 1).

Fig. 1

The points $z_1, z_2, \rho _{-\varepsilon }(z_1), \rho _{\varepsilon }(z_2)$ in Lemma 4. The potential increases at every point in the subarc $\widehat{\rho _\varepsilon (z_2) \rho _{-\varepsilon }(z_1)}$ when $(z_1, z_2) \rightarrow (\rho _{-\varepsilon }(z_1), \rho _{\varepsilon }(z_2))$; see (9).

For $\phi \in \mathbb{R }$ and $z\in \mathbb{S }^1$, we let $\rho _\phi (z):=e^{i\phi }z$ denote the counterclockwise rotation of z by the angle $\phi$.

Lemma 4

([2]) Let $z_1, z_2\in \mathbb{S }^1$ and $0<\varepsilon <\gamma (\widehat{z_2z_1})/2$. Then with f as in Theorem 1,

$$\begin{aligned} U^f((z_1,z_2);z)\le U^f((\rho _{-\varepsilon }(z_1),\rho _\varepsilon (z_2));z) \end{aligned}$$

(9)

for z in the subarc $\widehat{\rho _\varepsilon (z_2) \rho _{-\varepsilon }(z_1)},$ while the reverse inequality holds for z in the subarc $\widehat{z_1 z_2}$. If f is strictly convex on $(0,\pi ]$, then these inequalities are strict. If $z_1=z_2$, then we set $\widehat{z_1 z_2}=\{z_1\}$ and $\widehat{z_2 z_1}=\mathbb{S }^1$.

We now assume that $\omega _n=(z_1 ,\ldots , z_n)$ is ordered in a counterclockwise manner and also that the indexing is extended periodically so that $z_{k+n}=z_k$ for $k\in \mathbb{Z }$. For $1\le k\le n$ and $\Delta \in \mathbb{R }$, we define $\tau _{k,\Delta }:(\mathbb{S }^1)^n\rightarrow (\mathbb{S }^1)^n$ by

$$\begin{aligned} \tau _{k,\Delta }(z_1,\ldots , z_k,z_{k+1},\ldots , z_n):=(z_1,\ldots , \rho _{-\Delta }(z_k),\rho _{\Delta }(z_{k+1}),\ldots , z_n). \end{aligned}$$

If $z_{k-1}\ne z_k$ and $z_{k+1}\ne z_{k+2}$, then $\tau _{k,\Delta }(\omega _n)$ retains the ordering of $\omega _n$ for $\Delta$ positive and sufficiently small. Given $\varvec{\Delta }:=(\Delta _1,\ldots , \Delta _n)^T\in \mathbb{R }^n$, let $\tau _{\varvec{\Delta }}\!:=\!\tau _{n,\Delta _n}\circ \cdots \circ \tau _{2,\Delta _2}\circ \tau _{1,\Delta _1}$ and $\omega _n^{\prime }\!:=\!\tau _{\varvec{\Delta }} (\omega _n).$ Letting $\alpha _k\!:=\!\gamma (\widehat{z_k z_{k+1}})$ and $\alpha _k^{\prime }:=\gamma (\widehat{z_k^{\prime } z_{k+1}^{\prime }})$ for $k=1,\ldots , n$, we obtain the system of n linear equations:

$$\begin{aligned} \alpha ^{\prime }_k=\alpha _k-\Delta _{k-1}+2\Delta _k-\Delta _{k+1} \quad (1\le k\le n), \end{aligned}$$

(10)

which is satisfied as long as $\sum _{k=1}^n\alpha _k^{\prime }=2\pi$ or, equivalently, if $\omega _n^{\prime }$ is ordered counterclockwise. Let

$$\begin{aligned} \text{ sep }(\omega _n):=\min _{1\le \ell \le n} \alpha _\ell . \end{aligned}$$

Then (10) holds if

$$\begin{aligned} \max _{1\le k\le n}|\Delta _k|\le (1/4)\text{ sep }(\omega _n), \end{aligned}$$

(11)

in which case, the configurations

$$\begin{aligned} \omega _{n,\varvec{\Delta }}^{(\ell )}:=\tau _{n,\Delta _\ell }\circ \cdots \circ \tau _{2,\Delta _2}\circ \tau _{1,\Delta _1}(\omega _n) \quad (\ell =1,\ldots ,n) \end{aligned}$$

(12)

are all ordered counterclockwise. If the components of $\varvec{\Delta }$ are nonnegative, then we may replace the ‘(1/4)’ in (11) with ‘(1/2)’.

Lemma 5

Suppose $\omega _n=(z_1 ,\ldots , z_n)$ and $\omega _n^{\prime }=(z^{\prime }_1 ,\ldots , z^{\prime }_n)$ are n-point configurations on $\mathbb{S }^1$ ordered in a counterclockwise manner. Then there is a unique $\varvec{\Delta }^*=(\Delta _1^*,\ldots , \Delta _n^*)\in \mathbb{R }^n$ so that

• (a) $\Delta _k^*\ge 0, \quad k=1,\ldots , n$,

• (b) $\Delta _{j }^*=0$    for some $j \in \{1,\ldots , n\}$, and

• (c) $\tau _{\varvec{\Delta ^*}}(\omega _n)$ is a rotation of $\omega _n^{\prime }$.

Proof

The system (10) can be expressed in the form

$$\begin{aligned} A\varvec{\Delta }=\varvec{\beta }, \end{aligned}$$

(13)

where

$$\begin{aligned} A:=\left( \begin{array}{cccccc} 2 &{}\quad -1&{}\quad 0 &{}\quad 0 &{}\quad \cdots &{} -1\\ -1 &{}\quad 2 &{}\quad -1&{}\quad 0&{}\quad \cdots &{}\quad 0 \\ \vdots &{}\quad &{} &{} &{} &{} \vdots \\ 0 &{}\quad 0 &{}\quad \cdots &{}\quad -1 &{}\quad 2 &{}\quad -1\\ -1 &{}\quad 0 &{}\quad \cdots &{}\quad 0&{}\quad -1 &{}2 \end{array} \right) ; \quad \varvec{\Delta }:=\left( \begin{array}{c} \Delta _1 \\ \Delta _2\\ \vdots \\ \\ \Delta _n \end{array} \right) , \quad \text{ and }\quad \varvec{\beta }:=\left( \begin{array}{cc} \alpha _1^{\prime }-\alpha _1\\ \alpha _2^{\prime }-\alpha _2\\ \vdots \\ \\ \alpha _n^{\prime }-\alpha _n \end{array} \right) . \end{aligned}$$

It is elementary to verify that $\ker A=(\text{ range }A)^\perp = \text{ span } (\varvec{1})$, where $\varvec{1}=(1,1,\ldots ,1)^T$. Since $\varvec{\beta }^T\varvec{1}=\sum _{k=1}^n (\alpha _k^{\prime }-\alpha _k)=0$, the linear system (13) always has a solution $\varvec{\Delta }$. Let $j\in \{1, \ldots , n\}$ satisfy $\Delta _{j}= \min _{1\le k\le n} \Delta _k$. Then subtracting $\Delta _{j} \varvec{1}$ from $\varvec{\Delta }$, we obtain the desired $\varvec{\Delta }^*$. Since $\ker A=\text{ span }\,\varvec{1}$, there is at most one solution of (13) satisfying properties (a) and (b), showing that $\varvec{\Delta ^*}$ is unique.

Part (c) holds as a direct result of the fact that both $\omega _n$ and $\omega _n^{\prime }$ are ordered counterclockwise.

Lemma 6

Let $\Omega _n=(z_1,\ldots , z_n)$ be a configuration of $n$ distinct points on $\mathbb{S }^1$ ordered counterclockwise, and with f as in Theorem 1, suppose $\varvec{\Delta }=(\Delta _1,\ldots , \Delta _n)\in \mathbb{R }^n$ is such that

• (a) $0\le \Delta _k \le (1/2) \mathrm{sep}(\Omega _n)$    for $k=1,\ldots , n$, and

• (b) there is some $j\in \{1,\ldots , n\}$ for which $\Delta _j=0$.

Let $\Omega _n^{\prime }:=\tau _{\varvec{\Delta }}(\Omega _n)=(z^{\prime }_1,\ldots , z^{\prime }_n)$. Then $\widehat{z^{\prime }_j z^{\prime }_{j+1}}\subset \widehat{z_jz_{j+1}}$ and

$$\begin{aligned} U^f(\Omega _n;z) \le U^f(\Omega _n^{\prime };z) \quad (z\in \widehat{z_j^{\prime }z_{j+1}^{\prime }}). \end{aligned}$$

(14)

If f is strictly convex on $(0,\pi ]$ and $\Delta _k>0$ for at least one k, then the inequality (14) is strict.

We remark that $\Delta _k=0$ for all $k=1,\ldots , n$ is equivalent to saying that the points are equally spaced.

Proof

Recalling (12), it follows from condition (a) that $(z^{(\ell )}_1,\ldots , z^{(\ell )}_n):= \omega _{n,\varvec{\Delta }}^{(\ell )}$ are counterclockwise ordered. Since $\Delta _j=0$ and $\Delta _k\ge 0$ for $k=1,\ldots ,n$, the points $z^{(\ell )}_j$ and $z^{(\ell )}_{j+1}$ are moved at most once as $\ell$ varies from 1 to n and move toward each other, while remaining in the complement of all other subarcs $\widehat{z^{(\ell )}_k z^{(\ell )}_{k+1}}$, i.e.,

$$\begin{aligned} \widehat{z^{\prime }_jz^{\prime }_{j+1}}=\widehat{z^{(n)}_jz^{(n)}_{j+1}}\subseteq \widehat{z^{(\ell )}_jz^{(\ell )}_{j+1}}\subseteq \widehat{z^{(\ell )}_{k+1}z^{(\ell )}_k}, \end{aligned}$$

for $k\in \{1,\ldots ,n\}\setminus \{j\}$ and $\ell \in \{1,\ldots , n\}$. Lemma 4 implies that, for $\ell =1,\ldots , n$, we have $U^f(\omega ^{(\ell -1)}_n;z) \le U^f(\omega ^{(\ell )}_n;z)$ for $z\in \widehat{z^{(\ell )}_j z^{(\ell )}_{j+1}}$ (where $\omega ^{(0)}_n:=\omega _n$) and the inequality is strict if $\Delta _\ell >0$. Hence, (14) holds and the inequality is strict if f is strictly convex and $\Delta _k>0$ for some $k=1,\ldots , n$. $\square$

We now proceed with the proof of Theorem 1. Let $\omega _n=(z_1,\ldots , z_n)$ be a non-equally spaced configuration of n (not necessarily distinct) points on $\mathbb{S }^1$ ordered counterclockwise. By Lemma 5, there is some equally spaced configuration $\omega _n^{\prime }$ (i.e., $\alpha ^{\prime }_k=2\pi /n$ for $k=1,\ldots , n$) and some $\varvec{\Delta ^*}=(\Delta _1^*,\ldots , \Delta _n^*)$ such that (a) $\omega _n^{\prime }=\tau _{\varvec{\Delta ^*}}(\omega _n)$, (b) $\Delta ^*_k\ge 0$ for $k=1,\ldots ,n$, and (c) $\Delta ^*_j=0$ for some $j\in \{1,\ldots ,n\}$. Then (10) holds with $\alpha _k:=\gamma (\widehat{z_k,z_{k+1}})$ and $\alpha ^{\prime }_k:=2\pi /n$. Since $\omega _n$ is not equally spaced, we have $\Delta ^*_k>0$ for at least one value of k.

For $0\le t\le 1$, let $\omega _n^t:=\tau _{(t\varvec{\Delta ^*})}(\omega _n)=(z_1^t,\ldots , z_n^t)$ and, for $k=1,\ldots , n$, let $\alpha _k^t:=\gamma (\widehat{z_k^t z_{k+1}^t})$. Recalling (10), observe that

$$\begin{aligned} \alpha _k^t&= \alpha _k-t(\Delta _{k-1}+2\Delta _k-\Delta _{k+1})\\&= \alpha _k+t(2\pi /n-\alpha _k)\\&= (1-t)\alpha _k+t(2\pi /n), \end{aligned}$$

for $0\le t\le 1$ and $k=1,\ldots , n$, and so $\text{ sep }(\omega _n^t)\ge t(2\pi /n)$. Now let $0<t<s<\min (1,t(1+\pi /(nD)))$, where $D:=\max \{\Delta _k : 1\le k\le n\}$. Then Lemma 6 (with $\Omega _n=\omega _n^t, \varvec{\Delta }=(s-t)\varvec{\Delta ^*}$, and $\Omega _n^{\prime }=\tau _{\varvec{\Delta }}(\Omega _n)=\omega _n^s$) implies that $\widehat{z_j^s z_{j+1}^s}\subseteq \widehat{z_j^t z_{j+1}^t}$ and that

$$\begin{aligned} U^f(\omega _n^t;z) \le U^f(\omega _n^s;z) \quad (z\in \widehat{z_j^sz_{j+1}^s}), \end{aligned}$$

(15)

where the inequality is sharp if f is strictly convex.

Consider the function

$$\begin{aligned} h(t):=\min \{U^f(\omega _n^t;z): z\in \widehat{z_j^t z_{j+1}^t}\}, \quad (0\le t\le 1). \end{aligned}$$

Observe that

$$\begin{aligned} h(t)\le \min \{U^f(\omega _n^t;z): {z\in \widehat{z_j^s z_{j+1}^s}}\}\le \min \{U^f(\omega _n^s;z): {z\in \widehat{z_j^s z_{j+1}^s}}\}= h(s), \end{aligned}$$

for $0<t<s<\min (1,t(1+\pi /(nD)))$. It is then easy to verify that h is non-decreasing on $(0,1)$. Since $\omega _n^t$ depends continuously on t, the function h is continuous on $[0,1]$ and thus h is non-decreasing on $[0,1]$.

We then obtain the desired inequality

$$\begin{aligned} M^f(\omega _n;\mathbb{S }^1)\le h(0) \le h(1)=M^f(\omega _n^{\prime };\mathbb{S }^1), \end{aligned}$$

where the last equality is a consequence of the fact that $\omega _n^{\prime }$ is an equally spaced configuration and so the minimum of $U^f(\omega _n^{\prime };z)$ over $\mathbb{S }^1$ is the same as the minimum over $\widehat{z_j^{\prime }z_{j+1}^{\prime }}$. If f is strictly convex, then $h(0)<h(1)$ showing that any optimal f-polarization configuration must be equally spaced. This completes the proof of Theorem 1. $\square$