Tracing Compressed Curves in Triangulated Surfaces

Abstract

A simple path or cycle in a triangulated surface is normal if it intersects any triangle in a finite set of arcs, each crossing from one edge of the triangle to another. A normal curve is a finite set of disjoint normal paths and normal cycles. We describe an algorithm to “trace” a normal curve in $O(\min \{ X, n^2\log X \})$ time, where $n$ is the complexity of the surface triangulation and $X$ is the number of times the curve crosses edges of the triangulation. In particular, our algorithm runs in polynomial time even when the number of crossings is exponential in $n$. Our tracing algorithm computes a new cellular decomposition of the surface with complexity $O(n)$; the traced curve appears in the 1-skeleton of the new decomposition as a set of simple disjoint paths and cycles. We apply our abstract tracing strategy to two different classes of normal curves: abstract curves represented by normal coordinates, which record the number of intersections with each edge of the surface triangulation, and simple geodesics, represented by a starting point and direction in the local coordinate system of some triangle. Our normal-coordinate algorithms are competitive with and conceptually simpler than earlier algorithms by Schaefer et al. (Proceedings of 8th International Conference Computing and Combinatorics. Lecture Notes in Computer Science, vol. 2387, pp. 370–380. Springer, Berlin 2002; Proceedings of 20th Canadian Conference on Computational Geometry, pp. 111–114, 2008) and by Agol et al. (Trans Am Math Soc 358(9): 3821–3850, 2006).

Un poète doit laisser des traces de son passage, non des preuves.

Seules les traces font rêver.

— René Char, La Parole en Archipel (1962)

A typical simple closed curve on a surface is complicated, from the point of view of someone tracing out the curve.

— William P. Thurston, “On the geometry and dynamics of diffeomorphisms of surfaces” (1988)

1 Introduction

Curves on abstract surfaces are usually represented by describing the interaction between the curve and a decomposition of the surface into elementary pieces. For example, given a triangulation of the surface, any sufficiently well-behaved curve that avoids the vertices of the triangulation can be described by listing the sequence of edges that the curve crosses, in order along the curve. (See Sect. 2 for more precise definitions.) This crossing sequence identifies the curve up to a continuous deformation that avoids the vertices. We call a subpath of a curve between two consecutive edge crossings an elementary segment.

For simple curves, however, there are several more compact representations. For example, given a triangulation of the surface, any sufficiently well-behaved simple curve can be described by listing the number of elementary segments connecting each pair of edges in each triangle. These numbers are called the normal coordinates of the curve [28, 40]. Any vector of normal coordinates identifies a unique simple curve (again up to continuous deformation), because there is only one way to fill each triangle with the correct number of elementary segments without intersection. The normal coordinate representation is remarkably compact; only $O(n\log (X/n))$ bits are needed to list the normal coordinates of a curve with $X$ crossings on a triangulated surface with complexity $n$. Several algorithms in two- and three-dimensional topology owe their efficiency to the compactness of the normal-coordinate representation [1, 10, 11, 29, 63, 64, 66, 68, 75].

Schaefer et al. [63, 66, 75] consider several algorithmic questions about normal curves, such as computing the number of components of a curve, deciding whether two given curves are isotopic, and computing algebraic and geometric intersection numbers of pairs of curves. Classical algorithms for these problems require explicit traversal or crossing sequences as input.

By connecting normal coordinates with grammar-based text compression [45, 46, 49, 61] and word equations [18, 57, 59, 60], Schaefer et al. developed algorithms whose running times are polynomial in the bit complexity of the normal coordinate vector, which they call the normal complexity of the curve. These algorithms rely on a complex algorithm of Plandowski and Rytter [57] to compute compressed solutions of word equations. We are unaware of any precise time analysis, but as Plandowski and Rytter’s algorithm uses a nested sequence of quadratic- and cubic-time reductions, its running time is quite high. Štefankovic [75] described simpler algorithms for some of these problems in time linear in the normal complexity, or $O(n\log (X/n))$ time in our notation, by reducing them to an elegant algorithm of Robson and Deikert [59, 60] to solve word equations with a certain special structure.

Some of the problems considered by Schaefer et al. can also be solved in polynomial time using the polynomial-time orbit-counting algorithm of Agol et al. [1], which was originally designed to compute the number of components of normal surfaces in triangulated 3-manifolds in polynomial time, but in fact (like the word-equation algorithms of Schaefer et al. [63, 66, 75]) works for similar problems in any dimension. Agol et al. do not claim a precise time bound, but a direct reading of their analysis implies a running time of $O(n^4\log ^3 (X/n))$. Dynnikov and Wiest [19] later developed a special case of the orbit-counting algorithm to reconstruct braids from their planar curve diagrams; Dehornoy et al. [16] refer to this variant as the transmission-relaxation method.

Other compact representations of curves include weighted train tracks [5, 6, 25, 26, 56], Dehn-Thurston coordinates (with respect to a fixed pants decomposition of the surface) [15, 25, 26, 55, 77], and compressed intersection sequences [66, 75].

1.1 New Results: Normal Curves

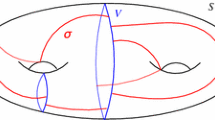
We propose an alternate strategy to efficiently compute with curves on surfaces. Instead of using complex compression techniques to avoid unpacking the crossing sequence of the input curve, our algorithms modify the underlying cellular decomposition of the surface so that the curve has a small explicit description with respect to the new decomposition. Specifically, given the normal coordinates of a curve $\gamma$ on a triangulated surface with $n$ edges, we compute a new cellular decomposition of the surface with complexity $O(n)$, called a street complex, such that $\gamma$ is a simple path or cycle in the 1-skeleton. After reviewing some background terminology, we formally define the street complex in Sect. 2; see Fig. 4 for an example.

At a high level, our algorithm simply traces the curve, continuously updating the street complex to reflect the portion of the curve traced so far. A naïve implementation of our tracing strategy runs in $O(X)$ time, where $X$ is the total number of edge crossings; each time the curve enters a triangle by crossing an edge, we can easily determine in $O(1)$ time which of the other two edges of the triangle to cross next. The main result of this paper is a tracing algorithm that runs in $O(n^2\log X)$ time, an exponential improvement over the naïve algorithm for any fixed surface triangulation.

Our new algorithm relies on two simple ideas. First, we observe that for typical curves, most of the decisions made by the brute-force tracing algorithm are redundant. If a curve enters a triangle $\varDelta$ between two older elementary segments that leave $\varDelta$ through the same edge, the new elementary segment must also leave $\varDelta$ through that edge; see Fig. 1. The street complex allows us to skip these redundant decisions automatically.

Fig. 1

Tracing three segments of a curve through a triangle. Tracing the third segment does not require any decisions

Second, even with redundant decisions filtered out, the naïve algorithm may repeat the same series of crossings many times when the input curve contains a spiral [19, 54, 65, 67]. Our algorithm detects spirals as they occur, quickly determines the depth of the spiral (the number of repetitions), and then skips ahead to the first crossing after the spiral. See Fig. 8 below.

We describe our generic tracing algorithm in Sect. 3 and analyze its running time in Sect. 4. We also describe and analyze a symmetric untracing algorithm in Sect. 5, which works backward from the street complex of a curve to its normal coordinates.

The street complex allows us to answer several fundamental topological questions about simple curves using elementary algorithms. For example, to determine whether a curve represented by normal coordinates is connected, we can trace one component of the curve, and then check whether the number of edge crossings we encountered is equal to the sum of the normal coordinates. To determine whether a connected normal curve is contractible, we can trace the curve and then apply a $O(n)$-time depth-first search in the dual of the resulting street complex [23]. To find the normal coordinates of a single component of a curve, we can trace just that component, discard the untraced components, and then untrace the street complex.

In Sect. 6, we describe algorithms to solve these and several other related problems for normal curves in $O(n^2\log X)$ time. All of the problems we consider were previously solved in (large) polynomial time by Schaefer et al. [63]; however, our algorithms are significantly faster and simpler. Our algorithms are also faster than the orbit-counting algorithm of Agol et al. [1] and more general than Dynnikov and Wiest’s transmission-relaxation method [16, 19]. For some of the problems we consider, our algorithms appear to be slower by a factor of $n$ than algorithms described by Štefankovic [75]; however, we optimistically conjecture that this gap can be closed with more careful time analysis.

1.2 New Results: Geodesics

Finally, in Sect. 7, we describe an extension of our tracing algorithm to simple geodesic paths on piecewise-linear surfaces. Here, the input surface is presented as a set of $n$ triangles, each with its own local Euclidean coordinate system, with some pairs of equal-length edges identified; the geodesic path is specified by a starting point and a direction, in the local coordinate system of one of the triangles. In particular, we do not assume that the input surface is embedded (or embeddable) in any Euclidean space. As an example application, we sketch an algorithm to find the first point of self-intersection on a geodesic path in $O(n^2\log X)$ time.

We regard our algorithm as a first step toward efficiently computing shortest paths on arbitrary piecewise-linear surfaces. Many algorithms have already been proposed to compute both exact and approximate shortest paths in piecewise-linear surfaces; Mitchell [48] and Bose et al. [7] provide exhaustive surveys. However, despite some claims to the contrary [14], these algorithms are efficient (and some are correct) only under the assumption that any shortest path crosses any edge of the input complex at most a constant number of times. This crossing assumption is reasonable in practice; for example, it holds if the input complex is PL-embedded in $\mathbb R ^d$ for any $d$ (in which case any shortest path crosses any edge at most once), or if all face angles are larger than some fixed constant. However, this assumption does not hold in general. As an elementary bad example, consider the piecewise-linear annulus defined by identifying the non-horizontal edges of the parallelogram with vertices $(0,0)$, $(1,0)$, $(x,1)$, $({x+1},1)$, for some arbitrarily large integer $x$; as shown in Fig. 2. This annulus is isometric to a “toilet paper tube” cut by $x$ turns of a helix; although this tube is curved, its Gaussian curvature is zero everywhere. The shortest path in this annulus between its two vertices is a vertical segment that crosses the oblique edge $x-1$ times; all existing shortest-path algorithm require at least constant time for each crossing. Essentially the same example appears as Fig. 1 in a seminal paper of Alexandrov [2].

Fig. 2

A shortest path in a piecewise-linear toilet paper tube

A shortest-path map for a surface ${\varSigma }$ with source point $s$ is a subdivision of $\varSigma$ into regions, such that for each region, all shortest paths from $s$ to that region cross the same sequence of edges of $\varSigma$. Suppose $\varSigma$ is a piecewise-linear surface such that the sum of angles around every vertex is at most $2\pi$. Alexandrov’s theorem [2] implies that $\varSigma$ is isometric to the surface of a convex polyhedron; it follows that the edges of any shortest-path map on $\varSigma$ are themselves geodesics. (Without the angle assumption, some edges of shortest-path maps may be hyperbolic arcs.) The results of Schaefer et al. [63] imply that any shortest-path map on $\varSigma$ has a compressed representation of complexity $O(n^2\log X)$, where $X$ is the number of intersections between edges of the shortest-path map and edges of $\varSigma$. Mount [52] described a similar compressed representation of size $O((n+m)\log (m+n))$ for a decomposition of $\varSigma$ into disks by $m$ interior-disjoint geodesic paths, but only under the explicit assumption that each geodesic traverses each edge of $\varSigma$ at most once. Mount’s data structure stores the sequence of intersections along each edge of $\varSigma$ in a binary tree; to save space, common subtrees are shared between edges. Schreiber and Sharir [69, 70] extended and applied Mount’s data structure in their algorithm to compute shortest paths on convex polyhedra in $O(n\log n)$ time. The compressed intersection sequences of Schaefer et al. [63] (and our equivalent tracing history, defined in Sect. 3.3) can be viewed as a generalization of Mount’s representation.

In light of these results, it is natural to ask whether compressed shortest-path maps can be constructed in time polynomial in $n$ and $\log X$; our research in this paper was originally motivated by this open problem. We leave further exploration of these ideas to future papers.

1.3 Computational Assumptions

Most of our time bounds are stated as functions of two variables: the number $n$ of triangles in the input triangulation and the total crossing number $X$ of the traced curve. We assume that $X = \varOmega (n^2)$, since otherwise our analysis yields a time bound slower than the trivial bound $O(n+X)$; this assumption implies that $\log (X/n) = \varTheta (\log X)$.

We formulate and analyze our algorithms for normal curves in the standard unit-cost integer RAM with $w$-bit words, where $w = \varOmega (\log X)$; that is, we assume that the sum of the normal coordinates can be stored in a single memory word. This assumption implies that all necessary integer arithmetic operations (comparison, addition, subtraction, multiplication, and division) required by our tracing algorithm can be executed in constant time. The $O(n\log X)$ time bound for Štefankovic’s word-equation algorithms [59, 60, 75] and the $O(n^4\log ^3 X)$ time bound for the Agol–Hass–Thurston orbit-counting algorithm [1] require the same model of computation.¹ For integer RAMs with smaller word sizes (for example, if the word size is only large enough to the largest individual normal coordinate), all these running times increase by at most a polylogarithmic factor in $X$.

However, like many other exact geometric shortest-path algorithms, the geodesic-tracing algorithm we describe in Sect. 7 requires the real RAM model of computation, to avoid prohibitive numerical issues; the real RAM model supports exact real addition, subtraction, multiplication, division, and square roots in constant time [58]. Specifically, we require exact real arithmetic to efficiently compute and apply transformations between the local coordinate systems of faces of the input surface. (Square roots are not required if the input surface is given as a set of triangles in the plane specified by vertex coordinates, but they are necessary for other reasonable input representations, such as polyhedra in $\mathbb R ^3$ or planar triangles specified by their edge lengths.)

2 Background

We begin by establishing some terminology and notation. In Sects. 2.1–2.3, we recall several standard definitions from combinatorial topology; for further background, see Edelsbrunner and Harer [20] or Stillwell [76]. We define the street complex and its components in Sect. 2.4. We defer background on piecewise-linear surfaces and geodesics to Sect. 7.1.

2.1 Surfaces, Curves, and Isotopy

A surface (more formally, a 2-manifold with boundary) is a Hausdorff space in which every point has an open neighborhood homeomorphic to either the plane $\mathbb R ^2$ or the closed halfplane $\{ (x,y) \mid x\ge 0 \}$. The set of points in a surface $\varSigma$ with halfplane neighborhoods is the boundary of the surface, denoted $\partial \!\varSigma$; the boundary is homeomorphic to a finite set of disjoint circles. A surface is orientable if it does not contain a subset homeomorphic to the Möbius band. We consider only compact, connected, orientable surfaces in this paper; we use a fixed but arbitrary orientation of the surface to distinguish between “left” and “right” and between “clockwise” and “counterclockwise”.

Formally, a simple cycle in a surface $\varSigma$ is a continuous injective map $\gamma :S^1\rightarrow \varSigma$. A simple path is (the image of) a continuous injective map $\pi :[0,1]\rightarrow \varSigma$; a simple arc is a simple path $\alpha$ whose endpoints $\alpha (0)$ and $\alpha (1)$ lie on the boundary $\partial \!\varSigma$. Except where explicitly noted, our algorithms deal with undirected curves; we do not normally distinguish between a cycle or arc and its reversal, or between different parametrization of the same cycle or arc. A simple arc is properly embedded if it intersects $\partial \!\varSigma$ only at its endpoints; similarly, a simple cycle is properly embedded if it avoids $\partial \!\varSigma$ entirely. A properly embedded curve is a finite collection of disjoint, properly embedded arcs and cycles. We emphasize that curves may have multiple components.

A homotopy between two curves is a continuous deformation of one curve to the other; if the curve remains properly embedded during the entire deformation, the homotopy is called a (proper) isotopy. More formally, a homotopy between two cycles $\gamma$ and $\gamma ^{\prime }$ is a continuous map $h:[0,1] \times S^1 \rightarrow \varSigma$ such that $h(0, \cdot ) = \gamma$ and $h(1,\cdot ) = \gamma ^{\prime }$; the homotopy is an isotopy if $h(t,\cdot )$ is a properly embedded cycle for all $t\in [0,1]$. Similarly, a homotopy between two arcs $\alpha$ and $\alpha ^{\prime }$ is a continuous map $h:[0,1] \times [0,1] \rightarrow \varSigma$ such that $h(0, \cdot ) = \alpha$ and $h(1,\cdot ) = \alpha ^{\prime }$; again, the homotopy is a proper isotopy if $h(t,\cdot )$ is a properly embedded arc for all $t\in [0,1]$. The formal definitions of homotopy and proper isotopy extend naturally to properly embedded curves with multiple components; in particular, a proper isotopy is a continuous deformation of the entire curve, so that the entire curve is always properly embedded. Two curves are isotopic, or in the same isotopy class, if there is an isotopy between them; homotopic curves are defined similarly. A simple cycle or arc is contractible if it is homotopic to a point.

An ambient isotopy is a continuous deformation of the entire surface, that is, a continuous function $H:[0,1]\times \varSigma \rightarrow \varSigma$ such that $H(0,\cdot )$ is the identity map and $H(t,\cdot )$ is a homeomorphism for all $t$. Classical results of Epstein [22] imply that two properly embedded curves $\gamma$ and $\gamma ^{\prime }$ are isotopic if and only if there is an ambient isotopy $H$ such that $H(1,\gamma ) = \gamma ^{\prime }$; see also Hirsch [33, Theorem 1.3].

The genus of a surface is the maximum number of disjoint simple cycles that can be removed without disconnecting the surface. Up to homeomorphism, there is exactly one orientable surface with genus $g$ and $b$ boundary components for any non-negative integers $g$ and $b$.

2.2 Triangulations and Euler Characteristics

An embedding of a graph $G$ on a surface $\varSigma$ is a function mapping the vertices of $G$ to distinct points in $\varSigma$ and the edges of $G$ to paths in $\varSigma$ that are simple and disjoint except at common endpoints. The faces of the embedding are maximal connected subsets of $\varSigma$ that are disjoint from the image of the graph. An embedding is cellular if every face is homeomorphic to an open disk; in particular, $\partial \!\varSigma$ must be the image of a set of disjoint cycles in $G$. A triangulation of $\varSigma$ is a cellularly embedded graph in which a walk around the boundary of any face has length three. Equivalently, a triangulation expresses $\varSigma$ as a set of disjoint triangles with certain pairs of edges identified; the 1-skeleton of the resulting cell complex is the induced graph of vertices and edges.

We assume that our input surfaces are presented as triangulations, either as a set of triangles and gluing rules, or as an abstract graph with a rotation system [39, 51] specifying the counterclockwise order of edges around each vertex. We do not assume that triangulations are simplicial complexes. That is, triangulations may contain parallel edges and loops; two triangles may share more than a single vertex or a single edge; and the same triangle may be incident to a vertex or edge more than once.

The Euler characteristic of a triangulation $T$ is the number of vertices and faces minus the number of edges; the Euler characteristic $\chi (\varSigma )$ of a surface $\varSigma$ is the Euler characteristic of any triangulation of $\varSigma$. A classical extension of Euler’s formula, originally due to l’Huillier [43, 44], implies that $\chi (\varSigma ) = 2-2g-b$ for the orientable surface $\varSigma$ with genus $g$ and $b$ boundary components.

Lemma 2.1

The components of a properly embedded curve on a surface with genus $g$ and $b$ boundary cycles fall into at most $9g + 6b - 8$ isotopy classes.

Proof

Fix a properly embedded curve $\gamma$ on a surface $\varSigma$. We separately bound the contractible components, noncontractible cycles, and noncontractible arcs in $\gamma$; thus, our analysis is not tight.

Two contractible arcs are isotopic if and only if their endpoints lie on the same boundary cycle of $\varSigma$; thus, contractible arcs fall into at most $b$ isotopy classes. All contractible cycles in $\varSigma$ are isotopic. We conclude that $\gamma$ has at most $b+1$ contractible components.

Let $\fancyscript{C}$ be a maximal set of pairwise-disjoint noncontractible cycles in distinct isotopy classes. Cutting the surface along any cycle leaves its Euler characteristic unchanged. Each component of $\varSigma \setminus \fancyscript{C}$ is either a pair of pants bounded by three cycles in $\fancyscript{C}$ or an annulus bounded by a cycle in $\fancyscript{C}$ and a boundary cycle of $\varSigma$; a component of any other topological type would contain a non-contractible cycle that is not isotopic to any cycle in $\fancyscript{C}$. A pair of pants has Euler characteristic $-1$; an annulus has Euler characteristic $0$; and each annular component of $\varSigma \setminus \fancyscript{C}$ contains exactly one boundary cycle of $\varSigma$. Thus, $\varSigma \setminus \fancyscript{C}$ consists of exactly $-\chi (\varSigma ) = 2g+b-2$ pairs of pants and $b$ annuli, which implies that $\mathopen | \fancyscript{C} \mathclose | = (3(2g+b-2) + b)/2 = 3g+2b-3$.

Similarly, let $\fancyscript{A}$ be a maximal set of pairwise-disjoint noncontractible arcs in distinct isotopy classes. Each component of $\varSigma \setminus \fancyscript{A}$ is a disk bounded by exactly three arcs in $\fancyscript{A}$ and three boundary arcs. Contracting each boundary cycle of $\varSigma$ to a point transforms $\fancyscript{A}$ into a $b$-vertex triangulation of a surface of genus $g$ with no boundary. Thus, Euler’s formula implies that $b - \mathopen | \fancyscript{A} \mathclose | + \tfrac{2}{3}\mathopen | \fancyscript{A} \mathclose | = 2-2g$, or equivalently, $\mathopen | \fancyscript{A} \mathclose | = 6g+3b-6$. $\square$

2.3 Normal Curves, Normal Isotopy, and Normal Coordinates

Let $T$ be a triangulation of a surface $\varSigma$ and let $n$ be the number of triangles in $T$. A properly embedded curve $\gamma$ in $\varSigma$ is normal with respect to $T$ if (1) $\gamma$ avoids the vertices of $T$; (2) every intersection between $\gamma$ and an edge of $T$ is transverse; and (3) the intersection of $\gamma$ with any triangular face of $T$ is a finite set of disjoint elementary segments: simple paths whose endpoints lie on distinct sides of the triangle. A normal isotopy between two normal curves is a proper isotopy $h$ such that $h(t,\cdot )$ is a normal curve for all $t$. Two curves are normal isotopic, or in the same normal isotopy class, if there is a normal isotopy between them.

A normal cycle is trivial if it bounds a disk in $\varSigma$ containing a single vertex of $T$. We call a normal curve $\gamma$ reduced if no component of $\gamma$ is a trivial cycle and no two components of $\gamma$ are normal isotopic.

Any normal curve can be identified, up to normal isotopy, by two different vectors of $O(n)$ non-negative integers. There are three types of elementary segments within any face $\varDelta$, each separating one corner of $\varDelta$ from the other two; the corner coordinates of $\gamma$ list the number of elementary segments of each type in each face of $T$. The edge coordinates of $\gamma$ list the number of times $\gamma$ intersects each edge of $T$. See Fig. 3. We collectively refer to the corner and edge coordinates of a curve as its normal coordinates.² Given either normal coordinate representation, it is easy to compute the other representation in $O(n)$ time. Not every vector of non-negative integers gives rise to a normal curve; the sum of corner coordinates within each triangle must be even, and the edge coordinates on the boundary of each triangle must satisfy the triangle inequality.

The total crossing number of a normal curve is the sum of its edge coordinates; this number is also equal to the sum of the curve’s corner coordinates plus the number of arc components of the curve.

Fig. 3

Corner and edge coordinates of a normal curve with two components in a triangulated disk

2.4 Ports, Blocks, Junctions, and Streets

We now introduce the street complex and its components.

The intersections between any normal curve $\gamma$ and the edges of any triangulation $T$ partition $\gamma$ into elementary segments and partition the edges of $T$ into segments called ports. The overlay graph $T\Vert \gamma$ is the cellularly embedded graph whose edges are these elementary segments and ports. Every vertex of $T\Vert \gamma$ is either a vertex of $T$ or an intersection point of $\gamma$ and some edge of $T$. Every face of $T\Vert \gamma$ is a subset of some face $\varDelta$ of $T$. We call each face a junction if it is incident to all three sides of its containing face $\varDelta$, and a block if it is incident to only two sides of $\varDelta$; these are the only two possibilities. Each face of $T$ contains exactly one junction. Each block is bounded either by two elementary segments and two ports, or by one elementary segment and two ports that share a vertex of $T$.

The following useful observation is essentially due to Kneser [40].

Lemma 2.2

A reduced normal curve in a surface triangulation with $n$ triangles has at most ${\lfloor (3n-1)/2 \rfloor } = O(n)$ components.

Proof

Fix a reduced normal curve $\gamma$ on a triangulation $T$ with $n$ triangles and $v$ vertices; obviously, $v\ge 1$. Consider the non-reduced normal curve $\gamma ^{\prime }$ obtained from $\gamma$ by adding $v$ trivial cycles and arcs, one around each vertex of $T$. Orient each component of $\gamma ^{\prime }$ arbitrarily, and consider the faces of $T\Vert \gamma ^{\prime }$ immediately to the left of some nontrivial component $\gamma _i$. Because $\gamma _i$ is nontrivial, none of these faces is a triangular block. If all of these faces were quadrilateral blocks, the component just to the left of $\gamma _i$ would be normal-isotopic to $\gamma _i$, contradicting our assumption that $\gamma$ is reduced. Thus, at least one face on the left side of $\gamma _i$ is a junction; symmetrically, at least one face on the right side of $\gamma _i$ is a junction. Similarly, each trivial component of $\gamma ^{\prime }$ is incident to at least one junction. The overlay graph $T\Vert \gamma ^{\prime }$ has exactly $n$ junctions, each incident to at most three components of $\gamma ^{\prime }$. We conclude that $\gamma ^{\prime }$ has at most $\lfloor (3n-v)/2 \rfloor$ non-trivial components. $\square$

We call a port redundant if it separates two blocks; because each face of $T$ contains exactly one junction, each edge of $T$ contains at most two non-redundant ports. Removing all the redundant ports from the overlay graph $T\Vert \gamma$ merges contiguous sets of blocks into streets. Each street is either a single open disk with exactly two non-redundant ports on its boundary (called the ends of the street), an open annulus bounded by a trivial component of $\gamma$ and a vertex of $T$, or an annulus bounded by two parallel components of $\gamma$. In particular, if $\gamma$ is reduced, all streets are of the first type. For any reduced normal curve $\gamma$, the street complex $S(T, \gamma )$ is the complex of streets and junctions in the overlay $T\Vert \gamma$. Figure 4 shows the street complex of the normal curve in Fig. 3. Streets and junctions are two-dimensional analogues of the product regions and guts of normal surfaces, defined by Jaco et al. [35] and Jaco and Rubinstein [36].

Fig. 4

The street complex of the normal curve in Fig. 3. Unshaded faces are junctions; shaded faces are streets; one street is shaded darker (green) for emphasis

By construction, the components of any reduced normal curve $\gamma$ appear as disjoint paths and cycles in the 1-skeleton of the street complex. Although the complexity of the overlay graph $T\Vert \gamma$ can be arbitrarily large, even when the curve $\gamma$ is connected, the street complex $S(T,\gamma )$ of a reduced normal curve is never more than a constant factor more complex than the original triangulation.

Lemma 2.3

Let $T$ be a surface triangulation with $n$ triangles. For any reduced normal curve $\gamma$ in $T$, the street complex $S(T,\gamma )$ has complexity $O(n)$.

Proof

The triangulation $T$ trivially has at most $3n$ vertices and at most $3n$ edges. Each interior edge of $T$ contains at most two non-redundant ports, so $S(T,\gamma )$ has $O(n)$ interior vertices. Each boundary vertex of $S(T,\gamma )$ is either a boundary vertex of $T$ or an endpoint of one of the $O(n)$ components of $\gamma$, so $S(T,\gamma )$ has $O(n)$ boundary vertices. Each vertex of $S(T,\gamma )$ is either a vertex of $T$ or has degree at most $4$, so $S(T, \gamma )$ has $O(n)$ edges. Each non-redundant port is an end of at most one street, so $S(T, \gamma )$ has $O(n)$ streets. Finally, $S(T, \gamma )$ has exactly $n$ junctions, one in each triangle of $T$. $\square$

Our restriction to reduced curves has two motivations. First, the street complex of any non-reduced curve $\gamma$ contains annular faces, which would complicate our algorithms (but probably not seriously). More importantly, the street complex of a non-reduced curve can have arbitrarily high complexity, since the curve can have arbitrarily many components. Fortunately, as we argue in Sect. 6, it is easy to avoid tracing trivial components or more than one component in the same normal isotopy class.

The crossing sequence of a street is the sequence of edges in the original triangulation $T$ crossed by any path that traverses the street from one end to the other. The crossing length of a street is the length of its crossing sequence, or equivalently, the number of constituent blocks plus one. To simplify our analysis, we regard any port between two junctions, as well as any boundary port incident to a junction, as a street with crossing length 1. The sum of the crossing lengths of the streets in any street complex $S(T,\gamma )$ is the total crossing number of $\gamma$ plus the number of edges in $T$.

Any normal curve $\gamma ^{\prime }$ that is disjoint from $\gamma$ subdivides each port in $S(T, \gamma )$ into smaller ports, each street in $S(T,\gamma )$ into narrower “blocks”, and each junction in $S(T, \gamma )$ into blocks and exactly one smaller junction. Removing all redundant ports from this refinement gives us the refined street complex $S(T, \gamma \cup \gamma ^{\prime })$. Conversely, the intersection of $\gamma ^{\prime }$ with any street or junction in $S(T,\gamma )$ is a set of elementary arcs. There are three types of elementary arcs within any junction, each connecting two of the junction’s three ports. The junction coordinates of $\gamma ^{\prime }$ list the number of elementary arcs of each type in each junction of $S(T,\gamma )$. Similarly, the street coordinates of $\gamma ^{\prime }$ list the number of such arcs within each street of $S(T,\gamma )$. Junction and street coordinates have the same simple linear relationship as corner and edge coordinates; in fact, the normal coordinates of a curve $\gamma$ are just the junction and street coordinates of $\gamma$ in the trivial street complex $S(T,\varnothing )$.

Our tracing strategy must handle normal curves that are partially drawn on the surface; we slightly extend our definitions to include such curves. A normal path is any simple path whose endpoints lie in the interior of edges of $T$ and that can be extended to a normal curve on $\varSigma$. Let $\gamma$ be composed of a normal curve $\gamma ^{\prime }$ and possibly a normal path $\pi$ disjoint from $\gamma ^{\prime }$. A fork is the union of two ports that share one of the endpoints of $\pi$; for most purposes, we can think of a fork as a degenerate junction. Formally, we call a port redundant if it separates two blocks and it is not part of a fork; modified definitions of streets and the street complex follow immediately. The modified street complex $S(T,\gamma )$ clearly still has complexity $O(n)$. See Fig. 5.

Fig. 5

Street complexes for two subcurves of the curve in Fig. 3, with street and junction coordinates. On the left, the arc component is being traced; on the right, the arc has been completely traced, but there is another untraced component. Zero coordinates are omitted for clarity. Compare with Fig. 4

3 Tracing Connected Normal Curves

In this section, we describe our algorithm to trace connected normal curves. Given a triangulation $T$ of an orientable surface $\varSigma$ and the corner and edge coordinates of a connected normal curve $\gamma$, our tracing algorithm computes the street complex $S(T,\gamma )$. We extend our algorithm to reduced curves with multiple components in Sect. 4, and we consider arbitrary normal curves in Sect. 6.

Our algorithm maintains a normal subpath $\pi$ of $\gamma$ that is growing at one end, along with the street complex $S(T, \pi )$ and the junction and street coordinates of the complementary path $\gamma \setminus \pi$. If $\gamma$ is an arc, we trace it from one endpoint to the other. If $\gamma$ is a cycle, we trace it starting at some intersection point with an edge of $T$. In either case, $\pi$ is initially a single crossing point, which splits some edge into two smaller segments, each of which is a street with crossing length $1$. If $\gamma$ is a cycle, these two segments also define a fork. During the rest of the tracing algorithm, existing streets are extended, but no other streets are created or destroyed, except at the very last step if $\gamma$ is a cycle, when two pairs of streets are merged together at the initial fork; see the middle of Fig. 7.

During the rest of the tracing algorithm, no new streets are created and no streets are destroyed (except at the last step when $\gamma$ is a cycle); however, existing streets are extended.

3.1 Steps

In each step of our algorithm, we extend the path $\pi$ through one junction or fork, and then through one street, updating both the street complex and the junction and street coordinates. After each step, we call the streets on either side of the last segment added to $\pi$ the left and right active streets. (Recall that “left” and “right” are defined with respect to a fixed but arbitrary orientation of the surface $\varSigma$.)

Suppose $\pi$ is about to enter a junction. We call the streets adjacent to the junction but not to the endpoint of $\pi$ the left exit and the right exit. Suppose the local junction coordinates are $a$, $b$, and $c$, and the active street coordinates are $l$ and $r$, as shown in Fig. 6. These coordinates satisfy the equation $l+r+1=a+c$, so either $l<a$ or $r<c$. If $l<a$, we extend $\pi$ through the junction and through its left exit into the next junction; the left active street grows to the end of the left exit, and the left exit becomes the new right active street. We call this case a left turn; the symmetric case $r<c$ is called a right turn. In either case, we update the street and junction coordinates as shown in Fig. 6. A similar case analysis applies when $\pi$ crosses a fork; see Fig. 7.

Fig. 6

Tracing a curve through a junction

Fig. 7

Tracing a curve through a fork

The tracing algorithm ends when $\pi$ hits either the boundary of $\varSigma$ or the starting point of the trace. In all other cases, each step makes one active street longer, replaces the other active street, and makes the new active street narrower. All necessary operations for a single step—comparing and updating the junction and street coordinates and updating the street complex—can be performed in $O(1)$ time.

3.2 Phases and Spirals

Unfortunately, executing each step by brute force is not necessarily efficient. To improve the brute-force algorithm, we more coarsely partition the tracing process into phases. Each phase is a maximal sequence of either left turns or right turns. Every step in a phase consisting of left turns extends the same left active street; similarly, every step in a right phase extends the same right active street. In either case, each phase extends a single active street.

During each phase, we maintain a sequence of directed streets and junctions traversed during that phase. If the growing path $\pi$ ever enters a street for the second time, in the same direction, during the same phase, then $\pi$ has entered a spiral. In fact, the reentered street is the first street traversed during the current phase; for the remainder of the phase, $\pi$ repeatedly traverses the same sequence of directed streets and junctions. The length of a spiral is the total number of streets it traverses, counted with multiplicity, and the depth of the spiral is the number of times it repeats the entire sequence of directed streets and junctions. If the spiral has length $\ell$ and traverses $m$ distinct directed streets, its depth is $\lceil \ell /m \rceil -1$. Figure 8 shows a left spiral with length $\ell =16$ and depth $d=3$ through $m=5$ distinct streets, plus the first step of the next phase.

Fig. 8

A left spiral, plus one step of the next phase

Instead of tracing the spiral step by step, we compute the depth of the spiral directly in $O(m)$ time as follows. Let $J_0, J_1, \ldots , J_{m-1}$ be the junction coordinates modified during the first iteration of the spiral. Let $w$ denote the width of the active street, defined as the corresponding street coordinate plus $1$. The depth of the spiral is $d = \min _i \lfloor J_i/w \rfloor$, and the spiral ends at the first junction whose coordinate $J_i$ is smaller than $dw$. Once we compute $d$, we can update the street complex $S(T,\pi )$ and the appropriate street and junction coordinates in $O(m)$ time. In particular, as long as the depth of the spiral is at least $2$, the combinatorial structure of $S(T,\pi )$ (the 1-skeleton and the rotation system encoding its embedding in $\varSigma$) depends only on the last $\ell \text{ mod } m$ steps of the spiral.

The lengths and widths of the streets, as well as junction and street coordinates of the remainder of the curve, can all be updated in $O(m)$ time. The length of the active street increases by $d$ times the total length of the $m$ distinct directed streets in the spiral, plus the total length of the last $\ell \text{ mod } m$ streets; no other street changes length. Each undirected street in the spiral is traversed $d$, $d+1$, $2d$, $2d+1$ or $2d+2$ times, depending on whether the street is traversed in one or both directions, and which of those traversals occur in the last $\ell \text{ mod } m$ steps of the phase. We can compute all such numbers in $O(m)$ time, after which updating the widths of the streets traversed by the spiral is straightforward.

The crude upper bound $m = O(n)$ immediately implies that each phase of our tracing algorithm can be executed in $O(n)$ time. We analyze the number of phases, as a function of the total crossing number of the traced curve, in Sect. 4.

3.3 History

For some applications of our tracing algorithm, it is useful to maintain the history of the street complex, which records the evolution of each street during the algorithm’s execution. We identify each street by a distinct numerical index. For each phase of the tracing algorithm, the history records the tuple $(a;~ \ell ;~ m;~ i_0, i_1, \ldots , i_{m-1})$, where

• $a$ is the index of the street that is active for the entire phase;

• $\ell$ is the number of steps in the phase;

• $m$ is the number of distinct directed streets traversed during the phase; and

• $i_0, i_1, \ldots , i_{m-1}$ are the indices of these $m$ directed streets in the order they are traversed.

If the same street is traversed in both directions during the phase, the index of that street will appear twice in the sequence $i_0, i_1, \ldots , i_{m-1}$.

The resulting history encodes a context-free grammar whose terminals correspond to the edges of $T$ and most of whose productions have the following form, where $d = \lceil l/m \rceil - 1$:

$$\begin{aligned} X_a&\rightarrow X_b\, (X_{i_0}\, X_{i_1}\, \ldots \, X_{i_{m-1}})^d\, X_{i_0}\, X_{i_1}\, \ldots \, X_{i_{(\ell -1)\text{ mod } m}}\\ {\overline{X}}_a&\rightarrow {\overline{X}}_{i_{(\ell -1)\text{ mod } m}} \, \ldots \, {\overline{X}}_{i_1}\, {\overline{X}}_{i_0} ({\overline{X}}_{i_{m-1}} \,\ldots \, {\overline{X}}_{i_1}\, {\overline{X}}_{i_0})^d\, {\overline{X}}_b. \end{aligned}$$

(We refer readers unfamiliar with context-free grammars to Hopcroft et al. [34, Chapter 5], or Sipser [74, Chapter 4].) The language of each non-terminal $X_i$ is a single string, recording the crossing sequence of the street at the end of some phase. In the example above, $X_a$ is the crossing sequence of the active street just after the phase ends; $X_b$ is the crossing sequence of the active street just before the phase begins; and ${\overline{X}}_i$ denotes the reversal of $X_i$. If the same street is traversed in both directions during a phase, we will have ${X_{i_j} = {\overline{X}}_{i_k}}$ for some indices $j\ne k$, so both the forward and reverse productions are necessary; otherwise, the indices $i_j$ are distinct. The grammar also contains terminal productions of the form $X_i \rightarrow e_i$ and ${\overline{X}}_i \rightarrow e_i$ for each edge $e_i$ in the input triangulation. (We can encode signed crossing sequences, which record the direction of each crossing in addition to the crossed edge, by changing these terminal productions to $X_i \rightarrow e_i$ and ${\overline{X}}_i \rightarrow \overline{e}_i$.)

This context-free grammar can be transformed into Chomsky normal form by replacing each production in the form above with $O(m + \log d)$ productions of the form $A\rightarrow B\,C$. Context-free grammars whose language contains a single string are sometimes called straight-line programs [37] or grammar-based codes [38]. Thus, our history data structure is equivalent to the compressed intersection sequence constructed by Schaefer et al. [66, 75]. We analyze the complexity of our history data structure and the resulting compressed intersection sequence in the next section.

4 Analysis

We now bound the running time of our tracing algorithm. In Sect. 4.1, we bound the time required to trace a connected normal curve; we extend our analysis to reduced curves with multiple components in Sect. 4.2 and to the complexity of compressed intersection sequences in Sect. 4.3. Throughout our analysis, we let $N$ denote the current number of streets in the evolving street complex; $N$ is constant if we are tracing a connected normal curve, but for disconnected curves, $N$ increases or decreases by at most $2$ when we start or finish tracing each component. Because we actually trace only reduced curves, Lemma 2.3 implies that $N = \varTheta (n)$ at all times.

Our analysis can be viewed as a generalization of Lamé’s classical analysis of Euclid’s GCD algorithm in terms of Fibonacci numbers [41, 73]. This connection is not a coincidence; when tracing a single cycle on the unique triangulation of the torus with two triangles, our algorithm actually reduces to Euclid’s algorithm. In particular, handling each phase in $O(n)$ time, instead of constant time per step, generalizes the use of division in Euclid’s algorithm instead of repeated subtraction. Euclid’s algorithm is invoked explicitly by the orbit-counting algorithm of Agol et al. [1] and by the compressed pattern-matching algorithms [37, 49, 61] underlying the results of Schaefer et al. [66, 75]. See also related results of Moeckel [50] and Series [71, 72] on encoding (infinite) geodesics in surfaces of constant curvature by continued fractions.

In retrospect, our analysis (at least for connected curves) is nearly identical to Dynnikov and Weist’s analysis of their transmission-relaxation method [16, 19], although the algorithms themselves appear to be quite different. In particular, the potential function $\Phi$ in the proof of Lemma 4.1 closely resembles their definition of the AHT-complexity of a braid (named after Agol, Hass, and Thurston). Dehornoy et al. [16, p. 196] draw a similar analogy between their approach and the fast Euclidean algorithm.

4.1 Abstract Tracing

In each phase of our tracing algorithm, the crossing length of the active street increases by the sum of the crossing lengths of the other traversed streets, counted with appropriate multiplicity. The algorithm AbstractTrace, shown in Fig. 9, abstractly models this growth. For any positive integer $k$, we write $[k]$ to denote the set $\{ 1,2,\ldots ,k \}$.

Fig. 9

Our abstract tracing algorithm

AbstractTrace maintains an array $x[1\ldots N]$ of positive integers, corresponding to the crossing lengths of the streets maintained in our tracing algorithm, along with the index $a$ of the current active street. Each iteration of the outer loop of AbstractTrace models a phase of our tracing algorithm. The inner loops update the crossing length $x[a]$ of the active street as the curve traverses a spiral of length $\ell$ and depth $d$, containing $m$ distinct streets whose indices are in the vector $(i_0, i_1, \ldots , i_{m-1})$. The last street traversed in the current phase becomes the active street for the next phase. For purposes of analysis, we assume that the termination condition for the outer loop and the parameters $\ell$, $m$, and $(i_0, i_1, \ldots , i_{m-1})$ of each iteration are determined

instead of the topology of the input curve.

To analyze AbstractTrace, we derive an upper bound on the number of phases required to reach any fixed values of $x[1\ldots N]$; equivalently, we derive a lower bound on the values $x[1\ldots N]$ for a given number of phases. To minimize the increase in $x[a]$ and therefore maximize the number of phases, we can assume conservatively that $m = 1$ in every phase; equivalently, we can ignore the contribution to the active street’s crossing length from all but the last street in every spiral. (We could also conservatively assume that $\ell =1$ at this point, but it will be useful later to consider larger values of $\ell$). Thus, we consider the simpler algorithm SimpleTrace shown in Fig. 10. The new variable $\delta$ is the number of times the last street in the spiral is traversed; specifically, $\delta =d$ if $\ell /m$ is an integer and $\delta =d+1$ otherwise.The other new variable $\varDelta$ is used only in the analysis. Note that an upper bound on the number of phases of AbstractTrace is implied by a lower bound on the summation of $x_i$’s.

Fig. 10

A simplified tracing algorithm for analysis

Lemma 4.1

At the end of each iteration of SimpleTrace, we have $\varDelta \!\le \! 2\sum _{i=1}^N \lg x[i]$.

Proof

Consider the potential function $\varPhi := 2\sum _{i=1}^N \lg x[i] - \lg x[a].$ Initially we have $\varPhi = 0$. There are two cases to consider, depending on whether $x[a]$ is smaller or larger than $x[i]$ at the start of each iteration of the loop.

• If $x[a] \le x[i]$, then the assignment $x[a] \leftarrow x[a] + \delta \cdot x[i]$ increases $\varPhi$ by at least $\lg (\delta +1)$, and the assignment $a\leftarrow i$ does not decrease $\varPhi$.

• If $x[a] \ge x[i]$, then the assignment $x[a] \leftarrow x[a] + \delta \cdot x[i]$ does not decrease $\varPhi$, and the assignment $a\leftarrow i$ increases $\varPhi$ by at least $\lg (\delta +1)$.

In both cases, $\varPhi$ increases by at least $\lg (\delta +1)$ in each iteration. It immediately follows by induction that $\varDelta \le \varPhi \le 2\sum _{i=1}^N \lg x[i]$ at the end of every iteration. $\square$

Lemma 4.2

AbstractTrace $(N)$ runs for at most $2L = O(N\log X)$ phases, where $L$ is the final value of $\sum _{i=1}^N \lg x[i]$ and $X$ is the final value of $\sum _{i=1}^N x[i]$.

Proof

To maximize the number of phases, we assume that $m=\ell =1$ in every phase. This assumption allows us to simplify the execution to an instance of SIMPLE-TRACE where $\delta =1$ in every phase, and therefore $\varDelta$ is simply the number of phases. Lemma 4.1 implies that the algorithm terminates after at most $2L$ phases. The parameter $L$ is maximized as a function of $N$ and $X$ when $x[i] = X/N$ for all $i$. (Our assumption that $X=\varOmega (n^2)$ implies that $\log (X/N) = \varTheta (\log X)$.) $\square$

The trivial inequality $m\le N$ now implies the following time bound:

Corollary 4.3

AbstractTrace $(N)$ runs in $O(NL) = O(N^2\log X)$ time, where $L$ is the final value of $\sum _{i=1}^N \lg x[i]$ and $X$ is the final value of $\sum _{i=1}^N x[i]$.

Theorem 4.4

Let $T$ be a surface triangulation with $n$ triangles, and let $\gamma$ be a connected normal curve in $T$ with total crossing number $X$. Given the normal coordinates of $\gamma$, we can trace $\gamma$ in $O(n^2\log X)$ time.

There is an interesting tension between the two steps of our analysis. To bound the number of phases in Lemma 4.2, we conservatively assume that each phase traverses only a constant number of streets; however, to bound the total number of steps in Corollary 4.3, we conservatively assume that each phase traverses a constant fraction of the streets. Despite this tension, both bounds are asymptotically tight in the worst case, at least when $X$ is sufficiently large.

Lemma 4.5

AbstractTrace $(N)$ executes $\varOmega (N \log X)$ phases in the worst case.

Proof

Suppose the adversary chooses $i = (a \text{ mod } N) + 1$ and $\delta = 1$ in every phase of SimpleTrace. An easy inductive argument implies that for any integer $r\ge 1$, at the end of $r\cdot (N-1)$ phases we have $x[i] \le 2^r$ for all $i$. Thus, SimpleTrace must perform at least $(N-1)\lg (X/N) = \varOmega (N \log X)$ iterations before $\sum _i x[i] = X$. $\square$

Lemma 4.6

AbstractTrace $(N)$ runs in $\varOmega (N^2 \log X)$ time in the worst case, assuming $X = \varOmega (N^{2+\varepsilon })$ for some $\varepsilon >0$.

Proof

Suppose $N = 2k$ for some integer $k\ge 2$, and in every phase of AbstractTrace, the adversary chooses $\ell = m = k+1$ (and therefore $d=0$) and $(i_0, i_1, \ldots , i_k) = (k+1, k+2, \ldots , 2k, (a \text{ mod } k)+1)$. In other words, the adversary mimics the strategy described in the previous proof in the lower half $x[1\ldots k]$ of the array, but uses the upper half $x[k+1\ldots 2k]$ to add $k$ additional steps to the start of each phase. The values in $x[k+1\ldots 2k]$ never change; at all times, we have $a\le k$ and $x[i] = 1$ for all $i>k$. Thus, the additional steps have little impact on the growth of the sum $\sum _i x[i]$.

A straightforward inductive argument implies that for any integer $r\ge 1$, at the end of $r\cdot (k-1)$ phases, we have $\sum _{i=1}^k x[i] < (2^r-1)k^2 + k < 2^r k^2 - k$ and therefore $\sum _{i=1}^N x[i] < 2^r N^2/4$. Thus, AbstractTrace must execute at least ${(N-1)}\times \lg (4X/N^2) = \varOmega (N \log X)$ phases before $\sum _{i=1}^N x[i] = X$. Each phase requires $\varOmega (N)$ time. $\square$

We leave open the possibility that our analysis is not tight for instances that actually arise from tracing normal curves on triangulated surfaces. We conjecture that Lemma 4.2 is still tight in this context, but that Corollary 4.3 is not.

4.2 Tracing Reduced Curves

Now consider the more general case where $\gamma$ is a reduced curve, possibly with more than one component. (For the applications we describe in Sect. 6, this is the most general case we need to consider.) Our tracing algorithm requires little modification to handle these curves; we simply trace the components one at a time, in arbitrary order. Each component refines the street complex defined by the previous components. Lemma 2.3 immediately implies that the resulting algorithm runs in $O(n^3\log X)$ time, but this time bound can be improved with more careful analysis.

Theorem 4.7

Let $T$ be a surface triangulation with $n$ triangles, and let $\gamma$ be a reduced normal curve in $T$ with total crossing number $X$. Given the normal coordinates of $\gamma$, we can trace all components of $\gamma$ in $O(n^2\log X)$ total time.

Proof

Consider the effect of ending one component and starting another on the vector of crossing lengths modeled by the array $x[1\ldots N]$ in SimpleTrace. When we begin tracing a new cycle component, we split some street into three smaller streets by introducing a fork; one of the three new streets becomes the active street for the first phase of the new component. This update can be modeled in SimpleTrace by adding the following lines:

When we finish tracing a cycle component, we merge the four streets adjacent to the initial fork into two longer streets; see the center of Fig. 7. This update can be modeled in SimpleTrace by adding the following lines:

Similarly, when we begin tracing a new arc component, we split some street (ending on the boundary of $\varSigma$) into two narrower streets. This update can be modeled in SimpleTrace by adding the following lines:

No additional changes are necessary when we end an arc component. Again, for purposes of analysis, we assume that the decision of when to end one component and begin another, whether each new component is an arc or a cycle, and the array elements involved in starting or ending a component are all chosen

instead of being determined by the topology of a curve.

Altogether, ending one component and starting a new one decreases the potential function $\varPhi$ by at most $O(\log X)$. An easy modification of the proof of Lemma 4.1 now implies that after each iteration of SimpleTrace, we have $\varDelta \le 2\sum _{i=1}^N \lg x[i] + O(t\lg X)$, where $t$ is the number of components we have completely traced so far. Lemma 2.2 implies that any reduced normal curve has $O(n)$ components. We conclude that SimpleTrace $(N)$ executes at most $O(N\log X) = O(n\log X)$ phases; each phase trivially requires $O(n)$ time. $\square$

When we trace curves with multiple components, we also record the start and end of each component in the tracing history. We omit the straightforward but tedious details.

4.3 Logarithmic Spiral Cost

Recall from Sect. 3.3 that our history data structure can be transformed into a context-free grammar in Chomsky normal form, also known as a straight-line program, that encodes the crossing sequence of every component of the traced curve $\gamma$. For each phase of the tracing algorithm, this grammar contains $O(m + \log d)$ productions, where $m$ is the number of distinct streets traversed in that phase and $d$ is the depth of that phase’s spiral.

Lemma 4.1 immediately implies that the total size of this grammar is $O(n^2\log X)$ for any connected normal curve. In particular, the sum of all the $O(\log d)$ terms is only $O(n\log X)$; this sum is bounded by the parameter $\varDelta$ maintained in SimpleTrace. The sum of all the $O(m)$ terms is bounded by the running time of the tracing algorithm, which is $O(n^2\log X)$ by Corollary 4.3. The proof of Theorem 4.7 extends this analysis to reduced curves with multiple components.

Theorem 4.8

Let $T$ be a surface triangulation with $n$ triangles, and let $\gamma$ be a reduced normal curve in $T$ with total crossing number $X$. Given the normal coordinates of $\gamma$, we can compute a straight-line program of length $O(n^2\log X)$ that encodes the crossing sequences of every component of $\gamma$, in $O(n^2\log X)$ total time.

Štefankovic [75,  Lemma 3.4.2] (also [66,  Lemma 3.1]) proves that the crossing sequence of any connected normal curve can be compressed into a straight-line program of length $O(n\log X)$, which can be computed in $O(n\log X)$ time; his time and length bounds are smaller than the bounds in Theorem 4.8 by a factor of $O(n)$. However, Štefankovic’s result does not generalize immediately to disconnected curves, at least with the same time and length bounds; the most direct generalization of his algorithm would require advance knowledge of the crossing length of each component.

The geodesic tracing algorithm described in Sect. 7 requires $O(m + \log d)$ time to trace a spiral of depth $d$ through $m$ distinct streets; thus, the same analysis implies that the overall running time of that algorithm is also $O(n^2\log X)$. We defer further details to Sect. 7.

5 Untracing

Several of the problems we consider ask for the normal coordinates of one or more components of the input curve, with respect to the input triangulation. These coordinates can be recovered from the street complex and some additional information, essentially by running the tracing algorithm backward. We emphasize that recovering the normal coordinates of a curve from the street complex alone is impossible; two curves may have combinatorially isomorphic street complexes even if they are not normal isotopic.

5.1 Untracing from History

The simplest method to untrace a curve uses the full history of the street complex, as defined in Sect. 3.3. The normal coordinates of any normal curve $\gamma$ can be recovered from a straight-line program of length $T$ encoding the crossing sequences of $\gamma$’s components, by straightforward dynamic programming, in $O(nT)$ time [27, 66, 75]. Theorem 4.8 immediately implies that we can extract the normal coordinates of any subcurve of $\gamma$ in $O(n^3\log X)$ time from the tracing history. Our untracing algorithm improves this approach by a factor of $O(n)$.

Our untracing algorithm maintains the street coordinates of the already-untraced components in the devolving street complex. Initially, all street coordinates are equal to zero; when the curve is completely untraced, the streets degenerate to edges, and the street coordinates are the required edge coordinates. We can then easily recover the corner coordinates in $O(n)$ time.

Lemma 5.1

Let $T$ be a surface triangulation with $n$ triangles, let $\gamma$ be a reduced normal curve in $T$ with total crossing number $X$, and let $\lambda$ be the union of any subset of components of $\gamma$. Given the street complex $S(T, \gamma )$ and its history, we can compute the normal coordinates of $\lambda$ with respect to $T$ in $O(n^2\log X)$ time.

Proof

Our untracing algorithm maintains an array $st[1\ldots N]$ of street coordinates, initially all equal to zero, and a bit $\phi$ that indicates whether we are currently untracing a component of $\lambda$. We consider the phases stored in the history in reverse order. To undo a phase with parameters $(a; \ell ; m; i_0, i_1, \ldots , i_{m-1})$, we update the street coordinates as follows:

$$\begin{aligned}&{d} \leftarrow \lceil \ell /m \rceil -1\\&\text{ for } \, j\leftarrow 0 \ \text{ to } \, m-1\\&\qquad st[i_j] \leftarrow st[i_ j] + d \cdot (st[a] + \phi )\\&\text{ for } \, j \leftarrow 0 \ \text{ to } \, (\ell -1) \text{ mod } m\\&\qquad st[i_j] \leftarrow st[i_j] + (st[a] + \phi ) \end{aligned}$$

(Compare with the AbstractTrace algorithm in Fig. 9.) Some additional bookkeeping is required at the beginning and end of each component of $\gamma$; we omit the straightforward but tedious details. Note that the street coordinates $st[\mathord {\cdots }]$ do not actually change until we start untracing a component of $\lambda$. When the algorithm ends, the array $st[\mathord {\cdots }]$ contains the edge coordinates of $\lambda$; we can then easily recover the corner coordinates of $\lambda$ in $O(n)$ time.

Since we spend $O(m)$ time untracing each phase, the total time to untrace the entire curve is the same as the time spent tracing the curve, up to small constant factors. The $O(n^2\log X)$ time bound now follows directly from Theorem 4.7. $\square$

5.2 Untracing Without History

Even without the complete tracing history, we can untrace a curve $\gamma$ given only the crossing lengths of every street in street complex $S(T,\gamma )$. In fact, it is not necessary to follow the tracing algorithm backward; we can untrace the components of $\gamma$ in any order, starting each cycle component at any crossing.

Lemma 5.2

Let $T$ be a surface triangulation with $n$ triangles, let $\gamma$ be a reduced normal curve in $T$ with total crossing number $X$, and let $\lambda$ be the union of any subset of components of $\gamma$. Given the street complex $S(T, \gamma )$ and the crossing length of every street, we can compute the normal coordinates of $\lambda$ with respect to $T$ in $O(n^2\log X)$ time.

Proof

Our untracing algorithm maintains the devolving street complex, its associated street and junction coordinates (all initially zero), and an array $x[1.. N]$ storing the crossing lengths of each street. Our algorithm untraces every component of $\gamma \setminus \lambda$ (in arbitrary order), resets all street and junction coordinates to $0$, and then untraces the components of $\lambda$ (again in arbitrary order). When the algorithm terminates, all crossing lengths are equal to $1$, and the street and junction coordinates are just the normal coordinates of $\lambda$.

First consider the untracing process for a single component of $\gamma$. Following the intuition of the tracing algorithm, we maintain a normal subpath $\pi$ that is shrinking from one end toward the other. The last segment of $\pi$ either separates two streets or separates a street and a junction. We can easily remove the last segment of $\pi$ and update the appropriate street coordinates and crossing lengths in $O(1)$ time, by time-reversing the case analysis in Figs. 6 and 7.

To complete the proof, it remains only to prove that we can untrace any spiral of any depth through $m$ distinct streets in $O(m)$ time. The last segment of $\pi$ separates two streets; call the longer of these the active street. The last segment of $\pi$ is a spiral if and only if the active street is incident to itself at the junction where $\pi$ ends; see Figs. 8 and 11. This condition can be tested easily in constant time at each step.

Without loss of generality, suppose the active street lies to the left of the last segment of $\pi$, so we are untracing a left spiral, as shown in Fig. 11. The $m$ directed streets and junctions traversed by the spiral are all incident to the right side of the active street. Thus, we can recover the number $m$ and indices $i_0, i_1, \ldots , i_{m-1}$ of the relevant streets in $O(m)$ time by traversing $\pi$ backward until some edge is incident on the left. The depth of the spiral is

$$\begin{aligned} d := \left\lfloor {\frac{{x[a]}}{{\sum \nolimits _{{j = 0}}^{{m - 1}} {x[i_{j} ]} }}} \right\rfloor . \end{aligned}$$

To untrace $d$ complete turns of the spiral, we add $d\cdot (st[a]+1)$ to the $m$ relevant street and junction coordinates (where $st[a]$ is the street coordinate of the active street) and subtract $d\cdot \sum _{j=0}^{m-1} x[i_j]$ from the active crossing length $x[a]$.We then untrace the last $\ell \text{ mod } m$ steps of the spiral by brute force in constant time each. Although computing the length $\ell$ of the spiral is straightforward, it is not actually necessary. The total time to untrace the entire spiral is $O(m)$, as required. $\square$

Fig. 11

After tracing a spiral, the active street is incident to itself at the terminal junction

5.3 Abstract Untracing

We can also analyze our untracing algorithm directly by considering the growth of the street coordinates, just as we analyzed the forward tracing algorithm by the evolution of crossing lengths. Moreover, because our tracing and untracing algorithms have the same running time (up to constant factors), we obtain a new analysis of our tracing algorithm. Although our backward analysis leads to the same asymptotic time bound $O(n^2\log X)$, we obtain more refined bounds for connected normal curves in terms of the bit-complexity of the normal coordinates. As in Sect. 4, $N=\varTheta (n)$ denotes the number of streets in the current street complex.

First, suppose we are untracing a connected normal curve. Again, we ignore the actual topology of the curve and consider instead the abstract untracing algorithm shown in Fig. 12. This algorithm includes the instructions described in the proof of Lemma 5.1 to update the street coordinates, with $\phi$ fixed to $1$ for purposes of analysis.

Fig. 12

Our abstract untracing algorithm

The values in the array $st[1.. N]$ correspond to the street coordinates of the $N$ streets. At the end of each backward phase, the current $a$ctive street becomes one of the streets traversed (and therefore widened) in the next phase; we re-index the streets in each spiral so that $i_0$ is always the index of the previous active street. As in the forward analysis, we conservatively assume that the parameters of each phase and the termination condition for the main loop are determined

instead of by the topology or tracing history of the curve.

As in the forward analysis, to maximize the number of phases, we can assume conservatively that $m = 1$ in every phase, which simplifies the abstract algorithm to the form shown in Fig. 13. To simplify the algorithm further, we work with an array $w[1,..\,N]$ of street widths, where $w[i] = st[i] + 1$ for all $i$. Again, we introduce a new variable $\varDelta$ strictly for purposes of analysis. Except for variable names, SimpleUntrace is identical to our earlier algorithm SimpleTrace, so our earlier analysis applies immediately.

Fig. 13

Our simplified abstract untracing algorithm; compare with Fig. 10

Lemma 5.3

AbstractUntrace $(N)$ runs for at most $2W = O(N\log X)$ phases and $O(nW) = O(n^2\log X)$ total time, where $W$ is the final value of $\sum _{i=1}^N \lg w[i]$ and $X$ is the final value of $\sum _{i=1}^N w[i]$.

Again, both bounds in Lemma 5.3 are tight in the worst case.

Ignoring lower-order terms, the parameter $W$ is the number of bits needed to store the edge coordinates of the traced curve $\gamma$; Schaefer et al. [63, 66, 75] call $W$ the normal complexity of $\gamma$. Recall from Sect. 4.1 that $L$ is the total number of bits needed to store the crossing lengths in the street complex $S(T, \gamma )$. Both $W$ and $L$ are between $\varOmega (n+\log X)$ and $O(n \log X)$, which implies the crude bounds $W = O(nL)$ and $L = O(nW)$. In fact, these crude bounds are tight in the worst case, even for actual curves; we leave the proof as an amusing exercise for the reader.

Corollary 5.4

Let $T$ be a surface triangulation with $n$ triangles, let $\gamma$ be a connected normal curve in $T$. Given the normal coordinates of $\gamma$, we can trace $\gamma$ in ${O(n\cdot \min \{ L, W \})}$ time, where $W$ is the total bit-length of the normal coordinates of $\gamma$, and $L$ is the total bit-length of all crossing lengths in the resulting street complex $S(T,\gamma )$.

The backward analysis can be extended to disconnected reduced curves, exactly as in Sect. 4. However, since the resulting time bound does not improve our earlier analysis, we omit further details.

6 Normal Coordinate Algorithms

In this section, we describe efficient algorithms for several problems involving normal curves represented by their normal coordinates. For each of our algorithms, the input consists of a surface triangulation $T$ with $n$ triangles and the edge and corner coordinates of either one or two normal curves with total crossing length at most $X$. All of the problems we consider were previously solved by Schaefer et al. [63, 66, 75]. Table 1 summarizes our results and the best previous result for each problem. We list only the time bounds explicitly claimed by Schaefer et al.; however, it seems likely that more of these bounds can be improved using Štefankovic’s techniques [75].

Table 1 Summary of our normal-coordinate algorithms

6.1 Connectedness

Theorem 6.1

Let $T$ be a surface triangulation with $n$ triangles, and let $\gamma$ be a normal curve in $T$ with total crossing length $X$, represented by its normal coordinates. We can determine whether $\gamma$ is connected in $O(n^2\log X)$ time.

Proof

The input curve $\gamma$ is connected if and only if, after tracing an arbitrary component of $\gamma$, every street coordinate in the resulting street complex is equal to zero. Because we need only trace one component of $\gamma$, the result now follows immediately from Theorem 4.4.

Štefankovic described an algorithm to test whether a normal curve $\gamma$ is connected in $O(W) = O(n\log X)$ time, where $W$ is the bit-complexity of $\gamma$’s normal coordinates [75, Observation 3.3.1]. Our backward analysis in Sect. 5.3 implies that our algorithm actually runs in $O(nW^{\prime })$ time, where $W^{\prime }$ is the bit-complexity of the normal coordinates of just the traced component of $\gamma$.

6.2 One Component

Theorem 6.2

Let $T$ be a surface triangulation with $n$ triangles, and let $\gamma$ be a normal curve in $T$ with total crossing length $X$, represented by its normal coordinates; and let $x$ be any intersection point of $\gamma$ with an edge of $T$, represented by its index along that edge. We can compute the normal coordinates of the component of $\gamma$ containing $x$ in $O(n^2\log X)$ time.

Proof

Suppose $x$ is the $i$th crossing point along some edge $e$; let $\gamma (e)$ denote the number of crossings between $\gamma$ and $e$; and let $\gamma _x$ denote the component of $\gamma$ containing $x$. We trace $\gamma _x$ starting at $x$, by splitting $e$ into two smaller edges with street coordinates $i-1$ and $\gamma (e) - i$; these two new edges and $e$ define a fork. If $\gamma _x$ is a cycle, the tracing algorithm eventually reaches $x$ again. Otherwise, when the tracing algorithm reaches an endpoint $y$ of $\gamma _x$, we continue the trace from $x$ to the other endpoint, as if starting a new component of $\gamma$. (Alternatively, we can simply start over and trace $\gamma _x$ from $y$ to the other endpoint.) In all cases, tracing $\gamma _x$ requires $O(n^2\log X)$ time. Finally, to recover the normal coordinates of $\gamma _x$, we reset all the street and junction coordinates in $S(T,\gamma _x)$ to zero and then untrace $\gamma _x$, using either Lemmas 5.1 or 5.2. $\square$

Štefankovic described an algorithm for this problem that runs in time $O(nW) = O(n^2\log X)$; see the proof of Lemma 3.3.3 in his thesis [75]. Like the previous theorem, more careful analysis implies that our algorithm runs in $O(nW^{\prime })$ time, where $W^{\prime }$ is the bit-complexity of the normal coordinates of $\gamma _x$.

6.3 Forward and Reverse Indexing

Let $x$ be a point of intersection between $\gamma$ with an edge $e$ of the surface triangulation. The edge-index of $x$ is the position of $x$ in the sequence of intersection points along $e$ (directed arbitrarily). Similarly, if $x$ lies on an arc component of $\gamma$, the arc-index of $x$ is the position of $x$ in the sequence of intersection points along that arc (again, directed arbitrarily). Schaefer et al. [63] describe an algorithm to compute the arc-index of an intersection point from its edge-index in time polynomial in $n\log X$. We can more efficiently transform either index into the other using our tracing and untracing algorithms.

Theorem 6.3

Let $T$ be a surface triangulation with $n$ triangles; let $\gamma$ be a normal arc in $T$ with total crossing length $X$, represented by its normal coordinates; and let $x$ be any intersection point of $\gamma$ with an edge $e$ of $T$, represented by its edge-index. We can compute the arc-index of $x$ in $O(n^2\log X)$ time.

Proof

We trace $\gamma$ against its chosen indexing direction, starting at $x$. As we trace $\gamma$, we maintain the crossing lengths of all streets in the evolving street complex. Also, whenever we traverse a street, we add its crossing length to a running counter. When the trace reaches the boundary of the surface, the counter contains the arc-index of $x$.

Theorem 6.4

Let $T$ be a surface triangulation with $n$ triangles; let $\gamma$ be a normal arc in $T$ with total crossing length $X$, represented by its normal coordinates; and let $x$ be any intersection point of $\gamma$ with an edge of $T$, represented by its arc-index. We can compute the edge of $T$ containing $x$ and the index of $x$ along that edge in $O(n^2\log X)$ time.

Proof

We trace $\gamma$ along its chosen indexing direction, starting at one boundary point, maintaining the crossing lengths of all streets. Whenever the tracing algorithm traverses a street, we add its crossing length to a running counter. When the counter reaches the curve-index of $x$, we stop the tracing algorithm and add a fork to the street complex at the point $x$. Note that $x$ may lie in the interior of the last street traversed by the trace. We then untrace the traced subpath of $\gamma$, again starting at the boundary endpoint and untracing toward $x$. When the untracing algorithm reaches $x$, the desired edge-index is one of the street coordinates of the fork. $\square$

6.4 Normal Isotopy Classes

Theorem 6.5

Let $T$ be a surface triangulation with $n$ triangles, and let $\gamma$ be a normal curve in $T$ with total crossing length $X$, represented by its normal coordinates. We can compute the number of normal isotopy classes of components of $\gamma$ and the number of components in each normal isotopy class in $O(n^2\log X)$ time.

Proof

We begin by counting and deleting the trivial components of $\gamma$. Each trivial component is a cycle that separates an interior vertex $v$ form the other vertices; the number of such cycles is just the minimum of the corner coordinates incident to $v$. Thus, we can easily count trivial cycles and delete them from $\gamma$, by reducing the appropriate normal coordinates, in $O(n)$ time.

Next, we repeatedly trace one component of $\gamma$ and then count and remove all other components in the same normal isotopy class, as follows. Suppose we have already traced components $\gamma _1, \ldots , \gamma _{i-1}$. Let $\hat{\gamma }_{<i}$ denote the reduced normal curve $\gamma _1 \cup \cdots \cup \gamma _{i-1}$, and let $\gamma _{\ge i}$ denote the union of all components of $\gamma$ that are not normal-isotopic to any component of $\hat{\gamma }_{<i}$. In particular, we have $\hat{\gamma }_{<1} = \varnothing$ and $\gamma _{\ge 1} = \gamma$. By assumption, we have computed the street complex $S(T, \hat{\gamma }_{<i})$ as well as the street and junction coordinates of $\gamma _{\ge i}$. Let $x$ be the leftmost intersection point between $\gamma _{\ge i}$ and some non-redundant port $p$ in $S(T, \hat{\gamma }_{<i})$, and let $\gamma _i$ denote the component of $\gamma _{\ge i}$ that contains $x$. We trace $\gamma _i$ through $S(T, \hat{\gamma }_{<i})$ to produce the street complex $S(T, \hat{\gamma }_{<(i+1)})$, along with the street and junction coordinates of $\gamma _{\ge i} \setminus \gamma _i$. The number of other components of $\gamma$ that are normal isotopic to $\gamma _i$ is the minimum of the junction coordinates just to the right of $\gamma _i$ in the new street complex $S(T, \hat{\gamma }_{<(i+1)})$. Thus, we can easily count these components and reduce the appropriate street and junction coordinates in $O(n)$ time, thereby computing the street and junction coordinates of $\gamma _{\ge (i+1)}$.

The total time spent tracing all components $\gamma _i$ is $O(n^2\log X)$, by Theorem 4.7. Lemma 2.1 implies that there are at most $O(n)$ normal-isotopy classes of components in $\gamma$, so the total time spent counting and removing parallel components of $\gamma$ is only $O(n^2)$. $\square$

The output of our algorithm is the street complex $S(T, \hat{\gamma })$, where $\hat{\gamma }$ is the reduced normal curve consisting of all traced components of $\gamma$. Each normal isotopy class in $\gamma$ appears as a single cycle or arc in $\hat{\gamma }$, and thus is represented by a simple walk or cycle in the 1-skeleton of $S(T, \hat{\gamma })$. Štefankovic described an algorithm to count normal isotopy classes in $O(n^3\log ^2 X)$ time [75, Lemma 3.3.3]; his algorithm actually computes the normal coordinates of one component in each class. We can compute the same output representation by independently untracing each component of $\hat{\gamma }$, using either Lemmas  5.1 or 5.2. Lemma 2.2 implies that the total time to untrace all components is $O(n^3\log X)$, which is still slightly faster than Štefankovic’s algorithm.

Corollary 6.6

Let $T$ be a surface triangulation with $n$ triangles, and let $\gamma$ be a normal curve in $T$ with total crossing length $X$, represented by its normal coordinates. We can compute the normal coordinates of each normal-isotopy class of components of $\gamma$ in $O(n^3\log X)$ time.

Theorem 6.5 also implies immediately that we can compute the number of components of a given normal curve in $O(n^2\log X)$. Štefankovic described an algorithm that solves this problem in $O(n\log X)$ time [75, Observation 3.3.1].

Corollary 6.7

Let $T$ be a surface triangulation with $n$ triangles, and let $\gamma$ be a normal curve in $T$ with total crossing length $X$, represented by its normal coordinates. We can compute the number of components of $\gamma$ in $O(n^2\log X)$ time.

6.5 Isotopy Classes

Recall that two properly embedded cycles or arcs are isotopic if one can be continuously deformed to the other, keeping the curve properly embedded at all times. Our algorithm for counting isotopy classes uses the following classical characterizations of contractible and isotopic cycles and arcs. Parts (a) and (b) were proved by Epstein [22, Theorem 1.7 and Lemma 2.4]; parts (c) and (d) follow easily by considering the surface obtained by gluing two copies of $\varSigma$ along corresponding boundary points.

Lemma 6.8

Let $\varSigma$ be an arbitrary orientable 2-manifold, possibly with boundary.

• (a) A simple cycle in $\varSigma$ is contractible if and only if it is the boundary of a disk in $\varSigma$.

• (b) Two disjoint simple non-contractible cycles in $\varSigma$ are isotopic if and only if they are the boundary of an annulus in $\varSigma$.

• (c) A simple arc in $\varSigma$ is contractible if and only if there is a disk in $\varSigma$ whose boundary consists of that arc and a segment of $\partial \!\varSigma$.

• (d) Two disjoint simple arcs in a surface $\varSigma$ are isotopic if and only if there is a disk in $\varSigma$ whose boundary consists of those two arcs and two segments of $\partial \!\varSigma$.

Theorem 6.9

Let $T$ be a surface triangulation with $n$ triangles, and let $\gamma$ be a normal curve in $T$ with total crossing length $X$, represented by its normal coordinates. We can compute the number of isotopy classes of components of $\gamma$ and the number of components in each isotopy class in $O(n^2\log X)$ time.

Proof

We begin by computing the number and multiplicities of the normal isotopy classes of components of $\gamma$ in $O(n^2\log X)$ time, as described in the proof of Theorem 6.5. Let $\hat{\gamma }$ be the reduced curve containing one component of $\gamma$ in each non-trivial normal isotopy class, and let $\gamma _1, \gamma _2, \ldots$ denote the components of $\hat{\gamma }$. The rest of the algorithm requires only $O(n)$ time.

Next we compute the Euler characteristic of the components of $\varSigma \setminus \hat{\gamma }$, where $\varSigma$ is the surface triangulated by $T$; to avoid confusion, we will refer to the components of $\varSigma \setminus \hat{\gamma }$ as pieces. Because each curve $\gamma _i$ is a simple arc or cycle in the 1-skeleton of the street complex $S(T, \hat{\gamma })$, we can compute the Euler characteristic of every piece in $O(n)$ time using a depth-first search in the dual graph of $S(T, \hat{\gamma })$ [23]. In particular, we can identify which pieces are disks ($\chi =1$) and annuli ($\chi =0$).

We can now cluster the components of $\hat{\gamma }$ into isotopy classes as follows. Call a cycle or arc $\gamma _i$ obviously contractible if it is the only component of $\hat{\gamma }$ on the boundary of a disk piece. Call two arcs $\gamma _i$ and $\gamma _j$ obviously isotopic if they are the only components of $\hat{\gamma }$ on the boundary of a disk piece. Finally, call two cycles $\gamma _i$ and $\gamma _j$ obviously isotopic if they comprise the boundary of an annulus piece. Let $G$ be the graph whose nodes are the components of $\hat{\gamma }$ and whose edges connect obviously isotopic components. This graph has $O(n)$ nodes and $O(n)$ edges, and we can easily construct it in $O(n)$ time.

Lemma 6.8 implies by induction that an arc or cycle in $\hat{\gamma }$ is contractible if and only if it lies in the same component of $G$ as an obviously contractible arc or cycle, and two arcs or cycles in $\hat{\gamma }$ are isotopic if and only if they lie in the same component of $G$. Thus, we can easily cluster the components of $\hat{\gamma }$ into isotopy classes in $O(n)$ time. We can also compute the number of components of $\gamma$ in each isotopy class in $O(n)$ time by adding the sizes of the appropriate normal-isotopy classes. $\square$

Schaefer et al. [63] describe an algorithm to compute isotopy classes of normal curves in time polynomial in $n\log X$.³ Their algorithm actually computes the normal coordinates of one component in each isotopy class. We can compute these normal coordinates by untracing one component in each isotopy class; Lemma 2.1 implies that there are at most $O(g+b)$ classes to consider.

Corollary 6.10

Let $T$ be a surface triangulation with $n$ triangles, and let $\gamma$ be a normal curve in $T$ with total crossing length $X$, represented by its normal coordinates. We can compute the normal coordinates of each isotopy class of components of $\gamma$ in $O((g+b)n^2\log X)$ time.

6.6 Algebraic Intersection Numbers

Finally, suppose $\gamma ^+$ and $\delta ^+$ are directed curves that intersect only transversely and only at a finite number of points. We call an intersection point in $\gamma \cap \delta$ a positive (resp. negative) crossing if $\gamma ^+$ crosses $\delta ^+$ from left to right (resp. from right to left) at that point; see Fig. 14. The algebraic intersection number $\hat{\iota }(\gamma ^+,\delta ^+)$ is the number of positive crossings minus the number of negative crossings. We easily observe that $\hat{\iota }(\gamma ^+,\delta ^+) = -\hat{\iota }(\delta ^+, \gamma ^+) = -\hat{\iota }(\gamma ^-, \delta ^+)$, where $\gamma ^-$ is the reversal of $\gamma ^+\!$. Algebraic intersection numbers are invariant under isotopy.⁴

Fig. 14

Positive and negative crossings

The signed edge coordinates of a directed normal curve $\gamma ^+$ are a list of the algebraic intersection numbers of $\gamma ^+$ with each (arbitrarily oriented) edge in the triangulation. Similarly, the signed corner coordinates of $\gamma ^+$ record, for each corner of the triangulation, the number of counterclockwise elementary segments in that corner, minus the number of clockwise segments. Reversing the direction of a normal curve negates all of its signed normal coordinates.

Given the (unsigned) normal coordinates of an undirected normal arc or cycle $\gamma$, we can compute the signed normal coordinates of some orientation $\gamma ^+$ of $\gamma$ as follows. We begin by tracing $\gamma$ in the chosen direction. We give each street in the resulting street complex $S(T, \gamma )$ an arbitrary reference direction. Then we untrace $\gamma$, maintaining signed street coordinates. Thus, in each untracing step, we either add or subtract the active street coordinates, depending on whether the directions of the active streets on either side of $\gamma$ agree or disagree. The additional bookkeeping increases the running time of the untracing algorithm by only a small constant factor. When the untracing algorithm ends, we have the signed edge coordinates of $\gamma ^+$; computing the signed corner coordinates in $O(n)$ additional time is straightforward.

Corollary 6.11

Let $T$ be a surface triangulation with $n$ triangles, and let $\gamma$ be a connected normal curve in $T$ with total crossing length $X$, represented by its unsigned normal coordinates. We can compute the signed normal coordinates of some orientation of $\gamma$ in $O(n^2\log X)$ time.

Signed normal coordinates do not determine a unique curve up to normal isotopy; nevertheless, given the signed normal coordinates of $\gamma ^+$ and $\delta ^+$, we can compute $\hat{\imath }(\gamma ^+,\delta ^+)$ in $O(n)$ time by choosing an appropriate drawing of the two curves [63]. For each edge of the triangulation, we move all intersections with $\gamma ^+$ close to one of the endpoints, chosen arbitrarily, and all intersections with $\delta ^+$ close to the other endpoint, and we then draw every elementary segment as a straight line segment, as shown in Fig. 15. Then it is easy to compute the number of positive and negative crossings within each triangle in constant time, by multiplying at most six pairs of signed corner coordinates.

Fig. 15

Intersection patterns of two normal curves within a single triangle

The algebraic intersection number of two undirected normal curves $\gamma$ and $\delta$ is well-defined only if both curves are connected, and then only up to a sign change. Formally, we define $\hat{\iota }(\gamma ,\delta ) = \mathopen | \hat{\iota }(\gamma ^+,\delta ^+) \mathclose |$, where the directions of $\gamma ^+$ and $\delta ^+$ are chosen arbitrarily.

Corollary 6.12

Let $T$ be a surface triangulation with $n$ triangles, and let $\gamma$ and $\delta$ be connected normal curves in $T$ with total crossing length $X$, represented by their normal coordinates. We can compute the algebraic intersection number $\hat{\iota }(\gamma ,\delta )$ in $O(n^2\log X)$ time.

Štefankovic described algorithms to compute signed normal coordinates and algebraic intersection numbers in $O(n\log X)$ time [75, Observation 3.6.1], which is a factor of $O(n)$ faster than our algorithms.

7 Tracing Geodesics

Finally, we extend our tracing algorithm to simple geodesic paths on piecewise-linear triangulated surfaces. The input to our algorithm is a piecewise-linear surface $\varSigma$ (specified by triangles and gluing rules), along with a starting point $p$ and a direction vector $v$ in the local coordinate system of some face of $\varSigma$ that contains $p$. As an example application, we sketch an algorithm to trace the geodesic path $\gamma$ that starts at $p$ in direction $v$ up to its first point of self-intersection. However, we can easily impose other stopping conditions, such as an upper bound on Euclidean length or the number of edge crossings.

7.1 Background

Before describing our tracing algorithm, we recall some standard definitions for piecewise-linear surfaces and geodesics.

A piecewise-linear surface is a 2-manifold, possibly with boundary, constructed from a finite number of closed Euclidean polygons by identifying pairs of equal-length edges. The interiors of the constituent polygons are called faces of the surface; without loss of generality, we assume that all faces are triangles. The vertices and edges of the surface are the equivalence classes of vertices and edges of the polygons, respectively. One of the simplest examples of a piecewise-linear surface is the boundary of a convex polyhedron in $\mathbb R ^3$; however, we do not assume that our input surfaces are embedded polyhedra. Indeed, most piecewise-linear surfaces cannot be embedded in any Euclidean space so that every face is flat; consider, for example, the flat torus obtained by identifying opposite sides of the unit square.⁵ Our algorithms assume only that the surface is orientable and that each face has its own local coordinate system; affine transformations between the local coordinate systems of neighboring faces can be derived from the gluing rules.

A path $\gamma :[0,1]\rightarrow \varSigma$ is geodesic if it is locally as short as possible; for any real $t\in [0,1]$, and for any sufficiently small $\varepsilon >0$, the restriction of $\gamma$ to the interval $[0,1]\cap [t-\varepsilon ,t+\varepsilon ]$ is a shortest path. If $\gamma$ is a geodesic in a piecewise-linear surface $\varSigma$, any subpath of $\gamma$ that lies entirely within a face of $\varSigma$ is a straight line segment. Similarly, a subpath of $\gamma$ that crosses an edge of $\varSigma$ from one face $A$ to another face $B$ is a line segment in the polygon obtained by unfolding $A$ and $B$ into a common planar coordinate system [17, 47]. A geodesic is simple if it does not self-intersect. We emphasize that a simple geodesic may cross each face of a piecewise-linear surface arbitrarily many times, or even infinitely many times; again, consider the flat torus. Every simple geodesic of finite length is also a normal path.

7.2 Brute-Force Tracing

To simplify our exposition, we assume that both the surface $\varSigma$ and the direction vector $v$ are generic; thus, the geodesic $\gamma$ does not intersect any vertex of $\varSigma$ but does eventually intersect itself. ⁶ We emphasize that even for generic inputs, the total crossing number of $\gamma$ is not bounded a priori by any function of $n$.

Any simple geodesic path $\gamma$ that starts and ends on edges of the triangulation is a normal path. Thus, the street complex of $\gamma$ is well-defined and has complexity $O(n)$ by Lemma 2.3. Moreover, each of the $O(n)$ faces of the street complex is isometric to a convex polygon with at most six sides; in particular, every street is either a triangle or a convex quadrilateral. (The street complex may have $\varOmega (n)$ vertices on the boundary of a single street, but at most four are actually corners of the quadrilateral that corresponds to the street.)

Although we do not know the normal coordinates of $\gamma$ in advance, we can still easily decide in constant time at each step of our tracing algorithm whether a geodesic $\gamma$ entering a junction leaves through its left exit, leaves through its right exit, or hits an earlier segment of $\gamma$. Geometrically, this decision is equivalent to a ray-shooting query in a convex polygon with at most six sides. Thus, we can easily adapt the brute force tracing algorithm described in Sect. 3.1 to the geodesic setting. However, to achieve a running time of $O(n^2\log X)$, we require a new algorithm to efficiently compute the depth of a geodesic spiral. We develop such an algorithm in the next two subsections.

7.3 Annular Ray Shooting

Computing spiral depth eventually reduces to the following annular ray shooting problem, which may be of independent interest: Given a ray $\rho$ on a piecewise-linear annulus $\fancyscript{A}$, how many times does $\rho$ wrap around $\fancyscript{A}$ before hitting the boundary? More formally, suppose we are given a triangulated simple polygon $P$ in the plane, with two edges $e_0$ and $e_1$ of equal length, and a ray $\rho$ that starts on $e_0$ and points into $P$. Identifying the edges $e_0$ and $e_1$ transforms $P$ into the annulus $\fancyscript{A}$. Equivalently, $e_0$ and $e_1$ are portals; when the ray exits $P$ at any point on $e_1$, it immediately reenters $P$ through the corresponding point on $e_0$ at the same incidence angle [21, 53, 79–81]. An annular ray shooting query asks for the number of times that $\rho$ crosses the portal(s) before hitting a non-portal edge of $P$.

For the rest of this section, let $n$ denote the number of vertices in $P$, and let $t^*$ denote the integer output of the annular ray-shooting query. We explicitly consider only generic polygons $P$; in particular, we assume that $e_0$ and $e_1$ are not parallel. (Adapting our algorithm to polygons with parallel portals is straightforward.) Without loss of generality, we assume that the edge $e_0$ is vertical, the polygon $P$ lies locally to the right of $e_0$, and that the transformation $\tau$ is a counterclockwise rotation by some angle $0 < \theta < \pi$. This assumption immediately implies that $t^* \le \lceil \pi /\theta \rceil$; however, we emphasize that $t^*$ is not bounded a priori by any function of $n$.

The naïve solution to this problem requires $O(n + t^*\log n)$ time: Preprocess $P$ for standard ray-shooting queries in $O(n)$ time, and then perform $t^*+1$ queries, each in $O(\log n)$ time [32]. Our algorithm improves this naïve bound exponentially.

Lemma 7.1

The annular ray-shooting problem can be solved in $O(n + \log t^*)$ time and space, where $n$ is the number of edges in $P$ and $t^*$ is the output value.

Proof

Assume that $t^* \ge 10$, since otherwise, the naïve algorithm already satisfies the desired time bound. (In fact, we could safely assume that $t^* \ge n/\log n$.) This assumption implies that $\theta \le \pi /11$.

First we observe that we need only consider polygons $P$ with a special geometric structure. Following Chazelle and Guibas [13], we define the hourglass $H$ of $P$ as the union of all shortest paths from points in $e_0$ to points in $e_1$; see Fig. 16. The hourglass is bounded by the shortest paths in $P$ between corresponding endpoints of the two portals; we call these shortest paths $A$ (“above”) and $B$ (“below”). Our assumption that $t^*\ge 1$ implies that $\rho$ reaches $e_1$ without intersecting either $A$ or $B$; thus, $A$ and $B$ are disjoint convex chains [3, 78]. In particular, $H$ is contained in the convex hull of the portals $e_0$ and $e_1$. Because $P$ is already triangulated, it is straightforward to construct its hourglass in $O(n)$ time [12, 42, 78]. Any line segment from $e_0$ to $e_1$ intersects a non-portal edge of $P$ if and only if it intersects a non-portal edge of $H$; it follows that annular ray-shooting queries in $P$ and in $H$, with the same ray, yield exactly the same answer. Thus, it suffices to describe an algorithm to answer annular ray-shooting queries in $H$.

Fig. 16

The hourglass between the portals of a polygon

Our algorithm considers, but does not actually construct, finite portions of the universal cover of the annulus determined by $H$. Let $\tau :\mathbb R ^2\rightarrow \mathbb R ^2$ denote the unique rigid motion that maps $e_0$ onto $e_1$; our genericity assumption implies that $\tau$ is a rotation. For each integer $i>0$, let $\tau ^i = \tau \circ \tau ^{i-1}$, and let $e_i = \tau (e_{i-1}) = \tau ^i(e_0)$. Similarly, let $H_0 = H$, and for any integer $i>0$, let $H_i = \tau (H_{i-1}) = \tau ^i(H_0)$; by construction, the segment $e_i$ is an edge of both $H_{i-1}$ and $H_i$. Finally, for any non-negative integer $t$, let $H_{<t}$ denote the topological disk obtained from the polygons $H_0, H_1, \ldots , H_{t-1}$ by identifying corresponding edges $e_j$ in $H_{j-1}$ and $H_j$, for all $j$ between $1$ and $t-1$. The disk $H_{<k}$ grows to the right and curves upward as the parameter $k$ increases. (The disk $H_{<k}$ is actually a simple polygon for all $k \le \lfloor 2\pi /\theta \rfloor$, but we never use this fact.)

The output $t^*$ of the annular ray-shooting query is the maximum of all integers $t$ such that $\rho$ intersects edges $e_0$ and $e_t$ but no other edge of $H_{<t}$. Our algorithm finds $t^*$ using a standard unbounded search strategy due to Bentley and Yao [4]. We emphasize that our algorithm does not actually construct $H_{<t^*}$ or any significant portion thereof, but instead computes on the fly only the vertices and edges required for the search.

Let $a_0, a_1, \ldots , a_\alpha$ denote the vertices of $A$ in order from left to right, and let $b_0, b_1, \ldots , b_\beta$ denote the vertices of $B$ in order from left to right. Thus $e_0 = a_0b_0$ and $e_1 = a_\alpha b_\beta$; we also have $\alpha +\beta \le n+2$. For any indices $i$ and $j$, let $a_{i,j} = \tau ^j(a_i)$ denote the vertex of $H_j$ corresponding to $a_i$, and let $b_{i,j} = \tau ^j(b_i)$ denote the vertex of $H_j$ corresponding to $b_i$. In particular, we have $a_{0,j} = a_{\alpha ,j-1}$ and $b_{0,j} = b_{\beta ,j-1}$ for every positive integer $j$.

We define two families of segments that connect adjacent copies of $A$ and $B$. For any index $j$, let $c_j$ (“the $j$th ceiling”) denote the lower common tangent of $A_{j-1}$ and $A_j$. By symmetry, there are indices $l$ and $r$ such that $c_j = a_{l,j-1} a_{r,j}$ for every index $j$. Similarly, let $f_j$ (“the $j$th floor”) denote the upper common tangent of $B_{j-1}$ and $B_j$. By symmetry, there are indices $p$ and $q$ such that $f_j = b_{p,j-1} b_{q,j}$ for every index $j$. Because $\tau$ is a counterclockwise rotation, we have $r\le l$ and $p\le q$; thus, segments $c_j$ and $c_{j+1}$ are interior-disjoint, but segments $f_j$ and $f_{j+1}$ intersect inside $H_j$. See Fig. 17.

Our algorithm applies a standard unbounded search strategy of Bentley and Yao [4] to find the smallest positive value of $t$ that satisfies at least one of the following conditions:

• (A) Segment $c_t$ contains a point below $\rho$.

• (A$^{\prime }$) The angle of $c_t$ (relative to the positive $x$-axis) is larger than the angle of $\rho$.

• (B) Segment $f_t$ contains a point above $\rho$.

By definition of $t^*$, the ray $\rho$ intersects either $A_{t^*}$ or $B_{t^*}$. If $\rho$ hits $A_{t^*}$ first, then either condition $(A)$ or $(A^{\prime })$ holds for all $t$ such that $t^* < t \le t^* + \lfloor \pi /\theta \rfloor \le 2t^* - 1$. In particular, condition $(A^{\prime })$ is necessary to detect the situation where $\rho$ crosses $A_{t^*}$ twice between the ceiling endpoints $a_{r,t^*}$ and $a_{l,t^*}$. On the other hand, if $\rho$ hits $B_{t^*}$ first, then condition $(B)$ holds for all $t$ such that $t^* < t \le t^* + \lfloor \pi /\theta \rfloor \le 2t^* - 1$. Finally, none of the conditions holds for any positive $t < t^*$.

Fig. 17

Floors and ceilings in the universal cover of the annulus

Starting with the estimate $t=1$, our algorithm repeatedly doubles $t$ until at least one of these four conditions is satisfied, and then performs a binary search for the critical value of $t$. To avoid messy boundary conditions when $t^* \approx \pi /\theta$, we actually check the conditions for all $t$ between $2^k$ and $2^k + 3$ in the $k$th iteration of the doubling search. When the unbounded search ends, there are three cases to consider, depending on which conditions are satisfied.

• (A) Suppose $c_t$ contains a point below $\rho$ but $c_{t-1}$ does not. Then $\rho$ must hit either $A_{t-1}$ or $A_t$; that is, either $t^* = t-1$ or $t^* = t$. We can distinguish between these two cases in $O(n)$ time by brute force.

• (A$^{\prime }$) Suppose $c_{t-1}$ and $c_t$ both lie above $\rho$, and the angle of $\rho$ lies between the angles of $c_{t-1}$ and $c_t$. Then either $\rho$ hits $A_{t-1}$, or $\rho$ does not intersect any upper chain $A_j$. Again, we can distinguish between these two cases in $O(n)$ time by brute force. If $\rho$ hits $A_{t-1}$, we return $t^* = t-1$. Otherwise, we perform a second unbounded search to find the first chain $B_{t^*}$ hit by $\rho$.

• (B) Finally, if $f_t$ contains a point above $\rho$ but $f_{t-1}$ does not, then $\rho$ must hit either $B_{t-1}$ or $B_t$. Again, we can distinguish between these two cases in $O(n)$ time by brute force.

If the critical value of $t$ satisfies more than one termination condition, we perform the relevant computation for all satisfied conditions and return the smallest value found.

An important subtlety in the algorithm is that computing the coordinates of $c_t$ or $f_t$ from scratch requires $\varTheta (\log t)$ time, because we do not assume a model of computation that supports exact constant-time trigonometric and inverse trigonometric functions. However, by computing an array of $O(\log t^*)$ rotations of the form ${\tau ^{2^i}}$ during the doubling phase of the unbounded search, we can compute the coordinates of the appropriate segments $c_t$ or $f_t$ in $O(1)$ time in each iteration of the search.

To summarize: Our algorithm spends $O(n)$ time constructing the hourglass $H$ and and the segments $c_1$ and $f_1$; performs an unbounded binary search to approximate $t^*$ up to a small additive constant, spending $O(1)$ time per iteration; and then spends $O(n)$ postprocessing time to find the precise value of $t^*$. $\square$

7.4 Tracing Geodesic Spirals

Now we describe our reduction from the problem of tracing a geodesic spiral to the annular ray-shooting problem. At a high level, the reduction is straightforward. If the growing geodesic $\gamma$ enters the same street in the same direction during the same phase, we construct $P$ by unfolding all the streets and junctions traversed so far in that phase, perform an annular ray-shooting query with $\gamma$ as the ray, and then perform $O(n)$ more steps by brute force to finish tracing the spiral. However, there are three important subtleties that must be taken into account.

First, the topological disk $P$ that we obtain by unfolding streets and junctions into a common plane may not be a simple polygon; some streets and junctions may overlap. However, because $P$ contains a line segment between the two portals, the hourglass $H$ of $P$ is a simple polygon. Moreover, we can construct $H$ by extending the shortest paths $A$ and $B$ through one street or junction at a time, as described by Hershberger and Snoeyink [31]. There is no need to construct the disk $P$ explicitly.

Second, we actually require the following minor modification: Given a polygon $P$ with equal-length portal edges and a ray $\rho$, we need to determine how many times $\rho$ crosses the portal before hitting either a non-portal edge of $P$ or some earlier point in $\rho$. Assuming $\rho$ always passes through each street in only one direction during the current phase, every self-intersection point along $\rho$ has the form $\rho \cap \tau ^k(\rho )$ for some integer $k$; because $\tau$ is a simple rotation, the first such crossing (if any) occurs at the point $\rho \cap \tau (\rho )$. Thus, we need to compute the largest integer $t$ such that $\rho$ does not intersect $A_{<t}$ or $B_{<t}$ and does not cross the ray $\tau (\rho )$ inside the polygon $H_{<t}$. To solve this modified problem, we add a fourth termination condition to the unbounded search:

• (C) The rays $\rho$ and $\tau (\rho )$ intersect inside the convex quadrilateral $\mathrm{conv }\{ e_{t-1}, e_t \}$.

Adding this condition increases the running time of the unbounded search algorithm by only a small constant factor.

Finally, it is possible for a geodesic to traverse a single street in both directions during a single phase of the tracing algorithm; in this case, merely adding condition $(C)$ to the unbounded search algorithm might fail to detect a self-intersection. To avoid this possibility, we partition each street that does not end at the boundary of $\varSigma$ into two lanes with a geodesic segment we call the median. (If a street ends at the boundary of $\varSigma$, it obviously cannot be traversed more than once.) The endpoints of the median are vertices of the triangular faces (in the original surface triangulation $T$) incident to the ends of the street, as shown in Fig. 18. Straightforward case analysis implies that $\gamma$ crosses a median only in the last step of each phase. For example, if $\gamma$ enters a street with a left turn, either it exits the street with another left turn and does not cross the median, or it crosses the median and then exits the street with a right turn, thereby ending the current phase. Informally, the geodesic “drives on the left” during left-turning phases and “drives on the right” during right-turning phases; see Fig. 18.

Fig. 18

Top: $\gamma$ enters a street with a left turn, traverses the left lane, and exits the street with a left turn. Bottom $\gamma$ enters a street with a right turn, crosses the median, and exits the street with a left turn

Similarly, each junction is partitioned into fragments by the medians of the three streets incident to that junction. Each fragment has constant only one direction during a phase (if it is traversed at all). Thus, to compute the depth of a spiral, we compute the $m$ lanes and $m$ junction fragments traversed by the spiral on the fly, in O(1) time each; unfold these lanes and fragments into a common plane in $O(m)$ time; compute the hourglass of the resulting (possibly self-overlapping) polygon in $O(m)$ time; and finally invoke our modified annular ray-shooting algorithm.

Lemma 7.2

The depth $d$ of a geodesic spiral through $m$ distinct directed streets can be computed in $O(m + \log d)$ time.

7.5 Summary

The proof of Theorem 4.8 now immediately implies that our geodesic tracing algorithm runs in $O(n^2\log X)$ time, where $X$ is the number of times the geodesic crosses an edge of the input triangulation $T$. The output of our tracing algorithm is the final street complex $S(T,\gamma )$, the face of $S(T,\gamma )$ that contains the first self-intersection point $x$, and the local coordinates of $x$ within that face.

Finally, we can also locate $x$ in the input triangulation in $O(n^2\log X)$ additional time as follows. Each street and junction in the street complex $S(T,\gamma )$ has its own local coordinate system. Each junction inherits its local coordinate system from the triangle of $\varSigma$ that contains it; similarly, each street inherits its local coordinate system from one of the triangles incident to the corresponding edge in the initial triangulation. During the tracing algorithm, for each edge $e$ of the evolving street complex, we maintain the rigid motion $\tau _e:\mathbb R ^2\rightarrow \mathbb R ^2$ that maps from the local coordinates on one side of $e$ to the local coordinates on the other side. The matrices encoding these rigid motions can be updated in $O(m + \log d)$ time in each phase of the tracing algorithm.

After locating $x$ in the street complex $S(T,\gamma )$, we untrace $\gamma$, keeping track of which face of the devolving street complex contains $x$ and the local coordinates of $x$ within that face. There are three cases to consider in each phase of the untracing algorithm. If $x$ lies inside a junction, we can stop untracing immediately. Otherwise, if $x$ does not lie in the active street of the current phase, its local coordinates do not change during that phase. Finally, if $x$ lies in the active street of the phase, we can determine its new local coordinates in $O(m + \log d)$ time.

We conclude:

Theorem 7.3

Let $\varSigma$ be a triangulated piecewise-linear surface with $n$ triangles. Given the starting point and direction of a geodesic $\gamma$ in $\varSigma$, we can compute the first self-intersection point in $\gamma$ in $O(n^2\log X)$ time, where $X$ is the number of edges $\gamma$ crosses before it self-intersects.