Is full annuitization socially optimal?

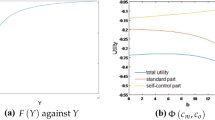
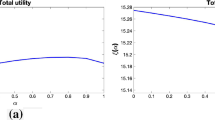
Abstract

A seminal result Yaari holds that all pension savings should be in life-annuities. Annuities offer a higher return than standard assets and diversify mortality risk and therefore it is individually optimal to save in annuities only. This is a cornerstone result in the pensions literature where many attempts have been made to explain that individual savings in annuities is very low, the socalled annuity puzzle. But is the result that all pension savings should be in life-annuities also socially optimal? We show in a standard setting with fair annuities and dynamic efficiency that full annutization of all pensions saving is not socially optimal. Less than full annutization implies unintentional bequests and thus transfers from the old to the young, which is welfare improving under dynamic efficiency. Further, we show that no annutization can implement the Golden Rule capital stock level and analyse whether some annutization is socially optimal using a numerical analysis, which shows that it is the case under a wide range of parameter constellations.

Appendices

Appendices

A Optimal annutization under endogenous factor prices

For later use note that (using (12) and (13))

$$\begin{aligned} \frac{\partial {\overline{R}}}{\partial {k}}=\left[ \frac{\lambda }{\pi } +1-\lambda \right] f_{kk}\left( k\right)&\quad \frac{\partial g}{\partial k}= \left[ 1-\pi \right] \left[ 1-\lambda \right] \left[ f_{kk}\left( k\right) k+f_{k}\left( k\right) \right] \nonumber \\ \frac{\partial {\overline{R}}}{\partial \lambda }=\left[ \frac{1}{\pi }-1 \right] f_{k}\left( k\right)&\quad \frac{\partial g}{\partial \lambda }=- \left[ 1-\pi \right] f_{k}\left( k\right) k \end{aligned}$$

(17)

Life-time utility in equilibrium is given by

$$\begin{aligned} \Omega =u(c^{y})+\frac{\pi }{1+\delta }u(c^{o}) \end{aligned}$$

where

$$\begin{aligned} c^{y}= & {} w\left( k\right) -k+g\left( \lambda ,k\right) \end{aligned}$$

(18)

$$\begin{aligned} c^{o} &= {} {\overline{R}}\left( \lambda ,k\right) k \end{aligned}$$

(19)

The optimal savings (capital stock) satisfies

$$\begin{aligned} u_{c}(c^{y})=\frac{\pi }{1+\delta }{\overline{R}}\left( \lambda ,k\right) u_{c}(c^{o}) \end{aligned}$$

(20)

which implicitly defines the captial stock level k as a function of the level of annutization $\lambda$. It follows that

$$\begin{aligned} \frac{\partial k}{\partial \lambda }=\frac{\frac{\pi }{1+\delta }u_{c}\left( c^{o}\right) \left[ 1-\sigma \right] \frac{\partial {\overline{R}}\left( \cdot \right) }{\partial \lambda }-u_{cc}(c^{y})\frac{\partial g\left( \cdot \right) }{\partial \lambda }}{\Delta } \end{aligned}$$

(21)

where $\sigma \equiv -\frac{{\overline{R}}\left( \cdot \right) ku_{cc}\left( c^{o}\right) }{u_{c}\left( c^{o}\right) }$ is the coefficient of relative risk aversion (old age consumption), and

$$\begin{aligned} \Delta\equiv & \,{} u_{cc}(c^{y})\left[ \frac{\partial w\left( \cdot \right) }{ \partial k}-1+\frac{\partial g\left( \cdot \right) }{\partial k}\right] \\&-\frac{\pi }{1+\delta }u_{c}\left( c^{o}\right) \left[ 1-\sigma \right] \frac{\partial {\overline{R}}\left( \cdot \right) }{\partial k}-\frac{\pi }{ 1+\delta }{\overline{R}}\left( \cdot \right) ^{2}u_{cc}\left( c^{o}\right) \\> & {} 0 \end{aligned}$$

where the sign follows from the stability condition (see Appendix C). Using (10)–(13) and (17) gives

$$\begin{aligned} \frac{\partial k}{\partial \lambda }=\frac{\left[ 1-\pi \right] f_{k}\left( k\right) \left[ \frac{1}{1+\delta }u_{c}\left( c^{o}\right) \left[ 1-\sigma \right] +u_{cc}(c^{y})k\right] }{\Delta } \end{aligned}$$

implying that

$$\begin{aligned} \frac{\partial k}{\partial \lambda }\,\lesseqqgtr \,0\text { iff }\sigma \,\gtreqqless \,1+\frac{u_{cc}(c^{y})k}{\frac{1}{1+\delta }u_{c}\left( c^{o}\right) } \end{aligned}$$

where $\frac{u_{cc}(c^{y})k}{\frac{1}{1+\delta }u_{c}\left( c^{o}\right) }<0$ .

The welfare effect of a change in the level of annutization $\lambda$ is

$$\begin{aligned} \frac{\partial \Omega }{\partial \lambda }= & {}\, u_{c}(c^{y})\left[ \left[ \frac{\partial w\left( \cdot \right) }{\partial k}-1+\frac{\partial g\left( \cdot \right) }{\partial k}\right] \frac{\partial k\left( \cdot \right) }{ \partial \lambda }+\frac{\partial g\left( \cdot \right) }{\partial \lambda } \right] \\&+\frac{\pi }{1+\delta }u_{c}\left( c^{o}\right) \left[ \left[ \frac{ \partial {\overline{R}}\left( \cdot \right) }{\partial k}k+{\overline{R}}\left( \cdot \right) \right] \frac{\partial k}{\partial \lambda }+\frac{\partial {\overline{R}}\left( \cdot \right) }{\partial \lambda }k\right] \\= & {} \frac{\pi }{1+\delta }u_{c}(c^{o}) \\&\times \left[ \left[ {\overline{R}}\left( \cdot \right) \left[ \frac{ \partial w\left( \cdot \right) }{\partial k}+\frac{\partial g\left( \cdot \right) }{\partial k}\right] +\frac{\partial {\overline{R}}\left( \cdot \right) }{\partial k}k\right] \frac{\partial k}{\partial \lambda }+\overline{ R}\left( \cdot \right) \frac{\partial g\left( \cdot \right) }{\partial \lambda }+\frac{\partial {\overline{R}}\left( \cdot \right) }{\partial \lambda }k\right] \end{aligned}$$

where (20) has been used. Hence,

$$\begin{aligned} \frac{\partial \Omega }{\partial \lambda }\,\gtreqqless \,0\text { iff }\left[ {\overline{R}}\frac{\partial w\left( \cdot \right) }{\partial k}+k\frac{ \partial {\overline{R}}\left( \cdot \right) }{\partial k}\right] \frac{ \partial k}{\partial \lambda }+{\overline{R}}\left( \cdot \right) \frac{ \partial g\left( \cdot \right) }{\partial k}\frac{\partial k}{\partial \lambda }+{\overline{R}}\left( \cdot \right) \frac{\partial g\left( \cdot \right) }{\partial \lambda }+\frac{\partial {\overline{R}}\left( \cdot \right) }{\partial \lambda }k\,\gtreqqless \,0 \end{aligned}$$

(22)

1.1 A.1 Optimality of full annutization

For full annutization ($\lambda =1$) being optimal it is necessary that $\left. \frac{\partial \Omega }{\partial \lambda }\right| _{\lambda =1}\ge 0$. Evaluating the condition (22) at full annutization $\lambda =1$, and using $\frac{\partial g}{\partial k}=0$ for $\lambda =1$ cf. (17), implies $\left. \frac{\partial \Omega }{\partial \lambda }\right| _{\lambda =1}\ge 0$ iff

$$\begin{aligned} \text { }\left[ {\overline{R}}\frac{\partial w\left( \cdot \right) }{\partial k} +k\frac{\partial {\overline{R}}\left( \cdot \right) }{\partial k}\right] \frac{ \partial k}{\partial \lambda }+{\overline{R}}\left( \cdot \right) \frac{ \partial g\left( \cdot \right) }{\partial \lambda }+\frac{\partial \overline{ R}\left( \cdot \right) }{\partial \lambda }k\ge 0 \end{aligned}$$

(23)

Using (10)–(13) and (17), (23) can be rewritten

$$\begin{aligned} -\frac{1}{\pi }\left[ f_{k}\left( k\right) -1\right] \left[ f_{kk}\left( k\right) k\frac{\partial k}{\partial \lambda }+\left[ 1-\pi \right] f_{k}\left( k\right) k\right] \ge 0 \end{aligned}$$

Under dynamic efficiency $f_{k}\left( k\right) >1$, a necessary condition for full annutization ($\lambda =1$) being socially optimal is thus

$$\begin{aligned} f_{kk}\left( k\right) \frac{\partial k}{\partial \lambda }+\left[ 1-\pi \right] f_{k}\left( k\right) \le 0 \end{aligned}$$

Using (21) (recall, $\Delta >0$), the condition can be written

$$\begin{aligned} f_{kk}\left( k\right) \left[ 1-\pi \right] f_{k}\left( k\right) \left[ \frac{ 1}{1+\delta }u_{c}\left( c^{o}\right) \left[ 1-\sigma \right] +u_{cc}(c^{y})k \right] \le -\Delta \left[ 1-\pi \right] f_{k}\left( k\right) \end{aligned}$$

Since (after using (10)–(13) and (17))

$$\begin{aligned} \Delta =u_{cc}(c^{y})\left[ -kf_{kk}\left( k\right) -1\right] -\frac{\pi }{ 1+\delta }u_{c}\left( c^{o}\right) \left[ 1-\sigma \right] \frac{1}{\pi } f_{kk}\left( k\right) -\frac{\pi }{1+\delta }\left[ \frac{1}{\pi } f_{k}\left( k\right) \right] ^{2}u_{cc}\left( c^{o}\right) \end{aligned}$$

(24)

for $\lambda =1$, the condition (24) can be written

$$\begin{aligned}&f_{kk}\left( k\right) \left[ 1-\pi \right] f_{k}\left( k\right) \left[ \frac{1}{1+\delta }u_{c}\left( c^{o}\right) \left[ 1-\sigma \right] +u_{cc}(c^{y})k\right] \\\le & {} \\&-\left\{ \begin{array}{c} u_{cc}(c^{y})\left[ -kf_{kk}\left( k\right) -1\right] -\frac{\pi }{1+\delta } u_{c}\left( c^{o}\right) \left[ 1-\sigma \right] \frac{1}{\pi }f_{kk}\left( k\right) \\ -\frac{\pi }{1+\delta }\left[ \frac{1}{\pi }f_{k}\left( k\right) \right] ^{2}u_{cc}\left( c^{o}\right) \end{array} \right\} \\&\times \left[ 1-\pi \right] f_{k}\left( k\right) \end{aligned}$$

or

$$\begin{aligned} 0\le u_{cc}(c^{y})+\frac{\pi }{1+\delta }\left[ \frac{1}{\pi }f_{k}\left( k\right) \right] ^{2}u_{cc}\left( c^{o}\right) \end{aligned}$$

which can never hold. Hence, we can conclude that $\left. \frac{\partial \Omega }{\partial \lambda }\right| _{\lambda =1}<0$ and full annutization is not socially optimal under endogenous factor prices.

1.2 A.2 Optimality of non-zero annutization

Next consider whether it is socially optimal to have any annutization at all, which has $\left. \frac{\partial \Omega }{\partial \lambda }\right| _{\lambda =0}>0$ as a sufficient condition. Evaluating the condition (22) at zero annutization $\lambda =0$ gives $\left. \frac{\partial \Omega }{\partial \lambda }\right| _{\lambda =0}>0$ (using (10)–(13) and (17)) iff

$$\begin{aligned}&\left[ \left[ 1-f_{k}\left( k\right) \right] kf_{kk}\left( k\right) +\left[ 1-\pi \right] f_{k}\left( k\right) \left[ kf_{kk}\left( k\right) +f_{k}\left( k\right) \right] \right] \frac{\partial k}{\partial \lambda } \\&+\left[ \frac{1}{\pi }-f_{k}\left( k\right) \right] \left[ 1-\pi \right] f_{k}\left( k\right) k>0 \end{aligned}$$

A necessary and sufficient condition for $\left. \frac{\partial \Omega }{ \partial \lambda }\right| _{\lambda =0}>0$, after using (21 ) and (10)–(13) and (17) evaluated at $\lambda =0$ (recall, $\Delta >0$), is

$$\begin{aligned}&\left[ \left[ 1-f_{k}\left( k\right) \right] kf_{kk}\left( k\right) +\left[ 1-\pi \right] f_{k}\left( k\right) \left[ kf_{kk}\left( k\right) +f_{k}\left( k\right) \right] \right] \\&\times \left[ \frac{1}{1+\delta }u_{c}\left( c^{o}\right) \left[ 1-\sigma \right] +u_{cc}(c^{y})k\right] \\> & {} -\Delta \left[ \frac{1}{\pi }-f_{k}\left( k\right) \right] k \end{aligned}$$

Using that (after using (10)–(13) and (17))

$$\begin{aligned} \Delta= & {} \,u_{cc}(c^{y})\left[ -kf_{kk}\left( k\right) -1+\left[ 1-\pi \right] \left[ kf_{kk}\left( k\right) +f_{k}(k)\right] \right] \\&-\frac{\pi }{1+\delta }u_{c}\left( c^{o}\right) \left[ 1-\sigma \right] f_{kk}\left( k\right) -\frac{\pi }{1+\delta }\left[ f_{k}(k)\right] ^{2}u_{cc}\left( c^{o}\right) \end{aligned}$$

for $\lambda =0$, the condition can be written

$$\begin{aligned}&\left[ \left[ 1-\pi f_{k}\left( k\right) \right] kf_{kk}\left( k\right) + \left[ 1-\pi \right] \left[ f_{k}\left( k\right) \right] ^{2}\right] \left[ \frac{1}{1+\delta }u_{c}\left( c^{o}\right) \left[ 1-\sigma \right] +u_{cc}(c^{y})k\right] \\> & {} \\&-\left\{ \begin{array}{c} u_{cc}(c^{y})\left[ -1+\left[ 1-\pi \right] f_{k}\left( k\right) -\pi f_{kk}\left( k\right) k\right] \\ -\frac{\pi }{1+\delta }u_{c}\left( c^{o}\right) \left[ 1-\sigma \right] f_{kk}\left( k\right) -\frac{\pi }{1+\delta }\left[ f_{k}\left( k\right) \right] ^{2}u_{cc}\left( c^{o}\right) \end{array} \right\} \\&\times \left[ \frac{1}{\pi }-f_{k}\left( k\right) \right] k \end{aligned}$$

which after some routine steps can be written as

$$\begin{aligned}&\frac{\left[ 1-\sigma \right] \left[ 1-\pi \right] }{1+\delta }u_{c}\left( c^{o}\right) \left[ f_{k}\left( k\right) \right] ^{2}+\frac{1}{\pi } u_{cc}(c^{y})k\left[ f_{k}\left( k\right) -1\right] \\> & {} \frac{\pi }{1+\delta }u_{cc}\left( c^{o}\right) \left[ f_{k}\left( k\right) \right] ^{2}k\left[ \frac{1}{\pi }-f_{k}\left( k\right) \right] \end{aligned}$$

or by use of $\sigma \equiv -\frac{f_{k}\left( k\right) ku_{cc}\left( c^{o}\right) }{u_{c}\left( c^{o}\right) }$ as

$$\begin{aligned} \frac{1-\pi }{1+\delta }\left[ f_{k}\left( k\right) \right] ^{2}>-\frac{1}{ \pi }\left[ \frac{u_{cc}(c^{y})}{u_{c}\left( c^{o}\right) }+\frac{\pi }{ 1+\delta }\frac{u_{cc}\left( c^{o}\right) }{u_{c}\left( c^{o}\right) }\left[ f_{k}\left( k\right) \right] ^{2}\right] k\left[ f_{k}\left( k\right) -1 \right] \end{aligned}$$

Using the equilibrium condition in (20) evaluated at $\lambda =0$ the conditon for $\left. \frac{\partial \Omega }{\partial \lambda } \right| _{\lambda =0}>0$ reads

$$\begin{aligned} \left[ 1-\pi \right] f_{k}\left( k\right) >-\left[ \frac{u_{cc}(c^{y})}{ u_{c}(c^{y})}+\frac{u_{cc}\left( c^{o}\right) }{u_{c}\left( c^{o}\right) } f_{k}\left( k\right) \right] k\left[ f_{k}\left( k\right) -1\right] \end{aligned}$$

(25)

1.2.1 A.2.1 Numerical analysis

Assuming a CES utility function $u\left( c\right) =\frac{c^{1-\sigma }-1}{ 1-\sigma }$, where $\sigma >0$ is the coefficient of relative risk aversion (as before), and using (18) and (19) evaluated at $\lambda =0$ gives (25) as

$$\begin{aligned} \left[ 1-\pi \right] f_{k}\left( k\right) \left[ \frac{f\left( k\right) }{k} -\pi f_{k}\left( k\right) -1\right] >\sigma \left[ \frac{f\left( k\right) }{k }-\pi f_{k}\left( k\right) \right] \left[ f_{k}\left( k\right) -1\right] \end{aligned}$$

where $\frac{f\left( k\right) }{k}$ is the output-capital ratio and $f_{k}\left( k\right)$ is the gross return on capital. Further, assuming a Cobb-Douglas production function $f\left( k\right) =k^{\alpha }$, where $0<\alpha <1$, gives the condition as

$$\begin{aligned} \left[ 1-\pi \alpha \right] \left[ \left[ 1-\pi -\sigma \right] \alpha k^{\alpha -1}+\sigma \right] >\alpha \left[ 1-\pi \right] \end{aligned}$$

Assuming the empirically relevant $\alpha =\frac{1}{3}$ gives the condition as

$$\begin{aligned} \frac{1-\pi -\sigma }{k^{\frac{2}{3}}}+3\sigma >\frac{1-\pi }{1-\frac{\pi }{3 }} \end{aligned}$$

(26)

giving the sufficient condition in (25) given the specific functional forms and assuming $\alpha =\frac{1}{3}$.

The left hand side (LHS) of (26) is a function of the parameters $\pi$, $\sigma$ and $\delta$ (since k is implicitly a function of $\delta$) while the right hand side (RHS) is only a function of $\pi$. An increase in $\delta$ results in a lower equilibrium capital stock k, which can be seen using (10)–(13) and ( 17)–(20) and the functional forms evaluated at $\lambda =0$ and $\alpha =\frac{1}{3}$

$$\begin{aligned} \frac{\partial k}{\partial \delta }=-\frac{3kc^{y}}{2\left[ 1+\delta \right] \left[ \sigma k+c^{y}\right] }<0 \end{aligned}$$

Hence, for any given values of $\pi \in \left( 0,1\right)$ and $\sigma >0$, there exist positive $\delta$-as satisfying the condition.

Below, we consider the three case; $\pi +\sigma <1$, $\pi +\sigma =1$ and $\pi +\sigma >1.$ First, consider the case where $\pi +\sigma =1$. Then (26) becomes

$$\begin{aligned} \pi <2 \end{aligned}$$

which always holds. It can therefore be concluded that the sufficient condition for positive annutization being optimal (in (26)) is fulfilled for all $\delta >0$, $\pi \in \left( 0,1\right)$ and $\sigma >0$ for which $\pi +\sigma =1$.

Second, consider the case where $\pi +\sigma <1$. Since the LHS in (26) is strictly increasing in $\delta$ for $\pi +\sigma <1$ and the RHS is independent of $\delta$, showing that the (26) holds when $\delta =0$ is sufficent to show that it holds for all $\delta >0$ . Using (10)–(13) and (17)–(20) and the specific functional forms evaluated at $\lambda =0$, $\alpha =\frac{1}{3}$ and $\delta =0$ to calculate the equilibrium capital stock for various $\pi$ and $\sigma$ such that $\pi +\sigma <1$ gives the following results for the difference between the LHS and RHS in (26).

Table 1 $LHS-RHS$ in (26) for various $\pi$ and $\sigma$ such that $\pi +\sigma <1$ and $\delta =0$

The table shows that (26) holds for various combinations of $\pi$ and $\sigma$ ($\pi +\sigma <1$) when $\delta =0$ implying the sufficient condition for positive annutization being optimal (in (26)) is fulfilled for all $\delta >0$, $\pi \in \left( 0,1\right)$ and $\sigma >0$ such that $\pi +\sigma <1$.

Finally, consider the case when $\pi +\sigma >1$. We now restrict our analysis to case where relative risk aversion is $\sigma \in \left( 0,1\right)$ - a well known condition in the literature. Since the LHS in ( 26) is strictly decreasing in $\delta$ when $\pi +\sigma >1$ and the RHS is independent of $\delta$, there exists a value of $\delta$, i.e. ${\bar{\delta }}$, for which (26) holds for all $\delta <\bar{ \delta }$. Using (10)–(13) and (17)–(20) and the specific function forms evaluated at $\lambda =0$ and $\alpha =\frac{1}{3}$ to calculate the equilibrium capital stock for various $\delta$, $\pi$ and $\sigma$ such that $\pi +\sigma >1$ gives the following results for ${\bar{\delta }}$:

Table 2 Maxmimum $\delta$ (${\bar{\delta }}$) where (26) holds for various $\pi$ and $\sigma$ such that $\pi +\sigma >1$

As an example, the condition (26) holds for all $\delta <2.3$ if $\pi =\sigma =0.5$. Assuming that each period is 30-year long in our two period OLG model, this implies that the sufficient condition for positive annutization being optimal (in (26)) is fulfilled if the annual discount rate is less than $4\%$ when $\pi =\sigma =0.5$.

B Implementing the Golden Rule allocation

The opitmal $\lambda$ is determined by the condition (from (22))

$$\begin{aligned} \left[ {\overline{R}}\frac{\partial w\left( \cdot \right) }{\partial k}+k\frac{ \partial {\overline{R}}\left( \cdot \right) }{\partial k}\right] \frac{ \partial k}{\partial \lambda }+{\overline{R}}\left( \cdot \right) \frac{ \partial g\left( \cdot \right) }{\partial k}\frac{\partial k}{\partial \lambda }+{\overline{R}}\left( \cdot \right) \frac{\partial g\left( \cdot \right) }{\partial \lambda }+\frac{\partial {\overline{R}}\left( \cdot \right) }{\partial \lambda }=0 \end{aligned}$$

Using (10)–(13) and (17) and imposing a Golden Rule allocation (k is such that $f_{k}\left( k\right) =1$) gives

$$\begin{aligned} \left[ \frac{\lambda }{\pi }+1-\lambda \right] \left[ f_{kk}\left( k\right) k+1\right] \frac{\partial k}{\partial \lambda }=-\frac{1-\pi }{\pi }k \end{aligned}$$

(27)

Using (10)–(13) and (17) and imposing $f_{k}\left( k\right) =1$ in (21) gives

$$\begin{aligned} \frac{\partial k}{\partial \lambda }=\frac{\left[ 1-\pi \right] \left\{ \frac{1}{1+\delta }u_{c}\left( c^{o}\right) \left[ 1-\sigma \right] +u_{cc}(c^{y})k\right\} }{\Delta } \end{aligned}$$

where

$$\begin{aligned} \Delta\equiv & {} -\left[ \frac{\lambda }{\pi }+1-\lambda \right] \\&\times \left\{ \begin{array}{c} u_{cc}(c^{y})\pi \left[ f_{kk}\left( k\right) k+1\right] +\frac{\pi }{ 1+\delta }u_{c}\left( c^{o}\right) \left[ 1-\sigma \right] f_{kk}\left( k\right) \\ +\frac{\pi }{1+\delta }\left[ \frac{\lambda }{\pi }+1-\lambda \right] u_{cc}\left( c^{o}\right) \end{array} \right\} \\> & {} 0 \end{aligned}$$

Using these in (27) gives

$$\begin{aligned} u_{c}\left( c^{o}\right) \left[ 1-\sigma \right] =\left[ \frac{\lambda }{\pi }+1-\lambda \right] ku_{cc}\left( c^{o}\right) \end{aligned}$$

Finally, using $\sigma \equiv -\frac{\left[ \frac{\lambda }{\pi }+1-\lambda \right] ku_{cc}\left( c^{o}\right) }{u_{c}\left( c^{o}\right) }$ this implies

$$\begin{aligned} u_{c}\left( c^{o}\right) =0 \end{aligned}$$

which can never hold. Hence, it can be concluded that the social optimal degree of annutization $\lambda \in \left[ 0,1\right]$, does not implement the Golden Rule level of capital stock.

C Local stability condition

Life-time utility of a household born at time t is

$$\begin{aligned} \Omega _{t}=u(w\left( k_{t}\right) -k_{t+1}+g\left( \lambda ,k_{t}\right) )+ \frac{\pi }{1+\delta }u({\overline{R}}\left( \lambda ,k_{t+1}\right) k_{t+1}) \end{aligned}$$

and the equilibrium capital stock satisfies

$$\begin{aligned} u_{c}(w\left( k_{t}\right) -k_{t+1}+g\left( \lambda ,k_{t}\right) )=\frac{ \pi }{1+\delta }{\overline{R}}\left( \lambda ,k_{t+1}\right) u_{c}({\overline{R}} \left( \lambda ,k_{t+1}\right) k_{t+1}) \end{aligned}$$

It follows that

$$\begin{aligned} \frac{\partial k_{t+1}}{\partial k_{t}}=\frac{u_{cc}(c_{t}^{y})\left[ \frac{ \partial w\left( \cdot \right) }{\partial k_{t}}+\frac{\partial g\left( \cdot \right) }{\partial k_{t}}\right] }{\frac{\pi }{1+\delta }\frac{ \partial {\overline{R}}\left( \cdot \right) }{\partial k_{t+1}} u_{c}(c_{t+1}^{o})+\frac{\pi }{1+\delta }{\overline{R}}\left( \cdot \right) u_{cc}(c_{t+1}^{o})\left[ \frac{\partial {\overline{R}}\left( \cdot \right) }{ \partial k_{t+1}}k_{t+1}+{\overline{R}}\left( \cdot \right) \right] +u_{cc}(c_{t}^{y})} \end{aligned}$$

and evaluated at steady state we have

$$\begin{aligned} \frac{\partial k_{t+1}}{\partial k_{t}}_{k_{t}=k_{t+1}=k}=\frac{u_{cc}(c^{y}) \left[ \frac{\partial w\left( \cdot \right) }{\partial k}+\frac{\partial g\left( \cdot \right) }{\partial k}\right] }{\frac{\pi }{1+\delta }\frac{ \partial {\overline{R}}\left( \cdot \right) }{\partial k}u_{c}(c^{o})+\frac{ \pi }{1+\delta }{\overline{R}}\left( \cdot \right) u_{cc}(c^{o})\left[ \frac{ \partial {\overline{R}}\left( \cdot \right) }{\partial k}k+{\overline{R}}\left( \cdot \right) \right] +u_{cc}(c^{y})} \end{aligned}$$

The steady state is locally stable if $0<\frac{\partial k_{t+1}}{\partial k_{t}}_{k_{t}=k_{t+1}}<1$, or

$$\begin{aligned} 0<\frac{u_{cc}(c^{y})\left[ \frac{\partial w\left( \cdot \right) }{\partial k }+\frac{\partial g\left( \cdot \right) }{\partial k}\right] }{\frac{\pi }{ 1+\delta }\frac{\partial {\overline{R}}\left( \cdot \right) }{\partial k} u_{c}(c^{o})+\frac{\pi }{1+\delta }{\overline{R}}\left( \cdot \right) u_{cc}(c^{o})\left[ \frac{\partial {\overline{R}}\left( \cdot \right) }{ \partial k}k+{\overline{R}}\left( \cdot \right) \right] +u_{cc}(c^{y})}<1 \end{aligned}$$

(28)

The numerator in this expression is negative, since

$$\begin{aligned}&u_{cc}(c^{y})\left[ \frac{\partial w\left( \cdot \right) }{\partial k}+ \frac{\partial g\left( \cdot \right) }{\partial k}\right] \\= & {} u_{cc}(c^{y}) \\&\times \left[ -kf_{kk}\left( k\right) +\left[ 1-\pi \right] \left[ 1-\lambda \right] \left[ f_{kk}\left( k\right) k+f_{k}\left( k\right) \right] \right] \\= & {} u_{cc}(c^{y}) \\&\times \left[ \left[ 1-\pi \right] \left[ 1-\lambda \right] f_{k}\left( k\right) -\left[ 1-\left[ 1-\pi \right] \left[ 1-\lambda \right] \right] f_{kk}\left( k\right) k\right] \\< & {} 0 \end{aligned}$$

The stability condition thus requires the denominator in (28) to be negative. We therefore have

$$\begin{aligned}&u_{cc}(c^{y})\left[ \frac{\partial w\left( \cdot \right) }{\partial k}+ \frac{\partial g\left( \cdot \right) }{\partial k}\right] \\> & {} \\&\frac{\pi }{1+\delta }\frac{\partial {\overline{R}}\left( \cdot \right) }{ \partial k}u_{c}(c^{o})+\frac{\pi }{1+\delta }{\overline{R}}\left( \cdot \right) u_{cc}(c^{o})\left[ \frac{\partial {\overline{R}}\left( \cdot \right) }{\partial k}k+{\overline{R}}\left( \cdot \right) \right] +u_{cc}(c^{y}) \end{aligned}$$

or:

$$\begin{aligned} u_{cc}(c^{y})\left[ \frac{\partial w\left( \cdot \right) }{\partial k}-1+ \frac{\partial g\left( \cdot \right) }{\partial k}\right] -\frac{\pi }{ 1+\delta }u_{c}\left( c^{o}\right) \left[ 1-\sigma \right] \frac{\partial {\overline{R}}\left( \cdot \right) }{\partial k}-\frac{\pi }{1+\delta } {\overline{R}}\left( \cdot \right) ^{2}u_{cc}\left( c^{o}\right) >0 \end{aligned}$$

which shows that $\Delta >0$ evaluated at a locally stable steady state capital stock.

D Distribution of bequests

Consider the case where the young whose parents do not survive into old age receive their parents’ entire bequests while the young whose parents survive receive zero bequests

$$\begin{aligned} g &= {} 0\text { for fraction }\pi \\ g &= {} \frac{\left[ 1-\pi \right] R_{b}b}{1-\pi }=R_{b}b \\ &= {} \left[ 1-\lambda \right] R_{b}s>0\text { for }\lambda <1\text { for fraction }1-\pi \end{aligned}$$

To ensure the existance of the annuities (insurance) market, it is assumed that survival probabilities are independent of whether ones own parents survived into old age. Here, bond holding b and savings s can be thought of as average bond holding $b=\pi b_{n}+\left[ 1-\pi \right] b_{g}$ and average savings $s=\pi s_{n}+\left[ 1-\pi \right] s_{g}$ since the young receiving g are independently drawn from parents receiving bequests (holding bond $b_{g}$ and saving $s_{g}$) and parents receiving no bequests (holding bond $b_{n}$ and saving $s_{n}$), where the subscript “n” stands for no bequests and “g” stands for positive bequests.

Expected life-time utility is

$$\begin{aligned} \Omega _{n} &= {} u\left( c_{n}^{y}\right) +\frac{\pi }{1+\delta }u\left( c_{n}^{o}\right) \\ \Omega _{g} &= {} u\left( c_{g}^{y}\right) +\frac{\pi }{1+\delta }u\left( c_{g}^{o}\right) \end{aligned}$$

where

$$\begin{aligned} c_{n}^{y} &= {} w-s_{n} \\ c_{n}^{o} & ={} {\overline{R}}s_{n} \\ c_{g}^{y} &= {} w-s_{g}+g \\ c_{g}^{o} &= {} {\overline{R}}s_{g} \end{aligned}$$

implying that optimal savings are given by

$$\begin{aligned} u_{c}(c_{n}^{y})= {} \frac{\pi }{1+\delta }{\overline{R}}u_{c}(c_{n}^{o}) \end{aligned}$$

(29)

$$\begin{aligned} u_{c}(c_{g}^{y})= {} \frac{\pi }{1+\delta }{\overline{R}}u_{c}(c_{g}^{o}) \end{aligned}$$

(30)

Further, we have for later use

$$\begin{aligned} \left. \frac{\partial g}{\partial \lambda }\right| _{\lambda =1} &= {}\, 0 \text { for fraction }\pi \\ \left. \frac{\partial g}{\partial \lambda }\right| _{\lambda =1} &= {} -R_{b}s\text { for fraction }1-\pi \end{aligned}$$

The welfare objective is

$$\begin{aligned} \Omega= & {} \,\pi \left[ u(w-s_{n})+\frac{\pi }{1+\delta }u({\overline{R}}s_{n}) \right] \\&+\left[ 1-\pi \right] \left[ u(w-s_{g}+g)+\frac{\pi }{1+\delta }u( {\overline{R}}s_{g})\right] \end{aligned}$$

Hence

$$\begin{aligned} \frac{\partial \Omega }{\partial \lambda }= & {} \,\pi \left[ -u(c_{n}^{y})\frac{ \partial s_{n}}{\partial \lambda }+\frac{\pi }{1+\delta }u_{c}(c_{n}^{o}) \left[ s_{n}\frac{\partial {\overline{R}}}{\partial \lambda }+{\overline{R}} \frac{\partial s_{n}}{\partial \lambda }\right] \right] \\&+\left[ 1-\pi \right] \left[ -u_{c}(c_{g}^{y})\frac{\partial s_{g}}{ \partial \lambda }+u_{c}(c_{g}^{y})\frac{\partial g}{\partial \lambda }+ \frac{\pi }{1+\delta }u_{c}(c_{g}^{o})\left[ s_{g}\frac{\partial {\overline{R}} }{\partial \lambda }+{\overline{R}}\frac{\partial s_{g}}{\partial \lambda } \right] \right] \end{aligned}$$

or, by using (29)–(30) and (6)

$$\begin{aligned} \frac{\partial \Omega }{\partial \lambda }= & {} \,\frac{\pi ^{2}}{1+\delta } u_{c}(c_{n}^{o})s_{n}\left[ \frac{1}{\pi }-1\right] R_{b} \\&+\left[ 1-\pi \right] \frac{\pi }{1+\delta }u_{c}(c_{g}^{o})\left[ \left[ \frac{\lambda }{\pi }+1-\lambda \right] \frac{\partial g}{\partial \lambda } +s_{g}\left[ \frac{1}{\pi }-1\right] \right] R_{b} \end{aligned}$$

Using that $\left. \frac{\partial g}{\partial \lambda }\right| _{\lambda =1}=-R_{b}s$ and that $g=0$ and hence $s_{g}=s_{n}\equiv s$ and $c_{g}^{o}=c_{n}^{o}\equiv c^{o}$ for $\lambda =1$ gives

$$\begin{aligned} \left. \frac{\partial \Omega }{\partial \lambda }\right| _{\lambda =1}=- \frac{1-\pi }{1+\delta }u_{c}(c^{o})R_{b}s\left[ R_{b}-1\right] <0 \end{aligned}$$

which is the main result of the paper; full annuitization ($\lambda =1$) is not socially optimal under dynamic efficiency ($R_{b}>1$). Hence, allowing for this kind of heterogeneity does not affect the main result of the paper.