Wave propagation in elasto-plastic granular systems

Abstract

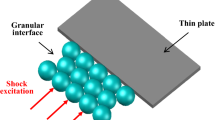
Due to the nonlinear nature of the inter-particle contact, granular chains made of elastic spheres are known to transmit solitary waves under impulse loading. However, the localized contact between spherical granules leads to stress concentration, resulting in plastic behavior even for small forces. In this work, we investigate the effects of plasticity in wave propagation in elasto-plastic granular systems. In the first part of this work, a force–displacement law between contacting elastic-perfectly plastic spheres is developed using a nonlinear finite element analysis. In the second part, this force–displacement law is used to simulate wave propagation in one-dimensional granular chains. In elasto-plastic chains, energy dissipation leads to the formation and merging of wave trains, which have characteristics very different from those of elastic chains. Scaling laws for peak force at each contact point along the chain, velocity of the leading wave, local contact and total dissipation are developed.

Appendix: Energy dissipation

The energy dissipation at a contact is given by the expression (31), where $\alpha = \alpha _{max}$ is the maximum relative displacement attained at the contact. The total energy dissipated in the system upto location $x_N$, as described by Eqs. (28–30) is given by (32), where $\tilde{x} = x/R^*$ and $E_t = d_0\left( \tilde{x}_t - \tilde{x}_1\right) + d_1 a\tilde{I} b \left( e^{-b\tilde{x}_1} - e^{-b\tilde{x}_t} \right) + 2 d_2 \left( a\tilde{I}\right) ^2 b \left( e^{-2 b \tilde{x}_1} - e^{-2 b \tilde{x}_t}\right)$ is the energy dissipated by the contact points in the first regime.

$$\begin{aligned} \tilde{E}_{dis}\!&= \! \dfrac{1}{F_y \alpha _y}\int \limits _{0}^{\alpha } \left( F_{load} \!-\! F_{unload} \right) d\alpha \nonumber \\ \!&= \! \left\{ \begin{array}{l} \left( \dfrac{3}{1.6}\right) \dfrac{ c_1 }{2} \left( \left( c_4 \tilde{\alpha } + c_5\right) ^2 \left( c_4 \alpha _0 \!+\! c_5 \right) ^2 \right) \\ + \left( \dfrac{3}{1.6} \right) \dfrac{c_2 }{c_3^2}\left( -e^{-c_3\left( \tilde{\alpha } \!-\! 1\right) } \left( c_3 \tilde{\alpha } \!+\! c_4 \!+\! c_3 c_5 \right) \right. \\ \left. + e^{-c_3\left( \alpha _0-1\right) }\left( c_3 \alpha _0 \!+\! c_4 \!+\! c_3 c_5 \right) \right) \\ + \left( \dfrac{3}{1.6}\right) \dfrac{c_1 \sigma _y }{c_6 \!+\! 1}\left( \alpha ^{c_6\!+\!1}_0 \!-\! 1 \right) \\ + \left( \dfrac{3}{1.6}\right) \dfrac{c_2 e^{c_3} }{c_3^{c_6+1}} \left( \varGamma \left( c_6\!+\!1,c_3\right) \!- \!\varGamma \left( c_6\!+\!1 , c_3 \alpha _0\right) \right) \\ + \dfrac{2}{5} \!-\! \dfrac{ \tilde{F}\left( \tilde{\alpha } - \tilde{\alpha }_R\right) }{n} \quad \quad \text{ if } \,\, \alpha _0 \le \tilde{\alpha } \\ \left( \dfrac{3}{1.6}\right) \dfrac{c_1 \sigma _y }{c_6 \!+\! 1}\left( \tilde{\alpha }^{c_6+1} \!-\! 1 \right) \\ + \left( \dfrac{3}{1.6} \right) \dfrac{c_2 e^{c_3} }{c_3^{c_6+1}} \left( \varGamma \left( c_6+1,c_3\right) - \varGamma \left( c_6+1 , c_3 \tilde{\alpha } \right) \right) \\ + \dfrac{2}{5} - \dfrac{ \tilde{F}\left( \tilde{\alpha } \!-\! \tilde{\alpha }_R\right) }{n} \quad \quad \text{ if } 1\! <\! \tilde{\alpha } < \alpha _0 \\ 0 \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \text{ otherwise, } \end{array}\right. \end{aligned}$$

(31)

where the constants $c_i$ are as defined in Sect. 2 and $\varGamma (.,.)$ is the Gamma function. The total energy dissipation is

$$\begin{aligned} \dfrac{4 E_{tot}}{F_y \alpha _y}\!=\! \left\{ \begin{array}{l} d_0 \left( \tilde{x}_N \!-\! \tilde{x}_1\right) \!+\! d_1 a\tilde{I} b\left( e^{-b \tilde{x}_1} \!-\! e^{-b \tilde{x}_N } \right) \\ + 2 d_2 \left( a\tilde{I}\right) ^2 b \left( e^{-2 b \tilde{x}_1} \!-\! e^{-2 b \tilde{x}_N } \right) ,\quad \hbox { if }\, \tilde{x_N} \!<\! \tilde{x}_t \\ {E}_t \!+\! d_0 (\tilde{x}_N\!-\! \tilde{x}_t) \!+\! d_1 C \tilde{I} \ln \left( \dfrac{x_N}{x_t}\right) \\ - d_2 \left( C \tilde{I}\right) ^2 \left( \dfrac{1}{\tilde{x}_N} \!-\! \dfrac{1}{\tilde{x}_t}\right) , \quad \hbox { otherwise}. \end{array}\right. \end{aligned}$$

(32)