Influence of packing density and stress on the dynamic response of granular materials

Abstract

Laboratory geophysics tests including bender elements and acoustic emission measure the speed of propagation of stress or sound waves in granular materials to derive elastic stiffness parameters. This contribution builds on earlier studies to assess whether the received signal characteristics can provide additional information about either the material’s behaviour or the nature of the material itself. Specifically it considers the maximum frequency that the material can transmit; it also assesses whether there is a simple link between the spectrum of the received signal and the natural frequencies of the sample. Discrete element method (DEM) simulations of planar compression wave propagation were performed to generate the data for the study. Restricting consideration to uniform (monodisperse) spheres, the material fabric was varied by considering face-centred cubic lattice packings as well as random configurations with different packing densities. Supplemental analyses, in addition to the DEM simulations, were used to develop a more comprehensive understanding of the system dynamics. The assembly stiffness and mass matrices were extracted from the DEM model and these data were used in an eigenmode analysis that provided significant insight into the observed overall dynamic response. The close agreement of the wave velocities estimated using eigenmode analysis with the DEM results confirms that DEM wave propagation simulations can reliably be used to extract material stiffness data. The data show that increasing either stress or density allows higher frequencies to propagate through the media, but the low-pass wavelength is a function of packing density rather than stress level. Prior research which had hypothesised that there is a simple link between the spectrum of the received signal and the natural sample frequencies was not substantiated.

1 Introduction

Investigations of the nature of wave propagation through granular materials provide essential material properties and are often conducted for engineering applications. For example, the velocity of the propagating wave can be related to the small-strain stiffness of granular materials and is important in geophysics, geotechnical engineering and fundamental research into granular materials [1,2,3]. In these dynamic geophysics tests, the wave velocity can be obtained using either time domain techniques (e.g. [4, 5]) or frequency domain techniques (e.g. [6,7,8,9]). This paper explores whether additional information, i.e. in addition to the elastic stiffness parameters, can be obtained about the tested samples by relatively simple analyses of the received signal. A testing scenario is considered which involves a controlled disturbance to generate an inserted signal at one sample boundary and monitoring of the received signal at another sample boundary.

Two research questions are considered here:

• 1. Granular materials act as a low-pass filter to seismic (stress) or acoustic waves. Santamarina and Aloufi [10] and Santamarina et al. [11] related the maximum transmitted frequency $(f_{low-pass})$ and the associated wavelength $(\lambda _{low-pass})$ to particle size, while Mouraille and Luding [12] related $\lambda _{low-pass}$ to the layer spacing. In their analysis of bender element tests and simulations, O’Donovan et al. [13] found that the relationship between particle size and $f_{low-pass}$ differs from that proposed by Santamarina and Aloufi [10] and Santamarina et al. [11]. Data presented in O’Donovan [14] indicates that $f_{low-pass}$ varies with confining pressure in randomly packed monodisperse materials. Lawney and Luding [15] examined a 1-D chain of spheres and observed that a narrower band of frequencies is transmitted when there is a variation in the sphere masses, in comparison with the case of perfectly uniform spheres. At a given stress and void ratio, the contact model also alters the frequency limit [16]. A better understanding of the material characteristics that determine $f_{low-pass}$ would enable us to assess whether measurement of $f_{low-pass}$ in laboratory seismic tests can provide useful information about how to characterise the material. In addressing these issues here, the influence of confining stress and void ratio on $f_{low-pass}$ and $\lambda _{low-pass}$ are discussed.

• 2. The study also examines whether comparison of inserted and received signals in the frequency domain can provide details on the fundamental vibration modes of the sample. Taking a simple fast Fourier transform (FFT) of the received signal in a laboratory test reveals a number of local maxima, i.e. high amplitudes associated with specific frequencies. Alvarado and Coop [17] proposed that the frequencies of fundamental vibration modes can be identified from the local maxima of the ratio of the Fourier transforms of the received and inserted signals. They based their hypothesis on a simple analysis of a single degree of freedom system. This idea was further developed in continuum analyses of the overall sample dynamics by O’Donovan et al. [13]. The current study adopts a more rigorous approach where the eigenfrequencies of a model granular material created with DEM are directly compared with the received signal obtained in a simulated seismic test.

Considering DEM simulations of wave propagation O’Donovan et al. [13] showed that the system response observed in DEM simulations of dynamic tests gives a reasonable match to that observed in equivalent physical laboratory tests. The particle-scale data available in the DEM simulations enable a range of analyses to better understand the system response and so they can be used to explore the two research questions stated above. The dynamic response of a system is determined by its natural vibration frequencies/periods and corresponding modes. These frequencies and modes cannot be directly obtained from the responses observed in the DEM simulations or laboratory geophysics tests. Adopting techniques used in matrix structural analysis [18] enables an eigenvalue decomposition to obtain these data. The dispersion relation of a propagating wave is also investigated following Mouraille et al. [19] and compared with results of eigenmode analysis considering all the particles as used in DEM simulations. The use of three different approaches to analyse the system enabled a more comprehensive picture to be developed than would be the case if DEM simulations alone were considered. Furthermore, agreement between the results of the three methods serves as a verification that each model formulation is reasonable and has been correctly implemented.

2 DEM simulations

DEM simulations were performed using a modified version of the LAMMPS molecular dynamics code [20]. Uniformly sized spheres with a radius (R) of 1.27 mm were used with a particle density $\rho _{p} = 2230\,\hbox {kg/m}^{3}$. Using monodisperse particles enables the effects of fabric to be isolated from any particle inertia effects. A simplified Hertz–Mindlin (HM) contact model was considered with Young’s modulus $E_{p} = 60\,\hbox {GPa}$ and particle Poisson’s ratio $\nu _{p} = 0.2$, which are typical properties for borosilicate glass ballotini. This system configuration was also considered in Otsubo et al. [16].

Table 1 Specification of test cases and results

Fig. 1

Examples of samples: a FCC sample b random sample (test case 22) at $\sigma = 100~\hbox {kPa}$. Coordination number $(C_{N})$ per particle is plotted for the random sample

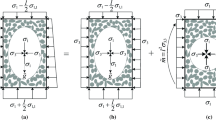
Referring to Table 1, a regular FCC packing and various random packings were considered. Representative sample images are presented in Fig. 1; Fig. 1a is a FCC sample and Fig. 1b is a random sample (test case 22, Table 1), both of which are isotropically compressed to 100 kPa. Use of random samples enables consideration of the effects of geometric disorder on wave propagation, developing on the contributions of [12, 15]. As was the case in earlier contributions [12, 16, 19], the lateral boundaries were periodic while the boundaries in the longitudinal direction were fixed walls with the same material properties as the contacting spheres. The FCC sample consisted of 3200 particles ($4\times 4\times 200$ layers) and so is equivalent to that considered by Mouraille et al. [19] and Mouraille and Luding [12]; it was created by considering the lattice geometry of the packing. For the FCC samples, a coefficient of friction $\mu _{comp} = 0$ was used during controlled compression to the stress levels ($\sigma$) listed in Table 1. The random samples all consisted of 35,201 particles. They were prepared by applying a controlled compression to initial “clouds” of non-contacting spheres to achieve isotropic confining stresses, $\sigma$, of between 10 kPa and 10 MPa. The borosilicate ballotini which are nominally considered in the DEM simulations would most likely be crushed at $\sigma > 10\,\hbox {MPa}$; however particle crushing is not considered here. To vary the packing density, values of the inter-particle friction coefficient, $\mu _{{comp}}$, were varied during this compression process, as listed in Table 1, to create a total of 32 samples. The sample lengths (L) were between 141D and 146D, where D stands for the particle diameter, with aspect ratios $\simeq$10. The void ratio (e) and mean coordination number $(C_{N})$ of the isotropic, random samples are summarised in Table 1.

Referring to Fig. 1, P-waves were generated by moving the lower source boundary (at $\hbox {z} = 0$) in the longitudinal (Z) direction. A single-period, sinusoidal pulse with phase shifted by $270^{\circ }$, maximum double amplitude (2A) of 5 nm and frequency $(f_{input})$ of 100 kHz was used for most of the simulations (Fig. 2a) so that A/$L \quad \simeq 7.0 \times 10^{-9}$ and $A/D = 9.8 \times 10^{-7}$. A nominal 100 kHz frequency pulse can excite a broad range of frequencies including main frequencies of up to 200 kHz (Fig. 2b). As discussed below, a higher nominal frequency of $f_{input} = 200\,\hbox {kHz}$ was used for two of the FCC simulations (test cases 3 and 4) when frequency domain analysis was performed (and so frequencies of up to 400 kHz were inserted). During wave propagation, the particle displacements in the Z direction and the stress responses in the Z direction at the source wall ($\hbox {z} = 0$) and receiver wall ($\hbox {z} = \hbox {L}$) were recorded.

Fig. 2

Displacement and normalised spectral amplitude of the source wall for input frequencies of 100 and 200 kHz

The present study used an inter-particle friction coefficient of 0.1 for the FCC samples during wave propagation simulations $(\mu _{wave})$. Mouraille and Luding [21] varied the inter-particle friction coefficient ($\mu$) values for their FCC DEM samples and reported a sensitivity to $\mu$ at $\mu < 0.01$ for their simulated test conditions. In the current study, for the random samples, if a coefficient of friction $\mu _{wave }= \mu _{comp}$ had been used during wave propagation the samples would not have exhibited an elastic response due to slip at the contacts, as many of the contacts carried a tangential contact force that was close to friction limit ($\mu \,{N}$ where N is the normal contact force) under isotropic confinement. Therefore, before applying the input motion, $\mu _{wave}$ was increased to give $\mu _{wave }=\mu _{comp}+ 0.1$. A check confirmed that an increment in friction coefficient exceeding 0.1 does not affect the sample response during wave propagation. Table 1 lists the friction coefficient values $(\mu _{wave})$ used during the wave propagation simulations. Viscous damping was applied once the sample packing became stable at the required confining pressure to remove any kinetic energy imparted to the particles during isotropic compression. No damping was applied to the particles during wave propagation.

The displacements of particles along a line connecting the source wall to the receiver wall were considered to give insight into the dynamic response. Representative particle displacements in the Z-direction at distances of approximately $z = 10D,\, 50D$ and 100D from the source wall are plotted in Fig. 3 for the FCC packing, and the dense and loose random samples at $\sigma =0.1\,\hbox {MPa}$. The compression wave (P-wave) propagates faster in the denser packing and arrives earlier at the monitored particles. It is also clear that the frequency of particle motion is affected by packing density. The amplitude of particle displacements is attenuated as the wave propagates particularly in looser samples. Dispersion of the wave, conversion of energy into either rotation or displacement in other directions, and frictional dissipation all contributed to this attenuation. However, frictional dissipation was not significant in the simulations as the inter-particle friction was increased by 0.1 before applying the stress disturbance. The simplified Hertz–Mindlin contact model used does not allow for frictional energy dissipation prior to sliding.

The influence of an increased confining stress on the samples’ responses is illustrated in Fig. 4 where displacements of a particle in the Z direction at about $z = 50D$ are compared for an input frequency $f_{input} = 100\,\hbox {kHz}$. Increasing isotropic stress reduces the void ratio of the samples as illustrated in the legend of Fig. 4. The amplitude of particle displacements increases clearly with increasing stress and the wave arrival time is reduced considerably with increasing stress.

The particle displacements along a line from the source wall to the receiver wall at various distances from the source wall (z) are displayed in Fig. 5 for representative FCC and random dense samples at $\sigma = 0.1\,\hbox {MPa}$ (test cases 2 and 6). For the random sample, rattler particles that are not involved in the coherent movement were excluded. In similar FFT analyses of received signals in wave propagation experiments, Jia [3] observed a low-frequency ballistic component followed by higher frequency inherent (scattered) waves. A similar trend is confirmed in the DEM data for the random samples; low amplitude high-frequency (or short-wavelength) waves that followed the more coherent low-frequency waves are evident at least over a short distance from the source as shown in Figs. 3 ($e = 0.687$) and 5b.

Fig. 3

Particle displacement at distances of $z = 10D$, 50D and 100D from the source wall at $\sigma = 100\,\hbox {kPa}$ (test cases 2, 6 and 30)

Fig. 4

Particle displacement at a distances of $z = 50D$ from the source wall at $\sigma = 0.1$, 1 and 10 MPa (test cases 2–4, 6–8 and 30–32). Input frequency of 100 kHz was used for all cases presented here

Fig. 5

Spatial and temporal plot of particle displacement at $\sigma = 100\,\hbox {kPa}$. a FCC sample (test case 2), b random dense sample (test case 6)

Referring to Fig. 5a, b, the first peaks propagate almost linearly with time and distance from the wall, the gradients of straight lines fitted to these data were used to obtain the P-wave velocities $(V_{P})$ for each sample. This approach was adopted for all samples. These $V_{P}$ data are summarised for all the stress levels and densities considered in Table 1 (as $V_{P,dL/dt}$) and Fig. 6. For all stress levels considered, $V_{P}$ increases with increases packing density (reducing void ratio) (Fig. 6a). When compared with the random samples, the FCC samples exhibit larger velocities (i.e. the extrapolated trend lines for the random samples lie below the FCC data points on Fig. 6a). Data on Fig. 6b are grouped by the void ratio at 1 kPa, $e_{1\,\mathrm{kPa}}$. $V_{P}$ increases with increasing stress (Fig. 6b) and as predicted by Hertzian contact theory, the power coefficient (b) in the $V_{P}-\sigma$ relationship is approximately 1/6 for the FCC samples where the changes in e are small and $C_{N}$ stays constant. The random samples show $b > 1/6$; in this case both e and $C_{N}$ change with stress and b increases with increases $e_{1\,\mathrm{kPa}}$.

Fig. 6

P-wave velocity ($V_{P}$, labelled as dL / dt in Table 1) for all test cases

Effective medium theory (EMT) enables estimation of the sample stiffness and elastic wave velocity [22]. The sample shear modulus $(G_{0})$ estimated using EMT was compared with DEM data in [16] where it was shown that for the FCC samples, EMT and DEM data agree well, while EMT overestimates $G_{0}$ for the random samples. The reason may be related to the assumption of affine displacements made in EMT as discussed in [23].

3 Eigenmode anaysis

If the mass and stiffness matrices of a system can be created, for example in a finite element or structural matrix analysis, the fundamental natural vibration modes can be found via eigenvalue decomposition, where the eigenvector gives the fundamental shape of vibration associated with an angular frequency ($\omega$) equal to the square root of the corresponding eigenvalue (e.g. [18]). As discussed in O’Sullivan and Bray [24] and Otsubo et al. [25], the particles in a DEM simulation are analogous to the nodes in a finite element model, while the contacts are roughly equivalent to the elements. This conceptual model of a granular material is used in implicit discrete element method formulations such as the particulate form of discontinuous deformation analysis (DDA) as outlined in [26,27,28]. For the 3-D analyses considered here, each particle has 3 translational degrees of freedom and 3 rotational degrees of freedom and so the diagonal mass matrix (M) includes the mass (m) and rotational inertia values for each particle.

The global stiffness matrix (K) can be created using the stiffness matrix assembly techniques described in [28] once the local contact stiffness matrix describing pairwise interaction of two particles is obtained. Here the local contact stiffness matrix was created using the data available in the DEM model once the inter-particle friction was set at $\mu _{wave}$. The local contact stiffness matrix is a $12\times 12$ element matrix; expressions for this matrix are given in [29] and the entries depend on the particle coordinates and contact stiffnesses. For the analyses presented here, the parameters required to construct the local stiffness matrix (particle coordinates, contact orientations and contact stiffnesses) were obtained from the DEM sample configurations following isotropic compression. For a sample composed of n particles, there are $6\times n$ degrees of freedom; for the systems considered here (K) consisted of up to 211,206$\times$211,206 elements for the random samples. The contact stiffnesses between particles and boundaries were also included in K. The eigenvalue decomposition is achieved by solving:

$$\begin{aligned} \left( {\mathbf{K}-{\varvec{\omega }}^{\mathbf{2}}{} \mathbf{M}} \right) {\varvec{\upvarphi }}=0 \end{aligned}$$

(1)

where ${\varvec{\omega }}^{2}$ are the eigenvalues and ${\varvec{\upvarphi }}$ are the eigenvectors; each eigenvalue $\omega _{i}^{2}$ is associated with a particular eigenvector $\varphi _{i}$. The frequency of the ith mode is $f_{i} = \omega _{i}/2\pi$. Here, built-in MATLAB functions (MathWorks, 2015) were used to obtain the eigenvalues and eigenvectors.

Previous researchers have used this approach to analyse the dynamic response of granular materials. Based on their 1-D chain model, Lawney and Luding [15] showed that the low-frequency eigenmodes are not affected by small random variations in particle mass. Somfai et al. [30] considered a 2-D configuration of disks, and linked eigenmodes to peaks observed in the received signal frequency spectrum. They also noted that the eigenmodes corresponding to the low non-zero eigenfrequencies have a similar vibration mode during wave propagation. Marketos and O’Sullivan [31] performed an eigenmode analysis for 2-D regular arrays and linked to a DEM simulation for the same packing. Application of eigenmode analysis to a 3-D packing is challenging, not just due to the increased number of degrees of freedom, but also because the eigenvector (mode) shapes are more complex.

Fig. 7

a Cumulative and b density distribution of eigenfrequencies for FCC sample (test case 2), random dense sample (test case 6) and random loose sample (test case 30) at $\sigma = 100\,\hbox {kPa}$

Fig. 8

Stress-dependency of maximum eigenfrequency using FCC sample, random dense sample (R0), random loose sample (R04), FCC sample excluding rotational degrees of freedom, and theory of dispersion relation for P-wave propagation (Eq. 10)

The natural frequencies, $f_{i}$, are plotted against the normalised mode number in Fig. 7a for the FCC sample and random dense and loose packings at 100 kPa (test cases 2, 6, 30); the corresponding density distributions are given in Fig. 7b. Figure 7a includes data for a FCC sample where the rotational degrees of freedom are ignored (FCC trans. only), this is discussed further below. Excluding consideration of FCC trans. only, the natural frequencies are distributed between 0.7534 and 211.2 kHz for the FCC sample and between 0 and 216.1 kHz, and 0 and 214.1 kHz for the random dense and loose samples, respectively. The very low frequency data ($\approx$0 kHz) are associated with the presence of rattler particles [30]. The density distribution indicates several peaks (local maxima) for the FCC packing which are not evident in the data for the random samples. Figure 8 illustrates the variation in the maximum eigenfrequency $(f_{i,max})$ with stress level for the three sample types, again data for the FCC sample where rotational degrees of freedom are suppressed are also included. The three samples exhibit similar values where the differences between them were <3% across the wide range of stresses between 10 kPa and 10 MPa. The maximum eigenfrequency relates to the element with the highest stiffness:mass ratio in the system [32], so that a lower mass gives a higher eigenfrequency. Following O’Sullivan and Bray [24], the mass of each particle is distributed to its contacts (which represent the elements) so when the contact density is higher, less mass is assigned to each contact. Assuming a uniform distribution of contact stiffness, the maximum value of the stiffness:mass ratio is therefore determined by the particle with the greatest number of contacts. While the random samples have average coordination numbers that are significantly lower than the FCC coordination number ($C_{N,1kPa}=5.91$ and 3.84 in comparison with 12), in each case there are local regions of dense packing so that particles with contact numbers of 11–12 exist in all the random dense samples and contact numbers of 9–10 are locally found in the random loose samples. Even though only a few particles show these high contact numbers this explains the lack of sensitivity of the maximum eigenfrequency to the packing.

Fig. 9

Correlation indices against eigenfrequencies for a FCC sample (test case 2) and a random dense sample (test case 6) at $\sigma = 100\,\hbox {kPa}$

To find the fundamental eigenmodes associated with P-wave propagation, a correlation index $(\chi _{zi})$ was calculated for each mode, i:

$$\begin{aligned} \chi _{zi} =\frac{1}{n}\sum _{s=1}^n {\overline{u} _{zi,s}^2 } \end{aligned}$$

(2)

where $\bar{{u}}_{{ zi,s}}= \hbox {Z}$ component of the normalised eigenvector for particle s. When $\chi _{zi} = 1$ the displacement of all the particles is in the Z-direction (i.e. the eigenvectors have no X or Y components). Processing Eq. 2 for the full-set of eigenvectors is computationally expensive, and so for the analyses presented here a linear chain of particles connecting the source and receiver wall boundaries was considered. The index $\chi _{zi}$ is plotted against $f_{i}$ for both a FCC and a random sample at $\sigma = 0.1~\hbox {MPa}$ in Fig. 9a. For the FCC packing, modes giving $\chi _{zi} = 1$ were observed across the entire range of eigenfrequencies. For the random dense sample, modes with $\chi _{zi} > 0.9$ are evident for $f_{i} \le 10\,\hbox {kHz}$; however, the maximum $\chi _{zi}$ value observed at a given frequency drops to about 0.33 for $f_{i} >15\,\hbox {kHz}$, indicating arbitrary displacements occurring in any directions. For loose samples the maximum $\chi _{zi}$ value observed tends to decrease below 0.9 at lower $f_{i}$ values in comparison with the data on Fig. 9b, while at a higher stress the maximum $\chi _{zi}$ values attained are higher (>0.9) and these high $\chi _{zi}$ values are observed at higher $f_{i}$ values than those illustrated on Fig. 9b.

Fig. 10

Normalised eigenvectors in the Z-direction at fundamental resonant modes at $\sigma = 100\,\hbox {kPa}$. a–f correspond to $\hbox {r} = 1, 2, 5, 10, 50, 200$ resonant modes for FCC sample (test case 2), and g–l correspond to $\hbox {r} = 1, 2, 5, 10, 15, 20$ resonant modes for random dense sample (test case 6)

Mode shapes associated with typical resonant frequencies are illustrated in Fig. 10 for the FCC and random packings. The boundary conditions in the Z-direction considered in this analysis are the fixed-wall boundaries used in the DEM simulations. Thus the wavelength $(\lambda _{r})$ and wave number $(\kappa _{r})$ for resonant mode r can be expressed as:

$$\begin{aligned} \lambda _r= & {} \frac{2L}{r} \end{aligned}$$

(3)

$$\begin{aligned} \kappa _r= & {} \frac{2\pi }{\lambda _r }=\frac{\pi }{L}r \end{aligned}$$

(4)

The agreement between the frequencies corresponding to peaks in $\chi _{zi}$ values and resonant modes of the sample is confirmed in Fig. 10. In Fig. 10a–d the mode shapes (determined from the z-component of eigenvector) associated with the 1st, 2nd, 5th, 10th maxima of $\chi _{zi}$ are shown; the wavelengths associated with these sinusoidal mode shapes agree with Eq. 3. The mode shapes illustrated in Fig. 10e, f also correspond with $\chi _{zi} = 1$; however, referring to Figs. 7b and 9a, at these eigenfrequencies there are a larger number of eigenmodes present with very similar eigenfrequencies. Therefore the fundamental modes were identified both from the $\chi _{zi}$ value and visual observation of the mode shapes. Thus the 1st mode of resonance (Fig. 10a) at 1.06 kHz gives a wave length $\lambda = 2 L$, while the 200th mode of resonance (Fig. 10f) at 137.6 kHz gives $\lambda =L/100$. At the 1st mode of resonant vibration, all the particles move in the same direction ($\Delta \,\hbox {z}>0$), while for the 200th mode neighbouring layers move in opposite directions; in all cases the horizontal (x, y) components of the eigenvectors were negligible. As shown in Fig. 9a, fundamental frequencies higher than 137.6 kHz exist for the FCC sample; however, these modes excite rotational components and the corresponding eigenvectors were more complex than the purely compressional modes with displacement restricted to be in the Z-(vertical) direction. For the random packing the modes are more easily identifiable by simply considering the maxima of $\chi _{zi}$ in Fig. 9b. Referring to Fig. 10g–k the lowest resonant modes were clearly identifiable just as in the case of FCC packing and in agreement with the observations of Somfai et al. [30]. As $f_{i}$ increases and $\chi _{zi}$ decreases, the resonant eigenvectors identified do not have a clean sinusoidal shape. For the random samples the rattler particles are not involved in any mode of vibration. The combinations of $f_{r}$ and $\kappa _{r}$ obtained for the first 10 resonant modes for all the packings considered at $\sigma = 0.1~\hbox {MPa}$ are tabulated in Table 2.

Table 2 Resonant frequency $(f_{r})$ and corresponding wavenumber $(\kappa _{r})$ for various void ratio at $\sigma = 100\,\hbox {kPa}$

A comparison of data from the eigenmode analysis with the DEM wave propagation simulation serves to verify the ability of the DEM model to correctly give data on the system’s elastic properties. Using the measurements of stress recorded at the source and receiver walls, and applying frequency domain analyses [9] the group and phase velocities were found at $\sigma = 0.1~\hbox {MPa}$ as given in Fig. 11a, b for the FCC and random dense samples, respectively. Note that the inserted signal contains a range of frequencies and the phase velocity, $V_{phase}$, is the velocity of a particular component. The group velocity, $V_{group}$, is the velocity with which the overall waveform propagates through the sample. While there are some fluctuations in the data for the random sample, in both cases the group and phase velocities approach each other at low frequencies, as expected. These velocities are also similar to the $V_{P}$ based on direct measurements (dL / dt) as listed in Table 1. The group and phase velocities were also directly calculated from the eigenmode data as $V_{group} =\frac{d\omega }{d\kappa }$ and $V_{phase} =\frac{\omega }{\kappa }$, where $\omega (=\! 2\pi f$) and $\kappa$ are the angular frequency and wave number for the fundamental modes, respectively; these can be derived from the data in Table 2. This analysis of the eigenmode data is plotted in Fig. 11c, d, and for the initial (low frequency) modes considered, the group and phase velocity data calculated using both methods agree and they agree with $V_{p,dL/dt}$. Note that [16] considered alternative methods of interpreting the DEM dataset in the time and frequency domain and obtained a good match between the shear wave velocity values obtained from direct measurement (dL/dt), the peak-to-peak method, the approach given in [9], and 2-D dispersion. The direct comparison with the eigenmode analysis presented here further increases confidence in the use of simple interpretation of the received signal to infer elastic properties for these systems.

Fig. 11

Group velocity and phase velocity at $\sigma = 0.1\,\hbox {MPa}$ in comparison with directly measured P-wave velocity, $V_{P}$ (dL / dt). a FCC sample (test case 2), b Random dense sample (test case 6), c FCC sample in comparison with results of eigenmode analysis, d Random dense sample in comparison with results of eigenmode analysis

4 Dispersion relation for FCC packing

The dispersion relation describes the relationship between angular frequency $\omega$ and wave number $\kappa$. The derivation of the dispersion relation for a 1-D chain of identical spheres has been previously shown [33]. The theory can be extended to a 3-D regular array of equal spheres [33,34,35] to give:

$$\begin{aligned} \omega =2\sqrt{\frac{C}{m}}\left| {\sin \frac{l}{2}\kappa } \right| \end{aligned}$$

(5)

where $C=$ stiffness constant between neighbouring layers, $l =$ distance between the neighbouring layers and $m=$ mass of a particle. As $\kappa \rightarrow 0$ (long wave limit):

$$\begin{aligned} V_{longwave} =V_{group,\max } =V_{phase,\max } =l\sqrt{\frac{C}{m}} \end{aligned}$$

(6)

For ideal regular packings, there is a linear relationship between the maximum transmitted frequency, i.e. low-pass frequency $(f_{low-pass})$ and the long wave velocity $(V_{longwave})$:

$$\begin{aligned} V_{longwave} =\pi l\, f_{low-pass} \end{aligned}$$

(7)

The layer stiffness for a FCC packing $(C^{FCC})$ in the Z-direction associated with a compressional distortion can be expressed using the normal and tangential contact stiffnesses ($k_{N}$ and $k_{T}$, respectively) considering its geometry:

$$\begin{aligned} C^{FCC}=2 \left( {k_N^{^{FCC}} +k_T^{^{FCC}} } \right) \end{aligned}$$

(8)

Thus, $k_{T}$ also contributes to the layer stiffness; however rotation of spheres is not involved in the motion considered. Here the $k_N^{FCC}$ and $k_T^{FCC}$ data were extracted from DEM results to calculate $C^{FCC}$. In the absence of DEM data, the $k_N^{FCC}$ and $k_T^{FCC}$ values can be estimated as explained in [36, 37]; a cross-check confirmed that this approach gives equivalent data. For P-wave propagation in a FCC packing, the dispersion relationship is then given by:

$$\begin{aligned} \omega =2\sqrt{\frac{C^{FCC} }{m}}\left| {\sin \frac{l^{FCC} }{2}\kappa } \right| \end{aligned}$$

(9)

where $l^{FCC}$ is the layer distance and is approximately $\sqrt{2}R$ for the considered direction. The maximum transmitted frequency, i.e. the low-pass frequency limit, $f_{low-pass}$, is then:

$$\begin{aligned} f_{low-pass} =\frac{\omega _{low-pass} }{2\pi }=\frac{1}{\pi }\sqrt{\frac{C^{FCC} }{m}} \end{aligned}$$

(10)

The low-pass frequencies obtained for FCC samples at various stress levels using Eq. 10 are given in Table 1 as $f_{low-pass}^{theory}$.

Fig. 12

Frequency spectra at varying distances from the source wall at $\sigma = 100\,\hbox {kPa}$. a $e = 0.353$, FCC sample (test case 2), b $e = 0.544$ (test case 6), c $e = 0.646$ (test case 22), and d $e = 0.687$ (test case 30)

5 Frequency domain response

Using the DEM dataset in combination with the eigenvalue decomposition and the dispersion relationship enabled a comprehensive picture of the frequency domain response of the system to be developed. The synthesis of the available data focussed on two aspects of the response: the maximum transmitted frequency and resonance.

5.1 Maximum transmitted frequency

As noted above, granular materials act as low-pass filters to inserted seismic/stress/acoustic waves, removing the high-frequency contents of the signal with distance. The low-pass frequency limit depends on the particle characteristics and the porosity of the assembly [38]. Following Mouraille and Luding [12], the variation in the frequency content of the particle displacement responses with the distance from the source wall can be investigated by considering a linear chain of particles connecting the source and the receiver. Figure 12 was developed by repeatedly applying a fast Fourier transform (FFT) to the particle displacements along such a chain to create a plot of frequency versus distance from the source wall where the shading gives the associated amplitude. Four samples were considered, given as test cases 2, 6, 22 and 30 in Table 1, all at $\sigma = 0.1\,\hbox {MPa}$. The regular lattice structure of the FCC packing enables significantly larger frequencies to be transmitted in comparison with the random packings. The maximum transmitted frequency $(f_{low-pass})$ varies with distance in all cases. The trend for $f_{low-pass}$ to decrease with distance for the FCC sample (Fig. 12a) resulted from the short recording time period [12]. The recording time was limited to exclude interference in the signals due to reflection at the receiver wall. For random packings, high frequencies are evident close to the source wall (<0.05 m), and these high frequencies are removed gradually as the waves propagate. A constant, stable value of maximum frequency was attained after a distance from the source wall and $f_{low-pass}$ was defined for this stable frequency. The $f_{low-pass}$ values considered here correspond to the coherent low-frequency wave rather than the high-frequency (or short-wavelength) scattered waves measured near the source wall. The stress-dependency of $f_{low-pass}$ was examined; Fig. 13 confirms the observations based on data in [13] and shows that $f_{low-pass}$ increases with stress for the random dense packing (test cases 7 and 8).

Fig. 13

Frequency spectra at varying distances from the source wall. a $\sigma = 1\,\hbox {MPa}$, $e = 0.539$, b $\sigma = 10\,\hbox {MPa}$, $e = 0.516$

To quantify $f_{low-pass}$ for each sample, a specific threshold value had to be determined to avoid the effects of the low amplitude high-frequency data (noise) that always appeared during the wave propagation simulations. This noise was partially a consequence of the lack of damping in the wave propagation simulations. In this study, the $f_{low-pass}$ value was taken to be the frequency associated with a displacement amplitude of 2% of the maximum value. This threshold was decided based on visual analysis using the $f_{low-pass}$ - distance plot (e.g. Fig. 12). However, the $f_{low-pass}$ values obtained depended on the threshold value, with the random samples being more sensitive than the FCC samples. The $f_{low-pass}$ values determined using a 1% threshold exceeded those obtained using a 2% threshold whereas the $f_{low-pass}$ values were similar when thresholds of either 2 or 3% were used. Further analyses of the sensitivity of both $f_{low-pass}$ and $\lambda _{low-pass}$ to the threshold value indicate that where thresholds of 1% or less are used the calculated $f_{low-pass}$ and $\lambda _{low-pass}$ values are affected by the noise in the data. For completeness, Table 1 summarises the $f_{low-pass}$ data based on thresholds of 1 and 2%; the following discussions and associated figures are based on using a 2% threshold.

For the FCC sample, the three approaches agree; maximum transmitted frequencies of $f_{low-pass} = 137.7$, 137.6 and 138.1 kHz are obtained using dispersion theory (Eq. 10), eigenmode analysis and DEM simulation (Table 2), respectively. It is also interesting to examine the link between $f_{low-pass}$ and the maximum eigenfrequency, $f_{i,max}$. Referring to Fig. 8, when the rotational degrees of freedom are included, the $f_{i,max}$ values are significantly larger than $f_{low-pass}$; e.g. for the random dense sample at 100 kPa $f_{i,max} = 216.1\,\hbox {kHz}$, while $f_{low-pass}$ is 21.9 kHz. However, for the FCC sample, when the rotational degrees of freedom are excluded from the eigenvalue decomposition analysis, $f_{low-pass}\approx f_{i,max}$; the $f_{low-pass}$ data obtained from dispersion theory for the FCC sample are overlain on Fig. 8. This is an interesting result as it links the natural vibration frequencies of the sample to the low-pass frequency limit.

Fig. 14

Dispersion relation of particle displacement at $\sigma = 100\,\hbox {kPa}$. a $e = 0.353$, FCC sample (test case 2), b $e = 0.544$ (test case 6), c $e = 0.646$ (test case 22), and d $e = 0.687$ (test case 30)

The dispersion relation can be obtained from the DEM data [12]. Figures 14 and 15 show the dispersion relation for the samples discussed in Figs. 12 and 13. The results of eigenmode analysis summarised in Table 2 are overlain on the DEM data in Figs. 14 and 15 as open white circular symbols for the random sample and open black circular symbols for the FCC sample. For the FCC sample the theoretical dispersion relationship (Eq. 9) is also shown as a dashed line. For the random samples, initially the relationship is linear, and this is captured by eigenmode analysis. However, the curvature of the dispersion relation at higher wave numbers (or frequencies) is not observed as in the case of the FCC packing.

Fig. 15

Dispersion relation of particle displacement. a $\sigma = 1\,\hbox {MPa}$, $e = 0.539$, b $\sigma = 10\,\hbox {MPa}$, $e = 0.516$

Fig. 16

Low-pass frequency $(f_{low-pass})$ for all test cases

Figure 16 summarises the combined influences of void ratio and stress on $f_{low-pass}$. For the FCC samples at $\sigma = 1$ MPa and 10 MPa, $f_{input} = 200\,\hbox {kHz}$ was used (Fig. 2) so that the low-pass frequency could be observed clearly. The observed trends exhibited a similarity with the $V_{P}$ data in Fig. 6; $f_{low-pass}$ is observed to increase with increased stress and packing density. This suggests a relationship between $V_{P}$ and $f_{low-pass}$; Fig. 17 shows the $V_{P }-f_{low-pass}$ relationship in which the FCC sample responses exhibit a linear relationship. This agrees with the dispersion relation theory where the maximum frequency is proportional to $V_{P}$ (long wave velocity, Eq. 7). On the other hand, the relationship for the random samples was slightly different. If the data are grouped by $e_{1\,\mathrm{kPa}}$, the $V_{P }-f_{low-pass}$ relationship is again linear, with a slope of between 1.2 and 1.4; this slope increases with reducing packing density. Note that these data were generated assuming an (arbitrary) amplitude threshold of 2% of the maximum displacement; if the threshold amplitude is reduced the data shift upwards, but the overall trends are invariant.

Fig. 17

Relationship between P-wave velocity $(V_{P})$ and low-pass frequency $(f_{low-pass})$ for all test cases

Fig. 18

Influence of void ratio on low-pass wavelength $(\lambda _{low-pass})$ normalised by particle diameter for all test cases

The low-pass wavelength $(\lambda _{low-pass})$ which corresponds to $f_{low-pass}$ for each sample was obtained using the DEM dispersion relation plot (as illustrated for example in Figs. 14, 15) (recall that $\lambda =2\pi$/$\kappa$); $\lambda _{low-pass}$ values considered here correspond to the coherent low-frequency wave as in the case for $f_{low-pass}$. The resultant $\lambda _{low-pass}$ data are tabulated in Table 1 based on both the 1 and 2% thresholds and Fig. 18 illustrates the variation in $\lambda _{low-pass }$ (based on the 2% threshold) with void ratio. The geometry of the FCC samples is invariant and so the resultant $\lambda _{low-pass}$ is insensitive to changes in void ratio and stress, which contrasts with the observations for $V_{P}$ or $f_{low-pass}$. $\lambda _{low-pass}$ increases with increasing void ratio and seems to be independent of stress level. In contrast, for the random samples there are variations in the sample topology with stress or $\mu _{comp}$. The data here give $\lambda _{low-pass}$ values of between about 7 and 18 times the particle diameter (D) for the 2% threshold, and 5 to 12D for the 1% threshold. Santamarina et al. [11] and Santamarina and Aloufi [10] assumed the particle diameter to be an internal scale ( $\alpha$) of granular materials where $\lambda _{low-pass} = 2 \alpha$, while Mouraille and Luding [12] took $\alpha$ to be the layer distance for a FCC sample, i.e. $\alpha = \sqrt{2}R$. The DEM and eigenmode analysis data for the FCC packing support the observation by Mouraille and Luding [12]. For the random samples; $\lambda _{low-pass}$ is density dependent (Fig. 18). It seems logical that there must be some link between void ratio and layer distance; a lower void ratio indicating a smaller layer distance, however in a random packing this link cannot be determined simply. It seems more appropriate to qualify the conclusions in [10, 11] and state that $\lambda _{low-pass}$ depends on both void ratio and particle size.

Fig. 19

Gain factor. a FCC sample at $\sigma = 0.1$, 1, 10 MPa (test cases 2–4), b Random dense sample at $\sigma = 0.1$, 1, 10 MPa (test cases 6–8), c FCC sample at $\sigma = 0.1~\hbox {MPa}$ plotted with resonant frequencies, d Random dense sample at $\sigma = 0.1\, \mathrm{Mpa}$ plotted with resonant frequencies

5.2 Resonance

Following earlier geomechanics contributions [9, 17], a frequency domain technique was applied that considered the gain factor: the ratio of the frequency spectra of the stress responses at the source and receiver walls. Taking the stress responses at the boundary walls as the input for FFT analyses, gain factor data for the FCC samples and random samples at $\sigma = 0.1$, 1.0 and 10 MPa (test cases 2–4 and 6–8) are illustrated in Fig. 19a, b across the entire range of received frequencies. The maximum value of the gain factors exceeds 1 because of the fixed-end condition at the receiver wall, i.e. the kinetic energy is converted into strain energy. In general, the gain factor decreases with increasing frequency. As is clear from the data presented in Figs. 12 and 13, higher frequencies propagate through the FCC samples in comparison with the random samples. Restricting consideration to the low frequency data <10 kHz, Fig. 19c, d compare the gain factor with the resonant frequencies data from Table 2. The frequency interval at which local maxima in the gain factor are observed roughly corresponds to the frequency interval at which natural (resonant) frequencies are observed. The peaks in the gain factor neither correspond exactly with resonant modes exhibiting mode shapes that reflect the applied disturbance; nor do they correspond with resonant frequencies having more complex mode shapes. This contrasts with the discussions/hypotheses in [17]. Somfai et al. [30] also did not find a perfect match between the resonant frequencies and actually excited frequencies for their 2-D DEM analyses.

6 Conclusions

This contribution aimed to address two questions arising from previous research and a review of the literature:

• 1. What are the factors that determine the low-pass frequency limit, $f_{low-pass}$, and can measurement of $f_{low-pass}$ provide useful information about the sample?

• 2. Can the fundamental vibration modes of a sample be easily identified from the received signals in laboratory seismic tests?

To address these questions, data were generated using a series of DEM simulations of planar compression wave propagation in both FCC and randomly generated samples. In all cases the particles used were monodisperse spheres to isolate inertia effects from the observed response. Applying approaches used in implicit DEM formulations and matrix structural analysis, mass and stiffness matrices were formed and eigenmode analyses were carried out. In addition, for the FCC samples, a theoretical dispersion expression was derived. The group velocity and phase velocity obtained from stress responses at the source and receiver wall using DEM simulation exhibited good agreement between the velocities estimated using eigenmode analysis where the dispersion theory also agreed. The good agreement in the data serves as a cross-validation of the three approaches considered. The agreement also verifies the use of simple analysis of received signals to infer elastic parameters from laboratory geophysics experiments.

Considering the frequency limit, the P-wave velocity, $V_{P}$, and the low-pass frequency limit, $f_{low-pass}$, exhibited similar sensitivities to variations in stress and packing density. Increasing either stress or density resulted in a larger $V_{P}$ and higher $f_{low-pass}$. For the FCC samples with a stable regular lattice packing, Hertzian contact theory gives a linear relationship between $V_{P}$ and $f_{low-pass}$; this was confirmed from the DEM simulation data. On the other hand, the configuration of a random packing depends on packing density and stress level. The resultant relationship between $V_{P}$ and $f_{low-pass}$ differed slightly from that for a FCC packing; however a linear relationship was still observed. The low-pass wavelength $\lambda _{low-pass}$ was not sensitive to stress level but was affected considerably by packing density. For the FCC samples where the packing was invariant $\lambda _{low-pass}$/$D \approx \sqrt{2}$, i.e. $\lambda _{low-pass}$ is twice the layer spacing. Considering the low-frequency compression waves the ratio $\lambda _{low-pass}$/D observed for the random samples varied between 5 and 18 depending on the void ratio and the threshold used to identify $f_{low-pass}$. This observation does not relate to the low amplitude high-frequency scattered waves that emerged subsequent to the main low frequency response. These data highlight that for non-crystalline materials it is difficult to quantitatively relate $\lambda _{low-pass}$ to a characteristic of the sample. The layer spacing relates to void ratio and particle size and establishing a link between layer spacing and these two parameters is non-trivial.

The natural (fundamental) frequencies of the samples were obtained using eigenvalue decomposition of the mass and stiffness matrices derived from the DEM data. The resonant modes were identified by searching for the eigenvectors that had negligible components in the X- and Y-directions, i.e. those mode shapes were exclusively vertical. For the FCC samples, up to 200 resonant modes were found; i.e. the number of resonant modes agreed with the number of layers in the sample. The mode shapes were sinusoidal and, in agreement with theory, for a given mode, the relationship between the wavelength $\lambda _{r}$ and the mode number (r) was given by $\lambda _r =\frac{2L}{r}$. For the random samples the mode shapes associated with shorter wavelengths/higher frequencies could not easily be identified using eigenmode analysis (using the DEM data the dispersion relation could also not easily be identified for these wavelength:frequency combinations). In principle, if the data for the high frequency responses were clearer, the number of modes could be determined with confidence to get a measurement of the layer spacing which then could be related to $\lambda _{low-pass}$. The resonant frequencies and corresponding wavelengths agreed with the dispersion relation obtained using DEM data; for the FCC samples there was also agreement with the theoretical dispersion relationship. The relationship between the low pass frequency limit $(f_{low-pass})$ and the maximum eigenfrequency $(f_{i,max})$ of samples was also investigated. For P-wave propagation, $f_{low-pass} < f_{i,max}$ for all the samples; however, $f_{low-pass} \approx f_{i,max}$ was observed for FCC samples where the rotational degrees of freedom were excluded from the eigenvalue decomposition analysis. The ratio between the spectrum of the received signal and the spectrum of the inserted signal was taken as the gain factor. While resonant frequencies were found close to the local maxima in the gain factor, the data presented here do not support earlier hypotheses linking these maxima to resonant frequencies, as the local maxima in the gain factor do not coincide with resonant frequencies corresponding to a motion that agreed with the applied disturbance, nor do they give an exact match with any other resonant frequency.