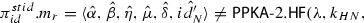Pragmatic authenticated key agreement for IEEE Std 802.15.6

Abstract

The IEEE Std 802.15.6 is the latest international standard for Wireless Body Area Networks. The security of communication in this standard is based upon four elliptic-curve-based key agreement protocols. These protocols have been shown to exhibit serious security vulnerabilities but surprisingly, do not provision any privacy guarantees. To date, no suitable key agreement protocol has been proposed which fulfills all the requisite objectives for IEEE Std 802.15.6. In this paper, two key agreement protocols are presented which, in addition to being efficient and provisioning advance security properties, also offer the essential privacy attributes of anonymity and unlinkability. We develop a formal security and privacy model in an appropriate complexity-theoretic framework and prove the proposed protocols secure in this model.

1 Introduction

Wireless Body Area Networks (WBANs) consist of miniaturized computing devices which can be fitted inside or around the human body [7]. Through use of short range communication technologies, these devices talk to a designated centralized node (Hub) which further communicates with external networks via a Gateway [23]. The general layout of a typical WBAN is illustrated in Fig. 1. Note that the Hub and Gateway are functionally two separate entities, but are usually combined into a single physical node. Mindful of the peculiarities of communicating in and around the human body, the IEEE published IEEE Std 802.15.6 [3] for WBAN communications in 2012. As high power transmissions are harmful to humans and nodes in a WBAN are energy constrained, this standard provisioned an optional two-hop communication architecture to enable resource-constrained nodes to minimize transmissions when communicating with the Hub.

In addition to conventional security guarantees, privacy is of utmost importance for typical target application areas such as healthcare and the military [29]. The elliptic-curve-based session key agreement methods of IEEE Std 802.15.6 have been shown to have security weaknesses [28], but also do not provide the privacy features that should be expected of a WBAN [20]. In this paper, we present two key agreement protocols which render a comprehensive range of security and privacy properties, which are regarded as essential [20] for WBANs. We start by presenting a network and adversary model for WBAN key agreement and elaborating upon the desired security, privacy and functional objectives.

Fig. 1

Generic architecture of a typical WBAN

1.1 Network and adversary model

We begin by describing a system model suitable for the deployment scenarios of WBANs. In this model, a System Administrator (SA) initializes the network. The network is composed of three types of nodes; a Hub Node (HN), Intermediary Nodes (IN) and Normal Nodes (N). As the HN is usually a resourceful device with better hardware protection mechanisms in place, we assume it to be trusted and its long-term secret Master Key to be protected. As the role of HN is usually undertaken by a modern smart phone in a generic WBAN, this argument is supported aptly by the real world example of the FBI-Apple encryption dispute [2] where even for resourceful parties like government agencies it is not easy to crack into a smart phone. Normal nodes N are resource constrained and their transmission range is assumed to be limited; in particular, they are not always able to communicate directly with HN. Intermediary nodes IN are also located in and around the body but, at a particular time instance, are in direct communication with both N and HN, thus acting as intermediary nodes for the purpose of relaying traffic between HN and N when required. We assume a Dolev-Yao [12] adversary ${\mathcal {A}}$   who can listen, modify and synthesize any message of his choice in this model.

1.2 Desired objectives

The security of traffic in IEEE Std 802.15.6 is protected using authenticated encryption, which requires the establishment of symmetric session keys. The procedure for agreeing these keys is thus critical to the overall security and privacy of a WBAN. Next we list down the requisite properties (and where required the associated rationale) of a Privacy-Preserving Key Agreement (PPKA) protocol to be executed between a node N and HN

1.2.1 Security properties

Mutual entity authentication Entity authentication is the process by which one entity (the verifier) is assured of the identity of a second entity (the claimant) [27]. The PPKA should provision mutual entity authentication between N and HN.

Mutual “implicit” key authentication The assurance that only a particularly identified other party may possibly know the negotiated key [27]. Mutual “implicit” key authentication is required between N and HN.

Known key security An adversary compromising a session key in a single session should not impose any threat to the session key security in any other sessions.

Key randomness The assurance that any successful key agreement should output a uniformly distributed session key among the set of all possible session keys [26].

Partial forward secrecy The compromise of the long-term secret of a node N should not enable an adversary to compromise previously established session keys of that node. Partial Forward Secrecy (PrFS) is crucial as client nodes (unlike HN) in typical WBAN deployment scenarios are not tamper-proof and their internal storage can be accessed by an adversary easily. Note that as already explained earlier in Sect. 1.1, we do not consider the compromise of the long-term secret of HN. This enables us to consider a more pragmatic version of forward secrecy for WBANs. PrFS is a well documented [6] and discussed [5, 8, 9, 24] security notion for key exchange protocols which considers the compromise of the long-term keys of a subset of protocol participants. We remark that PrFS is distinct from the related notion of Weak Forward Secrecy (WFS) [17] where the concerned adversary is a passive one. PrFS considers an active adversary.

Key compromise impersonation (KCI) resilience Suppose N’s long-term secret gets disclosed. Clearly an adversary that knows this value can now impersonate N, since it is precisely this value that identifies N. However, it is highly desirable that this loss should not enable an adversary to impersonate other entities to N [19]. Consider the scenario where a cardiac pacemaker is part of a WBAN deployed upon a chronic patient by a hospital for remote administration and monitoring purposes. The leakage of the pacemaker’s long-term secret should not enable the adversary to issue “stop” commands to the pacemaker by impersonating as the hospital administrator. Such a case could potentially lead to a life threatening situation.

Replay prevention An adversary should not be able to successfully replay previously captured copies of legitimate messages between the protocol participants.

Desynchronization resistance If the authentication parameters get updated during the protocol execution, then usually the participants need to have the same updated values at the end of a protocol run. Otherwise, they will not authenticate each other in later sessions and we say they have been desynchronized. In a desynchronization attack, the adversary forces the protocol participants to update their authentication parameters to different values. A PPKA needs to be resistant to these types of attacks.

1.2.2 Privacy properties

We focus on two privacy aspects:

Node anonymity An adversary ${\mathcal {A}}$, who is observing all communications, should not be able to learn the identity of any node N who is participating in a PPKA protocol with HN. The privacy attribute of anonymity is a necessity for typical application scenarios of WBANs, such as healthcare and military.

Session unlinkability An adversary ${\mathcal {A}}$, who is observing communications, should not be able to link one successfully executed PPKA session of node N to another successfully completed session of the same node. Session unlinkability is imperative in addition to anonymity. Although the PPKA sessions could be anonymous, if the adversary is able to link various PPKA sessions and group them together then ${\mathcal {A}}$ would be able to attribute a group to a particular node with high probability, due to his knowledge of the operations of the WBAN. For example, consider a medical WBAN in which a pacemaker is supposed to communicate with the remote healthcare providers every five minutes, while the body temperature sensor communicates only three times per day.

1.2.3 Functional requirements

Support for multi-hop communication As discussed in Sect. 1.1, depending upon the network topology, nodes would either be communicating directly with the Hub Node HN or via an Intermediary Node IN. Therefore, the PPKA protocol should be designed to be suitable for both single-hop and two-hop communication modes of [3].

Energy consumption As nodes in a WBAN are severely energy constrained, the PPKA protocol needs to be minimalistic in terms of computation, communication and storage overhead. Energy consumption in WBANs is dominated by radio communications [10], which mainly depends on the number of bits to be transmitted within the network. Consequently, the PPKA protocol should be designed such that the number of bits to be exchanged between the protocol participants and the computational overhead for nodes N should be minimal.

Stateless HN HN is the consistent nucleus of the network whose lack of accessibility will have devastating effects on the complete WBAN. As the network topology in WBANs is dynamic where client nodes join and leave the network on a frequent basis; it is imperative for HN’s accessibility that it be independent of such dynamism. Consequently, an important requirement is that the PPKA protocol should not require HN to maintain a state of the WBAN nodes.

Table 1 Comparison of security and privacy features

1.3 Design principles

1.3.1 Offloading of expensive operations

As nodes in a WBAN are resource constrained, it makes sense to offload energy-expensive operations to more resourceful entities such as SA and HN. An example of this is discussed in more detail in Sect. 4.2.

1.3.2 Minimizing the implementation footprint

Ideally, the proposed solution should not introduce new cryptographic primitives as this will adversely affect the implementation footprint (hardware and memory). Specifically, we aim to use the already specified block cipher function in [3] for achieving the various security and privacy objectives. A more detailed discussion is given in Sect. 4.2.

1.3.3 Reducing management costs

A PPKA solution should not place management costs on the WBAN nodes after the network initialization. Consider the situation where a third party wants to add its node (for example a fitness tracker) to an already deployed WBAN. The third party should be able to contact the SA, who (after registration of the new node) would dispatch it to the WBAN owner, who begins using the new device upon receipt. Note that all this was done without interacting with the currently operational WBAN.

1.4 Related work

Toorani [28] discovered various security weaknesses in the key agreement methods of IEEE Std 802.15.6, all of which were susceptible to Key Compromise Impersonation attacks as well as attacks on forward secrecy. Wang and Zhang [30] proposed a key agreement scheme for WBANs that claimed to provide anonymity and unlinkability in addition to the requisite security guarantees. However, Jiang et al. [14] show that [30] is vulnerable to client impersonation attack and thus lacks mutual authentication. They proposed an authenticated key agreement scheme which rectified this flaw. However, their scheme was based on computing bilinear pairings; which is not suitable for deployment in resource constrained WBANs. To avoid the overhead of managing public-key certificates, He et al. proposed a certificateless authentication scheme [13], which provides anonymity and unlinkability. However, the computation and communication overheads associated with their scheme also render it unsuitable for WBAN deployment. Recently, Li et al. [21] presented an authenticated key agreement scheme based only upon symmetric cryptographic primitives. This is an attractive proposal since there is no requirement of any additional infrastructure and the associated computation and communication overheads are negligible. The authors claimed that this scheme achieved almost all of the security and privacy objectives defined in Sect. 1.2.

1.5 Contributions and paper organization

1.5.1 Previous version

This manuscript is full version of the paper presented at IEEE TrustCom, 2018 [15]. The main differences from the conference version are as follows: Firstly, the list of required security objectives is more comprehensive after inclusion of PrFS and KCI resilience. Moreover, the introduction section has been further enhanced by addition of the design principles of the proposed protocols. Furthermore, a new Sect. 4 providing discussion about various aspects of the proposed protocols is also part of this manuscript. This manuscript successfully answers the open question put forward in [15] regarding the feasibility of a privacy-preserving authenticated key agreement protocol for IEEE Std 802.15.6 offering PrFS and KCI resilience without any dependence on public key cryptography. The second key agreement protocol (termed PPKA2 within this manuscript) is one such protocol satisfying all the requisite security and privacy requirements. Further additional contributions of this manuscript are as below:

• We enhance our previous analysis [15] of [21] which, in addition to showing that Li et al. scheme does not provide session unlinkability and forward secrecy, also exhibits its vulnerability to KCI attacks.

• In addition to the key agreement protocol () proposed in [15], which provided session unlinkability and resolved the privacy flaws found in [21], we present another protocol ( 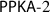) that additionally provisions PrFS and KCI resilience. Table 1 lists the security and privacy features provisioned by each protocol.

• We develop a formal security and privacy model in an appropriate complexity-theoretic framework and prove the proposed protocols secure in this model.

The remainder of this paper is organized as follows:

• Section 2 provides an overview and analysis of a WBAN key agreement scheme proposed in [21].

• The proposed protocols are detailed in Sect. 3.

• Section 4 discusses pertinent aspects of the proposed protocols.

• Sections 5 and 6 explain the formal security model and the associated analysis, respectively.

• Finally, Sect. 7 provides future research directions and concludes the paper.

2 Li et al. scheme

In this section, we present an overview and analysis of Li et al. scheme [21]. For ease of comparison we use the same notation (details in Table 2) as in [21].

Fig. 2

Li et al. Protocol

Table 2 Notations used in [21]

2.1 The key agreement protocol

Li et al. PPKA protocol between the Hub node (HN) and a node (N) consists of three phases. For a pictorial overview of the protocol see Fig. 2.

2.1.1 Initialization phase

The (SA) randomly samples a master secret key $k_{HN}$ and stores it in HN.

2.1.2 Registration phase

The SA randomly samples a unique secret identity $id_N$ for node N. It then randomly chooses the temporary secret parameter $k_N$ and calculates $a_N = id_N \oplus h(k_{HN},k_N)$ and $b_N ={k_{HN}}\oplus a_N \oplus k_N$. A unique relay identity $id'_{IN}$ for the intermediary node (IN) is chosen and the parameters $\langle {id_N,a_N,b_N}\rangle$ and $\langle {id'_{IN}}\rangle$ are stored in N and IN, respectively, while $id'_{IN}$ is stored by HN as the identity of IN when communicating in relay mode.

2.1.3 Authentication phase

We can think of the authentication phase of Li et al. scheme as a two-pass protocol. The individual steps are outlined below:

Step 1 $N \rightarrow IN: \langle {tid_N,y_N,a_N,b_N,t_N}\rangle$. N picks a random $r_N$ and creates timestamp $t_N$. Then it computes $x_N = a_N \oplus id_N$, $y_N = x_N \oplus r_N$ and $tid_N = h(id_N \oplus t_N,r_N)$ and forwards the tuple $\langle {tid_N,y_N,a_N,b_N,t_N}\rangle$ to IN.

Step 2 $IN \rightarrow HN: \langle {tid_N,y_N,a_N,b_N,t_N,id'_{IN}}\rangle$. IN adds its relay identity $id'_{IN}$ to the tuple and forwards it to HN. Note that IN when operating in relay mode uses $id'_{IN}$ not $id_{IN}$.

Step 3 $HN \rightarrow IN: \langle {\alpha ,\beta ,\eta ,\mu ,id'_{IN}}\rangle$. After receiving the parameters from IN, HN verifies the relay identity $id'_{IN}$ from its database and substantiates the validity of the timestamp $t_N$. Upon success of these checks, it computes $k^*_N = k_{HN} \oplus a_N \oplus b_N,\ x^*_N = h(k_{HN},k^*_N),\ id^*_N = x^*_N \oplus a_N,\ r^*_N = x^*_N \oplus y_N$ and $tid^*_N = h(id^*_N \oplus t_N,r^*_N)$. It then verifies whether $tid_N \overset{?}{=} tid^*_N$. Then, a random $f_N$ is chosen and $\alpha = x_N \oplus f_N$ and $\gamma = r_N \oplus f_N$ are computed. Then a new $k^+_N$ is picked and $a^+_N = id_N \oplus h(k_{HN},k^+_N),\ b^+_N = k_{HN} \oplus a^+_N \oplus k^+_N,\ \eta = \gamma \oplus a^+_N,\ \mu = \gamma \oplus b^+_N,\ \beta = h(x_N,r_N,f_N,\eta ,\mu )$ are computed. The shared session key is computed as $k_S = h(id_N,r_N,f_N,x_N)$ and is stored in memory. Finally, HN forwards the tuple $\langle {\alpha ,\beta ,\eta ,\mu ,id'_{IN}}\rangle$ to IN.

Step 4 $IN \rightarrow N: \langle {\alpha ,\beta ,\eta ,\mu }\rangle$. IN removes the relay identity $id'_{IN}$ from the received tuple and forwards $\langle {\alpha ,\beta ,\eta ,\mu }\rangle$ to N.

Step 5; Upon receipt of the response from IN, N computes $f^*_N = x_N \oplus \alpha$ and $\beta ^* = h(x_N,r_N,f^*_N,\eta ,\mu )$ and verifies that $\beta ^*\overset{?}{=}\beta$. If true, N computes $\gamma = r_N \oplus f_N$, $a^+_N = \gamma \oplus \eta$ and $b^+_N = \gamma \oplus \mu$. The shared session key $k_S$ is computed as

$h(id_N,r_N,f_N,x_N)$ and the authentication parameters $(a_N,b_N)$ are replaced by $(a^+_N,b^+_N)$.

2.2 Analysis of the Li et al. scheme

In this section we discuss vulnerabilities and attacks on the security of the Li et al. scheme.

2.2.1 Security analysis

In addition to provisioning of mutual “direct” authentication [11], Li et al. scheme fulfills all the security criteria as defined in Sect. 1.2 except KCI resilience and PrFS. Moreover, the scheme also protects the master secret ($k_{HN}$) in the event of compromise of various nodes of the WBAN. For sake of brevity, we will restrict our security analysis to highlight only the vulnerabilities of Li et al. scheme.

Discussion about forward secrecy Li et al. claimed a forward security property of their scheme. Their definition of forward secrecy varies from the generally accepted one. According to Li et al., the goal of forward secrecy is to protect other (past / future) session keys in the event of compromise of the current session key $k_S$. However, the conventional definition of forward secrecy states that in the event of compromise of the long term secrets of the protocol participant(s), an adversary should not be able to obtain any of the past session keys [22]. While Li et al. scheme is forward secure according to their own definition, it is not forward secure in a conventional sense.

KCI attack We demonstrate a KCI attack on Li et al. scheme. ${\mathcal {A}}$ observes the first pass of the protocol and notes the message contents. As the value $id_N$ is known to ${\mathcal {A}}$, he calculates the following values as follows:

$$\begin{aligned}x_N = a_N \oplus id_N; \quad r_N = y_N \oplus x_N.\\\end{aligned}$$

${\mathcal {A}}$ chooses a random $f_N$ and calculates $\alpha = f_N \oplus x_N$. ${\mathcal {A}}$ then chooses arbitrary values of $\eta$ and $\mu$ and calculates $\beta$ as:

$$\begin{aligned}\beta = h(x_N,r_N,f_N,\eta ,\mu ).\end{aligned}$$

Finally, ${\mathcal {A}}$ sends out the tuple $\langle {\alpha ,\beta ,\eta ,\mu }\rangle$ back to node N. N cannot detect this KCI attack as N’s computed value $\beta$ is the same as in the received tuple. As a result, node N would be sharing the session key $k_S = h(id_N,r_N,f_N,x_N)$ with ${\mathcal {A}}$, incorrectly believing itself to be sharing $k_S$ with HN.

2.2.2 Privacy analysis

The anonymity dilemma It is known apriori to the attacker that all nodes ultimately communicate with HN. As the node identifier $id_{N}$ is always masked (by taking an XOR of it with a fresh random value), anonymity in Li et al. protocol is preserved from “direct” privacy attacks. However, now consider the situation depicted in Fig. 3, where an intermediary node IN is providing the relaying service to various nodes N.

Fig. 3

The privacy dilemma of Li et al. scheme

In the second pass of Li et al. scheme, it is not clear how the intermediary node IN would be able to identify the original node N out of the “anonymity set” [25] for onward forwarding of the tuple $\langle {\alpha ,\beta ,\eta ,\mu }\rangle$ received from HN. One naive way to resolve this is to allow IN to broadcast the second pass of protocol for all nodes. However, this approach is unsuitable for already energy-constrained WBAN nodes as they will need to perform additional communication (radio reception) and computational steps for each transmission.

Session unlinkability While Li et al. claim their scheme provides session unlinkability, we show this to be untrue. We highlight a weakness in Li et al. key agreement protocol, which allows a passive attacker to easily link two or more sessions of the same node N. The attack proceeds as follows:

Session # 1 Suppose that a run of Li et al.’s key agreement protocol is carried out between node N and HN. A passive attacker ${\mathcal {A}}$ observes the contents of the messages being exchanged. From Step 1 of Sect. 2.1.3, ${\mathcal {A}}$  records the value $y_N = x_N \oplus r_N$. Then, from Step 3 of Sect. 2.1.3, ${\mathcal {A}}$ records $\alpha = x_N \oplus f_N$. Now, ${\mathcal {A}}$ obtains the value $\gamma = r_N \oplus f_N = \alpha \oplus y_N$. Further, ${\mathcal {A}}$  records the values $\eta$ and $\mu$ from Step 3 of Sect. 2.1.3 and uses $\gamma$ to compute:

$$\begin{aligned} a^+_N = \gamma \oplus \eta ;\quad b^+_N = \gamma \oplus \mu .\end{aligned}$$

Table 3 Overheads associated with Li et al. scheme

Session # 2 Now, ${\mathcal {A}}$ observes key exchange protocol sessions between various nodes and HN. ${\mathcal {A}}$ compares the values of the parameters $a_N$ and $b_N$ from Step 1 of the protocol with the saved values of $a^+_N$ and $b^+_N$. When ${\mathcal {A}}$ finds a match, ${\mathcal {A}}$ concludes with almost certainty that another key exchange session has been initiated by the same node N. This is correct because node N uses the updated authentication parameters $a^+_N$ and $b^+_N$ in its next run of the protocol. In this way, ${\mathcal {A}}$ can track and link sessions of node N, demonstrating that Li et al. scheme does not achieve session unlinkability.

2.2.3 Functional requirements

Li et al. scheme can be easily adapted for direct communication between N and HN without the involvement of IN. Since this scheme employs only symmetric cryptographic primitives, it is extremely efficient from a computation, communication and storage overhead perspective and there is no requirement of any additional network infrastructure. Assuming a hash function with a digest length of B bits and 16 bit intermediary node IDs (i.e. $id'_{IN}$), Table 3 highlights the communication, computation and storage overhead of Li et al. scheme. In this table, h denotes one hash operation, $\oplus$ denotes an XOR operation and m denotes the number of intermediary nodes in the WBAN. Note that, contrary to the assumption made by Li et al. in Sect. 5.4 of [21] about the arbitrary length of the timestamp field, it is implicitly the same length as the hash function digest because, as described earlier in Sect. 2.1.3, $tid_N = h(id_N \oplus t_N,r_N)$. This is not commensurate with the length of the timestamp field as defined in IEEE Std 802.15.6, which is three octets or 24 bits. Regarding state maintenance by HN, in case of [21], HN needs to maintain states concerning the relay nodes IN, which is an undesirable feature as already explained in Sect. 1.2.3.

3 Our PPKA protocols

In this section, we propose two PPKA protocols which rectify the problems highlighted in Sect. 2.2. While devising these PPKA protocols, we have tried to preserve the original elegance, simplicity and efficiency of the scheme in [21]. The first PPKA protocol addresses the privacy flaws of unlinkability and anonymity dilemma faced by IN (Sect. 2.2.2) in Li et al.’s scheme. The second protocol, additionally provides PrFS and KCI resilience (in case of compromise of the long-term secret of node N). Note that though in our protocols the intermediary node IN is not an active participant from a cryptographic standpoint (this was a conscious design consideration), we have included IN in our protocol description for verification of the resolution of the anonymity dilemma of IN. Detail of additional notation used in our PPKA protocols is given in Table 4.

Table 4 Detail of additional symbols

3.1 PPKA protocol 1

The phases of PPKA Protocol 1 are separated into three distinct phases. An Initialization Phase, that generates the long-term secret values of the Hub Node HN. A Registration Phase, that generates the long-term values of the end-nodes N and stores them with HN. Finally, an Authentication Phase where the nodes N and HN generate an authenticated shared secret key, and update the authentication parameters.

3.1.1 Initialization phase

This is identical to the Initialization Phase as presented in [21]. Specifically, the (SA) randomly samples a master secret key $k_{HN}$ and stores it in HN.

3.1.2 Registration phase

The intermediary node (IN) is not provided with a relay identity $id'_{IN}$. Instead, parameters $\langle {id_N,a_N,b_N}\rangle$ are stored in N. Note that the user identity $id_N$ is sampled in a fully random fashion. The identities in case of a WBAN in general and IEEE 802.15.6 in specific, do not require a structure as in other communication settings like mobile telephony, etc [16]. Also note that the proposed scheme does not impose any limitations on the length of $id_N$ and is flexible enough to accommodate the identity field of any length.

3.1.3 Authentication phase

The various steps of the authentication phase are depicted in Fig. 4 and are as follows:

Step 1 $N \rightarrow IN: \langle {tid_N,y_N,a_N,b_N,t_N,id'_N}\rangle$. N picks a random $r_N$ and creates timestamp $t_N$. It then computes $x_N = a_N \oplus id_N$, $y_N = x_N \oplus r_N$. It further picks a random pseudonym $id'_N$ to be used as a temporary identifier for this session only, calculates $tid_N = h(id_N,id'_N,t_N,r_N)$ and sets the “Relay Field” of the underlying “MAC Header” to value 1, according to sub-clause 6.10 of [3].

Step 2 $IN \rightarrow HN: \langle {tid_N,y_N,a_N,b_N,t_N,id'_N}\rangle$. IN checks the value of “Relay Field” and forwards the tuple to HN.

Step 3 $HN \rightarrow IN: \langle {\alpha ,\beta ,\eta ,\mu ,id'_N}\rangle$. After receipt of the tuple from IN, HN verifies the validity of the timestamp $t_N$. Upon success of this check, it computes $k^*_N = k_{HN} \oplus a_N \oplus b_N,\ x^*_N = h(k_{HN},k^*_N),\ id^*_N = x^*_N \oplus a_N,\ r^*_N = x^*_N \oplus y_N$ and $tid^*_N = h(id^*_N,id'_N,t_N,r^*_N)$. It then verifies whether $tid_N \overset{?}{=} tid^*_N$. Then, a random $f_N$ is chosen and $\alpha = x_N \oplus f_N$, $\gamma = r_N \oplus f_N \oplus h(id_N,t_N)$ and $\gamma ' = r_N \oplus f_N \oplus h(id_N,t_N,r_N,id'_N)$ are computed. Then, a new $k^+_N$ is picked and $a^+_N = id_N \oplus h(k_{HN},k^+_N),\ b^+_N = k_{HN} \oplus a^+_N \oplus k^+_N,\ \eta = \gamma \oplus a^+_N,\ \mu = \gamma ' \oplus b^+_N,\ \beta = h(x_N,r_N,f_N,\eta ,\mu ,id'_N)$ are computed. Finally, the shared session key $k_S = h(id_N,r_N,f_N,x_N)$ is computed and stored in memory, and the value of the underlying “Relay Field” is set to 1.

Step 4 $IN \rightarrow N: \langle {\alpha ,\beta ,\eta ,\mu ,id'_N}\rangle$. IN checks the “Relay Field” of the message received from the Hub node. If “Relay Field” value is set to 1, then it notes the identifier $id'_N$ received in the tuple for onward forwarding of the tuple to node N.

Step 5; Upon receiving a response from IN, N computes $f^*_N = x_N \oplus \alpha$ and $\beta ^* = h(x_N,r_N,f^*_N,\eta ,\mu ,id'_N)$ and verifies that $\beta ^*\overset{?}{=}\beta$. If so, N computes $\gamma = r_N \oplus f_N \oplus h(id_N,t_N)$, $\gamma ' = r_N \oplus f_N \oplus h(id_N,t_N,r_N,id'_N)$, $a^+_N = \gamma \oplus \eta$ and $b^+_N = \gamma ' \oplus \mu$. The shared session key $k_S$ is computed as $h(id_N,r_N,f_N,x_N)$, and the authentication parameters $(a_N,b_N)$ are updated by being replaced with $(a^+_N,b^+_N)$.

3.2 PPKA protocol 2

The second PPKA protocol is structurally similar to PPKA Protocol 1, with three phases and similar goals. We describe the execution of PPKA Protocol 2 below.

3.2.1 Initialization phase

This phase is unchanged from [21].

3.2.2 Registration phase

The registration phase is mostly identical to PPKA Protocol 1. However, SA additionally computes $z_N = h(k_{HN}, id_N, k_N)$. Parameters $\langle {id_N,a_N,b_N,z_N}\rangle$ are stored in N.

3.2.3 Authentication phase

Fig. 4

PPKA Protocols 1 and 2 (Values/operations defined within curly brackets $\{~~\}$ are valid only for PPKA 1, while those defined within square brackets $[~~]$ are valid only for PPKA 2)

The authentication phase of PPKA Protocol 2 is depicted in Fig. 4 and detailed as follows:

Step 1 $N \rightarrow IN: \langle {tid_N,y_N,a_N,b_N,t_N,id'_N}\rangle$. This is identical to Step 1 in PPKA 1 except that the value of $tid_N$ is calculated as $h(id_N,id'_N,z_N,t_N,r_N)$.

Step 2 $IN \rightarrow HN: \langle {tid_N,y_N,a_N,b_N,t_N,id'_N}\rangle$. This is identical to Step 2 in PPKA 1

Step 3 $HN \rightarrow IN: \langle {\alpha ,\beta ,\eta ,\mu ,\delta ,id'_N}\rangle$. After receipt of the tuple from IN, HN proceeds identically to Step 3 in PPKA 1. Additionally $z^*_N$ is calculated as $h(k_{HN},id_N,k_N)$ and $tid^*_N$ as $h(id^*_N,id'_N,z^*_N,t_N,r^*_N)$. It then verifies whether $tid_N \overset{?}{=} tid^*_N$. Then, $\alpha$, $\eta$ and $\mu$ are computed as in PPKA 1. $k_S$ is computed as $h(id_N,z_N,r_N,f_N,x_N,1)$ while an additional key $k_Z$ is computed as $h(z_N,id_N,r_N,f_N,x_N,0)$. HN then computes $z^+_N = h(k_{HN},id_N,k^+_N)$ and encrypt it with $k_z$ as $\delta = \texttt {Enc}(k_z,z^+_N)$. Lastly, $\beta$ is calculated as $h(x_N,z_N,r_N,f_N,\delta ,\eta ,\mu ,id'_N)$.

Step 4 $IN \rightarrow N: \langle {\alpha ,\beta ,\eta ,\mu ,\delta ,id'_N}\rangle$. This is identical to Step 4 in PPKA 1

Step 5; This is identical to Step 5 in PPKA 1, except that $\beta ^*$ is calculated as $h(x_N,z_N,r_N,f^*_N,\delta ,\eta ,\mu ,id'_N)$ and the shared session key $k_S$ is computed as $h(id_N,z_N,r_N,f_N,x_N,1)$. Additionally, node N decrypts $z^+_N = \texttt {Dec}(k_z,\delta )$ and replaces $z_N$ with $z^+_N$.

4 Discussion

4.1 Why a Bespoke solution?

If we consider the scenario of direct communication between N and HN (without the involvement of IN), at first glance, it seems to be similar to that of RFID; where a tag needs to be authenticated in a secure and private manner by the reader. However, there is a fundamental distinction between the two scenarios. As discussed in Sect. 1.2.3, in our case the HN does not maintain any state about the network nodes and is oblivious to the identity management of the network, while in the RFID setting, the reader has access to the back-end database server(s) which maintain nodes’ status in the RFID network. This means that, in the case of RFID, SA needs to update the status at the back-end servers whenever it introduces a new node or removes an old one from the system. As explained in Sect. 1.2.3, this is problematic for WBANs.

4.2 Random number generation on WBAN nodes

A WBAN Cryptographically Secure Pseudo Random Number Generator (CSPRNG) needs to be computationally inexpensive and there should be no requirement for entropy collection from environmental resources, as this would entail extra communication. We recommend the approach outlined in [18]. During the “Registration Phase”, SA can allocate each node N with a unique (randomly chosen) secret key K. Thereafter, node N can encrypt the sequence $\{0,1,2,3,...\}$ under key K using AES (already available for message security purposes) as the block cipher. This arrangement can securely generate $2^{60}$ bytes without the need for re-seeding the key K.

4.3 Why timestamps?

Timestamps as a replay prevention tool are generally avoided in key agreement protocols as they present various practical problems, such as the need for a reliable source of time. Here, we would like to draw the reader’s attention to Sect. 1.2.3, which discusses the requirement of the HN being stateless. Any other technique for replay prevention (nonces, sequence numbers, etc.) will require the HN to maintain a state about the clients and consequently will impose design limitations which we are specifically trying to avoid. Given the peculiar situation of WBANs and availability of various time-synchronization avenues within the standard (Clause 6.11 of [3] which provisions for HN to act as the central time source for the WBAN and regularly broadcasts time-synchronization beacons), replay prevention via timestamps seems to be the way forward. This may not be the most desirable solution but it still is a step forward from the current standard which offers no replay protection at all.

4.4 Security versus usability

It was a conscious design choice to keep HN free of any client related data (refer Sects. 1.2.3 and 1.3). While security can be improved manifold via diffusion of secret parameters between the client nodes and HN and attacks like impersonation of some other non-compromised node by a compromised client node could be avoided; this would adversely affect the usability features (no management cost, etc) we are trying to achieve. Hence, the cleanness predicates (Sect. 5.4) in our security model define the exact combination of secrets that the adversary can compromise. Our security model allows the adversary to leak the long-term secret key of the node ($id_N$) but not along with the previously established per-stage secret state ($a_N$, $b_N$). What we are trying to achieve here is the delicate balance between security and usability via this approach.

5 Security model

We now introduce our security models for the analysis of privacy-preserving key agreement (PPKA) protocols. Our first security experiment is based on standard key-exchange models in the tradition of Bellare-Rogaway [4] key indistinguishability games. This allows our model to easily capture known key secrecy, as well as generically capture key randomness notions, since our adversary is tasked merely with the goal of distinguishing the targeted session key from a random session key from the same distribution. Our second security experiment allows us to capture privacy notions of sessions, by challenging an adversary to determine which of two previously selected nodes ran a given protocol execution. Our cleanness predicates (see Sect. 5.4) allows us to model KCI attacks by allowing the adversary to reveal the long-term key of the node running the PPKA protocol, as well as the notions of partial forward secrecy. We begin by describing the execution environment for our security frameworks.

5.1 Execution environment

Consider an experiment played between a challenger ${\mathcal {C}}$ and an adversary ${\mathcal {A}}$. ${\mathcal {C}}$ maintains a single node $HN$, running a number of instances of the PPKA protocol $\varPi$, and a set of (up to) $n_N$ nodes $N_1, \ldots , N_{n_N}$ (representing nodes communicating with the hub node $HN$), each potentially running one stage of (up to) $n_S$ consecutive stages of $\varPi$. The PPKA protocol $\varPi$ is represented as a tuple of algorithms $\varPi$ = $(\textsf {HKeyGen}, \textsf {HF}, \textsf {NKeyGen}, \textsf {NF}, \textsf {StateGen})$. We abuse notation and use $\pi ^{stid}_{id}$ to refer to both the identifier of the $stid$-th stage of $\varPi$ being run by node $N_{id}$ and the collection of per-session variables maintained for this stage. We describe the algorithms below:

$\varPi .\textsf {HKeyGen}(\lambda ) \overset{\$}{\rightarrow }(k_{HN})$ is a probabilistic symmetric key generation algorithm taking as input a security parameter $\lambda$ and outputting a long-term hub node secret key $(k_{HN})$.

$\varPi .\textsf {HF}(\lambda ,k_{HN},m) \overset{\$}{\rightarrow }(m')$ is a (potentially) probabilistic algorithm that takes a security parameter $\lambda$, the long-term key of the hub node $k_{HN}$, and an arbitrary bit string $m \in \{0,1\}^*\cup \{\emptyset \}$, and outputs a response $m'\in \{0,1\}^*\cup \{\emptyset \}$ and an updated per-session state $\pi '$.

$\varPi .\textsf {NKeyGen}(\lambda ) \overset{\$}{\rightarrow }(ltk)$ is a probabilistic symmetric key generation algorithm taking as input a security parameter $\lambda$ and outputting a long-term hub node secret key $(ltk)$. Note that in our proposed PPKA protocols, we denote this long-term secret key with $id_N$.

$\varPi .\textsf {NF}(\lambda ,\pi ,m) \overset{\$}{\rightarrow }(m',\pi ')$ is a probabilistic algorithm taking a security parameter $\lambda$, the set of per-session variables $\pi$ and an arbitrary bit string $m \in \{0,1\}^*\cup \{\emptyset \}$, and outputs a response $m'\in \{0,1\}^*\cup \{\emptyset \}$ and an updated per-session state $\pi '$.

$\varPi .\textsf {StateGen}(\lambda , k_{HN},ltk) \overset{\$}{\rightarrow }(psstate)$ is a probabilistic symmetric key generation algorithm taking as input a security parameter $\lambda$ and the long-term secret keys of the hub node and the “normal” node, outputting secret state information for node N $(psstate)$. In PPKA Protocol 1, this per-stage secret state is $\langle a_N, b_N \rangle$. In PPKA Protocol 2, this is $\langle a_N, b_N, z_N\rangle$.

$\varPi .\textsf {StateUpdate}(\lambda , \pi ) \overset{\$}{\rightarrow }(psstate)$ is a probabilistic symmetric key generation algorithm taking as input a security parameter $\lambda$ and a set of per-session variables, outputting the next stage’s per-stage secret state $(psstate)$ for node N.

The experiment begins with ${\mathcal {C}}$ running $\varPi .\textsf {HKeyGen}$ once to generate a long-term secret key for the hub node $(k_{HN})$, and randomly sampling a bit $b \in \{0,1\}$. ${\mathcal {A}}$ then interacts with ${\mathcal {C}}$ via the queries listed in Sect. 5.2, eventually terminating and outputting a guess bit $b'$ of ${\mathcal {C}}$’s bit b. ${\mathcal {A}}$ wins the key-indistinguishability game if $b'=b$ and the session $\pi ^{stid}_{id}$ such that ${\mathcal {A}}$ issued $\mathsf {\mathbf {Test}}(id,stid)$ satisfies the cleanness predicate $\mathsf {clean}$, which we discuss in Sect. 5.4. Each session maintains the following set of per-session variables:

• $ltk\in \{0,1\}^{\lambda }$ - the long-term symmetric-secret of $N_{id}$.

• $id\in \{1, \ldots , n_N\}$ - the index of the node $N_{id}$.

• $m_s \in \{0,1\}^*\cup \{\bot \}$ - the concatenation of messages sent by the node, initialised by $\bot$.

• $m_r \in \{0,1\}^*\cup \{\bot \}$ - the concatenation of messages received by the node, initialised by $\bot$.

• $psstate\in \{0,1\}^*\cup \{\bot \}$ - the per-stage secret state of the node, initialised by $\bot$.

• $sk\in \{0,1\}^*\cup \{\bot \}$ - the session key, initialised by $\bot$.

• $stid\in \{1, \ldots , n_S\}$ - the index of the most recently completed stage, initialised by 1 and increased monotonically.

• $\alpha \in \{\mathtt {active}, \mathtt {accept}, \bot \}$ - the current status of the node, initialised by $\bot$.

Finally, the challenger manages the following set of registers, which indicate ${\mathcal {A}}$’s compromise of secrets:

• Long-term symmetric keys $\{\mathsf {LSKflag}_{1}, \ldots , \mathsf {LSKflag}_{n_N}\}$, where $\mathsf {LSKflag}_{i} \in \{\mathtt {corrupt},\mathtt {clean},\bot \} ~\forall$ $i \in [n_N]$.

• Per-stage secret state $\{\mathsf {PSSflag}^{1}_{1}, \mathsf {PSSflag}^{1}_{2}, \ldots , \mathsf {PSSflag}^{1}_{n_S}$, $\ldots$ $\mathsf {PSSflag}^{n_N}_{1}, \mathsf {PSSflag}^{n_N}_{2}, \ldots , \mathsf {PSSflag}^{n_N}_{n_S}\}$ where $\forall i \in n_N$, $j \in n_S$, $\mathsf {PSSflag}^{i}_{j} \in \{\mathtt {corrupt}, \mathtt {clean},\bot \}$.

• Session keys $\{\mathsf {SKflag}^{1}_{1}, \mathsf {SKflag}^{1}_{2}, \ldots , \mathsf {SKflag}^{1}_{n_S}$, $\ldots$ $\mathsf {SKflag}^{n_N}_{1}$, $\mathsf {SKflag}^{n_N}_{2}, \ldots , \mathsf {SKflag}^{n_N}_{n_S}\}$ where $\forall i \in n_N$, $j \in n_S$, $\mathsf {SKflag}^{i}_{j} \in \{\mathtt {corrupt},\mathtt {clean},\bot \}$.

5.2 Adversarial interaction

In the game, the adversary ${\mathcal {A}}$ is able to communicate with the challenger and thus interact with the parties/sessions via the following set of queries:

Register$(\lambda ) \rightarrow id$: Allows ${\mathcal {A}}$ to register a new node with security parameters $\lambda$ and gives ${\mathcal {A}}$ an identifier for the node $id$ (which we denote $N_{id}$). For protocols where nodes do not have a public identifier, the index of the node is given to ${\mathcal {A}}$.

$NextKey(\lambda , id) \rightarrow m$: Allows ${\mathcal {A}}$ to indicate that the node with public identifier $id$ should attempt a new key agreement using (potentially) the new/updated security parameters $\lambda$. The challenger then returns any protocol messages m.

$Corrupt(id)\rightarrow ltk$: Allows ${\mathcal {A}}$ to compromise the long-term key of the node $\pi _{id}.ltk$ with public identifier $id$.

$Reveal(id,stid)\rightarrow sk$: Allows ${\mathcal {A}}$ to compromise the session key established between the hub node and the node $N_{id}$ in stage $stid$. Note that $stid$ indicates the index of the session key established between the node $id$ and the hub node. The challenger responds with the session key $\pi ^{stid}_{id}.sk$.

$StateReveal(id,stid)\rightarrow psstate$: Allows ${\mathcal {A}}$ to compromise the per-stage secret state $psstate$ of the node with public identifier $id$. Note that $stid$ indicates the index of the stage-specific state, and the challenger responds with $\pi ^{stid}_{id}.psstate$.

$Send(id,m)\rightarrow m'$: Allows ${\mathcal {A}}$ to send a message m to the node with identifier $id$ currently running a protocol execution. Note that the node will update its per-session variables and potentially output a new message $m'$.

$Test(id,stid)\rightarrow sk$: If the node $N_{id}$ has completed its $stid$-stage key agreement, then the challenger uses the randomly-sampled bit $b \in \{0,1\}$. If $b=0$ the challenger responds with $\pi ^{stid}_{id}.sk$, otherwise the challenger responds with a random key from the same distribution.

We now formalise the advantage of a PPT algorithm ${\mathcal {A}}$ in winning the PPKA key-indistinguishability game:

Definition 1

(Key Indistinguishability) Let $\varPi$ be a PPKA protocol and $n_N$, $n_S\in \mathbb {N}$. For a given cleanness predicate $\mathsf {clean}$, and a PPT algorithm ${\mathcal {A}}$, we define the advantage of ${\mathcal {A}}$ in the key-indistinguishability game to be:

$$\begin{aligned}&{\text {Adv}}_{{\varPi ,n_{N} ,n_{S} ,{\mathcal {A}}}}^{{{\text {PPKA - SU,clean}}}} (\lambda ) \nonumber \\&= \left| {2 \cdot \left( {\Pr \left[ {{\text {EXP}}_{{\varPi ,n_{N} ,n_{S} ,{\mathcal {A}}}}^{{{\text {PPKA - SU,clean}}}} (\lambda ) = 1} \right] - \frac{1}{2}} \right) } \right| \end{aligned}$$

We say that $\varPi$ is -secure if, for all ${\mathcal {A}}$, is negligible in security parameter $\lambda$.

5.3 Session unlinkability

The experiments for PPKA key-indistinguishability and session unlinkability are mostly identical. However, instead of using the $\mathsf {\mathbf {Test}}(id,stid)$ query, at some point ${\mathcal {A}}$ will stop and output $(id_0,id_1)$. When ${\mathcal {A}}$ outputs $(id_0,id_1)$, ${\mathcal {C}}$ runs $\mathsf {\mathbf {NextKey}}(\lambda ,id_0)$ and responds to queries as before. We will refer to this as the “challenge” node. However, when $\pi ^{stid}_{id_0}.\alpha \leftarrow \mathtt {accept}$, ${\mathcal {C}}$ then refers to the random bit b sampled at the beginning of the experiment and:

• if $b=0$, then ${\mathcal {C}}$ runs $\mathsf {\mathbf {NextKey}}(\lambda ,id_0)$

• if $b=1$, then ${\mathcal {C}}$ runs $\mathsf {\mathbf {NextKey}}(\lambda ,id_1)$ instead.

${\mathcal {A}}$ now uses the $\mathsf {\mathbf {SendTest}}(m)$ query to send messages to the node $N_{id_b}$ in order to avoid trivial identification. We will refer to this as the “unnamed node”. ${\mathcal {A}}$ at some point terminates and outputs a guess bit $b'$. If $b'=0$, then ${\mathcal {A}}$ is indicating that the unnamed node $N_{id_b}$ was linked to the challenge node $N_{id_0}$. If $b'=1$, then ${\mathcal {A}}$ is indicating that the unnamed node $N_{id_b}$ was not linked to the challenge node $N_{id_0}$.

We now formalise the advantage of a PPT algorithm ${\mathcal {A}}$ in winning the PPKA session-unlinkability game:

Definition 2

(Session Unlinkability) Let $\varPi$ be a PPKA protocol, and $n_N$, $n_S\in \mathbb {N}$. For a given cleanness predicate $\mathsf {clean}$, and a PPT algorithm ${\mathcal {A}}$, we define the advantage of ${\mathcal {A}}$ in the session-unlinkability game to be:

We say that $\varPi$ is -secure if, for all ${\mathcal {A}}$, is negligible in the security parameter $\lambda$.

5.4 Cleanness predicates

The cleanness predicates are used in the security experiments to define the exact combination of secrets that ${\mathcal {A}}$ is able to compromise without trivially breaking the PPKA protocol. In order to capture key-compromise-impersonation (KCI) attacks and PrFS notions, we allow ${\mathcal {A}}$ to leak the long-term secret key of the “normal” nodes if ${\mathcal {A}}$ has not also leaked any previously established per-stage secret state. Our analysis is focused primarily on the normal nodes, and we do not allow the compromise of the hub node secrets, as all security in all stages is lost in this scenario. We additionally describe a cleanness predicate for PPKA protocols that do not achieve PrFS or KCI resilience.

Definition 3

(PrFS-KCI-clean) A session $\pi ^{stid}_{id}$ such that $\pi ^{stid}_{id}.\alpha$ $=$ $\mathtt {accept}$ in the experiment defined in Fig. 5 is if $\mathsf {SKflag}^{stid}_{id} \ne \mathtt {corrupt}$ and if $\mathsf {LSKflag}_{id} = \mathtt {corrupt}$ then $\forall$ $s \le stid$ $\mathsf {PSSflag}^{s}_{id} \ne \mathtt {corrupt}$.

Definition 4

(nPrFS-clean) A session $\pi ^{stid}_{id}$ such that $\pi ^{stid}_{id}.\alpha = \mathtt {accept}$ in the experiment defined in Fig. 5 is if $\mathsf {SKflag}^{stid}_{id} \ne \mathtt {corrupt}$.

Finally, we describe a cleanness predicate for our session-unlinkability game. It is straightforward to realise that if $\mathsf {\mathbf {Corrupt}}(id_0)$ or $\mathsf {\mathbf {Corrupt}}(id_1)$ were to be issued, it would trivially allow ${\mathcal {A}}$ to win in either of our PPKA protocols by simply reconstructing the $tid_N$ field sent by the unnamed node. Similarly, we cannot allow the adversary to reveal the per-stage secret state for the current stage $stid$ of the unnamed node $N_{id_b}$.

Definition 5

(SU-clean) A session $\pi ^{stid}_{id}$ in the experiment defined in Fig. 5 is if $\mathsf {LSKflag}_{id} \ne \mathtt {corrupt}$ and $\mathsf {PSSflag}^{stid}_{id} \ne \mathtt {corrupt}.$

Fig. 5

An algorithmic description of the $\mathsf {PPKA}$-$\mathsf {IND}$ and $\mathsf {PPKA}$-${{\mathsf {S}}}{{\mathsf {U}}}$ security experiments

6 Analysis of our proposed PPKA Protocols

6.1 Security and privacy analysis

Before we begin, we show that an adversary ${\mathcal {A}}$ is unable to recover the hub node secret $k_{HN}$ (with non-negligible probability) even if ${\mathcal {A}}$ reveals all long-term secrets $id_N$ of all nodes and all per-stage secret states $psstate$. In our proofs we work within the random oracle model, and ${\mathcal {A}}$ cannot learn anything about $k_{HN}$ from hash outputs $h(k_{HN}, X)$ (where X is any concatenation of arbitrary values). We turn to ${\mathcal {A}}$ attempting to learn $k_{HN}$ that has been “blinded” through exclusive-or (XOR) operations. We give below the generic construction of messages that include $k_{HN}$:

• $b_N = k_{HN} \oplus k_N \oplus id_{N} \oplus h(k_{HN}, k_{N})$

• $\mu = k_{HN} \oplus k_N^+ \oplus id_{N} \oplus h(k_{HN}, k_{N}^+)$ $\oplus h(id_N, t_{N}, r_N, id_N')\oplus$ $f_N \oplus r_N$

Taking $\mu$ first, we note that $k_N^+$ (independently sampled by the hub node, uniformly-at-random, in each stage) acts as the key in a one-time-pad, perfectly hiding the long-term secret key $k_{HN}$ of the hub node, the long-term secret key $id_N$ of the normal node and the value $h(k_{HN},k_N)$. $k_N^+$ is an internal value that is known only to the challenger implementing the Hub Node, as it cannot be compromised by ${\mathcal {A}}$ via $\mathsf {\mathbf {Reveal}}$, $\mathsf {\mathbf {Corrupt}}$ or $\mathsf {\mathbf {StateReveal}}$ queries. For $b_N$, we note that $k_N$ (randomly sampled by the hub node in a previous stage) is still acting as the same key $k_N^+$ in a one-time-pad, and thus still perfectly hiding the same message, i.e. the long-term secret key $k_{HN}$ of the hub node, the long-term secret key $id_N$ of the normal node and the value $h(k_{HN},k_N)$. We argue then that ${\mathcal {A}}$ cannot recover the hub node secret key $k_{HN}$. We can further conclude that an adversary that compromises fewer internal states and long-term secret keys will also be unable to recompute $k_{HN}$. We can continue our proof knowing that the best strategy for ${\mathcal {A}}$ to recover the long-term secret key of the hub node $k_{HN}$ is to attempt to brute-force the value.

We now show that an adversary ${\mathcal {A}}$ that does not issue a $\mathsf {\mathbf {Corrupt}}(id)$ query cannot recover the long-term secret key $id_N$ of node $N_{id}$. As before, we note that since we instantiate the hash function as a random oracle, that the adversary cannot invert hash outputs of the form $h(id_{N},X)$ (where X is some arbitrary concatenation of values) in order to learn $id_N$. We can now focus on the adversary attempting to learn $id_N$ from “blinded” values by XORing them with other values. In each stage of the protocol execution, this is available to ${\mathcal {A}}$ in the following generic ways:

• $a_N = id_{N} \oplus h(k_{HN}, k_{N})$

• $b_N = k_{HN} \oplus k_N \oplus id_{N} \oplus h(k_{HN}, k_{N})$

• $\eta = r_N \oplus f_N \oplus id_{N} \oplus k_{HN} \oplus k_N \oplus h(id_{N}, f_{N}) \oplus h(k_{HN}, k_{N}^+)$

• $\mu = r_N \oplus f_N \oplus id_{N} \oplus k_{HN} \oplus k_N^+ \oplus h(id_{N}, t_N, r_N, id_N') \oplus$ $h(k_{HN}, k_{N}^+)$

If this is the first stage of the protocol execution for node $N_{id}$, then $a_N$ and $b_N$ are established in some out-of-band way. Thus $h(k_{HN}, k_{N})$ and $k_N$ act as uniformly random and independent keys in a one-time pad, perfectly hiding $id_N$ and $k_{HN} \oplus id_{N} \oplus h(k_{HN}, k_{N})$ (for $a_N$ and $b_N$ respectively). Since, by the previous argument, the best strategy for ${\mathcal {A}}$ to recover $k_{HN}$ is simply to guess, (and we instantiate the hash function with a random oracle), in order to recompute $h(k_{HN},k_{N})$ ${\mathcal {A}}$ must either guess $k_{HN}$ or to guess $h(k_{HN}, k_{N})$. Since they are the same bit-length, the probability of ${\mathcal {A}}$ doing either is the same: $2^{-\lambda }$.

If this is not the first stage of the protocol execution, then $a_N$ and $b_N$ they were sent as “sub-XOR” of a previous stage $\eta$ and $\mu$. We argue that $h(k_{HN}, k_{N}^+)$ and $k_{N}^+$ act as keys to one-time-pads for $\eta$ and $\mu$, respectively, and remain the keys to the one-time-pad perfectly hiding $id_N$ and $k_{HN} \oplus id_{N} \oplus h(k_{HN}, k_{N})$ (for $a_N$ and $b_N$ respectively) in the following stage. It follows then that the best strategy ${\mathcal {A}}$ has in recovering $id_{N}$ is to merely guess $id_{N}: 2^{-\lambda }$.

We now prove the key-indistinguishability of our PPKA protocols given in Fig. 4. We begin with , as it captures the strongest notions of security, capturing PrFS, KCI resilience, key randomness, known key security and hub-node authentication. Afterwards, we turn to proving the session unlinkability of . We then prove key indistinguishability and session unlinkability of . As is essentially a truncated version of , this allows us to omit the most repetitive details of the proofs.

Theorem 1

(Key Indistinguishability of ) The privacy preserving key agreement protocol given in Fig. 4 is $\mathsf {PPKA}$-$\mathsf {IND}$-secure with cleanness predicate (capturing PrFS and KCI resilience) and assuming all hash functions are random oracles. For any PPT algorithm ${\mathcal {A}}$ against the key indistinguishability game, is negligible in the security parameter $\lambda$.

Proof

For our proof, we assume that a test query $\mathsf {\mathbf {Test}}(id,stid)$ has been issued, and separate into the following three cases:

• $\pi ^{stid}_{id}$ has accepted such that $\pi _{{id}}^{{st\,id}} .m_{r} \ne {\text {PPKA - }}2.{\text {HF}} (\lambda ,\,k_{{HN}} ,\,\pi _{{id}}^{{st\,id}} .m_{r} )$.

• $\pi ^{stid}_{id}$ has accepted such that $\pi _{{id}}^{{st\,id}} .m_{r} \ne {\text {PPKA - }}2.{\text {HF}} (\lambda ,\,k_{{HN}} ,\,\pi _{{id}}^{{st\,id}} .m_{r} )$ and $\mathsf {\mathbf {Corrupt}}(id)$ has not been issued.

• $\pi ^{stid}_{id}$ has accepted such that $\pi _{{id}}^{{st\,id}} .m_{r} \ne {\text {PPKA - }}2.{\text {HF}} (\lambda ,\,k_{{HN}} ,\,\pi _{{id}}^{{st\,id}} .m_{r} )$ and $\mathsf {\mathbf {Corrupt}}(id)$ has been issued. By the definition of the cleanness predicate , we assume that the per-stage secret state has not been revealed for any stage $s \le stid$.

Case 1 In this case, we show that the probability the session $\pi ^{stid}_{id}$ such that $\mathsf {\mathbf {Test}}(id,stid)$ was issued set $\pi ^{stid}_{id}.\alpha$ $\leftarrow$ $\mathtt {accept}$ such that is negligible.

Game 0 This is a normal PPKA key-indistinguishability game. Thus we have: .

Game 1 In this game, we guess the index $(id,stid)$ of the session $\pi ^{stid}_{id}$, and abort if during the execution of the experiment, a query $\mathsf {\mathbf {Test}}(i^*,s^*)$ is received and $(i^*, s^*) \ne (id,stid)$. Thus we have: $\Pr (break_{0}) \le n_Nn_S\cdot \Pr (break_{1})$.

Game 2 In this game, we replace the $h(k_{HN}, k_{N})$ value computed within $\pi ^{stid}_{id}$ (and, potentially, in the hub node processing $\pi ^{stid}_{id}.m_s$) with a uniformly-random value $\widetilde{h(k_{HN}, k_{N})}$. We note that since we instantiate the hash function with a random oracle that the distribution is identical to $h(k_{HN}, k_{N})$. Thus, the only way that ${\mathcal {A}}$ can detect this change is to query $(k_{HN}, k_{N})$ to the random oracle. Since the only way for ${\mathcal {A}}$ to do this is to recover $k_{HN}$ fully, and we argued previously that ${\mathcal {A}}$’s probability of success in this endeavour is $2^{-\lambda }$, we have: $\Pr (break_{1}) \le 2^{-\lambda } + \Pr (break_{2})$.

Game 3 In this game we argue that the adversary ${\mathcal {A}}$ has a negligible probability of producing a value ${\hat{\beta }} = h(\widetilde{h(k_{HN},k_N)},$ $\hat{z_N},\hat{r_N},\hat{f_N},{\hat{\delta }},{\hat{\eta }},{\hat{\mu }},\hat{id_N'})$. Note that for $\pi ^{stid}_{id}.\alpha$ to reach $\mathtt {accept}$, ${\mathcal {A}}$ must produce such a value ${\hat{\beta }}$. We know by the definition of Case 1 that the following must be true:

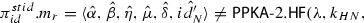• $\pi ^{stid}_{id}.m_s)$

Since all message fields are included in the computation of ${\hat{\beta }}$, and the message received by the test session does not match any output from an honest hub node, we know that the only way that ${\mathcal {A}}$ can cause $\pi ^{stid}_{id}$ to reach $\mathtt {accept}$ is to query $\widetilde{h(k_{HN},k_N)},\hat{z_N},\hat{r_N},\hat{f_N},{\hat{\delta }},{\hat{\eta }},{\hat{\mu }},\hat{id_N'}$ to the random oracle. However, since by Game 2, $\widetilde{h(k_{HN},k_N)}$ is a uniformly-random value sampled independently from the protocol flow, the only way for ${\mathcal {A}}$ to produce such an input is to guess $\widetilde{h(k_{HN},k_N)}$. Thus, we have: $\Pr (break_{2}) \le 2^{-\lambda }+ \Pr (break_{3})$.

It is clear that if the session $\pi ^{stid}_{id}$ such that $\mathsf {\mathbf {Test}}(id,stid)$ must be issued (by Game 1) cannot reach $\pi ^{stid}_{id}.\alpha \leftarrow \mathtt {accept}$, then in Game 3 the experiment proceeds identically regardless of the bit b sampled by the challenger. Thus: $\Pr (break_{3}) = 0$. We can now begin treating Case 2: that $\mathsf {\mathbf {Corrupt}}(id)$ has not been issued for the appropriate node.

Case 2 In this case, we show that an adversary who issues a $\mathsf {\mathbf {Test}}(stid,id)$ query (and does not also issue a $\mathsf {\mathbf {Corrupt}}(id)$ query) cannot win the key-indistinguishability game with non-negligible probability.

Game 0 This is a normal PPKA key-indistinguishability game. Thus we have:

Game 1 In this game, we guess the index $(id,stid)$ of the session $\pi ^{stid}_{id}$, and abort if during the execution of the experiment, a query $\mathsf {\mathbf {Test}}(i^*,s^*)$ is received and $(i^*, s^*) \ne (id,stid)$. Thus, we have: $\Pr (break_{0}) \le n_Nn_S\cdot \Pr (break_{1})$.

Game 2 In this game, we replace the session key $k_S$ computed by the node $N_{id}$ in stage $stid$ with a uniformly-random and independent value $\widetilde{k_S}$. First we note that $k_S$ is computed as $k_S = h(id_N, z_N,r_N,f_N,x_N)$. Since we instantiate the hash function as a random oracle, the distribution of $\widetilde{k_S}$ and $k_S$ is identical. In order to distinguish this change, ${\mathcal {A}}$ must be able to query the random oracle with the input $(id_N,r_N,f_N,x_N)$. Since we argued previously that in order to recover $id_N$ (the long-term secret key of the node $N_{id}$), ${\mathcal {A}}$’s only strategy to distinguish this change would be to guess the long-term secret $id_N$. The probability of ${\mathcal {A}}$ distinguishing this replacement is $2^{-\lambda }$ where $\lambda$ is the bit-length of $id_N$.

After this change, the session key returned to ${\mathcal {A}}$ as the response to the $\mathsf {\mathbf {Test}}(stid,id)$ query is a uniformly-random value independent of the protocol execution regardless of the bit b sampled by the challenger. Thus, we have: $\Pr (break_{1}) \le 2^{-\lambda }$.

Case 3

In this case, we show that an adversary who issues a $\mathsf {\mathbf {Test}}(stid,id)$ query (and does not issue $\mathsf {\mathbf {StateReveal}}$ queries for all per-stage secret states established before stage $stid$) cannot win the key-indistinguishability game.

Game 0 This is a normal PPKA key-indistinguishability game. Thus we have:

Game 1 In this game, we guess the index $(id,stid)$ of the session $\pi ^{stid}_{id}$, and abort if during the execution of the experiment, a query $\mathsf {\mathbf {Test}}(i^*,s^*)$ is received and $(i^*, s^*) \ne (id,stid)$. Thus we have: $\Pr (break_{0}) \le n_Nn_S\cdot \Pr (break_{1})$.

Game 2 In this game, we replace the $z_N = h(k_{HN}, id_N, k_N)$ value held in secret stage by the node $N_{id}$ with a uniformly random value $\widetilde{z_N}$ independent from the protocol execution. Since we instantiate the hash function with a random oracle, the distributions of $z_N$ and $\widetilde{z_N}$ are identical. Thus, in order to detect this change, ${\mathcal {A}}$ must query the random oracle with the input $k_{HN}, id_N, k_N$. Since, by earlier arguments, the best strategy ${\mathcal {A}}$ has to recover $k_{HN}$ is simply to guess $k_{HN}$, the probability that ${\mathcal {A}}$ is able to do this is $2^{-\lambda }$. Thus $\Pr (break_{1}) = 2^{-\lambda } + \Pr (break_{2})$.

Game 3 In this game, we replace the computation of the $z_N^+$ encryption key $k_z = h(\widetilde{z_N},id_N,r_N,f_N,0)$ with a uniformly-random and independent value $\widetilde{k_z}$. We note that $\widetilde{z_N}$ (by Game 2) is already a uniformly random value, and the hash function is instantiated with a random oracle, this replacement is sound and indistinguishable from the perspective of ${\mathcal {A}}$. Thus $\Pr (break_{2}) = \Pr (break_{3})$.

Game 4 In this game, we replace the contents of ciphertext $\delta$ with a random string of the same length, and abort if the ciphertext $\delta$ sent by the hub node $HN$ is not the ciphertext received by $N_{id}$, but the output of decrypting $\delta$ is not $\bot$. We do so by constructing an algorithm ${\mathcal {B}}$ that interacts with an challenger in the following way: ${\mathcal {B}}$ acts identically as in Game 3, except for the hub node protocol execution that computes $\widetilde{k_z}$. Instead, when ${\mathcal {B}}$ computes $\delta$, ${\mathcal {B}}$ selects a uniformly-random string $\widetilde{z_N^+}$ (of the same length as $z_N^+$) and submits $(z_N^+,\widetilde{z_N^+})$ to the encryption oracle $\mathsf {Enc}$.

When the random bit b sampled by the challenger is 0, then $\delta$ contains the encryption of $z_N^+$, so ${\mathcal {B}}$ is a perfect simulation of Game 3. However, when the bit b sampled by the challenger is 1, then $\delta$ contains a random string $\widetilde{z_N^+}$ and thus ${\mathcal {B}}$ is a perfect simulator of Game 4. Since in Game 3, the $z_N^+$ encryption key $\widetilde{k_z}$ is uniformly-random and independent of the protocol execution, this replacement is sound. Any adversary capable of distinguishing this change can break the confidentiality of the encryption scheme and guess b with perfect success. Thus .

Game 5 We now note that by Game 4, $z_N^+$ has been established in an out-of-band way, reminiscent of the first stage run by node $N_{id}$. We now repeat the process of Games 2, 3, and 4 $(stid-2)$ times to establish a $z_N$ value for stage $stid$ run by node $N_{id}$ that is indistinguishable from establishing $z_N$ in some out-of-band way. Thus .

Game 6 We replace $z_N$ with a uniformly-random and independent value $\widetilde{z_N}$ in stage $stid$ of node $N_{id}$ by the same argument as Game 2. Thus $\Pr (break_{5}) = 2^{-\lambda } + \Pr (break_{6})$.

Game 7 In this game, we replace the computation of the session key $k_s = h(id_N,\widetilde{z_N},r_N,f_N,1)$ with a uniformly-random and independent value $\widetilde{k_s}$. We note that $\widetilde{z_N}$ (by Game 6) is already a uniformly random value, and the hash function is instantiated with a random oracle, this replacement is sound and indistinguishable from the perspective of ${\mathcal {A}}$. Thus $\Pr (break_{6}) = \Pr (break_{7})$. We finally note that the session key established by $\pi ^{stid}_{id}$ is now uniformly random and independent of the protocol flow, and of the bit b sampled by the $\mathsf {PPKA}$-$\mathsf {IND}$ challenger. Thus $\Pr (break_{7}) = 0$. $\square$

We follow our proof of the key-indistinguishability of by proving the session-unlinkability of .

Theorem 2

(Session Unlinkability of ) The PPKA given in Fig. 4 is $\mathsf {PPKA}$-${{\mathsf {S}}}{{\mathsf {U}}}$-secure with cleanness predicate and assuming all hash functions are random oracles. For any PPT algorithm ${\mathcal {A}}$ against the session-unlinkability game described in Fig. 5, is negligible in the security parameter $\lambda$.

Proof

We begin by restating the cleanness predicate, and reiterating the impact upon our proof. For both nodes $N_{id_0}$ and $N_{id_1}$, we know that the queries $\mathsf {\mathbf {Corrupt}}(id_0)$ and $\mathsf {\mathbf {Corrupt}}(id_1)$ have not been issued. In addition, for the stage $stid_b$ run by the unnamed node $N_{id_b}$, we know that a $\mathsf {\mathbf {StateReveal}}(id_b)(stid_b)$ query has not been issued.

Game 0 This is a normal PPKA session-unlinkability game. Thus we have:

Game 1 In this game, in the unnamed session $\pi ^{stid_b}_{id_b}$, we replace the hash outputs of the form $h(id_N,X)$ (where X is a concatenation of arbitrary stings) with a uniformly random values $\widetilde{h(id_N,X)}$ chosen independently of the protocol flow. As before, since we instantiate (in our proof) the hash function with a random oracle, the distribution of this change is indistinguishable. In order to detect this change then, ${\mathcal {A}}$ must query the random oracle with the input $(id_N,X)$. As per our previous arguments, in order to query $id_N$ to the random oracle, ${\mathcal {A}}$ must first recover $id_N$. Since the best strategy to recover $id_N$ is to simply guess the value of $id_N$, the probability of ${\mathcal {A}}$ distinguishing this change is $2^{-\lambda }$. Thus we have: $\Pr (break_{0}) = 2^{-\lambda } + \Pr (break_{1}).$

Game 2 In this game, in the unnamed session $\pi ^{stid_b}_{id_b}$, we replace the hash outputs of the form $h(k_{HN},X)$ (where X is either $k_N$ or $k_N^+$) with a uniformly random values $\widetilde{h(k_{HN},X)}$ chosen independently of the protocol flow. As before, since we instantiate (in our proof) the hash function with a random oracle, the distributions of Game 1 and Game 2 are indistinguishable. In order to detect this change then, ${\mathcal {A}}$ must query the random oracle with the input $(k_{HN},X)$. As per our previous arguments, in order to query $k_{HN}$ to the random oracle, ${\mathcal {A}}$ must first recover $k_{HN}$. Since the best strategy to recover $k_{HN}$ is, to simply guess the value of $k_{HN}$, the probability of ${\mathcal {A}}$ distinguishing this change is $2^{-\lambda }$. Thus we have: $\Pr (break_{1}) = 2^{-\lambda } + \Pr (break_{2}).$

Game 3 In this game, in the message output by the hub node for the unnamed session $\pi ^{stid_b}_{id_b}$, we replace the hash outputs $\beta = h(\widetilde{h(k_{HN},k_{N}^+)},z_N, r_N, f_N, \delta , \eta ,\mu ,id_N')$ with a uniformly random value $\widetilde{\beta }$ chosen independently of the protocol flow. As previous arguments, the distributions of Game 2 and Game 3 are indistinguishable. In order to detect this change then, ${\mathcal {A}}$ must query the random oracle with the input $(\widetilde{h(k_{HN},k_{N}^+)},z_N, r_N, f_N, \delta , \eta ,\mu ,id_N')$. Since $\widetilde{h(k_{HN},k_{N}^+)}$ is already a uniformly random value independent of the protocol flow (by Game 2), the best strategy to distinguish this change is to simply guess the value of $\widetilde{h(k_{HN},k_{N}^+)}$. Thus we have: $\Pr (break_{2}) = 2^{-\lambda } + \Pr (break_{3}).$

Game 4 In this game, in the unnamed session $\pi ^{stid_b}_{id_b}$ we replace the computation of the $z_N^+$ key $k_z = h(z_N,id_N,r_N,f_N,0)$ with a uniformly-random and independent value $\widetilde{k_z}$. We note that since we instantiate the hash function with a random oracle, that the distribution of $\widetilde{k_z}$ and $k_z$ is indistinguishable. Thus, in order to detect this change, ${\mathcal {A}}$ must query the random oracle with the input $z_N,id_N,r_N,f_N,0$. By earlier arguments, the best strategy ${\mathcal {A}}$ has to recover $id_{N}$ is simply to guess $id_{N}$. Thus $\Pr (break_{3}) = 2^{-\lambda } + \Pr (break_{4})$.

Game 5 In this game we replace the value $\delta$ send by the hub node to the unnamed session $\pi ^{stid_b}_{id_b}$ with a uniformly random and independent values $\widetilde{\delta } \overset{\$}{\leftarrow }\{0,1\}^{\lambda }$. We do so by constructing an algorithm ${\mathcal {B}}$ that interacts with a $\mathsf {PRF}$ challenger in the following way: ${\mathcal {B}}$ acts identically as in Game 4, expect for the hub node protocol execution that computes $\widetilde{k_z}$. Instead, ${\mathcal {B}}$ initialise a $\mathsf {PRF}$ challenger and queries $(z_n^+)$, and uses the output $\widetilde{\delta }$ from the $\mathsf {PRF}$ challenger to replace the computation of $\delta$. Since by Game 4, $\widetilde{k_z}$ is a uniformly random and independent value, this replacement is sound. If the test bit sampled by the $\mathsf {PRF}$ challenger is 0, then $\widetilde{\delta } \leftarrow \mathsf {Enc}(\widetilde{k_z}, z_N^+)$ and we are in Game 4. If the test bit sampled by the $\mathsf {PRF}$ challenger is 1, then $\widetilde{\delta } \overset{\$}{\leftarrow }\{0,1\}^{\lambda }$ and we are in Game 5. Thus any adversary ${\mathcal {A}}$ capable of distinguishing this change can be turned into a successful adversary against the $\mathsf {PRF}$ security of the encryption scheme $\mathsf {Enc}$, and we find: $\Pr (break_{4}) \le \mathsf {Adv}^{\mathsf {PRF}}_{\mathsf {Enc},{\mathcal {A}}}(\lambda ) + \Pr (break_{5})$

We pause here to reflect on the consequences of these changes. The first message sent by the unnamed node is $\langle \widetilde{tid_N}, y_N, a_N, b_N, t_N, id_N' \rangle$. Since $t_N$ is a timestamp and $id_N'$ is sampled identically regardless of the identity of the unnamed node, the distributions of these fields is similarly identical independent of the choice of the randomly sampled bit b. $\widetilde{tid_N}$ is a uniformly-random valued and independent of the protocol flow (by Game 1), as it is the output of a random oracle query that is of the form $(id_{N_b}, id_N',t_n,r_n)$. This is true regardless of the choice of the randomly sampled bit b of the challenger. For $y_N$ we remark that $r_N$ is a uniformly-random value sampled identically from the same distribution regardless of the node identity. This value acts as the key in a one-time-pad, perfectly hiding $\widetilde{h(k_{HN},k_N)}$. $r_N$ is not reused (as a key) in any message in any stage, and thus $y_N$ is a uniformly-random value, regardless of node identity. $a_N$ is also a uniformly random value. Here, $\widetilde{h(k_{HN},k_N)}$ acts as the key in a one-time-pad, perfectly hiding the long-term secret key $id_N$ of the node by Game 2. Since $\widetilde{h(k_{HN},k_N)}$ is not reused (as a key) in any message in any stage, $a_N$ is a uniformly random value, regardless of the node identity, or the bit b randomly sampled by the challenger. Finally, we turn to $b_N$. We note that this time, $k_N$ (randomly sampled by the hub node in a previous stage, uniformly-at-random) acts as the key in a one-time-pad, perfectly hiding the long-term secret key $k_{HN}$ of the hub node, the long-term secret key $id_N$ of the node and the value $\widetilde{h(k_{HN},k_N)}$. $k_N$ is not reused (as a key) in any message in any stage, and thus $b_N$ is a uniformly-random value, regardless of node identity.

We examine the first message received by the unnamed node, $\langle \alpha , \beta , \eta , \mu , \delta , id_N' \rangle$. Again, $id_N'$ is sampled identically regardless of the identity of the unnamed node; the distributions of the fields are similarly identical independent of the choice of the randomly sampled bit b. For $\alpha$ we remark that $f_N$ is a uniformly-random value sampled identically from the same distribution regardless of the node identity. This value acts as the key in a one-time-pad, perfectly hiding $\widetilde{h(k_{HN},k_N^+)}$. $f_N$ is not reused (as a key) in any message in any stage, and thus $\alpha$ is a uniformly-random value, regardless of node identity. $\eta$ is also a uniformly random value. Here, $\widetilde{h(id_N,t_N)}$ acts as the key in a one-time-pad, perfectly hiding the values $r_N$, $f_N$ and $a_N^+$ by Game 1. Since $\widetilde{h(id_{N},t_N)}$ is not reused (as a key) in any message in any stage, $\eta$ is a uniformly random value, independent of the node identity, or the bit b randomly sampled by the challenger. A similar argument apples for $\mu$, substituting $\widetilde{h(id_N,t_N,r_N,id_N')}$ for $\widetilde{h(id_N,t_N)}$. $\widetilde{\beta }$ is a uniformly-random valued and independent of the protocol flow (by Game 3), as it is the output of a random oracle query that is of the form $(\widetilde{h(k_{HN},k_{N}^+)},z_N, r_N, f_N,$ $\delta , \eta ,\mu ,id_N')$. This is true regardless of the choice of the randomly sampled bit b of the challenger. Finally, we rely on the $\mathsf {PRF}$ security of the encryption scheme $\mathsf {Enc}$ to replace the $\delta$ field returned by the hub node. By Game 5, the value $\widetilde{\delta }$ is uniformly-random and independent of the protocol regardless of the node identity $id_b$. We note then that all message fields have the same distribution regardless of the challenger’s randomly-sampled bit b; thus we have: $\Pr (break_{5}) = 0$. $\square$

We now prove key-indistinguishability of our proposed , capturing known key security, and key randomness, but not forward-secrecy. It follows identically from Case 2 of the proof of key-indistinguishability, as it does not capture PrFS or KCI resilience. However, it still captures known key security, and key randomness and (obviously) key-indistinguishability.

Theorem 3

(Key Indistinguishability of ) The PPKA Protocol 1 given in Fig. 4 is $\mathsf {PPKA}$-$\mathsf {IND}$-secure with cleanness predicate (capturing neither PrFS nor KCI resilience) and assuming all hash functions are random oracles. For any PPT algorithm ${\mathcal {A}}$ against the key-indistinguishability game, is negligible in the security parameter $\lambda$.

Proof

For our proof, we note that we cannot prove partial-forward-secrecy or key-compromise-impersonation resilience for the proposed PPKA Protocol 1. Thus, unlike , the cleanness predicate ensures that $\mathsf {\mathbf {Corrupt}}(id)$ has not been issued. In this case, we assume that the per-stage secret state has been compromised at any (or perhaps, at all) previous stages. Since sends the per-stage secret state $\langle a_N, b_N \rangle$ in the clear, this has no bearing on our security proof of .

Similarly to the proof for , we begin by showing that the adversary is unable to recover the Hub Node secret key $k_{HN}$ (with non-negligible probability) even if ${\mathcal {A}}$ completely reveals the long-term secret keys of every normal node and the per-stage secret states of the nodes. This argument follows identically to the argument for the secrecy of $k_{HN}$ in the proof of , and we can continue our proof knowing that the best strategy ${\mathcal {A}}$ has in recovering $k_{HN}$ is to merely guess $k_{HN}.$

In this proof, we show that an adversary that issues a $\mathsf {\mathbf {Test}}(stid,id)$ query (and does not also issue a $\mathsf {\mathbf {Corrupt}}(id)$ query) cannot win the key-indistinguishability game with negligible probability. Before we begin in earnest, we wish to show that an adversary that does not issue a $\mathsf {\mathbf {Corrupt}}(id)$ query cannot recover the long-term secret key $id_N$ of node $N_{id}$. This argument follows identically to the argument for the secrecy of $id_{N}$ in the proof of , and we can continue our proof knowing that the best strategy ${\mathcal {A}}$ has in recovering $id_{N}$ is to merely guess $id_{N}.$

Game 0 This is a normal PPKA key-indistinguishability game. Thus we have:

Game 1 In this game, we guess the index $(id,stid)$ of the session $\pi ^{stid}_{id}$, and abort if during the execution of the experiment, a query $\mathsf {\mathbf {Test}}(i^*,s^*)$ is received and $(i^*, s^*) \ne (id,stid)$. Thus we have: $\Pr (break_{0}) \le n_Nn_S\cdot \Pr (break_{1})$.

Game 2 In this game, we replace the session key $k_S$ computed by the node $N_{id}$ in stage $stid$ with a uniformly-random and independent value $\widetilde{k_S}$. First we note that $k_S$ is computed as $k_S = h(id_N,r_N,f_N,x_N)$. Since we instantiate the hash function as a random oracle, the distribution of $\widetilde{k_S}$ and $k_S$ is identical, thus in order to distinguish this change, ${\mathcal {A}}$ must be able to query the random oracle with the input $(id_N,r_N,f_N,x_N)$. Since we argued previously that in order to recover $id_N$ (the long-term secret key of the node $N_{id}$), ${\mathcal {A}}$’s only strategy in distinguishing this change would be to guess the long-term secret key $id_N$. Thus the probability of ${\mathcal {A}}$ in distinguishing this replacement is $2^{-\lambda }$ where $\lambda$ is the bit-length of $id_N$.

After this change, the session key returned to ${\mathcal {A}}$ as the response to the $\mathsf {\mathbf {Test}}(stid,id)$ query is a uniformly-random value independent of the protocol execution regardless of the bit b sampled by the challenger. Thus we have: $\Pr (break_{1}) \le 2^{-\lambda } + 0$. $\square$

Finally, we finish our security analysis by proving the session-unlinkability of .

Theorem 4

(Session Unlinkability of ) The PPKA given in Fig. 4 is $\mathsf {PPKA}$-${{\mathsf {S}}}{{\mathsf {U}}}$-secure with cleanness predicate and assuming all hash functions are random oracles. For any PPT algorithm ${\mathcal {A}}$ against the session-unlinkability game described in Fig. 5, is negligible in the security parameter $\lambda$.

Proof

The proof of the session-unlinkability of follows near-identically to the proof of session-unlinkability for , (with the exception of Game 4 and Game 5, since does not have $z_N$ state, nor a $\delta$ field in the hub node’s response) and so we omit repeating it here. $\square$

6.2 Functional Analysis

The proposed PPKA protocols can easily be adapted for direct communication between N and HN by removal of Steps 2 and 4 out of their respective Authentication Phases. As our PPKA protocols are also based on symmetric cryptographic primitives, they preserve the efficiency of the original scheme from a computation, communication and storage perspective without the aid of any additional network infrastructure. Note that the length of the identity field $id_N$ is something not under the control of the authors. The current IEEE 802.15.6 standard utilizes 24-bits to represent $id_N$ as specified under Clause 9 of IEEE Std 802-2001. The proposed scheme doesn’t impose any limitations on the length of $id_N$ and is flexible enough to accommodate the identity field of any length. Moreover, in our protocols the timestamp field can also be of any arbitrary length to suit the underlying protocol layers, unlike [21]. Assuming a B bit hash digest and 16 bit pseudo identity $id'_N$ for node N, Tables 5 and 6 depict the various overheads associated with PPKA Protocols 1 and 2, respectively. In these tables, h denotes an instance of a hash operation and $\oplus$ denotes an XOR operation. From a computational perspective, single instances of hash operation and encryption operation have been considered equal [1].

Table 5 Overheads associated with PPKA Protocol 1

Table 6 Overheads associated with PPKA Protocol 2

7 Conclusion and future research directions

We have proposed two authenticated key agreement protocols suitable for WBANs. The protocols are based upon symmetric cryptographic components only and are thus highly efficient and avoid the additional burden of deploying and managing an associated public key infrastructure. Our protocols are suitable for any application scenario where efficiency is of essence and the network can be initialized by a System Administrator. In addition to the requisite security guarantees, the proposed protocols also offer appropriate privacy attributes suitable for a wide variety of application scenarios. In order to ensure confidence in our proposals, we introduce formal security frameworks for the analysis of privacy-preserving key agreement protocols, and analyze our constructions. The proposed protocols emerge as attractive alternatives to the current key exchange methods described in the IEEE 802.15.6 standard, which are based upon legacy public key-based primitives and do not offer any privacy features. One of the protocols offers the advance security properties of partial forward secrecy and KCI resilience in case of compromise of the long-term secret of the sensor/client node. It would be interesting to investigate whether future research can yield a scheme which is based on symmetric primitives and still offers (full) forward secrecy in the (additional) event of compromise of the long-term secret of the Hub node or KCI resilience in the (additional) event of the compromise of node’s ephemeral parameters.