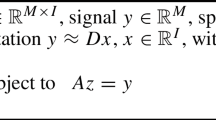Skip to main content
SpringerLink
Log in

Learning Functions of Few Arbitrary Linear Parameters in High Dimensions

  • Published:
Foundations of Computational Mathematics Aims and scope Submit manuscript

Abstract

Let us assume that f is a continuous function defined on the unit ball of ℝd, of the form f(x)=g(Ax), where A is a k×d matrix and g is a function of k variables for k≪d. We are given a budget m∈ℕ of possible point evaluations f(x i ), i=1,…,m, of f, which we are allowed to query in order to construct a uniform approximating function. Under certain smoothness and variation assumptions on the function g, and an arbitrary choice of the matrix A, we present in this paper

  1. 1.

    a sampling choice of the points {x i } drawn at random for each function approximation;

  2. 2.

    algorithms (Algorithm 1 and Algorithm 2) for computing the approximating function, whose complexity is at most polynomial in the dimension d and in the number m of points.

Due to the arbitrariness of A, the sampling points will be chosen according to suitable random distributions, and our results hold with overwhelming probability. Our approach uses tools taken from the compressed sensing framework, recent Chernoff bounds for sums of positive semidefinite matrices, and classical stability bounds for invariant subspaces of singular value decompositions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

References

  1. R. Ahlswede, A. Winter, Strong converse for identification via quantum channels, IEEE Trans. Inf. Theory 48(3), 569–579 (2002).

    Article  MathSciNet  MATH  Google Scholar 

  2. E. Arias-Castro, Y.C. Eldar, Noise folding in compressed sensing, IEEE Signal Process. Lett. 18(8), 478–481 (2011).

    Article  Google Scholar 

  3. R.G. Baraniuk, M. Davenport, R.A. DeVore, M. Wakin, A simple proof of the restricted isometry property for random matrices, Constr. Approx. 28(3), 253–263 (2008).

    Article  MathSciNet  MATH  Google Scholar 

  4. H. Bauschke, H. Borwein, On projection algorithms for solving convex feasibility problems, SIAM Rev. 38(3), 367–426 (1996).

    Article  MathSciNet  MATH  Google Scholar 

  5. E.J. Candès, Harmonic analysis of neural networks, Appl. Comput. Harmon. Anal. 6(2), 197–218 (1999).

    Article  MathSciNet  MATH  Google Scholar 

  6. E.J. Candès, Ridgelets: estimating with ridge functions, Ann. Stat. 31(5), 1561–1599 (2003).

    Article  MATH  Google Scholar 

  7. E.J. Candès, D.L. Donoho, Ridgelets: a key to higher-dimensional intermittency? Philos. Trans. R. Soc., Math. Phys. Eng. Sci. 357(1760), 2495–2509 (1999).

    Article  MATH  Google Scholar 

  8. E.J. Candès, J. Romberg, T. Tao, Stable signal recovery from incomplete and inaccurate measurements, Commun. Pure Appl. Math. 59(8), 1207–1223 (2006).

    Article  MATH  Google Scholar 

  9. E.J. Candès, T. Tao, The Dantzig selector: statistical estimation when p is much larger than n, Ann. Stat. 35(6), 2313–2351 (2007).

    Article  MATH  Google Scholar 

  10. A. Cohen, W. Dahmen, R.A. DeVore, Compressed sensing and best k-term approximation, J. Am. Math. Soc. 22(1), 211–231 (2009).

    Article  MathSciNet  MATH  Google Scholar 

  11. A. Cohen, I. Daubechies, R.A. DeVore, G. Kerkyacharian, D. Picard, Capturing ridge functions in high dimensions from point queries, Constr. Approx. 35(2), 225–243 (2012).

    Article  Google Scholar 

  12. R. Courant, D. Hilbert, Methods of Mathematical Physics, II (Interscience, New York, 1962).

    Google Scholar 

  13. R.A. DeVore, G. Petrova, P. Wojtaszczyk, Instance optimality in probability with an ℓ 1-minimization decoder, Appl. Comput. Harmon. Anal. 27(3), 275–288 (2009).

    Article  MathSciNet  MATH  Google Scholar 

  14. D.L. Donoho, Compressed sensing, IEEE Trans. Inf. Theory 52(4), 1289–1306 (2006).

    Article  MathSciNet  Google Scholar 

  15. M. Fazel, Matrix rank minimization with applications, Ph.D. thesis, Stanford University, Palo Alto, CA, 2002.

  16. M. Fornasier, Numerical methods for sparse recovery, in Theoretical Foundations and Numerical Methods for Sparse Recovery, ed. by M. Fornasier, Radon Series on Computational and Applied Mathematics (De Gruyter, Berlin, 2010).

    Chapter  Google Scholar 

  17. M. Fornasier, H. Rauhut, Compressive sensing, in Handbook of Mathematical Methods in Imaging, vol. 1, ed. by O. Scherzer (Springer, Berlin, 2010), pp. 187–229.

    Google Scholar 

  18. S. Foucart, A note on ensuring sparse recovery via ℓ 1-minimization, Appl. Comput. Harmon. Anal. 29(1), 97–103 (2010).

    Article  MathSciNet  MATH  Google Scholar 

  19. G. Golub, C.F. van Loan, Matrix Computations, 3rd edn. (Johns Hopkins University Press, Baltimore, 1996).

    MATH  Google Scholar 

  20. F. John, Plane Waves and Spherical Means Applied to Partial Differential Equations (Interscience, New York, 1955).

    MATH  Google Scholar 

  21. M. Ledoux, The Concentration of Measure Phenomenon (American Mathematical Society, Providence, 2001).

    MATH  Google Scholar 

  22. B.F. Logan, L.A. Shepp, Optimal reconstruction of a function from its projections, Duke Math. J. 42(4), 645–659 (1975).

    Article  MathSciNet  MATH  Google Scholar 

  23. E. Novak, H. Woźniakowski, Tractability of Multivariate Problems, Volume I: Linear Information, EMS Tracts in Mathematics, vol. 6 (Eur. Math. Soc., Zürich, 2008).

    Book  MATH  Google Scholar 

  24. E. Novak, H. Woźniakowski, Approximation of infinitely differentiable multivariate functions is intractable, J. Complex. 25, 398–404 (2009).

    Article  MATH  Google Scholar 

  25. R.I. Oliveira, Sums of random Hermitian matrices and an inequality by Rudelson, Electron. Commun. Probab. 15, 203–212 (2010).

    Article  MathSciNet  MATH  Google Scholar 

  26. S. Oymak, K. Mohan, M. Fazel, B. Hassibi, A simplified approach to recovery conditions for low-rank matrices, in Proc. Intl. Symp. Information Theory (ISIT) (2011).

    Google Scholar 

  27. A. Pinkus, Approximation theory of the MLP model in neural networks, Acta Numer. 8, 143–195 (1999).

    Article  MathSciNet  Google Scholar 

  28. B. Recht, M. Fazel, P. Parillo, Guaranteed minimum rank solutions to linear matrix equations via nuclear norm minimization, SIAM Rev. 52(3), 471–501 (2010).

    Article  MathSciNet  MATH  Google Scholar 

  29. M. Rudelson, R. Vershynin, Sampling from large matrices: an approach through geometric functional analysis, J. ACM 54(4), 21 (2007) 19 pp.

    Article  MathSciNet  Google Scholar 

  30. W. Rudin, Function Theory in the Unit Ball of ℂn (Springer, New York, 1980).

    Book  Google Scholar 

  31. K. Schnass, J. Vybíral, Compressed learning of high-dimensional sparse functions, in Proc. ICASSP11 (2011).

    Google Scholar 

  32. G.W. Stewart, Perturbation theory for the singular value decomposition, in SVD and Signal Processing, II, ed. by R.J. Vacarro (Amsterdam, Elsevier, 1991).

    Google Scholar 

  33. J.A. Tropp, User-friendly tail bounds for sums of random matrices, Found. Comput. Math. (2011). doi:10.1007/s10208-011-9099-z.

    Google Scholar 

  34. P.-A. Wedin, Perturbation bounds in connection with singular value decomposition, BIT 12, 99–111 (1972).

    Article  MathSciNet  MATH  Google Scholar 

  35. H. Weyl, Das asymptotische Verteilungsgesetz der Eigenwerte linearer partieller Differentialgleichungen (mit einer Anwendung auf die Theorie der Hohlraumstrahlung), Math. Ann. 71, 441–479 (1912).

    Article  MathSciNet  MATH  Google Scholar 

  36. P. Wojtaszczyk, ℓ 1 minimisation with noisy data, Preprint (2011).

Download references

Acknowledgements

Massimo Fornasier would like to thank Ronald A. DeVore for his kind and warm hospitality at Texas A&M University and for the very exciting daily joint discussions which later inspired part of this work. We acknowledge the financial support provided by the START-award “Sparse Approximation and Optimization in High Dimensions” of the Fonds zur Förderung der wissenschaftlichen Forschung (FWF, Austrian Science Foundation). We would also like to thank the anonymous referees for their very valuable comments and remarks.

Author information

Authors and Affiliations

  1. Faculty of Mathematics, Technische Universität München, Boltzmannstraße 3, 85748, Garching, Germany

    Massimo Fornasier

  2. Johann Radon Institute for Computational and Applied Mathematics, Austrian Academy of Sciences, Altenbergerstraße 69, 4040, Linz, Austria

    Karin Schnass & Jan Vybiral

Authors
  1. Massimo Fornasier
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Karin Schnass
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Jan Vybiral
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Massimo Fornasier.

Additional information

Communicated by Emmanuel Candès.

Dedicated to Ronald A. DeVore on his 70th birthday.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Fornasier, M., Schnass, K. & Vybiral, J. Learning Functions of Few Arbitrary Linear Parameters in High Dimensions. Found Comput Math 12, 229–262 (2012). https://doi.org/10.1007/s10208-012-9115-y

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10208-012-9115-y

Keywords

Mathematics Subject Classification (2010)

Search

Navigation