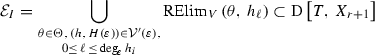A Baby Step–Giant Step Roadmap Algorithm for General Algebraic Sets

Abstract

Let $\mathrm {R}$ be a real closed field and $\mathrm{D}\subset \mathrm {R}$ an ordered domain. We present an algorithm that takes as input a polynomial $Q \in \mathrm{D}[X_{1},\ldots ,X_{k}]$ and computes a description of a roadmap of the set of zeros, $\mathrm{Zer}(Q,\,\mathrm {R}^{k}),$ of Q in $\mathrm {R}^{k}.$ The complexity of the algorithm, measured by the number of arithmetic operations in the ordered domain $\mathrm{D},$ is bounded by $d^{O(k \sqrt{k})},$ where $d = \deg (Q)\ge 2.$ As a consequence, there exist algorithms for computing the number of semialgebraically connected components of a real algebraic set, $\mathrm{Zer}(Q,\,\mathrm {R}^{k}),$ whose complexity is also bounded by $d^{O(k \sqrt{k})},$ where $d = \deg (Q)\ge 2.$ The best previously known algorithm for constructing a roadmap of a real algebraic subset of $\mathrm {R}^{k}$ defined by a polynomial of degree d has complexity $d^{O(k^{2})}.$

Appendix: Computing the Limit of Bounded Points and Curve Segments

1.1 Limit of a Bounded Point

Before computing the limit of a bounded point we need to explain how to perform some useful computations modulo a quasi-monic triangular Thom encoding $\mathcal {F},\,\sigma$ representing a point $t\in \mathrm {R}^{m}.$

We associate to $t\in \mathrm {R}^{m}$ specified by a triangular Thom encoding $\mathcal {F},\,\sigma ,$

$$\begin{aligned} {\mathcal {F}}=\left( f_{[1]},\ldots ,f_{[m]}\right) ,\quad f_{[i]}\in \mathrm{D}\left[ T_{1},\ldots ,T_{i}\right] , \end{aligned}$$

the ordered domain $\mathrm{D}[t]$ contained in $\mathrm {R}$ and generated by t.

We now aim at describing the pseudo-inverse of a nonzero element in the domain $\mathrm{D}[t]$ specified by $\mathcal {F},\,\sigma .$

Definition 8.1

A pseudo-inverse of $f\in \mathrm{D}[t]$ is an element $g\in \mathrm{D}[t]$ such that $f g\in \mathrm{D}$ is strictly positive.

This notion is delicate because the computation of the pseudo-inverse sometimes requires us to update the quasi-monic triangular Thom encoding specifying t, in the spirit of dynamical methods in algebra (e.g., [7]). We start with a motivating example.

Example 8.2

We consider t, specified as the root of

$$\begin{aligned} f(T)=T^{4}-T^{2}-2, \end{aligned}$$

giving signs $(+,\,+,\,+,\,+)$ to the set $\mathrm{Der}(f)$ of derivatives of f.

Consider $T^{2}+1.$ It is easy to see, using, for example, [2], Algorithm 10.13 (Sign Determination Algorithm)] applied to f and the list $\mathrm{Der}(f),\,T^{2}+1,$ that the sign of $T^{2}+1$ at t is positive. To compute its pseudo-inverse, we perform [2], Algorithm 8.22 (Extended Signed Subresultant)] of f and $T^{2}+1.$ If $f(T)$ and $T^{2}+1$ were coprime, we would obtain the pseudo-inverse of $T^{2}+1$ modulo $f(T)$ since the last subresultant would be a nonzero constant in $\mathrm{D}.$ But $f(T)$ and $T^{2}+1$ are not coprime and their greatest common divisor (gcd) is $T^{2}+1.$ So we divide $f(T)$ by $T^{2}+1,$ obtain a new polynomial $g(T)=T^{2}-2$, and check that the root t of $f(T)$ giving signs $(+,\,+,\,+,\,+)$ to the set $\mathrm{Der}(f)$ coincides with $\sqrt{2}$, which is the root of $T^{2}-2$, making the derivative $g^{\prime }(T)=2T$ positive, using again, for example, [2], Algorithm 10.13 (Sign Determination Algorithm)]. It is now possible to compute a pseudoreduction of $T^{2}+1$ modulo $g(T),$ which gives 3.

In other words, during the process of computing the pseudo-inverse of $T^{2}+1$, we discovered the factor $g(T)$ of $f(T)$ having t as a root and coprime with $T^{2}+1.$ Using this new description of t we were able to compute a pseudo-inverse of $T^{2}+1.$

We can now describe the computation of the pseudo-inverse in general.

Description 8.3

Given $t=(t_{1},\ldots ,t_{m}) \in \mathrm {R}^{m}$ specified by the quasi-monic triangular Thom encoding $\mathcal {F}=(f_{[1]},\ldots ,f_{[m]}),\,\sigma =(\sigma _{1},\ldots ,\sigma _{m}),$ we describe how to compute a pseudo-inverse of a nonzero element of $\mathrm{D}[t].$

We proceed by induction on the number $m$ of variables of $\mathcal {F}.$

If $m=0,$ there is nothing to do since $\mathrm{D}$ is an ordered domain.

If $m\not = 0,$ then let $t^{\prime }=(t_{1},\ldots ,t_{m-1})$ specified by $\mathcal {F}^{\prime }=(f_{[1]},\ldots ,f_{[m-1]}),\,\sigma =(\sigma _{1},\ldots ,\sigma _{m-1}).$

We consider f a polynomial in $T_{m}$ whose coefficients, which are elements of

$$\begin{aligned} \left\{ h\in \mathrm{D}\left[ T_{1},\ldots ,T_{m-1}\right] \mid \deg _{T_{i}}(h)<\deg _{T_{i}}\left( f_{[i]}\right) ,\, i=1,\ldots ,m-1\right\} , \end{aligned}$$

represent elements of $\mathrm{D}[t^{\prime }].$

We first decide the sign of f at t, which is done by [2], Algorithm 12.19 (Triangular Sign Determination Algorithm)].

If $f(t)\not =0,$ then we try to pseudo-invert f modulo $\mathcal {F}.$ We perform [2], Algorithm 8.22 (Extended Signed Subresultant)] for f and $f_{[m]},$ with respect to the variable $T_{m}$, and compute a $\gcd (f,\,f_{[m]})\in \mathrm{D}[t^{\prime }]$ (the last nonzero subresultant polynomial) as well as the cofactors $u,\,v\in \mathrm{D}[t^{\prime }]$ with $uf+vf_{[m]}=\gcd (f,\,f_{[m]}).$

• (1) If $\gcd (f,\,f_{[m]})$ is of degree 0 in $T_{m}$, then $u$ is a quasi-inverse of f.

• (2) If $\gcd (f,\,f_{[m]})$ is of degree $>$0 in $T_{m}$, then we have discovered a factor of $f_{[m]}.$ We define h as the quasi-monic polynomial proportional to $f_{[m]}/\gcd (f,\,f_{[m]})$ obtained by [2], Algorithm 8.22 (Extended Signed Subresultant)] (see [2], Algorithm 10.1 (Gcd and Gcd-free part)]). We perform [2], Algorithm 12.19 (Triangular Sign Determination)] applied to $f_{[m]}$ and $\mathrm{Der}(f_{[m]}),\,\mathrm{Der}(h)$ to identify the Thom encoding $\tau$ of $t_{[m]}$ as a root of h. We replace $f_{[m]}$ with h and $\sigma _{[m]}$ with $\tau$ in $\mathcal {F}.$ Now f and the new $f_{[m]},$ considered as polynomials in $T_{[m]}$, are coprime, and we can invert f modulo $f_{[m]}.$

Proposition 8.4

Let $\mathrm{D}$ be an ordered domain contained in a real closed field $\mathrm {R},$ and let $t=(t_{1},\ldots ,t_{m})\in \mathrm {R}^{m}$ be specified by a quasi-monic triangular Thom encoding $\mathcal {F},\,\sigma ,$

$$\begin{aligned} \mathcal {F}=\left( f_{[1]},\ldots ,f_{[m]}\right) ,\quad f_{[i]}\in \mathrm{D}\left[ T_{1},\ldots ,T_{i}\right] . \end{aligned}$$

Let d be a bound of the degree of $f_{[i]}$ with respect to each $T_{j},\,1\le j\le i,\,1\le i\le m.$

• (a) If $g\in \mathrm{D}[T_{1},\ldots ,T_{m}]$ is a polynomial of degree $D,$ then the complexity of computing a pseudoreduction $(c,\,\bar{g})$ of g modulo $\mathcal {F}$ is $(D d)^{O(m)}$ arithmetic operations in $\mathrm{D}.$

• (b) The complexity of the computation of the pseudo-inverse of an element of $\mathrm{D}[t]$ is $d^{O(m)}$ arithmetic operations in $\mathrm{D}.$

Proof

(a) Suppose that $C_{g}\in \mathrm{D}$ is such that $C_{g} T_{1}^{i_1}\cdots T_{m}^{i_{m}} g$ has a reduction in $\mathrm{D}$ modulo $\mathcal {F}$ for every $(i_{1}, \ldots i_{m})$, with $i_{j}<\mathrm{deg}(f_{[j]},\,T_{j}),\,1\le j\le m.$ We denote by $\mathrm{Mat}(C_{g} g)$ the matrix of multiplication by $C_{g} g$ modulo $(\mathcal {F})$ with respect to monomial bases. The entries of $\mathrm{Mat}(C_{g} g)$ are in $\mathrm{D}.$ Its rows and columns are indexed by $(i_{1}, \ldots , i_{m}),\,i_{j}<\mathrm{deg}(f_{[j]},\,T_{j}),\,1\le j\le m$, and the $(j_{1},\ldots ,j_{m})$th entry of the column indexed by $(i_{1},\ldots ,i_{m})$ is the coefficient of $T_{1}^{j_{1}}\cdots T_{m}^{j_{m}}$ in the reduction of $C_{g} T_{1}^{i_{1}}\cdots T_{m}^{i_{m}} g$ modulo $\mathcal {F}.$ Note that $\mathrm{Mat}(C_{g} C_{h} gh)=\mathrm{Mat}(C_{g} g)\mathrm{Mat}(C_{h} h).$ Note also that the entries of the first column of $\mathrm{Mat}(C_{g} g)$ [indexed by $(0,\ldots ,0)$] are the coefficients of the reduction of $C_{g} g$ modulo $\mathcal {F}.$

We first compute $C_{T_{j}}$ such that $C_{T_{j}} T_{1}^{i_{1}}\cdots T_{m}^{i_{m}} T_{j}$ has a reduction in $\mathrm{D}$ modulo $\mathcal {F}$ for every $(i_{1}, \ldots i_{m}),\,i_{h}<\mathrm{deg}(f_{[h]},\,T_{h}),\,1\le h\le m.$ The algorithm proceeds by induction on j.

For $j=1,$ let $c_{1}\in \mathrm{D}$ be the leading coefficient of $f_{[1]}\in \mathrm{D}[T_{1}],\,d_{1}=\mathrm{deg}(f_{[1]},\,T_1),$ and let $C_{T_1}=c_{1}.$ The matrix $\mathrm{Mat}(c_{1} T_{1})$ is simply obtained by replacing each occurrence of $c_{1} T_{1}^{d_{1}}$ by $f_{[1]}-c_{1}T_{1}^{d_{1}}$ in

$$\begin{aligned} c_1 T_1^{d_1-1} T_{2}^{i_2}\cdots T_{m}^{i_m} T_1, \end{aligned}$$

with $i_h<d_h,\,2\le h\le m$ and writing the result as a linear combination of the monomials $T_{1}^{j_1}\cdots T_{m}^{j_m},\,j_i<d_i,\,1\le i \le m.$ Compute $\mathrm{Mat}(C_{T_1}^{h} T_1^{h})=\mathrm{Mat}(c_1 T_1)^{h},\,h<2d,$ and define $C_1=c_1^{2d-1}.$

Suppose by induction that for every monomial M in $T_1,\ldots , T_j$ of degree $<$2d, $C_M T_1^{i_1}\cdots T_m^{i_m} M$ has a reduction in $\mathrm{D}$ modulo $\mathcal {F}$ for every $(i_1, \ldots , i_m),\,i_j<\mathrm{deg}(f_{[j]},\,T_j),\,1\le j \le m.$ Also, suppose that $\mathrm{Mat}( C_{M} M)$ has been computed. Denote by $C_{j}\in \mathrm{D}$ the product of $C_M$ for all the monomials M of degree $<$2d in the j variables $T_1,\ldots ,T_j.$

Let $c_{j+1}\in \mathrm{D}$ be the leading coefficient of $f_{[j+1]}\in \mathrm{D}[T_1,\ldots ,T_{j+1}]$ with respect to $T_{j+1}$ and $d_{j+1}=\mathrm{deg}(f_{[j+1]},\,T_{j+1}),$ and take $C_{T_{j+1}}=c_{j+1} C_{j}.$ The matrix $\mathrm{Mat}(C_{T_{j+1}} T_{j+1})$ is obtained by replacing each occurrence of $C_{T_{j+1}} T_{j+1}^{d_{j+1}}$ by $C_{j}f_{[j+1]}-C_{T_{j+1}} T_{j+1}^{d_{j+1}}$ in

$$\begin{aligned} C_{T_{j+1}} T_{1}^{i_1}\cdots T_{j}^{i_j}T_{j+1}^{d_{j+1}-1}T_{j+2}^{i_{j+2}}\cdots T_{m}^{i_m} T_{j+1}, \end{aligned}$$

with $i_\ell <d_\ell .$

Notice that the polynomials obtained in this way have degrees at most $2d$ in $T_1,\ldots ,T_j$ and degrees $<d_h$ in $T_h$ for $h > j.$ Reduce all such monomials using the matrices of multiplication computed previously.

Finally, compute for every monomial M of degree $\le D$, in $T_1,\ldots ,T_m,\,C_M$ and $\mathrm{Mat}(C_{M} M)$ by taking products of the $C_{T_i}$ and the matrices $\mathrm{Mat}(C_{T_i} T_i)$ (respectively), and let $C_g$ be the product of the $C_M$ for all monomials M of degree $\le D.$ Now determine $\mathrm{Mat}(C_{g} g)$ by taking an appropriate linear combination of $\mathrm{Mat}(C_{M} M)$ and in that way obtain the reduction of $C_g g$ modulo $\mathcal {F}.$

Notice that the complexity of computing the $C_{T_{j+1}}$ and $\mathrm{Mat}(C_{T_{j+1}} T_{j+1})$ is bounded by $d^{O(m)}.$ In the last step, there are $O(D)^m$ monomials of degree at most D, and hence at most $O(D)^m$ matrix multiplications to perform, and the sizes of the matrices are $d_1\cdots d_m \le d^m.$ Thus, the complexity is $(Dd)^{O(m)}.$

(b) The proof proceeds by induction on the number of variables m of ${\mathcal {F}}.$

If $m=1,$ then the computation of a gcd takes $(d+1)^{c}$ operations in the domain $\mathrm{D},$ for some universal constant $c > 0,$ using the complexity analysis of [2], Algorithm 8.22 (Extended Signed Subresultant)] and [2], Algorithm 10.13 (Sign Determination)].

If $m>1$, let $t=(t^{\prime },\,u),$ and we suppose by the induction hypothesis that the complexity of arithmetic operations including pseudo-inverse in $\mathrm{D}[t^{\prime }]$ is $(d+1)^{c(m-1)}$ arithmetic operations in the ordered domain $\mathrm{D}.$ The claim is clear since the arithmetic operations in the domain $\mathrm{D}[t]$ use $(d+1)^{c}$ operations in the domain $\mathrm{D}[t^{\prime }]$ using the complexity analysis of [2], Algorithm 8.22 (Extended Signed Subresultant)] and [2], Algorithm 10.13 (Sign Determination)]. $\square$

We can now give the description of Algorithm 3 (Limit of a Bounded Point).

Description of Algorithm 3 (Limit of a Bounded Point)

The precise input and output of this algorithm appear in Sect. 6.2.

Procedure Remove from $g(\varepsilon )(T_1,\ldots ,T_m,\,U)$ the coefficients vanishing at the point $(t_1,\ldots ,t_m)$ using [2], Algorithm 12.19 (Triangular Sign Determination)]. Supposing without loss of generality that not all the coefficients of

$$\begin{aligned} g(\varepsilon )\left( t_1,\ldots ,t_m,\,U\right) \end{aligned}$$

are multiples of $\varepsilon ,$ denote by $g(T_1,\ldots ,T_m,\,U)$ the polynomial obtained by substituting $0$ for $\varepsilon$ in $g(\varepsilon )(T_1,\ldots ,T_m,\,U).$

Similarly, denote by $G(T_1,\ldots ,T_m,\,U)$ the polynomials obtained by substituting $0$ for $\varepsilon$ in $G(\varepsilon )(T_1,\ldots ,T_m,\,U).$

Compute the set $\varSigma$ of Thom encodings of roots of $g(t,\,U)$ using [2], Algorithm 12.19 (Triangular Sign Determination)]. Denoting by $\mu _\sigma$ the multiplicity of the root of $g(t,\,U)$ with Thom encoding $\sigma ,$ define $G_\sigma$ as the $(\mu _\sigma -1)$th derivative of G with respect to U.

Identify the Thom encoding $\sigma$ and $G_\sigma$ representing z, using [2], Algorithm 12.19 (Triangular Sign Determination)], by checking whether a ball of infinitesimal radius $\delta$ ($1\gg \delta \gg \varepsilon >0$) around the point x represented by the real univariate representation $g,\,\sigma ,\,G_\sigma$ contains $z(\varepsilon ).$

Pseudo-invert the leading coefficient of the univariate representation, denote by $\mathcal {F}^{\prime },\,\sigma ^{\prime }$ the new triangular Thom encoding describing $t$, and compute a pseudoreduction of the output modulo $\mathcal {F}^{\prime }.$

Complexity analysis follows from the complexity of [2], Algorithm 12.19 (Triangular Sign Determination)].

1.2 Limit of a Curve

Computing the limit of a curve is not immediate when some part of the curve has a vertical limit, as seen in the following example.

Example 8.5

Consider the s-a curve $\gamma :\,[0,\,\varepsilon ]\rightarrow \mathrm {R}\langle \varepsilon \rangle ^3,$ parametrized by the $X_1$-coordinate defined by

$$\begin{aligned} \gamma \left( x_1\right) = \left( x_1,\,\gamma _2\left( x_1\right) ,\,\gamma _3\left( x_1\right) \right) ,\quad x_1 \in [0,\,\varepsilon ], \end{aligned}$$

where $(\gamma _2(x_1),\,\gamma _3(x_1))$ is the solution of the triangular system

$$\begin{aligned} X_2 - x_1/\varepsilon = 0, \\ X_2^2 + X_3^2 - 1 = 0, \end{aligned}$$

with Thom encoding $(0,\,+),\,(0,\,+,\,+).$

Notice that the image of $\gamma$ is contained in the cylinder of unit radius, with the $X_1$-axis as the axis, and is bounded over $\mathrm {R}.$ The image of $\gamma$ under the $\lim _\varepsilon$ map is contained in a circle in the plane $X_1=0$ and can no longer be described as a curve parametrized by the $X_1$-coordinate.

However, it is possible to reparametrize $\gamma$ by the $X_2$-coordinate. In doing so we obtain another s-a curve $\varphi :\,[0,\,1] \rightarrow \mathrm {R}\langle \varepsilon \rangle ^3$ (having the same image as $\gamma$) defined by

$$\begin{aligned} \varphi \left( x_2\right) = \left( \varphi _1\left( x_2\right) ,\,x_2,\,\varphi _3\left( x_2\right) \right) ,\quad x_2 \in [0,\,1], \end{aligned}$$

where $(\varphi _1(x_2),\,\varphi _3(x_2))$ is the real solution of the triangular system

$$\begin{aligned} X_1-\varepsilon x_2 = 0, \\ X_3^2 + x_2^2 - 1 = 0, \end{aligned}$$

with Thom encoding $(0,\,-),\,(0,\,+,\,+).$ Notice that the image under $\lim _\varepsilon$ of the curve that is the graph of $\varphi$ can be easily described as the curve represented by the following triangular system parametrized by $x_2 \in [0,\,1]$:

$$\begin{aligned} X_1 = 0, \\ X_3^2 + x_2^2 - 1 = 0, \end{aligned}$$

and Thom encoding $(0,\,-1),\,(0,\,+,\,+).$

This is why some kind of reparametrization is necessary before computing the limit.

1.2.1 Reparametrization of Curve Segments

We define the notion of a well-parametrized curve and prove that the limit of a well-parametrized curve is easy to describe.

Definition 8.6

A differentiable s-a curve

$$\begin{aligned} \gamma = \left( \gamma _1,\ldots ,\gamma _k\right) :\,(a,\,b)\rightarrow \mathrm {R}^k, \end{aligned}$$

parametrized by $X_1$ [i.e., $\gamma _1(x_1)=x_1$] is well parametrized if for every $x_1 \in (a,\,b)$

$$\begin{aligned} \sum _{i=1}^k \left( \frac{\partial \gamma _i}{\partial X_1}\right) ^2 \le k. \end{aligned}$$

Let $t\in \mathrm {R}^m$ be represented by a triangular Thom encoding $\mathcal {F},\,\sigma$, and let

$$\begin{aligned} f_1,\,\sigma _1,\, f_2,\, \sigma _2,\,g,\, \tau ,\,G \end{aligned}$$

be a curve segment with parameter $X_j$ over t on $(\alpha _1,\,\alpha _2)$, where $\alpha _1$ and $\alpha _2$ are the elements of $\mathrm {R}$ represented by the Thom encodings $f_1,\,\sigma _1$ and $f_2,\,\sigma _2.$

The curve segment

$$\begin{aligned} f_1,\,\sigma _1,\, f_2,\, \sigma _2,\,g,\, \tau ,\,G \end{aligned}$$

is well parametrized if the s-a curve $\gamma :\,(\alpha _1,\,\alpha _2)\rightarrow \mathrm {R}\langle \varepsilon \rangle ^k$ defined by

$$\begin{aligned} \gamma \left( x_j\right) = \left( \frac{g_{1} (t,\,x_j,\, u(x_j))}{g_0 (t,\,x_j,\,u(x_j))}, \ldots , \frac{g_k (t,\,x_j,\, u(x_j))}{g_0 (t,\,x_j,\, u(x_j))} \right) , \end{aligned}$$

is well parametrized, where $u:\,(\alpha _1,\,\alpha _2) \rightarrow \mathrm {R}$ maps each $x_j \in (\alpha _1,\,\alpha _2)$ to the root of $g(t,\,x_j,\,U)$ with Thom encoding $\tau .$ This means that

$$\begin{aligned} \sum _{i=1}^k\left( \left( \frac{g_i (t,\,x_j,\,u(x_j))}{g_0 (t,\,x_j,\,u(x_j))} \right) ^{\prime }\right) ^2 \le k, \end{aligned}$$

where the derivative is taken with respect to $x_j.$

Example 8.5 is not a well-parametrized curve segment.

If a curve segment defined over $\mathrm {R}\langle \varepsilon \rangle$ is well parametrized and represents a curve bounded over $\mathrm {R},$ then the image of the curve under the $\lim _\varepsilon$ map can be easily described. The following proposition explains why this is true.

Proposition 8.7

Let $(a(\varepsilon ),\,b(\varepsilon ))\subset \mathrm {R}\langle \varepsilon \rangle ,\,a(\varepsilon ),\,b(\varepsilon )$ be bounded over $\mathrm {R},\,r < j \le k,\,z(\varepsilon ) \in \mathrm {R}\langle \varepsilon \rangle ^{r},$ and let

$$\begin{aligned} \gamma (\varepsilon ) =:(a(\varepsilon ),\,b(\varepsilon ))\rightarrow \{z(\varepsilon )\} \times \mathrm {R}\langle \varepsilon \rangle ^{k - r} \end{aligned}$$

be a s-a differentiable curve parametrized by $X_j$ and bounded over $\mathrm {R}.$ If $\gamma (\varepsilon )$ is well parametrized, then:

• (1) There exists a continuous extension of $\gamma (\varepsilon )$ to a continuous s-a curve,

  $$\begin{aligned} \gamma (\varepsilon ) = :[a(\varepsilon ),\,b(\varepsilon )] \rightarrow \{z(\varepsilon )\} \times \mathrm {R}\langle \varepsilon \rangle ^{k - r}, \end{aligned}$$

  defined over the closed interval $[a(\varepsilon ),\,b(\varepsilon )]$;

• (2) For each $x \in [\lim _\varepsilon ( a(\varepsilon )),\,\lim _\varepsilon (b(\varepsilon ))]$ and any $x(\varepsilon ) \in [a(\varepsilon ),\,b(\varepsilon )]$, with $\lim _\varepsilon (x(\varepsilon )) = x,\,\gamma (x):=\lim _\varepsilon (\gamma (\varepsilon )(x)) = \lim _\varepsilon (\gamma (\varepsilon )(x(\varepsilon )))$;

• (3) $\lim _\varepsilon (\gamma (\varepsilon )([a(\varepsilon ),\,b(\varepsilon )])) = \gamma ([\lim _\varepsilon (a(\varepsilon )),\,\lim _\varepsilon (b(\varepsilon ))]).$

In other words, the graph of the s-a function $\gamma (-):= \lim _\varepsilon (\gamma (\varepsilon )(-))$ is the image under $\lim _\varepsilon$ of the graph of $\gamma (\varepsilon ).$

Proof

Since $\gamma (\varepsilon )$ is bounded, it follows that there exists a continuous extension of $\gamma (\varepsilon )$ to the endpoints of the interval $(a(\varepsilon ),\,b(\varepsilon )).$ It also follows from the definition of being well parametrized that $||\gamma (\varepsilon )^{\prime }(x)|| \le \sqrt{k}$ for all $x\in (a(\varepsilon ),\,b(\varepsilon )).$ By the s-a mean value theorem [2], Exercice 3.4], we have that for each $x \in (a(\varepsilon ),\,b(\varepsilon ))\cap \mathrm {R}$ and any $x(\varepsilon ) \in (a(\varepsilon ),\,b(\varepsilon ))$, with $\lim _\varepsilon ( x(\varepsilon )) = x,$

$$\begin{aligned} ||\gamma (\varepsilon )(x) - \gamma (\varepsilon )(x(\varepsilon ))|| =||\gamma (\varepsilon )^{\prime }(w(\varepsilon ))|||x-x(\varepsilon )| \end{aligned}$$

for some $w \in (x,\,x(\varepsilon ))$ [assuming without loss of generality that $x < x(\varepsilon )$]. Taking the image under $\lim _\varepsilon$ and noticing that $||\gamma (\varepsilon )^{\prime }(w(\varepsilon ))||$ is bounded over $\mathrm {R}$ by the previous observation, we obtain that

$$\begin{aligned} \lim _\varepsilon (\gamma (\varepsilon )(x)) = \lim _\varepsilon (\gamma (\varepsilon )(x(\varepsilon ))), \end{aligned}$$

proving (1). This implies that the function $\gamma :\,(\lim _\varepsilon (a(\varepsilon )),\,\lim _\varepsilon (b(\varepsilon ))) \rightarrow \mathrm {R}^k$ defined by $\gamma (x) = \lim _\varepsilon (\gamma (\varepsilon )(x))$ is a continuous, bounded [since $\gamma (\varepsilon )$ is bounded over $\mathrm {R}$] s-a function and, hence, can be extended to a continuous, bounded s-a function on the closed interval $[\lim _\varepsilon ( a(\varepsilon )),\,\lim _\varepsilon (b(\varepsilon ))].$ Moreover, it is clear that $\gamma (\lim _\varepsilon (a(\varepsilon ))) = \lim _\varepsilon (\gamma (\varepsilon )(a(\varepsilon )))$ and $\gamma (\lim _\varepsilon (b(\varepsilon ))) = \lim _\varepsilon (\gamma (\varepsilon )(b(\varepsilon )))$ since

$$\begin{aligned} \gamma (\lim _\varepsilon (a(\varepsilon ))),\,\gamma (\lim _\varepsilon (b(\varepsilon ))) \in \overline{\gamma ((\lim _\varepsilon (a(\varepsilon )),\,\lim _\varepsilon (b(\varepsilon ))))}=\lim _\varepsilon (\gamma (\varepsilon )([a(\varepsilon ),\,b(\varepsilon )])). \end{aligned}$$

It is then clear that (2) follows.

A s-a curve is in general not well parametrized. However, subdividing if necessary the curve into several pieces, it is possible to choose for each such piece a parametrizing coordinate that makes the piece well parametrized. This is what we do in Algorithm 8 (Reparametrization of a Curve).

Proof of correctness. Let

$$\begin{aligned} \left( f_1,\,\sigma _1,\,f_2,\,\sigma _2,\,g,\, \tau ,\,G\right) \end{aligned}$$

be a curve segment parametrized by $X_1$ over t representing the curve $\gamma :\,(a,\,b) \rightarrow \mathrm {R}^k.$

Let $(c,\,d)$ be a subinterval of $(a,\,b)$ such that for every $x_1\in (a,\,b)$

$$\begin{aligned} G_\ell \left( t,\,x_1,\,u\left( x_1\right) \right) = k F_\ell ^2\left( t,\,x_1,\,u\left( x_1\right) \right) - \sum _{j=1}^{k}F_j^2\left( t,\,x_1,\,u\left( x_1\right) \right) \ge 0 \end{aligned}$$

(8.1)

(using the notation of Steps 1 and 2).

This implies

$$\begin{aligned} \left| \frac{\partial \gamma _\ell }{\partial X_1} \right| \ge \frac{1}{\sqrt{k}}, \end{aligned}$$

and hence the mapping $\gamma _\ell$ from $(c,\,d)$ to $(c^{\prime },\,d^{\prime })$, with $c^{\prime }=\gamma _\ell (c),\,d^{\prime }=\gamma _\ell (d)$, is invertible. Defining $\bar{\gamma }(x_\ell )=\gamma (\gamma _\ell ^{-1}(x_\ell )),\,\bar{\gamma }((c^{\prime },\,d^{\prime }))=\gamma ((c,\,d))$ is well parametrized by $X_\ell .$

Moreover, at each point $x_1 \in (a,\,b)$ such a choice of $\ell$ exists since there must exist an $\ell ,\, 1 \le \ell \le k$ such that $\displaystyle {\left( \frac{\partial \gamma _\ell }{\partial X_1}\right) ^2}$ is at least the average value $\displaystyle {\frac{1}{k}\sum \nolimits _{i=1}^k \left( \frac{\partial \gamma _i}{\partial X_1}\right) ^2}.$ Notice also that for such a choice of $\ell$ we have, by the chain rule,

$$\begin{aligned} \sum _{i=1}^k \left( \frac{\partial \gamma _i}{\partial X_\ell }\right) ^2 = \frac{\sum _{i=1}^k \left( \frac{\partial \gamma _i}{\partial X_1}\right) ^2}{\left( \frac{\partial \gamma _\ell }{\partial X_1}\right) ^2}\le k. \end{aligned}$$

(8.2)

In Step 2 of the algorithm we obtain a partition of the interval $(a,\,b)$ into points and open intervals such that over each subinterval $(c_{j-1},\,c_j)$ of the partition there exists an index $\ell = \ell (j)$ such that (8.1) is satisfied at each point $v \in (c_{j-1},\,c_j),$ and the curve segment over this interval is well parametrized by $X_\ell$ by (8.2).

Each curve segment corresponding to elements of $\mathcal {V}$ output by the algorithm is thus well parametrized. The remaining property of the output is a consequence of the correctness of Algorithm 1 (Curve Segments) and [2], Algorithm 12.19 (Triangular Sign Determination)]. $\square$

Complexity analysis. Let $\mathrm{D}$ be a bound on the degrees of the polynomials in the input. The complexity of Steps 1 and 2 is bounded by $k^{O(1)} \mathrm{D}^{O(m)}$ from the complexity of [2], Algorithm 11.19 (Restricted Elimination)] and [2], Algorithm 12.23 (Triangular Sample Points)], noting that the number of polynomials in $\mathcal {L}$ is bounded by $k^{O(1)} \mathrm{D}^{O(m)}.$

In Steps 3 and 4 Algorithm 1 (Curve Segments) and [2], Algorithm 12.19 (Triangular Sign Determination)] are both called with a constant number of variables in the input. Using the complexity analysis of these algorithms, the total complexity is bounded by $k^{O(1)} D^{O(m)}.$ $\square$

1.2.2 Limit of a Curve

We are now ready to describe Algorithm 4 (Limit of a Curve).

Description of Algorithm 4 (Limit of a Curve)

The algorithm proceeds by reparametrizing the curve and computing the limit of the well-parametrized curve segments thus obtained, as explained in what follows. Its precise input and output appear in Sect. 6.2.

Procedure.

Step 1. :

Let $T=(T_1,\ldots ,T_m),\,X^{\prime }=(X_{1},\ldots ,X_{r}).$ Call a slight variant of [2], Algorithm 12.18 (Parametrized Bounded Algebraic Sampling)], computing pseudoreductions of the intermediate computations modulo $\mathcal {F}$ (using Proposition 8.4), with input

$$\begin{aligned} \sum _{A\in \mathcal {H}(\varepsilon )}A^2\in \mathrm{D}[\varepsilon ,\,T,\,X^{\prime }] \end{aligned}$$

and parameters $\varepsilon ,\,T,$ and output the set $\mathcal {U}_{\varepsilon }$ of parametrized univariate representations with variable U. For every $(h(\varepsilon ),\,H(\varepsilon )) \in \mathcal {U}(\varepsilon ),$ use [2], Algorithm 12.20 (Triangular Thom Encoding)], with the triangular system $(\mathcal {F},\,h(\varepsilon ))$ as input, to compute the Thom encodings of the real roots of $h(\varepsilon )(y,\,U).$ If

$$\begin{aligned} \mathcal {H}(\varepsilon )=\left( h_{[1]},\ldots ,h_{[r]}\right) , \end{aligned}$$

with $h_{[i]}\in \mathrm{D}[T,\,X_1,\ldots ,X_i]$, substitute the variables $X^{\prime }$ into

$$\begin{aligned} \bigcup _{0,\ldots ,r} \mathrm{Der}_{X_i}\left( h_{[i]}\right) , \end{aligned}$$

using $H(\varepsilon )$ by Notation 4.5, and define a family $\mathcal {A}$ of polynomials in $\varepsilon ,\,T,\,U.$ Using [2], Algorithm 12 (Triangular Sign Determination)], compute the signs of the polynomials of $\mathcal {A}$ at the roots of $h(\varepsilon )(y,\,U).$ Comparing the Thom encodings, identify a specific $(h(\varepsilon ),\,\tau (\varepsilon ),\,H(\varepsilon ))$ representing $z(\varepsilon )$ over t. Then apply Algorithm 3 (Limit of a Bounded Point) with input

$$\begin{aligned} (h(\varepsilon ),\,\tau (\varepsilon ),\,H(\varepsilon )), \end{aligned}$$

representing $z(\varepsilon )$ over t, to obtain a real univariate representation $p_z,\,\rho _z,\,P_z$ representing z over t.

Step 2. :

Using Algorithm 8 (Reparametrization of a Curve), reparametrize the input curve segment.

Step 3. :

For every well-parametrized curve segment $S(\varepsilon )$ computed in Step 2 and represented by

$$\begin{aligned} \left( f(\varepsilon )_{1},\,\sigma (\varepsilon )_{1},\,f(\varepsilon )_{2},\,\sigma (\varepsilon )_{2},\,g(\varepsilon ),\,\tau (\varepsilon ),\,G(\varepsilon )\right) , \end{aligned}$$

do the following. First reorder the variables to ensure that the parameter of $S(\varepsilon )$ is $X_{r+1}.$ Then compute a description of $\lim _\varepsilon (S(\varepsilon )).$ This process will generate a finite list of open intervals and points above which the representation of the restriction of the curve $\lim _\varepsilon (S(\varepsilon ))$ by a curve segment is fixed. This is done as follows.

Step 3(a). :

Denote by $\alpha (\varepsilon )_{1}$ the element of $\mathrm {R}\langle \varepsilon \rangle$ represented by

$$\begin{aligned} f(\varepsilon )_{1}\left( T,\,X^{\prime },\,X_{r+1}\right) ,\,\sigma (\varepsilon )_{1} \end{aligned}$$

over $(t,\,z(\varepsilon )).$ Call a slight variant of [2], Algorithm 12.18 (Parametrized Bounded Algebraic Sampling)], computing a pseudoreduction of the intermediate computations modulo $\mathcal {F}$ of the output modulo $\mathcal {F}$ (using Proposition 8.4), with input

$$\begin{aligned} \sum _{A\in \mathcal {H}(\varepsilon )}A^2+f(\varepsilon )_{1}\left( T,\,X^{\prime },\,X_{r+1}\right) ^2 \in \mathrm{D}\left[ \varepsilon ,\,T,\,X^{\prime },\,X_{r+1}\right] \end{aligned}$$

and parameters $\varepsilon ,\,T,$ and output a set $\mathcal {U}^{\prime }_{\varepsilon }$ of parametrized univariate representations with variable U. For every $(h(\varepsilon ),\,H(\varepsilon )) \in \mathcal {U}^{\prime }_{\varepsilon },$ use [2], Algorithm 12.20 (Triangular Thom Encoding)], with the triangular system $(\mathcal {F},\,h(\varepsilon ))$ as input, to compute the Thom encodings of the real roots of $h(\varepsilon )(y,\,U).$ If

$$\begin{aligned} \mathcal {H}(\varepsilon )=\left( h_{[1]},\ldots ,h_{[r]}\right) , \end{aligned}$$

with $h_{[i]}\in \mathrm{D}[T,\,X_1,\ldots ,X_i],$ substitute the variables $X^{\prime },\,X_{r+1}$ into

$$\begin{aligned} \mathrm{Der}_{X_{r+1}}f(\varepsilon )_{1}\left( T,\,X^{\prime },\,X_{r+1}\right) ,\,X_{r+1}\cup \bigcup _{1,\ldots ,r} \mathrm{Der}_{X_i}\left( h_{[i]}\right) \end{aligned}$$

using Notation 4.5, and define a family $\mathcal {B}$ of polynomials in $\varepsilon ,\,T,\,U.$ Using [2], Algorithm 12 (Triangular Sign Determination)], compute the signs of the polynomials of $\mathcal {B}$ at the roots of $h(\varepsilon )(y,\,U).$ Comparing the Thom encodings, identify a specific $(h(\varepsilon ),\,\tau (\varepsilon ),\,H(\varepsilon ))$ representing $(z(\varepsilon ),\,\alpha (\varepsilon )_{1})$ over t. Then apply Algorithm 3 (Limit of a Bounded Point) with input

$$\begin{aligned} (h(\varepsilon ),\,\tau (\varepsilon ),\,H(\varepsilon )) \end{aligned}$$

representing $(z(\varepsilon ),\,\alpha (\varepsilon )_{1})$ over t to obtain a quasi-monic real univariate representation $p_{z,\alpha _1},\,\rho _{z,\alpha _1},\,P_{z,\alpha _1}$ representing $(z,\,\alpha _1)$ over t, with $\alpha _1=\lim _\varepsilon (\alpha (\varepsilon )_{1}).$ Obtain a Thom encoding over t of $\alpha _1$ using [2], Algorithm 15.1 (Projection)]. Similarly, for $\alpha (\varepsilon )_{2}$ the element of $\mathrm {R}\langle \varepsilon \rangle$ represented by

$$\begin{aligned} f(\varepsilon )_{2}\left( T,\,X^{\prime },\,X_{r+1}\right) ,\,\sigma (\varepsilon )_{2}, \end{aligned}$$

over $(t,\,z(\varepsilon )),$ compute a Thom encoding over t of $\alpha _2=\lim _\varepsilon (\alpha (\varepsilon )_{2}).$

Step 3(b). :

Perform a slight variant of [2], Algorithm 12.18 (Parametrized Bounded Algebraic Sampling)], computing pseudoreductions of intermediate computations modulo $\mathcal {F}$ of the output modulo $\mathcal {F}$ (using Proposition 8.4), with input

$$\begin{aligned} \sum _{A\in \mathcal {H}(\varepsilon )}A^2+g(\varepsilon )\left( T,\,X^{\prime },\,X_{r+1},\,V\right) ^2 \in \mathrm{D}\left[ \varepsilon ,\,T,\,X^{\prime },\,X_{r+1},\,U\right] \end{aligned}$$

and parameters $\varepsilon ,\,T,\,X_{r+1}$, and output a set $\mathcal {V}(\varepsilon )$ of parametrized univariate representations with parameter $\varepsilon ,\,T,\,X_{r+1}$ and variable V. Denote by $\mathbf {\varTheta }(\varepsilon )$ the set of polynomials $\theta (\varepsilon )$ such that there exists $\varTheta (\varepsilon )$, with $(\theta (\varepsilon ),\,\varTheta (\varepsilon ))\in \mathcal {V}(\varepsilon ).$ Note that $\theta (\varepsilon ) \in \mathrm{D}[\varepsilon ,\,T,\,X_{r+1},\,V].$

Step 3(c). :

Compute the family of coefficients $\mathcal {C}\subset \mathrm{D}[T,\,X_{r+1}]$ of the polynomials $\theta (\varepsilon ) \in \mathbf {\varTheta }(\varepsilon )$ considered as elements of $\mathrm{D}[T,\,X_{r+1}][\varepsilon ,\,V]$ and the list $\mathcal {L} \subset \{=0,\,\ne 0\}^{\mathcal {C}}$ of nonempty conditions $=0,\,\not = 0$ satisfied by $\mathcal {C}$ in $\mathrm {R}$ using [2], Algorithm 12.23 (Triangular Sample Points)]. Note that for every $x_{r+1}$ in the realization of $\tau \in \mathcal {L},$ the orders in $\varepsilon$ of the coefficients of the polynomials in $\mathbf {\Theta }(\varepsilon )(t,\,x_{r+1})\subset \mathrm{D}[\varepsilon ,\,V]$ are fixed. For every $\theta (\varepsilon ) \in \mathbf {\varTheta }(\varepsilon )$ we denote by $o(\theta (\varepsilon ),\,\tau )$ the minimal order in $\varepsilon$ of the coefficients of $\theta (\varepsilon )(t,\,x_{r+1})$ on the realization of $\tau$ and by $\mathbf {\varTheta }_\tau \subset \mathrm{D}[T,\,X_{r+1},\,V]$ the set of polynomials obtained by substituting $0$ for $\varepsilon$ in $\varepsilon ^{-o(\theta (\varepsilon ),\tau )}\theta (\varepsilon ).$

Step 3(d). :

Define

$$\begin{aligned} \mathbf {\Theta }=\bigcup _{\tau \in \mathcal {L}} \mathbf {\Theta }_\tau \subset \mathrm{D}\left[ T,\,X_{r+1},\,V\right] . \end{aligned}$$

Compute

$$\begin{aligned} \mathcal {E}=\mathcal {C} \cup \bigcup _{\theta \in \mathbf {\Theta }} \mathrm{RElim}_V(\theta ,\,\mathrm{Der}(\theta ))\subset \mathrm{D}\left[ T,\,X_{r+1}\right] , \end{aligned}$$

using [2], Algorithm 11.19 (Restricted Elimination)], so that the Thom encodings of the real roots of $\theta (t,\,x_{r+1},\,V)$ are fixed when $x_{r+1}$ varies in an open interval defined by the roots of the polynomials $\mathcal {E}(t).$

Step 3(e). :

Compute using [2], Algorithm 12.19 (Triangular Sign Determination)] the Thom encodings of the real roots of the polynomials in $\mathcal {E}(t)$ and the ordered list $c_1<\cdots < c_{h-1}$ of the roots of the polynomials in $\mathcal {E}(t)$ in the interval $(c_0,\,c_h),$ with $c_0=\alpha _1,\,c_h=\alpha _2.$ Denote by $C_j,\,\rho _j$ a polynomial in $\mathcal {E}(t)$ and a Thom encoding representing $c_j.$

Step 3(f). :

For every j from 1 to $h-1,$ and for every $\theta \in \mathbf {\Theta },$ determine, using [2], Algorithm 12.19 (Triangular Sign Determination)], the Thom encoding

$$\begin{aligned} \theta \left( t,\,c_j,\,V\right) ,\,\tau _j \end{aligned}$$

of a root $v_j$ such that $v_j=\lim _\varepsilon (v(\varepsilon )),$ where $v(\varepsilon )$ is the root of $\theta (\varepsilon )(t,\,c_j,\,V)$, with Thom encoding $\tau (\varepsilon ).$ The multiplicity $\mu _j$ of the root $v_j$ is determined by $\tau _j.$

Step 3(g). :

For every j from 1 to h, define $I=(c_{j-1},\,c_j).$ For every $\theta \in \mathbf {\Theta }$ determine, using [2], Algorithm 12.19 (Triangular Sign Determination)], the Thom encoding $\theta _{I}(t,\,x_{r+1},\,V),\,\tau _{I}$ of a root $v_{I}(x_{r+1})$ of multiplicity $\mu _I$ such that for every $x_{r+1}\in I,\,v_{I}(x_{r+1})=\lim _\varepsilon (v(\varepsilon ))$, where $v(\varepsilon )$ is the root of $\theta (\varepsilon )(t,\,x_{r+1},\,V)$ with Thom encoding $\tau (\varepsilon ).$ The multiplicity $\mu _I$ of the root $v_{I}(x_{r+1})$ is determined by $\tau _{I}.$

Step 3(h). :

Given $(\theta (\varepsilon ),\,\Theta (\varepsilon ))$ in $\mathcal {U}(\varepsilon )$, denote by $(g_{\Theta (\varepsilon )},\,G_{\Theta (\varepsilon )})$ the $k-r+1$-tuple of polynomials obtained by substituting into $(g(\varepsilon ),\,G(\varepsilon ))$ the variables $X^{\prime },\,U$ by $F(\varepsilon )$ (Notation 4.5). Denote by $\mathcal {V}^{\prime }(\varepsilon )\subset \mathrm{D}[\varepsilon ,\,T,\,X_j,\,V]$ the set of $k-r+1$-tuples of polynomials $(g_{\Theta (\varepsilon )},\,G_{\Theta (\varepsilon )}).$

Step 3(i). :

For every j from 1 to $h-1$ and every $(h(\varepsilon ),\,H(\varepsilon ))\in \mathcal {V}^{\prime }(\varepsilon ),$ with $H(\varepsilon )=(h(\varepsilon )_{0},\,h(\varepsilon )_{r+2},\ldots , h(\varepsilon )_{k})$, determine the order in $\varepsilon$ of

$$\begin{aligned} h_{\varepsilon }(t,\,c_j,\,v_j),\,h(\varepsilon )_{i}(t,\,c_j,\,v_j). \end{aligned}$$

This is done by determining the signs of the coefficient $h_{\ell },\,h_{i,\ell }$ of $\varepsilon ^\ell$ in $h(t,\,c_j,\,v_j),\,h_i(t,\,c_j,\,v_j)$ using [2], Algorithm 12.19 (Triangular Sign Determination)]. Retain those $(h(\varepsilon ),\,H(\varepsilon ))$ such that $o(h(\varepsilon )_{0})\le o(h(\varepsilon )_{i})$ for all i from $r+2$ to k, and replace $\varepsilon$ with $0$ in

$$\begin{aligned} (\varepsilon ^{-o(h_{\varepsilon })}h(\varepsilon ),\,\varepsilon ^{-o(h(\varepsilon )_{0})}H(\varepsilon )), \end{aligned}$$

which defines a set $\mathcal {H}_j.$ Inspecting every $(h,\,H)\in \mathcal {H}_j,$ determine, using [2], Algorithm 12.19 (Triangular Sign Determination)], a $k-r+1$-tuple $(h_j,\,H_j)$ with the following property. Let $d_j$ be the point represented by the real univariate representation

$$\begin{aligned} \left( h_j\left( T,\,X_{r+1},\,V\right) ,\,\tau _j,\,H_j^{(\mu _j-1)}\left( T,\,X_{r+1},\,V\right) \right) \end{aligned}$$

over $t,\,u.$ The image under $\lim _\varepsilon$ of the point of $S(\varepsilon )$ with the $X_{r+1}$-coordinate $(c_j)$ is $(z,\,c_j,\,d_j).$

Step 3(j). :

For every j from 1 to h, define $I=(c_{j-1},\,c_j).$ For every $(h(\varepsilon ),\,H(\varepsilon ))\in \mathcal {V}^{\prime }(\varepsilon ),$ with $H(\varepsilon )=(h(\varepsilon )_{0},\,h(\varepsilon )_{r+2},\ldots , h(\varepsilon )_{k})$, subdivide I so that the order in $\varepsilon$ of $h(\varepsilon )(t,\,c_j,\,v_j)$ and $h_i(\varepsilon )(t,\,x_{r+1},\,v_{I}(x_{r+1}))$ is fixed. This is done by computing

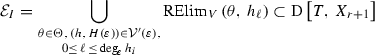
and

using [2], Algorithm 11.19 (Restricted Elimination)]. Defining

$$\begin{aligned} \mathcal {E}^{\prime }_I=\mathcal {E}_I\cup \bigcup _{i\in {0,r+2,\ldots ,k}} \mathcal {E}_{I,i}, \end{aligned}$$

compute the Thom encodings of the roots of the polynomials in $\mathcal {E}^{\prime }_{I}(t)$ using [2], Algorithm 12.19 (Triangular Sign Determination)]. On each open interval J between two successive roots, the order in $\varepsilon ,$ denoted by $o(h_{\varepsilon }),\,o(h(\varepsilon )_{i})$ of the polynomials

$$\begin{aligned} h(\varepsilon )\left( t,\,x_{r+1},\,v_{J}\left( x_{r+1}\right) \right) ,\,h_i(\varepsilon )\left( t,\,x_{r+1},\,v_{J}\left( x_{r+1}\right) \right) , \end{aligned}$$

remains fixed. Retain those $(h(\varepsilon ),\,H(\varepsilon ))$ such that $o(h(\varepsilon )_{0})\le o(h(\varepsilon )_{i})$ for all i from $r+2$ to k, and replace $\varepsilon$ with $0$ in $\varepsilon ^{-o(h(\varepsilon )_{0})}(h,\,H(\varepsilon )),$ which defines a set $\mathcal {H}_J.$ Inspecting every $(h,\,H)\in \mathcal {H}_J,$ determine, using [2], Algorithm 12.19 (Triangular Sign Determination)], a $k-r+1$-tuple $(h_J,\,H_J)$ such that the point represented by

$$\begin{aligned} \left( h_J\left( t,\,x_{r+1},\,v_{I}\right) ,\,H_J^{(\mu _J-1)}\left( t,\,x_{r+1},\,v_{I}\right) \right) \end{aligned}$$

is the image under $\lim _\varepsilon$ of the point of $S(\varepsilon )$ with the $X_{r+1}$-coordinate $x_{r+1},$ where $\mu _J$ is the multiplicity of $u_{J}(x_{r+1})$ as a root of $h_{J}(x_{r+1},\,V).$ Let $w_J$ be the curve represented by the curve segment representation

$$\begin{aligned} h_{I}\left( T,\,X_{r+1},\,U\right) ,\,\tau _j,\,H_J^{(\mu _J-1)}\left( T,\,X_{r+1},\,U\right) , \end{aligned}$$

with parameter $X_{r+1}$ over $t,\,u.$

Step 3(k). :

Let $c_1< \cdots < c_{N-1}$ denote the set of all elements of $\mathrm {R}$ computed earlier in Steps 2(d) and (i), and $c_N=c.$ Reindex each $v_j$ computed in Step 3(h) such that $d_j$ lies above $c_j.$ Similarly, reindex each $w_I$ computed in Step 3(i) by some $j,\,1 \le j \le N,$ so that $w_j$ lies above the interval $(c_{j-1},\,c_j).$ Output the lists consisting of $d_1,\ldots ,d_{N-1}$ and $w_1,\ldots ,w_N.$

Proof of correctness. Let $\gamma (\varepsilon ):\,(\alpha (\varepsilon )_{1},\,\alpha (\varepsilon )_{2}) \rightarrow \mathrm {R}\langle \varepsilon \rangle ^k$ be the curve represented by a well-parametrized curve segment

$$\begin{aligned} f(\varepsilon )_{1},\,\sigma (\varepsilon )_{1},\,f(\varepsilon )_{2},\,\sigma (\varepsilon )_{2},\,g(\varepsilon ),\,\tau (\varepsilon ),\,G(\varepsilon ) \end{aligned}$$

computed in Step 2.

Let $G:\,(\alpha _1,\,\alpha _2) \rightarrow \mathrm {R}^k$ be a curve whose image equals the image of $\gamma (\varepsilon )$ under $\lim _\varepsilon .$ Since the input curve segment is well parametrized, it follows from Proposition 8.7 that in order to compute for any $x_1 \in (c_0,\,c_N),\,G(x_1)$, it suffices to compute $\lim _\varepsilon \gamma (\varepsilon )(x_1).$ The proof of correctness of the algorithm is then similar to the proof of correctness of Algorithm 3 (Limit of a Bounded Point). $\square$

Complexity analysis. Let $\mathrm{D}$ be a bound on the degrees of all polynomials appearing in the input. We first bound the degrees in the various variables, $\varepsilon ,\,T,\,X^{\prime },\,X_{r+1},\,U,\,V$, of the polynomials computed in various steps of the algorithm. In Step 1, the degrees of the polynomials in $\mathcal {U}(\varepsilon )$ are bounded as follows. The degrees in $\varepsilon ,\,U$ are bounded by $D^{O(r)}$ by the complexity analysis of [2], Algorithm 12.18 (Parametrized Bounded Algebraic Sampling)], and the degrees in the $T_i$ are bounded by $\mathrm{D}$ because of the pseudoreduction. Moreover, the complexity of this step is bounded by $\mathrm{D}^{O(m+r)}$ from the complexity of [2], Algorithm 12.18 (Parametrized Bounded Algebraic Sampling)] and the complexity of pseudoreduction (Definition 4.2).

The degrees in $\varepsilon ,\,T_i,\,X^{\prime },\,U$ in the output of Step 2 are all bounded by $D^{O(1)}$, and the complexity of Step 2 is bounded by

$$\begin{aligned} (k-r)^{O(1)} \mathrm{D}^{O(m+r)} = k^{O(1)}\mathrm{D}^{O(m+r)} \end{aligned}$$

using the complexity analysis of Algorithm 8 (Reparametrization of a Curve).

The degrees of the polynomials in Step 3(a) are bounded as follows. In the output of the call to [2], Algorithm 12.18 (Parametrized Bounded Algebraic Sampling)], the degrees in $\varepsilon ,\,U$ are bounded by $\mathrm{D}^{O(r)},$ and the degrees in the $T_i$ are bounded by $\mathrm{D}.$ Now, from the complexity analysis of Algorithm 3 (Limit of a Bounded Point) it follows that the degrees in the $T_i$ of the polynomials output are bounded by $\mathrm{D}$, and those in $\varepsilon ,\,U$ are bounded by $\mathrm{D}^{O(r)}.$ Moreover, the complexity of Step 3(a) is bounded by $D^{O(m+r)}$ from the complexity of [2], Algorithm 12.18 (Parametrized Bounded Algebraic Sampling)], the complexity of Algorithm 3 (Limit of a Bounded Point), and the complexity of the pseudoreduction (Proposition 8.4).

The degrees of the polynomials in Step 3(b) are bounded as follows. In the output of the call to [2], Algorithm 12.18 (Parametrized Bounded Algebraic Sampling)], the degrees in $\varepsilon ,\,X_{r+1},\,V$ are bounded by $D^{O(r)},$ and the degrees in the $T_i$ are bounded by $\mathrm{D}.$ The complexity of Step 3(b) is bounded by $D^{O(m+r)}$ from the complexity of [2], Algorithm 12.18 (Parametrized Bounded Algebraic Sampling)] and the complexity of pseudoreduction (Definition 4.2).

The complexity of Step 3(c) is bounded by $D^{O(m+r)}$ using the degree bounds from the complexity analysis of the previous steps and the complexity of [2], Algorithm 12.23 (Triangular Sample Points)].

It now follows from the complexity analysis of [2], Algorithm 12.19 (Triangular Sign Determination)], [2], Algorithm 11.19 (Restricted Elimination)], and the degree estimates proved previously that the complexity of the remaining steps are all bounded by $k^{O(1)} \mathrm{D}^{O(m+r)}.$ Thus, the complexity of the algorithm is bounded by $k^{O(1)} \mathrm{D}^{O(m+r)}.$