1 Introduction

In many estuaries, regions are found with sediment concentrations exceeding those directly upstream or downstream. The region where the highest sediment concentration is found is called the estuarine turbidity maximum (ETM). Quite often multiple peaks of high concentration are found in estuaries (see, e.g., Lin and Kuo (2001) and references therein). This trapping of sediment is the result of the complex interaction of the water motion (forced by tides, river discharge, density gradients) and sediment dynamics (availability of sediment, sediment size, flocculation). At the locations with high sediment concentrations, depleted levels of oxygen (and hence degraded environmental conditions) are often observed (De Jonge 1983; Talke et al. 2009a). Since anthropogenic and natural changes (e.g., sea-level rise, land subsidence, etc.) in estuaries can influence the locations where sediment is trapped and/or the amount of sediment being trapped, it is important to understand the physical mechanisms resulting in the trapping of sediment and how these mechanisms are influenced by changes to the system.

An example of an estuary where major changes took place over the past 25 years is the Ems estuary, located on the border between The Netherlands and Germany. Recent observations on the river Ems document an increase in tidal range and suspended sediment concentration (SSC) and the development of hypoxic conditions between 1980 and the present as a response to maintenance dredging and deepening (Krebs and Weilbeer 2008; Talke et al. 2009a, b). The tidal river has also shifted from a sandy bed to a silty bed (Krebs and Weilbeer 2008). Further details about the estuary and changes are provided in Section 4.1 and Table 1. The ETM has moved upstream, but the physical mechanism producing this change is still debated. Talke et al. (2009a) show that observed changes can be reproduced with a simple model of gravitational circulation and river discharge; however, other studies speculate that tidal pumping and tidal asymmetry are important (Wurpts and Torn 2005).

Table 1 Model input parameters representing 1980 and 2005 measurements carried out along the Ems/Dollard estuary, respectively
Full size table

To understand this kind of changes in estuarine dynamics, large-scale numerical models are often applied (see, e.g., Weilbeer 2007 for the Ems estuary). Because 3D numerical models are computationally expensive and include the sum of many processes (e.g., baroclinic circulation, tidal straining, tidal pumping, flocculation, settling and scour lag, nonlinear interactions, etc.), it becomes difficult to isolate the magnitude and importance of particular processes or investigate parameter sensitivity. These limitations motivate the development of idealized models in which specific physical mechanisms can be studied in isolation. The advantage of an idealized model is that it is complex enough to reproduce the physical behavior of the system well, yet it is relatively simple to construct analytical solutions using standard mathematical techniques, avoiding high computational costs.

Various mechanisms have been identified that can result in the trapping of sediment. For example, using a tidally averaged numerical model, Festa and Hansen (1978) investigated the convergence zone of sediment due to the balance between gravitational circulation (Hansen and Rattray 1965; Officer 1976) and freshwater discharge. Recently, the Festa and Hansen approach was extended to include the influence of longitudinal suspended sediment concentration gradients on the tidally averaged flows and the trapping of sediment (Talke et al. 2009b). The importance of tidally varying processes on the formation of residual (tidally averaged) flows and sediment fluxes is discussed in many publications (Simpson et al. 1990; Geyer 1993; Jay and Musiak 1994; Burchard and Baumert 1998). Recently, an idealized model was developed to study the depth-dependent water motion on the tidal time scale in an estuarine cross section (Huijts et al. 2009) and its interaction with the entrapment of sediment in the lateral direction (Huijts et al. 2006). However, no such model has been developed that describes these processes in the longitudinal direction.

The main aim of the present paper is to develop an analytical model that simulates the along-channel flows resulting from various forcings such as the semi-diurnal and first overtide external forcing, the horizontal density gradient, and the river discharge. Based on the water motion, we calculate the sediment concentration in morphodynamic equilibrium in the estuary. Using the model, we are able to investigate the relative importance of various forcing mechanisms and parameters (e.g., tidal dynamics, sediment grain size, residual flows, etc.) on the changes that occurred between 1980 and 2005. In this paper, we address the following research questions. Why did the tidal range increase by 1.5 m in the upstream reaches between 1980 and 2005? Which mechanisms result in the trapping of sediment and in the variation of the trapping location for sediment with a different grain size under the same hydrodynamic conditions? Why is there an upstream shift of the turbidity zone in 2005 compared to 1980?

In Section 2, we discuss the model equations we use to model the water motion and sediment dynamics: the width-averaged shallow water and advection-diffusion equations, respectively. We make a perturbation analysis and provide analytic solutions of the problem in Section 3. Comparison with observations and results is provided in Section 4, followed by a discussion in Section 5 and conclusions in Section 6.

2 Model formulation

To focus on the water motion and sediment dynamics in the longitudinal direction, we develop a width-averaged model for an estuary that is constrained by a weir at the landward side. The seaward boundary of the estuary is located at x = 0, and the weir is found at x = L (see Fig. 1). The estuary is assumed to be exponentially converging, i.e., the width B(x) of the estuary is given by

$$ B(x)=B_0e^{-x/L_b}, $$
(1)

with B 0 the width of the estuary at the seaward side and L b the exponential convergence length. The bed profile is described by z = − H(x), z = 0 denotes the undisturbed water level, and z = ζ(t, x) denotes the water surface.

Fig. 1
figure 1

Sketch of the model geometry. The upper panel depicts the side view of the estuary and the lower one presents the top view. A Cartesian coordinate system is used, with x the along-channel coordinate directed landwards, y the transverse coordinate, and z the vertical coordinate pointing upwards. Other variable are introduced in the text

Full size image

The flow in the longitudinal direction is modeled by the width-averaged shallow water equations:

$$ u_x+\emph{w}_z-\frac{u}{L_b}=0, $$
(2a)
$$ u_t+uu_x+\emph{w}u_z+g\zeta_x-\frac{g\rho_x}{\rho_0}(z-\zeta)-(A_\emph{v}u_z)_z=0. $$
(2b)

Here, x(u) and z(w) denote the along-channel and vertical coordinate (velocity), respectively. Time is denoted by t, g ∼ 10 m2/s is the gravitational acceleration, \(\rho_0\sim\text{1,020}\) kg m − 3 is the reference density, and A v is the vertical eddy viscosity coefficient.

The along-channel density of the estuarine water is denoted by ρ(x) and varies in general due to the salinity s, suspended sediment concentration c, and temperature. To simplify, we neglect the density gradients caused by suspended sediment concentration (SSC) and temperature and assume that the temporal variations of the salinity field are small compared to the time-averaged salinity field. Furthermore, we assume that the salinity is vertically well-mixed. Hence, the along-channel density ρ is modeled as

$$ \rho(s)=\rho_0(1+\beta<s(x)>), $$
(3)

where β∼7.6 × 10 − 4 psu − 1 converts salt to density and the angular brackets < . > denote a tidal average. Here, < s(x) > is the observed along-channel time- and depth-averaged salinity profile which describes the gradual decrease of the salinity from the sea to the river (i.e., the model is diagnostic in salinity). The salinity profile is prescribed as a hyperbolic tangent profile along the estuary that depends on the freshwater discharge (see Talke et al. 2009a).

Following Friedrichs and Hamrick (1996), the vertical eddy viscosity coefficient A v is parameterized as

$$ A_\emph{v}(x)=A_{\emph{v}0}\frac{H(x)}{H_0}, $$
(4)

with H 0 the water depth at the entrance of the estuary.

At the free surface z = ζ, the boundary conditions are the no stress condition and the kinematic boundary condition:

$$ A_\emph{v}u_z=0\ \ \ \mbox{ and }\ \ \ \emph{w}=\frac{\partial \zeta}{\partial t}+u\frac{\partial \zeta}{\partial x}. $$
(5)

As boundary condition at the bottom, z = − H(x), we assume the bed to be impermeable, i.e.,

$$ \emph{w}=-u\frac{\partial H}{\partial x} $$
(6)

and prescribe a partial slip condition:

$$ \tau_b\equiv\rho_0A_\emph{v}u_z=\rho_0su\ \ \ \mbox{ at }\ \ \ z=-H(x). $$
(7)

Note that this condition must be evaluated at the top of the constant stress layer instead of at the true bed. The bottom stress τ b is proportional to friction velocity squared. By linearizing the quadratic friction law (Zimmerman 1992), τ b can be related to the velocity at the bed and reads τ b  = ρ 0 su. Hence, the partial slip condition can be rewritten as \(A_\emph{v}u_z=su\) (Schramkowski et al. 2002). Here, the parameter s is the so-called stress or slip parameter that can still depend on the longitudinal coordinate. Following Friedrichs and Hamrick (1996) and Schramkowski et al. (2002), this dependency is taken to be linear in the local water depth, i.e.,

$$ s=s_0\frac{H(x)}{H_0}. $$

The water motion is forced by a prescribed tidal elevation at the seaward side of the estuary that consists of a semi-diurnal (M 2) constituent and its first over tide (M 4)

$$ \zeta(t,x)=A_{M_2}\cos\sigma t+A_{M_4}\cos(2\sigma t-\phi), $$

where σ = 1.4 · 10 − 4 s − 1 is the tidal frequency of the M 2 semi-diurnal tidal constituent and \(A_{M_2}\) and \(A_{M_4}\) are the amplitude of the M 2 and M 4 (externally forced) tidal constituent, respectively. The relative phase ϕ is the phase difference between the M 4 and M 2 tidal components, defined by \(\phi=\phi_{\zeta_{M_4}}-2\phi_{\zeta_{M_2}}\), where \(\phi_{\zeta_{M_2}}\) (\(\phi_{\zeta_{M_4}}\)) denotes the phase of the M 2 (M 4) tidal constituent. Apart from the externally prescribed M 4 overtide, overtides are generated internally by nonlinear interactions. The combination of the M 2 and M 4 constituents results in so-called tidal asymmetry: an estuary is called flood (ebb) dominant if flood currents are stronger (weaker) than ebb currents.

At the riverine side, a constant river discharge Q is prescribed and the tidal discharge is required to vanish

$$ B(x)\int\limits^{\zeta}_{-H}udz = Q\ \ \ \mbox{ at }\ \ \ x=L. $$
(8)

Sediment is assumed to consist of noncohesive fine particles that have a uniform grain size (constant settling velocity) and are transported primarily as suspended load. The governing equation for the sediment dynamics is the width-averaged sediment mass balance equation (for a derivation, see electronic supplement S1)

$$ c_t+uc_x+\emph{w}c_z=\emph{w}_sc_z + (K_hc_x)_x + (K_\emph{v}c_z)_z - \frac{1}{L_b}K_hc_x, $$
(9)

where c denotes the width-averaged sediment concentration and \(\emph{w}_s\sim 0.2--5\) mm s − 1 the settling velocity. The turbulent vertical eddy diffusivity coefficient \(K_\emph{v}\) is assumed to be equal to \(A_\emph{v}\). The horizontal diffusivity coefficient is denoted by K h . Suspended sediment is transported due to diffusive contributions, temporal (or local) settling lag effects (related to tidal asymmetry and local inertia, see Groen 1967), and spatial settling lag effects (which are related to the finite time for sediment particles to settle, see Postma 1954; De Swart 2009).

At the surface, we require that no sediment particles enter or leave the domain, i.e., the normal component of the settling and diffusive flux balance

$$ \emph{w}_sc+K_\emph{v}c_z-K_hc_x\zeta_x=0\ \ \ \mbox{ at }\ \ \ z=\zeta. $$
(10)

The normal component of the sediment flux at the bottom due to erosion is given by

$$ E_s\equiv-K_\emph{v}\frac{\partial c}{\partial z}n_z-K_h\frac{\partial c}{\partial x}n_x=\emph{w}_sc_\ast\ \ \ \mbox{ at }\ \ \ z=-H(x). $$
(11)

Here, \(\overrightarrow{n}=(n_x,n_z)\) is the unit normal vector at the bottom and c  ∗  is a reference concentration. It is defined as

$$ c_\ast(t,x)=\rho_s\frac{|\tau_b(t,x)|}{\rho_0g'd_s}a(x), $$
(12)

where the density of sediment is denoted by ρ s , the dimensionless bed shear stress by τ b /(ρ 0 g′d s ) with τ b defined in Eq. 7 and the erosion coefficient by a(t, x). Furthermore, d s is the grain size of the sediment and g′ = g(ρ s  − ρ 0)/ρ 0 is the reduced gravity. The erosion coefficient a(x)∼10 − 5 models the along-channel distribution of easily erodible sediment, available in mud reaches.

Following Friedrichs et al. (1998) and Huijts et al. (2006), we will consider our system to be in morphodynamic equilibrium, which means that there is no evolution of the bed over a tidal period. This approach is valid when the easily erodible sediment is redistributed on a much shorter timescale than the typical timescale at which the external forcing changes significantly. Hence, there is a balance between the tidally averaged erosion and deposition at the bottom z = − H(x). The erosion flux is defined in Eq. 11, and the depositional sediment flux is defined by

$$ D=\emph{w}_scn_z\ \ \ \mbox{ at }\ \ \ z=-H(x). $$

Assuming that < E > − < D > = 0, a condition for morphodynamic equilibrium is obtained by integrating the sediment mass balance equation (Eq. 9) over depth. Using boundary conditions 5, 6, and 10 and averaging the result over a tidal period, the morphodynamic equilibrium condition reads (for details, see electronic supplement S2)

$$ \left\langle\int\limits_{-H}^{\zeta}(uc-K_hc_x)dz\right\rangle=0, $$
(13)

where we assumed that there is no residual sediment flux at the weir.

The sediment concentration in morphodynamic equilibrium still depends on the unknown erosion coefficient a(x). Since the sediment concentration depends linearly on the erosion coefficient, the morphodynamic equilibrium condition 13 can be rewritten as a first-order linear differential equation for the erosion coefficient a(x)

$$ F\frac{da}{dx}+Ta=0. $$
(14)

where \(\footnotesize{F=\left\langle \int\limits^{\zeta}_{-H}-K_h\dfrac{c}{a}dz\right\rangle}\) and \(\footnotesize{T=\left\langle \int\limits^{\zeta}_{-H} \left(u\dfrac{c}{a}\right.\right.}\) \(\footnotesize{-K_h \left.\left. \left(\dfrac{c}{a}\right)_x\right)dz \right\rangle}\).

By prescribing the total amount of sediment available at the bottom for resuspension, the integration constant can be determined by requiring

$$ \frac{\displaystyle\int\limits_{0}^{L}B(x)a(x)dx}{\displaystyle\int\limits_{0}^{L}B(x)dx}=a_\ast, $$
(15)

where a ∗ is the average amount of sediment available for resuspension.

3 Perturbation analysis and solutions

In this section, we will approximate the system of equations discussed in Section 2 to obtain a (semi-) analytic solution. Here, we will only give a short outline of the procedure used to construct the reduced system of equations, for a detailed description of this procedure, and the solution method used to solve the resulting reduced system of equations, see electronic supplement S3.

First, the relative importance of the various terms in the model equations is established by performing a scaling analysis, using parameter values representative for the Ems estuary (see Table 1, which is discussed in detail in Section 4). One of the dimensionless parameters that appears in the scaled equations is the ratio of the M 2 tidal amplitude \(A_{M_2}\) and the undisturbed water depth H 0. This ratio, denoted by ε, is much smaller than one, i.e., \(\varepsilon=A_{M_2}/H_0\ll 1\). The other dimensionless parameters are compared to this small parameter ε.

Next, we approximate the solution of the dimensionless equations and the boundary conditions by expanding the physical variables in power series of the small parameter ε. This expansion is substituted in the scaled equations, and terms of the zeroth (first) order of ε are collected, resulting in a leading (first-order) system of equations. The leading order system is presented in Section 3.1, the first-order system in Section 3.2, and the morphodynamic equilibrium condition is discussed in Section 3.3.

3.1 Leading order system of equations

In leading order, i.e., \(\mathcal{O}(\varepsilon^0)\), the dimensional system of equations describing the water motion reads

$$ u^{02}_x+\emph{w}^{02}_z-\frac{u^{02}}{L_b}=0, $$
(16a)
$$ u^{02}_t+g\zeta^{02}_x-(A_\emph{v}u^{02}_z)_z=0. $$
(16b)

The first superscript denotes the order of ε, and the second superscript is the index of the lunar constituent under consideration, i.e. in leading order, only an M 2 signal is present in the water motion.

The boundary condition at the riverine side requires the depth-averaged velocity to vanish at the weir. At the entrance, the system is forced by an externally prescribed semi-diurnal tide. These conditions read

$$ \zeta^{02}=A_{M_2}\cos(\sigma t)\ \ \ \mbox{ at }\ \ \ x=0, $$
(17a)
$$ \int\limits_{-H}^0u^{02}dz=0\ \ \ \mbox{ at }\ \ \ x=L. $$
(17b)

At the free surface z = 0, the boundary conditions are given by

$$ \emph{w}^{02}=\zeta^{02}_t, $$
(18a)
$$ A_\emph{v}u^{02}_z=0. $$
(18b)

At the bottom z = − H(x), the boundary conditions read

$$ \emph{w}^{02}=-u^{02}\frac{\partial H}{\partial x}, $$
(19a)
$$ A_\emph{v}u^{02}_z=su^{02}. $$
(19b)

The solution of Eqs. 16–19 describes the propagation of a tidal wave in a medium with effectively a homogeneous density and a varying depth. It is solved by reducing the system to a homogeneous ordinary boundary-value problem for the sea surface elevation ζ 0 (see Ianniello (1977) and the electronic supplement S3.1 for details).

The dynamics of the sediment concentration in leading order is given by

$$ c_t^0-\emph{w}_sc_z^0=(K_\emph{v}c_z^0)_z. $$
(20)

Hence, in leading order, the evolution of the sediment concentration is governed by local inertia, settling and vertical mixing of sediments.

Boundary conditions at the free surface z = 0 require no flux through the boundary,

$$ \emph{w}_sc^0+K_\emph{v}c_z^0=0. $$
(21)

At the bottom, z = − H(x), the boundary condition reads

$$ -K_\emph{v}c_z^0=\emph{w}_s\rho_s\frac{s|u^0(t,x)|}{g'd_s}a(x). $$
(22)

Since the water motion only consists of an M 2 tidal signal in leading order, it follows that the concentration has a residual (tidally averaged) component and all constituents with frequencies that are an even multiple of the M 2 tidal frequency, hence

$$ c^0=c^{00}+c^{04}+\ldots. $$
(23)

The sediment concentration c 0 still depends on the unknown erosion coefficient a(x).

For the solution method and analytical expressions of the semi-diurnal tidal velocity and sediment concentration components, see electronic supplement S3.1.

3.2 Higher-order system of equations

In this section, the first-order system of equations is given. The water motion is discussed in Section 3.2.1 and sediment dynamics in Section 3.2.2.

3.2.1 Water motion

The dimensional hydrodynamic equations in first order, i.e., \(\mathcal{O}(\varepsilon^1)\), are given by

$$ u_x^1+\emph{w}_z^1-\dfrac{u^1}{L_b}=0, $$
(24a)
$$ u^1_t + \underline{u^{02}u^{02}_x + \emph{w}^{02}u^{02}_z} + g\zeta^1_x - \underline{g\beta \left\langle s\right\rangle _xz} = (A_\emph{v}u^1_z)_z, $$
(24b)

where the underlines \(\underline{\ \ . \ \ }\) denote individual forcing terms, which are discussed later.

At the free surface z = 0, the boundary conditions read

$$ \emph{w}^{1}=\zeta^{1}_t \underline{ -\zeta^{02}\emph{w}^{02}_z + u^{02}\zeta^{02}_x }, $$
(25a)
$$ A_\emph{v}u^{1}_z + \underline{ A_\emph{v}\zeta^{02}u^{02}_{zz} }=0, $$
(25b)

and at the bottom z = − H(x)

$$ \emph{w}^{1}=-u^{1}\frac{\partial H}{\partial x}, $$
(26a)
$$ A_\emph{v}u^{1}_z=su^{1}. $$
(26b)

The boundary conditions at the riverine side and entrance are given by

$$ \int\limits_{-H}^{0}u^{1}dz = \underline{Q/B}\ \ \ \mbox{ at }\ \ \ x=L, $$
(27)
$$ \zeta^{1}=\underline{A_{M_4}\cos\left( 2\sigma t-\phi \right)} \ \ \ \mbox{ at }\ \ \ x=0. $$
(28)

Careful inspection of Eqs. 24–28 shows that the order ε velocity fields \(u^1, \emph{w}^1\) and the sea surface elevation ζ 1 consist of the residual contributions (\(u^{10},\emph{w}^{10},\zeta^{10}\)) and contributions (\(u^{14},\emph{w}^{14},\zeta^{14}\)) which oscillate with twice the frequency of the semi-diurnal tide. These contributions are discussed separately in the following paragraphs. For the solution method, see the electronic supplement S3.2.

Residual flow

By averaging over a tidal period, a forced linear system that describes the residual flow is obtained:

$$ u_x^{10}+\emph{w}_z^{10}-\dfrac{u^{10}}{L_b}=0, $$
(29a)
$$ \underbrace{\left\langle u^{02}u^{02}_x + \emph{w}^{02}u^{02}_z\right\rangle}_{\text{TS}} + g\zeta^{10}_x - \underbrace{g\beta\left\langle s\right\rangle _xz}_{\text{GC}} = (A_\emph{v}u^{10}_z)_z. $$
(29b)

where the underbraces \(\underbrace{.}_{}\) denote the individual residual forcing terms. The semi-diurnal tidal components u 02, \(\emph{w}^{02}\), ζ 02 were obtained in Section 3.1.

At the free surface z = 0, the boundary conditions are given by

$$ \emph{w}^{10}= \underbrace{-\left\langle \zeta^{02}\emph{w}^{02}_z - u^{02}\zeta^{02}_x \right\rangle}_{\text{SD}}, $$
(30a)
$$ A_\emph{v}u^{10}_z + \underbrace{\left\langle A_\emph{v}\zeta^{02}u^{02}_{zz}\right\rangle}_{\text{SC}} = 0. $$
(30b)

At the bottom z = − H(x), the boundary conditions read

$$ \emph{w}^{10}=-u^{10}\frac{\partial H}{\partial x}, $$
(31a)
$$ A_\emph{v}u^{10}_z=su^{10}. $$
(31b)

The boundary condition at the riverine side is that the depth and tidally averaged velocity equals the river discharge at the weir and at the entrance the tidally averaged sea surface elevation in first order is zero. Those conditions read

$$ \int\limits_{-H}^{0}u^{10}dz=\underbrace{\dfrac{Q}{B}}_{\text{RI}}\ \ \ \mbox{ at }\ \ \ x=L, $$
(32a)
$$ \zeta^{10}=0\ \ \ \mbox{ at }\ \ \ x=0. $$
(32b)

Equation 29 together with boundary conditions 30–32 describe the residual water motion in the estuary which is driven by the residual forcing terms. First, the water motion is forced by the residual constituent of nonlinear interactions of the leading order M 2 tide due to advective contribution (TS). Second, there is a time-independent forcing (GC) due to the presence of a salinity gradient \(\left\langle s\right\rangle_x\) (gravitational circulation). Third, there is the tidal return transport (SD), which is the residual transport that compensates for the correlation between horizontal and vertical water motion (Stokes drift). Fourth, there is the residual constituent due to the no-stress condition at the surface (SC). Finally, there is a river discharge prescribed at the weir, resulting in a residual water motion in the estuary (RI).

Since this system of equations is linear, we can study the importance of each forcing mechanism separately, i.e., the resulting solution for the residual velocity fields u 10 and w 10 and the sea surface elevation ζ 10 reads

$$ \mathbf{\chi}^{10} = \mathbf{\chi}^{10}_{\text{TS}} + \mathbf{\chi}^{10}_{\text{GC}} + \mathbf{\chi}^{10}_{\text{SD}} + \mathbf{\chi}^{10}_{\text{SC}} + \mathbf{\chi}^{10}_{\text{RI}}, $$
(33)

where \(\mathbf{\chi}^{10}=(u^{10}, \emph{w}^{10}, \zeta^{10})\).

First overtide (M4) flow

The M 4 constituent of the water motion is described by the following system of forced equations

$$ u^{14}_x+\emph{w}^{14}_z-\frac{u^{14}}{L_b}=0, $$
(34a)
$$ u^{14}_t + \underbrace{\left[ u^{02}u^{02}_x+\emph{w}^{02}u^{02}_z\right]}_{\text{AC}} + g\zeta^{14}_x = (A_\emph{v}u^{14}_z)_z, $$
(34b)

where braces [.] denote the M 4 contribution and the underbraces \(\underbrace{.}_{}\) are the individual M 4 forcing terms.

At the free surface z = 0, the boundary conditions are given by

$$ \emph{w}^{14}=\zeta^{14}_t+\underbrace{[u^{02}\zeta^{02}_x-\zeta^{02}\emph{w}^{02}_z]}_{\text{FS}}, $$
(35a)
$$ A_\emph{v}u^{14}_z+\underbrace{A_v[\zeta^{02}u^{02}_{zz}]}_{\text{NS}}=0. $$
(35b)

At the bottom z = − H(x), the boundary conditions read

$$ \emph{w}^{14}=-u^{14}\frac{\partial H}{\partial x}, $$
(36a)
$$ A_\emph{v}u^{14}_z=su^{14}. $$
(36b)

The boundary conditions at the entrance and riverine side are identical to those of the leading order conditions, but at the entrance the system is forced by the externally prescribed M 4 tide. These conditions are

$$ \zeta^{14}=\underbrace{A_{M_4}\cos\left( 2\sigma t-\phi \right)}_{\text{EF}}\ \ \ \mbox{ at }\ \ \ x=0, $$
(37a)
$$ \int\limits_{-H}^{0}u^{14}dz=0\ \ \ \mbox{ at }\ \ \ x=L.$$
(37b)

System 34 and boundary conditions 35–37b describe the M 4 water motion in the estuary driven by the M 4 constituent of nonlinear interactions of the leading order M 2 tide due to advective contribution (AC), the M 4 transport (FS) that compensates for the correlation between horizontal and vertical water motion, and the M 4 constituent of no-stress condition at the surface (NS). The AC, FS and NS constituents are produced within the estuary and are referred to as the internally generated overtide. Moreover, the water motion is forced by an externally prescribed overtide (forcing term EF). These four components result in a M 4 tidal motion in the estuary.

As with the residual flow, the solution to Eq. 34 can be decomposed into different contributions, each induced by an individual forcing mechanism:

$$ \mathbf{\chi}^{14} = \mathbf{\chi}^{14}_{\text{AC}} + \mathbf{\chi}^{14}_{\text{FS}} + \mathbf{\chi}^{14}_{\text{NS}} + \mathbf{\chi}^{14}_{\text{EF}}, $$
(38)

where \(\mathbf{\chi}=(u^{14}, \emph{w}^{14}, \zeta^{14})\). Thus, we can investigate the influence of each forcing separately.

3.2.2 Sediment dynamics

The sediment mass balance equation (Eq. 9) and its boundary conditions at first order are equivalent to those in leading order, with the first-order component of the bed shear stress given by

$$ |\tau_b^1|=\rho_0 s u^1 \frac{u^{02}}{|u^{02}|}\ \ \ \mbox{at}\ \ \ z=-H. $$
(39)

Based on Eq. 39, it can be concluded that the first-order sediment concentration is a result of the leading order and the first-order tidal flow interaction. Applying a Fourier analysis to the bottom boundary condition 11 for the sediment concentration equation, it can be deduced that the higher-order concentration consists of all tidal components

$$ c^1=c^{10}+c^{12}+\ldots . $$
(40)

3.3 Morphodynamic equilibrium condition

The leading order morphodynamic equilibrium condition reads (for details, see electronic supplement S3.3)

$$\begin{array}{lll} &&{\kern-6pt}\int\limits^{0}_{-H} \left( u^{10}c^{00}+\left\langle u^{02}c^{12}\right\rangle +\left\langle u^{14}c^{04}\right\rangle-K_h \left\langle c^{00}_x\right\rangle \right)dz \\ &&{\kern3pt}+\left\langle\zeta^0 [u^{02}c^0]_{z=0}\right\rangle =0. \end{array}$$
(41)

Here, the first contribution models the residual transport of sediment due to interactions of the residual velocity and the time-averaged sediment concentration. Note that we can decompose this flux even further as we have separate expressions for the residual flow components due to different forcing agents (see Eq. 33). The second term describes the semi-diurnal sediment transport which occurs due to the interactions of the semi-diurnal velocity and the M 2 concentration. The third component represents the first overtide transport of sediment and is a result of the interactions of the first overtide velocity and the M 4 concentration. The horizontal diffusive flux and a flux due to the correlation between the tidal return flow and concentration are represented by the fourth and fifth terms, respectively. Note that, as in the case with the residual sediment flux, we can perform further decomposition of the aforenamed fluxes.

The sediment concentration in the morphodynamic equilibrium condition still depends linearly on the unknown erosion coefficient a(x), i.e., c 00 = a(x)c 00a, c 04 = a(x)c 04a, and c 12 = a(x)c 12a, where c 00a, c 04a, and c 12a are independent of a(x). This results in a linear first-order ordinary differential equation for the erosion coefficient a(x)

$$ F\frac{da}{dx}+Ta=0, $$
(42)

with

$$ F=\left\langle\displaystyle\int\limits^{0}_{-H}-K_hc^{00a}dz\right\rangle, $$
$$\begin{array}{rll} T&=&\underbrace{ \displaystyle\int\limits^{0}_{-H}u^{10}c^{00a}dz + \bigg<\zeta^0\left[u^{02}c^{0a}\right]_{z=0}\bigg> }_{T_{\text{res}}} + \underbrace{\displaystyle\int\limits^{0}_{-H}\left\langle u^{02}c^{12a}\right\rangle dz}_{T_{M_2}} \\ &&+\underbrace{\displaystyle\int\limits^{0}_{-H}\left\langle u^{14}c^{04a}\right\rangle dz}_{T_{M_4}} - \underbrace{\displaystyle\int\limits^{0}_{-H}K_h\left\langle c_x^{00a}\right\rangle dz}_{T_{\text{diff}}}. \end{array}$$

Here, the underbraces \(\underbrace{.}\) denote different contributions of the transport function T, induced by various interactions between the velocity and concentration: \(T_{\text{res}}\) is the transport, which results from the interaction of the residual velocity with the residual concentration; \(T_{M_2}\) is the transport due to the M 2 velocity and M 2 concentration interaction; \(T_{M_4}\) is the transport due to the M 4 velocity and M 4 concentration interaction; and \(T_{\text{diff}}\) is the diffusive transport. These contributions are discussed in detail in Section 5.2.1.

4 Results

In this section, the model developed in Sections 2 and 3 is used to gain insight into both the hydrodynamics and sediment dynamics in the Ems estuary. There has been a distinct change in both the water motion and sediment dynamics over the past 30 years in this estuary. These changes and the general characteristics of the Ems estuary are briefly discussed in Section 4.1. Using the observations carried out in 1980 and 2005 on the Ems estuary, we will investigate the ability of the model to reproduce the main characteristics of the hydro- and sediment dynamics (Section 4.2), resulting in a physical explanation for why the dynamics changed so drastically. The water motion results are discussed in Section 4.3, followed by Section 4.4 in which the sediment dynamics and the trapping of sediment in the estuary are discussed.

4.1 Characteristics of the Ems estuary

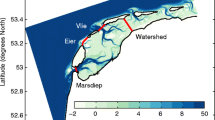
The Ems estuary is situated on the border between The Netherlands and Germany and runs from the island of Borkum to the tidal weir in Herbrum. Its length from the geographical entrance (the barrier islands) to the tidal weir is approximately 100 km. In this paper, the zero of the along-channel coordinate axis x is located at Knock, with x increasing toward the weir at Herbrum (see Fig. 2). Moreover, in the remainder of the article, the term entrance denotes the model entrance, which is km 0 in our coordinate system (Knock), and not the geographical entrance of the Ems estuary.

Fig. 2
figure 2

Map of the Ems estuary from the barrier island of Borkum in the North Sea up to the tidal weir in Herbrum

Full size image

The Ems estuary is exponentially converging with a convergence length L b of 30 km. The system is partially mixed and the landward limit of the salt intrusion varies with the river discharge and is usually found between 20 and 30 km (Talke et al. 2009a).

Approximately 90% of the freshwater input comes from the Ems river, the remaining 10% from other tributaries. The river discharge exhibits seasonal variations. The discharge is approximately 30 m3/s during low flow conditions (June–October) while 150 m3/s is observed during high flow conditions (November–April). The yearly average freshwater discharge is 70 m3/s.

The solid red line in Fig. 3 shows the bathymetry of 1980. The depth of the navigation channel, i.e., the region between Emden and Papenburg, was approximately 4–5 m. At the entrance, the tidal range was 3.1 m and the main tidal constituent was the M 2 tide with an amplitude of 1.43 m. The first overtide had an amplitude of approximately 0.25 m and a relative phase of − 171.9°. The tidal range decreased upstream (near Papenburg it was approximately 2.3 m). Surface measurements registered that average SSC steeply increased from an average of 70 mg/l in Knock (km 0) to a maximum of 400 mg/l in Terborg (approximately km 25) and decreased sharply further upstream (De Jonge 1983).

Fig. 3
figure 3

Bathymetry of the Ems estuary in 1980 and 2005

Full size image

Between 1980 and 2005, portions of the Ems river were deepened from 4–5 to 7 m. The solid blue line in Fig. 3 depicts the 2005 water depth (WSA Emden). At the entrance, the mean tidal range is now 3.2 m (the spring-neap tidal range is 3.5 and 2.7 m, respectively) and the main tidal constituent is the M 2 tide with an amplitude of 1.35 m. The first overtide has an amplitude of approximately 0.19 m and a relative phase of − 174.6°. The tidal range increases upstream (near Papenburg it is approximately 3.8 m). Measurements between Pogum (km 15) and Rhede (km 59) in 2005–2006 found an average SSC of 950 mg/l with no distinct peak (V. de Jonge, personal communication).

A variety of measurements were used to calibrate the model to present conditions (labeled the “2005” case for convenience) and historical conditions (labeled “1980” for convenience). The variation of M 2 and M 4 water level at eight locations (between km 0, 13, 19.6, 27.4, 37.1, 44.4, 48, and 63.5 in our coordinate system) along the estuary were obtained from measurements over 24 hours by the Wasser and Schiffartsamt (WSA), Emden on February 29th, 1980, during median tidal conditions. Concurrent measurements of water level and velocity from a nearly 14 hour period on April 25, 1984 are used to estimate the historical phasing of flow and pressure. Velocity was estimated using hand held instruments every 15 min at 0.3–0.5 m increments in the water column at three locations on two cross sections located on Ems km 38.5 and 41.1. The phase difference between water level and flow used in the model is obtained from the average harmonic fit of near-surface measurements from the four available digitized data sets and is approximately 65°.

Considerably more data were available to calibrate the “2005” model condition, which is subsequently better constrained. Continuous water level measurements (5–30-min increments) from 2005 and 2006 were obtained from the Niedersaechsicher Landesbetrieb fuer Wasserwirtschaft, Kuesten- und Naturschutz (NLWKN) at the same locations as the 1980 data (between the towns of Knock and Herbrum). Additionally, velocity measurements from surface-moored Aandera RCM-9 probes deployed by WSA Emden were used to define the phase angle between surface tidal flows and water level at a total of six along-channel locations between January–April 2006. Because instruments were serviced occasionally or moved to different along-channel locations, some data gaps exist and the total data set spans approximately 2–2.5 months at each site. Bathymetry for the “2005” and “1980” case were obtained from surveys by WSA Emden in December 2004 and 1984, respectively.

Over most of the modeled estuary, bottom sediment consists primarily of silt (70–80%), with approximately 20–25% fine sand and 5% clay (M. Krebs, personal communication). The channel bed before deepening was primary sandy (Krebs and Weilbeer 2008). Observed flocculation settling velocities in the Ems vary from < 0.0001 to 0.008 m s − 1 (van Leussen and Cornelliese 1993, 1996; van der Lee 2000).

4.2 Model setup

Historical bathymetry, digitized from an old charts, was only available between Emden and Herbrum. To be able to simulate the water motion and sediment dynamics for 1980, we have extended the available bathymetry of 1980 from Emden downstream to Knock and from Papenburg up to Herbrum by using the 2005 bathymetry. This is a fair assumption, since channel deepening was mainly carried out between Emden and Papenburg. Moreover, because we focus on flow and sediment pattern on the basin scale, the bathymetries were smoothed using a lowpass filter. Most other model parameters are directly obtained from the observations outlined in Section 4.1 and are summarized in Table 1.

The vertical eddy viscosity coefficient A v0 and the stress parameter s 0, which are unknown, are obtained by calibrating the model to the measured data. We minimize the difference between the observed and modeled semi-diurnal tidal amplitude (\(\zeta_{M_2}\)) and the phase difference between the semi-diurnal horizontal and vertical tide (\(\phi_{\zeta_{M_2}}-\phi_{u_{M_2}}\)) in a least square sense. The other observations, such as the residual and M 4 tidal amplitude and velocity at the surface, are then used to validate the model. The resulting vertical eddy viscosity coefficient A v0 has decreased from 0.019 m2 s − 1 in 1980 to 0.012 m2 s − 1 in 2005. Apart from this decrease of A v0, A v (x) (see Eq. 4) decreased everywhere as well compared to the 1980 case. For the stress parameter, we found 0.098 m s − 1 in 1980 and 0.049 m s − 1 in 2005 as best fit.

The river discharge that we use is 65 m3/s. It is assumed that the turbulent vertical eddy diffusivity K v is equal to the vertical mixing coefficient A v . The horizontal diffusivity coefficient K h is taken to be 100 m2/s.

4.3 Water motion

Figure 4a, c show the comparison of observations and model predictions of the semi-diurnal tidal amplitude, and Fig. 4b, d represent the phase difference between the semi-diurnal horizontal and vertical tide in 1980 and 2005, respectively. Unless explicitly stated otherwise, all velocities are taken at the sea surface. Here, the solid blue line represents the model results using parameter values given in Table 1, and the red square marks the observed values. In dashed lines, we plotted the locations where the measurements were made in 2005. Comparison of these figures and additional model computations (see electronic supplement S4) shows that the tidal motion is closer to resonance in 2005 than 1980, as the M 2 amplitude increases and the phase difference between the horizontal velocity and water level is closer to 90°.

Fig. 4
figure 4

Comparison between observations and model predictions of the semi-diurnal tidal amplitude and phase difference between the semi-diurnal horizontal and vertical tide. The blue curves represent model predictions; the red squares show measured data at various measuring locations. The dashed lines depict locations at which the measurements were made in 2005. The left panels represent tidal amplitude along the estuary, and the right ones depict relative phase shift between the free surface elevation and along-channel velocity component. The upper panels show 1980 case; the lower panels are 2005

Full size image

Figure 5a shows the ratio of the M 4 over M 2 horizontal velocity at the surface. The solid blue (black) line represents the model results for the 2005 (1980) case, using parameter values given in Table 1 and the red square (cross) marks the observed values for 2005 (1980). The ratio of the M 4 over M 2 velocity amplitude has decreased from 1980 to 2005 in the first 20 km from the entrance and has increased everywhere else. Figure 5b depicts the relative phase of the sea surface elevation, which is defined as \(\phi_{\zeta_{M_4}}-2\phi_{\zeta_{M_2}}\), where \(\phi_{\zeta_{M_2}}\) (\(\phi_{\zeta_{M_4}}\)) is the phase of the M 2 (M 4) tidal elevation. The relative phase defines the duration of the rise and fall of the tide. Both observations and the model suggest that the duration of the falling tide is greater than the rising tide everywhere in the estuary, with no striking quantitative differences observed between 1980 and 2005. In Fig. 5c, the relative phase of the horizontal velocity (\(\phi_{u_{M_4}}-2\phi_{u_{M_2}}\)) is shown. The relative phase between the semi-diurnal tidal velocity and its first overtide, i.e., the M 4 velocity, determines whether there is flood or ebb dominance (Aubrey and Speer 1985). If the relative phase is between − 90° and 90°, the estuary is flood dominant; otherwise, the estuary is ebb dominant. Model results presented in Fig. 5c suggest that the ebb/flood dominance changed between the two years. In 1980, there was only a pronounced flood dominance in the last 30 km of the estuary with a small ebb dominated region at the entrance. In 2005, however, the estuary was flood dominated everywhere.

Fig. 5
figure 5

The water motion model results. The blue curves represent model predictions; the red marks show measured data at various locations. Scattered data at the same location means that measurements were done at various times. The dotted lines show locations at which the measurements were made in 2005. The upper left panel depicts the ratio of the M 4 over M 2 horizontal velocity at the surface, and the upper right one represents the relative phase of the sea surface elevation. The lower panel shows the relative phase of the horizontal velocity at the surface. Changes from parameter regions with ebb and flood dominance are indicated by the green solid lines

Full size image

In Fig. 6, the horizontal component of the residual velocity along the estuary is shown for 1980 (Fig. 6a) and 2005 (Fig. 6b). The maximum velocity magnitude of 0.4 m/s in both cases is located at the weir and results primarily from river discharge. From the weir toward the entrance, the velocity gradually decreases. At the entrance, there is a region near the bed where the residual velocity changes direction from downstream to upstream (the zero contour is indicated by the black solid line). The model suggests that between 1980 and 2005, the region with upstream directed velocity has advanced into the estuary by as much as 5 km.

Fig. 6
figure 6

The residual velocity model result. The black solid line depicts the zero contour. The left panel shows the 1980 case and the right one depicts 2005

Full size image

4.4 Sediment Dynamics

To reflect the observed variation in the grain size distribution, we modeled fine silt with a settling velocity w s of approximately 0.0005 m s − 1 and a coarser silt with a settling velocity of 0.002 m s − 1. All other parameters have their default values (see Table 1).

Figure 7a, b show the tidally averaged SSC for fine silt in morphodynamic equilibrium, and Fig. 7c, d represent coarse silt in 1980 and 2005, respectively. In 1980 for both fine and coarse silt, Fig. 7a, c indicate that the trapping region is located near the upward limit of salt intrusion (from here on we define trapping of sediment at this location as the ETM at the classical location). For fine silt, this region is shifted upstream by approximately 7 km compared to coarse silt. In 2005 for fine silt, the trapping region has shifted upstream into the freshwater zone by approximately 19 km compared to the 1980 case. For coarse silt, we observe two ETMs: one at the classical location and the other one further upstream at km 42.5.

Fig. 7
figure 7

Tidally averaged suspended sediment concentration (SSC) in morphodynamic equilibrium. The upper panels show the SSC for fine silt and the lower ones depict coarse silt

Full size image

Note that the erosion coefficient a(x) in the morphodynamic equilibrium condition is determined up to a constant a ∗ (see Eq. 15). Here, we used \(a_\ast = 10^{-5}\) to get the SSC at the surface of approximately 300 mg/l for fine sediment in 1980. An increase (decrease) of the constant a ∗ results in higher (lower) SSC. For both 1980 and 2005, we used the same a ∗ for consistency.

5 Discussion

In this section, we will use the analytical model to explain the model results presented in the previous section. Section 5.1 provides an analysis of the hydrodynamic conditions in the estuary. In Section 5.2, we will study the changes of trapping locations between 1980 and 2005 for fixed settling velocity w s and river discharge Q and compare the difference in grain sizes for the same year. In Section 5.3, we will discuss the sensitivity of trapping locations to the settling velocity and river discharge.

5.1 Hydrodynamics

We start the analysis of the hydrodynamic conditions in the estuary by investigating the difference of the M 2 and M 4 tidal characteristics between 1980 and 2005. As shown in Fig. 4, the dimensionless M 2 tidal amplitude (the ratio of the M 2 tidal amplitude over its value at the entrance) at the landward side increased from approximately 0.74 to 1.12 between 1980 and 2005. Furthermore, the relative phase between the horizontal velocity and water level is closer to 90° in 2005 compared to 1980, i.e., the character of wave has become more that of a standing wave and the estuary is closer to resonance. A similar amplification for the M 4 tide is observed.

We investigate the amplification of the M 2 tide by looking at two different scenarios (details are given in electronic supplement S4). Deepening the estuary to the 2005 depth, but keeping the 1980 A v and s parameter values, results in an increase of the dimensionless M 2 tidal amplitude at the landward boundary to 0.89. Keeping the 1980 depth but using the 2005 parameter values for A v and s results in the dimensionless M 2 tidal amplitude of approximately 0.99 at the landward side. Hence, we can conclude that, although the reduction of the vertical eddy diffusivity and stress parameter has more effect on the tidal resonance in the case of the Ems estuary, the observed amplification of the dimensionless M 2 tidal amplitude to approximately 1.12 in 2005 is a result of both factors acting simultaneously.

Next, we study the observed and modeled ebb and flood dominance in the estuary. The estuary is everywhere flood dominant in 2005, while in 1980 a small region at the entrance of the estuary was ebb dominated. The M 2 velocity phase curves have a similar trend, and they do not change the flood dominance between years (see Fig. 8a). The two contributions to the M 4 phase of the horizontal velocity at the surface are shown in Fig. 8b. The blue line denotes the internally generated contribution which is caused by nonlinear interactions, and the black line shows the externally forced contribution. Dashed lines depict the 1980 case and solid lines the 2005 case. The externally generated M 4 velocity phase shows qualitatively similar behavior for both years. The character of the internal M 4 velocity phase has changed significantly: in the region where we observe ebb dominance in 1980, the phase rapidly increases from approximately − 250° to − 100°, while in 2005 the phase is always about − 100°, resulting in a stronger flood dominance in 2005 compared to 1980. So we can conclude that the main changes in ebb/flood dominance, as observed in the Ems, are a result of changes in the phase of the internally generated overtide.

Fig. 8
figure 8

The left panel shows the M 2 horizontal velocity phase at the surface and the right panel depicts the M 4 horizontal velocity phase at the surface

Full size image

Next, we focus on changes in the ratio of the modeled M 4 over M 2 horizontal velocity at the surface, plotted in Fig. 5a. The M 2 and M 4 horizontal velocity at the surface are shown in Fig. 9. Figure 9a indicates that the behavior of the M 2 velocity component did not change between 1980 and 2005. The only change is an average 12% amplification of the M 2 velocity in 2005 compared to 1980. In Fig. 9b, we plotted both the externally forced and internally generated M 4 velocity amplitude at the surface for both years. In Section 4.3, we discriminated between two distinct regions. In a region within 20 km of the entrance the first region, located close to the entrance, the M 4/M 2 ratio has decreased from 1980 to 2005. This is caused by a local decrease of the M 4 internally generated velocity in 1980. Everywhere else we observe the opposite: an increase of the M 4/M 2 ratio in 2005 compared to 1980. This can be explained by a rapid damping of the M 4 externally forced signal toward the end of the estuary in 1980, which is not the case in 2005. Moreover, the internally generated M 4 velocity amplitude is more amplified in 2005 than in 1980 everywhere in the estuary.

Fig. 9
figure 9

The left panel represents M 2 velocity amplitude at the surface and right one the M 4 velocity amplitude at the surface

Full size image

Finally, we analyze the residual flow. The residual flow is the sum of five separate contributions, each from an individual forcing mechanism: gravitational circulation, river inflow, tidal return flow, surface contribution, and tidal stresses (see Section 3.2). In Fig. 10, the three largest residual horizontal velocity components are presented. The other two components are negligible. The top row shows the gravitational circulation in 1980 (Fig. 10a) and 2005 (Fig. 10b), respectively. These figures suggest that the gravitation circulation has intensified over the years. The reason for that is a combination of increased estuarine depth and a decrease of vertical mixing (Talke et al. 2009a, b). At the same time, the tidal return flow, depicted in Fig. 10c, d, has decreased between 1980 and 2005. One would expect an increase of this contribution due to a decrease of the vertical mixing. On the other hand, the increase of water depth and decrease of the stress parameter s (resulting in a wave with a stronger standing wave character) result in a decrease of the tidal return flow. In this case, based on additional model computations, the latter effect is stronger. The lower panels, Fig. 10e, f, represent the river velocity in 1980 and 2005, respectively. The river velocity has decreased by less than 5% in 2005 due to deepening, but there are no significant changes between 1980 and 2005. Therefore, the combination of the increased gravitational circulation and the decrease of the tidal return flow resulted in the residual flow changes described in Section 4.3.

Fig. 10
figure 10

The residual velocity constituents, namely the gravitational circulation is depicted on the upper panels, the tidal return flow is shown on the middle panels, and the river outflow on the lower panels

Full size image

5.2 Analysis of the sediment fluxes

In Fig. 7, we observe different sediment trapping regions between different years and/or grain sizes. For fine silt, the trapping region is found at the classical location in 1980, i.e., near the upward limit of salt intrusion. In 2005, the trapping region has shifted further upstream by 19 km. Coarse silt is trapped at the classical location in 1980 as well, whereas in 2005 two trapping regions are observed. One ETM is located at the classical location and the other trapping region is far upstream into the freshwater zone. To understand the physical mechanisms resulting in these different trapping regions, we analyze the sediment fluxes discussed in Section 3.3.

To clarify our analysis method, we take as an example the sediment fluxes for fine silt in 1980. These fluxes are shown in Fig. 11. In this figure, the solid red line represents the residual sediment flux due to the transport of the residual concentration by the residual velocity. If this flux is negative (i.e., between approximately 15 and 45 km), the sediment is transported in the seaward direction. If the flux is positive (from the entrance up to approximately 15 km), the sediment transport is directed upstream. Similarly, the solid green, black, and magenta lines denote the residual sediment transport due to the interaction of the M 2 concentration with the M 2 velocity, the M 4 concentration, and the M 4 velocity and diffusion (i.e., \(aT_{\text{diff}}+a_xF\)), respectively. Since the system is in morphodynamic equilibrium, these fluxes balance, i.e., the sum of the different contributions vanishes everywhere in the estuary, resulting in no residual sediment transport anywhere. The erosion coefficient that results in this morphodynamic equilibrium (and is calculated using Eq. 42) is the dashed blue line in Fig. 11. The location of the maximum corresponds to the location of the ETM and is at the classical location. In the sediment balance, all fluxes have a significant contribution. There is no approximate balance between the diffusive flux \(a(x)T_{\text{diff}}+a_xF\) and the \(a(x)T_{\text{res}}\) flux as used in (Talke et al. 2009b).

Fig. 11
figure 11

Residual sediment fluxes in morphodynamic equilibrium in 1980 due to the residual velocity/residual concentration (solid red line), M 2 velocity/M 2 concentration (solid green line), M 4 velocity/M 4 concentration interaction (solid black line), and diffusion (solid magenta line). Erosion coefficient a(x) that results in morphodynamic equilibrium is shown with dashed blue line. Results are obtained for the settling velocity of 0.5 mm/s − 1 and river discharge 65 m3/s

Full size image

From Eq. 42, it follows that a (local) maximum or minimum in sediment concentration is found in the vicinity of the location where the transport function T = 0. At these locations, da/dx = 0, and since a(x) itself is nonzero, T(x) has to be zero. Hence, to determine the ETM locations (i.e., a (local) maximum of sediment concentration) one has to investigate the zeros of T. Differences in trapping regions, as observed in Fig. 7, result from an up- or downstream shift of the convergence point or the occurrence of a new location with T = 0.

The physical reason for changes in trapping location can be found by studying the different contributions of T (see Eq. 42). As an example of such a decomposition of the dimensionless transport function T (T divided by its maximum absolute value) and its components for 1980 (fine sediment) are shown in Fig. 12. The blue line represents the total function T and its zero crossing (marked with a blue circle) corresponds to the location of the ETM in Fig. 11. The red, green, black, and magenta lines in Fig. 12 are the contributions to the transport function T, which result from the interaction of the residual velocity with the residual concentration (\(T_{\text{res}}\)), M 2 velocity with M 2 concentration (\(T_{M_2}\)), M 4 velocity with M 4 concentration (\(T_{M_4}\)), and diffusion (\(T_{\text{diff}}\)), respectively. From the seaward boundary up to approximately 18 km, the sediment is transported up-estuary mainly by \(T_{M_2}\) (the arrows in Fig. 12 show the direction of the sediment transport, with its color representing the main transport mechanism. Here, the green arrow indicates the import of sediment), while from 18 to 63 km transport is down-estuary mainly by \(T_{\text{res}}\) (the export of sediment is indicated by the red arrow). Hence, there is a convergence of sediment around 18 km. By analyzing the sediment transport components and comparing them for different grain sizes and/or years, we can conclude which fluxes are responsible for the sediment trapping and the observed differences in the sediment trapping between the years (Section 5.2.1) and for different grain size (Section 5.2.2).

Fig. 12
figure 12

Dimensionless transport function T (solid blue line) in 1980. Results are obtained for the settling velocity of 0.5 mm/s − 1. Red, green, black, and magenta lines depict contributions of T that result from the residual velocity/residual concentration, M 2 velocity/M 2 concentration, M 4 velocity/M 4 concentration interaction, and diffusion, respectively. The two arrows show the direction of the residual export and import of sediment, respectively. The color of the arrows represents the main contribution, responsible for the sediment transport, i.e., the residual import of sediment is mainly due to \(T_{M_2}\) (represented by the green arrow) and the residual export is primarily caused by \(T_{\text{res}}\) (shown with the red arrow)

Full size image

5.2.1 Changes between 1980 and 2005

From Fig. 13, it follows that for fine sediment in both 1980 and 2005 the main import of sediment into the estuary is due to the M 2 transport (\(T_{M_2}\)) and the major export is caused by the residual transport (\(T_{\text{res}}\); see arrows in Fig. 13a, b). For coarse sediment in 1980, the main import of sediment in the upstream region is due to \(T_{M_2}\) (green arrow in Fig. 13c) and the export is due to a combination of \(T_{\text{res}}\), \(T_{M_2}\), and \(T_{M_4}\) transports (green/red arrow). In 2005, coarse sediment was primarily imported in the upstream reaches by \(T_{M_2}\) and exported by \(T_{\text{res}}\), whereas sediment to the downstream ETM is imported due to a combined transport of \(T_{M_2}\) and \(T_{M_4}\) and exported due to \(T_{\text{res}}\) and \(T_{M_2}\) (see arrows in Fig. 13d).

Fig. 13
figure 13

Dimensionless transport function T and its components. The upper panels show fine silt and the lower ones coarse silt. The left panels represent 1980 and the right ones represent 2005. Arrows show the direction of export and import of sediment, and their color(s) represent(s) the main contribution(s) responsible for transport

Full size image

From Fig. 13a, b, we see that for fine silt the global behavior of the transport function T changed between 1980 and 2005. Closer inspection shows that this change is mainly due to a change in \(T_{M_2}\). In 1980, \(T_{M_2}\) is approximately constant and positive up until 20 km, after which it starts to decrease. In 2005, \(T_{M_2}\) only starts to decrease after approximately 50 km. Therefore, the transport function T becomes negative farther upstream in 2005 than in 1980. This results in a shift of the convergence point between 1980 and 2005 by approximately 19 km.

For coarser silt, we observe one convergence point in the 1980 case and two convergence points in 2005 (see Fig. 13c, d). In both cases, the first convergence point is still at the classical location, even though its position has shifted upstream by approximately 5 km in 2005 compared to 1980. The second convergence point is well into the freshwater region. The change in the transport function T is again mainly due to changes in the \(T_{M_2}\) contribution. In 1980, \(T_{M_2}\) becomes negative at approximately km 18, whereas in 2005 this point is located closer to the weir at km 52.

It follows that for both fine and coarse silt the \(T_{M_2}\) contribution play an important role in the changes of the sediment trapping location in the Ems estuary between 1980 and 2005. In the next paragraphs, we analyze the \(T_{M_2}\) contribution in more detail. For detailed analysis of the other components of the transport function, see electronic supplement S5.

To understand which mechanism is responsible for this significant change of \(T_{M_2}\), \(T_{M_2}\) will be decomposed into different components. The M 2 concentration (see Section 3.2.2) is forced by the M 2 component of the bed shear stress. From Eq. 39, it follows that the M 2 component of the bed shear stress is a result of the interaction of both the residual and the M 4 velocities with the M 2 velocity. Contributions of \(T_{M_2}\) that involve the residual velocity components are denoted by \(T_{M_2}^{\text{res}}\) and \(T_{M_2}^{M_4}\) denotes the contribution of \(T_{M_2}\) due to the overtide velocity components (for details, see electronic supplement S5).

In Fig. 14, \(T_{M_2}\) and its components \(T_{M_2}^{\text{res}}\), \(T_{M_2}^{M_4}\) are shown by the dashed green, solid red, and solid blue lines, respectively. The qualitative change in \(T_{M_2}\) is mainly determined by the \(T_{M_2}^{M_4}\) contribution. In 1980, the \(T_{M_2}^{M_4}\) flux begins to decrease at approximately km 20, whereas in 2005 it is elevated over much of the estuary and begins decreasing only upstream of km 50.

Fig. 14
figure 14

Dimensionless transport function \(T_{M_2}\) and its components

Full size image

The \(T_{M_2}^{M_4}\) contribution can be decomposed further into four contributions: \(T_{M_2}^{M_4} = T_{M_2}^{\text{AC}} + T_{M_2}^{\text{FS}} + T_{M_2}^{\text{NS}} + T_{M_2}^{\text{EF}}\). Here, the M 4 velocity components that contribute to \(T_{M_2}^{M_4}\) are advective contributions, denoted by \(T_{M_2}^{\text{AC}}\); free surface contribution, denoted by \(T_{M_2}^{\text{FS}}\); no-stress contribution, denoted by \(T_{M_2}^{\text{NS}}\); and the M 4 external forcing, denoted by \(T_{M_2}^{\text{EF}}\) (see Eq. 38 and electronic supplement S5 for details). The \(T_{M_2}^{M_4}\) components of the transport function \(T_{M_2}\) are shown in Fig. 15. For both fine silt (Fig. 15a, b) and coarse silt (Fig. 15c, d), we see that the changed behavior of \(T_{M_2}^{M_4}\) (the dashed blue line) is primarily determined by the \(T_{M_2}^{\text{EF}}\) contribution which results from the externally forced M 4 tide (the solid magenta line). The other three contributions are much smaller. In 1980, the transport due to the external overtide decreases from km 16, whereas in 2005 an abrupt decrease starts only at approximately km 40. Hence, the main change between 1980 and 2005 is due to the difference in residual sediment transport by tidal asymmetry, resulting in less import of sediment in 1980 compared to 2005, both for fine and coarser silt.

Fig. 15
figure 15

Dimensionless transport function \(T_{M_2}^{M_4}\) and its components

Full size image

As overall conclusion, it follows that the changes in trapping location between 1980 and 2005, for both years, is a result of changes in the sediment transport due to tidal asymmetry, i.e., changes of the external overtide.

5.2.2 Grain size sensitivity

In the previous section, our focus was on the changes between 1980 and 2005 for sediment with the same grain sizes. Here, we analyze the difference in the sediment distribution for different grain sizes for the same year. As shown by (Groen 1967), the temporal settling lag mechanism is quite efficient in transporting suspended sediment in one direction (upstream in our case) when there is tidal asymmetry.

In Fig. 16a, b, we show the transport function T with (solid lines) and without (dashed lines) the temporal settling lag (TSL) effects in 1980 and 2005, respectively (see Eq. 9). As we can see from Fig. 16a, in 1980, there is virtually no import of sediment into the estuary in the absence of the temporal settling lag (the dashed lines). Temporal settling lag (the solid lines) results in an import of sediment upstream and is, as expected, more efficient in transporting fine silt (from the entrance up to approximately 20 km) than coarse silt (up to approximately 12 km). In the 2005 case shown in Fig. 16b, we observe two trapping locations for both fine and coarse silt in absence of the temporal settling lag mechanism (the dashed lines). One ETM is located at the classical location and the other one further upstream at km 45. For fine silt, the temporal settling lag (the solid lines in Fig. 16b) qualitatively changes the trapping locations: instead of two trapping locations, fine silt is deposited only at one location at approximately km 37. For coarse silt, temporal settling lag is not as efficient and we observe an insignificant shift of the trapping locations upstream (the blue dashed and solid lines in Fig. 16b).

Fig. 16
figure 16

Dimensionless transport function T for both fine and coarse silt with and without temporal settling lag (TSL) effect. The blue (red) line represents the coarse (fine) silt. The dashed lines depict the transport function T in the absence of the temporal settling lag effect. The left panel shows 1980 and the right one 2005

Full size image

From Fig. 16, we conclude that the difference between the sediment distribution of different grain sizes is a result of the temporal settling lag mechanism.

5.3 Parameter sensitivity

The analysis of the specific cases with river discharge Q = 65  m3/s and settling velocity w s of 0.0005 and 0.002 m s − 1 (see Section 5.2.1) gives a good insight into processes in the estuary, but only for these specific parameters. To study the sensitivity of the turbidity maxima to river outflow and settling velocity, we analyze the transport function T for a range of settling velocity w s (0.0002–0.002 m s − 1) and river discharge Q (20–140 m3 s − 1). For each w s and Q, we constructed a plot, which is similar to Fig. 12 and determined the location where an ETM occurs. We summarize these locations in Fig. 17a for 1980 and Fig. 17b for 2005. On the x-axis, the location in the estuary is plotted, on the y-axis the settling velocity. If trapping occurs at a certain location for a specific settling velocity, the associated river outflow is given by the color code. If no trapping occurs for a settling velocity at a certain location for a river outflow between 20 and 150 m3/s, then this (x,w s ) coordinate is left blank.

Fig. 17
figure 17

Occurrence of ETMs in the estuary. The horizontal axis is the position in the estuary, and the vertical axis represents the settling velocity. If trapping occurs at a certain location for a specific settling velocity, the associated river outflow is given by the color code; otherwise, this (x,w s ) coordinate is left blank. The river outflow is varied between 20 and 150 m3/s

Full size image

From Fig. 17, we conclude that in 1980 the trapping location of both fine and coarse silt is found at the upstream limit of salt intrusion (i.e., the classical location). In 1980, the sediment is found more into the estuary only for very small river outflow (at most 30 m3 s − 1). Furthermore, we observe two trapping locations only for coarse silt (with settling velocity between 0.001 and 0.002 m s − 1) and river discharge corresponding to low flow conditions (at most 22 m3 s − 1). In 2005, fine silt is either trapped at the classical location (for very high river discharge of 100–140 m3 s − 1) or in the freshwater zone (river discharge of approximately 30–80 m3 s − 1), which depends on specific magnitude of river discharge Q and settling velocity w s . For coarser silt in 2005, two trapping regions are observed even for relatively high river outflow (40–75 m3 s − 1). One ETM is found at the classical location; the other one is located more upstream in the freshwater zone.

6 Conclusions

This paper presents a width-averaged analytical model of water and sediment dynamics in an estuary constrained upstream by a weir. Using the morphodynamic equilibrium condition, the trapping of sediment can be described in this estuary. The estuary is assumed to be exponentially converging and vertically well-mixed. The water motion is modeled by the width-averaged shallow water equations, the concentration by the width-averaged advection-diffusion equation. The sediment concentration still depends on a spatially varying erosion coefficient which models the availability of erodible sediment and is found using the condition of morphodynamic equilibrium. Analytic solutions are obtained using a perturbation approach in which physical variables are expanded in power series of the ratio of the semi-diurnal tidal amplitude and the undisturbed water depth at the entrance.

To test the applicability of our model, we consider the Ems estuary. Here, anthropogenic changes altered the water motion and sediment trapping locations significantly between 1980 and 2005. Two distinct bathymetries are considered which represents these two years. Most parameter values are obtained from measurements directly. The vertical eddy viscosity coefficient and stress parameter are obtained by calibrating the model to measured data by minimizing the difference between the observed and modeled semi-diurnal tidal amplitude and the phase difference between the semi-diurnal horizontal and vertical tide in a least square sense. Other observations are used to validate the model. Model results suggest a 50% and 37% reduction in the stress parameter and vertical eddy viscosity coefficient, respectively, in 2005 compared to 1980. The decreased friction and mixing suggests less hydraulic roughness, possibly because bed forms have been removed by dredging or because of the fluid mud that currently covers much of the turbid zone (Talke et al. 2009b).

The model results suggest that the water motion of the estuary is more amplified in 2005. This occurs both due to the deepening of the estuary and to the decreased vertical eddy viscosity and stress parameter. The shift toward greater flood dominance in 2005 is a result of changes in the internally generated overtides. The increased depth and decreased vertical mixing and stress parameter have intensified the gravitational circulation and weakened the tidal return flow in 2005 compared to 1980.

The modeled concentration profiles show that in 1980 both fine and coarse silt is trapped near the upward limit of salt intrusion, with the ETM moving further upstream only for small river outflow (less than 35 m3/s). In 2005, fine silt is either trapped near the upward limit of salt intrusion or in the freshwater zone, depending on the specific magnitude of river discharge and settling velocity. The main import of fine sediment into the estuary is due to the M 2 transport and the major export is caused by the residual transport in both 1980 and 2005. For coarser silt, two trapping regions are observed even for relatively high river outflow (40–75 m3 s − 1). One is found at the classical location, the other one upstream in the freshwater zone. In 1980, the main import of coarse sediment to the ETM is due to the M 2 transport and the export is due to a combination of the residual, M 2 and M 4 transports. In 2005, coarse sediment was primarily imported to the upstream ETM by the M 2 transport and exported by the residual transport, whereas sediment is imported to the downstream ETM due to a combined transport of M 2 and M 4 and exported due to the residual and M 2 transport.

The upstream shift of the estuarine turbidity maximum between 1980 and 2005 and the trapping of sediment in the freshwater zone is primarily a result of changes in tidal asymmetry (the external overtide). The amplification and change of behavior of the externally forced M 4 tide results in a shift of the estuarine turbidity maximum into the freshwater zone in 2005. The difference between the sediment distribution of different grain sizes under the same hydrodynamic conditions (i.e., for the same year) is a result of the temporal settling lag mechanism.

A number of processes that might be important for the trapping of sediment are not taken into account: spatial settling lag, the high sediment concentration, and the SIPS mechanism (strain-induced periodic stratification) discussed for example by (Burchard and Baumert 1998). Note that this kind of model does not allow us to explain an increase of the SSC from 400 to 950 mg/l observed between 1980 and 2005. Furthermore, in our model, the SSC is not found close to the weir. Preliminary results show that the spatial settling lag effect, for example, is important in a region of approximately 20 km downstream from the weir and is negligible in the rest of the estuary. Hence, it probably will enhance the shift of the ETM that is located in the freshwater zone upstream, whereas the ETMs that occur at the classical location will not be affected by this effect.