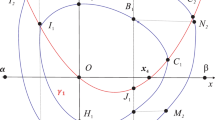
Abstract
In this paper, we investigate the number, location and stability of limit cycles in a class of perturbed polynomial systems with (2n + 1) or (2n + 2)-degree by constructing detection function and using qualitative analysis. We show that there are at most n limit cycles in the perturbed polynomial system, which is similar to the result of Perko in [8] by using Melnikov method. For n = 2, we establish the general conditions depending on polynomial’s coefficients for the bifurcation, location and stability of limit cycles. The bifurcation parameter value of limit cycles in [5] is also improved by us. When n = 3 the sufficient and necessary conditions for the appearance of 3 limit cycles are given. Two numerical examples for the location and stability of limit cycles are used to demonstrate our theoretical results.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Wang, Y.Q., Jing, Z.J. Cubic Lienard equations with quadratic damping (II). Acta Mathematicae Applicatae Sinica (English Series), 18(1): 103–116 (2002)
Han, Maoan. On the number and distributions of limit cycles in a cubic system. Chin. Ann. of Math., 23A(2): 143–152 (2002)
Ilieve, I.D., Perko, I.M. Higher order bifurcations of limit cycles. J. Diff. Eqns., 154: 339–363 (1999)
Rychkov, G.S. The maximum number of limit cycles of the system x′ = y − a 0 x − a 1 x 3 − a 2 x 5, y′ = −x is two. Diff. Eqns., 11: 380–391 (1973)
Ye, Y.Q. The theory of limit cycles. Trans Math Monographs 66, Am Math Soc, New York, 1986
Li, J.B., Huang, Q.M. Bifurcations of limit cycles forming compound eyes in the cubic system. Chin. Ann. Math., 8B: 391–403 (1987)
Liu, Z.R., Yang, Z.Y., Jiang, T. The same distribution of limit cycles in five perturbed cubic Hamiltonian systems. International Joural of Bifurcation and Chaos, 13(1): 243–249 (2003)
Perko, L. Differential equations and dynamical system, Second Edition. Springr-Verlag, New York, 1996
Melnikov, V K. On the stability of the center for time periodic perturbations. Trans. Moscow Math. Soc., 12: 1–57 (1963)
Arnold, V I. Loss of stability of self-oscillation close to resonance and versal deformations of equivariant vector fields. Funct. Anal. Appl., 11: 1–10 (1977)
Li, C.Z., Li, W.G., Llibre, J., et al. Polynomial systems: a lower bound for the weakened 16th Hilbert problem. Extracta Mathematicae, 16(3): 441–447 (2001)
Helena E Nusse, James A Yorke. Dynamics: Numerical explorations (Accompanying Computer Program Dynamics Coauthored by Eric J Kostelich). Springer-Verlag, New York, 1998
Author information
Authors and Affiliations
Additional information
1 Supported by Natural Science Foundation of China (10261008) and "Creative Project" (KZCZ2-SW-118) in Chinese Academy of Sciences.
Rights and permissions
About this article
Cite this article
Yang1, Cx., Wang, Rq. Number and Location of Limit Cycles in a Class of Perturbed Polynomial Systems. Acta Mathematicae Applicatae Sinica, English Series 20, 155–166 (2004). https://doi.org/10.1007/s10255-004-0158-y
Received:
Issue Date:
DOI: https://doi.org/10.1007/s10255-004-0158-y