Introduction

The effects of the Einstein general relativity (GR, Einstein et al. 1938) in the parameterized post-Newtonian (PPN) approximation can be considered as perturbing forces acting on earth-orbiting satellites which change the motion, the geometry, and the orientation of the Keplerian orbits (Infeld 1957; Kopeikin and Potapov 1994; Brumberg 2007). The relativistic gravitomagnetic effects changing the angular orbital elements Ω (ascending node) and ω (perigee) have been confirmed using observations of Mercury and pulsars (Kopeikin and Potapov 1994; Will 2018), artificial satellites such as LAser GEOdynamic Satellites (LAGEOS-1 and -2; Ciufolini et al. 1998; Lucchesi 2003), LAser RElativistic Satellite (LARES, Ciufolini et al. 2016), and Gravity Probe B (Everitt et al. 2011). However, the direct observations of orbit geometry deformation based on measured distances to planets or satellites, including the observations of the size and shape changes of the orbit due to GR, have not been conducted so far.

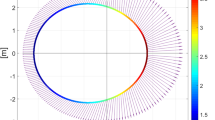
The satellite orbits of the Global Navigational Satellite Systems (GNSS), such as GPS, GLONASS, and Galileo, are determinable with an exceptionally high accuracy allowing for the recovery of small-scale perturbations with magnitudes below 10–9 m/s2 (Hugentobler and Montenbruck 2017; Bury et al. 2020). On August 22, 2014, the first pair of the Fully Operational Capability (FOC) Galileo satellites, E14 and E18 (or GSAT-0202 and GSAT-0201, respectively), was accidentally launched by Soyuz ST rocket into highly eccentric orbits. Instead of a nominal altitude of 23,225 km above the earth’s surface with an inclination of 56° and a revolution period of 14h05m, the satellites orbit at heights between 17,180 and 26,020 km with an inclination of 50° and a revolution period of 12h56m (Steigenberger and Montenbruck 2017; Sośnica et al. 2018; Hadas et al. 2019).

The Galileo satellites with differences between the perigee and apogee heights of 8,840 km (Fig. 1) constitute perfect probes for verifying effects emerging from the GR due to high-precision onboard clocks and two techniques for precise orbits determination, broadcasted L-band GNSS signals and Satellite Laser Ranging (Bury et al. 2019b; 2021; Sośnica et al. 2019). So far, only Galileo clocks onboard E14 and E18 have been used to verify GR effects (Delva et al. 2018; Herrmann et al. 2018; Kouba 2019, 2021; Formichella et al. 2021). The onboard clocks require, however, calibration of biases and corrections to the orbit modeling errors.

Fig. 1
figure 1

GPS (blue), GLONASS (red), and Galileo (green) satellites shown as a function of satellite inclination angle and distance from the perigee and apogee from geocenter with associated satellite PRN numbers

Full size image

This study shows the measurements of satellite geometry deformations caused by GR using Galileo E14 and E18 satellites in highly eccentric orbits as well as GPS, GLONASS, and Galileo in near-circular orbits. The measurements of the orbit deformations give the first metric values of the impact of spacetime curvature on the geometry changes of satellite orbits, because the changes of the semimajor axis of the orbit due to GR have never been directly observed before.

General relativistic effects acting on earth-orbiting satellites

The main relativistic effects on earth-orbiting satellites in the PPN approximation can be described by the Schwarzschild field of the earth (Schwarzschild 1916), which considers the earth a symmetric spherical non-rotating celestial body, by the Lense–Thirring or frame-dragging effect (Lense and Thirring 1918), which considers non-static stationary distributions of mass-energy induced by rotating earth, and the De Sitter effect or geodetic precession (De Sitter 1916), which can be considered a Coriolis-like force induced by the sun (Brumberg and Kopejkin 1989; Damour et al. 1994; Sośnica et al. 2021). The relativistic correction to the acceleration of an artificial earth satellite for spherically symmetric and uniformly rotating bodies derived in PPN approximation reads as (e.g., Brumberg and Kopejkin 1989, Petit and Luzum 2010):

$$ \begin{aligned} \bf{a}_{rel} = & \frac{{{\text{GM}}_{ \oplus } }}{{c^{2} r^{3} }}\left\{ {\left[ {2\left( {\beta + \gamma } \right)\frac{{{\text{GM}}_{ \oplus } }}{r} - \gamma \dot{\bf{r}} \cdot \dot{\bf{r}}} \right]\bf{r} + 2\left( {1 + \gamma } \right)\left( {\bf{r} \cdot \dot{\bf{r}}} \right)\dot{\bf{r}}} \right\} \\ & + \frac{{{\text{GM}}_{ \oplus } }}{{c^{2} r^{3} }}\left( {1 + \gamma } \right)\left[ {\frac{3}{{r^{2} }}\left( {\bf{r} \times \dot{\bf{r}}} \right)\left( {\bf{r} \cdot \bf{J}_{ \oplus } } \right) + \left( {\dot{\bf{r}} \times \bf{J}_{ \oplus } } \right)} \right] \\ & + \left( {1 + 2\gamma } \right)\left[ {\dot{\bf{R}} \times \left( {\frac{{ - {\text{GM}}_{S} \bf{R}}}{{c^{2} R^{3} }}} \right)} \right] \times \dot{\bf{r}} \\ \end{aligned}$$
(1)

where \({\text{G}}{\text{M}}_{ \oplus }\) is the standard earth gravitation product, \({\text{G}}{\text{M}}_{{\text{S}}}\) is the standard solar gravitation product, and β and γ are PPN parameters equal to 1 in GR. The speed of light is c, and \(\mathbf{{r}}\) and \({\dot{\mathbf{r}}}\) are the position and velocity of a satellite with respect to the geocenter. \({\dot{\mathbf{R}}}\) and \({\dot{\mathbf{R}}}\) are position and velocity of the earth with respect to the sun. \({{\mathbf{J}}}_{ \oplus }\) is the earth’s angular momentum per unit mass. The β parameter is related to the degree of nonlinearity in the gravitational field, whereas γ is related to the amount of spatial curvature generated by mass. The first line describes the so-called Schwarzschild term, the second is the frame-dragging gravitomagnetic Lense–Thirring effect, whereas the third corresponds to the De Sitter effect, also known as geodetic precession. For Galileo in eccentric orbits, the accelerations caused by general relativity equal at maximum 388.3, − 25.3, and 4.6 ⋅10−12 m⋅s−2 due to the Schwarzschild, De Sitter, and Lense–Thirring effect, respectively. Some GNSS analysis centers consider only the dominating Schwarzschild term. However, the impact of De Sitter effect may also be important for high-quality GNSS solutions, because it induces a secular drift of the ascending node at Galileo heights of 7.2 mm/day (Sośnica et al. 2021). The De Sitter effect can also change the inclination angle depending on the relative geometry between the sun, earth, and the satellites, whereas all GR effects change the argument of perigee.

Sośnica et al. (2021) used first-order Gaussian perturbations and GNSS orbit simulations to derive theoretical effects emerging from GR on Keplerian orbit parameters to identify which perturbations are detectable using the current accuracy of GNSS orbits. The mean offset is expected for the semimajor axis of all earth satellites, the periodical variations of the semimajor axis should be present for eccentric satellites, whereas the eccentricity should be exposed to periodical variations independent from the initial value of the eccentricity (Sośnica et al. 2021). This study aims at confirming the theoretical GR effects on the size and shape of GNSS orbits.

Methodology

To verify how the GR deforms the geometry of satellite orbits, we process 3 years of continuous GPS, GLONASS, and Galileo L-band data with the 180 s sampling interval for 2017.0–2020.0 based on the global network of 106 International GNSS Service (IGS, Johnston et al. 2017) stations, all of which track GPS, GLONASS, and Galileo satellites and belong to the multi-GNSS Experiment Pilot Project (Montenbruck et al. 2017). The double-difference phase observations using two frequencies are generated based on the common satellite-station visibilities, thus eliminating the satellite and receiver clock errors. The double-difference phase observations are characterized by a mean error of 1.4 mm. Table 1 provides the list of background models and GNSS data processing specifications.

Table 1 Specification of the processing strategy and background models used
Full size table

We determine satellite orbits, GNSS station coordinates, earth rotation parameters, and troposphere signal delays in one common adjustment following the methodology described in Zajdel et al. (2019; 2020). Solutions are conducted in the Bernese GNSS Software (Dach et al. 2015; Prange et al. 2020) with additional implementations of advanced handling of GR effects and direct solar radiation pressure (SRP) modeling for Galileo using satellite macromodels (Bury et al. 2019a; 2020). The standard version of the Bernese GNSS Software considers only the Schwarzschild effect; thus, the Lense–Thirring and De Sitter effects had to be added. Moreover, the possibility of the estimation of the PPN parameters β and γ has been implemented. Table 2 lists all estimated parameters with the specification of the constraints used.

Table 2 Specification of the estimated parameters
Full size table

Based on Galileo metadata published by the European GNSS Agency, we developed the Galileo a priori macromodel that considers the detailed construction and surface properties of satellite buses and solar panels to account for the direct SRP, earth’s albedo, and earth’s infrared radiation. Similar satellite models based on empirically adjusted surface parameters provided by IGS are employed for GPS and GLONASS satellites due to the lack of official detailed information about the satellite construction for all military spacecraft. The uncertainty of the box-wing model for Galileo is about 3% (Bury et al. 2020), whereas the remaining fluctuations of SRP, as well as small accelerations caused by and the misalignment of the solar panels with respect to the direction of the sun when assuming the yaw-steering mode are accounted for by estimating empirical orbit parameters using the 5-parameter ECOM model.

Table 3 lists the main non-gravitational, gravitational, and relativistic accelerations acting on Galileo satellites and their uncertainties. Other perturbations, such as interactions with the earth magnetic field, influence mostly the atomic clocks but not the orbits (Delva et al. 2018). The major unmodeled perturbing accelerations are caused by the thermal re-radiation and the missmodeling of accelerations acting on rotating satellite bus. The satellite thermal re-radiation effect is partially absorbed by the estimated parameters, however, not for eclipsing seasons for which greater orbit errors are expected. The uncertainties of most perturbing forces have a different nature than the effects emerging from GR, e.g., direct SRP and thermal effects depend on the distance of the satellites from the sun, whereas the Schwarzschild effect depends on the distance from the earth. Therefore, GR effects can be separated from non-gravitation orbit perturbations, except those for albedo and earth infrared radiation.

Table 3 Perturbing forces acting on Galileo satellites and their uncertainties in 10−9 m·s−2
Full size table

Three independent solutions are generated. In the first solution, no GR is considered. In the second solution, we assume that GR is true; thus, we incorporate all GR effects as recommended by the International Earth Rotation Service and Reference Systems (IERS) Conventions 2010 (Petit and Luzum, 2010) with γ = 1 and β = 1. In the third solution, we consider GR effects; however, the PPN parameters β and γ are estimated as dynamical orbit parameters. Thus, we allow satellites to find their optimum spacetime curvature and nonlinearity as provided by estimated γ and β values from raw GNSS observations. Finally, we derive differences between satellite orbits determined from the second and the first solution, as well as the third and the first solution. We compare the obtained differences with the theoretical values predicted by GR. Orbit differences are estimated every 15 min for each GPS, GLONASS, and Galileo satellite.

Impact of the GR on semimajor axis

The geometry of the instantaneous satellite orbit at a particular epoch can be described by two Keplerian osculating elements: the semimajor axis \(a\) (size) and eccentricity \(e\) (shape). The first-order Gaussian orbital perturbations of the semimajor axis with the integration constant due to the Schwarzschild accelerations read as (Sośnica et al. 2021):

$${\Delta }a = - 4\frac{{{\text{G}}{\text{M}}_{ \oplus } }}{{c^{2} }} + \left( {\frac{{{\text{G}}{\text{M}}_{ \oplus } }}{{c^{2} \left( {1 - e^{2} } \right)^{2} }}\left[ {\left( { - 14 - 6e^{2} } \right)e\cos \nu - 5e^{2} \cos 2\nu } \right]} \right) + O\left( {c^{ - 4} } \right)$$
(2)

where \(\nu\) is the true anomaly, which is a function of the argument of latitude (u) and perigee (ω), \(\nu = u - \omega\). Equation 2 contains a constant and a periodic component, both of which are independent of the semimajor axis \(a\). The amplitude of the periodic term increases with the increase in the orbital eccentricity.

The change of the semimajor axis for circular orbits (\(e = 0\)) is independent of the orbital height and equals \({\Delta }a = - 4\frac{GM_{ \oplus }}{{c^{2} }} = - 17.74\) mm for all earth-orbiting satellites (Sośnica et al. 2021). The mean change of the semimajor axis is thus twice larger than the Schwarzschild radius of the earth, i.e., the radius of a black hole with the same mass as the mass of the earth.

The Schwarzschild effect for circular orbits can be explained by a small change in the gravitational constant product \({\text{G}}{\text{M}}_{ \oplus }\) when considering satellites at the same height. When using multiple satellites in circular orbits at different heights, the offset of \({\Delta }a = - 17.74\) mm due to the Schwarzschild effect can be assigned to the antenna calibration offset, a range bias in direct range measurements, or may be absorbed by the up station coordinate components affecting the global GNSS scale. Therefore, using elliptical orbits or satellites at different heights allows for the discrimination between the Schwarzschild effect, the gravitational constant, and antenna or range measurement errors. For non-circular orbits, the Schwarzschild effect is not a central force, as opposed to the circular orbits. Schwarzschild accelerations change as \(r^{ - 3}\) with the height, whereas the Newton accelerations change as \(r^{ - 2}\), hence both effects can be well separated for elliptical orbits. Please note that in this study, the value of \({\text{G}}{\text{M}}_{ \oplus }\) and the Shapiro effect correction (Ashby 2003; Petit and Luzum 2010) remain the same for all tests to extract the effects affecting the orbit dynamics only.

De Sitter and Lense–Thirring cause small offsets of the semimajor axis of about + 0.46 and − 0.07 mm, respectively, for Galileo in eccentric orbits, and negligible periodical variations of the order of 10–14–10–12 m (Sośnica et al. 2021). The mean Lense–Thirring -induced offset is reduced to zero when considering higher-order effects. Hence, the mean theoretical offset of the semimajor axis should be − 17.35 mm when considering all three main GR effects.

Figure 2 shows how the main three terms of GR modify the observed osculating semimajor axis of Galileo E30 in a circular orbit and Galileo E18 in an eccentric orbit as a function of time and altitude. Assuming that β = 1 and γ = 1, the mean offsets are − 16.7 and − 16.9 mm for Galileo E18 and E30, respectively (Fig. 2 top left and top right). For circular orbits, the difference with the theoretical derivations is 0.5 mm and the semimajor axis change does not depend on the satellite height, as opposed to the satellites in eccentric orbits.

Fig. 2
figure 2

Observed changes of the semimajor axis due to general relativity of Galileo satellites E30 (circular orbit, left column) as a function of time and E18 (eccentric orbit, right column) as a function of satellite height. Top row solutions assume that the PPN parameters equal β = 1 and γ = 1. For bottom row solutions, β and γ are estimated as free parameters. The blue points correspond to orbit differences every 15 min. The red line is the least-squares fit, and the greenish line represents the expected PPN effect from the first-order approximations (Eq. 2). Eclipsing periods have been excluded from the analysis

Full size image

When considering the solution with the estimation of PPN parameters, the deviation of the mean offset from theoretical values is 6.1 and 3.1 mm for E14 and E18, respectively (Table 4). However, this difference depends on the satellite considered. The mean difference is also larger for satellites in circular orbits, e.g., E30 and E08. The measurement noise from the solution with the PPN estimation is much higher than the corresponding noise from the solution with β = 1 and γ = 1, affecting the estimated values and reducing the GR-induced height differences between perigee and apogee (Fig. 3). The β and γ parameters estimated based on Galileo in eccentric orbits are underestimated with respect to the expected values and are correlated with the \(a\) and \(e\), which may explain differences in the recovery of the total effect on the semimajor axis. The PPN values calculated with equal weights from all constellations considered are β − 1 = 0.09 and γ − 1 = 0.14, whereas the values based only on Galileo E14 and E18 equal β − 1 =  − 0.33, and γ − 1 =  − 0.55.

Table 4 Changes of the semimajor axis due to GR effects, the sum of the Schwarzschild, Lense–Thirring, and De Sitter effects acting on Galileo E14&E18 and E30&E08 based on theoretical values and values derived from solution with PPN = 1 and estimating PPN values with formal solution uncertainty
Full size table
Fig. 3
figure 3

Changes of the semimajor axis of Galileo E18 due to general relativity as a function of the fraction of a day and satellite altitude. PPN = 1 (left), and estimating PPN parameters (right). Units: meters

Full size image

For eccentric orbits, such as Galileo E14 and E18, GR predicts that the semimajor axis change is different in perigee and apogee by − 7.8 and − 28.3 mm, respectively. The changes of the semimajor axis equal − 6.6 and − 8.6 mm in perigee and − 19.0 and − 23.8 mm in apogee for E14 and E18, respectively, in the solutions with the estimated PPN parameters, which gives the maximum relative error of 33%. Nevertheless, the GR effects changing the semimajor axis of GNSS orbits are sufficiently large to be detected by the current GNSS precise orbit determination methods.

Impact of the GR on eccentricity

Sośnica et al. (2021) derived theoretical effects of the eccentricity changes due to Schwarzschild, Lense–Thirring, and De Sitter. The change of the eccentricity is \(- 6.09\) to \(+ 3.51 \cdot 10^{ - 10}\) for Galileo in eccentric orbits in perigee and apogee, respectively, and \(- 4.68\) to \(+ 4.53 \cdot 10^{ - 10}\) for Galileo in circular orbits (the change of the eccentricity of \(4.5 \cdot 10^{ - 10}\) corresponds to a distance of 12.9 and 13.6 mm for Galileo in eccentric and circular orbits, respectively). Despite that E08 and E30 are excellent proxies of circular orbits (see Fig. 1), the difference of the height in perigee and apogee is still about 20 km.

The first-order Gaussian orbit perturbations for the eccentricity changes caused by the main Schwarzschild term read as:

$${\Delta }e = - \frac{{{\text{G}}{\text{M}}_{ \oplus } }}{{c^{2} ae\left( {1 - e^{2} } \right)}}\left[ {\left( {3 + 7e^{2} } \right)e\cos \nu + \frac{5}{2}e^{2} \cos 2\nu } \right] + O\left( {c^{ - 4} } \right).$$
(3)

Much smaller periodical variations are caused by Lense–Thirring and De Sitter (for equations, see Sośnica et al. 2021). The maximum \(a \cdot {\Delta }e\) values for E14 and E18 equal 16.37, 0.19, and 0.11 mm due to Schwarzschild, De Sitter, and Lense–Thirring, respectively; thus, these are of a similar order of magnitude to the changes of the semimajor axis. However, the semimajor axis variations are always negative, whereas the variations of the eccentricity change the sign in apogee and perigee. For Galileo satellites in eccentric orbits, the change of the semimajor axis is negative in the perigee and the apogee, with the maximum change in the perigee; thus, the size of the orbit is always reduced. The eccentricity change is negative in the perigee, which implies a more circular orbit as the perigee goes higher, and positive in the apogee, which implies a more eccentric orbit, as the apogee also goes higher from the geocenter perspective. The GR changes thus the shape and the size of the orbit instantaneously in opposite directions; however, both effects compensate each other to a certain extent.

Interestingly, the change of the eccentricity due to GR does not depend on the initial eccentricity of the satellite when assuming e2 to be negligible. The periodical changes of eccentricities are at a similar order of magnitude for satellites with height differences at perigee and apogee of several kilometers (e.g., GPS or Galileo in circular orbits), as well as dozens of thousands of kilometers, as in the case of Galileo E14 and E18.

Figure 4 illustrates that the predicted theoretical effect is reconstructed very well for GPS G28 for the solutions with β = 1 and γ = 1, whereas Galileo E18 shows an offset. The discrepancies are related to the assumption that all Keplerian parameters are perturbed separately, whereas in real GNSS solutions, the parameters are strongly correlated, which means that changes in other parameters can absorb some perturbations in one parameter. The semimajor axis is correlated with eccentricity with a correlation coefficient of even 0.9, whereas the correlations between β and γ, \(a\) and \(e\) are between 0.2 and 0.7.

Fig. 4
figure 4

Observed changes of the eccentricity of GPS G28 (left column) and Galileo E18 (eccentric orbit, right column) due to general relativity as a function of height. Top row solutions assume that the PPN parameters equal β = 1 and γ = 1, bottom row solutions allow each satellite to find its best β and γ values, i.e., β and γ are estimated as free parameters. Blue points correspond to orbit differences every 15 min, the red line is the least-squares fit, whereas the greenish line represents the expected PPN effect from the first-order approximations

Full size image

For Galileo E18, the eccentricity change in perigee equals − 6.09, − 6.73, and − 5.74 \(\cdot \) 10–10 according to theoretical values, the solution with PPN = 1, and solution with PPN estimated, respectively, whereas the eccentricity change in apogee is + 3.51, + 2.69, + 2.72 \(\cdot \) 10–10 for the solutions in the same order. The solution with the PPN estimation is obviously more scattered (Fig. 5). Table 5 compares the theoretical first-order GR perturbations with those derived from solutions with different handling of PPN parameters. The maximum differences in perigee and apogee reach 20–30% of the predicted theoretical effect with fixing PPN, and 20–40% when PPN are estimated.

Fig. 5
figure 5

Changes of the eccentricity of Galileo E18 due to general relativity as a function of the fraction of a day and satellite altitude: PPN = 1 (left) and estimating PPN parameters (right)

Full size image
Table 5 Changes of the eccentricity axis due to GR effects, the sum of the Schwarzschild, Lense–Thirring, and De Sitter effects acting on the eccentric Galileo E14&E18 and circular E30&E08. Eclipsing periods have been removed from statistics
Full size table

Impact on all GNSS satellites

Figure 6 shows the impact of GR effects on all GPS, GLONASS, and Galileo satellites as a difference between the solution with no GR effects and from the solution with fixing β and γ to 1 (top) and the estimation of β and γ (bottom), thus allowing each satellite to find its optimum spacetime curvature. From the solution with fixed PPN, the mean changes of the semimajor axis correspond well to the theoretical values. Only E14 and E18 and some GPS satellites have larger variations due to their eccentricities (Fig. 1).

Fig. 6
figure 6

Changes of the semimajor axis for GPS, GLONASS, and Galileo satellites due to GR assuming that PPN = 1 (top) and PPN parameters estimated (bottom) based on orbit differences every 15 min. All values are expressed in meters. The box extends from Q1 to Q3 quartile (the interquartile range, IQR), orange lines denote the median, and whiskers extend to 1.5 \(\cdot \) IQR. Dashed horizontal lines indicate the mean value from the set. Color dashed line denotes the theoretical value of the semimajor axis change due to GR

Full size image

Despite different heights, eccentricities, and different inclination angles of GPS, GLONASS, and Galileo satellites, the mean semimajor axis change oscillates around the value of \(-17.35\) mm, which is approximately the double value of the Schwarzschild radius, as predicted from the theory. The accuracy of the solution strongly depends on the accuracy of the radial orbit component, which is limited by the modeling of earth's albedo, infrared re-radiation, and satellite thermal effects and the correlations between determined parameters. The mean semimajor axis offset based on all satellites from the solution with the estimation of PPN is \(-17.41\pm 2.90\) mm, which gives a relative error with respect to the expected value of 0.36%.

Figure 7 illustrates changes of orbital eccentricity due to GR. It is almost impossible to distinguish Galileo in eccentric orbits from other GNSS satellites on the basis of the eccentricity change. The GR-induced eccentricity changes do not depend on the initial value of the eccentricity; thus, the variations for Galileo E14 and E18 do not deviate from those of near-circular orbiting satellites. Only a small asymmetry of the boxes with medians slightly shifted toward positive values can disclose which satellites are in eccentric orbits. The shift is caused by the fact that regular intervals of 15 min were used for comparisons, whereas eccentric satellites “spend” more time in the apogee region than in the perigee.

Fig. 7
figure 7

Changes of the eccentricity for GPS, GLONASS, and Galileo satellites due to GR assuming that PPN = 1 (top) and estimating PPN parameters (bottom) based on orbit differences every 15 min. The definition of the boxes is the same as in Fig. 6

Full size image

The observed mean change of the eccentricity for all satellites and the solution with the estimation of PPN (Fig. 7) is 3.17 \(\cdot \) 10–17 with the standard deviation of 7.52 \(\cdot \) 10–11, which is very close to the expected value of zero. The χ2 test from Table 6 shows that we can reject the hypothesis that GR does not change the semimajor axis, whereas we cannot reject the hypothesis that eccentricity change differs from zero and the semimajor axis differs from the value \(-17.35\) mm expected from theory.

Table 6 χ2 statistics for the assumption of the mean semimajor axis change of a0 = 0.00 mm and a1=\(-17.35\) mm and the mean eccentricity change of \(e=0\) due to GR from the solution with the estimation of PPN parameters
Full size table

Radial orbit displacements and correlations

To test a potential impact on the ground reference frame and the satellite orbits, we run two transformations; the Helmert transformation for the ground network and the transformation for satellite orbits. The comparison of the orbits resulted in a difference in the radial orbit component of − 4.4 and − 4.7 mm for all satellites from the solution, assuming that the PPN parameters equal β = 1 and γ = 1 and when estimating PPN parameters, respectively (Fig. 8).

Fig. 8
figure 8

Differences of the radial orbit component due to general relativity of Galileo satellites E30 (circular orbit, left column) as a function of time and E18 (eccentric orbit, right column) as a function of satellite height. The top row shows differences between the solution with the PPN parameters equal β = 1 and γ = 1 and the solution with no GR effects. The bottom row shows differences between the solution with β and γ estimated and the solution with no GR effects. The blue points correspond to orbit differences every 15 min. The red line is the least-squares fit, and the greenish line (below the red line) represents the expected effect. Eclipsing periods have been excluded from the analysis

Full size image

Following the third Kepler law, the mean change of the radial orbit component due to the accelerations in the radial direction R0 reads as (Bury et al. 2020):

$${\Delta }r = - \frac{1}{3}\frac{{{a}^{3} R_{0} }}{{{\text{G}}{\text{M}}_{ \oplus } }}$$
(4)

For a simplified version of the Schwarzschild accelerations in the radial direction, we obtain:

$$R_{0} = 3\frac{{{ }\left( {{\text{G}}{\text{M}}_{ \oplus } } \right)^{2} }}{{c^{2} {a}^{3} }}$$
(5)

Therefore, considering Eqs. 4 and 5, the expected orbit difference in the radial direction equals:

$${\Delta }r = - \frac{{{\text{G}}{\text{M}}_{ \oplus } }}{{c^{2} }}$$
(6)

which gives \({\Delta }r\)=  − 4.4 mm and explains the observed offsets from Fig. 8.

The mean changes of the semimajor axis are on average a factor of four larger than the orbit changes in the radial direction (cf. Equations 2 and 6), because the temporal variations of the eccentricity compensate to a great extent the semimajor axis variations. Moreover, GR effects modify the mean motion and thus also the revolution period by − 45.5 μs in the case of Galileo in circular orbits (Sośnica et al. 2021). No evident variations as a function of satellite height are visible for Galileo E18 in the eccentric orbit (Fig. 8).

Moreover, the noise of the solution with estimating β and γ parameters is only 1.5 times larger than the noise of the solution with fixing β and γ to 1. For the semimajor axis and eccentricity, this ratio exceeds the value of 5. Figure 9 depicts the correlation coefficients between estimated parameters: Keplerian (a, e, i, ω, Ω, u), ECOM (D0, Y0, B0, BC, BS), and PPN (β, γ) for a satellite in a circular orbit and Galileo E18 in eccentric orbit. The semimajor axis is strongly correlated with eccentricity with a correlation coefficient of − 0.8 and 0.9 with a time-variable sign and value. The PPN β parameter is also correlated with a and e, whereas γ is correlated with Ω and ECOM parameters, such as B0 and BS. Due to the considerable correlations between PPN parameters, semimajor axis, and eccentricity, the changes in these parameters are difficult to separate; however, the sum of all effects remains relatively stable for the differences of the orbit radial components, as shown in Fig. 8.

Fig. 9
figure 9

Correlation coefficients between Keplerian, PPN, and ECOM parameters in one daily solution for GPS G28 (left) and Galileo E18 (right)

Full size image

As a result, the radial orbit differences due to GR effects are rather small and assume similar values in apogee and perigee in the case of Galileo satellites in eccentric orbits, because GR changes the orbit size and shape in opposite directions. The differences in the GNSS station coordinates due to GR orbital effects are even smaller than radial orbit differences. From the Helmert transformation, the scale of the reference frame is shifted by − 0.24 mm, which is negligible in respect to the current accuracy of the GNSS antenna calibrations. Therefore, the orbital GR effects are absorbed mainly by the orbit parameters and do not substantially affect the estimated station coordinates.

Summary and conclusions

We empirically confirm the theoretical orbit geometry misshaping caused by the effects emerging from GR. The measurements from 83 artificial earth satellites collected by 106 stations were used for the detection of the orbit size and shape changes caused mainly by the Schwarzschild effect with a minor contribution from the Lense–Thirring and De Sitter effects.

The change of the satellite semimajor axis due to the three GR effects equals \(\Delta a =-28.3\) and \(-7.8\) mm when eccentric Galileo satellites are in their perigees and apogees, respectively. When considering the full constellation of GPS, GLONASS, and Galileo, the mean observed offset is \(-17.41\) mm, which gives a relative error versus the expected value of 0.36% from the solution with β and γ estimated as free parameters, thus allowing each satellite to find its best spacetime curvature and nonlinearity. The mean GR change of the semimajor axis does not depend on the satellite height and is equal to the double Schwarzschild radius with a small contribution from Lense–Thirring and De Sitter effects.

For eccentric Galileo, GR changes the orbital perigee in such a way that the orbit becomes smaller (perigee goes lower due to the semimajor axis changes) but more circular (perigee goes higher due to eccentricity change). In the apogee, the semimajor axis also decreases (apogee goes lower), but eccentricity increases (apogee goes higher), and thus the orbit becomes more eccentric. Hence, the orbital size variabilities for eccentric orbits are greatly compensated by the orbital shape changes, and thus the total effect of satellite height change is much smaller than the effects for the size and the shape of the orbit, individually and equals on average \(-4.4\) mm. For circular orbits, no semimajor axis variations occur as opposed to the variations of the eccentricities, which are similar for circular and eccentric orbits.

The earlier confirmations of the Schwarzschild effect, which is the main GR effect, were based on the observations of periapsis rates. For the first time, this study shows that direct range measurements to artificial earth satellites allow for the observations of GR effects from the orbit geometry variations. This opens a number of new applications of high-accuracy GNSS solutions in fundamental physics. In addition, the first pair of Galileo FOC satellites in eccentric orbits discloses phenomena related to the instantaneous orbit geometry variations otherwise unobserved.