Skip to main content
SpringerLink
Log in

\({\mathscr{H}}\)-matrix approximability of inverses of discretizations of the fractional Laplacian

  • Published:
Advances in Computational Mathematics Aims and scope Submit manuscript

Abstract

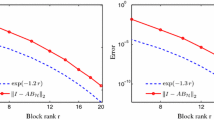
The integral version of the fractional Laplacian on a bounded domain is discretized by a Galerkin approximation based on piecewise linear functions on a quasiuniform mesh. We show that the inverse of the associated stiffness matrix can be approximated by blockwise low-rank matrices at an exponential rate in the block rank.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Acosta, G., Bersetche, F.M., Borthagaray, J.P.: A short FE implementation for a 2d homogeneous Dirichlet problem of a fractional Laplacian. Comput. Math Appl. 74(4), 784–816 (2017)

    MathSciNet  MATH  Google Scholar 

  2. Acosta, G., Borthagaray, J.P.: A fractional Laplace equation: regularity of solutions and finite element approximations. SIAM J. Numer. Anal. 55(2), 472–495 (2017)

    MathSciNet  MATH  Google Scholar 

  3. Adams, R.A., Fournier, J.J.F.: Sobolev Spaces, Volume 140 of Pure and Applied Mathematics (Amsterdam), 2nd edn. Elsevier/Academic Press, Amsterdam (2003)

    Google Scholar 

  4. Ainsworth, M., Glusa, C.: Aspects of an adaptive finite element method for the fractional Laplacian: a priori and a posteriori error estimates, efficient implementation and multigrid solver. Comput. Methods Appl. Mech. Engrg. 327, 4–35 (2017)

    MathSciNet  Google Scholar 

  5. Bebendorf, M.: Approximation of boundary element matrices. Numer. Math. 86(4), 565–589 (2000)

    MathSciNet  MATH  Google Scholar 

  6. Bebendorf, M.: Hierarchical LU decomposition-based preconditioners for BEM. Computing 74(3), 225–247 (2005)

    MathSciNet  MATH  Google Scholar 

  7. Bebendorf, M.: Why finite element discretizations can be factored by triangular hierarchical matrices. SIAM J. Numer. Anal. 45(4), 1472–1494 (2007)

    MathSciNet  MATH  Google Scholar 

  8. Bonito, A., Lei, W., Pasciak, J.E.: On sinc quadrature approximations of fractional powers of regularly accretive operators. ArXiv e-prints (2017)

  9. Bonito, A., Pasciak, J. : Numerical approximation of fractional powers of elliptic operators. Math. Comp. 84(295), 2083–2110 (2015)

    MathSciNet  MATH  Google Scholar 

  10. Börm, S.: Approximation of solution operators of elliptic partial differential equations by \({\mathscr{H}}^{2}\)-matrices. Numer. Math. 115(2), 165–193 (2010)

    MathSciNet  MATH  Google Scholar 

  11. Börm, S.: Efficient Numerical Methods for Non-Local Operators, Volume 14 of EMS Tracts in Mathematics. European Mathematical Society (EMS), Zürich (2010)

    Google Scholar 

  12. Börm, S., Grasedyck, L.: Hybrid cross approximation of integral operators. Numer. Math. 101(2), 221–249 (2005)

    MathSciNet  MATH  Google Scholar 

  13. Cabré, X., Sire, Y.: Nonlinear equations for fractional Laplacians, I Regularity, maximum principles, and Hamiltonian estimates. Ann. Inst. H. Poincaré, Anal. Non Linéaire 31(1), 23–53 (2014)

    MathSciNet  MATH  Google Scholar 

  14. Cabré, X., Tan, J.: Positive solutions of nonlinear problems involving the square root of the Laplacian. Adv. Math. 224(5), 2052–2093 (2010)

    MathSciNet  MATH  Google Scholar 

  15. Caffarelli, L., Silvestre, L.: An extension problem related to the fractional Laplacian. Comm. Partial Diff. Equ. 32(7-9), 1245–1260 (2007)

    MathSciNet  MATH  Google Scholar 

  16. Caffarelli, L., Stinga, P.: Fractional elliptic equations, Caccioppoli estimates and regularity. Ann. Inst. H. Poincaré, Anal. Non Linéaire 33(3), 767–807 (2016)

    MathSciNet  MATH  Google Scholar 

  17. Capella, A., Dávila, J., Dupaigne, L., Sire, Y.: Regularity of radial extremal solutions for some non-local semilinear equations. Comm Partial Diff. Equ. 36(8), 1353–1384 (2011)

    MathSciNet  MATH  Google Scholar 

  18. Corona, E., Martinsson, P.-G., Zorin, D.: An O(N) direct solver for integral equations on the plane. Appl. Comput. Harmon. Anal. 38(2), 284–317 (2015)

    MathSciNet  MATH  Google Scholar 

  19. Deny, J., Lions, J.L.: Les espaces du type de Beppo Levi. Ann. Fourier, Grenoble 5, 305–370 (1955). 1953–54

    MathSciNet  MATH  Google Scholar 

  20. Dölz, J., Harbrecht, H., Schwab, C.: Covariance regularity and \({\mathscr{H}}\)-matrix approximation for rough random fields. Numer. Math. 135(4), 1045–1071 (2017)

    MathSciNet  MATH  Google Scholar 

  21. Duan, R., Lazarov, R., P.J.: Numerical approximation of fractional powers of elliptic operators. Technical report, arXiv:1803.10055 (2018)

  22. Faustmann, M., Melenk, J.M., Praetorius, D.: \({\mathscr{H}}\)-matrix approximability of the inverses of FEM matrices. Numer. Math. 131(4), 615–642 (2015)

    MathSciNet  MATH  Google Scholar 

  23. Faustmann, M., Melenk, J.M., Praetorius, D.: Existence of \({\mathscr{H}}\)-matrix approximants to the inverses of BEM matrices: the simple-layer operator. Math. Comp. 85(297), 119–152 (2016)

    MathSciNet  MATH  Google Scholar 

  24. Faustmann, M., Melenk, J.M., Praetorius, D.: Existence of \({\mathscr{H}}\)-matrix approximants to the inverse of BEM matrices: the hyper-singular integral operator. IMA J. Numer. Anal. 37(3), 1211–1244 (2017)

    MathSciNet  MATH  Google Scholar 

  25. Gagliardo, E.: Caratterizzazioni delle tracce sulla frontiera relative ad alcune classi di funzioni in n variabili. Rend. Sem. Mat. Univ. Padova 27, 284–305 (1957)

    MathSciNet  MATH  Google Scholar 

  26. Gavrilyuk, I.P., Hackbusch, W., Khoromskij, B.N.: Hierarchical tensor-product approximation to the inverse and related operators for high-dimensional elliptic problems. Computing 74(2), 131–157 (2005)

    MathSciNet  MATH  Google Scholar 

  27. Gillman, A., Martinsson, P.G.: A direct solver with O(N) complexity for variable coefficient elliptic PDEs discretized via a high-order composite spectral collocation method. SIAM J. Sci. Comput. 36(4), A2023–A2046 (2014)

    MathSciNet  MATH  Google Scholar 

  28. Gol’dshtein, V., Ukhlov, A.: Weighted Sobolev spaces and embedding theorems. Trans. Amer. Math. Soc. 361(7), 3829–3850 (2009)

    MathSciNet  MATH  Google Scholar 

  29. Grasedyck, L.: Theorie und Anwendungen Hierarchischer Matrizen. Doctoral thesis Kiel (2001)

  30. Grasedyck, L.: Adaptive recompression of \({\mathscr{H}}\)-matrices for BEM. Computing 74(3), 205–223 (2005)

    MathSciNet  MATH  Google Scholar 

  31. Grasedyck, L., Hackbusch, W.: Construction and arithmetics of \({\mathscr{H}}\)-matrices. Computing 70(4), 295–334 (2003)

    MathSciNet  MATH  Google Scholar 

  32. Grasedyck, L., Hackbusch, W., Kriemann, R.: Performance of \({\mathscr{H}}\)-LU preconditioning for sparse matrices. Comput. Methods Appl. Math. 8(4), 336–349 (2008)

    MathSciNet  MATH  Google Scholar 

  33. Grasedyck, L., Kriemann, R., Le Borne, S.: Parallel black box \({\mathscr{H}}\)-LU preconditioning for elliptic boundary value problems. Comput. Vis. Sci. 11(4-6), 273–291 (2008)

    MathSciNet  Google Scholar 

  34. Greengard, L., Gueyffier, D., Martinsson, P., Rokhlin, V.: Fast direct solvers for integral equations in complex three-dimensional domains. Acta Numer. 18, 243–275 (2009)

    MathSciNet  MATH  Google Scholar 

  35. Hackbusch, W.: A sparse matrix arithmetic based on \({\mathscr{H}}\)-matrices. Introduction to \({\mathscr{H}}\)-matrices. Computing 62(2), 89–108 (1999)

    MathSciNet  MATH  Google Scholar 

  36. Hackbusch, W.: Hierarchical Matrices: Algorithms and Analysis, Volume 49 of Springer Series in Computational Mathematics. Springer, Heidelberg (2015)

    Google Scholar 

  37. Hackbusch, W., Khoromskij, B., Sauter, S.: On \({\mathscr{H}}^{2}\)-matrices. Lect. Appl. Math., 9–29 (2000)

  38. Hackbusch, W., Khoromskij, B.N.: A sparse \({\mathscr{H}}\)-matrix arithmetic: general complexity estimates. J. Comput. Appl. Math. 125(1-2), 479–501 (2000)

    MathSciNet  MATH  Google Scholar 

  39. Hackbusch, W., Khoromskij, B.N.: A sparse \({\mathscr{H}}\)-matrix arithmetic. II. Application to multi-dimensional problems. Computing 64(1), 21–47 (2000)

    MathSciNet  MATH  Google Scholar 

  40. Hale, N., Higham, N.J., Trefethen, L.N.: Computing A \(^{{\alpha }},\log (A)\), and related matrix functions by contour integrals. SIAM J. Numer. Anal. 46(5), 2505–2523 (2008)

    MathSciNet  MATH  Google Scholar 

  41. Harizanov, S., Lazarov, R., Margenov, S., Marinov, P., Vutov, Y.: Optimal solvers for linear systems with fractional powers of sparse SPD matrices. Numer Linear Algebra Appl. 25(5), e2167,24 (2018)

    MathSciNet  MATH  Google Scholar 

  42. Heidel, G., Khoromskaia, V., Khoromskij, B., Schulz, V.: Tensor approach to optimal control problems with fractional d-dimensional elliptic operator in constraints. Technical report, arXiv:1809.01971 (2018)

  43. Ho, K., Greengard, L.: A fast direct solver for structured linear systems by recursive skeletonization. SIAM J. Sci Comput. 34(5), A2507–A2532 (2012)

    MathSciNet  MATH  Google Scholar 

  44. Ho, K.L., Ying, L.: Hierarchical interpolative factorization for elliptic operators: differential equations. Comm. Pure Appl. Math. 69(8), 1415–1451 (2016)

    MathSciNet  MATH  Google Scholar 

  45. Ho, K.L., Ying, L.: Hierarchical interpolative factorization for elliptic operators: integral equations. Comm. Pure Appl. Math. 69(7), 1314–1353 (2016)

    MathSciNet  MATH  Google Scholar 

  46. Kufner, A.: Weighted Sobolev Spaces. A Wiley-Interscience Publication. Wiley, New York (1985). Translated from the Czech

    Google Scholar 

  47. Kwaśnicki, M.: Ten equivalent definitions of the fractional Laplace operator. Fract. Calc. Appl. Anal. 20(1), 7–51 (2017)

    MathSciNet  MATH  Google Scholar 

  48. Le Borne, S., Grasedyck, L.: \({\mathscr{H}}\)-matrix preconditioners in convection-dominated problems. SIAM J. Matrix Anal. Appl. 27 (4), 1172–1183 (2006). (electronic)

    MathSciNet  MATH  Google Scholar 

  49. Li, I., Mao, Z., Song, F., Wang, H., Karniadakis, G.: A fast solver for spectral element approximation applied to fractional differential equations using hierarchical matrix approximation. Technical report https://arxiv.org/pdf/1808.02937.pdf (2018)

  50. Li, S., Gu, M., Wu, C., Xia, J.: New efficient and robust HSS Cholesky factorization of SPD matrices. SIAM J. Matrix Anal. Appl. 33(3), 886–904 (2012)

    MathSciNet  MATH  Google Scholar 

  51. Lischke, A., Pang, G., Gulian, M., Song, F., Glusa, C., Zheng, X., Mao, Z., Cai, W., Meers chaert, M., Ainsworth, M., Karniadakis, G.: What is the fractional Laplacian? Technical report, arxiv:1801.09767, 01 (2018)

  52. Martinsson, P.: A fast direct solver for a class of elliptic partial differential equations. J. Sci. Comput. 38(3), 316–330 (2009)

    MathSciNet  MATH  Google Scholar 

  53. Martinsson, P., Rokhlin, V.: A fast direct solver for boundary integral equations in two dimensions. J. Comput. Phys. 205(1), 1–23 (2005)

    MathSciNet  MATH  Google Scholar 

  54. Muckenhoupt, B.: Hardy’s inequality with weights. Studia Math. 44, 31–38 (1972). Collection of articles honoring the completion by Antoni Zygmund of 50 years of scientific activity, I

    MathSciNet  MATH  Google Scholar 

  55. Nochetto, R.H., Otárola, E., Salgado, A.J.: Piecewise polynomial interpolation in Muckenhoupt weighted Sobolev spaces and applications. Numer. Math. 132(1), 85–130 (2016)

    MathSciNet  MATH  Google Scholar 

  56. Schmitz, P., Ying, L.: A fast direct solver for elliptic problems on general meshes in 2D. J. Comput. Phys. 231(4), 1314–1338 (2012)

    MathSciNet  MATH  Google Scholar 

  57. Scott, L.R., Zhang, S.: Finite element interpolation of nonsmooth functions satisfying boundary conditions. Math. Comp. 54(190), 483–493 (1990)

    MathSciNet  MATH  Google Scholar 

  58. Stinga, P., Torrea, J.: Extension problem and Harnack’s inequality for some fractional operators. Comm. Partial Diff. Equ. 35(11), 2092–2122 (2010)

    MathSciNet  MATH  Google Scholar 

  59. Xia, J.: Efficient structured multifrontal factorization for general large sparse matrices. SIAM J. Sci. Comput. 35(2), A832–A860 (2013)

    MathSciNet  MATH  Google Scholar 

  60. Xia, J., Chandrasekaran, S., Gu, M., Li, X.: Superfast multifrontal method for large structured linear systems of equations. SIAM J Matrix Anal. Appl. 31(3), 1382–1411 (2009)

    MathSciNet  MATH  Google Scholar 

  61. Zhao, X., Hu, X., Cai, W., Karniadakis, G.E : Adaptive finite element method for fractional differential equations using hierarchical matrices. Comput. Methods Appl. Mech Engrg. 325, 56–76 (2017)

    MathSciNet  Google Scholar 

  62. Zygmund, A.: Trigonometric Series. Cambridge Mathematical Library, 3rd edn., vol. I, II. Cambridge University Press, Cambridge (2002). With a foreword by Robert A. Fefferman

Download references

Funding

MK was supported by Conicyt Chile through project FONDECYT 1170672. JMM was supported by the Austrian Science Fund (FWF) project F 65.

Author information

Authors and Affiliations

  1. Departamento de Matemática, Universidad Técnica Federico Santa María, Avenida España 1680, Valparaíso, Chile

    Michael Karkulik

  2. Institut für Analysis und Scientific Computing, Technische Universität Wien, Wiedner Hauptstrasse 8-10, Vienna, Austria

    Jens Markus Melenk

Authors
  1. Michael Karkulik
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jens Markus Melenk
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Michael Karkulik.

Additional information

Communicated by: Ivan Oseledets

Publisher’s note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Karkulik, M., Melenk, J.M. \({\mathscr{H}}\)-matrix approximability of inverses of discretizations of the fractional Laplacian. Adv Comput Math 45, 2893–2919 (2019). https://doi.org/10.1007/s10444-019-09718-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10444-019-09718-5

Keywords

Mathematics Subject Classification (2010)

Search

Navigation