Remanufacturing supply chain coordination under the stochastic remanufacturability rate and the random demand

Abstract

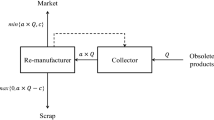
As an effective mode for resource recovery, remanufacturing has been widely recognized in practice and academia. However, coordination is needed and multi-uncertainties exist in a remanufacturing supply chain (RSC). Under a retailer collection mode, this paper extends the existing studies on a revenue-sharing mechanism for a forward supply chain to examine how to coordinate a RSC between a remanufacturer and a retailer by developing a mathematical model. This model considers two types of uncertainties, they are, the stochastic remanufacturability rate from the supply side of used products and the random demand occurring in remarketing of remanufactured products. This study fills the research gap on RSC coordination under the multi-uncertainty environment. Moreover, it introduces an iterative algorithm (the Newton–Raphson Method) to deal with difficulty in solving the implicit function of the payment to consumers under the non-uniform demand distribution by finding the approximate value. The research results show that a revenue-sharing contract for a RSC with multi-uncertainties can increase profit for the whole RSC as well as the remanufacturer and the retailer by eliminating double marginalization. Besides, the government subsidy to the remanufacturer can motivate the retailer to collect more used products under a revenue-sharing case since the retailer can share benefits of the whole RSC. A case study of remanufactured truck engines demonstrates benefits of the proposed revenue-sharing mechanism and the profit increase for the whole RSC with the government subsidy.

Appendices

Appendix 1: The list of symbols used in the paper

Expected profit:

$\prod _r^D$ :

retailer’s expected profit in decentralized case (wholesale-case)

$\prod _m^D$ :

remanufacturer’s expected profit in decentralized case (wholesale-case)

$\prod _{SC}^D$ :

supply chain’s expected profit in decentralized case (wholesale-case)

$\prod _r^C$ :

retailer’s expected profit in centralized case

$\prod _m^C$ :

remanufacturer’s expected profit in centralized case

$\prod _{SC}^C$ :

supply chain’s expected profit in centralized case

$\prod _r^{RS}$ :

retailer’s expected profit under revenue-sharing contract

$\prod _m^{RS}$ :

remanufacturer’s expected profit under revenue-sharing contract

$\prod _{SC}^{RS}$ :

supply chain’s expected profit under revenue-sharing contract

Uncertainty factors (Stochastic variables):

$\xi$ :

the remanufacturablity rate, and it is a percentage of used products that can be remanufactured. It is a stochastic variable and the distribution is known

$E(\xi )$ :

the expectation of remanufacturablity rate $\xi$

D :

the demand for remanufactured products, and it is a stochastic variable. CDF of D is F(x), PDF of D is f(x), expectation of D is $E(D)=\mu$. $F^{-1}(x)$ is the inverse distribution function of F(D)

For retailer:

$p_r$ :

unit price to consumers for used products acquisition

$p_r^D$ :

optimal unit price to consumers for used products acquisition in decentralized case

$p_r^C$ :

optimal unit price to consumers for used products acquisition in centralized case

$w^{d}$ :

transfer payment charged by a retailer on a remanufacturer per used product

$c_{ri}$ :

unit inventory cost in retailer’s location

$c_{rf}$ :

unit freight cost from a retailer to a remanufacturer

q :

the quantity of remanufactured products delivered from a remanufacturer, and it rely on $\xi$

$c_{rh}$ :

handing cost of selling product at the retailer

For remanufacturer:

P :

selling price of remanufactured products

$c_{me}$ :

unit examination cost at a remanufacturer, when used products are transported to remanufacturer, it would be examined to check whether it can be remanufactured or not

$c_{ms}$ :

unit sorting cost by the remanufacturer (including dismantling cost)

$c_{mr}$ :

unit remanufacturing cost (including testing cost)

$c_{md}$ :

unit disposal cost, for used products that cannot be remanufactured, it suffers a cost of disposal fee

$c_{mi}$ :

unit inventory cost during holding at the remanufacturer

$c_{mf}$ :

unit freight cost from remanufacturer to retailer

S(q):

expected sales, considering demand is D, $S(q)=q-\int \limits _0^q {F(y)dy}$

l :

leftover value per remanufactured product after selling season

s :

shortage cost per remanufactured product when demand is unsatisfied

$k_s$ :

government subsidies per remanufactured product

Revenue-sharing contact parameters:

$\{w_r ,\phi \}$ :

a pair of parameters in revenue-sharing contact

$w_r$ :

the parameter in revenue-sharing contract that represents the wholesale-price offered by remanufacturer to retailer for each used product collected

$\phi$ :

the parameter in revenue-sharing contract that represents a percentage of the revenue for remanufactured products offered by remanufacturer to retailer

T :

transfer payment between retailer and remanufacturer, and $T=T(w_r ,\phi )$

$w_r^{\max }$ :

the maximum value of $w_r$ under the constraint that the RSC achieves coordination

$\phi ^{\max }$ :

the maximum value of $\phi$ under the constraint that the RSC achieves coordination

Appendix 2: Proof of theorems and observations

Proof of Theorem 1

(A) Take $p_r^D$ as unknown variable in Eq. (9). (B) According to $Q=a\cdot p_r$. (C) It is obviously. End of proof. $\square$

Proof of Theorem 2

Make the partial derivative with respect to $p_r$ in profit function of remanufacturer. End of proof. $\square$

Proof of Observation 1

Compare Eqs. (7) and (19), it finds that ${p_r^C }/{p_r^D }>\frac{4(B-A)+a(P+s-l)\left( {E(\xi )} \right) ^{2}}{2(B-A)+a(P+s-l)\left( {E(\xi )} \right) ^{2}}>1.$ One gets $p_r^C >p_r^D$. End of proof. $\square$

Proof of Theorem 3

(A) Take $p_r^C$ as unknown variable in Eq. (20). (B) According to $Q=a\cdot p_r$. End of proof. $\square$

Proof of Theorem 4

Similar to the proof of Theorem 2. End of proof. $\square$

Proof of Theorem 5

The deformation of Eq. (17) and (25) is below,

$$\begin{aligned} E\left( {\prod \nolimits _{SC}^C } \right)= & {} -p_r Q-\frac{c_{ri} Q}{2}- c_{rf} Q-\frac{c_{ri} Q\xi }{2}-c_{rh} Q\xi +Pq-c_{me} Q-c_{ms} Q-c_{mr} Q\xi \\&-\,c_{md} Q(1-\xi )-\frac{c_{mi} Q}{2}-c_{mf} Q\xi -(P+s-l)\int \limits _0^q {F(x)} dx-s\left( {E(D)-q} \right) \\ E\left( {\prod \nolimits _m^{RS} } \right)= & {} -c_{me} Q-c_{ms} Q-c_{mr} Q\xi -c_{md} Q(1-\xi )-\frac{c_{mi} Q}{2}-c_{mf} Q\xi -w_r Q \\&+\,\phi \cdot Pq-\left( {\phi \cdot (P-l)+s} \right) \int \limits _0^q {F(x)} dx-s\left( {E(D)-q} \right) \end{aligned}$$

Since $E\left( {\prod _m^{RS} } \right) =\lambda \cdot E\left( {\prod _{SC}^C } \right)$, one gets two equations below,

$$\begin{aligned} \begin{array}{l} \lambda \cdot \left( {\begin{array}{l} -p_r Q-\frac{c_{ri} Q}{2}-c_{rf} Q-\frac{c_{ri} Q\xi }{2}-c_{rh} Q\xi +Pq-c_{me} Q-c_{ms} Q-c_{mr} Q\xi \\ \quad -c_{md} Q(1-\xi )-\frac{c_{mi} Q}{2}-c_{mf} Q\xi -s\left( {E(D)-q} \right) \\ \end{array}} \right) \\ \quad =-c_{me} Q-c_{ms} Q-c_{mr} Q\xi -c_{md} Q(1-\xi )-\frac{c_{mi} Q}{2}-c_{mf} Q\xi -w_r Q\\ \quad \quad +\,\phi \cdot Pq-s\left( {E(D)-q} \right) \end{array} \end{aligned}$$

And

$$\begin{aligned} \lambda (P+s-l)\int \limits _0^q {F(x)} dx=\left( {\phi \cdot (P-l)+s} \right) \int \limits _0^q {F(x)} dx \end{aligned}$$

Simultaneous two equations above, one gets the equations below with three variables $\lambda$, $w_r$ and $\phi$,

$$\begin{aligned} \left\{ {{\begin{array}{l} {\begin{array}{l} \lambda \cdot \left( {\begin{array}{l} -p_r Q-\frac{c_{ri} Q}{2}-c_{rf} Q-\frac{c_{ri} Q\xi }{2}-c_{rh} Q\xi +Pq-c_{me} Q-c_{ms} Q-c_{mr} Q\xi \\ \quad -c_{md} Q(1-\xi ) -\frac{c_{mi} Q}{2}-c_{mf} Q\xi -s\left( {E(D)-q} \right) \\ \end{array}} \right) \\ =-c_{me} Q-c_{ms} Q-c_{mr} Q\xi -c_{md} Q(1-\xi )-\frac{c_{mi} Q}{2}-c_{mf} Q\xi \\ \quad -w_r Q+\phi \cdot Pq-s\left( {E(D)-q} \right) \end{array}} \\ {\lambda (P+s-l)=\phi \cdot (P-l)+s} \\ \end{array} }} \right. \end{aligned}$$

Then, delete $\lambda$ in those two equations above, one gets

$$\begin{aligned} w_r= & {} -\frac{\phi \cdot (P-l)+s}{P+s-l}\left( -p_r -\frac{c_{ri} }{2}-c_{rf} -\frac{c_{ri} \xi }{2}-c_{rh} \xi +P\xi -c_{me} -c_{ms} -c_{mr} \xi \right. \nonumber \\&\left. -\,c_{md} (1-\xi )-\frac{c_{mi} }{2}-c_{mf} \xi -s\left( {\frac{E(D)}{Q}-\xi } \right) \right) \\&+\,\phi \cdot P\xi -c_{me} -c_{ms} -c_{mr} \xi -c_{md} (1-\xi )-\frac{c_{mi} }{2}-c_{mf} \xi -s\left( {\frac{E(D)}{Q}-\xi } \right) \end{aligned}$$

Besides, based on the assumption, $E\left( {\prod _m^{RS} } \right) =\lambda \cdot E\left( {\prod _{SC}^C } \right)$, so $E\left( {\prod _{SC}^{RS} } \right) =E\left( {\prod _{SC}^C } \right)$ (the objective function is exactly the same: $E\left( {\prod _{SC}^C } \right)$ and $\lambda \cdot E\left( {\prod _{SC}^C } \right) )$. End of proof. $\square$

Proof of Observation 2

$P<\Lambda$

$$\begin{aligned}&\Leftrightarrow \\&\frac{s\xi }{P-l}P>\Omega =\left( {\begin{array}{l} p_r +\frac{c_{ri} }{2}+c_{rf} +\frac{c_{ri} \xi }{2}+c_{rh} \xi +c_{me} +c_{ms} +c_{mr} \xi \\ +c_{md} (1-\xi )+\frac{c_{mi} }{2}+c_{mf} \xi +s\left( {\frac{E(D)}{Q}-\xi } \right) \\ \end{array}} \right) \\&\Leftrightarrow \\&\frac{\partial w_r }{\partial \phi }=\frac{(P-l)}{P+s-l}\left( {\begin{array}{l} \frac{s}{P-l}P\xi -p_r -\frac{c_{ri} }{2}-c_{rf} -\frac{c_{ri} \xi }{2}-c_{rh} \xi -c_{me} -c_{ms} -c_{mr} \xi \\ -c_{md} (1-\xi )-\frac{c_{mi} }{2}-c_{mf} \xi -s\left( {\frac{E(D)}{Q}-\xi } \right) \\ \end{array}} \right) >0. \end{aligned}$$

End of proof. $\square$

Proof of Observation 3

In Theorem 5, let $\phi =0$, then the maximum value of $w_r$ can be got. And it is easy to see that if $w_r^{\max } >0$, there is no positive terms in remanufacturer’s profit function. End of proof. $\square$

Proof of Observation 4

In Theorem 5, let $w_r =0$, the proof is similar to Observation 3. End of proof. $\square$

Proof of Theorem 6

In decentralized case, let’s assume that $w=w_r$, $\Pi _m^d \ge 0$ and $\Pi _r^d \ge 0$. It is known that $\Pi _{SC}^d =\Pi _m^d +\Pi _r^d$ and the RSC couldn’t get optimal profit in decentralized case.

Hence in this respect, after coordination process, the RSC profit in revenue-sharing contract surely become larger than the wholesale-price contract, $\Pi _{SC}^{RS} \ge \Pi _{SC}^d$. In other words, $\Pi _m^{RS} +\Pi _r^{RS} \ge \Pi _m^d +\Pi _r^d$. Considering the set of contract parameters lies on a continuous straight line, which means the profit can allocate arbitrarily, consequently, there exists at least one point on the line $w_r =w_r \left( \phi \right) ,0\le \phi \le 1$, that meets one of those three cases below,

$$\begin{aligned} \begin{array}{l} \Pi _m^{RS} >\Pi _m^d \, and\, \Pi _r^{RS} =\Pi _r^d \\ or \\ \Pi _r^{RS} >\Pi _r^d \, and\, \Pi _m^{RS} =\Pi _m^d \\ or \\ \Pi _m^{RS} >\Pi _m^d \, and\, \Pi _r^{RS} >\Pi _r^d \\ \end{array} \end{aligned}$$

End of proof. $\square$

Proof of Theorem 7

Similar to Theorem 5. End of proof. $\square$

Proof of Theorem 8

According to Theorem 1 in decentralized case, add $k_s \xi$ into the Equation (12), considering

$$\begin{aligned} Q_{with\,subsidies} -Q_{without\,subsidies} =a\cdot \left( {\left( {p_r^D } \right) _{with\,subsidies} -\left( {p_r^D } \right) _{without\,subsidies} } \right) , \end{aligned}$$

so $Q_{with\,subsidies} -Q_{without\,subsidies} =\frac{a\left( {B-A} \right) k_s \xi }{4(B-A)+a\cdot \xi ^{2}\left( {P+s-l} \right) }$.

$E_{with\,subsidies} \left( {\prod _{SC}^D } \right) -E_{without\,subsidies} \left( {\prod _{SC}^D } \right) =k_s \xi \cdot \Delta Q=k_s \xi \cdot \frac{a\left( {B-A} \right) k_s \xi }{4(B-A)+a\cdot \xi ^{2}\left( {P+s-l} \right) }.$ End of proof. $\square$

Proof of Theorem 9

Similar to Theorem 8. End of proof. $\square$

Appendix 3: Introduction and MATLAB code of the Newton–Raphson method

Let’s assume the problem is finding the root of function $f(x)=0,x\in \left[ {A,B} \right]$, and f(x) is a continuously differentiable function on interval $\left( {A,B} \right)$.

Let’s assume the current guess is $x_n$ and this is incorrect by an amount h. Consequently $x_n +h$ is the required value. It remains for us to determine h now or find an approximation to $x_n +h$ at least. The Taylor expansion for the function f(x) at point $x+h$ is given by

$$\begin{aligned} f(x_n +h)=f(x_n )+hf^{{\prime }}(x_n )+O(h^{2}). \end{aligned}$$

which means the value of the function f(x) at $x_n +h$ is nearly equal to the value of the function f(x) at $x_n$ plus the gradient at $x_n$ times the distance between $x_n +h$ and $x_n$. And the error is a second order of h. Loosely this error equals to something the same size as $h^{2}$. In fact, $O(h^{2})$ also means differentiated with respect to x the argument of the function. Considering $x_n +h$ is the required value, $f(x_n +h)=0$. After discarding the higher-order terms $O(h^{2})$ one finds that

$$\begin{aligned} h\approx \frac{f(x)}{f^{{\prime }}(x)}. \end{aligned}$$

This allows us to construct the iterative scheme

$$\begin{aligned} x_{n+1} =x_n -\frac{f(x_n )}{f^{{\prime }}(x_n )},n=0,1,2,\ldots . \end{aligned}$$

In these Iterative derivations the function is taken to be approximated by a “straight line” in order to determine the next point. And the “straight line” is the tangent on the point $\left( {x_n ,f\left( {x_n } \right) } \right)$.

The MATLAB Code of Newton–Raphson method is provided:

%

% Newton_Raphson_method.m

%

x = input(“Starting from one guess point:”)

tolerance = 1e-6;

iterations = 0;

while $(iterations<100)$ & $(abs(func(x))>tolerance)$

      x = x-func(x)./func_prime(x);

      iterations = iterations + 1;

end

if iterations==100

      disp(’No root is found’)

else

      disp([’The Root of function = ’ num2str(x,10) ’is found in ’ int2str(iterations)’ iterations.’])

end

%below is the function func_prime(x)

%

%func_prime.m

%

function [derivative] = func_prime(x)

%” derivative” will change based on your function, for example $f(x) = e^{x}+7x^{2}-17,$ then

derivative=e. $\hat{\,}$ x+14.* x;