1 Introduction

The 2019 novel coronavirus has proven to be one of the deadliest diseases that the world has ever seen. The pandemic has raised substantial challenges globally, disrupting commerce and severely impacting national economies as well as imposing harsh pressures on the medical sector (Fernandes, 2020). Efforts to shift operations online have met with uneven and limited success. As such, it is critical to explore the dynamics of the virus’ spread to obtain insights on its impacts and devise ways to reduce or slow its transmission (Yang et al., 2020).

The COVID-19 virus broke out in Wuhan China in December 2019, and gradually spread across the country. As the magnitude of the problem became evident, the World Health Organisation (WHO) launched the 2019 novel-coronavirus (2019-nCoV) emergency, and a strict lockdown strategy and social distancing measures have been implemented in most countries (Huang et al., 2020; Fernandes, 2020; Sohrabi et al., 2020). Nonetheless, more than 49.1 million people around the world have been affected by the virus. The global mortality rate has reached approximately 4%, and approximately 2.24 million deaths have been recorded (Worldmeters, 2020). The global medical sector is experiencing challenges in their efforts to develop a vaccine, and more than nine months after the disease outbreak, the governments are struggling to develop effective plans to ensure public health. Since governments across the world have implemented a strict lockdown policy, the business sector has been shattered, and economies have faced a substantial revenue loss. Delays in the development of a drug to resolve the issue has raised substantial difficulties for the countries around the world (Lai et al., 2020; Choi, 2020; Govindan et al., 2020).

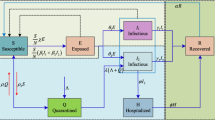
An expanded form of Susceptible Infectious Recovered (SIR) models, Susceptible-Exposed-Infectious-Removed (SEIR) models are widely used mathematical models used to analyse infection data during the different stages of an epidemic outbreak (Prem et al., 2020; Pujari & Shekatkar, 2020; Yang et al., 2020). Most early studies have emphasized on how to predict the vertical transmission using SEIR mathematical modelling. There are two types of transmission of viruses in the human body, namely the horizontal and vertical transmissions. In vertical transmission, virus would transmit from mothers to their offspring. In horizontal transmission, virus transmits among individuals of the same generation and COVID is an example of horizontal transmission. Horizontal transmission occurs either by direct contacts (licking, touching, biting etc.), or indirect contacts (vectors or fomites) with no physical contact. Note that seminal contributions have been made by a number of studies (Fine, 1975; Busenberg et al., 1983; Lu et al., 2002; Alberto d’Onofrio, 2005) to predict the vertical transmission using SEIR modelling. However, epidemic prediction problems dealing with the analysis of diseases that are horizontally transmitted are relatively under-explored. Columbia University applied a SEIR model called the Severe COVID-19 model & Mapping Tool to identify the number of hospitalisations, critical cases, critical care, and deaths and found that inadequate preparations could result in 4029–11,420 excess deaths due to inaccessible critical care (Branas et al., 2020). Similarly, the University of Pennsylvania adopted a diversified approach with its COVID-19 Hospital Impact Model for Epidemics (CHIME) (https://penn-chime.phl.io/) model to analyse upcoming worst- and best-case scenarios for the total number of coronavirus hospitalisations, ICU bed and ventilator demand, and the number of days such demands would exceed hospitals’ capacities (Santosh, 2020). Efimov and Ushirobira (2020) proposed an uncertainty model to analyse the course of COVID-19 in France, Italy, Spain, Germany, Brazil and Russia and investigated social feedback on the pandemic and effects of social isolation. The parameters of their SEIR model were identified by using publicly available data in the above-named countries, and the developed model was applied for the prediction of virus propagation under conditions of confinement. López and Rodo (2020) used exponential coefficients to project mortality and recovery rates and found that whereas the former is decreasing over time, the latter is increasing.

Recent theoretical developments based on variations of the SEIR model have indicated that if constant parameter values are used, the spread of the virus slows down only after the majority of the population have been infected or preventive measures are active (Mwalili et al., 2020; Pandey et al., 2020; Omori et al., 2020). However, classical SEIR models tend to yield pessimistic predictions. Many studies obtained high basic reproduction index values (depicted as R0), which caused alarm worldwide when used in basic SEIR models, many of which projected that the virus would affect upward of 50% of the world’s population. For example, the Medical Research Council (MRC) used a non-pharmaceutical intervention (NPI) SEIR model to reduce the coronavirus mortality rate and projected a worst-case scenario of more than two million deaths in the U.S. alone (Ferguson et al., 2020a, b). A recent study developed a SEIR model by using polynomial regression to project future COVID-19 prevalence based on the number of infection cases in India from January 22 to March 30, 2020 and projected that that if no measures are taken, 80% of susceptible individuals would be infected within several months (Pandey et al., 2020). Mwalili et al. (2020) used an extended SEIR model that subdivided the human population into people who were susceptible, exposed, asymptomatic infectious, symptomatic infectious and recovered and incorporated environmental pathogens as variables to calculate a basic reproduction number. The resulting value of 2.03 suggests that the pandemic will persist in the absence of strong control measures such as physical distancing, wearing of masks and frequent washing of hands.

In SEIR modelling, the attenuation of the spread of infection with a small number of infected people is possible only if the parameters are changed. To overcome this problem (He, Peng, et al., 2020; He, Tang, et al., 2020) used optimisation methods to fit model with real data of infection cases in Hubei. They published a study in June 2020 in which they considered single individuals rather than whole populations as a basic unit to analyse the non-linear dynamics of COVID-19 propagation. Their SEIR model incorporated hospitalisations, quarantines and external inputs as general control strategies, and an optimisation algorithm was used to calculate the model parameters that provided the best fit with actual data on the number of infected in Hubei province. Their resulting value of 45,563 is approximately 0.08% of the population of Hubei; however, as of September 2, 2020, there were 6.05 million cases, which represents about 2% of population.

Logistic models are a simplified analysis of infection propagation without respect to rate of conversion between susceptible, infected, exposed and recovered. Zhou et al. (2020) compared SEIR and logistic models and argued that logistic models are not effective for forecasting future pandemic dynamics if the known dynamics are exponential. Mathematically, logistic model assumes that prediction power and curve fitting of the model depends on the historical dataset so logistic model can predict the infection ratio accurately if it is controlled by population and growth rate. Carcione et al. (2020) analysed how the value of R0 impacts COVID-19 dynamics assuming that the rate of infection depends on measures taken and predicted a death toll of approximately 2.7 million infected individuals and 15,600 casualties in Lombardy, Italy by the end of the pandemic.

Most of the state-of-the-art prediction models utilised to critically and comprehensively understand the spread of COVID-19 have largely proved ineffective, and many have failed to obtain accurate and timely information about hospitals, beds, capacity, settings, demographics, population density, poverty rates, and available commodities to survive the deadly influx of coronavirus (Pandey et al., 2020; Mwalili et al., 2020; Zhou et al., 2020; He, Tang, et al., 2020; He, Peng, et al., 2020; Ivanov, 2020a, b). Indeed, most have either over- or underestimated the number of viral cases and resulting deaths. The above-described studies also fail to provide reasons for epidemic attenuation when only a small number of people have been infected due to the adoption of restrictive measures, and they do not explain the mechanisms by which infection continues to fade even when restrictive measures are cancelled. Moreover, it is difficult to determine which measures most contribute to propagation prevention because the methods that authorities use to prevent COVID-19 propagation vary from region to region. In particular, to our knowledge, no study has considered a combination of different resistance levels to the virus among individuals, which may have impacted R0 at the beginning of the pandemic and the efficiency of preventive measures. People who are more vulnerable to the virus will cause a high number of cases in the initial stages of a pandemic; however, after a significant fraction of such people are infected, the numbers begin to attenuate.

The substantial failure of current strategies highlights the need to rely on diversified strategies that are capable of addressing uncertain situations such as coronavirus (Santosh, 2020). Accordingly, in this research, we introduce idea of infection vulnerability stratification to SEIR modelling. After a critical review of the literature, we decided to combine SEIR modelling with agent-based and curve-fitting models. Most of the research in this field is aimed at developing COVID-19 model parameter fittings and predictions; however, our research aims to uncover the reasons that parameters change. Taking into consideration the characteristics of coronavirus and its impacts on the world, If we check the historical details of Influenza Pandemic (also known as "Spanish flu"), we see that the highest mortality rate in this pandemic was related to the second wave of the disease in 1918. The “second wave” of Spanish Flu was monitored to “peak” by the end of November but was followed by yet another wave of this disease in the mid-winter period (Cox and Subbarao, 2000). Prediction of the second wave is a complicated problem. Researchers usually associate the second wave with the lifting of restrictions (Pedro et al., 2020; de Castro, 2020), seasonal factors (Bukhari et al., 2020) and tracking people behavior (Grekousis et al., 2021; Edward, 2020), even though none of these factors are perfect indicators. Previous studies have explained existing dynamics of epidemic and the key factors affecting the ability to measure it. It is important to note that classical SEIR models usually provide pessimistic predictions. Calculations using a SEIR model with vulnerability stratification can show that the maximum positive effects can be achieved with long-lasting but moderate measures. The main challenge to have an accurate epidemic prediction is the presence of many unknown and dynamic factors. In a scientific sense, epidemic can be regarded as an unstable dynamic system in which a small change in parameter values can cause a very significant qualitative change of dynamics. Therefore, forecasts are usually “approximate”, showing various possible development scenarios. In the case of COVID, uncovering the reasons that prediction parameters change and analysing the prevalence rate of the disease and population behaviour in the second and even later waves are focal points of this study. Note that most prior research in this field has focused on developing COVID-19 model parameter fittings and predictions. However, different from them, our research aims to uncover the reasons that parameters change. Taking into consideration the characteristics of COVID-19 and its impacts on the world, we aim to demonstrate that our models are viable and can work effectively and efficiently to rectify external and internal issues. We test vulnerability stratification for the U.S. and the seven most populous European countries, and show that the infection vulnerability stratification parameter does not affect pandemic dynamics in the early stages; however, it is crucial in later stages. We also obtain the optimal strategies for “restrictive measures” and we interestingly show that moderately strict measures with a long duration are most effective. This is another important contribution of this study.

Therefore, building from these current gaps, we pose three research questions that are highly relevant in the current COVID outbreak:

RQ1: Can we develop an extended SEIR model to forecast possible pandemic dynamics by investigating the effects of infection vulnerability stratification and measures on preventing the spread of infection?

RQ2: Can we measure the impact of “infection vulnerability stratification” and “dynamics of basic reproduction index” parameters in SEIR model in the dynamics of epidemic?

RQ3: What are the roles of optimization of restrictions measures in the prediction of pandemic’s second wave to high seasonal fluctuations and a low vulnerability stratification coefficient?

The remainder of this paper proceeds as follows. Section 2 provides a description of the dataset and the SEIR model with infection vulnerability stratification. In Sect. 3, we evaluate fluctuations of data and weekly cycles and introduce an approach to filter out those fluctuations. In Sect. 4, we solve the problem of optimizing duration and preventative measures. Finally, Sect. 5 presents the study’s implications and conclusion.

2 Data description and SEIR modelling

2.1 Dataset description

We used daily data about COVID-19 dynamics in each U.S. state (COVID Tracking Project, 2020) and European countries (Open Data, 2020) used. These datasets only contain the number of infected and recovered people; we assume that whole population is susceptible. Data for each state was divided by population. Data obtained from (www.covidtracking.com Copyright©2020 by The Atlantic Monthly Group, 2020) has errors that could distort the results, including reducing the number of dead people on some days, empty fields, NaN (not a number) values and zero new positive individuals on some days. In order to resolve these issues, we replaced empty rows NaNs values (missing values in data set) with previous known values, and if there is no value, then we replaced it with zero. Thus, all newly infected and recovered statistics will be represented in next day.

The EU’s Open Data website contains the cumulative number of cases and deaths as well as the total population in each country in the world, which enables the calculation of the number of infected individuals as a fraction of the country’s population. We used data from December 31, 2019 (Day 1) to September 13, 2020 for the U.S. and the seven most populated European countries. A graphical representation of the data used for analysis is shown in Fig. 1.

Fig. 1
figure 1

Dynamics of COVID-19 propagation

Full size image

2.2 Model parameters

This section provides a description of the dataset and the modified SEIR model with consideration of infection vulnerability stratification. In its most basic form, following Herbert (2000), SEIR can be written as follows:

$$ \begin{gathered} S^{\prime}\left( t \right) = - \beta S\left( t \right)I\left( t \right) \hfill \\ E^{\prime}\left( t \right) = \beta S\left( t \right)I\left( t \right) - \alpha E\left( t \right) \hfill \\ I^{\prime}\left( t \right) = \alpha E\left( t \right) - \gamma I\left( t \right) \hfill \\ R^{\prime}\left( t \right) = \gamma I\left( t \right) \hfill \\ \end{gathered} $$
(1)

where S, E, I, R represent the fraction of susceptible, exposed, infected, recovered, respectively, β is the day−1 infectivity rate, α−1 is the daily average incubation period, γ−1 denotes the daily average recovery rate. The variables in equation system 1 are subject to the initial conditions:

$$ {\text{S(0) = 1}} - \sigma {\text{, E(0) = 0, I(0) = }}\sigma {\text{, R(0) = 0 }} $$
(2)

where σ is the initial fraction of infected people.

The average infected person can infect susceptible individuals for γ−1 days; therefore, the basic reproduction number can be written as:

$$ R_{0} = \frac{\beta }{\gamma }S\left( t \right) $$
(3)

The parameters used in SEIR model are defined in Table 1.

Table 1 List of variables
Full size table

Pandemic growth will occur as long as the value of β exceeds 1, and cumulative number of infected will grow even during the decay stage. β is the only parameter that can be controlled by measures; the duration of the infection and incubation periods is not controlled. The set of measures introduced to reduce β are hygiene and safe behaviour propaganda, social distancing, lockdowns, quarantines, and travel bans. Although those measures reduce infection rates, most can also be very harmful for economic and social stability.

Based on the classic SEIR model without vulnerability stratification, the value of β only depends on active measures to prevent infection spread. If drastic measures are necessary to slow the spread of infection, it is assumed they would be necessary until the infection’s extinction or the number of susceptible people was reduced through vaccination. We propose an alternative approach in this paper: the infection rate depends on the susceptible fraction, representing the probability that people who are prone to infection will catch the virus first, following which the infection rate will decrease. The idea of the infection rate depending on the fraction of susceptible individuals can be represented as in the form of monotonic decreasing function \(\beta = \beta \left( S \right)\). Introducing an unknown function to SEIR substantially complicates fitting because it increases the number of degrees of freedom, thereby possibly causing model overfitting. In order to overcome problems caused by complexity, we assume that \(\beta = \beta_{0} S^{k}\), where k is an infection vulnerability stratification parameter that can be fitted much more simply than function (He, Peng, et al., 2020; He, Tang, et al., 2020).

The SEIR model with vulnerability stratification coefficient k is stated as follows:

$$ \begin{gathered} S^{\prime}\left( t \right) = - \beta_{0} S^{k + 1} \left( t \right)I\left( t \right) \hfill \\ E^{\prime}\left( t \right) = \beta_{0} S^{k + 1} \left( t \right)I\left( t \right) - \alpha E\left( t \right) \hfill \\ I^{\prime}\left( t \right) = \alpha E\left( t \right) - \gamma I\left( t \right) \hfill \\ R^{\prime}\left( t \right) = \gamma I\left( t \right) \hfill \\ \end{gathered} $$
(4)

This equation is solved with the initial conditions of Eq. (2); assume that the value of β can be controlled by preventive measures, whereas vulnerability stratification cannot be controlled. Due to the discrete nature of data modelled by Eq. (4), the Euler method with a time-step of one day is used. The resulting numeric scheme is as follows:

$$ \begin{gathered} S\left( {t + 1} \right) = S\left( t \right) - \beta_{0} S^{k + 1} \left( t \right)I\left( t \right) \hfill \\ E\left( {t + 1} \right) = E\left( t \right) + \beta_{0} S^{k + 1} \left( t \right)I\left( t \right) - \alpha E\left( t \right) \hfill \\ I\left( {t + 1} \right) = I\left( t \right) + \alpha E\left( t \right) - \gamma I\left( t \right) \hfill \\ R\left( {t + 1} \right) = R\left( t \right) + \gamma I\left( t \right) \hfill \\ \end{gathered} $$
(5)

Calculations are performed until \(E\left( t \right) + I\left( t \right) < \varepsilon\), where epsilon is a small number.

2.3 Scenario results

This section describes the results of scenarios with different values of the basic SEIR parameters and infection vulnerability stratification. This factor often neglected in epidemic prediction, thereby causing significant overestimations of possible consequences. Table 2 shows the effect of applying the parameters in a series of calculations on the infected fraction of the population, which is presented in the last column and can be determined as a limit of the fraction of removed at infinity time. The dynamics of infection propagation for those parameters are shown in Figs. 2, 3 and 4.

Table 2 Effect of changing extended SEIR parameters on the final number of infected
Full size table
Fig. 2
figure 2

Effect of α change on dynamics of infection propagation

Full size image
Fig. 3
figure 3

Effect of proportional changes of β and γ on dynamic of infection propagation

Full size image
Fig. 4
figure 4

Effect of vulnerability stratification k change on infection propagation

Full size image

Figure 2 shows the cumulative number of exposed and infected over time depending on incubation period duration. The effect of incubation period on the total fraction of infected population is within 0.5% in the simulation. A longer incubation period slows down infection propagation and reduces the peak fraction of infected, thereby preventing health system overload. However, a lengthy incubation period also makes tracking the contacts of infected individuals more difficult.

Figure 3 shows the effect of proportional change infection and recovery rates. Proportional increases of infection and recovery rates β and γ do not impact the basic reproduction number R0; however, it reduces the duration of infection for each individual and increases the chance that they will infect others. Variation in those coefficients has a small effect on the final cumulative fraction of infected within 1%. A classical SEIR model assumes a constant infection rate for each infected person; however, in real life, the highest risk of infection is within the first days after infection, when symptoms are mild and the infected person is not yet isolated (He, Peng, et al., 2020; He, Tang, et al., 2020). The results of SEIR model simulations cannot be matched with US statistics data because states use substantially different methodologies of considered individual as ‘recovered’ (Covid Tracking Project, 2020). The EU’s statistical data does not include the number of recovered people (Publications Office of the European Union, 2020).

Figure 4 shows the effect of vulnerability stratification k on infection spread. At initial stages, when the fraction of infected less 1%, the effect of stratification is not significant, however, a high value of k reduces infection spread at later stages because people who are more prone to infections have already been infected. After R0 becomes less than 1, infection propagation begins slowing down. However, the effect of vulnerability stratification is difficult to detect during the initial stages of a pandemic. Figure 4 shows that whereas other parameters begin to affect epidemic dynamics in early stages, the effect of vulnerability stratification is not significant when only a small fraction of people are infected. Vulnerability stratification is the only parameter that affects the fraction of people that have ever been infected.

Figure 5 shows the effect of periodic fluctuations of infection rate within half a year. A season multiplier was added to the infection rate \(\left[ {1 + A\sin \left( {\frac{4\pi t}{{365}}} \right)} \right]\). It is shown that vulnerability stratification had a small effect during the initial stages of the pandemic before day 120; however, subsequent dynamics depend on the vulnerability stratification coefficient at any value of amplitude of periodic fluctuations of infection rate (Edward, 2020). If this parameter is high, then there is a decrease in the fraction of new infected after day 150 (Fig. 5c, e), and a second wave appears after day 200. Moreover, the scale of second wave depends on the vulnerability stratification coefficient; a third pandemic wave is possible if the coefficient is low and the amplitude of periodic fluctuations of infection rate is high. However, the third wave is weaker than the second, and there is no fourth wave at any parameters within the ranges A < 0.5 and k < 10.

Fig. 5
figure 5

Seasonal effects on pandemic propagation (a, c, e—fraction of new infected; b, d, f—cumulative fraction of infected; a, b—A = 0.2; c, d—A = 0.35; e, f—A = 0.5)

Full size image

A high amplitude of periodic fluctuations of infection rate slightly increases the peak fraction of new infected people per day, and vulnerability stratification significantly impacts peak fraction. A high vulnerability stratification coefficient smooths peak value fractions at the second and third waves.

Seasonal fluctuations can cause healthcare systems to overload. It is difficult to obtain real seasonal fluctuations of infection rate values because a) its shape is not necessarily sinusoidal due to variable weather, and b) infection propagation depends on the effectiveness of preventive measures and people’s behaviour, among other factors (Edward, 2020). Nonetheless, the obtained results are qualitatively consistent with the actual dynamics of the pandemic.

3 COVID-19 data analysis and estimating the dynamics of basic reproduction number R 0

This section describes our analysis of real data using our SEIR model with vulnerability stratification. Such analysis includes fluctuations in data and weekly cycles and our method of filtering out those fluctuations and estimating how the dynamics of basic reproduction number R0 change over time.

Obtaining parameters values is the first step of the analysis. As indicated above, the EU dataset does not include information about the dynamics of recovery; therefore, it is impossible to obtain the numbers of currently infected people (Publication Office of the European Union, 2020). The U.S. conducts daily tracking of statistics about COVID-19 dynamics (The Covid Tracking Project, 2020). A prediction of future COVID dynamics can be obtained by solving the reversal problem based on the SEIR model. The duration of incubation period cannot be derived from the data on these websites. Researchers have obtained different values for the duration of the COVID-19 incubation period (Novel Coronavirus (2019-nCoV) Situation Report); whereas WHO reported an incubation period from 2–10 days. China’s National Health Commission estimated it as 10–14 days and the Centers for Disease Control and Prevention estimated it as 2–14 days (Coronavirus Disease 2019-COVID-19). Statistical research based on data obtained from Wuhan showed average incubation period equal to 5.2 days (Qun Li, Guan, et al., 2020; Li, Sun, et al., 2020). Based on the data above, we propose a value of \(\alpha = 0.2\,{\text{day}}^{ - 1}\).

The next step is retrieving matching data for the model variables (equation system 1). At the beginning of the modelling, the number of infected people was divided by the corresponding national population to obtain a fraction. Then, the number of infected people was calculated as the difference between cumulative infected, cumulative recovered and dead people. The results were used to obtain statistical data for the fractions of infected and recovered people I(t) and R(t). U.S. states that lacked data on the number of recovered individuals were excluded from the analysis. As mentioned in (The COVID Tracking Project, 2020):

States provide very disparate definitions on what constitutes a ‘recovered’ COVID-19 case…Types of ‘recovered’ cases include those who are discharged from hospitals, released from isolation after meeting CDC guidance on symptoms cessation, or those who have not been identified as fatalities after a number of days (30 or more) post disease onset. Specifics vary for each state or territory.

Therefore, the fraction of recovered individuals varies from state to state. Worldwide data for the number of cases, deaths and population of each country can be found in (US States Census Bureau, 2020, https://www.census.gov/data/tables/time-series/demo/popest/2010s-state-total.html).

We propose a simplified model that assumes that the number of infectious people is equal to number of newly infected within the last 14 days, as symptoms are typically mild on the first day after infection and there is higher chance that the infected did not take measures to prevent virus spread.

Calculating the number of exposed people is not a trivial endeavour. Obtaining data for the exposed fractions using incubation known fraction of infected and the incubation period fraction can be written as \(E\left( t \right) = \frac{1}{\alpha }\int\limits_{0}^{ + \infty } {\exp \left( { - \alpha \tau } \right)I\left( {t + \tau } \right)d\tau }\). This formula causes exponentially decreasing error depending on the number of days available after the current day. In order to estimate the number of exposed people, it is assumed that the number of infected people for periods after the last available day for which data are available can be calculated using the formula \(I\left( {t > t_{\max } } \right) = I\left( t \right)\).

The number of cases in the U.S. has fluctuated over time. Such fluctuations can be a source of panic because even if there is no stable trend in the growing number of new cases, this number will increase on some days. In order to investigate the nature of those fluctuations, we can analyse the structure of equation system 1.

Next, we can investigate possible fluctuations in the SEIR model using the analysis of ordinary differential equations. This analysis will show periodic epidemic dynamics based on the basic SEIR model (equation system 1).

Assuming that the infection spread is not wide and therefore \(E + I + R \ll 1\), equation system 1 becomes linear. The fraction of recovered is outside the scope of this analysis. A linearised system of equations for the exposed and infected population fraction can be depicted as:

$$ \begin{gathered} E^{\prime}\left( t \right) = \beta I\left( t \right) - \alpha E\left( t \right) \hfill \\ I^{\prime}\left( t \right) = \alpha E\left( t \right) - \gamma I\left( t \right) \hfill \\ \end{gathered} $$
(6)

Initially, there are no exposed people and only a small fraction of infected individuals, thereby matching the initial conditions in the formula: \(E\left( t \right) = 0\) and \(I\left( t \right) = \varepsilon\).

Unlike the number of infected people, the number of exposed cannot be monitored; therefore, we exclude E(t) from the system and transform it to a second-order differential equation. Differentiating the second equation of system 6 and adding it to second equation multiplied by α results in

$$ I^{^{\prime\prime}} \left( t \right) + \alpha I^{^{\prime}} \left( t \right) = \alpha E^{^{\prime}} \left( t \right) - \gamma I^{^{\prime}} \left( t \right) + \alpha^{2} E\left( t \right) - \alpha \gamma I\left( t \right) $$
(7)

Based on first equation of (6), substitute \(E^{^{\prime}} \left( t \right) + \alpha E\left( t \right) = \beta I\left( t \right)\)

$$ \begin{aligned} & I^{\prime\prime}\left( t \right) + \alpha I^{\prime}\left( t \right) = - \gamma I^{\prime}\left( t \right) + \alpha \beta I\left( t \right) - \alpha \gamma I\left( t \right) \\ & I^{\prime\prime}\left( t \right) + \left[ {\alpha + \gamma } \right]I^{\prime}\left( t \right) + \left[ {\alpha \left[ {\gamma - \beta } \right]} \right]I\left( t \right) = 0 \\ \end{aligned} $$
(8)

This equation has two common solutions in exponential form.

Analyse its characteristic equation

$$ \lambda^{2} + \left[ {\alpha + \gamma } \right]\lambda + \left[ {\alpha \left[ {\gamma - \beta } \right]} \right]I\left( t \right) = 0 $$
(9)

This is a quadratic equation in which the discriminant takes the form of

$$ D = \left[ {\alpha + \gamma } \right]^{2} + 4\left[ {\alpha \left[ {\beta - \gamma } \right]} \right] $$
(10)

The common solution of the differential equation can be written as

$$ \begin{aligned} I\left( t \right) & = C_{1} \exp \left( { - \left[ {\alpha + \gamma } \right] + \sqrt {\left[ {\alpha + \gamma } \right]^{2} + 4\left[ {\alpha \left[ {\beta - \gamma } \right]} \right]} } \right) \\ & \quad + C_{2} \exp \left( { - \left[ {\alpha + \gamma } \right] - \sqrt {\left[ {\alpha + \gamma } \right]^{2} + 4\left[ {\alpha \left[ {\beta - \gamma } \right]} \right]} } \right) \\ \end{aligned} $$
(11)

If the expression under the square root is negative, solution will have form

$$ \begin{aligned} I\left( t \right) & = C_{1} \exp \left( { - \left[ {\alpha + \gamma } \right]t} \right)\cos \left( {t\sqrt {\left[ {\alpha + \gamma } \right]^{2} + 4\left[ {\alpha \left[ {\beta - \gamma } \right]} \right]} } \right) \\ & \quad + C_{2} \exp \left( { - \left[ {\alpha + \gamma } \right]t} \right)\sin \left( {t\sqrt {\left[ {\alpha + \gamma } \right]^{2} + 4\left[ {\alpha \left[ {\beta - \gamma } \right]} \right]} } \right), \\ \end{aligned} $$
(12)

This solution can fluctuate; however, it cannot grow exponentially. An exponentially growing solution can only be obtained if the exponent is real. Neglect the lower exponent and obtain a solution in the form of

$$ I\left( t \right) = C_{1} \exp \left( { - \left[ {\alpha + \gamma } \right] + \sqrt {\left[ {\alpha + \gamma } \right]^{2} + 4\left[ {\alpha \left[ {\beta - \gamma } \right]} \right]} } \right) $$
(13)

Solution (13) is the only exponential growing solution for SEIR model. Periodical solution (12) is a product of exponentially decreasing and periodical function.

In contrast to the mathematical model, infection rates can change over time in real life. Such changes can be related to the following factors related to weekly cycles: a) delays in reporting new cases (cells containing zeros and NaNs in the table from [9] indicate the existence of this factor); b) delays in requesting medical care in cases of mild symptoms and c) infection risk depending on the day of week, such as work days (this factor effect was smoothed by the incubation period of COVID-19). As demonstrated above, there is not sufficient data to calculate effective parameter values for every day using statistical data due to different interpretations of the definition of being ‘recovered’. In this situation, the value of β in a classical SEIR model will substantially depend on a standard definition; however, the value of R0 does not depend on a common interpretation of ‘recovered’ if we assume that an individual is only contagious for 14 days. Based on this assumption, the reproduction index can be rendered as

$$ R_{0} \left( t \right) = t_{\inf } \frac{{I_{C} \left( t \right) - I_{C} \left( {t - 1} \right)}}{{I_{C} \left( {t - 1 - t_{e} } \right) - I_{C} \left( {t - 1 - t_{i} - t_{e} } \right)}}, $$
(14)

where IC is the cumulative fraction of the infected population (people who ever had COVID-19), \(t_{i} = 14\), i.e. the average duration of contagiosity, days; \(t_{e} = 5\), i.e. the average incubation period in days. Formula (14) is based on the assumption that the total number of infected people.

In order to reduce fluctuations, the daily average per week value of R0 was calculated using the following formula

$${R}_{0,j }= \frac{1}{\mathrm{n}}\sum_{i=0}^{n-1}{R}_{0 }({t}_{0 }+7i+j)$$
(15)

where t0 represents Apr 20, 2020, j = 0–6, i.e. the day of the week, and n = 19.

The results of weekly fluctuations in the U.S. and the seven European countries based on data from (US States Census Bureau, 2020, https://www.census.gov/data/tables/time-series/demo/popest/2010s-state-total.html) are shown in Table 3. Those values are normalised.

Table 3 Relationship between R0 fluctuations and the day of week
Full size table

Table 3 shows that in most countries, the highest number of cases are registered from Thursday–Saturday. The weekly fluctuations are widest in Germany, France and Italy, whereas the lowest fluctuations are observed in Russia and Turkey.

The average weekly R0 can be used for correction purposes. The corrected value of R0 can be calculated as

$${R}_{cor }\left(t\right)= \frac{{R}_{cor }\left(t\right)}{{R}_{0, mod (t,7)}}$$
(16)

where mod is the remainder following division by seven.

Fluctuations are caused by various factors. Strong data fluctuations hinder the investigation of pandemic dynamics. In order to resolve fluctuation problems, we used an alternative approach of filtering real data IC(t) based on an iterative algorithm.

$$ \begin{aligned} I_{C}^{0} \left( t \right) & = I_{C}^{{}} \left( t \right) \\ I_{C}^{n + 1} \left( t \right) & \leftarrow \min \left( {\max \left( {\frac{{I_{C}^{n} \left( {t - 1} \right) + 2I_{C}^{n} \left( t \right) + I_{C}^{n} \left( {t + 1} \right)}}{4},\left( {1 - \mu } \right)I_{C}^{{}} } \right),\left( {1 + \mu } \right)I_{C}^{{}} } \right) \\ I_{CF}^{{}} \left( t \right) & = I_{C}^{N} \left( t \right) \\ \end{aligned} $$
(17)

where \(I_{C}^{n} \left( t \right)\) represents data after n iterations of filtering, N is the total number of iterations of filtering algorithm, and \(\mu\) is the relative allowed data change due to filtering. A side effect of this filtering is introducing the relative error \(\mu\) to the cumulative fraction of infected.

Dynamics of \(R_{0} \left( t \right)\) for the U.S. and European countries based on filtered data are shown in Fig. 6. In all countries, a high value of R0 can be seen in the initial stages of the pandemic. This is caused by the lack of diagnostic knowledge when the virus first began to spread, which caused underestimations of case numbers. Following the early phase, there are fluctuations and a trend of decreasing R0. The least squares method is used to obtain the basic reproduction number without the effect of collective immunity R00 and coefficient of infection vulnerability stratification k. The minimised function takes the form of:

$$ \sum\limits_{{t = t_{1} }}^{{t_{2} }} {\left[ {R_{00} \left( {1 - I_{C} \left( t \right)} \right)^{k} - R_{0} \left( t \right)} \right]^{2} } \to \min $$
(18)
Fig. 6
figure 6

R0 estimations in the U.S. and top European countries (Day0 = Dec 30, 2019)

Full size image

The results of model fitting using the least squares method are shown in Table 4. Because reliable data about the effectiveness of government-imposed restrictions is practically impossible to obtain, this was not used as prediction variable. There is significant variation in k. Fitting real data to negative values of k means that other factors have more effect than vulnerability stratification.

Table 4 Basic reproduction index without the effects of collective immunity and vulnerability stratification coefficient of the U.S. and European countries
Full size table

Day 0 corresponds to December, 30 2019. There are no data for the first days, following which R0 values are high due to a lack of diagnostics and unpreparedness to fight a new virus. When diagnostics improve, the number of infected people detected increases. Delays in diagnostics efficiency were exacerbated by the need to produce a sufficient number of tests, and a lack of preventive measures caused virus propagation during the initial stages.

The results for different countries vary widely. The highest k values were obtained for Russia and Turkey. The high k value in Russia was caused by the slow decrease in R0 over time. The cumulative fraction of infected in Turkey is small; therefore, there would be smaller changes than in other countries. The U.S. and U.K. have vulnerability stratification coefficients near zero; R0 first decreases but then slowly begins to increase. The situation in Germany, Spain, France and Italy is worse; the increase of R0 above 1 over time is a sign of a possible second wave.

Analysis of the basic reproduction index shows that its value is stable around 1 in the U.S. and Russia following the initial outbreak period. Other countries that managed to reduce R0 below 1 later experienced an increase, which is expressed to varying degrees in different countries. The worst situation is in Spain. Germany and Turkey show small increases in R0.

The above findings evince that the basic reproduction index depends on factors not explained by SEIR model with constant parameters Those factors can be either external or related to the efficiency of preventive measures, which are only things that can be controlled in a pandemic situation. Possible factors influencing a second wave include low viral resistance, partial collective immunity (with consideration of vulnerability stratification), people’s behaviour, and authoritative actions.

4 Optimisation of restricting measures

Authorities can adopt measures to reduce infection rates during a pandemic; however, such policies are usually only temporary. A multi-criteria optimisation problem can be established, solving which yields the optimal restricting measures (Edward, 2020).

Assuming that restrictions reduce the infection rate coefficient, then

$$ \beta (t) = \left[ {1 - \beta_{ef} P\left( t \right)} \right]\beta_{0} S^{k} \left( t \right) $$
(19)

where P(t) is the temporal coefficient of measures intensity, which equals 1 at time of maximum implementation and 0 when all measures are cancelled. The level of intensity of measures can be expressed as:

$$ P\left( {t_{1} < t < t_{1} + t_{ef} } \right) > 0,\beta_{ef} $$
(20)

Problem of choice restrictions can be formulated as multi-criteria problem (Raboisson and Lhermie, 2020). We use following criteria for multi-criteria problem

  • \(t_{ef}\) is the duration of time when preventive measures are active;

  • \(\beta_{ef}\) denotes the strictness of measures;

  • \(I_{p} = \mathop {\max }\limits_{t} \left( {I\left( t \right)} \right)\) represents the peak value of the infected fraction; and

  • \(R_{\infty } = \mathop {\lim }\limits_{t \to \infty } R\left( t \right)\) is the cumulative value of infected fraction.

The first two criteria represent the costs of measures, and last two relate to the effects of measures. Peak value is important because the risk of negative consequences increases if it exceeds health system capacity.

4.1 Scenario 1

The intensity of preventive measures is constant during the entire period they are active. This is similar to the prevention measure model in Edward, (2020):

$$ P\left( t \right) = \left\{ \begin{gathered} 1,\quad t_{1} < t < t_{1} + t_{ef} \, \hfill \\ 0,\quad otherwise \hfill \\ \end{gathered} \right. $$
(21)

4.2 Scenario 2

De Castro (2020) investigates effects of confinement cancelling in Germany and Spain. The author shows that slower removing of confinement reduces the peak number of infected and number of deaths. Making reference to De Castro (2020), we have Scenario 2. In which preventive measures have their maximum intensity at the start, following which the intensity linearly decreases over time:

$$ P\left( t \right) = \left\{ {\begin{array}{*{20}l} {\frac{{t_{1} + t_{ef} - t}}{{t_{ef} }},} \hfill & {t_{1} < t < t_{1} + t_{ef} } \hfill \\ {0,} \hfill & {otherwise} \hfill \\ \end{array} } \right. $$
(22)

There is no single method for the scalarisation of multi-criteria problems. Pareto optimisation is the only reliable method to exclude ineffective solutions. However, if rules enable us to choose between two solutions, then that allows to exclude some of the solutions from the Pareto set. We assume that the cost of measures is growing faster than linear by \(\beta_{ef}\) and linear by \(t_{ef}\) because if multiple measures can be adopted, then the least costly ones will be adopted first. This assumption can be used to make a choice between solutions:

$$ \left( {t_{ef1} ,\beta_{ef1} ,I_{p} ,R_{\infty } } \right),\left( {t_{ef2} ,\beta_{ef2} ,I_{p} ,R_{\infty } } \right) $$
(23)

If \(t_{ef1} ,\beta_{ef1} < t_{ef2} ,\beta_{ef2} \,{\text{and}}\,t_{ef1} ,\beta_{ef2}\), then \(t_{ef1} ,t_{ef2}\) should be ignored when making a decision about Pareto efficiency.

Figure 7 shows the results of modelling preventive measures of various intensities and durations. The following parameters were used for the calculations:

$$ \beta_{0} = 0.15,\,k = 5,\,\alpha = 0.2,\,\gamma = 0.1 $$
(24)
$$ R_{0} = \frac{{\beta_{0} S^{k} }}{\gamma }S $$
(25)
Fig. 7
figure 7

Effects of preventive measures at k = 5 (a with constant intensity of preventive measures; b with linearly decreasing measures)

Full size image

Figure 7a shows measures with constant intensity and Fig. 7b combines linearly decreasing efficiency with doubled duration. The correlation between the peak and the total number exceeds 99%. It can be seen that the most effective result can be obtained with long-term but moderate measures. Weak preventive measures do not slow down infection propagation, and whereas overly strict measures can reduce R0 below 1, they cannot be maintained for a lengthy period due to economic concerns, and infection propagation resurges after their cancellation. When measures are moderate, the basic reproduction number becomes less than 1 when there are fewer infected people; therefore, the total number of cases during pandemic decay is reduced. The results of modelling preventive measures with consideration of the increasing value of vulnerability stratification are shown in Fig. 8. The key effects are the same as in Fig. 7. Real time control of the intensity of preventive measures is challenging due to the following issues: a) the incubation period causes feedback delays; b) fluctuations in number of cases, which can be smoothed, although doing so would also delay feedback; c) the unpredictable effects of the environment on infection rate (e.g. weather, seasonal changes); and d) the difficulty of making a quantitative estimation of the effectiveness of preventive measures. Despite these complications, using qualitative effects of typical scenarios is useful for decision-making, as Figs. 7 and 8 show that the effects of preventive measures depend on their maximum duration.

Fig. 8
figure 8

Effect of preventive measures at k = 10 (a with constant intensity of preventive measures, b with linearly decreasing measures)

Full size image

The dependence of total and peak numbers of infected individuals on the value of k is shown in Fig. 9. The impacts of preventive measures with constant intensity for 150 days and linearly decreasing efficiency for 300 days were tested. Figure 9 demonstrates that the total and peak number of infected logarithmically depends on infection vulnerability coefficient [k + 1]. Linearly intensive preventive measures are more effective than constant intensity measures. The peak number of infections is more strongly affected by preventive measures than the total number.

Fig. 9
figure 9

Effects of preventive measures at different values of k (a effects on total number of infected, b effects on peak numbers of infected)

Full size image

There are two main ways to halt a pandemic: elimination of the virus and reducing the basic reproduction index below 1. Neither of these solutions is possible over the long term in the absence of preventive measures. A pandemic cannot continue when there are neither infected nor exposed people; however, this elimination scenario does not appear to be realistic in the near future in the case of COVID-19. The latter is possible with measures such as improving healthcare (with better diagnostics, treatments, and a vaccine), social insurance (to support people with symptoms so they do not have to work) and collective immunity. Reducing basic reproduction index below 1 is a more reliable means of fighting a pandemic because it is resistant to the emergence of newly infected people. If a strategy of collective immunity is adopted, then a certain fraction of the population is likely to recover from infection. After the basic reproduction index has been reduced to 1, the number of actively infected people ceases to grow and the deceleration stage of the pandemic begins. However, this does not signal an end of the pandemic because the cumulative number of infected people will continue to increase depending on the values of the SEIR model variables at the start of the deceleration stage. Thus, minimising the cumulative number of infected individuals depends on deceleration stage. Assuming that pandemic dynamics are quasi-stationary at the start of the deceleration stage, we can calculate

$$ E^{\prime}\left( {t_{d} } \right) = 0,\,I^{\prime}\left( {t_{d} } \right) = 0 $$
(26)

Therefore, we can derive from (4) that

$$ \begin{aligned} & \beta_{0} S^{k + 1} \left( {t_{d} } \right)I\left( {t_{d} } \right) - \alpha E\left( {t_{d} } \right) = 0 \\ & \alpha E\left( {t_{d} } \right) - \gamma I\left( {t_{d} } \right) = 0 \\ \end{aligned} $$
(27)

Based in the assumption of quasi-stationary pandemic dynamics, we can derive the fractions of exposed and infected people:

$$ E\left( {t_{d} } \right) = \frac{\gamma }{\alpha }I\left( {t_{d} } \right) $$
(28)

The sum of the left side of Eq. (27) is

$$ \begin{aligned} & \beta_{0} S^{k + 1} \left( {t_{d} } \right)I\left( {t_{d} } \right) - \alpha E\left( {t_{d} } \right) + \alpha E\left( {t_{d} } \right) - \gamma I\left( {t_{d} } \right) = 0 \\ & \beta_{0} S^{k + 1} \left( {t_{d} } \right)I\left( {t_{d} } \right) - \gamma I\left( {t_{d} } \right) = 0 \\ & S\left( {t_{d} } \right) = \sqrt[{k + 1}]{{\frac{\gamma }{{\beta_{0} }}}} \\ \end{aligned} $$
(29)

The dynamics of the pandemic deceleration stage comprise a system of differential equations (Eq. 4) and initial conditions depending on the parameters

$$ \begin{aligned} S\left( {t_{d} } \right) & = \sqrt[{k + 1}]{{\frac{\gamma }{{\beta_{0} }}}} \\ R\left( {t_{d} } \right) & = \left( {1 - S\left( {t_{d} } \right)} \right)\left( {1 - I_{d} } \right) \\ E\left( {t_{d} } \right) & = \left( {1 - S\left( {t_{d} } \right) - R\left( {t_{d} } \right)} \right)\frac{\gamma }{\gamma + \alpha } \\ I\left( {t_{d} } \right) & = \left( {1 - S\left( {t_{d} } \right) - R\left( {t_{d} } \right)} \right)\frac{\alpha }{\gamma + \alpha }, \\ \end{aligned} $$
(30)

where k is the coefficient of stratification of infection vulnerability and Id is the fraction of infected and exposed at the start of deceleration phase.

Peak value is out of scope of this model because it was reached prior to the deceleration stage. We can solve the system of differential Eqs. (4) with the initial conditions in (30) depending on parameters k and Id.

The following parameter values can be used for modelling: \(\beta_0.15, \alpha=0.2, \gamma=0.1\)

In order to analyse tendencies of the deceleration stage, a cumulative deceleration infection ratio in following form can be used:

$$ I_{cdr} = \mathop {\lim }\limits_{t \to \infty } \frac{{S\left( {t_{d} } \right) - S\left( t \right)}}{1 - S\left( t \right)} $$
(31)

The nominator of expression under limit represents the fraction of the population that has been infected during the deceleration stage, and the denominator represents the fraction of the population infected prior to the deceleration stage. The results of modelling are shown in Fig. 10.

Fig. 10
figure 10

Relationship between the cumulative deceleration infection ratio and summary fractions of infected and exposed individuals at the start of this stage

Full size image

Figure 10 demonstrates, that the fraction of infected population can be substantially reduced by lowering the fraction of actively infected individuals at the start of the deceleration stage. The blue line ‘100%’ represents the limiting case when all people who are not susceptible are either exposed or infected (none removed). This case is not realistic; rather, it represents the theoretical upper bound. The red line ‘10%’ is the best match for the results of modelling presented in Table 3. Other lines evince the potential of further decreasing the number of infected people during the deceleration phase.

Coefficient of infection vulnerability stratification k does not have a substantial impact on the deceleration infection ratio, particularly when the fractions of infected and exposed are not high at the start of deceleration. On other hand, a high value of k reduces the cumulative fraction of infected population; therefore, when \(I_{cdr}\) does not change, it tends to lead to a proportional decrease in the total number of infected.

This section has presented an analysis of the relationship between the duration and intensity of preventive measures and the total fraction of infected people. Weak preventive measures have little-to-no effect, whereas excessively strict measures temporarily reduce the fraction of active infected; however, the epidemic will eventually resume. The highest effectiveness is achieved by implementing moderate long-term measures, which reduce the fraction of active infected population at the moment when R0 becomes less than 1 due to vulnerability stratification. We have shown that decreasing the fraction of the infected and exposed population by the start of deceleration helps to reduce the total number of infected individuals.

5 Conclusion

In this paper, we have proposed a modified SEIR model to analyse the dynamics of the COVID-19 pandemic and investigate how the model’s parameters affect those dynamics of s well as control strategies. A modified SEIR model with discrete time was used to model the effect of vulnerability estimation in combination with preventive measures. Our proposed model shows that ignoring preventing safety measures such as social distancing, frequent hand washing, mask wearing and non-essential travel has devastating effect on those who are most susceptible to the COVID-19 virus. Even if total elimination of the virus is currently impossible, the total number of infected people can be reduced during the deceleration stage. Our findings show a positive relationship between the cumulative deceleration infection ratio and summary fractions of infected and exposed individual at the start of pandemic deceleration. As we have shown, variations in vulnerability stratification did not impact the dynamics of the initial stage of the pandemic; however, the virus propagation rate decreases after the people most vulnerable to it have been infected. This factor cannot be predicted at the start of a pandemic; however, it has a significant impact on infection rates during later stages. Based on infection vulnerability stratification, we demonstrate effects brought by the fraction of infected persons in the population at the start of pandemic deceleration on the cumulative fraction of the infected population. We interestingly show that moderate and long-lasting preventive measures are more effective than more rigid measures, which tend to be eventually loosened or abandoned due to economic losses, delay the peak of infection and fail to reduce the total number of cases.

R0 values were calculated using statistical data on the number of COVID-19 cases in the U.S., Russia, Turkey, Germany, France, U.K., Italy, and Spain. The high value of the basic reproduction index during the initial stages of the pandemic was attributed to underdeveloped diagnostics and knowledge of the virus, which resulted in an exploding of number of infections, the underestimation of the number of cases, and the overestimation of R0. Those high R0 values caused panic worldwide when used in basic SEIR models, which projected that the virus would affect more than 50% of the world’s population. Classical SEIR models usually provide pessimistic predictions. Calculations using a SEIR model with vulnerability stratification showed that the maximum positive effects can be achieved with long-lasting but moderate measures. Overly strict measures, which can reduce the basic reproduction index below 1; however, these are often economically untenable, and there is nothing to prevent a resurgence of infections after they are eventually lifted.

We anticipate that a second, more severe wave of the novel coronavirus is likely to occur in the fall and winter of 2020. Therefore, it is critical for us to prepare for that wave in advance. Government and health agencies can use our results to limit the resurgence of COVID-19 and to inform future decision-making to prevent further devastation. In this research, we looked at the problem from mathematical modelling perspective and investigated several conditions. The least squares method was used to calculate the vulnerability stratification coefficients of eight countries, and negative coefficients in Germany, Spain, France, and Italy were related to infection rate increases due to the loosening of preventive measures and other external factors. Our findings indicate the possibility of a second wave of the pandemic in those countries. The vulnerability stratification coefficients in the U.S. and U.K. were found to be near zero, thereby suggesting the possibility of either a second wave or a slowing down of infection propagation in those countries. Russia and Turkey evinced higher positive coefficients and are deemed to be the country’s most likely to experience slowdowns.

The main limitation of this study is the lack of data with which to evaluate the statistical significance of factors impacting pandemic dynamics. Changes in seasonal infection rates, the effects of preventive measures, and infection vulnerability stratification cannot be distinguished because related data are only available for a single year. In addition, the number of cases recorded depends on criteria for who is tested for coronavirus, which varies across countries. Future research will be based on new data of R0 dynamics; which may enable us to better distinguish the effects of restrictions and other factors.