Inverse problem in ionospheric science: prediction of solar soft-X-ray spectrum from very low frequency radiosonde results

Abstract

X-rays and gamma-rays from astronomical sources such as solar flares are mostly absorbed by the Earth’s atmosphere. Resulting electron-ion production rate as a function of height depends on the intensity and wavelength of the injected spectrum and therefore the effects vary from one source to another. In other words, the ion density vs. altitude profile has the imprint of the incident photon spectrum. In this paper, we investigate whether we can invert the problem uniquely by deconvolution of the VLF amplitude signal to obtain the details of the injected spectrum. We find that it is possible to do this up to a certain accuracy. This leads us to the possibility of uninterrupted observation of X-ray photon spectra of solar flares that are often hindered by the restricted observation window of space satellites to avoid charge particle damages. Such continuous means of observation are essential in deriving information on time evolution of physical processes related to electron acceleration and interaction with plasma in solar atmosphere. Our method is useful to carry out a similar exercise to infer the spectra of more energetic events such as the Gamma Ray Bursts (GRBs), Soft Gamma-ray Repeaters (SGRs) etc., by probing even the lower part of the Earth’s atmosphere. We thus show that to certain extent, the Earth’s atmosphere could be used as a gigantic detector of relatively strong astronomical events.

Appendices

Appendix A: Observation limit and accuracy of spectra

In this section we estimate the accuracy with which we can estimate a spectrum of a solar flare in the range of our interest with the VLF observation of ionospheric modulation. The limit on accuracy is imposed by the minimum precision of the observed VLF data. This calculation is significant in two ways: first, it imposes an error bar on the calculated spectra and second, which is more important, it is equivalent to the resolving power of the assumed ionosphere-detector, (with VLF response analysis as read out mechanism) i.e., the resolution or minimum difference in spectral features that the detector can measure.

Since LWPC follows the Mode theory of VLF wave propagation in Earth-ionosphere waveguide, we adopt the calculations from this theory. For the propagation of VLF in the curved path between the Earth’s ionosphere and ground and assuming a uniform height along the path the vertical electric field strength between a vertical transmitter and receiver is given by (Wait 1960),

$$ (E = E_{0} W ), $$

(12)

where

$$\begin{aligned} \begin{aligned}[b] W &= \biggl(\frac{\frac{d}{a}}{\sin (\frac{d}{a})}\biggr)^{\frac{1}{2}} \biggl(\frac{d}{\lambda}\biggr)^{\frac{1}{2}} \frac{\lambda}{h}e^{i(\frac {2\pi d}{\lambda} - \frac{\pi}{4})} \\ &\quad {}\times\sum_{n=0}^{\infty}\varLambda_{n} G_{n} e^{-i2\pi\frac{C_{n}^{2}}{2}(\frac{d}{\lambda})} . \end{aligned} \end{aligned}$$

(13)

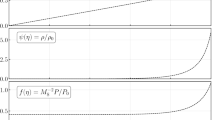
Here, $E_{0}$ is the field of the source at a great-circle distance $d$ in a flat perfectly conducting earth, $a$ is the radius of the Earth, $h$ is the height of the lower edge of the ionosphere and $\lambda$ is the free-space VLF wavelength. $\varLambda_{n}$ is the coupling excitation factor between VLF transmitter and different modes. $G_{n}$ represents the height gain factor at this wavelength and is normalized to 1 at the ground and $C_{n}$ is the cosine of angle of incidence of $n$th wave mode in the lower ionospheric layer.

The square of the amplitude of the field at the receiver can be written as

$$\begin{aligned} \bigl|W^{2}\bigr| \sim\biggl(\frac{\frac{d}{a}}{\sin (\frac{d}{a})}\biggr) \frac{d}{\lambda} \biggl(\frac{\lambda}{h}\biggr)^{2}\sum_{n=1}^{\infty} \sum_{m=1}^{\infty} e^{-i\frac{k}{2}(C_{n}^{2} - C_{m}^{*2})d}. \end{aligned}$$

(14)

The VLF signal received, i.e., the value of the power intensity averaged over width of the waveguide is obtained from $|\overline{E}^{2}| = |E_{0}^{2}||\overline{W}^{2}|$, where

$$\begin{aligned} \bigl|\overline{W}^{2}\bigr| &= \frac{1}{h} \int_{0}^{h} \bigl|W^{2} \bigr|dh \\ &= \biggl( \frac{\frac{d}{a}}{\sin (\frac{d}{a})}\biggr) \frac{d}{\lambda} \biggl(\frac{\lambda}{h} \biggr)^{2}\sum_{n=1}^{\infty}e^{-i\frac{k}{2}(C_{n}^{2} - C_{n}^{*2})d}. \end{aligned}$$

(15)

Noting

$$ C_{n}^{2} -C_{n}^{*2} = k\operatorname{Im} C_{n}^{2} , $$

(16)

assuming large distance (where very few (∼1) waveguide mode persist) and replacing $C_{n}$ by $C$ we have

$$\begin{aligned} \bigl|\overline{W}^{2}\bigr| \sim\frac{\frac{d}{a}}{\sin (\frac {d}{a})} \frac{d}{\lambda} \biggl(\frac{\lambda}{h}\biggr)^{2}e^{-\alpha d} e^{-(2G)^{\frac{1}{2}} \frac{d}{h}} , \end{aligned}$$

(17)

where

$$\begin{aligned} \alpha= k \operatorname{Im} \frac{C^{2}}{2} , \end{aligned}$$

(18)

and

$$\begin{aligned} G = \frac{\epsilon\omega}{\delta_{g} + i\epsilon_{g}\omega}, \end{aligned}$$

(19)

where, the $\epsilon$ and $\epsilon_{g}$ correspond to the dielectric constant of the lower ionosphere and ground respectively, $\delta_{g}$ is the ground conductivity and $\omega$ is the wave angular frequency (Wait and Spies 1964).

If the VLF signal amplitude corresponding to the ambient and flare conditions are $V_{a}$ and $V_{f}$ respectively, then the difference

$$\begin{aligned} \Delta V = V_{f} - V_{a} \approx20 \times2.3 \times \ln\biggl(\frac{\overline{W}_{f}^{2}}{\overline{W}_{a}^{2}}\biggr), \end{aligned}$$

(20)

where, $\overline{W}_{a}$ and $\overline{W}_{f}$ are the average power intensity during ambient and flare conditions.

From Eq. (17) we have,

$$\begin{aligned} \Delta V &\approx46.0 \times\biggl[2\biggl(\ln\frac{h_{1}}{h_{2}} \biggr) \\ &\quad {}+ \biggl(\frac{1}{h_{2}} - \frac{1}{h_{1}}\biggr) \bigl(2Gd^{2}\bigr)^{\frac{1}{2}} - (\alpha_{2} - \alpha_{1})d\biggr]. \end{aligned}$$

(21)

The above theory is for an assumed sharply bounded ionosphere, the effect of exponential variation of ionospheric conductivity can be included through the modification of the attenuation rate parameter $\alpha$. For VLF wave mode propagation the amplitude part of the mode resonance equation reads as

$$ e^{(-2d\alpha)} = |R_{i}||R_{g}| $$

(22)

where $R_{i}$ is the reflection coefficient of the lowest layer of the ionosphere and $R_{g}$ is that of the ground.

If $R_{i2}$ and $R_{i1}$ are the ionospheric reflection coefficients during the disturbed and ambient conditions respectively and corresponding attenuation coefficients are $\alpha_{2}$ and $\alpha_{1}$ respectively, then

$$ \alpha_{2} - \alpha_{1} = -\frac{1}{2d} \ln\bigg|\frac {|R_{i2}|}{|R_{i1}|}. $$

(23)

For lower D region the effective dielectric constant of the medium can be approximated by an exponential function, such that the relative permittivity can be put in the form (Wait and Walter 1963),

$$ K(h) = K_{0}\biggl(1-i\frac{1}{L}e^{\beta h}\biggr) , $$

(24)

where, $K_{0}$ is the reference permittivity and $L$ is a constant. The parameter $\beta$ is known as the conductivity gradient of the ionosphere and is given by

$$ \beta= 2.3 \frac{\log (\frac{\sigma}{\sigma_{0}})}{(h - h_{0})}, $$

(25)

where $\sigma$ and $\sigma_{0}$ are the conductivity at height $h$ and a reference height $h_{0}$ respectively. Then it can be shown that the amplitude of the reflection coefficient for $n$th mode for any type of polarization can roughly be expressed in the form,

$$ \bigl(|R_{i}|= e^{(-\frac{2\pi^{2}}{\lambda_{0} \beta}C)} \bigr). $$

(26)

From Eq. (23) and Eq. (26) we can see that

$$ \alpha_{2} - \alpha_{1} = \frac{\pi^{2}}{\lambda_{0} d C}\biggl( \frac {1}{\beta_{2}} - \frac{1}{\beta_{1}}\biggr). $$

(27)

Putting in Eq. (21) we get

$$\begin{aligned} \Delta V &\approx46 \times \biggl[2\biggl(\ln \frac{h_{1}}{h_{2}}\biggr) + \biggl(\frac{1}{h_{2}} - \frac{1}{h_{1}}\biggr) \bigl(2Gd^{2} \bigr)^{\frac{1}{2}} \\ &\quad {}- \frac{\pi ^{2}}{\lambda_{0} C}\biggl(\frac{1}{\beta_{2}} - \frac{1}{\beta_{1}}\biggr)\biggr]. \end{aligned}$$

(28)

In the process of finding the parameters $h^{\prime}$ and $\beta$ from VLF observation (Section, 3) during disturbed condition uncertainty may appear in the values of the parameters. So replacing $\beta_{2}$ by $\beta$ and $h_{2}$ by $h^{\prime}$ and taking the differential we get

$$\begin{aligned} 2\delta(\Delta V) \approx46 \times \biggl[\biggl(-\frac{2}{h^{\prime}} - \frac{(2Gd^{2})^{\frac{1}{2}}}{h^{\prime2}}\biggr) \delta h^{\prime}+ \frac{\pi ^{2}}{\lambda_{0} C} \frac{1}{\beta^{2}}\delta\beta\biggr]. \end{aligned}$$

(29)

The factor of 2 in the left hand side of the equation appears due to the fact that error or uncertainty may appear during the observational measurements of the VLF signal for both ambient and flare situations. In our case the minimum precision, i.e., the maximum error with which we can observe the VLF signal is $\delta(\Delta V) =0.1~\mbox{dB}$. The maximum uncertainty in $h^{\prime}$ and $\beta$ i.e., $\delta h^{\prime}$ and $\delta\beta$ can be calculated by putting the remaining terms equal to zero for each case.

Now taking logarithm and then differential of Eq. (11) we get

$$\frac{\delta N_{e}}{N_{e}} = \bigl(h-h^{\prime}\bigr)d\beta+ (0.65 - \beta )\delta h^{\prime}$$

or

$$ (\delta N_{e} = \gamma N_{e} ). $$

(30)

Putting the maximum uncertainties in the values of calculated parameters obtained from Eq. (29) in Eq. (30) we can find the maximum uncertainty in the calculated electron density as a function of height.

Now taking differential of Eq. (4) and substituting the value of $\delta N_{e}$ from Eq. (30) we have

$$ \delta q = \int\delta I_{0}(\nu, t)f(h, \nu)d\nu= \gamma(1+ \lambda) \biggl(\frac{dN_{e}}{dt} + 2\alpha N_{e}^{2}\biggr). $$

(31)

The quantity $\delta I_{0}(\nu, t)$ can be calculated with the iterative maximum likelihood method as described in Sect. 2.2. Two error bars can be put to the calculated spectra by adding and subtracting the values of $\delta I_{0}(\nu, t)$ with the calculated $I_{0}(\nu, t)$ values. With the value of $d = 5690~\mbox{km}$, calculated value of $G = 4.6 \times 10^{-4}$, $\lambda_{0} = 15~\mbox{km}$, $C \sim 0.1$ and corresponding values of $h^{\prime}$ and $\beta$ for the flares we find the values of $\gamma$ for the M and the X-class flares are respectively $1.1\times10^{-2}$ and $0.9\times10^{-2}$. The error bars calculated with these values from Eq. (31) are plotted in Fig. 5 with the corresponding calculated spectra.

Appendix B: Deconvolution using radial basis function decomposition

Clearly the basis functions described in Sect. 2.2 are not regular and orthogonal. We can approach this problem in a different way by choosing a set of appropriate radial basis functions since it can be shown that any continuous function on a compact interval can in principle be interpolated with arbitrary accuracy by a sum of these well behaved functions (Orr 1996).

Let us divide the height of consideration (60–80 km) into $N$ equal intervals. We choose $N$ Gaussian functions centered at the midpoint ($h_{n}$s) of those $N$ intervals as our radial basis functions. So the $n$th radial basis function has the form

$$ \phi= e^{\frac{-|h - h_{n}|}{2\sigma^{2}}}. $$

(32)

We divide the whole range of spectrum (say 1–100 keV) in $M$ separate intervals. We can write each of our original basis as linear combination of the radial basis functions, so that

$$ f(h,\nu_{m}) = \sum_{n} a_{nm}\phi_{n} , $$

(33)

where $\nu_{m}$ corresponds to the $m$th interval in photon energy. We calculate the coefficients $a_{nm}$ by matrix inversion method (for example, see Broomhead and Lowe 1988). Let us assume $a_{nm}$s form a matrix ($A$) of dimension $n \times m$. As each of the actual basis functions have their major contribution at different altitudes (as they are centered at different heights) the column vectors of matrix $A$ are clearly linearly independent. So the matrix $A$ is invertible.

Now the middle part of Eq. (4) at time ‘$t$’ can be written as

$$\begin{aligned} \int I_{0}(\nu, t)f(h, \nu)d\nu&= \sum _{m} I_{0m}\sum_{n} a_{nm}\phi _{n}, \\ &= \sum_{m} \sum_{n} I_{0m} a_{nm}\phi_{n}, \\ &= \sum_{n} \biggl(\sum _{m} a_{nm}I_{0m}\biggr) \phi_{n}. \end{aligned}$$

(34)

Similarly, we expand the left hand side of Eq. (4) at the same time with the radial Gaussian basis functions:

$$ q(h,t) = \sum_{n} q_{n} \phi_{n} . $$

(35)

Comparing Eq. (34) and Eq. (35) we have

$$ \sum_{n} a_{nm} I_{0m} = q_{n}. $$

(36)

This is a matrix equation, which can be written as

$$ AI_{0} = Q . $$

(37)

Inversion of this equation

$$ I_{0} = A^{-1}Q $$

(38)

gives the spectrum at the time of consideration.

This deconvolution method is an one step (matrix inversion) process and the existence of unique deconvolution is highly sensitive to the exact evaluation of the basis functions and the values of the parameters, namely $\alpha$ and $\lambda$. On the other hand, the method described in Sect. 2.3 is similar to an iterative spectrum fitting process and gives a result irrespective of variation (even large) of the parameter and basis values.