Abstract
The purpose of this work is to evaluate the effect of deformation inertia on tide dynamics, particularly within the context of the tide response equations proposed independently by Boué et al. (Celest Mech Dyn Astron 126:31–60, 2016) and Ragazzo and Ruiz (Celest Mech Dyn Astron 128(1):19–59, 2017). The singular limit as the inertia tends to zero is analyzed, and equations for the small inertia regime are proposed. The analysis of Love numbers shows that, independently of the rheology, deformation inertia can be neglected if the tide-forcing frequency is much smaller than the frequency of small oscillations of an ideal body made of a perfect (inviscid) fluid with the same inertial and gravitational properties of the original body. Finally, numerical integration of the full set of equations, which couples tide, spin and orbit, is used to evaluate the effect of inertia on the overall motion. The results are consistent with those obtained from the Love number analysis. The conclusion is that, from the point of view of orbital evolution of celestial bodies, deformation inertia can be safely neglected. (Exceptions may occur when a higher-order harmonic of the tide forcing has a high amplitude.)

















Similar content being viewed by others
Notes
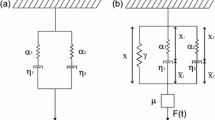
In order to understand this claim, it is enough to analyze the one degree of freedom harmonic oscillator \(\mu \ddot{x}+\eta \dot{x}+\gamma x=\cos (\omega t)\), with solution \(x(t)=a\cos (\omega t)-b\sin (\omega t)\), where \(a+ib\) plays the role of the Love number. Multiplying both sides of the equation by x and time-averaging gives \(\lim _{T\rightarrow \infty }\frac{1}{T}\int _0^T \cos (\omega t) x(t)\hbox {d}t=\frac{a}{2} =\lim _{T\rightarrow \infty }\frac{1}{T}\int _0^T [-\mu \dot{x}^2(t)+\gamma x^2(t)]\hbox {d}t\) that is the time-average balance of kinetic and potential energy. This same reasoning applied to the linear equations of tide dynamics, equation (47) in Ragazzo and Ruiz (2017), shows that the time-average tidal balance of energy is proportional to the real part of the Love number.
The value of \(\gamma /\gamma _{\,\mathrm I}\) for the Sun given in Table 1 does not coincide with that given in Ragazzo and Ruiz (2015). The value \({\mathrm{I}_\circ }/mR^2=0.059\) used in Ragazzo and Ruiz (2015) was taken from Yoder (1995, p. 26). The value \({\mathrm{I}_\circ }/mR^2=0.070\) used here is taken from https://nssdc.gsfc.nasa.gov/planetary/factsheet/sunfact.html. Using \({\mathrm{I}_\circ }/mR^2=0.070\), the new value of \(\gamma \) for the Sun is \(\gamma = 3.668\times 10^{-6}\,\mathrm{s}\).
These high-frequency oscillations are the source of difficulty for the numerical integration of the full equations of motion. The small inertia approximation in “Appendix” smooths out these oscillations by means of an averaging.
References
Antognini, F., Biasco, L., Chierchia, L.: The spin–orbit resonances of the Solar system: a mathematical treatment matching physical data. J Nonlinear Sci. 24, 473–492 (2014)
Bambusi, D., Haus, E.: Asymptotic behavior of an elastic satellite with internal friction. Math. Phys. Anal. Geom. 18(1), 1–18 (2015)
Bland, D.: Linear Viscoelasticity. Pergamon Press, Oxford (1960)
Boué, G., Correia, A.C.M., Laskar, J.: Complete spin and orbital evolution of close-in bodies using a Maxwell viscoelastic rheology. Celest. Mech. Dyn. Astron. 126, 31–60 (2016)
Celletti, A.: Analysis of resonances in the spin–orbit problem in celestial mechanics: the synchronous resonance (Part I). J. Appl. Math. Phys. (ZAMP) 41, 174–204 (1990)
Chandrasekhar, S.: Ellipsoidal Figures of Equilibrium. Dover, New York (1987)
Correia, A.C.M., Boué, G., Laskar, J., Rodríguez, A.: Deformation and tidal evolution of close-in planets and satellites using a Maxwell viscoelastic rheology. Astron. Astrophys. 571, A50 (2014)
Efroimsky, M.: Bodily tides near spin–orbit resonances. Celest. Mech. Dyn. Astron. 112(3), 283–330 (2012)
Efroimsky, M., Williams, J.G.: Tidal torques: a critical review of some techniques. Celest. Mech. Dyn. Astron. 104, 257–289 (2009)
Ferraz-Mello, S.: Tidal synchronization of close-in satellites and exoplanets. A rhephysical approach. Celest. Mech. Dyn. Astron. 116, 109–140 (2013)
Hale, J.K.: Ordinary Differential Equations, 2nd edn. Robert E. Krieger Publishing Company, New York (1980)
Kaper, T.J.: Systems theory for singular perturbation problems. In: Analyzing Multiscale Phenomena Using Singular Perturbation Methods: American Mathematical Society Short Course, vol. 56, Baltimore, MD, 5–6 Jan 1998 (1999)
Lamb, H.: Hydrodynamics, 6th edn. Cambridge Mathematical Library, Cambridge (1932)
Love, A.E.H.: Some Problems of Geodynamics: Being an Essay to which the Adams Prize in the University of Cambridge was Adjudged in 1911. CUP Archive (1911)
Mignard, F.: The evolution of the lunar orbit revisited I. Moon Planets 20, 301–315 (1979)
Munk, W., MacDonald, G.: The Rotation of the Earth. Cambridge University Press, New York (1960)
Nishida, K.: Earth’s background free oscillations. Annu. Rev. Earth Planet. Sci. 41, 719–740 (2013)
Petit, G., Luzum, B.: IERS Conventions. Technical report, DTIC Document (2010)
Ragazzo, C., Ruiz, L.: Dynamics of an isolated, viscoelastic, self-gravitating body. Celest. Mech. Dyn. Astron. 122(4), 303–332 (2015)
Ragazzo, C., Ruiz, L.: Viscoelastic tides: models for use in celestial mechanics. Celest. Mech. Dyn. Astron. 128(1), 19–59 (2017)
Ray, R.D., Eanes, R.J., Lemoine, F.G.: Constraints on energy dissipation in the Earth’s body tide from satellite tracking and altimetry. Geophys. J Int. 144, 471–480 (2001)
Rochester, M.G., Smylie, D.E.: On changes in the trace of the Earth’s inertia tensor. J. Geophys. Res. 79, 4948–4951 (1974)
Sanders, J.A., Verhulst, F., Murdock, J.A.: Averaging Methods in Nonlinear Dynamical Systems, vol. 59. Springer, New York (2007)
Williams, J.G., Boggs, D.H., Yoder, C.F., Todd Ratcliff, J., Dickey, J.O.: Lunar rotational dissipation in solid body and molten core. J. Geophys. Res. 106, 933–968 (2001)
Wisdom, J., Meyer, J.: Dynamic elastic tides. Celest. Mech. Dyn. Astron. 126, 1–30 (2016)
Yoder, C.: Astrometric and geodetic properties of Earth and the Solar System. In: Ahrens, T.J. (ed.) Global Earth Physics: A Handbook of Physical Constants, vol. 1, pp. 1–31. American Geophysical Union, Washington (1995)
Zlenko, A.A.: A celestial-mechanical model for the tidal evolution of the Earth–Moon system treated as a double planet. Astron. Rep. 59, 72–87 (2014)
Acknowledgements
We are grateful to Sylvio Ferraz Mello for having called our attention to the work of Love about the effect of inertia on tides. We also thank Yeva Gevorgyan who first pointed out the equivalence between the Association Principle and the Correspondence Principle in the frequency domain. C.R. is partially supported by FAPESP 2016/25053-8. A.C. is partially supported by CIDMA strategic project (UID/MAT/04106/2013), ENGAGE SKA (POCI-01-0145-FEDER-022217), and PHOBOS (POCI-01-0145-FEDER-029932), funded by COMPETE 2020 and FCT, Portugal.
Author information
Authors and Affiliations
Corresponding author
Additional information
This article is part of the topical collection on Recent advances in the study of the dynamics of N-body problem.
Guest Editors: Giovanni Federico Gronchi, Ugo Locatelli, Giuseppe Pucacco and Alessandra Celletti.
Appendix: The small inertia limit for the Maxwell oscillator
Appendix: The small inertia limit for the Maxwell oscillator
In this appendix, we apply three steps of averaging to the Maxwell oscillator in Eq. (3) that can be written as (see Eq. 49):
or
Let \(t=s\tau _4\) define a nondimensional time s, where \(\tau _4=\sqrt{\mu /(\alpha +\gamma )}\), and \(x^\prime (s)=\frac{\hbox {d}}{\hbox {d}s}x(s)\). Then in the nondimensional time scale the equation for the Maxwell oscillator becomes
where
Using the definitions
and \(\tau _3=\eta /\gamma \), the third-order equation can be written as
This equation can be explicitly solved when \(\varepsilon =0\). The solution motivates the change of variables \((u,v,w,t)\rightarrow (p,q,w,t)\) where
In the new variables, the equation becomes
Using the definitions
this equation can be written as
The following change of variables \((z,w,t)\rightarrow (y,w,t)\) was obtained after two steps of averaging Hale (1980),
Applying this change of variables, using \(\varGamma ^\prime =\sqrt{\varepsilon \frac{\tau _1}{\tau _2}}(\xi ^\prime \cdot z+\frac{\alpha }{\gamma }\varLambda )\) and \(\varLambda ^\prime =\{-\varGamma ^\prime +\sqrt{\varepsilon \frac{\tau _1}{\tau _2}}\tau _2^2\frac{\gamma }{\alpha }\ddot{H}\}\frac{\gamma }{\alpha }\), and averaging the resulting equations we obtain, after a long computation,
In the original time t, and neglecting the correction term, these equations become
The second of these equations implies the first equation in (27).
Notice that \(|y(t)|\rightarrow 0\) as \(t\rightarrow \infty \), so after some transient where |y(t)| decay as \(\exp [-t\tau _3/(2\tau _1\tau _2)]\) Eq. (62) implies
This and the relation \(x=w-v=w+\sin (s)p-\cos (s) q=w-\xi ^\prime (s)\cdot z\) imply
This equation plus the definition of \(\varLambda \) in Eq. (62) implies the second equation in (27).
Rights and permissions
About this article
Cite this article
Correia, A.C.M., Ragazzo, C. & Ruiz, L.S. The effects of deformation inertia (kinetic energy) in the orbital and spin evolution of close-in bodies. Celest Mech Dyn Astr 130, 51 (2018). https://doi.org/10.1007/s10569-018-9847-3
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10569-018-9847-3