Ritter’s dry-bed dam-break flows: positive and negative wave dynamics

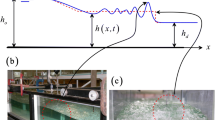
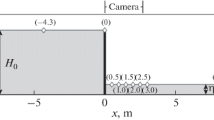
Abstract

Dam-break flood waves are associated with major environmental disasters provoked by the sudden release of water stored in reservoirs. Ritter found in 1892 an analytical solution to the wave structure of an ideal fluid released during an instantaneous dam failure, propagating over initially dry horizontal terrain. This solution, though ideal, hence frictionless, is widely used to test numerical solutions of the Shallow Water Equations (SWE), and as educational tool in courses of fluid mechanics, given that it is a peculiar case of the Riemann problem. However, the real wave structure observed experimentally differs in a major portion of the wave profile, including the positive and negative fronts. Given the importance of an accurate prediction of the dam break wave, the positive and negative wave portions originating from the breaking of a dam with initially dry land on the tailwater reach are revisited in this work. First, the propagation features of the dry-front are investigated using an analytical boundary-layer type model (Whitham/Dressler/Chanson model) constructed matching an (outer) inviscid dynamic wave to an (inner) viscous diffusive wave. The analytical solution is evaluated using an accurate numerical solution of the SWE produced using the MUSCL-Hancock finite-volume method, which is tested independently obtaining the solution based on the discontinuous Galerkin finite-element method. The propagation features of the negative wave are poorly reproduced by the SWE during the initial stages of dam break flows, and, thus, are then investigated using the Serre–Green–Naghdi equations for weakly-dispersive fully non-linear water waves, which are solved using a finite volume-finite difference scheme.

Appendices

Appendix 1: damping model for dispersive terms in Serre–Green–Naghdi equations

Current parametrizations of wave breaking are based on the assumption that the energy dissipation is adequately accounted for by the Rankine–Hugoniot jump conditions of shocks [52,53,54]. Therefore, a Boussinesq + Saint Venant matching approach is adopted. Basically, the wave profile is computed solving the Boussinesq-type equations and, after each time step, a wave breaking criteria is checked in the computational domain. In those cells marked as breaking, the dispersive terms are switched off (equivalent to setting ε = 0), and the SWE are solved there. Other wave-breaking models can be adopted, like the classical diffusive model extensively validated by Cienfuegos et al. [55] or the recent development by Tissier et al. [56]. The wave breaking model proposed by Hosoda and Tada [39] and Hosoda et al. [40], is, however, less known, despite its simplicity and good performance. The idea behind this parametrization is identical to that developed by Tonelli and Petti [41] in the sense that Boussinesq equations are “substituted” by the SWE at breaking cells. However, rather that producing a full (sharp) transition from Boussinesq to the SWE at breaking nodes, they proposed a gradual damping of the dispersive terms when the threshold criteria of wave breaking is exceeded. The method is as simple to implement as that of Tonelli and Petti [41], and permits a very stable behavior of the numerical computations. Below, the physical background of the method is explained.

The idea is to attenuate the dispersive terms of the Serre–Green–Naghdi equations if the local free surface slope exceeds a threshold value. To produce a gradual damping of dispersive terms Hosoda and Tada [39] and Hosoda et al. [40] proposed an exponential attenuation given by

$$ \varepsilon = \left\{ {\begin{array}{*{20}l} {\exp \left[ { - \varsigma \left( {\left| {\frac{\partial h}{\partial x}} \right| - \left| {\frac{\partial h}{\partial x}} \right|_{cr} } \right)} \right]} \hfill & {{\text{if }}{\kern 1pt} \quad \left| {\frac{\partial h}{\partial x}} \right| > \left| {\frac{\partial h}{\partial x}} \right|_{cr} } \hfill \\ 1 \hfill & {\text{else}} \hfill \\ \end{array} } \right., $$

(48)

A calibration parameter ς is introduced, and (∂h/∂x) _cr is the threshold value of the free surface slope above which wave breaking is initiated. This value was determined using the solitary wave as conceptual model, given that it is a particular solution of the Serre–Green–Naghdi equations. The solitary wave profile (Fig. 15a) is given by [24]

$$ \frac{h}{{h_{1} }} = 1 + \left( {\text{F}_{1}^{2} - 1} \right){\text{sech}}^{2} \left[ {\frac{{\left( {3\text{F}_{1}^{2} - 3} \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} }}{{\text{F}_{1} }}\frac{x}{{2h_{1} }}} \right], $$

(49)

where h ₁ is the undisturbed water depth and F₁ the corresponding Froude number. The question is then: What is the maximum value of the free surface slope in a solitary wave for incipient wave breaking? Successive differentiation of Eq. (49) produces

$$ \frac{\partial h}{\partial x} = B{\text{sech}}^{2} \left( {Ax} \right)\tanh \left( {Ax} \right),\quad \frac{{\partial^{2} h}}{{\partial x^{2} }} = AB{\text{sech}}^{2} \left( {Ax} \right)\left[ {{\text{sech}}^{2} \left( {Ax} \right) - 2\tanh^{2} \left( {Ax} \right)} \right], $$

(50)

where

$$ A = \frac{{\left( {3\text{F}_{1}^{2} - 3} \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} }}{{2h_{1} \text{F}_{1} }} , { }B = - \left( {\text{F}_{1}^{2} - 1} \right)\frac{{\left( {3\text{F}_{1}^{2} - 3} \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} }}{{\text{F}_{1} }}. $$

(51)

Fig. 15

a Solitary wave profile, b evolution of damping factor in test of Fig. 9

The maximum free surface slope occurs at the inflection point I in Fig. 15a. Thus, setting ∂² h/∂x ² = 0 results in

$$ x_{I} = \frac{{\ln \left( {2 \pm 3^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} } \right)}}{2A}, $$

(52)

and, using this value of the x-coordinate, the free surface slope at the inflection point is

$$ \left( {\frac{\partial h}{\partial x}} \right)_{\hbox{max} } = B\frac{{12\left[ {\left( {{5 \mathord{\left/ {\vphantom {5 3}} \right. \kern-0pt} 3}} \right) - 3^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} } \right]}}{{\left( {3 - 3^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} } \right)^{3} }}. $$

(53)

Based on undular bore experimental data of Favre waves, the limiting supercritical Froude number for wave breaking F₁ = 1.25 was adopted [39, 40]. Thus, from Eq. (53) results

$$ \left| {\frac{\partial h}{\partial x}} \right|_{cr} = 0.225. $$

(54)

This slope is adopted as a threshold value above which wave breaking occurs due to the action of turbulence.

To illustrate the performance of Eq. (48), the test case presented in Fig. 9 is reconsidered in Fig. 15b, where ε = ε(x/h _o ) is plotted at T = 1.13 and 2.76. Note the low value of ε just after the dam break, given that the damping model is activated by the upstream vertical water depth just as soon as computations are initiated. Its action is gradually reduced in magnitude and spatial extension as the wave evolves, given the reduction of the free surface slopes. For the remaining computational snapshots presented in Fig. 9 (e.g. T = 3.88, 5.01 and 6.64) the damping model is never activated (ε = 1).

Appendix 2: Ritter’s original work

In this appendix we reprint two original figures from Ritter [6], given their interest for educational purposes. In Fig. 16 we observe the original parabolic profile sketched by Ritter. The quantity (ga)^1/2 is denoted by U _o , and the celerity of the dry and backward fronts are clearly indicated. The initial water depth in the dam is a, and the critical water depth at the dam axis is (4/9)a.

Fig. 16

Parabolic wave solution by Ritter [6]

Ritter [6] noted that his parabolic profile was not in agreement with observations, and sketched a more realistic shape for the dam break curve, where all the profile has negative curvatures, as seen in Fig. 17.

Fig. 17

Parabolic wave solution and comparison with a more realistic shape for the dam break curve, after Ritter [6]