Skip to main content
SpringerLink
Log in

The State of Stress and Strain Adjacent to Notches in a New Class of Nonlinear Elastic Bodies

  • Published:
Journal of Elasticity Aims and scope Submit manuscript

Abstract

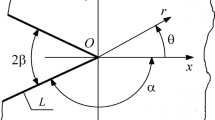
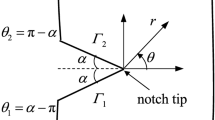
In this paper we study the deformation of a body with a notch subject to an anti-plane state of stress within the context of a new class of elastic models. These models stem as approximations of constitutive response functions for an elastic body that is defined within the context of an implicit constitutive relation between the stress and the deformation gradient. Gum metal and many metallic alloys are described well by such constitutive relations. We consider the state of anti-plane stress of a body with a smoothened V-notch within the context of constitutive relations for the linearized strain in terms of a power-law for the stretch. The problem is solved numerically and the convergence and the stability of the solution is studied.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

Notes

  1. Noll [42] later generalized the concept of his definition of a Simple Material but not to include implicit relationships. We shall not get into a discussion of the same here.

  2. Rajagopal [55] classified the material symmetry possessed by the sub-classes of bodies whose histories of the stress, deformation gradient, density, etc., are given in terms of an implicit constitutive relations.

  3. Bulíček et al. [7] study several mathematical aspects concerning strain limiting bodies.

  4. Since we consider constitutive relations of the type (4b), the anti-plane stress state is equivalent to the classical definition of anti-plane strain.

  5. We are not using the same model and obtaining two different sets of values for the material parameters under two loading conditions. The NLB and NLS models are two different models that provide equally good fits. We used different experiments to obtain the material parameters for the two different models. These different sets of values fit the data equally well for the both the experiments. Which of these two models better explains the response of the body can only be determined by having other experiments against which these models can be corroborated. Such experiments are not available at the present time.

References

  1. Alnæs, M., Blechta, J., Hake, J., Johansson, A., Kehlet, B., Logg, A., Richardson, C., Ring, J., Rognes, M.E., Wells, G.N.: The FEniCS project version 1.5. Arch. Numer. Softw. 3(100), 9–23 (2015). https://doi.org/10.11588/ans.2015.100.20553

    Article  Google Scholar 

  2. Beck, L., Bulíček, M., Málek, J., Süli, E.: On the existence of integrable solutions to nonlinear elliptic systems and variational problems with linear growth. Arch. Ration. Mech. Anal. 225(2), 717–769 (2017). https://doi.org/10.1007/s00205-017-1113-4

    Article  MathSciNet  MATH  Google Scholar 

  3. Blechta, J., Málek, J., Rajagopal, K.R.: On the classification of incompressible fluids (2019)

  4. Bonito, A., Girault, V., Süli, E.: Finite element approximation of a strain-limiting elastic model. arXiv:1805.04006 [math.NA] (2018)

  5. Bulíček, M., Gwiazda, P., Málek, J., Rajagopal, K.R., Świerczewska-Gwiazda, A.: On flows of fluids described by an implicit constitutive equation characterized by a maximal monotone graph. In: Robinson, J.C., Rodrigo, J.L., Sadowski, W. (eds.) Mathematical Aspects of Fluid Mechanics, pp. 23–51. Cambridge University Press, Cambridge (2012). https://doi.org/10.1017/cbo9781139235792.003

    Chapter  MATH  Google Scholar 

  6. Bulíček, M., Gwiazda, P., Málek, J., Świerczewska-Gwiazda, A.: On unsteady flows of implicitly constituted incompressible fluids. SIAM J. Math. Anal. 44(4), 2756–2801 (2012). https://doi.org/10.1137/110830289

    Article  MathSciNet  MATH  Google Scholar 

  7. Bulíček, M., Málek, J., Rajagopal, K.R., Süli, E.: On elastic solids with limiting small strain: modelling and analysis. EMS Surv. Math. Sci. 1(2), 283–332 (2014). https://doi.org/10.4171/emss/7

    Article  MathSciNet  MATH  Google Scholar 

  8. Bulíček, M., Gwiazda, P., Málek, J., Świerczewska-Gwiazda, A.: On steady flows of incompressible fluids with implicit power-law-like rheology. Adv. Calc. Var. 2(2), 109–136 (2009). https://doi.org/10.1515/ACV.2009.006

    Article  MathSciNet  MATH  Google Scholar 

  9. Bulíček, M., Gwiazda, P., Málek, J., Świerczewska-Gwiazda, A.: On scalar hyperbolic conservation laws with a discontinuous flux. Math. Models Methods Appl. Sci. 21(1), 89–113 (2011). https://doi.org/10.1142/S021820251100499X

    Article  MathSciNet  MATH  Google Scholar 

  10. Bulíček, M., Málek, J.: On unsteady internal flows of Bingham fluids subject to threshold slip on the impermeable boundary. In: Advances in Mathematical Fluid Mechanics, pp. 135–156. Birkhäuser, Basel (2016). https://doi.org/10.1007/978-3-0348-0939-9_8

    Chapter  Google Scholar 

  11. Bulíček, M., Málek, J.: Internal flows of incompressible fluids subject to stick-slip boundary conditions. Vietnam J. Math. 45(1–2), 207–220 (2017). https://doi.org/10.1007/s10013-016-0221-z

    Article  MathSciNet  MATH  Google Scholar 

  12. Bulíček, M., Málek, J., Rajagopal, K.R.: On Kelvin-Voigt model and its generalizations. Evol. Equ. Control Theory 1(1), 17–42 (2012). https://doi.org/10.3934/eect.2012.1.17

    Article  MathSciNet  MATH  Google Scholar 

  13. Bulíček, M., Málek, J., Rajagopal, K.R., Walton, J.: Existence of solutions for the anti-plane stress for a new class of “strain-limiting” elastic bodies. Calc. Var. Partial Differ. Equ. 54(2), 2115–2147 (2015). https://doi.org/10.1007/s00526-015-0859-5

    Article  MathSciNet  MATH  Google Scholar 

  14. Bulíček, M., Málek, J., Süli, E.: Analysis and approximation of a strain-limiting nonlinear elastic model. Math. Mech. Solids 20(1), 92–118 (2015). https://doi.org/10.1177/1081286514543601

    Article  MathSciNet  MATH  Google Scholar 

  15. Bustamante, R., Rajagopal, K.R.: On a new class of electroelastic bodies, I. Proc. R. Soc. A, Math. Phys. Eng. Sci. 469(2149), 20120521 (2012). https://doi.org/10.1098/rspa.2012.0521

    Article  ADS  MathSciNet  MATH  Google Scholar 

  16. Bustamante, R., Rajagopal, K.R.: On a new class of electro-elastic bodies, II: boundary value problems. Proc. R. Soc. A, Math. Phys. Eng. Sci. 469(2155), 20130106 (2013). https://doi.org/10.1098/rspa.2013.0106

    Article  ADS  MathSciNet  MATH  Google Scholar 

  17. Bustamante, R., Rajagopal, K.R.: Implicit constitutive relations for nonlinear magnetoelastic bodies. Proc. R. Soc. A, Math. Phys. Eng. Sci. 471(2175), 20140959 (2015). https://doi.org/10.1098/rspa.2014.0959

    Article  ADS  MathSciNet  MATH  Google Scholar 

  18. Cauchy, A.L.B.: Recherches sur l’équilibre et le mouvement intérieur des corps solides ou fluides, élastiques ou non élastiques. In: Bulletin de la Société Philomatique, pp. 9–13 (1823)

    Google Scholar 

  19. Coleman, B.D., Noll, W.: An approximation theorem for functionals, with applications in continuum mechanics. Arch. Ration. Mech. Anal. 6(1), 355–370 (1960)

    Article  MathSciNet  MATH  Google Scholar 

  20. COMSOL AB: Comsol multiphysics user’s guide. http://www.comsol.com (2008)

  21. Devendiran, V.K., Sandeep, R.K., Kannan, K., Rajagopal, K.R.: A thermodynamically consistent constitutive equation for describing the response exhibited by several alloys and the study of a meaningful physical problem. Int. J. Solids Struct. 108, 1–10 (2017). https://doi.org/10.1016/j.ijsolstr.2016.07.036

    Article  Google Scholar 

  22. Diening, L., Kreuzer, C., Süli, E.: Finite element approximation of steady flows of incompressible fluids with implicit power-law-like rheology. SIAM J. Numer. Anal. 51(2), 984–1015 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  23. Ebmeyer, C., Liu, S.W.: Quasi-norm interpolation error estimates for the piecewise linear finite element approximation of p-Laplacian problems. Numer. Math. 100(2), 233–258 (2005). https://doi.org/10.1007/s00211-005-0594-5

    Article  MathSciNet  MATH  Google Scholar 

  24. Feireisl, E., Liao, X., Málek, J.: Global weak solutions to a class of non-Newtonian compressible fluids. Math. Methods Appl. Sci. 38(16), 3482–3494 (2015). https://doi.org/10.1002/mma.3432

    Article  ADS  MathSciNet  MATH  Google Scholar 

  25. Gou, K., Mallikarjuna, M., Rajagopal, K.R., Walton, J.R.: Modeling fracture in the context of a strain-limiting theory of elasticity: a single plane-strain crack. Int. J. Eng. Sci. 88, 73–82 (2015). https://doi.org/10.1016/j.ijengsci.2014.04.018

    Article  MathSciNet  MATH  Google Scholar 

  26. Itou, H., Kovtunenko, V.A., Rajagopal, K.R.: Nonlinear elasticity with limiting small strain for cracks subject to non-penetration. Math. Mech. Solids (2016). https://doi.org/10.1177/1081286516632380

    Article  MATH  Google Scholar 

  27. Kreuzer, C., Süli, E.: Adaptive finite element approximation of steady flows of incompressible fluids with implicit power-law-like rheology. ESAIM: M2AN 50(5), 1333–1369 (2016). https://doi.org/10.1051/m2an/2015085

    Article  MathSciNet  MATH  Google Scholar 

  28. Kulvait, V., Málek, J., Rajagopal, K.R.: Anti-plane stress state of a plate with a V-notch for a new class of elastic solids. Int. J. Fract. 179(1–2), 59–73 (2013). https://doi.org/10.1007/s10704-012-9772-5

    Article  Google Scholar 

  29. Kulvait, V.: Mathematical analysis and computer simulations of deformation of nonlinear elastic bodies in the small strain range. PhD thesis. Charles University, Faculty of Mathematics and Physics (2017)

  30. Kulvait, V., Málek, J., Rajagopal, K.R.: Modeling gum metal and other newly developed titanium alloys within a new class of constitutive relations for elastic bodies. Arch. Mech. 69(1), 223–241 (2017)

    Google Scholar 

  31. Le Roux, C., Rajagopal, K.R.: Shear flows of a new class of power-law fluids. Appl. Math. 58(2), 153–177 (2013). https://doi.org/10.1007/s10492-013-0008-4

    Article  MathSciNet  MATH  Google Scholar 

  32. Logg, A., Mardal, K.A., Wells, G.: Automated Solution of Differential Equations by the Finite Element Method: The FEniCS Book. Springer, New York (2012)

    Book  MATH  Google Scholar 

  33. Málek, J.: Mathematical properties of flows of incompressible power-law-like fluids that are described by implicit constitutive relations. Electron. Trans. Numer. Anal. 31, 110–125 (2008)

    MathSciNet  MATH  Google Scholar 

  34. Málek, J., Průša, V.: Derivation of equations for continuum mechanics and thermodynamics of fluids. In: Giga, Y., Novotny, A. (eds.) Handbook of Mathematical Analysis in Mechanics of Viscous Fluids, pp. 1–70. Springer, Cham (2016)

    Google Scholar 

  35. Málek, J., Průša, V., Rajagopal, K.R.: Generalizations of the Navier-Stokes fluid from a new perspective. Int. J. Eng. Sci. 48(12), 1907–1924 (2010). https://doi.org/10.1016/j.ijengsci.2010.06.013

    Article  MathSciNet  MATH  Google Scholar 

  36. Málek, J., Rajagopal, K.R.: Compressible generalized Newtonian fluids. Z. Angew. Math. Phys. 61(6), 1097–1110 (2010). https://doi.org/10.1007/s00033-010-0061-8

    Article  MathSciNet  MATH  Google Scholar 

  37. Maringová, E., Žabenský, J.: On a Navier-Stokes-Fourier-like system capturing transitions between viscous and inviscid fluid regimes and between no-slip and perfect-slip boundary conditions. Nonlinear Anal., Real World Appl. 41, 152–178 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  38. Montero, S., Bustamante, R., Ortiz-Bernardin, A.: A finite element analysis of some boundary value problems for a new type of constitutive relation for elastic bodies. Acta Mech. 227(2), 601–615 (2016). https://doi.org/10.1007/s00707-015-1480-6

    Article  MathSciNet  MATH  Google Scholar 

  39. Noll, W.: On the continuity of the solid and fluid states. J. Ration. Mech. Anal. 4, 3–81 (1955)

    MathSciNet  MATH  Google Scholar 

  40. Noll, W.: On the Foundation of the Mechanics of Continuous Media. Technical Report Series. Books on Demand (1957)

  41. Noll, W.: A mathematical theory of the mechanical behavior of continuous media. Arch. Ration. Mech. Anal. 2(1), 197–226 (1958)

    Article  MathSciNet  MATH  Google Scholar 

  42. Noll, W.: A new mathematical theory of simple materials. Arch. Ration. Mech. Anal. 48(1), 1–50 (1972). https://doi.org/10.1007/BF00253367

    Article  MathSciNet  MATH  Google Scholar 

  43. Ortiz, A., Bustamante, R., Rajagopal, K.R.: A numerical study of a plate with a hole for a new class of elastic bodies. Acta Mech. 223(9), 1971–1981 (2012). https://doi.org/10.1007/s00707-012-0690-4

    Article  MathSciNet  MATH  Google Scholar 

  44. Ortiz, A., Bustamante, R., Rajagopal, K.R.: A numerical study of elastic bodies that are described by constitutive equations that exhibit limited strains. Int. J. Solids Struct. 51(3), 875–885 (2014). https://doi.org/10.1016/j.ijsolstr.2013.11.014

    Article  Google Scholar 

  45. Perlácová, T., Průša, V.: Tensorial implicit constitutive relations in mechanics of incompressible non-Newtonian fluids. J. Non-Newton. Fluid Mech. 216, 13–21 (2015). https://doi.org/10.1016/j.jnnfm.2014.12.006

    Article  MathSciNet  Google Scholar 

  46. Průša, V., Rajagopal, K.R.: On implicit constitutive relations for materials with fading memory. J. Non-Newton. Fluid Mech. 181, 22–29 (2012)

    Article  Google Scholar 

  47. Rajagopal, K.: A note on the linearization of the constitutive relations of non-linear elastic bodies. Mech. Res. Commun. (2017)

  48. Rajagopal, K., Srinivasa, A.: On a class of non-dissipative materials that are not hyperelastic. Proc. R. Soc. A, Math. Phys. Eng. Sci. 465(2102), 493–500 (2009). https://doi.org/10.1098/rspa.2008.0319

    Article  ADS  MathSciNet  MATH  Google Scholar 

  49. Rajagopal, K.R.: On implicit constitutive theories. Appl. Math. 48(4), 279–319 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  50. Rajagopal, K.R.: On implicit constitutive theories for fluids. J. Fluid Mech. 550, 243–249 (2006)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  51. Rajagopal, K.R.: The elasticity of elasticity. Z. Angew. Math. Phys. 58(2), 309–317 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  52. Rajagopal, K.R.: Conspectus of concepts of elasticity. Math. Mech. Solids 16(5), 536–562 (2011). https://doi.org/10.1177/1081286510387856

    Article  MathSciNet  MATH  Google Scholar 

  53. Rajagopal, K.R.: A new development and interpretation of the Navier–Stokes fluid which reveals why the “Stokes assumption” is inapt. Int. J. Non-Linear Mech. 50, 141–151 (2013). https://doi.org/10.1016/j.ijnonlinmec.2012.10.007

    Article  ADS  Google Scholar 

  54. Rajagopal, K.R.: On the nonlinear elastic response of bodies in the small strain range. Acta Mech. 225(6), 1545–1553 (2014). https://doi.org/10.1007/s00707-013-1015-y

    Article  MathSciNet  MATH  Google Scholar 

  55. Rajagopal, K.R.: A note on the classification of anisotropy of bodies defined by implicit constitutive relations. Mech. Res. Commun. 64, 38–41 (2015). https://doi.org/10.1016/j.mechrescom.2014.11.005

    Article  Google Scholar 

  56. Rajagopal, K.R., Saccomandi, G.: The mechanics and mathematics of the effect of pressure on the shear modulus of elastomers. Proc. R. Soc. A, Math. Phys. Eng. Sci. 465(2112), 3859–3874 (2009). https://doi.org/10.1098/rspa.2009.0416

    Article  ADS  MATH  Google Scholar 

  57. Rajagopal, K.R., Saccomandi, G.: A novel approach to the description of constitutive relations. Frontiers in Materials 3 (2016). https://doi.org/10.3389/fmats.2016.00036

  58. Rajagopal, K.R., Srinivasa, A.R.: On the response of non-dissipative solids. Proc. R. Soc. A, Math. Phys. Eng. Sci. 463(2078), 357–367 (2006). https://doi.org/10.1098/rspa.2006.1760

    Article  ADS  MathSciNet  MATH  Google Scholar 

  59. Rajagopal, K.R., Srinivasa, A.R.: Inelastic response of solids described by implicit constitutive relations with nonlinear small strain elastic response. Int. J. Plast. 71, 1–9 (2015). https://doi.org/10.1016/j.ijplas.2015.02.007

    Article  Google Scholar 

  60. Rajagopal, K.R., Walton, J.R.: Modeling fracture in the context of a strain-limiting theory of elasticity: a single anti-plane shear crack. Int. J. Fract. 169(1), 39–48 (2011). https://doi.org/10.1007/s10704-010-9581-7

    Article  MATH  Google Scholar 

  61. Rajagopal, K.R., Zappalorto, M.: Bodies described by non-monotonic strain-stress constitutive equations containing a crack subject to anti-plane shear stress. Int. J. Mech. Sci. 149, 494–499 (2018). https://doi.org/10.1016/j.ijmecsci.2017.07.060

    Article  Google Scholar 

  62. Süli, E., Tscherpel, T.: Fully discrete finite element approximation of unsteady flows of implicitly constituted incompressible fluids. arXiv:1804.02264 (2018)

  63. Truesdell, C., Moon, H.: Inequalities sufficient to ensure semi-invertibility of isotropic functions. J. Elas. 5(34) (1975)

  64. Zappalorto, M., Berto, F., Rajagopal, K.R.: On the anti-plane state of stress near pointed or sharply radiused notches in strain limiting elastic materials: closed form solution and implications for fracture assessments. Int. J. Fract. 199(2), 169–184 (2016). https://doi.org/10.1007/s10704-016-0102-1

    Article  Google Scholar 

Download references

Acknowledgements

Josef Málek thanks the Czech Science Foundation for support through the project 18-12719S. K.R. Rajagopal thanks the Office of Naval Research for support of this work.

Author information

Authors and Affiliations

  1. Charles University, Faculty of Mathematics and Physics, Mathematical Institute, Sokolovská 83, 186 75, Prague, Czech Republic

    Vojtěch Kulvait & Josef Málek

  2. Department of Mechanical Engineering, Texas A&M University, College Station, TX, 77843, USA

    K. R. Rajagopal

Authors
  1. Vojtěch Kulvait
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Josef Málek
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. K. R. Rajagopal
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to K. R. Rajagopal.

Additional information

Dedicated to the memory of Professor Walter Noll

Publisher’s Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kulvait, V., Málek, J. & Rajagopal, K.R. The State of Stress and Strain Adjacent to Notches in a New Class of Nonlinear Elastic Bodies. J Elast 135, 375–397 (2019). https://doi.org/10.1007/s10659-019-09724-0

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10659-019-09724-0

Keywords

Mathematics Subject Classification

Search

Navigation