1 Introduction

Multi-attribute group decision making (MAGDM) problems have been widely applied in various fields, such as investment decision-making, project evaluation, quality evaluation, resource allocation and comprehensive evaluation of economic benefits, etc. (Zhang et al. 2019; Zhang et al. 2020a, b; Wan et al. 2020; Liu and You 2019). With the development of the natural and economic environment, MAGDM problems have evolved from individual decision-making and small-scale group decision-making (GDM) to complex large-scale GDM (LSGDM) (Zhang et al. 2014; Jin et al. 2020; Xu et al. 2019a, b). Generally, LSGDM problems have the following characteristics (Xu et al. 2015; Lu et al. 2021; Guo et al. 2020; Quesada et al. 2015):

  1. (1)

    Decision makers (DMs) can participate in decision-making at different times and places by using network tools;

  2. (2)

    Generally, more than 20 DMs are used to handle LSGDM problems (Chen and Liu 2006), including people in both the same organization and different organizations, and, the knowledge, skills, experience and personality characteristics of each DM often vary. Besides, DMs both cooperate and compete;

  3. (3)

    The relationship between attributes is not only interrelated but also contradictory;

  4. (4)

    DMs’ assessments are uncertain and diverse, and consequently often quite conflicting. Thus, group consensus is very important to be able to increase agreement among DMs.

In the twenty-first century, with the digitalization process, LSGDM has become the focus of complex decision-making problems, especially in emergency decision-making. It requires experts from different fields to participate in the decision-making process and obtain the most effective decision results within a short period of time (Tang et al. 2020; Zhang et al. 2020c; Ou et al. 2018; Lin et al. 2020, 2021). The characteristics of LSGDM problems differ from those of GDM problems. For instance, the large number of DMs that are involved in LSGDM, the non-cooperative behavior shown by and minority opinions given by DMs, etc. The traditional consensus and GDM methods face many challenges in dealing with complex LSGDM problems (Labella et al. 2018; Gou et al. 2021; Bain and Hansen 2020; Liu et al. 2020; Chu et al. 2020; Zheng et al. 2020; Rodríguez et al. 2021b; Tang and Liao 2021; Chen et al. 2021). Therefore, previous models must be developed/evolved to deal with large-scale groups and to define new solution processes for LSGDM (Xu 2009; Xu and Chen 2018).

Complex real-word LSGDM problems in modern society and the economy cannot always be effectively managed and solved using crisp assessments. Moreover, it is natural for DMs to provide their assessments with linguistic variables (Zadeh 1975), which are intuitive and flexible enough to describe a DM’s knowledge, uncertainty and subjectivity. Although DMs elicit information using linguistic terms from a linguistic term set (LTS) (Herrera and Martinez 2000), sometimes they need more than one term to express their opinions. However, LTS cannot clearly reflect the importance and distribution assessments of different linguistic terms. To overcome such limitation, Zhang et al. (2014) introduced the concepts of linguistic distribution term sets (LDTSs) and linguistic distribution preference relations (LDPRs) and discussed operation laws for LDTSs. DMs’ social experience and cultural background, however, can lead to conflicts arising among them. In this situation, the application of a consensus reaching processes in LSGDM to build consensual opinions was successfully applied (Gong et al. 2020a, b). Therefore, consensus reaching process (CRP) is a key stage in the process of obtaining an acceptable solution for all DMs. There are many proposals for CRP models (Wang et al. 2019; Wu and Xu 2018; Wu et al. 2019; Gou et al. 2018; Ding et al. 2019), including the satisfaction achieving approaches with CRP (Zhang et al. 2018), adaptive CRP methods (Rodríguez et al. 2018), minimum-cost CPR models (Labella et al. 2020a, b). By defining the individual consensus measure and group consensus measure, Zhang et.al (2020a, b) devised a feedback mechanism and a consensus reaching algorithm. Based on personalized individual semantics, Li et al. (2019) developed a consensus method for LSGDM problems, in which the DMs’ willingness is increased by using the new clustering process and opposing consensus groups. Du et al. (2020) constructed a mixed CRP model by integrating the independent and supervised consensus-reaching models. Xu et al. (2019a, b) proposed a CRP model with uncertain linguistic preference relations, in which the element with lowest consensus level is modified to achieve the predefined consensus level. In order to decrease the impact of internal disagreements among DMs, Rodríguez et al. (2021a) designed a CRP model with restricted equivalence functions under the hesitant fuzzy linguistic term set environment. With the help of the reliability of DMs and Dempster–Shafer evidence theory, Liu et al. (2021) presented a novel CRP model for hesitant fuzzy linguistic GDM problems. Du et al. (2021) proposed a large-scale multi-attribute GDM consensus-reaching method to reach satisfactory consensus levels by considering the DMs’ knowledge structures. Xiao et al. (2020) first constructed a classification-based consensus framework and then developed an optimization model to derive the weights of DMs by maximizing consensus degrees among DMs.

Extant LSGDM methods rank alternatives to the decision-making problem by assuming that DMs are completely rational and neglecting DMs’ psychological behavior, like regret aversion. However, for complex and high risk LSGDM problems, DMs not only focus on the utility of alternatives chosen, but also on the results they would have obtained if they had chosen different alternative/s, in order to avoid regretting their choice. Therefore, regret theory is key to dealing with the DMs’ behavior of regret aversion (Bell 1982; Loomes and Sugden 1982; Zhou et al. 2017; Wang et al. 2020).

The large number of experts involved in LSGDM problems will inevitably lead to a large number of assessments, which can be utilized to deduce valuable decision-making information with statistical inference (Gong et al. 2020a; Ma et al. 2020). To put this in context, we note that with respect to group evaluation problems, Bu (2007) introduced a parameter estimation method with statistical inference theory and the AHP method, and developed a mathematical model to derive efficient and practical GDM results. Liu (2015) regarded the expert’s judgment results as a random sample of statistical inference GDM opinions, and established a green building group evaluation method based on statistical inference. Therefore, to accurately extract expert’s effective evaluation information and obtain reliable LSGDM results that reflect the personal preference of each expert, the statistical inference principle must be used to deal with LSGDM evaluation data.

Yet, despite it being of interest to multiple real-world decision-making problems, there are few reports on the consensus based linguistic distribution LSGDM (CLDLSGDM) method that consider the regret aversion psychological characteristics of DMs (Song et al. 2017). Therefore, this paper proposes a new CLDLSGDM method with regret theory, in which DM assessments are elicited by means of linguistic distribution elements (LDEs) to reflect the importance of assessments of different linguistic terms and their regret aversion behavior. The main contributions of this paper are listed as follows:

  • A CLDLSGDM is presented to improve agreement among DMs under the linguistic distribution information environment in multi-attribute LSGDM (MALCGDM) problems.

  • Based on the statistical inference principle, we develop two weight allocation methods for DMs and attributes.

  • A novel CLDLSGDM that ranks alternatives is proposed based on regret theory, in which we capture DM regret aversion psychological behavior.

  • A numerical example for evaluating the performance of public hospitals in China and the comparative analysis are provided to show the advantages of the proposed method.

The rest of the paper is set out according to the following scheme. Section 2 offers some basic knowledge about LDTSs, regret theory and MALSGDM. In Sect. 3, a novel CLDLSGDM method is designed, including CRP, DMs’ weight derivation process, attributes’ weight generation process and desirable alternative selection process. An illustration of the developed methods’ ranking orders of the Chinese public hospitals is given in Sect. 4. In Sect. 4, both a sensitivity analysis and a comparative analysis are performed to assess the stability and advantages of the proposed novel CLDLSGDM method. In Sect. 5 we point out the conclusions of this paper.

2 Preliminaries

In this section, we review the related knowledge about LDTSs, regret theory and LSGDM.

2.1 Linguistic Distribution Term Sets (LDTSs)

Let \(S = \left\{ {s_{\xi } \left| {\xi = 0,1, \ldots ,2\tau } \right.} \right\}\) be a fuzzy discrete LTS with odd cardinality, \(s_{\xi }\) indicates the linguistic term in \(S\) (Zadeh 1975; Li et al. 2017; Martínez and Herrera 2014; Martínez et al. 2010; Liu et al. 2010; Rodríguez et al. 2012; Labella et al. 2020a, b), which satisfy the following characteristics (Rodríguez and Martínez 2013): (1) If \(\xi \ge \zeta\), then \(s_{\xi } \ge s_{\zeta }\); (2) \(neg\;(s_{\xi } ) = s_{2\tau - \xi }\), especially \(neg\;(s_{\tau } ) = s_{\tau }\).

As LTS cannot accurately depict the distribution assessments associated with linguistic variables, Zhang et al. (2014) have generalized the LTSs to the LDEs in order to deal with this limitation.

Definition 1

(Zhang et al. 2014) Let \(S = \left\{ {s_{\xi } \left| {\xi = 0,1, \ldots ,2\tau } \right.} \right\}\) be a LTS, then a LDE can be denoted as follows:

$$ h = \left\{ {(s_{\xi } ,p_{{}}^{(\xi )} )\left| {\xi = 0,1, \ldots ,2\tau ,} \right.0 \le p^{(\xi )} \le 1,\sum\limits_{\xi = 0}^{2\tau } {p^{(\xi )} \le 1} } \right\}, $$
(1)

where \(s_{\xi } \in S\), \(p^{(\xi )} \in [0,1]\) is the corresponding probability of \(s_{\xi }\). LDE \(h\) can be seen as a discrete full probability distribution over the LTS \(S\).

Remark 1

In Definition 1, if \(\sum\nolimits_{\xi = 0}^{2\tau } {p^{(\xi )} } { = 1}\), then it means that all the probability information is considered in the LDE \(h\); If \(\sum\nolimits_{\xi = 0}^{2\tau } {p^{(\xi )} } { < 1}\), then LDE \(h\) can be normalized as (Zhang et al. 2014):

$$ \overline{h} = \left\{ {\left. {\left( {s_{\xi } ,{{p^{(\xi )} } \mathord{\left/ {\vphantom {{p^{(\xi )} } {\sum\limits_{\xi = 0}^{{{2}\tau }} {p^{(\xi )} } }}} \right. \kern-\nulldelimiterspace} {\sum\limits_{\xi = 0}^{{{2}\tau }} {p^{(\xi )} } }}} \right)} \right|\xi = 0,1, \ldots 2\tau } \right\}. $$
(2)

For convenience, the normalized LDE is still represented as \(h\) in this paper.

2.2 Regret Theory

In complex and risky decision-making problems, DMs are bounded rational and present different psychological behaviors, such as loss avoidance, decreasing sensitivity and distorted probability judgment. Regret theory (Bell 1982; Loomes and Sugden 1982) is an important behavioral decision-making theory, which can be applied to capture the DMs’ regret aversion.

Definition 2

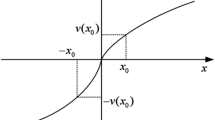
(Zhang et al. 2016) Assume that \(x\) and \(y\) are the evaluation values of alternatives \(A\) and \(B\), then the regret-rejoice function \(R( \cdot )\) is defined as:

$$ R(\vartriangle v) = 1 - exp\left( { - \delta \vartriangle v} \right),\delta > 0, $$
(3)

where \(\delta\) is the regret aversion coefficient of DM, \(\vartriangle v = pu(x) - pu(y)\) indicates the perceived utility deviation between alternatives \(A\) and \(B\), \(pu(x)\) and \(pu(y)\) represent the perceived utility values of \(x\) and \(y\).

Remark 2

In Definition 2, if \(\vartriangle v > 0\), then \(R(\vartriangle v)\) indicates the rejoice value of the DM choosing alternative \(x\) and giving up \(y\). If \(\vartriangle v < 0\), then \(R (\vartriangle v)\) indicates the regret value of the DM choosing alternative \(x\) and giving up \(y\). In addition, the parameter \(\delta\) is the regret aversion degree of the DM. The graphical representation of \(R (\vartriangle v)\) with different \(\delta\) is shown in Fig. 1. Let \(f (\delta ) = |R ( - \vartriangle v)|\)\(- R (\vartriangle v) = exp\left( {\delta \vartriangle v} \right) + exp\left( { - \delta \vartriangle v} \right) - 2\), then.

$$ f^{\prime}(\delta ) = \vartriangle v \cdot exp\left( {\delta \vartriangle v} \right) - \vartriangle v \cdot exp\left( { - \delta \vartriangle v} \right) = \vartriangle v \cdot \left( {exp\left( {\delta \vartriangle v} \right) - exp\left( { - \delta \vartriangle v} \right)} \right) > 0, $$
(4)

thus, \(f(\delta )\) is an increasing function with respect to parameter \(\delta\). Therefore, the bigger the parameter \(\delta\) is, the greater the deviation between \(|R( - \vartriangle v)|\) and \(R(\vartriangle v)\) is, and the more regret aversive a DM is.

Fig. 1
figure 1

Regret-rejoice function \(R(\vartriangle v)\) with different \(\delta\)

Full size image

2.3 Linguistic Distribution MALSGDM Problem

A MALSGDM problem with linguistic distribution preference information can be depicted as follows:

  • (i) Let \(E = \{ e_{1} ,e_{2} , \ldots ,e_{q} \}\) be a set of DMs and \(q(q \ge 20)\) be the number of DMs in the MALSGDM problem (Chen and Liu 2006). The weight vector of DMs is \(\omega = (\omega_{1} ,\omega_{2} , \ldots ,\omega_{q} )^{T}\), where \(\omega_{k} \ge 0,\sum\nolimits_{k = 1}^{q} {\omega_{k} } = 1\). The weight vector \(\omega\) is completely unknown.

  • (ii) A set of alternatives \(X = \{ x_{1} ,x_{2} , \ldots ,x_{m} \}\), a set of attributes \(A = \{ a_{1} ,a_{2} , \ldots ,a_{n} \}\). \(m(m \ge 2)\) and \(n(n \ge 1)\) are the number of alternatives and attributes in the MALSGDM problem, respectively. For DM \(e_{k}\), the weight vector of attributes is \(w_{k} = (w_{k1} ,w_{k2} , \ldots ,w_{kn} )^{T}\), where \(w_{kj} \ge 0,\sum\nolimits_{j = 1}^{n} {w_{kj} } = 1\). The weight vectors \(w_{k} (k = 1,2, \ldots ,q)\) are completely unknown.

  • (iii) DMs \(\{ e_{1} ,e_{2} , \ldots ,e_{q} \}\) evaluate the alternatives \(\{ x_{1} ,x_{2} , \ldots ,x_{n} \}\) with respect to attributes \(\{ a_{1} ,a_{2} , \ldots ,a_{m} \}\) with linguistic distribution information decision-making matrices \(H_{k} = (h_{ij}^{k} )_{m \times n} (k = 1,2, \ldots, q)\), where LDE \(h_{ij}^{k} = \left\{ {(s_{\xi } ,p_{ij(k)}^{(\xi )} )\left| {\xi = 0,1,\ldots, 2\tau } \right.} \right\}\) indicates the linguistic distribution preference information of alternative \(x_{i}\) with respect to attribute \(a_{j}\) provided by DM \(e_{k}\).

3 CLDLSGDM Method

In this section, a novel CLDLSGDM method is designed, including CRP, DM weight derivation process, attribute weight generation process and desirable alternative selection process. We first propose a LSGDM CRP with linguistic distribution information to achieve the consensus goal, then we develop DM and attribute weight allocation methods with a/the statistical inference principle. Based on the regret theory, the ranking order of the alternatives is eventually obtained, in which the regret aversion psychological characteristics of DMs are considered. The flow chart of the proposed CLDLSGDM method is shown in Fig. 2.

Fig. 2
figure 2

The developed CLDLSGDM method

Full size image

3.1 CRP for CLDLSGDM (Phase I)

For MALSGDM problems, group consensus is an important step to be taken to avoid conflicting decision results (Labella et al. 2018; 2020a, b). In the process of consensus improvement, the original evaluation information provided by DMs will inevitably be modified, with the aim of increasing the level of agreement among DMs (Palomares et al. 2014). Thus, a CRP model must be developed with the aim of retaining as many expert preferences as possible. Therefore, a new CRP with linguistic distribution information is introduced in order to try and reach an agreement by retaining the DMs’ preferences as much as possible. The flow chart of the new CRP is shown in Fig. 3.

Fig. 3
figure 3

Phase I: CRP for CLDLSGDM

Full size image

As DMs provide \(q\) linguistic distribution information decision-making matrices \(H_{k} =\) \((h_{ij}^{k} )_{m \times n} (k = 1,2,\ldots,q)\), where \(h_{ij}^{k} = \left\{ {(s_{\xi } ,p_{ij(k)}^{(\xi )} )\left| {\xi = 0,1,\ldots, 2\tau ,0 \le p_{ij(k)}^{(\xi )} \le 1,\sum\limits_{\xi = 0}^{2\tau } {p_{ij(k)}^{(\xi )} } = 1} \right.} \right\}\), then the similarity matrix \(SM^{kl} = (sm_{ij}^{kl} )_{m \times n}\) between DMs \(e_{k}\) and \(e_{l}\) can be obtained as follows:

$$ SM^{kl} = \left( {\begin{array}{*{20}c} {sm_{11}^{kl} } & {sm_{12}^{kl} } & \cdots & {sm_{1n}^{kl} } \\ {sm_{21}^{kl} } & {sm_{22}^{kl} } & \cdots & {sm_{2n}^{kl} } \\ \vdots & \vdots & \ddots & \vdots \\ {sm_{m1}^{kl} } & {sm_{m2}^{kl} } & \cdots & {sm_{mn}^{kl} } \\ \end{array} } \right), $$
(5)

where \(sm_{ij}^{kl} = 1 - \frac{1}{2}\sum\limits_{\xi = 0}^{2\tau } {\left| {p_{ij(k)}^{(\xi )} - p_{ij(l)}^{(\xi )} } \right|}\). It is obvious that \(0 \le sm_{ij}^{kl} \le 1,i = 1,2, \ldots ,m,j = 1,2, \ldots ,n\).

Therefore, there are \(q^{2}\) similarity matrices \(SM^{kl} (k,l = 1,2, \ldots ,q)\), and we can construct a super-similarity matrix \(SM = \left( {SM^{kl} } \right)_{q \times q}\) as follows:

$$ SM = \left( {\begin{array}{*{20}c} {SM^{11} } & {SM^{12} } & \cdots & {SM^{1q} } \\ {SM^{21} } & {SM^{22} } & \cdots & {SM^{2q} } \\ \vdots & \vdots & \ddots & \vdots \\ {SM^{q1} } & {SM^{q2} } & \cdots & {SM^{qq} } \\ \end{array} } \right). $$
(6)

As \(sm_{ij}^{kk} = 1 - \frac{1}{2}\sum\limits_{\xi = 0}^{2\tau } {\left| {p_{ij(k)}^{(\xi )} - p_{ij(k)}^{(\xi )} } \right|} = 1,sm_{ij}^{lk} = 1 - \frac{1}{2}\sum\limits_{\xi = 0}^{2\tau } {\left| {p_{ij(l)}^{(\xi )} - p_{ij(k)}^{(\xi )} } \right|} = 1 - \frac{1}{2}\sum\limits_{\xi = 0}^{2\tau } {\left| {p_{ij(k)}^{(\xi )} - p_{ij(l)}^{(\xi )} } \right|} = sm_{ij}^{kl}\), then we have \(SM^{kk} = \left( {\begin{array}{*{20}c} 1 & 1 & \cdots & 1 \\ 1 & 1 & \cdots & 1 \\ \vdots & \vdots & \ddots & \vdots \\ 1 & 1 & \cdots & 1 \\ \end{array} } \right)_{m \times n} ,k = 1,2, \cdots ,q\) and \(SM^{kl} = SM^{lk}\). Thus, super- similarity matrix \(SM\) is a symmetric matrix.

Based on the super-similarity matrix \(SM = \left( {SM^{kl} } \right)_{q \times q}\), we can derive the consensus matrix \(CM = \left( {cm_{kl} } \right)_{q \times q}\) as follows:

$$ CM = \left( {\begin{array}{*{20}c} {cm_{11} } & {cm_{12} } & \cdots & {cm_{1q} } \\ {cm_{21} } & {cm_{22} } & \cdots & {cm_{2q} } \\ \vdots & \vdots & \ddots & \vdots \\ {cm_{q1} } & {cm_{q2} } & \cdots & {cm_{qq} } \\ \end{array} } \right), $$
(7)

where \(cm_{kl} = \frac{1}{mn}\sum\nolimits_{i = 1}^{m} {\sum\nolimits_{j = 1}^{n} {sm_{ij}^{kl} } } \in [0,1]\) is defined as the consensus degree between DMs \(e_{k}\) and \(e_{l}\). As \(sm_{ij}^{kk} = 1,sm_{ij}^{lk} = sm_{ij}^{kl}\), then.

  • (i) \(cm_{kk} = \frac{1}{mn}\sum\nolimits_{i = 1}^{m} {\sum\nolimits_{j = 1}^{n} {sm_{ij}^{kk} } } = 1,\) which means that DM \(e_{k}\) has the highest degree of consensus DM \(e_{k}\) achieves is with themselves and is consistent with our intuitive perception.

  • (ii) \(cm_{kl} = \frac{1}{mn}\sum\nolimits_{i = 1}^{m} {\sum\nolimits_{j = 1}^{n} {sm_{ij}^{kl} } } = \frac{1}{mn}\sum\nolimits_{i = 1}^{m} {\sum\nolimits_{j = 1}^{n} {sm_{ij}^{lk} } } = cm_{lk} ,k,l = 1,2,\ldots,q\), which indicates the consensus degree between DMs \(e_{k}\) and \(e_{l}\) is unique and unidirectional.

Therefore, consensus matrix \(CM = \left( {cm_{kl} } \right)_{q \times q}\) is a symmetric matrix and the diagonal elements are equal to 1.

Definition 3

Let \(CM = \left( {cm_{kl} } \right)_{q \times q}\) be a consensus matrix of DMs \(\{ e_{1} ,e_{2} ,\ldots, e_{q} \}\), then the group consensus index (\(GCI\)) among DMs is defined as:

$$ GCI = \frac{2}{q(q - 1)}\sum\limits_{k = 1}^{q - 1} {\sum\limits_{l = k + 1}^{q} {cm_{kl} } } . $$
(8)

Now, we present a consensus adjustment algorithm to improve the group consensus degree.

Algorithm I

Input The linguistic distribution information decision-making matrices \(H_{k} = (h_{ij}^{k} )_{m \times n} (k = 1,2, ldots, q)\), the group consensus index threshold \(\theta (0 < \theta < 1)\), the cost of changing DMs \(e_{k}\)’s opinion 1 unit \(c_{k} (k = 1,2, \ldots q)\).

Output The adjusted linguistic distribution information decision-making matrices \(\tilde{H}_{k} =\) \((\tilde{h}_{ij}^{k} )_{m \times n} (k = 1,2 \ldots, q)\), the iterative times \(t\).

Step 1 Let \(t = 0\) and \(H_{k}^{(t)} = (h_{ij}^{k(t)} )_{m \times n} = H_{k} = (h_{ij}^{k} )_{m \times n} (k = 1,2,\ldots, q)\).

Step 2 Using Eqs. (5) and (7) to calculate similarity matrices \(SM^{kl(t)} (k,l = 1,2, \cdots ,q)\) and consensus matrix \(CM^{(t)} = \left( {cm_{kl}^{(t)} } \right)_{q \times q}\).

Step 3 Check the group consensus level with \(GCI^{(t)}\). If \(GCI^{(t)} \ge \theta\), then go to Step 8; Otherwise, go to Step 4.

Step 4Search for the lowest consensus level among DMs. Let \(cm_{{k^{*} ,l^{*} }}^{(t)} = \mathop {\min }\limits_{k < l} \{ cm_{kl}^{(t)} \}\), then the pair of DMs \((e_{{k^{*} }} ,e_{{l^{*} }} )\) has the lowest consensus level.

Step 5 Identifying the lowest similarity level in \(SM^{{k^{*} ,l^{*} ,(t)}}\). Let \(sm_{{i^{*} ,j^{*} }}^{{k^{*} ,l^{*} ,(t)}} = \mathop {\min }\limits_{i = 1,2,\ldots,m,j = 1,2,\ldots,n} \{ sm_{ij}^{{k^{*} ,l^{*} ,(t)}} \}\), then DMs \(e_{{k^{*} }}\) and \(e_{{l^{*} }}\) have the largest deviation on the judgement values of alternative \(x_{{i^{*} }}\) with respect to attribute \(a_{{j^{*} }}\), and we need to adjust LDE \(h_{{i^{*} ,j^{*} }}^{{k^{*} ,(t)}}\) or \(h_{{i^{*} ,j^{*} }}^{{l^{*} ,(t)}}\).

Step 6 Adjust the judgement values based on adjust cost. In order to decrease the deviation between \(h_{{i^{*} ,j^{*} }}^{{k^{*} ,(t)}}\) and \(h_{{i^{*} ,j^{*} }}^{{l^{*} ,(t)}}\), the adjustment direction is given as follows:

  • If \(c_{{k^{*} }} < c_{{j^{*} }}\), then DM \(e_{{k^{*} }}\) should change LDE \(h_{{i^{*} ,j^{*} }}^{{k^{*} ,(t)}}\) to \(h_{{i^{*} ,j^{*} }}^{{l^{*} ,(t)}}\).

  • If \(c_{{k^{*} }} > c_{{j^{*} }}\), then DM \(e_{{l^{*} }}\) should change LDE \(h_{{i^{*} ,j^{*} }}^{{l^{*} ,(t)}}\) to \(h_{{i^{*} ,j^{*} }}^{{k^{*} ,(t)}}\).

Step 7 Generate the new linguistic distribution information decision-making matrices \(H_{k}^{(t + 1)} = (h_{ij}^{k(t + 1)} )_{m \times n} (k = 1,2,\ldots,q)\). Let \(t = t + 1\), and go to Step 2.

Step 8 Let \(\tilde{H}_{k} = H_{k}^{(t)} (k = 1,2,\ldots,q)\), then output the adjusted linguistic distribution information decision-making matrices \(\tilde{H}_{k} (k = 1,2,\ldots,q)\), the iterative times \(t\).

Step 9 End.

Remark 3

From Algorithm I, it is clear that the obtained \(\tilde{H}_{k} = (\tilde{h}_{ij}^{k} )_{m \times n} (k = 1,2 \ldots,q)\) has a high level of consensus, and the iterative times \(t\) can directly reflect the number of adjusted elements.

The importance of each DM and attribute in MALSGDM problems differs. Although the weight vector of DMs \(\omega = (\omega_{1} ,\omega_{2} , \ldots ,\omega_{q} )^{T}\) and weight vectors of attributes \(w_{k} = (w_{k1} ,w_{k2} ,\ldots,w_{kn} )^{T} (k = 1,2 \ldots,q)\) are completely unknown, it can be calculated based on the DMs’ judgements. Therefore, in Subsections 3.2 and 3.3, by utilizing the statistical inference principle (Bu 2007; Liu 2015), we propose two DM and attribute weight allocation methods based on \(\tilde{H}_{k} =\)\((\tilde{h}_{ij}^{k} )_{m \times n} (k = 1,2 \ldots ,q)\), obtained in Subsection 3.1.

3.2 Deriving DMs’ Weights Based on Statistical Inference (Phase II)

It is obvious that the greater the number of consensus degrees associated with a DM in a consensus matrix \(C\tilde{M} = \left( {c\tilde{m}_{kl} } \right)_{q \times q}\), the closer the data distribution is to a normal distribution. Thus, the decision-making result is more accurate with the normal distribution method. For a MALSGDM problem, a large number of DMs participate in the complex decision-making problem. Therefore, in this subsection, we assume that the consensus data in the consensus matrix has normal distribution characteristics. Thus, we calculate the mathematical expectations and standard variances of these normal distribution data sequences. Finally, the normal distribution estimation is applied to calculate the DMs’ weights. The flow chart of Phase II can be seen in Fig. 4.

Fig. 4
figure 4

Phase II: Deriving DMs’ weights

Full size image

First, based on the adjusted linguistic distribution information decision-making matrices \(\tilde{H}_{k} = (\tilde{h}_{ij}^{k} )_{m \times n} (k = 1,2 \ldots ,q)\) that were derived from Algorithm I, we can obtain a new consensus matrix \(C\tilde{M} = \left( {c\tilde{m}_{kl} } \right)_{q \times q}\) by using Eqs. (5) and (7).

Based on the consensus matrix \(C\tilde{M} = \left( {c\tilde{m}_{kl} } \right)_{q \times q}\), let \(c\tilde{m}_{k}^{L} = \mathop {\min }\limits_{l \ne k} \{ c\tilde{m}_{kl} \} ,c\tilde{m}_{k}^{U} = \mathop {\max }\limits_{l \ne k} \{ c\tilde{m}_{kl} \} ,\) \(k = 1,2 \ldots ,q\), we obtain a sequence of interval numbers as follows: \(\left\{ {[c\tilde{m}_{1}^{L} ,c\tilde{m}_{1}^{U} ],[c\tilde{m}_{2}^{L} ,} \right.c\tilde{m}_{2}^{U} ],\left. { \ldots ,[c\tilde{m}_{q}^{L} ,c\tilde{m}_{q}^{U} ]} \right\}\), which can be divided into two real number sequences:

\(c\tilde{m}^{L} = \left\{ {c\tilde{m}_{1}^{L} ,c\tilde{m}_{2}^{L} , \ldots ,c\tilde{m}_{q}^{L} } \right\}\;{\text{and}}\;c\tilde{m}^{U} = \left\{ {c\tilde{m}_{1}^{U} ,c\tilde{m}_{2}^{U} , \ldots ,c\tilde{m}_{q}^{U} } \right\}\),

thus, the mathematical expectations \(\overline{cm}^{L} ,\overline{cm}^{U}\) and standard variances \(\overline{sv}^{L} ,\overline{sv}^{U}\) of two real number sequences \(c\tilde{m}^{L}\) and \(c\tilde{m}^{U}\) are calculated as:

$$ \overline{cm}^{L} = \frac{1}{q}\sum\limits_{k = 1}^{q} {c\tilde{m}_{k}^{L} } ,\;\overline{sv}^{L} = \sqrt {\frac{1}{q - 1}\sum\limits_{k = 1}^{q} {\left( {c\tilde{m}_{k}^{L} - \overline{cm}^{L} } \right)^{2} } } , $$
(9)
$$ \overline{cm}^{U} = \frac{1}{q}\sum\limits_{k = 1}^{q} {c\tilde{m}_{k}^{U} } ,\;\overline{sv}^{U} = \sqrt {\frac{1}{q - 1}\sum\limits_{k = 1}^{q} {\left( {c\tilde{m}_{k}^{U} - \overline{cm}^{U} } \right)^{2} } } , $$
(10)

where \(q\) is the number of data in a normal distribution data sequence \(\left\{ {c\tilde{m}_{1}^{L} ,c\tilde{m}_{2}^{L} , \ldots ,c\tilde{m}_{q}^{L} } \right\}\) or a normal distribution data sequence \(\left\{ {c\tilde{m}_{1}^{U} ,c\tilde{m}_{2}^{U} , \cdots ,c\tilde{m}_{q}^{U} } \right\}\).

As the variance of the consensus degrees in \(C\tilde{M} = \left( {c\tilde{m}_{kl} } \right)_{q \times q}\) is unknown, we apply a normal distribution estimation to compute the probability of interval number \([c\tilde{m}_{k}^{L} ,c\tilde{m}_{k}^{U} ]\), i.e.,

$$ Pro_{k} = P(x \le c\tilde{m}_{k}^{U} ) - P(x \le c\tilde{m}_{k}^{L} ),k = 1,2 \cdots ,q, $$
(11)

where (i) \(P(x \le c\tilde{m}_{k}^{L} ) = P\left( {\frac{{\overline{cm}^{L} - c\tilde{m}_{k}^{L} }}{{{{\overline{sv}^{L} } \mathord{\left/ {\vphantom {{\overline{sv}^{L} } {\sqrt q }}} \right. \kern-\nulldelimiterspace} {\sqrt q }}}}} \right)\), if \(c\tilde{m}_{k}^{L} < \overline{cm}^{L}\);

(ii) \(P(x \le c\tilde{m}_{k}^{L} ) = P\left( {\frac{{c\tilde{m}_{k}^{L} - \overline{cm}^{L} }}{{{{\overline{sv}^{L} } \mathord{\left/ {\vphantom {{\overline{sv}^{L} } {\sqrt q }}} \right. \kern-\nulldelimiterspace} {\sqrt q }}}}} \right)\), if \(c\tilde{m}_{k}^{L} > \overline{cm}^{L}\);

(iii) \(P(x \le c\tilde{m}_{k}^{U} ) = P\left( {\frac{{\overline{cm}^{U} - c\tilde{m}_{k}^{U} }}{{{{\overline{sv}^{U} } \mathord{\left/ {\vphantom {{\overline{sv}^{U} } {\sqrt q }}} \right. \kern-\nulldelimiterspace} {\sqrt q }}}}} \right)\), if \(c\tilde{m}_{k}^{U} < \overline{cm}^{U}\);

(iv) \(P(x \le c\tilde{m}_{k}^{U} ) = P\left( {\frac{{\overline{cm}^{U} - c\tilde{m}_{k}^{U} }}{{{{\overline{sv}^{U} } \mathord{\left/ {\vphantom {{\overline{sv}^{U} } {\sqrt q }}} \right. \kern-\nulldelimiterspace} {\sqrt q }}}}} \right)\), if \(c\tilde{m}_{k}^{U} > \overline{cm}^{U}\).

Let \(L_{{c\tilde{m}_{k} }} = c\tilde{m}_{k}^{U} - c\tilde{m}_{k}^{L} ,k = 1,2 \cdots ,q\). The larger value of \(L_{{c\tilde{m}_{k} }}\) is, the more scattered DM \(e_{k}\)’s consensus degrees is and the lower the consensus level of DM \(e_{k}\) is, which indicates that DM \(e_{k}\) is less important in MALSGDM problems. Therefore, one can derive DMs’ weights as follows:

$$ \omega_{k} = \frac{{1 - Pro_{k} }}{{\sum\nolimits_{k = 1}^{q} {\left( {1 - Pro_{k} } \right)} }},k = 1,2 \ldots ,q, $$
(12)

and \(\omega_{k} \in [0,1],\sum\nolimits_{k = 1}^{q} {\omega_{k} } = 1\).

3.3 Generating Attribute Weights Based on Statistical Inference (Phase III)

Similar to the process of deriving DM weights in Subsection 3.2, this subsection utilizes the statistical inference principle to derive the attributes’ weights with \(\tilde{H}_{k} = (\tilde{h}_{ij}^{k} )_{m \times n} (k = 1,2 \ldots ,q)\). First, we transform the linguistic distribution information decision-making matrices \(\tilde{H}_{k} = (\tilde{h}_{ij}^{k} )_{m \times n} (k = 1,2 \ldots ,q)\) into the utility matrices \(U_{k} = (u_{ij}^{k} )_{m \times n} (k = 1,2 \ldots ,q)\) with a utility function. Then, we determine the attributes’ weights utilizing the mathematical expectations and standard variances obtained. The flow chart of Phase III can be seen in Fig. 5.

Fig. 5
figure 5

Phase III: Generating attribute weights

Full size image

According to Definition 1, we know that a LDE can be viewed as a discrete full probability distribution over the LTS \(S = \{ s_{0} ,s_{1} , \ldots s_{\tau } , \ldots ,s_{2\tau } \}\). Therefore, for a LDE \(\tilde{h} = \left\{ {(s_{\xi } ,\tilde{p}_{{}}^{(\xi )} )\left| {\xi = } \right.} \right.\) \(\left. {0,1, \ldots ,2\tau ,0 \le \tilde{p}_{{}}^{(\xi )} \le 1,\sum\nolimits_{\xi = 0}^{2\tau } {\tilde{p}_{{}}^{(\xi )} } = 1} \right\}\), a utility function \(u(\tilde{h}) = \sum\nolimits_{\xi = 0}^{2\tau } {\Phi^{ - 1} (s_{\xi } ) \cdot \tilde{p}_{{}}^{(\xi )} } = \sum\nolimits_{\xi = 0}^{2\tau } {\xi \cdot \tilde{p}_{{}}^{(\xi )} }\) is used to calculate the utility value of LDE \(\tilde{h}\), and thus we can obtain the utility matrices \(U_{k} = (u_{ij}^{k} )_{m \times n} (k = 1,2 \ldots, q)\), where \(u_{ij}^{k} = \sum\nolimits_{\xi = 0}^{2\tau } {\xi \cdot \tilde{p}_{ij(k)}^{(\xi )} } ,i = 1,2, \ldots ,m,j = 1,2, \ldots ,n,k = 1,2 \ldots , q\).

Let \(u_{j}^{kL} = \mathop {\min }\limits_{i} \{ u_{ij}^{k} \} ,u_{j}^{kU} = \mathop {\max }\limits_{i} \{ u_{ij}^{k} \} ,j = 1,2, \ldots ,n,k = 1,2 \ldots ,q\), then we obtain the following interval matrix \(B = (b_{kj}^{{}} )_{q \times n} = \left( {[u_{j}^{kL} ,u_{j}^{kU} ]} \right)_{q \times n}\):

\(\begin{gathered} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;a_{1} \;\;\;\;\;\;\;\;\;\;\;\;\;\;a_{2} \;\;\;\;\;\;\;\; \cdots \;\;\;\;\;\;\;\;\;a_{n} \hfill \\ B = \begin{array}{*{20}c} {e_{1} } \\ {e_{2} } \\ {} \\ {e_{q} } \\ \end{array} \left( {\begin{array}{*{20}c} {[u_{1}^{1L} ,u_{1}^{1U} ]} & {[u_{2}^{1L} ,u_{2}^{1U} ]} & \cdots & {[u_{n}^{1L} ,u_{n}^{1U} ]} \\ {[u_{1}^{2L} ,u_{1}^{2U} ]} & {[u_{2}^{2L} ,u_{2}^{2U} ]} & \cdots & {[u_{n}^{2L} ,u_{n}^{2U} ]} \\ \vdots & \vdots & \ddots & \vdots \\ {[u_{1}^{qL} ,u_{1}^{qU} ]} & {[u_{2}^{qL} ,u_{2}^{qU} ]} & \cdots & {[u_{n}^{qL} ,u_{n}^{qU} ]} \\ \end{array} } \right) \hfill \\ \end{gathered}\).

We divide the interval sequence \(\left\{ {[u_{1}^{kL} ,u_{1}^{kU} ],[u_{2}^{kL} ,u_{2}^{kU} ], \ldots ,[u_{n}^{kL} ,u_{n}^{kU} ]} \right\}\) into the following two real number sequences \(\left\{ {u_{1}^{kL} ,u_{2}^{kL} , \ldots ,u_{n}^{kL} } \right\}\) and \(\left\{ {u_{1}^{kU} ,u_{2}^{kU} , \ldots ,u_{n}^{kU} } \right\}\). Therefore, their mathematical expectations \(\overline{u}^{kL} ,\overline{u}^{kU}\) and standard variances \(\overline{sv}^{kL} ,\overline{sv}^{kU}\) are calculated as:

$$ \overline{u}^{kL} = \frac{1}{n}\sum\limits_{j = 1}^{n} {u_{j}^{kL} } ,\;\overline{sv}^{kL} = \sqrt {\frac{1}{n - 1}\sum\limits_{j = 1}^{n} {\left( {u_{j}^{kL} - \overline{u}^{kL} } \right)^{2} } } ,k = 1,2, \ldots ,q, $$
(13)
$$ \overline{u}^{kU} = \frac{1}{n}\sum\limits_{j = 1}^{n} {u_{j}^{kU} } ,\;\overline{sv}^{kU} = \sqrt {\frac{1}{n - 1}\sum\limits_{j = 1}^{n} {\left( {u_{j}^{kU} - \overline{u}^{kU} } \right)^{2} } } ,k = 1,2, \ldots ,q, $$
(14)

where \(n\) is the number of data in the normal distribution data sequence \(\left\{ {u_{1}^{kL} ,u_{2}^{kL} , \ldots ,u_{n}^{kL} } \right\}\) or normal distribution data sequence \(\left\{ {u_{1}^{kU} ,u_{2}^{kU} , \ldots ,u_{n}^{kU} } \right\}\).

This is then followed by the generation of probability for the interval number \([u_{j}^{kL} ,u_{j}^{kU} ]\):

$$ Pro_{kj} = P\left( {x \le u_{j}^{kU} } \right) - P\left( {x \le u_{j}^{kL} } \right),k = 1,2 \cdots ,q,j = 1,2, \ldots ,n. $$
(15)

where (i) \(P\left( {x \le u_{j}^{kL} } \right) = P\left( {\frac{{\overline{u}^{kL} - u_{j}^{kL} }}{{{{\overline{sv}^{kL} } \mathord{\left/ {\vphantom {{\overline{sv}^{kL} } {\sqrt n }}} \right. \kern-\nulldelimiterspace} {\sqrt n }}}}} \right)\), if \(u_{j}^{kL} < \overline{u}^{kL}\);

(ii) \(P\left( {x \le u_{j}^{kL} } \right) = P\left( {\frac{{u_{j}^{kL} - \overline{u}^{kL} }}{{{{\overline{sv}^{kL} } \mathord{\left/ {\vphantom {{\overline{sv}^{kL} } {\sqrt n }}} \right. \kern-\nulldelimiterspace} {\sqrt n }}}}} \right)\), if \(u_{j}^{kL} > \overline{u}^{kL}\);

(iii) \(P\left( {x \le u_{j}^{kU} } \right) = P\left( {\frac{{\overline{u}^{kU} - u_{j}^{kU} }}{{{{\overline{sv}^{kU} } \mathord{\left/ {\vphantom {{\overline{sv}^{kU} } {\sqrt n }}} \right. \kern-\nulldelimiterspace} {\sqrt n }}}}} \right)\), if \(u_{j}^{kU} < \overline{u}^{kU}\);

(iv) \(P\left( {x \le u_{j}^{kU} } \right) = P\left( {\frac{{u_{j}^{kU} - \overline{u}^{kU} }}{{{{\overline{sv}^{kU} } \mathord{\left/ {\vphantom {{\overline{sv}^{kU} } {\sqrt n }}} \right. \kern-\nulldelimiterspace} {\sqrt n }}}}} \right)\), if \(u_{j}^{kU} > \overline{u}^{kU}\).

Let \(L_{kj} = u_{j}^{kU} - u_{j}^{kL} ,k = 1,2 \ldots, q,j = 1,2, \ldots, n\). In the process of MALSGDM problems, the larger the value of \(L_{kj} = u_{j}^{kU} - u_{j}^{kL}\) is, the more decentralized the attribute \(a_{j}\)’s utility values are, and the greater the difference of the utility values among different alternatives is with respect to attribute \(a_{j}\). Thus, the higher the degree of distinction among different alternatives occurs with attribute \(a_{j}\), which implies that attribute \(a_{j}\) provides the DMs with effective information, and that attribute \(a_{j}\) is more important in MALSGDM problems and should be assigned a bigger weight. Thus, the attributes’ weights are derived as follows:

$$ w_{kj} = \frac{{Pro_{kj} }}{{\sum\nolimits_{j = 1}^{n} {Pro_{kj} } }},k = 1,2 \ldots ,q,j = 1,2, \ldots ,n, $$
(16)

thus \(\sum\nolimits_{j = 1}^{n} {w_{kj} } = 1\) and \(w_{kj} \in [0,1],k = 1,2 \ldots ,q,j = 1,2, \ldots ,n\).

3.4 Determining the Ranking of Alternatives with Regret Theory (Phase IV)

DMs are bounded rational under the complex risk decision-making environment. Therefore, based on the obtained weight vector of DMs \(\omega = (\omega_{1} ,\omega_{2} , \ldots ,\omega_{q} )^{T}\) and weight vectors of attributes \(w_{k} = (w_{k1} ,w_{k2} , \ldots ,w_{kn} )^{T} (k = 1,2 \ldots ,q)\), we first construct the reference utility values, then the perceived utility matrices are obtained, which is followed by the integration of the comprehensive perceived utility matrix. In the end, we obtain the ranking of alternatives \(\{ x_{1} ,x_{2} , \ldots ,x_{n} \}\). The flow chart of Phase IV can be seen in Fig. 6.

Fig. 6
figure 6

Phase IV: Desirable alternative selection process

Full size image

Regret theory utilizes the regret-rejoice function to reflect the DM’s psychological perception that depends on the deviation of the utility values between the alternative they choose and the reference alternative. Now, we propose a decision-making approach to derive the ranking of alternatives with regret theory.

Algorithm II

Step 1. For the utility matrices \(U_{k} = (u_{ij}^{k} )_{m \times n} (k = 1,2 \ldots ,q)\), let \(u_{i}^{k} = \sum\nolimits_{j = 1}^{n} {w_{kj} u_{ij}^{k} } ,i = 1,2, \ldots ,m\), then \(\left( {u_{1}^{k} ,u_{2}^{k} , \ldots ,u_{m}^{k} } \right)^{T}\) can be deemed as a reference utility vector. According to regret-rejoice function (i.e., Eq. (4)), the perceived utility value of LDE \(\tilde{h}_{ij}^{k}\) is calculated as:

$$ pu(\tilde{h}_{ij}^{k} ) = u_{ij}^{k} + R\left( {u_{ij}^{k} - u_{i}^{k} } \right) = u_{ij}^{k} + 1 - exp\left( { - \delta \left( {u_{ij}^{k} - \sum\limits_{j = 1}^{n} {w_{kj} u_{ij}^{k} } } \right)} \right), $$
(17)

thus, the perceived utility matrices \(PU_{k} = \left( {pu(\tilde{h}_{ij}^{k} )} \right)_{m \times n} ,k = 1,2, \ldots ,q\) are constructed.

Step 2. By using the DMs’ weights \(\omega = (\omega_{1} ,\omega_{2} , \ldots ,\omega_{q} )^{T}\), we fuse these perceived utility matrices \(PU_{k} (k = 1,2, \cdots ,q)\) into a comprehensive perceived utility matrix \(PU =\) \(\left( {pu(\tilde{h}_{ij}^{{}} )} \right)_{m \times n}\), where

$$ pu(\tilde{h}_{ij}^{{}} ) = \sum\limits_{k = 1}^{q} {\omega_{k} \cdot pu(\tilde{h}_{ij}^{k} )} ,i = 1,2, \ldots ,m,j = 1,2, \ldots ,n. $$
(18)

Step 3. Let \(\varpi = (\varpi_{1} ,\varpi_{2} , \ldots ,\varpi_{n} )^{T}\), where \(\varpi_{j} = \sum\limits_{k = 1}^{q} {\omega_{k} w_{kj} } ,j = 1,2, \cdots ,n\). As \(\varpi_{j} \ge 0\) and

$$ \sum\limits_{j = 1}^{n} {\varpi_{j} } = \sum\limits_{j = 1}^{n} {\sum\limits_{k = 1}^{q} {\omega_{k} w_{kj} } } = \sum\limits_{k = 1}^{q} {\omega_{k} \left( {\sum\limits_{j = 1}^{n} {w_{kj} } } \right)} = \sum\limits_{k = 1}^{q} {\omega_{k} } = 1, $$
(19)

thus, \(\varpi = (\varpi_{1} ,\varpi_{2} , \cdots ,\varpi_{n} )^{T}\) can be regarded as the attribute weight vector of the comprehensive perceived utility matrix \(PU = \left( {pu(\tilde{h}_{ij}^{{}} )} \right)_{m \times n}\).

Step 4. Calculate the comprehensive perceived utility value of alternative \(x_{i}\) as follows:

$$ U(x_{i} ) = \sum\limits_{j = 1}^{n} {\varpi_{j} } \cdot pu(\tilde{h}_{ij}^{{}} ),i = 1,2, \cdots ,m, $$
(20)

Step 5. Determine the ranking order of alternatives with \(U(x_{i} )(i = 1,2, \cdots ,m)\), and select/obtain the best alternative \(x^{*}\), which is represented as \(\mathop {\max }\limits_{i} \left\{ {U(x_{i} )} \right\}\).

4 Case Study

Now, we will apply the developed CLDLSGDM method to the hospital assessment problem, then the sensitivity analysis and comparative analysis will be performed to illustrate the advantages of the developed CLDLSGDM method.

4.1 Application to Evaluate the Performance of Hospitals in China

Emergency health management in China has been proposed to deal with the risk of major public health incidents, such as COVID-19. Emergency health management refers to the government and other public medical institutions taking a series of necessary and effective steps towards protecting the safety of public life, health and property, and promoting the harmonious development of the society by establishing necessary response mechanisms and by applying science, technology, planning and management to the process of prevention, response, disposal and recovery of major public health incidents.

An important aspect of emergency health management is the effective evaluation of hospitals, so that the government might be able to coordinate and direct hospital resources in order to deal with major public health events effectively as soon as they occur. In this section, we give a numerical example to evaluate the performance of 4 listed public hospitals in Hefei, China, which illustrates the practicability and validity of the proposed CLDLSGDM method. The 4 listed public hospitals are The Second Affiliated Hospital of Anhui Medical University (\(x_{1}\)), Anhui Provincial Hospital (\(x_{2}\)), The First Affiliated Hospital of Anhui Medical University (\(x_{3}\)) and The First Affiliated Hospital of Anhui University of Traditional Chinese Medicine (\(x_{4}\)). Three evaluation attributes of hospitals are considered as follows: fixed assets (\(a_{1}\)), the number of full-time employees (\(a_{2}\)) and patient evaluation index (\(a_{3}\)). The above 4 public hospitals compete with each other as they all engage in medical services. Let \(S = \left\{ {s_{0} :very\;poor,} \right.\) \(\left. {s_{1} :poor,s_{2} :medium,s_{3} :good,\;s_{4} :very\;good} \right\}\) be a LTS, with a group consensus index threshold of \(\theta = 0.85\), let the costs be \((c_{1} ,c_{2} , \cdots ,c_{20} ) = (3,6,1,2,1,5,4,6,2,3,2,2,5,3,2,7,2,6,5,1)\) (Ben-Arieh et al. 2009; Gong et al. 2021), and the regret aversion coefficient \(\delta = 0.3\) (Zhang et al. 2016). To evaluate the medical and health service capacities of these hospitals \(\{ x_{1} ,x_{2} ,x_{3} ,x_{4} \}\), 20 DMs \(\{ e_{1} ,e_{2} , \ldots ,e_{20} \}\) provide their evaluation opinions, with LDEs, on four hospitals with respect to three attributes. Due to the complexity and ambiguity of the human mind, it is impracticable to require DMs to provide numerical judgements about four public hospitals. Thus, they are required to provide their preference using LDEs. For example, after DM \(e_{1}\) compares The Second Affiliated Hospital of Anhui Medical University (\(x_{1}\)) and The First Affiliated Hospital of Anhui Medical University (\(x_{3}\)), they think that the linguistic preference degree of The Second Affiliated Hospital of Anhui Medical University (\(x_{1}\)) over The First Affiliated Hospital of Anhui Medical University (\(x_{3}\)) may be \( very\;poor^{\prime\prime},poor,medium\) or \( very\;good\), and the their corresponding probabilities are 30%, 30%, 30%, and 10%, respectively. Thus, the evaluation information of The Second Affiliated Hospital of Anhui Medical University (\(x_{1}\)) over The First Affiliated Hospital of Anhui Medical University (\(x_{3}\)) from DM \(e_{1}\) can be depicted by LDE \( h_{{13}}^{1} = \{ (s_{0} ,0.3),(s_{1} ,0.3),(s_{2} ,0.3),(s_{3} ,0),(s_{4} ,0.1)\} \). Therefore, after interviewing 20 DMs and selecting the evaluation information in a similar way, twenty linguistic distribution information decision-making matrices \(H_{k} = (h_{ij}^{k} )_{4 \times 3} (k = 1,2, \cdots ,20)\) are obtained, which are shown in the Appendix.

We utilize the proposed CLDLSGDM method to appraise the relative performance of the 4 public hospitals and derive an overall ranking.

5 Phase I: CRP

By using Eqs. (5) and (7), we obtain the consensus matrix \(CM = \left( {cm_{kl} } \right)_{20 \times 20}\) as follows:

$$ CM = \left( {\begin{array}{*{20}c} {1.00} & {0.90} & {0.75} & {0.89} & {0.89} & {0.91} & {0.89} & {0.90} & {0.90} & {0.80} & {0.90} & {0.90} & {0.90} & {0.90} & {0.88} & {0.90} & {0.43} & {0.89} & {0.90} & {0.90} \\ {} & {1.00} & {0.74} & {0.81} & {0.87} & {0.87} & {0.86} & {0.88} & {0.87} & {0.76} & {0.86} & {0.87} & {0.88} & {0.83} & {0.85} & {0.87} & {0.46} & {0.85} & {0.84} & {0.84} \\ {} & {} & {1.00} & {0.77} & {0.74} & {0.74} & {0.71} & {0.71} & {0.71} & {0.42} & {0.75} & {0.75} & {0.73} & {0.73} & {0.72} & {0.70} & {0.40} & {0.74} & {0.71} & {0.71} \\ {} & {} & {} & {1.00} & {0.82} & {0.86} & {0.84} & {0.86} & {0.80} & {0.76} & {0.87} & {0.88} & {0.88} & {0.83} & {0.85} & {0.80} & {0.45} & {0.88} & {0.82} & {0.82} \\ {} & {} & {} & {} & {1.00} & {0.88} & {0.85} & {0.82} & {0.88} & {0.77} & {0.85} & {0.82} & {0.85} & {0.83} & {0.82} & {0.85} & {0.44} & {0.84} & {0.82} & {0.85} \\ {} & {} & {} & {} & {} & {1.00} & {0.89} & {0.85} & {0.88} & {0.75} & {0.86} & {0.87} & {0.86} & {0.86} & {0.80} & {0.91} & {0.91} & {0.83} & {0.83} & {0.85} \\ {} & {} & {} & {} & {} & {} & {1.00} & {0.88} & {0.86} & {0.75} & {0.87} & {0.87} & {0.83} & {0.83} & {0.84} & {0.88} & {0.44} & {0.88} & {0.83} & {0.84} \\ {} & {} & {} & {} & {} & {} & {} & {1.00} & {0.85} & {0.74} & {0.87} & {0.81} & {0.83} & {0.85} & {0.83} & {0.88} & {0.45} & {0.89} & {0.88} & {0.85} \\ {} & {} & {} & {} & {} & {} & {} & {} & {1.00} & {0.75} & {0.86} & {0.83} & {0.85} & {0.86} & {0.80} & {0.86} & {0.43} & {0.85} & {0.87} & {0.85} \\ {} & {} & {} & {} & {} & {} & {} & {} & {} & {1.00} & {0.75} & {0.77} & {0.76} & {0.77} & {0.75} & {0.76} & {0.41} & {0.76} & {0.77} & {0.75} \\ {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {1.00} & {0.85} & {0.86} & {0.85} & {0.86} & {0.89} & {0.43} & {0.89} & {0.87} & {0.83} \\ {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {1.00} & {0.85} & {0.88} & {0.82} & {0.87} & {0.46} & {0.87} & {0.83} & {0.83} \\ {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {1.00} & {0.84} & {0.85} & {0.86} & {0.43} & {0.86} & {0.85} & {0.83} \\ {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {1.00} & {0.81} & {0.86} & {0.43} & {0.86} & {0.87} & {0.86} \\ {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {1.00} & {0.82} & {0.44} & {0.82} & {0.83} & {0.85} \\ {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {1.00} & {0.43} & {0.85} & {0.85} & {0.86} \\ {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {1.00} & {0.46} & {0.45} & {0.46} \\ {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {1.00} & {0.85} & {0.85} \\ {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {1.00} & {0.88} \\ {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {1.00} \\ \end{array} } \right), $$

then we utilize Eq. (8) to get the DMs’ group consensus index \(GCI = 0.7936\). As \(GCI = 0.7936 < 0.85 = \theta\), we apply Algorithm I to improve the group consensus degree among DMs. As \(cm_{3,17}^{{}} = 0.40,cm_{3,10}^{{}} = 0.42\) and \(cm_{10,17}^{{}} = 0.41\) are the smallest three elements in consensus matrix \(CM = \left( {cm_{kl} } \right)_{20 \times 20}\), DMs \(e_{3} ,e_{10}\) and \(e_{17}\) need to adjust their evaluation opinions and another seventeen DMs do not need to modify their evaluation opinions, i.e., \(\tilde{H}_{k} = H_{k} (k = 1,2,4,5,6,7,8,9,11,12,13,14,15,16,18,19,20)\). The adjustment costs of DMs \(e_{3}\) and \(e_{10}\) are \(c_{3} = 1\) and \(c_{10} = 3\), respectively. According to Step 6 in Algorithm I, we have \(c_{3} < c_{10}\), and then we change DM \(e_{3}\)’s evaluation opinions toward to DM \(e_{10}\). Therefore, we obtain the adjusted linguistic distribution information decision-making matrices \(\tilde{H}_{3}\) as follows:

Similarly, one can obtain the adjusted linguistic distribution information decision-making matrices \(\tilde{H}_{k} (k = 10,17)\) which are derived as follows:

Then, one can determine the following new consensus matrix \(C\tilde{M} = \left( {c\tilde{m}_{kl} } \right)_{20 \times 20}\):

$$ C\tilde{M} = \left( {\begin{array}{*{20}c} {1.00} & {0.90} & {0.90} & {0.89} & {0.89} & {0.91} & {0.89} & {0.90} & {0.90} & {0.89} & {0.90} & {0.90} & {0.90} & {0.90} & {0.88} & {0.90} & {0.86} & {0.89} & {0.90} & {0.90} \\ {} & {1.00} & {0.86} & {0.81} & {0.87} & {0.87} & {0.86} & {0.88} & {0.87} & {0.85} & {0.86} & {0.87} & {0.88} & {0.83} & {0.85} & {0.87} & {0.83} & {0.85} & {0.84} & {0.84} \\ {} & {} & {1.00} & {0.86} & {0.87} & {0.86} & {0.87} & {0.85} & {0.85} & {0.84} & {0.88} & {0.86} & {0.87} & {0.86} & {0.83} & {0.83} & {0.85} & {0.85} & {0.85} & {0.84} \\ {} & {} & {} & {1.00} & {0.82} & {0.86} & {0.84} & {0.86} & {0.80} & {0.83} & {0.87} & {0.88} & {0.88} & {0.83} & {0.85} & {0.80} & {0.82} & {0.88} & {0.82} & {0.82} \\ {} & {} & {} & {} & {1.00} & {0.88} & {0.85} & {0.82} & {0.88} & {0.83} & {0.85} & {0.82} & {0.85} & {0.83} & {0.82} & {0.85} & {0.80} & {0.84} & {0.82} & {0.85} \\ {} & {} & {} & {} & {} & {1.00} & {0.89} & {0.85} & {0.88} & {0.85} & {0.86} & {0.87} & {0.86} & {0.86} & {0.80} & {0.91} & {0.91} & {0.83} & {0.83} & {0.85} \\ {} & {} & {} & {} & {} & {} & {1.00} & {0.88} & {0.86} & {0.83} & {0.87} & {0.87} & {0.83} & {0.83} & {0.84} & {0.88} & {0.82} & {0.88} & {0.83} & {0.84} \\ {} & {} & {} & {} & {} & {} & {} & {1.00} & {0.85} & {0.83} & {0.87} & {0.81} & {0.83} & {0.85} & {0.83} & {0.88} & {0.82} & {0.89} & {0.88} & {0.85} \\ {} & {} & {} & {} & {} & {} & {} & {} & {1.00} & {0.84} & {0.86} & {0.83} & {0.85} & {0.86} & {0.80} & {0.86} & {0.80} & {0.85} & {0.87} & {0.85} \\ {} & {} & {} & {} & {} & {} & {} & {} & {} & {1.00} & {0.83} & {0.84} & {0.83} & {0.83} & {0.80} & {0.85} & {0.81} & {0.85} & {0.84} & {0.84} \\ {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {1.00} & {0.85} & {0.86} & {0.85} & {0.86} & {0.89} & {0.83} & {0.89} & {0.87} & {0.83} \\ {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {1.00} & {0.85} & {0.88} & {0.82} & {0.87} & {0.80} & {0.87} & {0.83} & {0.83} \\ {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {1.00} & {0.84} & {0.85} & {0.86} & {0.80} & {0.86} & {0.85} & {0.83} \\ {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {1.00} & {0.81} & {0.86} & {0.83} & {0.86} & {0.87} & {0.86} \\ {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {1.00} & {0.82} & {0.79} & {0.82} & {0.83} & {0.85} \\ {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {1.00} & {0.82} & {0.85} & {0.85} & {0.86} \\ {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {1.00} & {0.83} & {0.85} & {0.83} \\ {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {1.00} & {0.85} & {0.85} \\ {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {1.00} & {0.88} \\ {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {1.00} \\ \end{array} } \right), $$

and the group consensus index is \(GCI = 0.8515 > 0.85 = \theta\). Thus, DMs achieve an acceptable consensus level.

6 Phase II: Derive DM Weights

Based on the obtained consensus matrix \(C\tilde{M} = \left( {c\tilde{m}_{kl} } \right)_{20 \times 20}\), we utilize Eqs. (9)–(12) to calculate the weight vector of DMs:

$$ \begin{gathered} \omega = (0.0518,0.0452,0.0517,0.0517,0.0512,0.0518,0.0517,0.0452,0.0517,0.0452, \hfill \\ \;\;\;\;\;\;\;\;0.0518,0.0452,0.0517,0.0452,0.0518,0.0512,0.0518,0.0518,0.0512,0.0512)^{T} . \hfill \\ \end{gathered} $$

7 Phase III: Generate Attribute Weights

According to the obtained linguistic distribution information decision-making matrices \(\tilde{H}_{k} (k = 1,2,\ldots,20)\), we can obtain the utility matrices \(U_{k} = (u_{ij}^{k} )_{m \times n} (k = 1,2 \ldots,20)\) as follows:

$$ \begin{gathered} U_{1} = \left( {\begin{array}{*{20}c} {2.00} & {1.60} & {1.30} \\ {2.10} & {1.80} & {1.30} \\ {2.50} & {2.90} & {2.90} \\ {1.10} & {1.30} & {0.90} \\ \end{array} } \right),U_{2} = \left( {\begin{array}{*{20}c} {1.90} & {1.70} & {1.40} \\ {2.00} & {2.10} & {1.40} \\ {2.60} & {2.80} & {3.00} \\ {1.20} & {1.50} & {1.20} \\ \end{array} } \right),U_{3} = \left( {\begin{array}{*{20}c} {1.90} & {1.40} & {1.30} \\ {2.20} & {2.10} & {1.70} \\ {2.90} & {2.90} & {2.80} \\ {1.10} & {1.20} & {1.10} \\ \end{array} } \right),U_{4} = \left( {\begin{array}{*{20}c} {2.10} & {1.70} & {1.20} \\ {2.20} & {1.90} & {1.40} \\ {2.60} & {3.10} & {2.80} \\ {1.40} & {1.40} & {0.80} \\ \end{array} } \right), \hfill \\ U_{5} = \left( {\begin{array}{*{20}c} {1.50} & {1.40} & {1.50} \\ {2.20} & {1.50} & {1.50} \\ {2.80} & {2.70} & {2.80} \\ {1.00} & {1.10} & {1.20} \\ \end{array} } \right),U_{6} = \left( {\begin{array}{*{20}c} {2.20} & {1.70} & {1.30} \\ {2.20} & {2.00} & {1.40} \\ {2.70} & {2.70} & {2.80} \\ {1.30} & {1.40} & {0.90} \\ \end{array} } \right),U_{7} = \left( {\begin{array}{*{20}c} {1.90} & {2.00} & {1.40} \\ {2.30} & {2.10} & {1.50} \\ {2.60} & {2.60} & {3.10} \\ {1.20} & {1.60} & {1.20} \\ \end{array} } \right),U_{8} = \left( {\begin{array}{*{20}c} {2.10} & {1.80} & {1.20} \\ {2.20} & {1.90} & {1.40} \\ {2.60} & {2.80} & {2.80} \\ {1.20} & {1.40} & {1.20} \\ \end{array} } \right), \hfill \\ U_{9} = \left( {\begin{array}{*{20}c} {2.20} & {1.40} & {1.40} \\ {2.20} & {2.10} & {1.60} \\ {1.90} & {2.90} & {2.80} \\ {1.00} & {1.10} & {1.20} \\ \end{array} } \right),U_{10} = \left( {\begin{array}{*{20}c} {1.70} & {1.80} & {1.30} \\ {2.00} & {1.80} & {1.40} \\ {2.80} & {3.00} & {3.10} \\ {0.70} & {2.10} & {0.90} \\ \end{array} } \right),U_{11} = \left( {\begin{array}{*{20}c} {1.80} & {1.50} & {1.10} \\ {2.50} & {1.90} & {1.40} \\ {2.40} & {3.00} & {2.90} \\ {1.30} & {1.50} & {1.00} \\ \end{array} } \right),U_{12} = \left( {\begin{array}{*{20}c} {2.10} & {1.80} & {1.20} \\ {2.30} & {1.90} & {1.40} \\ {2.60} & {2.60} & {2.80} \\ {1.20} & {1.40} & {1.00} \\ \end{array} } \right), \hfill \\ U_{13} = \left( {\begin{array}{*{20}c} {1.80} & {1.50} & {1.40} \\ {1.90} & {1.90} & {1.50} \\ {2.60} & {2.80} & {3.00} \\ {1.40} & {1.40} & {1.00} \\ \end{array} } \right),U_{14} = \left( {\begin{array}{*{20}c} {2.20} & {1.70} & {1.70} \\ {2.10} & {1.90} & {1.80} \\ {2.80} & {3.10} & {3.00} \\ {1.00} & {1.00} & {0.80} \\ \end{array} } \right),U_{15} = \left( {\begin{array}{*{20}c} {1.70} & {1.30} & {1.40} \\ {2.20} & {1.90} & {1.40} \\ {2.70} & {3.10} & {2.60} \\ {1.20} & {2.20} & {0.70} \\ \end{array} } \right),U_{16} = \left( {\begin{array}{*{20}c} {1.80} & {1.40} & {1.50} \\ {2.30} & {2.00} & {1.50} \\ {2.10} & {3.10} & {3.00} \\ {1.30} & {1.40} & {1.20} \\ \end{array} } \right), \hfill \\ \end{gathered} $$
$$ U_{17} = \left( {\begin{array}{*{20}c} {2.10} & {1.80} & {1.20} \\ {2.60} & {2.30} & {1.70} \\ {2.90} & {3.00} & {2.70} \\ {1.00} & {1.20} & {0.80} \\ \end{array} } \right),U_{18} = \left( {\begin{array}{*{20}c} {2.20} & {2.00} & {1.70} \\ {2.20} & {1.90} & {1.20} \\ {2.60} & {3.00} & {3.00} \\ {1.30} & {1.60} & {1.00} \\ \end{array} } \right),U_{19} = \left( {\begin{array}{*{20}c} {1.80} & {1.70} & {1.20} \\ {1.90} & {2.00} & {1.40} \\ {2.70} & {3.20} & {3.00} \\ {0.80} & {1.20} & {1.00} \\ \end{array} } \right),U_{20} = \left( {\begin{array}{*{20}c} {1.60} & {1.90} & {1.70} \\ {2.40} & {2.20} & {1.60} \\ {2.60} & {3.10} & {3.00} \\ {1.00} & {1.20} & {1.10} \\ \end{array} } \right). $$

Then, we utilize Eqs. (13)–(16) to calculate the attribute weight vectors:

$$ \begin{gathered} w_{1} = (0.3744,0.1287,0.4969)^{T} ,w_{2} = (0.5326,0.1503,0.3172)^{T} , \hfill \\ w_{3} = (0.4789,0.4292,0.0919)^{T} ,w_{4} = (0.4913,0.3763,0.1323)^{T} , \hfill \\ w_{5} = (0.3952,0.0218,0.5830)^{T} ,w_{6} = (0.3655,0.6314,0.0031)^{T} , \hfill \\ w_{7} = (0.7691,0.0883,0.1426)^{T} ,w_{8} = (0.2717,0.5106,0.2177)^{T} , \hfill \\ w_{9} = (0.1753,0.6793,0.1455)^{T} ,w_{10} = (0.1240,0.5901,0.2859)^{T} , \hfill \\ w_{11} = (0.0787,0.2806,0.6407)^{T} ,w_{12} = (0.1437,0.4308,0.4254)^{T} , \hfill \\ w_{13} = (0.4050,0.2217,0.3733)^{T} ,w_{14} = (0.3335,0.2252,0.4413)^{T} , \hfill \\ w_{15} = (0.0928,0.9062,0.0010)^{T} ,w_{16} = (0.1510,0.6923,0.1567)^{T} , \hfill \\ w_{17} = (0.4352,0.5442,0.0206)^{T} ,w_{18} = (0.3664,0.2365,0.3971)^{T} , \hfill \\ w_{19} = (0.3582,0.1312,0.5106)^{T} ,w_{20} = (0.6572,0.1216,0.2212)^{T} . \hfill \\ \end{gathered} $$

8 Phase IV: Determine the Ranking Order of Alternatives

First, with the perceived utility function (i.e., Eq. (17)), we construct perceived utility matrices \(PU_{k} = \left( {pu(\tilde{h}_{ij}^{k} )} \right)_{4 \times 3} (k = 1,2, \ldots ,20)\) as follows:

$$ \begin{gathered} PU_{1} = \left( {\begin{array}{*{20}c} {2.1129} & {1.5998} & {1.2056} \\ {2.2361} & {1.3354} & {1.2018} \\ {2.4220} & {2.9439} & {2.9439} \\ {1.1219} & {1.3788} & {0.8614} \\ \end{array} } \right), \;PU_{2} = \left( {\begin{array}{*{20}c} {1.9550} & {1.6966} & {1.3021} \\ {2.0682} & {1.6804} & {1.2844} \\ {2.5518} & {2.8128} & {3.0703} \\ {1.1964} & {1.5736} & {1.1864} \\ \end{array} } \right), \; PU_{3} = \left( {\begin{array}{*{20}c} {1.9777} & {1.3285} & {1.1959} \\ {2.2263} & {2.0967} & {1.5687} \\ {2.9028} & {2.9028} & {2.7724} \\ {1.0870} & {1.2170} & {1.0807} \\ \end{array} } \right), \hfill \\ PU_{4} = \left( {\begin{array}{*{20}c} {2.1777} & {1.6601} & {0.9918} \\ {2.2635} & {1.8753} & {1.2095} \\ {2.5335} & {3.1820} & {2.7956} \\ {1.4235} & {1.4235} & {0.6310} \\ \end{array} } \right), \; PU_{5} = \left( {\begin{array}{*{20}c} {1.5007} & {1.3702} & {1.5007} \\ {2.3193} & {1.4135} & {1.4135} \\ {2.8007} & {2.6702} & {2.8007} \\ {0.9637} & {1.0944} & {1.2241} \\ \end{array} } \right),\; PU_{6} = \left( {\begin{array}{*{20}c} {2.2911} & {1.6440} & {1.1094} \\ {2.2379} & {1.9784} & {1.1769} \\ {2.6999} & {2.6999} & {2.8295} \\ {1.2813} & {1.4114} & {0.7514} \\ \end{array} } \right), \hfill \\ PU_{7} = \left( {\begin{array}{*{20}c} {1.9186} & {2.0476} & {1.2597} \\ {2.3388} & {2.0793} & {1.2780} \\ {2.5784} & {2.5784} & {3.2207} \\ {1.1893} & {1.7036} & {1.1893} \\ \end{array} } \right),\;PU_{8} = \left( {\begin{array}{*{20}c} {2.1994} & {1.8146} & {1.0203} \\ {2.2935} & {1.9082} & {1.2477} \\ {2.5553} & {2.8162} & {2.8162} \\ {1.1689} & {1.4289} & {1.1689} \\ \end{array} } \right),\; PU_{9} = \left( {\begin{array}{*{20}c} {2.3796} & {1.3570} & {1.3570} \\ {2.2455} & {2.1164} & {1.4573} \\ {1.6249} & {2.9553} & {2.8266} \\ {0.9705} & {1.1009} & {1.2304} \\ \end{array} } \right), \hfill \\ PU_{10} = \left( {\begin{array}{*{20}c} {1.7165} & {1.8455} & {1.1911} \\ {2.0832} & {1.8265} & {1.3024} \\ {2.7370} & {2.9989} & {3.1284} \\ {0.3966} & {2.2436} & {0.6725} \\ \end{array} } \right),\; PU_{11} = \left( {\begin{array}{*{20}c} {1.9477} & {1.5674} & {1.0485} \\ {2.7304} & {1.9787} & {1.3296} \\ {2.2421} & {3.0328} & {2.9034} \\ {1.3400} & {1.5959} & {0.9496} \\ \end{array} } \right), \; PU_{12} = \left( {\begin{array}{*{20}c} {2.2424} & {1.8617} & {1.0766} \\ {2.4534} & {1.9455} & {1.2910} \\ {2.5741} & {2.5741} & {2.8339} \\ {1.1997} & {1.4579} & {0.4378} \\ \end{array} } \right), \hfill \\ PU_{13} = \left( {\begin{array}{*{20}c} {1.8627} & {1.4744} & {1.3432} \\ {1.9438} & {1.9438} & {1.4219} \\ {2.5402} & {2.8019} & {3.0600} \\ {1.4438} & {1.4438} & {0.9219} \\ \end{array} } \right), \; PU_{14} = \left( {\begin{array}{*{20}c} {2.2951} & {1.6487} & {1.6487} \\ {2.1518} & {1.8932} & {1.7625} \\ {2.7521} & {3.1423} & {3.0132} \\ {1.0261} & {1.0261} & {0.7659} \\ \end{array} } \right), \; PU_{15} = \left( {\begin{array}{*{20}c} {1.8031} & {1.2888} & {1.4187} \\ {2.2785} & {1.8918} & {1.2286} \\ {2.5852} & {3.1112} & {2.4512} \\ {0.8878} & {2.2279} & {0.1754} \\ \end{array} } \right), \hfill \\ PU_{16} = \left( {\begin{array}{*{20}c} {1.8926} & {1.3769} & {1.5072} \\ {2.3951} & {2.0099} & {1.3496} \\ {1.8160} & {3.1488} & {3.0198} \\ {1.2838} & {1.4138} & {1.1529} \\ \end{array} } \right),\; PU_{17} = \left( {\begin{array}{*{20}c} {2.1531} & {1.7629} & {0.9596} \\ {2.6531} & {2.2639} & {1.4596} \\ {2.8848} & {3.0148} & {2.6220} \\ {0.9681} & {1.2282} & {0.7043} \\ \end{array} } \right), \;PU_{18} = \left( {\begin{array}{*{20}c} {2.2711} & {2.0137} & {1.6208} \\ {2.3310} & {1.9492} & {1.0270} \\ {2.5210} & {3.0430} & {3.0430} \\ {1.3144} & {1.6992} & {0.9215} \\ \end{array} } \right), \hfill \\ \end{gathered} $$
$$ PU_{19} = \left( {\begin{array}{*{20}c} {1.8914} & {1.7637} & {1.1122} \\ {1.9701} & {2.0976} & {1.3196} \\ {2.6322} & {3.2809} & {3.0241} \\ {0.7525} & {1.2710} & {1.0135} \\ \end{array} } \right),PU_{20} = \left( {\begin{array}{*{20}c} {1.5823} & {1.9699} & {1.7123} \\ {2.4586} & {2.2004} & {1.4032} \\ {2.5542} & {3.1999} & {3.0725} \\ {0.9860} & {1.2450} & {1.1159} \\ \end{array} } \right). $$

By using Eq. (18), one can derive the following comprehensive perceived utility matrix:

$$ PU = \left( {\begin{array}{*{20}c} {2.0068} & {1.6509} & {1.2797} \\ {2.2863} & {1.9265} & {1.3352} \\ {2.5220} & {2.9477} & {2.9102} \\ {1.1032} & {1.4569} & {0.9322} \\ \end{array} } \right). $$

In addition, based on the obtained weight vector of DMs \(\omega = (\omega_{1} ,\omega_{2} , \cdots ,\omega_{20} )^{T}\) and attribute weight vectors \(w_{k} = (w_{k1} ,w_{k2} ,w_{k3} )^{T} (k = 1,2 \cdots ,20)\), we apply Eq. (19) to the attribute weight vector of comprehensive perceived utility matrix as follows:

$$ \varpi = (0.3521,0.3697,0.2781)^{T} . $$

Then, we calculate the comprehensive perceived utility values of public hospitals \(x_{i} (i = 1,2,3,4)\): \(U(x_{1} ) = 1.6730,U(x_{2} ) = 1.8887,U(x_{3} ) = 2.7874,U(x_{4} ) = 1.1864\). Therefore, we determine the ranking order of the four public hospitals to be \(x_{3} \succ x_{2} \succ x_{1} \succ x_{4}\).

8.1 Sensitivity Analysis

There is a parameter \(\delta\) in the developed CLDLSGDM method, where the parameter \(\delta > 0\) is the regret aversion coefficient of DMs and reflects the regret-rejoice psychological preference of DMs. Therefore, we have explored what impact the sensitivity analysis of parameter \(\delta\) might have on the complete ranking of the 4 public hospitals.

The sensitivity analyses of regret aversion coefficient \(\delta\) on the comprehensive perceived utility values of 4 public hospitals are shown in Table 1 and Fig. 7. The sensitivity analyses of regret aversion coefficient \(\delta\) on the complete ranking of 4 public hospitals are shown in Table 2 and Fig. 8.

Table 1 Comprehensive perceived utility values with different \(\delta\)
Full size table
Fig. 7
figure 7

Comprehensive perceived utility values with different \(\delta\)

Full size image
Table 2 The complete ranking results of 4 public hospitals with different \(\delta\)
Full size table
Fig. 8
figure 8

Ranking results of 4 public hospitals with different \(\delta\)

Full size image

From Table 1 and Fig. 7, it is shown that the comprehensive perceived utility values of 4 public hospitals monotonically decrease with respect to the regret aversion coefficient \(\delta\), which may lead to \(u_{ij}^{k} - \sum\limits_{j = 1}^{n} {w_{kj} u_{ij}^{k} } \le 0\). From Figs. 7 and 8, it can be observed that although the optimal public hospital remained unchanged, the complete ranking order of the 4 public hospitals has changed. Specifically, when regret aversion coefficient \(\delta \in (0,2.617)\), the complete ranking order of 4 public hospitals is \(x_{3} \succ x_{2} \succ x_{1} \succ x_{4}\), which indicates that the developed CLDLSGDM method has better robustness when \(\delta \in (0,2.617)\). The gap between public hospital \(x_{2}\) and public hospital \(x_{1}\) tended to decrease as the regret aversion coefficient \(\delta\) increased. When regret aversion coefficient \(\delta \in (2.617,4]\), the complete ranking order of the 4 public hospitals is \(x_{3} \succ x_{1} \succ x_{2} \succ x_{4}\), and the gap between public hospital \(x_{3}\) and public hospital \(x_{1}\) tended to decrease as the regret aversion coefficient \(\delta\) increased. When regret aversion coefficient \(\delta > 5.0493\), the ranking order of public hospital \(x_{3}\) and public hospital \(x_{1}\) changed. According to regret theory, it is known that the bigger the regret aversion coefficient \(\delta\) is, the greater the risk aversion of DMs is, and the more regret aversive a DM is.

8.2 Comparative Analysis

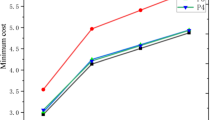
In this subsection, we present a comparison between our method and the methods used in Zhang et al. (2014), Liu and Li (2019), Zheng et al. (2020) and Liu et al. (2021). Differences between our method and the above literature have been summarized and are shown in Table 3.

Table 3 The difference for five methods
Full size table

Applying the methods proposed by Zhang et al. (2014), Liu and Li (2019), Zheng et al. (2020) and Liu et al. (2021), we derive the comprehensive evaluation values of 4 public hospitals, respectively, and then the ranking results of the 4 public hospitals are determined and displayed in Table 4 and Fig. 9.

Table 4 The evaluation results of 4 public hospitals with different methods
Full size table
Fig. 9
figure 9

Ranking results of 10 public hospitals with different methods

Full size image

From Table 4 and Fig. 9, it is obvious that The First Affiliated Hospital of Anhui Medical University (\(x_{3}\)) is the public hospital with the best performance. Although the 4 public hospitals obtain different comprehensive evaluation values with the methods in Zhang et al. (2014), Zheng et al. (2021) and the proposed probabilistic linguistic MALSGDM method, the ranking results of the 4 public hospitals are same, i.e., the complete ranking results of the 4 public hospitals are \(x_{3} \succ x_{2} \succ x_{1} \succ x_{4}\). In addition, the comprehensive prospect evaluation values of the 4 public hospitals obtained using Liu and Li (2019)’s method, in which there are five unknown parameters, could lead to unstable GDM results. Thus, Liu and Li (2019)’s method produces a different ranking order between The Second Affiliated Hospital of Anhui Medical University (\(x_{1}\)) and Anhui Provincial Hospital (\(x_{2}\)) than that obtained by the proposed probabilistic linguistic MALSGDM method. Liu et al. (2021)’s method is considered too complex to evaluate the relationship between DMs, thus Liu et al. (2021)’s method generates a different ranking order between The Second Affiliated Hospital of Anhui Medical University (\(x_{1}\)) and The First Affiliated Hospital of Anhui University of Traditional Chinese Medicine (\(x_{4}\)) than that obtained by the proposed probabilistic linguistic MALSGDM method.

According to the above comparison and sensitivity analysis, the advantages of the developed CLDLSGDM method are summarized as follows:

  1. (1)

    As LDE is a useful modelling tool used to express complex information in GDM, subsequently the CLDLSGDM method seems more reasonable and better suited to coping with LSGDM problems, in which DMs can elicit their opinions with qualitative evaluation information. Therefore, the developed CLDLSGDM method is more practical and can be widely used.

  2. (2)

    Although both the proposed method and Zhang et al. (2014)’s method obtain the same ranking results for the 4 public hospitals, the proposed method is more reasonable and reliable. On the one hand, the method proposed in Zhang et al. (2014) does not consider DMs’ agreements before making decisions and directly utilizes the linguistic distribution weighted averaging operator to integrate the individual attribute values into the overall attribute values, which may lead to unreliable results. On the other hand, the method proposed in Zhang et al. (2014)/this method disregards the psychological perception of DMs in the process of GDM. The proposed method, however, is based on CRP and regret theory and reduces disagreement among DMs with the aim of obtaining an agreed solution. It also considers the DMs are bounded rational under the complex GDM environment. Therefore, the developed CLDLSGDM method is more reasonable and reliable.

  3. (3)

    It can be observed in Table 4 that the ranking results of the 4 public hospitals, derived from both our method and Liu and Li (2019)’s method, are different. The method proposed in Liu and Li (2019) is based on prospect theory, thus, in the process of determining the comprehensive prospect evaluation values of the 4 public hospitals, one must consider how to select the five parameters provided by DMs. These include risk aversion coefficient, risk attitude coefficient, loss-aversion coefficient, gain coefficient and loss coefficient, which may lead to unstable and inaccurate GDM results. However, the proposed method takes the regret aversion psychological characteristics of DMs with only one parameter into account, which reduces the computational complexity. Therefore, the developed CLDLSGDM method is simpler and more efficient.

  4. (4)

    Comparison with the method proposed in Zheng et al. (2021): Although the ranking order of the 4 public hospitals is the same for both the proposed method and the Zheng et al. (2021) method, the proposed method is simpler and more effective. According to the method in Zheng et al. (2021), first, we need to utilize the bi-objective clustering method to divide the experts into different clusters, which is followed by the generation of cluster weights. Then, the comprehensive evaluation values and comprehensive ranking of the 4 public hospitals are obtained, which disregard the regret aversion psychological characteristics of DMs. However, as more DMs become involved in the LSGDM, the clustering method in Zheng et al. (2021) will be much harder to implement. As the proposed method derives the weights of DMs and attributes with the statistical inference principle, the comprehensive ranking of the 4 public hospitals is easy to obtain when considering the regret aversion psychological characteristics of DMs. Therefore, the developed CLDLSGDM method is simpler and more practical.

  5. (5)

    Comparison with method in Liu et al. (2021): Note that the method in Liu et al. (2021) and the proposed method derive different ranking orders of the 4 public hospitals, i.e., the ranking between The Second Affiliated Hospital of Anhui Medical University (\(x_{1}\)) and The First Affiliated Hospital of Anhui University of Traditional Chinese Medicine (\(x_{4}\)) is different. It can be observed that the method presented in Liu et al. (2021) is based on social network analysis in order to develop the consensus model and obtain a comprehensive ranking of the 4 public hospitals. However, although the social relationship among DMs perhaps improves the authenticity of GDM, it takes too much time and costs too much to analyze. In addition, in the original linguistic distribution information decision-making matrices \(H_{k} = (h_{ij}^{k} )_{4 \times 3} (k = 1,2, \ldots ,20)\) provided by DMs, it can be observed that \(h_{1j}^{k} \ge h_{4j}^{k} ,k = 1,2, \ldots ,20\), which indicates that The Second Affiliated Hospital of Anhui Medical University (\(x_{1}\)) is preferred to The First Affiliated Hospital of Anhui University of Traditional Chinese Medicine (\(x_{4}\)), i.e., \(x_{1} \succ x_{4}\). Therefore, the developed CLDLSGDM method in the paper is considered more reliable.

9 Conclusions

With the development of modern society and the economy, As LSGDM problems contain crisp data, the fact that DMs are generally provided qualitative evaluation information is not always effective. Therefore, this paper develops a CLDLSGDM method with linguistic distribution information based on statistical inference principle and regret theory. We first propose a LSGDM CRP with linguistic distribution information in a linguistic distribution information environment, in which the evaluation opinions of DMs are retained as much as possible, in order to improve the group consensus degree. Then, by utilizing the statistical inference principle, we develop two weight allocation methods for DMs and attributes. Furthermore, based on regret theory, we derive the comprehensively perceived utility values of alternatives and obtain the ranking order of alternatives, in which the regret aversion psychological characteristics of DMs are considered. Finally, a numerical example for evaluating the performance of the 4 public hospitals is presented to illustrate the implementation of the developed CLDLSGDM method. The stability analysis of the developed method is performed using a sensitivity analysis of parameter. The results of the comparative analysis demonstrate the advantages of the developed method.

However, the CLDLSGDM method sets a fixed group consensus index threshold and does not study how to determine appropriate group consensus index threshold. Therefore, in the future, based on the simulation experiment, we will further investigate the algorithm to determine the appropriate group consensus index thresholds. Also, the developed CLDLSGDM method can also be employed in other fields, such as social risk evaluation and hotel location selection.