Remarks on singular Cayley graphs and vanishing elements of simple groups

Abstract

Let $\Gamma$ be a finite graph and let $A(\Gamma )$ be its adjacency matrix. Then $\Gamma$ is singular if $A(\Gamma )$ is singular. The singularity of graphs is of certain interest in graph theory and algebraic combinatorics. Here we investigate this problem for Cayley graphs $\mathrm{Cay}(G,H)$ when G is a finite group and when the connecting set H is a union of conjugacy classes of G. In this situation, the singularity problem reduces to finding an irreducible character $\chi$ of G for which $\sum _{h\in H}\,\chi (h)=0.$ At this stage, we focus on the case when H is a single conjugacy class $h^G$ of G; in this case, the above equality is equivalent to $\chi (h)=0$. Much is known in this situation, with essential information coming from the block theory of representations of finite groups. An element $h\in G$ is called vanishing  if $\chi (h)=0$ for some irreducible character $\chi$ of G. We study vanishing elements mainly in finite simple groups and in alternating groups in particular. We suggest some approaches for constructing singular Cayley graphs.

1 Introduction

Let $\Gamma$ be a finite graph and let $A(\Gamma )$ be its adjacency matrix. Then $\Gamma$ is singular if $A(\Gamma )$ is a singular matrix. Alternatively, $\Gamma$ is singular if and only if its spectrum contains the eigenvalue 0. All graphs in this paper are undirected, without loops and without multiple edges; for all definitions please see Sect. 2.

Singular graphs play a significant role in graph theory, and there are many applications in physics and chemistry, see Sect. 2. While the literature on graph spectra is vast, it is not likely that a general theory of graph singularity per se will emerge. Some progress, however, can be made for graphs which admit a group of automorphisms that is transitive on the vertices of the graph. In some cases, the singularity problem then can be solved using techniques from ordinary character theory. The main purpose of this paper is to investigate these applications of character theory in graph theory.

In the following, G denotes a finite group and H denotes a connecting set in G. This is a subset of G such that  (i) H does not contain the identity element 1 of G,   (ii)  $H=H^{-1}:=\{h^{-1}\,|\,h\in H\}$  and  (iii) H generates G, that is, H does not lie in any proper subgroup of G. From these data, the Cayley graph $\Gamma =\mathrm{Cay}(G,H)$ with vertex set $V=G$ and connecting sets H can be defined, see Sect. 2. Here $\Gamma$ is a regular graph of degree |H| and the group G acts transitively on the vertices of $\Gamma .$ Note though that a graph may be the Cayley graph of more than one group and connecting set.

In this paper, we specify the singularity problem to Cayley graphs $\mathrm{Cay}(G,H)$ when the connecting set H is G-invariant, that is, H is a union of conjugacy classes of G. In this case, the following theorem (which is a special case of Theorem 1 in Zieschang [21]) reduces the singularity problem to a problem of character theory, see also the discussion in Sect. 2.

Theorem 1.1

Let G be a group with a G-invariant connecting set H. Then $\mathrm{Cay}(G,H)$ is singular if and only if there is an irreducible character $\chi$ of G with $\sum _{h\in H}\,\chi (h)=0.$ In particular, if $H=h^{G}$ is a single conjugacy class then $\mathrm{Cay}(G,H)$ is singular if and only if there is an irreducible character $\chi$ of G such that $\chi (h)=0.$

Comments:  1. Obviously, if $\chi (h)=0$ for all $h\in H$ then $\mathrm{Cay}(G,H)$ is singular. In addition, $\chi (h)=0$ if and only if $\chi (h^{-1})=0$. Therefore, for constructing singular Cayley graphs it suffices to specify an irreducible character $\chi$ of G and a set X generating G such that $\chi$ takes the value 0 on X. Then, setting $H=\cup _{ g\in G} \,\,g(X\cup X^{-1}) g^{-1},$ we conclude that H is a connecting set and so $\mathrm{Cay}(G,H)$ is singular.

2. Burnside’s theorem on character zeros [5, §32, Exercise 3] shows that every character $\chi$ of degree $>1$ takes the value $\chi (h)=0$ for some $h\in G.$ This implies that for every non-abelian group G there exists a singular Cayley graph on G,  see Proposition 2.1.

3. If the character table of a group G is available explicitly (which is the case for all sporadic simple groups, say) then one can determine in principle all singular Cayley graphs $\mathrm{Cay}(G,M\cup M^{-1})$ for G-invariant M.

In general, we have to look at elements g in G that take the value 0 for certain irreducible characters. Following [7], we say that g is non-vanishing if $\chi (g)\ne 0$ for every irreducible character $\chi$ of G,  otherwise we call gvanishing. Vanishing group elements are of particular interest in the block theory of finite groups. We postpone our comments on this matter until Sect. 4. Here we limit ourselves to the following well-known special case. Let |G| denote the order of G. If p is a prime then $|G|_p$ is the p-part of |G|, that is, $|G_{p}|$ is a power of p and $|G|/|G|_p$ is coprime to p. An element g in G is called p-singular if p divides the order of g.

Lemma 1.2

[5, Theorem 86.3] Let G be a finite group whose order is divisible by the prime p and let $\chi$ an irreducible character of G. Suppose that $\chi (1)$, the degree of $\chi ,$ is a multiple of $|G|_p$. Then $\chi (g)=0$ for every p-singular element $g\in G$.

In what follow p is a prime. The irreducible characters of degree divisible by $|G|_p$ are referred as those of defect 0 (or of p-defect 0 if p is not clear from the context). From this lemma and Theorem 1.1, we obtain the following general result on singular Cayley graphs.

Corollary 1.3

Suppose that p divides |G| and that G possesses an irreducible character of p-defect 0. Then the Cayley graph $\mathrm{Cay}(G,H)$ is singular whenever H is a G-invariant connecting set that consists of p-singular elements.

At the first sight, the existence of such characters do not appear to be a common phenomenon. However, this is not so as the following result shows:

Proposition 1.4

[8, Corollary 2] Let G be a non-abelian finite simple group and let $p>3$ be a prime dividing |G|. Then G has an irreducible character of p-defect 0. This remains true for $p=2,\,3$ unless G is a sporadic group (with known exceptions) or an alternating group.

It follows by Lemma 1.2 that in a non-abelian simple group G any element of order divisible by the prime $p>3$ vanishes at some irreducible character of G. Hence Theorem 1.1 applies and combining Proposition 1.4  with Theorem 1.1  we get

Theorem 1.5

Let $p>3$ be a prime. Let G be a non-abelian simple group and $M\subset G\setminus \{1\}$ a G-invariant subset consisting of p-singular elements. Then the Cayley graph $\mathrm{Cay}(G,M\cup M^{-1})$ is singular. This remains true for $p=2,3$ unless G is an alternating group or a sporadic simple group.

The exceptions in this theorem are genuine. They can be detected easily for alternating groups $A_n$ with $n=7,11, 13$ by inspection of the character tables. However, for arbitrary n the problem of describing all non-vanishing elements in $A_{n}$ is still open. In any case, Theorem 1.5 yields many examples of singular Cayley graphs.

We first state some elementary results which yield a variety of singular Cayley graphs when $G=A_{n}$. For $g\in G$ let $(c_1,\ldots ,c_k),$ with $c_1\ge c_2\ge \cdots \ge c_k,$ be the cycle lengths of g,  in the sense that g has k cycles where the longest cycle is of length $c_{1},$ the second longest of length $c_{2},$ and so on.

Theorem 1.6

Let $G=A_n$ with $n>4$ be the alternating group.

(1) Let $R_1=\{g\in G: c_k=1,c_{k-1}>1\}$ and let $M\subseteq R_1$ be a G-invariant subset. Then $H=M\cup M^{-1}$ is a connecting set and the Cayley graph $\mathrm{Cay}(G,M\cup M^{-1})$ is singular.

(2) Let $R_2=\{g\in G: c_{k-1}>1$ and $c_i\ne 2,4 \}$ for $i=1,\ldots ,k$. Let $M\subseteq R_2$ be G-invariant. Then $H=M\cup M^{-1}$ is a connecting set and the Cayley graph $\mathrm{Cay}(G,M\cup M^{-1})$ is singular.

Note that $R_1$ consists of all elements of $G=A_n$ fixing exactly one point of the natural G-set, whereas $R_2$ consists of elements fixing at most one point and having no 2- and 4-cycles in their cycle decomposition.

An element $g\in G$ is called real  if $g^{-1}$ is conjugate to g. In symmetric groups, all elements are real. This is not the case for alternating groups. From Theorem 1.6, we deduce the following

Theorem 1.7

Let $G=A_n$ with $n\ge 4$ and let $M\subset G$ be any set of non-real elements. Then there exists an irreducible character of G that vanishes on all elements of M. Furthermore, $H=M\cup M^{-1}$ is a connecting set and the Cayley graph Cay(G, H) is singular.

The proof of Theorem 1.6 is based on the Murnahgan–Nakayama formula for computing the values of irreducible characters of symmetric groups (see Sect. 4). In general, the problem of describing, for a given irreducible character $\chi$ of a given group G,  the set $\{g\in G: \chi (g)=0\}$ seems to be intractable, even when G is a symmetric or alternating group. However, the block theory of group characters supplies powerful tools for approaching this problem. In particular, we use block theory to prove Theorems 1.8 and 1.9.

Recall that for every prime p dividing the order of a finite group G the set of all irreducible characters of G is partitioned into blocks  (or p-blocks to be accurate)  and each block B determines a p-subgroup of G,  defined up to conjugacy in G. This group is the defect group of B. If $\chi \in B$ then $\chi (g)=0$ whenever the p-part of g is not contained in a defect group of B. To use this fact, it is important to know the blocks with the smallest defect groups. If $p>3$ then this smallest defect group is $\{1\}$ for $A_n,$ see [8], and this yields Proposition 1.4. (Note that blocks with trivial defect group are called blocks of defect 0.) For $G=A_{n}$ and $p=2$, the smallest defect groups can be easily determined (see Sect. 5), whereas for $p=3$ this is still an open problem. This is discussed in [3, Theorem 2.1], where, for $|G|_3=3^a$ and $n\ne 7$, the order of a smallest defect group is bounded from above by $3^{(a-1)/2}$. We improve this bound to $3^{(a-1)/3},$ see Proposition 6.5.

Now we turn to the simplest (in a sense) version of the singularity problem for Cayley graphs: we assume that $H=C\cup C^{-1}$ where $C\ne \{1\}$ is a single conjugacy class in G. Theorem 1.5 resolves this version of the singularity problem for Cayley graphs of the shape $\mathrm{Cay}(G,H)$ with G simple, except when $G=A_{n}$ and when the elements of C have order $2^\alpha 3^\beta$ for some $\alpha$ and $\beta .$ Theorem 1.7 reduces the problem to the case where $C=C^{-1}$, that is, where H is a single conjugacy class. Below we state some partial results. One of them is the following:

Theorem 1.8

Let $G=S_n$ or $A_n$ with $n\ge 5$ and $n\ne 7,11,$ and let $\omega (G)$ be the set of element orders of G. Let $\omega _{2,3}(G)$ be the set of all numbers in $\omega (G)$ that are not divisible by any prime $p>3$. Then G contains a vanishing element of order m for every $1\ne m\in \omega _{2,3}(G)$.

More can be said about the possible choices of h as an element of order m. By Theorem 1.5, there are no restrictions unless m is of the shape $2^\alpha 3^\beta$ for some $\alpha$ and $\beta .$ In the latter case, h can be chosen as any element of order mfixing a least number of members of the natural set $\{1,\ldots ,\,n\},$ see Theorem 6.8.

Theorem 1.9

Let $G=A_n$ with $n>4$ and let $g\in G.$ Suppose that 2|g| and 3|g| are not in $\omega (G)$. Then g is vanishing unless $n=7$.

This statement is new only for $|g|=2^\alpha 3^\beta ,$ otherwise it follows from Lemma 1.2 and Proposition 1.4. It is not true that all elements satisfying the condition in Theorem 1.9 vanish at the same character of G. But if $\alpha \beta =0$ then this is the case, see Corollary 3.2 and Proposition 6.4.

Notation Our notation for finite simple groups agrees with the Atlas [4]. In particular, $A_n$ means the alternating group on n letters, and $S_n$ is the symmetric group. The underlying set is often denoted by $\Omega _n$, and it can be identified with $\{1,\ldots ,n\}$. For a set $M\subset S_n$ the support  of M is $\mathrm{supp} (M):=\{x\in \Omega _n: gx\ne x$ for some $g\in M\}.$ In the other words, $\mathrm{supp} (M)$ is the complement in $\Omega _n$ of the set of the elements fixed by M.

If G is a group, then we write |G| for the order of G;  if p is a prime then $|G|_p$ is the p-part of |G|,  equivalently, the order of a Sylow $p$-subgroup of G. For nonzero integers $m,\,n$ we denote the g.c.d. of m, n by (m, n). If $g\in G$ then |g| is the order of g. The identity element of G is denoted by 1. For $h\in G$, we write $h^G$ for the conjugacy class of h in G. We write ${\mathrm{Irr}}G$ for the set of all irreducible characters of G. If $\chi$ is a character and $M\subset G$ then $\chi (M)=0$ means that $\chi (g)=0$ for all $g\in M$.

2 Singularity of graphs and Cayley graphs

Let $\Gamma =(V,E)$ be a graph with vertex set V and edge set E. Let $n:=|V|.$ Two distinct vertices u and v are adjacent to each other, denoted $u\sim v,$ if and only if $\{u,\,v\}\in E.$

Let ${\mathbb {F}}$ be a field of characteristic 0. Then we denote by ${\mathbb {F}}V$ the vector space over ${\mathbb {F}}$ with basis V. This is a permutation module for the automorphism group of $\Gamma .$ The natural inner product on ${\mathbb {F}}V$ is given by ${\big ( }v,v'{\big ) }=1$ if $v=v'$ and ${\big ( }v,v'{\big ) }=0$ if $v\ne v',$ for $v,\,v'\in V.$ The adjacency map$\alpha \!:\, {\mathbb {F}}V\rightarrow {\mathbb {F}}V$ is the linear map given by

(1)

for $v\in V.$ Since $v\sim v'$ for $v,\,v'\in V$ if and only if $v'\sim v$ we have ${\big ( }\alpha (v),v'{\big ) }={\big ( }v,\alpha (v'){\big ) }.$ Therefore, $\alpha$ is symmetric with respect to this inner product. The matrix of $\alpha$ with respect to the basis V is the adjacency matrix$A=A(\Gamma )$ of $\Gamma .$ Since A is symmetric, A is diagonalizable when ${\mathbb {F}}={\mathbb {R}}$ so all eigenvalues are real. The spectrum of $\Gamma$ are the eigenvalues $\lambda _{1},\,\lambda _{2},\,\ldots ,\,\lambda _{n}$ of A.

The graph $\Gamma$ is singular if $A(\Gamma )$ is a singular matrix. In other words, $\Gamma$ is singular if and only if 0 is an eigenvalue of $\Gamma .$ Singularity is connected to another special eigenvalue of graphs. The complement$\bar{\Gamma }$ of $\Gamma$ is the graph on the same vertex set with two distinct vertices connected in $\bar{\Gamma }$ if and only if they are not connected in $\Gamma .$ For regular graphs (each vertex has the same number of neighbors), one can show easily that $\Gamma$ is singular if and only if $-1$ is an eigenvalue of $\bar{\Gamma }.$ The nullity$\mathrm{null}(\Gamma )$ of $\Gamma$ is the multiplicity of eigenvalue 0 in $A(\Gamma ).$ So singular graphs are the graphs with $\mathrm{null}(\Gamma )>0.$ For instance, if $\Gamma$ is a bipartite graph with parts $V=V_{1}\,\dot{\cup }\,V_{2},$ then $\mathrm{null}(\Gamma )\ge \big ||V_{1}|-|V_{2}|\big |.$ This observation provides a wealth of examples of singular graphs.

The singularity of graphs plays an important role in several parts of mathematics and applications. It would be impossible to review the vast literature on graph spectra in this paper in order to determine the occurrence of 0 as an eigenvalue. In representation theory and finite incidence geometry, the containment of one permutation character in another often is easiest to establish by showing that a certain graph is non-singular or that its nullity is bounded in a particular way. An example of this technique appears in proofs of the Livingstone–Wagner Theorem [14] about the representations of a permutation group G on the k- and $(k+1)$-subsets of the set on which G acts.

We mention also the significance of graph singularity in systems analysis, physics and chemistry, see for instance the survey article [9]. Essentially, when modeling a discrete mechanical system (Hamiltonians), it is often necessary to work out a linear approximation of an operator where the constituents of the system and the relationships between them are represented by a finite graph. Many characteristics and observables of the system—its energy for instance—then typically involve the spectrum of this graph. This is one of the principles that underpins spectroscopy and Hückel Theory in chemistry [20]. In such applications, the singularity of a molecular graph of a feasible compound typically indicates that the compound is highly reactive, unstable, or nonexistent, see [9].

In order to investigate the singularity problem for graphs, we mention a few general facts so that our discussion here can be seen in a more general context. The problem becomes much more manageable for graphs which have a group of automorphisms that is transitive on the vertices of the graph. These includes in particular Cayley graphs for which we now give the basic definitions. It turns out that the singularity problem for vertex transitive graphs is equivalent to a nullity problem for Cayley graphs.

Let G denote a finite group with identity element 1. Then the subset H of G is a connecting set provided the following holds:

• (i) 1 does not belong to H, 

• (ii) $H^{-1}:=\{h^{-1}\,|\,h\in H\}=H$  and

• (iii) H generates G.

Suppose now that H is a connecting set. Then define the graph $\Gamma =(V,E)$ with vertex set $V=G$ by calling two vertices $u,v\in G$adjacent, denoted $u\sim v,$ if there is some h in H with $hu=v.$ The first condition above is equivalent to saying that $\Gamma$ has no loops. The second conditions hold if and only if all edges are undirected, that is $u\sim v$ if and only if $v\sim u.$ The last condition is equivalent to saying that $\Gamma$ is connected. This graph is the Cayley graph$\,\Gamma = \mathrm{Cay}(G,H)\,$onGwith connecting setH. Its adjacency map $\alpha \!:\, {\mathbb {F}}V\rightarrow {\mathbb {F}}V$ has the form

$$\begin{aligned} \alpha (v):=\sum _{h\in H}\,h^{-1}v \end{aligned}$$

(2)

for all vertices v in $V=G.$ Since $H=H^{-1}$, the set of all neighbors of $v\in \Gamma$ is the set Hv. In particular, $\Gamma$ is regular of degree |H|. Similarly, HHv is the set of all vertices of distance $\le 2$ from v,  and so on. The radius $r(\Gamma )$ of $\Gamma ,$ as a graph invariant, is useful for studying generating sets in a group. Evidently, $r=r(\Gamma )$ is the least number $r>0$ such that $H^{r}:=\{h_{1}h_{2}\cdots h_{r}\,|\, h_{i}\in H\}$ is equal to G,  see property (iii). This invariant is a subject of intensive study by group theorists.

For Cayley graphs, the eigenvalues of the adjacency map can be computed via the irreducible complex representations of the group, see Lovász [15], Babai [1], Zieschang [21], Brouwer and Haemers [2, Proposition 6.3.1], Diaconis and Shahsahani [6] and Ram Murty [18]. Theorem 1.1 is a part of Theorem 1 in [21] which states an explicit formula for eigenvalues when H is G-invariant. For the convenience of the reader, we provide a proof.

Proof of Theorem 1.1

Let $\rho$ be the left regular representation of G on ${\mathbb {C}}G={\mathbb {C}}V,$ given by $\rho (g)(v)=g^{-1}(v)$ for $g\in G$ and $v\in V=G.$ The adjacency map (2) above then becomes

$$\begin{aligned} \alpha (v)=\left( \sum _{h\in H}\,\rho (h)\right) (v). \end{aligned}$$

Note that $\rho (g)\alpha =\alpha \rho (g)$ for $g\in G$ as $g(\sum _{h\in H} \rho (h))g^{-1}=\sum _{h\in H} \rho (h)$.

Let $\lambda _{1},\,\lambda _{2},\ldots ,\,\lambda _{t}$ be the distinct eigenvalues of $\alpha$ and let $E_{1},\,E_{2},\,\ldots ,\,E_{t}$ be the distinct eigenspaces of $\alpha .$ So ${\mathbb {F}}V=E_{1}\oplus E_{2}\oplus \,\ldots \oplus E_{t}$ and each $E_i$$(i=1,\ldots ,t)$ is invariant under $\rho (g)$ for every $g\in G$. Let $\rho _{i}$ and $\alpha _{i}$ denote the restriction of $\rho$ and $\alpha$ to $E_{i},$ respectively. Thus

$$\begin{aligned} \alpha _{i}(x)=\left( \sum _{h\in H}\,\rho _{i}(h)\right) (x)=\lambda _{i} x\, \end{aligned}$$

for $x\in E_{i}.$ Now, if $\mathrm{Cay}(G,H)$ is singular, say $\lambda _{1}=0,$ then every irreducible representation $\rho _{1,i}$ appearing in $\rho _{1}$ satisfies $\sum _{h\in H}\,\chi _{1,i}(h)=0,$ where $\chi _{1,i}$ is the character of $\rho _{1,i}.$ Conversely, if $\chi _{j,i}$ is an irreducible character with $\sum _{h\in H}\,\chi _{j,i}(h)=0$ then $\rho _{j,i}$ appears in $\rho$ and so there is some $E_{j}$ on which $\lambda _{j}=0.$$\square$

Proposition 2.1

Let G be a non-trivial finite group whose order is not a prime. Then there exists a singular Cayley graph $\mathrm{Cay}(G,H)$ for some connecting set $H\subset G$.

Proof: If G is a non-abelian simple group, then the result follows from Burnside’s theorem on character zeros [5, §32, Exercise 3], saying that every nonlinear character (that is, of degree greater than 1) vanishes at some group element $g\in G$. Then we can take for H the union of the conjugacy classes of g and $g^{-1}$. If G has a proper normal subgroup $K\ne 1$ then the result follows from the following lemma (where we can take $H=G\setminus K$):

Lemma 2.2

Suppose that H is a connecting set of G which is a union of cosets of K. Then the adjacency matrix of $\mathrm{Cay}(G,H)$ is singular.

Proof

The adjacency matrix of $\mathrm{Cay}(G,H)$ has the form $A=A^*\otimes J$, where J is the $(|K|\times |K|)$-matrix with all entries equal to 1, and $A^*$ is the adjacency matrix of the Cayley graph $\mathrm{Cay}(G/K,H/K)$. As the rank of J is 1, we conclude that $\det A=0$, so $\mathrm{Cay}(G,H)$ is singular. $\square$

Next we consider automorphisms of Cayley graphs. Let H be a connecting set in the group G and let $\Gamma = \mathrm{Cay}(G,H).$ Then for $g\in G$ the right multiplication $x\mapsto xg$ for $x\in G$ is an automorphism of $\Gamma$ as is easy to see. Therefore, the right-regular representation of G on itself yields a regular group of automorphisms of $\Gamma .$ Cayley graphs are characterized by this property:

Theorem 2.3

(Sabidussi [19]) The graph $\Gamma$ is isomorphic to a Cayley graph if and only if $\mathrm{Aut}(\Gamma )$ contains a subgroup that acts regularly on the vertices of $\Gamma .$

By contrast, the left multiplication $x\mapsto g^{-1}x$ for g and $x\in G$ does not  yield an automorphism of $\Gamma$ in general. It is easy to show that $x\mapsto g^{-1}x$ is an automorphism of $\mathrm{Cay}(G,H)$ if and only if $gH=Hg.$ This is relevant for this paper as we are dealing with connecting sets that are unions of conjugacy classes. If H is a G-invariant connecting set then also left multiplication yields an automorphism of $\Gamma .$

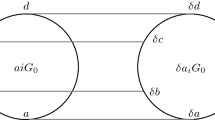
Finally we consider a connected graph $\Gamma =(V,E)$ which admits a vertex transitive group G of automorphisms. In this situation, Lovász [15] provides an associated Cayley graph $\Gamma ^{*}:=\mathrm{Cay}(G,H)$ from which the spectrum of $\Gamma$ can be determined. For the convenience of the reader, we recall this construction here. Fix a vertex $v\in V$ and let C be its stabilizer in G,  with $c:=|C|$. In view of Sabidussi’s theorem, assume that $c>1.$ Next let $H:=\{\,h\in G\,:\, v\sim v^{h}\,\}.$ Clearly $1\not \in H$ and $H=H^{-1}.$ Also, H generates G,  this follows from the transitivity of G on vertices and the connectedness of $\Gamma .$ Therefore, we have a Cayley graph $\Gamma ^{*}:=\mathrm{Cay}(G,H)$ associated to $\Gamma .$ It is imprimitive  in the sense that $a'\in Ca$ is adjacent to $b'\in Cb$ in $\Gamma ^{*}$ if and only if $v^{a}$ is adjacent to $v^{b}$ in $\Gamma$, for all $a,a',b,b'\in G.$ Hence, the adjacency matrix of $\Gamma ^{*}$ if of the form $A(\Gamma )\otimes J$ where J is the $c\times c$-matrix with all entries equal to 1. This implies the following

Theorem 2.4

[15] Let $\Gamma =(V,E)$ be a connected graph with a vertex transitive group G of automorphisms and let $\Gamma ^{*}$ be the associated Cayley graph. Suppose that the eigenvalues of $\Gamma$ are $\lambda _{1},\ldots ,\lambda _{n},$ with $n=|V|.$ Let c be the order of the stabilizer in G of a vertex of V. Then the eigenvalues of  $\Gamma ^{*}$ are $c\lambda _{1},..,\,c\lambda _{n}$ together with $0,\ldots ,\,0,$ of multiplicity $n(c-1).$ In particular, $\Gamma$ is singular if and only if $\mathrm{null}(\Gamma ^{*})>n(c-1).$

Comment:  We see that the singularity problem for vertex transitive graphs can be reduced - in principle at least - to the nullity problem for Cayley graphs. The theorem can also be used to construct singular graphs: any graph with a vertex transitive but not vertex regular group of automorphisms yields a singular Cayley graph with the same group of automorphisms.

3 Elementary observations on zeros of alternating group characters

The comments in Sect. 1 suggest to pay particular attention to the alternating groups. In fact, the reasonings in this paper are mostly concerned with these groups. In this section, we collect a number of well-known facts about characters of alternating groups and prove some results on the zeros of some of their irreducible characters.

We first recall certain notions of the representation theory of $S_n$. It is well known that the irreducible characters of $S_n$ are in bijection with the Young diagrams, and also with the partitions of n. So we write $\phi _Y$ for the irreducible representation or the irreducible character of $S_n$ corresponding to a Young diagram Y. For a Young diagram Y, we write |Y| for the number of boxes in it. A subdiagram of Y is a Young diagram of $S_m$ for $m<n$ which is contained in Y as a subset with the same top left hand corner. A box in Y is called extremal if there is no box either below or to the right of it. The set of all extremal boxes form the rim of Y.

The notion of a hook in a Young diagram Y is of common knowledge, see [12, page 55]. The number of boxes in a hook is called the length of it. A hook of length m is called an m-hook. The leg of a hook is the set of all boxes below the first row and ends in its foot. The number of the boxes in the leg is the leg length. The arm of the hook is its horizontal part, it ends in the hand of the hook, the right furthest box in the arm. Both foot and hand of the hook belong to the rim of Y.

To every m-hook $\Gamma$ of Y, there corresponds the set $\nu (\Gamma )$ of m contiguous boxes lying on the rim of Y which link the foot to the hand of $\Gamma .$ These boxes are the hook rim of Y,  see [12, pages 56 and 75] for details. Removing $\nu (\Gamma )$ from Y yields a Young subdiagram $Y\setminus \nu (\Gamma )$ with $|Y|-m$ boxes. Conversely, if $\nu$ is a sequence of m contiguous boxes on the rim of Y then the ends of $\nu$ are the foot and hand of a unique hook $\Gamma$ with $\nu =\nu (\Gamma ).$ We call $\nu$ an m-rim of Y if $\nu =\nu (\Gamma )$ for some hook $\Gamma$ of Y and refer to the leg length of $\Gamma$ as the leg length of $\nu .$

Below we need the Murnahgan–Nakayama formula [12, 2.4.7]. It expresses the character value of an irreducible character $\chi _Y$ in combinatorial terms. Let $g\in S_n$ and $g=ab$, where a is an m-cycle and where $b\in S_{n-m}\subset S_n$ is the permutation induced by g on the points fixed by a. The Murnahgan–Nakayama rule is the induction formula

$$\begin{aligned} \chi (g)=\sum (-1)^i\chi _{(Y\setminus \nu )}(b), \end{aligned}$$

(3)

where the sum runs over all m-rims $\nu$ of Y and where i is the leg length of $\nu$. (If no m-rim exists, then we have $\chi (g)=0$ by convention.)

As an illustration, we state the following

Lemma 3.1

Let $G= A_n$ or $S_n$ with $n\ge 7$ and let $M\subset G$ be the subset of all elements whose cycle decomposition has a cycle of length greater than $2\sqrt{n}+2$. Then $\chi (M)=0$ for some irreducible character $\chi$ of G.

Proof

Let m be the minimal number i such that $i^2>n$, so $m>\sqrt{n}$. Let $g\in M$ and let c(g) be maximal length of a cycle in the cycle decomposition of g. Then $c(g)>2 \sqrt{n}+2$. If $m(m-1)>n$ then set $Y=[m,\ldots ,m,n-m(m-1)]$ (m rows), if $m(m-1)=n$ then set $Y=[m,\ldots ,m]$ ($m-1$ rows), if $m(m-1)< n$ then set $Y=[m-1,\ldots ,m-1,n-(m-1)^2]$ (m rows). (So Y is a nearly square diagram.) In all cases, the hook lengths of Y does not exceed $2m-1$. By the Murnahgan–Nakayama formula (3), we have $\chi _Y(g)=0$ whenever $c(g)\ge 2m.$ As $c(g)>2 \sqrt{n}+2\ge 2(m-1)+2$, the result follows. $\square$

Corollary 3.2

Let $G=A_n$ with $n>4$ and let e be the maximum order of a 2-element of G. Let M be the set of elements of order e. Then $\chi (M)=0$ for some irreducible character $\chi$ of G.

Proof

Let g be an element of M. Observe that $| g|\ge n/2$. (In $S_n$ the inequality is strict.) If $\frac{n}{2}>2\sqrt{n}+2$, then the result follows from Lemma 3.1. Let $\frac{n}{2}\le 2\sqrt{n}+2$, equivalently, $n^2-24n+16\le 0$. This implies $n\le 23$. Let c be the maximal cycle length in the cycle decomposition of g. Then $c=16$ for $18\le n\le 23$ and $16>2\sqrt{n}+2$ so Lemma 3.1 applies. If $n= 6,8,10,12,15,17$ then G has a character of 2-defect 0 which vanishes at all 2-elements of G,  by Lemma 4.2. If $n=16, 14,13,11$ then $c=8.$ Let Y be as in the proof of Lemma 3.1. Then the maximal hook length of Y is at most 7 and so the result follows as above by the Murnahgan–Nakayama formula (3). For $n=7, 9$ the lemma follows by inspection of the character table of G. $\square$

Lemma 3.3

Let $g\in A_n$ with $n\ge 7$ and let $(c_1,\ldots ,c_k)$ with $c_1\ge c_2\ge \cdots \ge c_k$ be the cycle lengths of g. Let $\chi$ be the character labeled by the Young diagram $Y=[n-4,3,1]$. Suppose that $c_{k-1}\ne 1$ and $c_i\ne 2,4$ for $i=1,\ldots ,k$. Then $\chi (g)=0$.

Proof

For the reader’s convenience, we visualize the shape of  $Y=[15,3,1]$  for $n=19$:

We view $\chi$ as a character of $S_n$. Let $g=g_1b$ where $g_1$ is a cycle of size $c_1$ and the cycle lengths of b are $(c_2,\ldots ,c_k)$. By the Murnahgan–Nakayama rule (3) $\chi (g)=\sum (-1)^i\chi _{(Y\setminus \nu )}(b)$ where $\nu$ runs over the $c_1$-rims of Y and i is the leg length of $\nu$. (If no $c_1$-rim exists then $\chi (g)=0$.) Set $r=c_1$. It is clear from the diagram shape that an r-rim is either a part of the first row (and then $r\le n-7$) or $Y_1=Y\setminus \nu$ is one of the diagrams [2, 2, 1], $[2,1^2]$ or [2]. In each case, there is exactly one way to delete $\nu ,$ so the sum has at most one term.

Suppose first that $n-r<7$. There is no way to remove an r-rim to obtain $Y_1$ of size 6. So $\chi (g)=0$ if $n-r=6$. Let $n-r\le 5$; then $c_2+\cdots +c_k=n-r\le 5$, and hence $c_2=|b|=5,3$ or 1. The options $b=1$ and $|b|=3$ for $Y_1=[2,2,1]$ are ruled out as $c_2\ne 1$. Let $\chi _1$ be the character of $S_{n-r}$ corresponding to $Y_1$. Then $\chi _1(1)=5,3$ for $Y_1= [2,2,1]$, $[2,1^2]$, respectively. Therefore, $\chi _1$ is of $c_2$-defect 0, and hence $\chi _1(b)=0$ (one can also check this in the character tables of $S_5,S_4$). This implies $\chi (g)=0$ in these cases.

Let $n-r\ge 7$. Then $Y_1=[n-r, 3,1]$ and the leg length of the r-rim $\nu$ is 0. So $\chi (g)=\chi _1(b)$. So we can use induction on k. The case with $k=1$ follows from the above as then $n-r=0<7$. If $k>1$ then the cycle lengths of b are $(c_2,\ldots ,c_k)$, so the result follows by the induction assumption. $\square$

Proposition 3.4

Suppose that G is a doubly transitive permutation group on $\Omega .$ Then there is an irreducible character of G vanishing at every element $g\in G$ fixing exactly one point of $\Omega$. In particular, if $G=A_{n}$ with $n>3$ and if g fixes exactly one point then g vanishes at the irreducible character of degree $n-1$.

Proof

The permutation character is of the shape $\pi =1+\chi$ with $\chi$ irreducible. By assumption therefore $\chi (g)=\pi (g)-1=0.$$\square$

Proof of Theorem 1.6

This follows by combining Theorem 1.1 with Lemma 3.3 and Proposition 3.4. $\square$

Lemma 3.5

An element $g\in A_n$ is a real element if and only if one of the following conditions holds:

• (1) The cycle decomposition of g has a cycle of even length.

• (2) The cycle decomposition of g has two cycles of equal odd length. (Note that the fixed points are counted as cycles of length 1, so this includes any permutation that has two or more fixed points.)

• (3) All the cycles of g have distinct odd lengths $c_1,\ldots ,c_k$ and $\sum _{i=1}^k(c_i-1)/2$ is even. In other words, the number of $c_i$’s that are congruent 3 to modulo 4 is even.

Proof

Clearly, g is conjugate to $g^{-1}$ in $S_{n}.$ Note that the $S_{n}$-conjugacy class of g is an $A_{n}$-conjugacy class if and only if there is an odd permutation that centralizes g,  these are the conditions 1) and 2). In the remaining case, a cycle of odd length $2\ell +1$ is inverted by an element of sign $(-1)^{\ell },$ and this gives the condition 3). Here the $S_{n}$-conjugacy class of g splits in $A_n$, but g is conjugate to $g^{-1}$ in $A_{n}.$$\square$

Proof of Theorem 1.7

If $n\ge 7$, then any non-real element satisfies the assumption of Lemma 3.3, whence the result. If $n\le 6$ then either $n=6$, $|g|=5$ or $n=4$, $|g|=3$. In these cases, the result follows from Lemma 3.4. Finally, the claim that H is connected follows immediately if $n>4$ as $A_n$ is simple. If $n=4$ then H consists of all elements of order 3, so the claim follows by inspection of normal subgroups of $A_4$. $\square$

Proposition 3.6

Let G be a simple group and suppose that $g\in G$ is non-real. Then g is vanishing.

Proof

By Theorems 1.5 and 1.7, we are left to check the sporadic groups. It is observed in [11, p. 414] that $M_{22}$, $M_{24}$ are the only sporadic groups having non-identity non-vanishing elements, and these are of order 2, see the Atlas [4], and hence are real. $\square$

Lemma 3.7

Let $G=S_n$ with $n>2$ and let $M\subset (S_n\setminus A_n)$ be a subset. Then $\chi (M)=0$ for some irreducible character of G. Furthermore, if M generates G then the Cayley graph $\mathrm{Cay}(G,M\cup M^{-1})$ is singular.

Proof

Note that there exists a symmetric Young diagram of size n. Let $\phi$ be the irreducible representation of G labeled by this diagram. It is well known that $\phi$ is reducible under restriction to $A_n$ and that the irreducible constituents are non-equivalent. Let $h\in M$. By Clifford’s theorem, h permutes these constituents. So if V is the underlying space of $\phi$ then $V=V_1\oplus V_2$, and $hV_1=V_2$, $hV_2=V_1$. It is clear from this that the trace of h equals 0. So the character of $\phi$ vanishes on M. If M generates G then the set $H=M\cup M^{-1}$ is connecting, so the result follows by Theorem 1.1. $\square$

4 Blocks in symmetric groups and vanishing elements

In this section, we expose some part of representation theory of symmetric groups that is needed for the remainder of the paper. Recall the notation from Sect. 1. Let G be a finite group. For every prime p dividing |G| the irreducible characters of G partition into p-blocks. To every p-block, there corresponds a conjugacy class of p-subgroups of G and each of them is called a defect group  of the block. If $p^d$ is the order of a defect group then d is called the defect of the block. In particular, blocks of defect 0 are those whose defect groups consist of one element. In addition, G has a p-block of defect 0 if and only if there is an irreducible character of G which has p-defect 0. See for instance Navarro [17] or Curtis and Reiner [5], Chapter VII, for general theory of blocks. We use the following well-known fact:

Lemma 4.1

[10, Corollary 15.49] Let G be a finite group and let $g\in G$ be a p-singular element. Let $g=g_ph=hg_p$, where $g_p,h\in \langle g \rangle$, $g_p$ is a p-element and |h| is coprime to p. Let $\chi$ be an irreducible character of G. Suppose $g_p$ is not contained in any defect group for the p-block containing $\chi$. Then $\chi (g) =0$, in particular g is a vanishing element of G.

To use this lemma, one needs to know the defect groups of the p-blocks of $S_n$ (for $p=2$ and 3). These are described in [12, Theorems 6.2.39 and 6.2.45] for any prime p. However, first we discuss a special case of blocks and characters of defect 0.

4.1 Characters of defect 0

For non-abelian simple groups, there is the following criterion for the existence of p-blocks of defect 0.

Lemma 4.2

[8, Corollary 2] Every non-abelian finite simple group G has a p-block of defect 0 for every prime p,  except in the following special cases:

(1): G has no 2-block of defect 0 if and only if G is isomorphic to $M_{12}$; $M_{22}$; $M_{24}$; $J_2$; HS; $\mathrm{Suz};$$\mathrm{Ru};$$C_1$; $C_3$; BM, or $A_n$ where $n \ne 2m^2+m$ and $n\ne 2m^2 +m + 2$ for any integer m (not necessarily positive).

(2): G has no 3-block of defect 0 if and only if G is isomorphic to $\mathrm{Suz},$$C_3$, or $A_n$ with $3n+1 =m^2r$, where r is square-free and divisible by some prime $q \equiv 2 \pmod 3$.

Remarks

• 1. For $G=A_n$ the condition (1) can be expressed in an alternative way. If $m\ge 0$ then set $k=2m+1$. Then $2m^2+m=\frac{k(k-1)}{2}$. If $m<0$ then set $k=-2m$. Then $2m^2+m=\frac{k(k-1)}{2}$. So the set $\{2m^2+m:m\ne 0\}$ coincides with the set $\{\frac{k(k-1)}{2}:k>0\}$. So $A_n$ has a 2-block of defect 0 if and only if $n=\frac{k(k-1)}{2}$ or $2+\frac{k(k-1)}{2}$ for $k>0$.

• 2. For $p=3$, the condition (2) can be expressed in an alternative way. Specifically, $A_n$ has a 3-block of defect 0 if and only if n is of the form $n= 3(x_1^2+x^2_2 +x_1x_2)+x_1+2x_2$, where $x_1,x_2$ are integers, not necessary positive, see [13] or [8, p.333].

Corollary 4.3

If $n\equiv 3\pmod 4$ then $A_n$ has no 3-block of defect 0.

Proof

Write $n=4l+3$. Then $3n+1=2(6l+5)$, and the number $6l+5$ is odd. If we write $3n+1=2(6l+5)=m^2r$ then m is odd and $r=2r'$, where $r'$ is odd and square-free. It follows that 2r satisfies the condition in Lemma 4.2(2), whence the result. $\square$

Remarks

• (1) Applying Lemma 4.2 to a specific number n,  and decomposing $3n+1$ as a product of primes, we obtain the following list of $n<60$ with $n\not \equiv 3\pmod 4$ for which $A_n$ does not have a 3-block of defect 0: $n=13, 18,28,29,38,45,46,48,53,59$.

• (2) It is not true that if G does not have an irreducible character of 3-defect 0 then there exists a 3-singular element $g\in G$ such that $\chi (g)\ne 0$ for every irreducible character $\chi$ of G, see the character table of Suz.

Corollary 4.4

Let G be a perfect group, $h\in G$ and $C=h^G$ be the conjugacy class of h. Suppose that C generates G. Then the Cayley graph $\mathrm{Cay}(G,C\cup C^{-1})$ is singular except possibly when every simple quotient of G is isomorphic to $A_n$, $M_{22}$ or $M_{24}$ and the order of h is of the form $2^a3^b$ for some integers a, b.

Recall that every finite group G has a unique maximal normal nilpotent subgroup F(G),  called the Fitting subgroup of G. Lemma 4.2 can be extended to non-simple groups as follows.

Proposition 4.5

[7, Theorem A] Let G be a finite group, and let $h \in G$ be of order coprime to 6. Then either h belongs to the Fitting subgroup F(G) of G or h is vanishing.

For Cayley graphs, we therefore have the following general result:

Theorem 4.6

Let G be a non-cyclic finite group. Let $1\ne h\in G$ has order coprime to 6 and put $H:=h^G\cup (h^{-1})^G.$ Suppose that H generates G. Then the Cayley graph $\mathrm{Cay}(G,H)$ is singular.

Proof

Suppose first that $G\ne F(G)$. Then $h\notin F(G)$. By Proposition 4.5, $\chi (h)=0$ for some irreducible character $\chi$ of G. Recall that $\chi (h)=0$ implies $\chi (h^{-1})=0$. So the result follows by Theorem 1.1. Next, suppose that $G=F(G).$ Then all non-vanishing elements of G belongs to Z(G) [11, Theorem B]. Then $G= \langle H \rangle$ implies that G is cyclic. $\square$

We mention the following recent result on zeros of characters in $S_n$. This can be used to construct Cayley graphs of relatively high nullity.

Lemma 4.7

[16, Theorem 4.1] Let p be a prime, let $n\ge p$ be a natural number and $n=a_0+a_1p+\cdots +a_kp^k$ its p-adic expansion. Let h be a p-element of $S_n$ whose cycle structure is $1^{a_0}p^{a_1}(p^2)^{a_2}\ldots (p^k)^{a_k}$. Let $\chi$ be an irreducible character of $S_n$ such that p divides $\chi (1)$. Then $\chi (h)=0$. This remains true for $A_n$ provided $h\in A_n$. (See Remark following [16, Th 4.2]).

4.2 Blocks of symmetric groups

Let p be a prime. Every diagram that does not contain a p-hook is called a p-core. For instance, 2-cores are the diagrams of triangle shape $[k,k-1,\ldots ,1];$ in particular, $S_n$ has no 2-core of size n unless $n=1+\cdots +k=k(k+1)/2$ for some integer $k>0$. Every diagram Y contains a unique p-core subdiagram ${\tilde{Y}}$ which is maximal subject to condition $|Y|\equiv |{\tilde{Y}}|\pmod p$. The key result of block theory of symmetric groups states that two irreducible characters are in the same block if their Young diagram yields the same ${\tilde{Y}}$ [12, 6.1.21]. There is a simple algorithm to obtain ${\tilde{Y}}$ as follows.

If Y has no p-hook then $Y={\tilde{Y}}$. Otherwise remove arbitrary p-rim to obtain a subdiagram $Y_1$. If $Y_1$ has a p-hook, remove some p-rim from $Y_1$ to obtain a subdiagram $Y_2$ and so on. The process stops if and only if one gets a subdiagram ${\tilde{Y}}$ which is a p-core. By [12, Theorems 2.7.16], this final subdiagram ${\tilde{Y}}$ is unique (independently from the p-hooks choice), and called the p-core ofY. Thus, $|{\tilde{Y}}|=|Y|-pb$ for some uniquely determined integer $b\ge 0$, and this b is called the p-weight ofY (see [12, p. 80]). Note that the p-weight of a diagram is 0 if and only if the diagram is a p-core.

The following well-known fact follows easily from the dimension formula for irreducible characters in terms of hooks:

Lemma 4.8

Let $\chi$ be an irreducible character of $S_n$ labeled by a Young diagram Y. Then $\chi$ is of p-defect 0 if and only if Y is a p-core.

By [12, 6.1.35 and 6.1.42], there is a bijection between p-blocks of $S_n$ and the p-cores C such that $|C|\le |n|$ and $n-|C|\equiv 0\pmod p$.

Theorem 4.9

[12, Theorems 6.2.39] Let $\chi$ be an irreducible character of $S_n$ labeled by the Young diagram Y,  and let B be the p-block to which $\chi$ belongs. Let b be the p-weight of Y. Then a Sylow $p$-subgroup of $S_{pb}$ is a defect group of B.

Recall that the defect groups of a block are unique up to conjugacy. Here the group $S_{pb}$ is a natural subgroup of $S_n$ in the sense that this permutes pb elements of $\Omega _n$, and fixes the remaining elements. (Note that if $b=0$, then $S_{pb}$ is meant to be the identity group, and if $n=pb$ then $S_{pb}=S_n.$) Moreover, the character of $S_{n-pb}$ corresponding to ${\tilde{Y}}$ is of defect 0.

Corollary 4.10

Let D be a defect group of a p-block of $S_n$ and $g\in S_n$ a p-element. Then g is conjugate to an element of D if and only if $|\mathrm{supp} (g)|\le pb=|\mathrm{supp} (D)|$.

Corollary 4.11

(1) Let B be a p-block of $S_n$ with defect group D and p-core C. Then D fixes exactly |C| elements of $\Omega _n$.

It is easy to construct irreducible characters with given p-core C (provided $n-|C|$ is a multiple of p):

Corollary 4.12

Let $C=[l_1,\ldots ,l_k]$ be a p-core and $|C|=c$. Let $Y=[l_1+bp,l_2,\ldots ,l_k]$ be a diagram of $S_{c+bp}$, $\chi$ the character labeled by Y, and let D be a defect group of the p-block the character $\chi$ belongs to. Then $C={\tilde{Y}}$, and D is a Sylow $p$-subgroup of $S_{pb}$, which is the stabilizer of c elements of $\Omega$ in $S_n$. In particular, D stabilizes c elements of $\Omega _n$.

For our purpose, we are interested in the defect groups rather than in blocks themselves. Moreover, we can fix a defect group in every conjugacy class of defect groups in such a way that these defect groups form a chain with respect of inclusion. In fact, if the defect groups $D ,D '$ are Sylow p-subgroups in $S_{pb},S_{pb'}$, resp., and $b<b',$ then we can assume $D \subset D '$. (For this, one can order the elements of $\Omega$ and choose $S_{pb}$ to be the subgroup fixing elementwise the last $n-pb$ elements of $\Omega$.) Therefore, with this ordering of defect groups it is meaningful to speak of the minimal defect group of $S_n$, that is, the one with least possible b. Recall that the defect groups of a block are conjugate, and if D is one of them then the defect of a block is the number d such that $|D|=p^d$. So a minimal defect group is a defect group of a block of minimal defect. Note that the maximal defect group is always a Sylow $p$-subgroup of $S_n$. By Lemma 4.2, if $p>3$ then the minimal defect group is trivial (that is, the group of one element). (Formally, the lemma is stated for $A_n$ but it remains true for $S_n$.)

If $p>2$, then the defect groups of $A_n$ are exactly the same as those of $S_n$; if $p=2$ then the defect groups of $A_n$ are of shape $D\cap A_n$ for a defect group D of $S_n$. Moreover, if $\chi$ is an irreducible character of $S_n$ reducible on $A_n$ then irreducible constituents belong to blocks whose defect groups are conjugate in $S_n$, and hence have the same support. (This follows from [17, 9.26, 9.2].)

Lemma 4.13

Let B be a 2-block (resp., 3-block) of $S_n$ of nonzero defect. Then B contains an irreducible character that remains irreducible under $A_n$.

Proof

It is well known that the characters labeled by non-symmetric diagrams are irreducible under $A_n$. So we show that B contains a character whose Young diagram is not symmetric.

Let $Y=[l_1,\ldots ,l_k]$ be the 2-core (resp. 3-core) diagram determined by B, and $Y_1$ the diagram obtained from Y by adding $n-|Y|$ boxes to the first row of Y. As B is not of defect 0, $n\ne |Y|$, so $n-|Y|=2b$ (resp. 3b) for some integer $b>0$. If $l_1\ge k$ then $Y_1$ is not symmetric and the character labeled by $Y_1$ belongs to the block B (see Lemma 4.12). If $l_1<k$ (so $p=3)$ then take for $Y_1$ the diagram obtained from Y by adding 3b boxes to the first column, and conclude similarly. $\square$

Lemma 4.14

Let $G=S_n$ or $A_n$, $g\in G$, and let $D_2$ and $D_3$ be defect groups of a 2-block, or a 3-block, respectively. Suppose that $|g|=2^\alpha 3^\beta$ and $|\mathrm{supp} (g)|>|\mathrm{supp} (D_2)|+|\mathrm{supp} (D_3)|$. Then $\chi (g)=0$ for some irreducible character $\chi$ of G.

Proof

Let $G=S_n$ and let $g=g_2g_3=g_3g_2$, where $g_2$ is a 2-element and $g_3$ is a 3-element of G. It is easy to observe that $|\mathrm{supp} (g)|\le |\mathrm{supp} (g_2)|+|\mathrm{supp} (g_3)|$. So either $|\mathrm{supp} (g_2)|>|\mathrm{supp} (D_2)|$ or $|\mathrm{supp} (g_3)|>|\mathrm{supp} (D_3)|$. In the former case, $g_2$ is not conjugate to an element of $D_2$, so $\chi (g)=0$ for every irreducible character $\chi$ in a 2-block with defect group $D_2,$ by Lemma 4.1. Similarly, consider the latter case. Here the result follows for $G=S_n$. If $G=A_n$ then the result follows from that for $S_n$ and the fact stated prior Lemma 4.13. $\square$

Comments In view of Lemma 4.14, it is desirable to determine the minimal defect group for every n and $p=2$ or 3. If $p=2$ then the number $bp=2b$ must be of shape $k(k+1)/2$, so the minimal defect group of $S_n$ is a Sylow 2-subgroup of $S_{2b}$, where k is the maximal integer such that $n-2b=k(k+1)/2$ for some $b>0$. If $p=3$, we only prove the existence of a defect group D with $|\mathrm{supp} (D)|\le 2\sqrt{n}+4$ (Lemma 6.1), which is sufficient for our purpose.

5 Minimal defect group of $S_n$ for $p=2$

The following lemma is obvious in view of the above comments.

Lemma 5.1

Let $p=2$ and $d\ge 0$ an integer. Then $d=|\mathrm{supp} (D)|$ for some defect group D of a 2-block of $S_n$ if and only if d is even and $n-d=m(m+1)/2$ for some $m>0$. In particular, d is minimal if and only if m is a maximal number such that $n-m(m+1)/2\ge 0$ is even.

We first compute the minimal numbers in the set $\{|\mathrm{supp} (D)|: D$ is a defect group of a 2-block of $S_n, 13<n<34\}$. Note that these are equal to $n-t$, where t is the maximal number of shape $m(m+1)/2$ such that $n-t$ is even.

Note that $m(m+1)/2<34$ implies $m\le 7$ so $t\in \{1,3,6,10,15,21,28\}$.

Table 1 The minimal defect group support for 2-blocks of $S_n$ for $n<34$

Lemma 5.2

Let D be a minimal defect group of $S_n$ for $p=2$. If $n>13$ then $|\mathrm{supp} (D)|< 3\sqrt{2n-20}$.

Proof

Let $T_m$ be the triangular diagram $[m,m-1,\ldots ,1]$. Then $|T_{m+1}|-|T_m|=m+1$ as $T_{m+1}$ is obtained from $T_m$ by adding $m+1$ boxes.

Let $d=|\mathrm{supp} (D)|$ and let m be the maximal integer such that $m(m+1)/2\le n$. Set $a=n-m(m+1)/2$, so $a\le m$. If $a=0$ then $d=0$, and the lemma is trivial. If a is even then $d=a\le m$.

Suppose that a is odd. Then $T_m$ is not a 2-core of any diagram of $S_n$. So consider $T_{m-1}$. Then $n-|T_{m-1}|=a+m$. If m is odd then $a+m$ is even and then $d=a+m\le 2m$. Let m even. Then $a+m$ is odd and $a\le m-1$. It follows that $T_{m-1}$ is not a 2-core of any diagram of $S_n$. Consider $T_{m-2}$. Then $n-T_{m-2}=a+2m-1$ is even, so $d\le 3m-2$.

Therefore, $d\le 3m-2$ in any case. Then $3m-2<3\sqrt{2n-20}$ for $n>36$. (Indeed, this is equivalent to $(3m-2)^2<18n-180$, or $9 m^2-12m+184<18n$. As $m(m+1)/2<n$, we have $9m^2+9m<18n$, so it suffices to show that $18n+9 m^2-21m+184<18n$, or $184<21m$. This is true if $m\ge 9$, $n\ge 45$. Let $m<9$. If $m=8$ then $3m-2=22<3\sqrt{2n-3}$ for $n>36$.) For $n=36$, the lemma is true as $S_{36}$ has a block of 2-defect 0. Let $n<36$. Then $m\le 7$. As $m=7$ is odd, $d\le 2m=14<\sqrt{2n-3}$ for $n>21.$ Again $S_{21}$ has a block of 2-defect 0. Let $n<21$, so $m\le 6$. By inspection of Table 1, one is convinced that $d<\sqrt{2n-3}$ for $n>13.$$\square$

Recall that for $g\in S_n$ and a prime p we denote by $g_p$ the element such that $g=g_ph$, where $h\in \langle g \rangle$ and |h| is not a multiple of p. One observes that $|\mathrm{supp} (g_p)|$ is the sum of cycle lengths divisible by p in the cycle decomposition of g.

Lemma 5.3

Let $G=S_n$ or $A_n$ where $n>13$. Let $R=\{g\in G: |\mathrm{supp} (g_2)|\ge 3\sqrt{2n-20}\}$. Then there is a 2-block B of G such that $\chi (R)=0$ for every irreducible character $\chi$ of B.

Proof

Let T be the triangle diagram of maximal size $|T|\le n$ such that $n-|T|$ is even.

Suppose first that $|T|=n$. Then, by Lemma 4.8, $S_n$ has a character $\chi$ of 2-defect 0. Recall that $\chi$ is a unique character in a block it is contained in. So for $G=S_n$ the statement follows from Lemma 1.2. If $G=A_n$ then $\chi |_{A_n}$ is the sum of two irreducible characters of degree $\chi (1)/2$; moreover, each of them is of 2-defect 0 (indeed, an irreducible character $\chi$ of $A_n$ is of 2-defect 0 if and only if $\chi (1)$ is a multiple of $|S_n|_2$; as $|S_n|_2=2|A_n|_2$, it follows that $\chi (1)/2$ is a multiple of $|A_n|_2$). This implies the result for $A_n$.

Let $|T|<n$ and let Y be any diagram of size n containing T. Let $\chi$ be the irreducible character of $S_n$ labeled by Y. Then $\chi$ belongs to a block B, say, whose defect group D satisfies $|\mathrm{supp} (D)|=n-|T|$. By Lemma 5.2, $|\mathrm{supp} (g_2)|\ge 3\sqrt{2n-20}>n-|T|$, so $g_2$ is not conjugate to an element of D. By Lemma 4.1, $\chi (g)=0$ for every irreducible character $\chi$ of B, whence the result for $S_n$. It is known that the defect groups of blocks of $A_n$ to which the irreducible constituents of $\chi |_{A_n}$ belongs are $D\cap A_n$ and conjugate in $S_n$ (see comments prior Lemma 4.13). So $g_2$ is not conjugate to an element of $D\cap A_n$, and the result follows as above for $S_n$. By Lemma 4.13, Y can be chosen non-symmetric, so $\chi$ is irreducible under restriction to $A_n$. $\square$

We say that the element $g\in G\subseteq S_n$ has maximal support if $|\mathrm{supp} (g)|\ge |\mathrm{supp} (h)|$ whenever $h\in G$ and $|h|=|g|$. One easily observes that if g is of maximal support in $G= A_n$ and |g| is even then $|\mathrm{supp} (g)|\ge n-3$.

Corollary 5.4

Let $G=A_n$ or $S_n$ with $n>4$ and $n\ne 7,11,$ and let M be the set of all 2-elements of maximal support. Then $\chi (M)=0$ for some irreducible character $\chi$ of G.

Proof

Let $g\in G$ be a 2-element of maximal support. Then $|\mathrm{supp} (g)|\ge n-3$. If $n>13$ then $n-3\ge 3\sqrt{2n-20}$, and the result follows from Lemma 5.3. For $n\le 13$ and $n=5,6,8,10,12$ the result follows as $A_n$ has a 2-block of defect 0. So we are left with $n=9,13$, which can be inspected by the character table of G in [4]. Let $G=S_n$. Then we have to deal also with the cases with $n=5,8,12$. If $n=12$, the all elements of maximal support are in $A_{12}$. The cases with $n=5,8$ follows by inspection. $\square$

Remark

In $A_{7}$, the elements of order 2 are not vanishing while all elements of order 4 are vanishing. In $A_{11}$, the elements of order 2 and maximal support are non-vanishing while all other 2-elements are vanishing. In $A_{13}$, the elements of maximal support and all 2-elements of order greater than 2 are vanishing, whereas all other 2-elements are non-vanishing (they form two conjugacy classes).

6 Defect groups for $p=3$ and vanishing elements

We turn to the case $p=3$. Consider the following diagrams, where $r,s\ge 0$ are integers and $r+s>0$:

$C_{rs}=[r+2s,r+2s-2,\ldots ,r+2,r,r,r-1,r-1,\ldots ,1,1]$ and $C^-_{rs}=[r+1+2s,r+1+2(s-2),\ldots ,r+2,r,r,r-1,r-1, ,\ldots ,1,1].$ In particular,

$C_{0,s}=[2s,2s-2,2s-4,\ldots ,4,2]$ ($s>0$) and $C^-_{0,s}=[2s+1,2s-1,\ldots ,3,1]$$(s\ge 0).$

These diagrams appeared in [3, p. 1159]. One can show that these exhaust all 3-cores in $S_n.$

Note that $|C_{rs}|=rs+r(r+1)+s(s+1)$ and $|C^-_{rs}|=(r+1)(s+1)+r(r+1)+s(s+1)$. In addition, $C_{rs},C_{sr}$ and $C^-_{rs},C^-_{sr}$ are transposes of each other.

Examples. $C_{0,4}=[8,6,4,2]$; $~C_{0,3}^-= [7,5,3,1];$$~C_{2,3}^-= [9,7,5,3,2,2,1,1]$; $~C_{2,3}=[8,6,4,2,2,1,1]$

Lemma 6.1

Let $G=S_n$, $n>13$. Then G has a 3-block whose defect group support size is at most $2\sqrt{n}+4$.

Proof

We have to show that there is a 3-block with defect group D, say, such that $|\mathrm{supp} (D)|\le 2\sqrt{n}+4$. We can assume that $S_n$ has no block of defect 0 (otherwise $D=1$ and the statement is trivial).

Let s be the maximal number such that $s^2\le n$ (so $s\le \sqrt{n}$). Then $n<(s+1)^2$. Note that $|C^-_{0,s-1}|=s^2$, $|C_{1,s-1}|=s^2+1$ and $|C_{3,s-2}|=s^2+8$, and these three numbers have distinct residues modulo 3.

(i) Suppose that $n> s^2+8$. As $n>13$, we have $s\ge 3$. Then we choose the diagram $C\in \{C^-_{0,s-2}$, $C_{1,s-1}$, $C_{3,s-2}\}$ such that $3|(n-|C|)$. Then there is a diagram Y for $S_n$ such that $|{\tilde{Y}}|=C$. As $n<(s+1)^2$, we have $n-|{\tilde{Y}}|\le 2s\le 2\sqrt{n-9}$.

(ii) Let $n\le s^2+8$, so $s>2$ (since $n>13$). If the equality holds then $S_n$ has a block of defect 0. So $n\le s^2+7$. If $n= s^2+7,s^2+4$ then we choose for ${\tilde{Y}}$ the diagram $C_{1,s-1}$. Then $n-|{\tilde{Y}}| \ge s^2+7-(s^2+1)= 6$. If $n= s^2+6$ or $s^2+3$ then we choose for ${\tilde{Y}}$ the diagram $C_{1,s}$. Then $n-|{\tilde{Y}}| \ge s^2+6-s^2=6$.

Let $n= s^2+5$ or $s^2+ 2$. Then $n>13$ implies $s\ge 3$. We choose for ${\tilde{Y}}$ the diagram $C'\in \{C^-_{0,s-3}$, $C_{1,s-2}$, $C_{3,s-3}\}$ such that $3|(n-|C'|)$. Then $|{\tilde{Y}}|\ge (s-1)^2$, and hence $n-|{\tilde{Y}}| \ge s^2+5-(s-1)^2=2s+4\le 2\sqrt{n}+4$. $\square$

Remark

The bound $2\sqrt{n}+4$ in Lemma 6.1 is not sharp.

For $g\in G= S_n$ denote by $g_3$ the element such that $g=g_3h=hg_3$, where $g_3$ is a 3-element and |h| is coprime to 3.

Corollary 6.2

Let $G= S_n$ or $A_n$, and let $M=\{g\in G:|\mathrm{supp} (g_3)|> 2\sqrt{n}+4\}$. Then there is an irreducible character $\chi$ of G such that $\chi (M)=0$.

Proof

By Lemma 6.1, there is a 3-block of $S_n$ whose defect group support is at most $2\sqrt{n}+4$. So $g_3$ cannot lie in any defect group of this block. By Lemma 4.1, $\chi (g)=0$ for any irreducible character in this block and any $g\in M$. (Recall that the defect groups of a block are conjugate, so their supports are of the same size.) As the defect groups of 3-blocks of $A_n$ are the same as those of $S_n$, the result follows. $\square$

For further use, we record in Table 2 the list of maximal sizes of a core for 3-blocks of $S_n$ for $n<51$ provided $S_n$ has no 3-block of defect 0. (In the latter case, the size of some core equals n.) The numbers n to be inspected are in the first row of the table, see Corollary 4.3 and the comment following it. In the table, C is a core of maximal size $|C|\le n$ with $n\equiv |C|\pmod 3$, so $n-|C|=|\mathrm{supp} (D)|$, where D is a minimal defect group of $S_n$ for $p=3$.

Table 2 The minimal defect group support for 3-blocks of $A_n$ for $n<51$

The table shows that for every $n<49$ there is an irreducible character $\chi$ such that $\chi (g)=0$ whenever g is a 3-element of order at least 9. Note that if $n=51$ then $|C|=42$ and $n-|C|=9$.

Lemma 6.3

If $4<n<51$ then $S_n$ has a 3-block of defect 0 or 1, unless $n=18,31,38,48$ where there is a 3-block of defect 2.

Proof

This immediately follows by inspection of Table 2, as $A_{49}$, $A_{50}$ has a block of 3-defect 0, see the remark after Corollary 4.3 . $\square$

Proposition 6.4

Let $G=A_n$ with $n>4$ and $n\ne 7,$ and let e be the maximum order of a 3-element of G. Let M be the set of all elements of order e. Then $\chi (M)=0$ for some irreducible character of G.

Proof

Let $g\in M$. Observe that $|\mathrm{supp} (g)|> n/3$. If $\frac{n}{3}\ge 2\sqrt{n}+2$ then the result follows from Lemma 3.1. Suppose that $\frac{n}{3}< 2\sqrt{n}+2$. Then $n< 47$.

If $27\le n\le 46$ then $e=27>16>2\sqrt{n}+2$. For $9\le n\le 26$, we have $e=9$ and $|\mathrm{supp} (g)|> 9$. According to Table 2, there is a 3-block of defect group support at most 6, so g is not conjugate to an element of any such defect group. Therefore, $\chi (g)=0$ for any irreducible character in this block, whence the result. If $n=5,6,8$ then the groups $A_n,S_n$ have a 3-block of defect 0, so we are left with $n=7$ as claimed. $\square$

Proposition 6.5

Let $G=S_n$ or $A_n$ with $n>4,$$n\ne 7,$ and let $|G|=3^am$, where m is not a multiple of 3. Then there is a 3-block of defect at most $(a-1)/3$.

Proof

Suppose first that $\frac{n}{3}\ge |\mathrm{supp} (D)|,$ where D is a defect group of some 3-block B of G. Then $3|D|^3\le |G|_3$ for $n\ne 7$. Indeed, G contains a 3-subgroup X, say, isomorphic to the wreath product of D with $A_3$, and $|X|=3|D|^3$. Let $|D|=3^r$, so r is the defect of the block B. Then $|X|=3^{3r+1}$ and $3r+1\le a$. This implies $r\le (a-1)/3$.

Suppose that $n\ge 58$. Then $\frac{n}{3}> 2\sqrt{n}+4$. By Lemma 6.1  there is a 3-block of G whose defect group satisfies $|\mathrm{supp} (D)|\le 2\sqrt{n}+4$. So the result follows. Let $n< 58$. By Table 2, $\frac{n}{3}\ge |\mathrm{supp} (D)|$ unless $n=7$. $\square$

6.1 Elements of maximal support whose order is divisible by 3

Let $G= S_n$ or $A_n$ and $g\in G$. Recall that g is of maximal support in G if ${|\mathrm supp}(g)|\ge |\mathrm{supp}(h)|$ for any element h of the same order as g. In other words, the number of fixed points of such an h does not exceed the number of fixed points of g.

Note that for g in G to be of maximal support depends on whether $G=S_n$ or $A_n$. Say, if $g\in A_6$ is an involution (a double transposition) then g is of maximal support in $A_6$ but not in $S_6$. The following is easily verified:

Lemma 6.6

Let $G= S_n$ or $A_n$ and $g\in G$. Suppose that g is of maximal support.

• (1) Let $G= S_n$ and let |g| be even. Then $|\mathrm{supp}(g)|\ge n-1$.

• (2) Let $g\in A_n$ and let |g| be even. Then $|\mathrm{supp}(g)|\ge n- 3$.

• (3) Suppose that |g| is a multiple of 3. Then $|\mathrm{supp}(g)|\ge n- 2$.

• (4) Suppose that |g| is a multiple of 6. If $G=A_n$ then $|\mathrm{supp}(g)|\ge n- 2$, and if $G=S_n$ then $|\mathrm{supp}(g)|\ge n- 1$.

Lemma 6.7

Let $G=S_n$ or $A_n$ with $n>13$ and let $g=g_2g_3=g_3g_2\in G$, where $|g_2|=2^\alpha$ and $|g_3|=3^\beta$. Suppose that $|\mathrm{supp} (g_2)|> 3\sqrt{2n-20}$ or $|\mathrm{supp} (g_3)|> 2\sqrt{n}+4$. Then there is an irreducible character $\chi$ of G such that $\chi (g)=0$.

Proof

If $|\mathrm{supp} (g_2)|> 3\sqrt{2n-20}$ then $\chi (g)=0$ for some character $\chi$ of $S_n$ by Lemma 5.3. If $|\mathrm{supp} (g_3)|> 2\sqrt{n}+4$ then $\chi (g)=0$ for some irreducible character of G by Corollary 6.2. So the lemma follows for $G=S_n$.

Let $G=A_n$. If $\chi |_{A_n}$ is irreducible then we are done. Otherwise, $\chi |_{A_n}$ is the sum of two irreducible characters of equal degree. Recall (Lemma 1.2) that an irreducible character $\chi$ of G os of p-defect 0 if and only if $\chi (1)\equiv 0\pmod {|G|_p}$. Applying this to $S_n$ and $A_n$, one observes that if $\chi$ is of p-defect 0 (with $p\in \{2,3\}$) then so are the irreducible constituents of $\chi$. So in this case the lemma follows from Lemma 1.2. Suppose that $\chi$ is not of defect 0. Then, by Lemma 4.13, this block $\chi$ belongs to has an irreducible character $\chi '$ labeled by a non-symmetric Young diagram which is therefore irreducible under restriction to $A_n$. $\square$

Obviously, Theorem 1.8 follows from the following result:

Theorem 6.8

Let $G=S_n$ or $A_n$ with $n>4$ and let $g\in G.$ Suppose that g is of maximal support in G. Then $\chi (g)=0$ for some irreducible character of G, unless $n=7$ or 11.

Proof

In view of Theorem 1.5, we can assume that $|g|=2^\alpha 3^\beta ,$ and by Corollary 5.4, that $\beta \ne 0$. (Here $\alpha ,\beta \ge 0$ are integers.) By Lemma 3.7, we can assume that $g\in A_n$. Let $g=g_2g_3=g_3g_2$, where $|g_2|=2^\alpha$, $|g_3|=3^\beta$. By Lemma 4.1, we are done if $|\mathrm{supp} (g_2)|>|\mathrm{supp} (D_2)|$ or $|\mathrm{supp} (g_3)|>|\mathrm{supp} (D_3)|$ for some defect groups $D_2,D_3$ of some 2-block and 3-block of G, respectively. So we choose $D_2,D_3$ to be minimal.

Suppose first that $n>13$. By Lemma 6.7, we can assume that $|\mathrm{supp} (g_2)|\le 3\sqrt{2n-20}$ and $|\mathrm{supp} (g_3)|\le 2\sqrt{n}+4$. As g is of maximal support, we have $n-2\le |\mathrm{supp} (g)|\le |\mathrm{supp} (g_2)|+|\mathrm{supp} (g_3)|$ (Lemma 3.4), whence $n-2\le 3\sqrt{2n-20}+2\sqrt{n}+4$. This implies $n<45$.

Let $n<45$. One observes in Table 2 that $|\mathrm{supp} (D_3)|\le 6$ for n with $4<n<45$. (If $D_3=1$ then $|\mathrm{supp} (D_3)|=0$.) By Lemma 4.1, we are done unless $|\mathrm{supp} (g_3)|\le 6$. If so, we have $n-2\le |\mathrm{supp} (g)|\le |\mathrm{supp} (g_2)|+6$, whence $|\mathrm{supp} (g_2)|\ge n-8$. By Lemma 5.3, we are done if $|\mathrm{supp} (g_2)|\ge 3\sqrt{2n-20}$. The latter implies $3\sqrt{2n-20}> n-8$, whence $n\le 23$. The cases $13<n\le 23$ are verified by inspection, and we ignore the values of n such that $A_n$ and $S_n$ has a 3-block of defect 0. For the remaining cases $n=23,19,18,15$, we have $|\mathrm{supp} (D_2)| =2, 4,8,0$, respectively, for $S_n$. As the defect groups of 2-blocks for $A_n$ are $D_2\cap A_n$ when $D_2$ runs over the defect groups of 2-blocks of $S_n$, we have $|\mathrm{supp} (D_2)|\le 8$, so the result follows.

The cases with $n< 13$ can be examined from their character tables [4]. If $14>n>4$ and $n\ne 7,11$ then $A_n$ has a block of 3-defect 0. The non-vanishing elements $g\in G=A_{11}$ are in class 2B and 3A in notation of [4], and those in 3A are not of maximal support. Let $G=A_7$. Then an element of maximal support is in class 3B or 6A, the latter is non-vanishing, see  [4]. If $n=13$ then the character table is available in the GAP library. One observes that the only non-vanishing elements in $A_{13}$ are in classes 2A, 2B, 3A, and hence not of maximal support. This completes the proof. $\square$

Denote by $\omega (G)$, the set of element orders in the group G.

Lemma 6.9

Let $g\in G=A_n$. Suppose that $2|g|,3|g|\notin \omega (G)$.

• (1) We have $|\mathrm{supp} (g)|\ge n/2;$

• (2) Let $g=g_2g_3=g_3g_2$, where $|g_2|=2^\alpha$, $|g_3|=3^\beta$, $\alpha ,\beta >0$. Then $n< \min \{2^{\alpha +1}+|\mathrm{supp} (g_3)|+2, |\mathrm{supp} (g_2)|+3^{\beta +1}\}$.

Proof

(1) Suppose the contrary. Then $|\mathrm{supp} (g)|\le \frac{n}{2}-1$. Let $c_1,\ldots ,c_k,1,\ldots ,1$ be the cycle lengths of g, where $c_1,\ldots ,c_k>1$. So $|\mathrm{supp} (g)|=c_1+\cdots +c_k$. Let h be the permutation with cycle lengths $2c_1,\ldots ,2c_k,1,\ldots ,1$. Then $|h|=2|g|$ and $|\mathrm{supp} (h)|=2|\mathrm{supp} (g)|\le n-2$. If $h\notin A_n$ then replace h by the permutation $h'$ obtained from h by adding a 2-cycle. Then $h'\in A_n$ and $|h'|=2|g|$, which is a contradiction.

(2) Suppose the contrary. If $n\ge 2^{\alpha +1}+|\mathrm{supp} (g_3)|+2$ then consider an element $g_2'g_3$, where $|g_2'|=2^{\alpha +1}$ and $| \mathrm{supp} (g_2')\cap \mathrm{supp} (g_3)|=0$. Such element $g_2'\in A_n$ exists as $n- |\mathrm{supp} (g_3)|\ge 2^{\alpha +1}+2$. Then $|g_2'g_3|=2|g|$, a contradiction. Similarly, if $n\ge 3^{\beta +1}+|\mathrm{supp} (g_2)|$ then there is an element $g_3'$ such that $|g_3'|=3^{\beta +1}$ and $| \mathrm{supp} (g_2)\cap \mathrm{supp} (g_3')|=0$. Then $A_n$ contains an element $g_2g_3'$ of order 3|g|. $\square$

Proof of Theorem 1.9

Let $|g|=2^\alpha 3^\beta$. Suppose that $n>13$. By Lemma 6.7, we can assume that $|\mathrm{supp} (g_2)|< 3\sqrt{2n-20}$ and $|\mathrm{supp} (g_3)|< 2\sqrt{n}+4$. By Lemma 6.9, $|\mathrm{supp} (g)|\ge n/2$ and hence either $|\mathrm{supp} (g_2)|\ge n/4$ or $|\mathrm{supp} (g_3)|\ge n/4$. So either $3\sqrt{2n-20}> n/4$ or $2\sqrt{n}+4> n/4$. (Note that $3\sqrt{2n-20}> 2\sqrt{n}+4$ for $n>15$.)

Suppose that $n>15$ and $3\sqrt{2n-20}> n/4$. Then $n\le 297$. Then $|\mathrm{supp} (g_2)|< 3\sqrt{2n-20}<72$ for $n\le 297$ and $|\mathrm{supp} (g_3)|< 2\sqrt{n}+4<39$. Therefore, $2^\alpha \le 64,3^\beta \le 27$. Note that $|\mathrm{supp} (g)|= |\mathrm{supp} (g_2)|+ |\mathrm{supp} (g_3)|-| \mathrm{supp} (g_2)\cap \mathrm{supp} (g_3)|$. Therefore, $|\mathrm{supp} (g)|\le |\mathrm{supp} (g_2)|+ |\mathrm{supp} (g_3)|$. By Lemma 6.9(2), we have $n\le 3^4+72=153$.

This argument can be repeated: $|\mathrm{supp} (g_2)|< 3\sqrt{2n-20}<51$ for $n\le 153$ and $|\mathrm{supp} (g_3)|< 2\sqrt{n}+4<29$. Again by Lemma 6.9(2), we have $n\le 3^4+50=132$.

Again $|\mathrm{supp} (g_2)|< 3\sqrt{2n-20}<47$ for $n\le 132$ and $|\mathrm{supp} (g_3)|< 2\sqrt{n}+4<27$, whence $3^\beta \le 9$. Then $n\le 3^3+46=73$.

Once more $|\mathrm{supp} (g_2)|< 3\sqrt{2n-20}<34$ for $n\le 73$ and $|\mathrm{supp} (g_3)|< 2\sqrt{n}+4<22$, whence $n\le 3^3+32=59$.

Finally, $|\mathrm{supp} (g_2)|< 3\sqrt{2n-20}<30$ for $n\le 59$ and $|\mathrm{supp} (g_3)|< 2\sqrt{n}+4<20$. Therefore, $2^\alpha \le 16$ and $|\mathrm{supp} (g_3)| \le 18$. By Lemma 6.9(2), we have $n\le 2^5+18+2=52$.

If $n=52$ then G has a 3-block of defect 0, if $n=51$ then there is a 3-block of G with defect group support 9 (see comment after Table 2). In view of Lemma 4.1, we can assume that $|\mathrm{supp} (g_3)|\le 9$, and then $n\le 2^5+2+9=43$ by Lemma 6.9(2). For $n\le 43$ the group $G=A_n$ has a 3-block B with defect group support at most 6 (Table 2). Then, as above, $|\mathrm{supp} (g_3)|\le 6$, so $|g_3|=3$, $\beta =1$. Then Lemma 6.9(2) yields $n\le 2^5+2+3=37$.

For $n\le 37$, one observes from Table 2 that G has a 2-block with defect group support at most 16. Then $|\mathrm{supp} (g_2)|\le 16$, and $n\le 3^2+16\le 25$ by Lemma 6.9(2). For $n=25,24$ the group G has a 3-block of defect 0, so these values are ruled out too. If $n=23$ then G has a 2-block with defect group support 2, whence $|\mathrm{supp} (g_2)|\le 2$, which contradicts the inequality $n\le 9+4$ in Lemma 6.9(2). For $n=22,21,20$ the group G has a 3-block of defect 0. Let $n=19$. Then G has a 2-block with defect group support 4, whence $|\mathrm{supp} (g_2)|\le 4$, which contradicts the inequality $n\le 9+6$ in Lemma 6.9(2). So $n\le 18$.

Let $n=18$. Suppose that $|g_2|=8$. Consider the diagram $Y=[12,2,2,1,1]$:

Observe that there is a unique way to delete an 8-rim from Y. Let $\chi _Y$ be the irreducible character of $S_{18}$. Applying the Murnahgan–Nakayama formula (3) with $c=8$, we get $\chi _Y(g)=\chi _{Y_1}(h)$, where $Y_1=Y\setminus \nu =[4,2,2,1,1]$, $h\in S_{10}$ is obtained from g by removing the 8-cycle and $\chi _{Y_1}$ is an irreducible character of $S_{10}$. There is no way to delete a 3-rim from $Y_1$; so $\chi _{Y_1}$ is of 3-defect 0. As |h| is a multiple of 3, we have $\chi _{Y_1}(h)=0$, and hence $\chi _Y(g)=0$.

So the result follows if $|g_2|=8$. Let $|g_2|\le 4$. As $|\mathrm{supp} (g_3)|\le 6$, by Lemma 6.9(2) we have $n\le 6+2^3+2=16$, a contradiction.

If $n=17,16,14$ then G has a 3-block of defect 0, and if $n=15,12$ then G has a 2-block of defect 0. If $n\le 13$ then the result follows by inspection of the character table of G. $\square$