Microscopic simulation of RF noise in junctionless nanowire transistors

Abstract

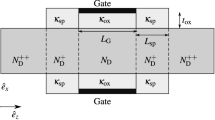
A deterministic solver for the analysis of microscopic noise and small-signal fluctuations in junctionless nanowire field-effect transistors is presented, which is based on a self-consistent and simultaneous solution of the Poisson/Schrödinger/Boltzmann equations. It is verified that the numerical framework fulfills the vital properties of reciprocity and passivity in the small-signal sense, and yields Johnson–Nyquist noise under equilibrium conditions. Key figures such as the cutoff frequency, drain excess noise factor, the Fano factor, and gate/drain correlation coefficient are presented at various bias conditions. In this work we show that similar to the inversion-mode MOSFETs, the gate and drain current noises mainly stem from the warm electrons at the source side, whereas the hot electrons do not have a significant contribution. Also, our results show that the device behaves similar to long-channel FETs in terms of its excess noise even for a channel length of 10 nm, due to the strong control of its electrostatics by the all-around gate.

Appendix

In order to calculate the small-signal terminal currents, we need to derive a formulation of the Ramo–Shockley theorem [17] that is consistent with our simulation framework, i.e., one-dimensional BE along the transport direction and two-dimensional SE in the transverse planes. In what follows, the details of such formulation are presented.

The small-signal current of the k-th contact can be expressed as:

$$\begin{aligned} {\underline{I}}_k = -\int _{\partial D_k} \Big ( \sum _\nu \mathbf {{\underline{J}}}^\nu (\mathbf{{r}})- i\omega \kappa (\mathbf{{r}})\nabla {\underline{\varphi }}(\mathbf{{r}}) \Big )\cdot {\mathrm{d}}\mathbf {A} \end{aligned}$$

(15)

where $\mathbf {{\underline{J}}}^\nu (\mathbf{{r}})$ is the three-dimensional small-signal current density and $\partial D_k$ comprises the set of points of the k-th contact. Defining the Ramo–Shockley test functions as the solutions to the Laplace equation within the device:

$$\begin{aligned}&\nabla \cdot \big ( \kappa (\mathbf{{r}})\nabla \tau _k(\mathbf{{r}}) \big ) = 0 , \nonumber \\&\quad \tau _k(\mathbf{{r}}) := \delta _{ki} \qquad {\text {for}} ~ \mathbf{{r}} \in \partial D_i \end{aligned}$$

(16)

we can safely extend the integration region to the whole surface and then employ the divergence theorem to get:

$$\begin{aligned} {\underline{I}}_k = \int _D \sum _\nu \mathbf {{\underline{J}}}^\nu (\mathbf{{r}}) \cdot \nabla \tau _k(\mathbf{{r}}) \;{\mathrm{d}}V - i\omega \sum _i C_{ik}{\underline{V}}_i^C \end{aligned}$$

(17)

with

$$\begin{aligned} C_{ik} := \int _D \kappa (\mathbf{{r}})\nabla \tau _i(\mathbf{{r}}) \cdot \nabla \tau _k(\mathbf{{r}}) \, \,{\mathrm{d}}V \end{aligned}$$

(18)

and the applied contact bias ${\underline{V}}_i^C$ at contact i. A bit more work has to be put into the first integral, because the only quantity we can directly compute is the current in transport direction. We divide the first term into two parts,

$$\begin{aligned} \int _D \nabla \tau _k(\mathbf{{r}}) \cdot \mathbf {{\underline{J}}}^\nu (\mathbf{{r}}) \;{\mathrm{d}}V =&\int _D \nabla \tau _k(\mathbf{{r}}) \cdot \mathbf {{\underline{J}}}_{\perp }^\nu (\mathbf{{r}}) \;{\mathrm{d}}V \nonumber \\&+ \int _D \nabla \tau _k(\mathbf{{r}}) \cdot \mathbf {{\underline{J}}}_z^\nu (\mathbf{{r}}) \;{\mathrm{d}}V , \end{aligned}$$

(19)

where $\mathbf {{\underline{J}}}_z^\nu (\mathbf{{r}})$ denotes the z-component of $\mathbf {{\underline{J}}}^\nu (\mathbf{{r}})$, and $\mathbf {{\underline{J}}}_{\perp }^\nu (\mathbf{{r}})$ is the component in $x-y$ plane perpendicular to the transport. Neglecting the transport in z-direction (i.e., $j^\nu (z)=0$), we have for the first integral:

$$\begin{aligned} {\mathscr {I}}_1&= \int \Big [\nabla \cdot \Big ( \tau _k(\mathbf{{r}})\mathbf {{\underline{J}}}_{\perp 0}^\nu (\mathbf{{r}}) \Big ) - \tau _k(\mathbf{{r}}) \nabla \cdot \mathbf {{\underline{J}}}_{\perp 0}^\nu (\mathbf{{r}}) \Big ] {\mathrm{d}}V \nonumber \\&= \underbrace{\oint _{\partial D} \tau _k(\mathbf{{r}})\mathbf {{\underline{J}}}_{\perp 0}^\nu (\mathbf{{r}}) \;{\mathrm{d}}\mathbf {A}}_{=0} \;+\; \int _D \tau _k(\mathbf{{r}}) \dfrac{\partial {\underline{\rho }}^\nu _{\perp 0}(\mathbf{{r}})}{\partial t} \;{\mathrm{d}}V \end{aligned}$$

(20)

where we have used the continuity equation:

$$\begin{aligned} \dfrac{\partial {\underline{\rho }}^\nu _{\perp }(\mathbf{{r}})}{\partial t} + \nabla \cdot \mathbf {{\underline{J}}}_{\perp 0}^\nu (\mathbf{{r}}) = 0 \, . \end{aligned}$$

(21)

and the fact that wavefunctions vanish on the boundary of the semiconductor region in transverse planes. The two-dimensional charge density $\rho ^\nu _\perp (\mathbf{{r}})$ can change with redistribution of electrons in the perpendicular plane either by changes in electrostatic potential or by scattering mechanisms. We need to capture both mechanisms here, while keeping in mind that time evolution of n(z) was already considered in solving the transport equation in order to avoid double-counting. This yields:

$$\begin{aligned}&{\mathscr {I}}_1 =\int _D \tau _k(\mathbf{{r}}) \Big [ 2i\omega n_\text {DC}(z) \psi ^\nu _\text {DC}(\mathbf{{r}}){\underline{\psi }}^\nu (\mathbf{{r}}) + {\underline{S}}_H^\nu (z)\vert \psi ^\nu _\text {DC}(\mathbf{{r}})\vert ^2 \Big ] \;{\mathrm{d}}V \end{aligned}$$

(22)

where ${\underline{S}}_H(z)$ represents the small-signal scattering term integrated over the total energy. Next, the contribution of $j^\nu (z)$ to $\mathbf {{\underline{J}}}_{\perp }^\nu (\mathbf{{r}})$ is calculated, which introduces a transverse current $\mathbf {J}_{\perp \text {IF}} ^\nu (\mathbf{{r}})$ when the wavefunctions change in z-direction. Hence, this component is attributed to the interface of adjacent z-boxes (see Fig. 11). Averaging this part over time for an arbitrary $\Delta t$ gives:

$$\begin{aligned}&\dfrac{1}{\Delta t} \int _0^{\Delta t} \int _D \nabla \tau _k(\mathbf{{r}}) \cdot \mathbf {J}_\perp ^\nu (\mathbf{{r}}) \;{\mathrm{d}}V{\mathrm{d}}t \nonumber \\&\quad = \dfrac{1}{\Delta t} \int _0^{\Delta t} \int _D \nabla \tau _k(\mathbf{{r}}) \cdot {\mathrm{d}}q \dfrac{{\mathrm{d}}{} \mathbf{{r}}(t)}{{\mathrm{d}}t}\delta (\mathbf{{r}} - \mathbf{{r}}(t)) \;{\mathrm{d}}V{\mathrm{d}}t \nonumber \\&\quad = \dfrac{{\mathrm{d}}q}{\Delta t} \int _{\mathbf{{r}}_\text {i}}^{\mathbf{{r}}_\text {f}} \nabla \tau _k(\mathbf{{r}}) \cdot {\mathrm{d}}{} \mathbf{{r}} = \dfrac{{\mathrm{d}}q}{\Delta t} \Big [ \tau _k(\mathbf{{r}}_\text {f}) - \tau _k(\mathbf{{r}}_\text {i}) \Big ] \end{aligned}$$

(23)

with:

$$\begin{aligned} {\mathrm{d}}q = j^\nu (z) \vert \psi _i^\nu (\mathbf{{r}}_\text {i})\vert ^2 {\mathrm{d}}A' \; \vert \psi _{i+1}^\nu (\mathbf{{r}}_\text {f})\vert ^2 {\mathrm{d}}A \Delta t . \end{aligned}$$

(24)

Fig. 11

Decomposition of the small-signal conduction current to three components

The discretized result for this part, therefore, is:

$$\begin{aligned} {\mathscr {I}}_2 =&\sum _i\int {\underline{j}}^\nu (z_{i+}) \Big [ \vert \psi ^\nu _{\text {DC},i}(\mathbf{{r}})\vert ^2 - \vert \psi ^\nu _{\text {DC},i+1}(\mathbf{{r}})\vert ^2 \Big ] \tau _k(\mathbf{{r}}) {\mathrm{d}}A \nonumber \\&+ 2\int j_\text {DC}^\nu (z_{i+}) \psi _{\text {DC},i}^\nu (\mathbf{{r}}){\underline{\psi }}_i^\nu (\mathbf{{r}}) \tau _k(\mathbf{{r}}){\mathrm{d}}A \nonumber \\&- 2\int j_\text {DC}^\nu (z_{i+}) \psi _{\text {DC},i+1}^\nu (\mathbf{{r}}){\underline{\psi }}_{i+1}^\nu (\mathbf{{r}}) \tau _k(\mathbf{{r}}){\mathrm{d}}A \end{aligned}$$

(25)

The last term in (19) is very straightforward to calculate, since the z-component of current density is obtained from the solution of Boltzmann equation:

$$\begin{aligned}&{\mathscr {I}}_3 =\int \dfrac{\partial \tau _k(\mathbf{{r}})}{\partial z} \Big [ {\underline{j}}^\nu (z)\vert \psi _\text {DC}^\nu (\mathbf{{r}}) \vert ^2 + 2j^\nu _\text {DC}(z) \psi ^\nu _\text {DC}(\mathbf{{r}}) {\underline{\psi }}^\nu (\mathbf{{r}}) \Big ] {\mathrm{d}}V. \end{aligned}$$

(26)