Abstract
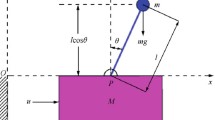
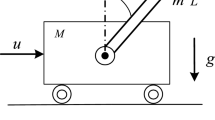
In this paper, we examine the stability of a linearized inverted pendulum system with two delayed position feedbacks. The semigroup approach is adopted in investigation for the well-posedness of the closed loop system. We prove that the spectrum of the system is located in the left complex half-plane and its real part tends to − ∞ when the feedback gains satisfy some additional conditions. The asymptotic eigenvalues of the system is presented. By estimating the norm of the Riesz spectrum projection of the system operator that does not have the uniformly upper bound, we show that the eigenfunctions of the system do not form a basis in the state Hilbert space. Furthermore, the spectrum determined growth condition of the system is concluded and the exponential stability of the system is then established. Finally, numerical simulation is presented by applying the MATLAB software.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
F. M. Atay. Balancing the inverted pendulum using position feedback. Appl. Math. Lett. 12 (1999), 51–56.
R. Datko, J. Lagnese, and M. P. Polis. An example on the effect of time delays in boundary feedback stabilization of wave equations. SIAM J. Control Optim. 24 (1986), No. 1, 152–156.
B. Z. Guo, J. M. Wang, and K. Y. Yang. Dynamic stabilization of an Euler–Bernoulli beam under boundary control and non-collocated observation. Systems Control Lett. 57 (2008), No. 9, 740–749.
T. Hagen. Asymptotic solutions of characteristic equations. Nonlinear Anal. Real World Appl. 6 (2005), No. 3, 429–446.
Z. J. Han and G. Q. Xu. Dynamical behavior of a hybrid system of nonhomogeneous Timoshenko beam with partial non-collocated inputs. J. Dynam. Control Systems 17 (2011), No. 1, 77–121.
H. Y. Hu. Using delayed state feedback to stabilize periodic motions of an oscillator. J. Sound Vibration 275 (2004), Nos. 3–5, 1009–1025.
M. Krstic. Control of an unstable reaction-diffusion PDE with long input delay. Systems Control Lett. 58 (2009), Nos. 10–11, 773–782.
H. Kwakernaak and R. Sivan. Linear optimal control systems. Wiley, New York (1972).
R. E. Langer. On the zeros of exponential sum and integrals. Bull. Am. Math. Soc. 7 (1931), 213–239.
B. Liu and H. Hu. Stabilization of linear undamped systems via position and delayed position feedbacks. J. Sound Vibration 312 (2008), 509–528.
Z. H. Luo, B. Z. Guo, and O. Morgul. Stability and stabilization of infinite-dimensional systems with applications. Springer-Verlag, London (1999).
A. Pazy. Semigroup of linear operators and applications to partial differential equations. Springer-Verlag, New York (1983).
J. P. Richard. Time-delay systems: an overview of some recent advances and open problems. Automat. J. IFAC 39 (2003), No. 10, 1667–1694.
A. A. Shkalikov. Boundary-value problems for ordinary differential equations with a parameter in the boundary conditions. J. Sov. Math. 33 (1986), 1311–1342.
N. C. Singer and W. P. Seering. Preshaping command inputs to reduce system vibration. ASME J. Dynam. Systems Measur. Control 112 (1990), 76–82.
E. D. Sontag. Mathematical control theory. Deterministic finite-dimensional systems. Springer-Verlag, New York (1990).
I. H. Suh and Z. Bien. Proportional minus delay controller. IEEE Trans. Automat. Control 24 (1979), No. 2, 370–372.
______, Use of time-delay actions in the controller design. IEEE Trans. Automat. Control 25 (1980), No. 3, 600–603.
J. M. Wang, B. Z. Guo, and M. Y. Fu. Dynamic behavior of a heat equation with memory. Math. Methods Appl. Sci. 32 (2009), No. 10, 1287–1310.
K. Youcef-Toumi and O. Ito. A time delay controller for systems with unknown dynamics. ASME J. Dynam. Systems Measur. Control 112 (1990), 133–142.
Author information
Authors and Affiliations
Corresponding author
Additional information
This work was partially supported by the National Natural Science Foundation of China and the Program for New Century Excellent Talents in University of China.
Rights and permissions
About this article
Cite this article
Zhao, DX., Wang, JM. Exponential stability and spectral analysis of the inverted pendulum system under two delayed position feedbacks. J Dyn Control Syst 18, 269–295 (2012). https://doi.org/10.1007/s10883-012-9143-6
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10883-012-9143-6