Skip to main content
SpringerLink
Log in

Bifurcation Analysis of a Predator–Prey System with Generalised Holling Type III Functional Response

  • Published:
Journal of Dynamics and Differential Equations Aims and scope Submit manuscript

Abstract

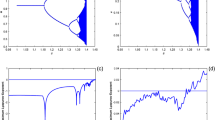
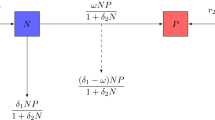
We consider a generalised Gause predator–prey system with a generalised Holling response function of type III: \(p(x) = \frac{mx^2}{ax^2+bx+1}\). We study the cases where b is positive or negative. We make a complete study of the bifurcation of the singular points including: the Hopf bifurcation of codimensions 1 and 2, the Bogdanov–Takens bifurcation of codimensions 2 and 3. Numerical simulations are given to calculate the homoclinic orbit of the system. Based on the results obtained, a bifurcation diagram is conjectured and a biological interpretation is given.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Andrews J.F. (1968). A mathematical model for the continuous culture of microorganisms utilizing inhibitory substrates. Biotechnol. Bioeng. 10: 707–723

    Article  Google Scholar 

  2. Bogdanov R.I. (1981). Versal deformation of singularity of a vector field on the plane in the case of zero eigenvalues. Selecta Math. Soviet. 1(4): 389–421

    Google Scholar 

  3. Bonin G. and Legault J. (1988). Comparaison de la méthode des constantes de Lyapunov et de la bifurcation de Hopf. Canad. Math. Bull. 31(2): 200–209

    MathSciNet  MATH  Google Scholar 

  4. Broer H.W., Naudot V., Roussarie R. and Saleh K. (2006). A predator–prey model with non-monotonic response function. Regul. Chaotic Dyn. 11: 155–165

    Article  MathSciNet  MATH  Google Scholar 

  5. Broer H.W., Naudot V., Roussarie R. and Saleh K. (2007). Dynamics of a predator–prey model with non- monotonic response function. Disc. Cont. Dyn. Sys. 18: 221–251

    Article  MathSciNet  MATH  Google Scholar 

  6. Caubergh M. and Dumortier F. (2004). Hopf–Takens bifurcations and centres. J. Differ. Equ. 202: 1–31

    Article  MathSciNet  MATH  Google Scholar 

  7. Chicone C. (1999). Ordinary differential equations with applications. Springer-Verlag, New York

    MATH  Google Scholar 

  8. Chow S.-N., Li C. and Wang D. (1994). Normal Forms and Bifurcation of Planar Vector Fields. Cambridge University Press, New York

    MATH  Google Scholar 

  9. Coutu, C.: Étude du diagramme de bifurcation d’un système prédateur-proie. Mémoire de maî trise, Université de Montréal (2003)

  10. Doedel E.J., Keller H.B. and Kernevez J.-P. (1991). Numerical analysis and control of bifurcation problems (II): bifurcation in infinite dimensions. Int. J. Bifurcations Chaos 1: 745–772

    Article  MathSciNet  MATH  Google Scholar 

  11. Dumortier F., Roussarie R. and Sotomayor J. (1987). Generic 3-parameter families of vector fields on the plane, unfolding a singularity with nilpotent linear part. The cusp case of codimention 3. Ergodic Theor. Dyn. Syst. 7(3): 375–413

    MathSciNet  MATH  Google Scholar 

  12. Freedman H.I. (1979). Stability analysis of a predator–prey system with mutual interference and density-dependent death rates. Bull. Math. Biol. 41: 67–78

    MathSciNet  MATH  Google Scholar 

  13. Freedman H.I. (1980). Deterministic Mathematical Models in Population Ecology. Marcel Dekker, Inc., New York

    MATH  Google Scholar 

  14. Freedman H.I. and Wolkowicz G.S.K. (1986). Predator–prey systems with group defence: the paradox of enrichment revisited. Bull. Math. Biol. 485(5/6): 493–508

    MathSciNet  Google Scholar 

  15. Gause G.F. (1969). The Struggle for Existence. Hafner Publishing Company, New York

    Google Scholar 

  16. Göbber F. and Willamowski K.-D. (1979). Ljapunov approach of multiple Hopf bifurcation. J. Math. Anal. Appl. 71: 333–350

    Article  MathSciNet  MATH  Google Scholar 

  17. Guckenheimer J. and Holmes P. (1983). Nonlinear Oscillations, Dynamical Systems and Bifurcations of Vector Fields. Springer-Verlag, New York

    MATH  Google Scholar 

  18. Holling C.S. (1965). The functional response of predators to prey density and its role in mimicry and population regulation. Mem. Entomol. Soc. Can. 45: 3–60

    Google Scholar 

  19. Jost J.L., Drake J.F., Fredrickson A.G. and Tsuchiya H.M. (1973). Interactions of Tetrahymena pyrisformis, Escherichia coli, Azotobacter vinelandii, and glucose in a minimal medium. J. Bacteriol. 113: 834–840

    Google Scholar 

  20. Jost J.L., Drake J.F., Tsuchiya H.M. and Fredrickson A.G. (1973). Microbial food chains and food webs. J. Theor. Biol. 41: 461–484

    Article  Google Scholar 

  21. Lamontagne, Y.: Étude d’un système prédateur-proie avec fonction de réponse Holling de type III généralisée. Mémoire de maîtrise, Université de Montréal (2006)

  22. Ruan S. and Xiao D. (2001). Global analysis in a predator–prey system with nonmonotonic functional response. SIAM J. Appl. Math. 61(4): 1445–1472

    Article  MathSciNet  MATH  Google Scholar 

  23. Wolkowicz G.S.K. (1988). Bifurcation analysis of a predator–prey system involving group defence. SIAM J. Appl. Math. 48(3): 592–606

    Article  MathSciNet  MATH  Google Scholar 

  24. Zhu H., Campbell S.A. and Wolkowicz G.S.K. (2002). Bifurcation analysis of a predator–prey system with nonmonotonic functional response. SIAM J. Appl. Math. 63(2): 636–682

    MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Collège Édouard-Montpetit, Longueuil, QC, Canada, J4H 3M6

    Yann Lamontagne & Caroline Coutu

  2. Département de Mathématiques, Université de Montréal, C.P. 6128, Succursale Centre-ville, Montréal, QC, Canada, H3C 3J7

    Christiane Rousseau

Authors
  1. Yann Lamontagne
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Caroline Coutu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Christiane Rousseau
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Christiane Rousseau.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Lamontagne, Y., Coutu, C. & Rousseau, C. Bifurcation Analysis of a Predator–Prey System with Generalised Holling Type III Functional Response. J Dyn Diff Equat 20, 535–571 (2008). https://doi.org/10.1007/s10884-008-9102-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10884-008-9102-9

Keywords

Mathematics Subject Classification (2000)

Search

Navigation