A Stable Fast Time-Stepping Method for Fractional Integral and Derivative Operators

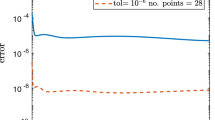
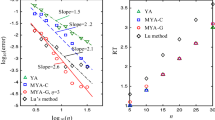
Abstract

A unified fast time-stepping method for both fractional integral and derivative operators is proposed. The fractional operator is decomposed into a local part with memory length $\varDelta T$ and a history part, where the local part is approximated by the direct convolution method and the history part is approximated by a fast memory-saving method. The fast method has $O(n_0+\sum _{\ell }^L{q}_{\alpha }(N_{\ell }))$ active memory and $O(n_0n_T+ (n_T-n_0)\sum _{\ell }^L{q}_{\alpha }(N_{\ell }))$ operations, where $L=\log (n_T-n_0)$, $n_0={\varDelta T}/\tau ,n_T=T/\tau$, $\tau$ is the stepsize, T is the final time, and ${q}_{\alpha }{(N_{\ell })}$ is the number of quadrature points used in the truncated Laguerre–Gauss (LG) quadrature. The error bound of the present fast method is analyzed. It is shown that the error from the truncated LG quadrature is independent of the stepsize, and can be made arbitrarily small by choosing suitable parameters that are given explicitly. Numerical examples are presented to verify the effectiveness of the current fast method.

Proofs

1.1 Proof of Theorem 1.

Proof

We follow the proof of Theorem 2.2 in [41]. We first expand $g(\lambda )=e^{-t\lambda }$ in terms of the Laguerre polynomials, i.e., $g(\lambda )=\sum _{n=0}^{\infty }a_nL_n^{(\alpha )}(\lambda ),$ where

$$\begin{aligned}a_n=\frac{\varGamma (n+1)}{\varGamma (n+1+\alpha )} \int _0^{\infty }\lambda ^{\alpha } e^{-\lambda } g(\lambda )L_n^{(\alpha )}(\lambda )\,\mathrm{d}\lambda =\frac{t^n}{(t+1)^{n+1+\alpha }}. \end{aligned}$$

The following property will be used, see [41],

$$\begin{aligned} \big |Q_N^{\alpha }[L_n^{(\alpha )}]\big | \le \left\{ \begin{aligned}&2\varGamma (1+\alpha ),{\quad }-1<\alpha \le 0,\\&2^{1+\alpha }{\varGamma (n+1+\alpha )}/{\varGamma (n+1)},{\quad }\alpha >0. \end{aligned}\right. \end{aligned}$$

With the above two equations and $J^{\alpha }[e^{-t\lambda }]- Q_N^{\alpha }[e^{-t\lambda }] =\sum _{n=2N}^{\infty }a_nQ_N^{\alpha }[L_n^{(\alpha )}]$ gives

$$\begin{aligned} \big |J^{\alpha }[e^{-t\lambda }]- Q_N^{\alpha }[e^{-t\lambda }]\big | \le \left\{ \begin{aligned}&2^{1+\alpha }\varGamma (1+\alpha )\sum _{n=2N}^{\infty }a_n ,{\quad }-1<\alpha \le 0,\\&c_{\alpha }2^{1+\alpha }\sum _{n=2N}^{\infty }n^{\alpha }a_n,{\quad }\alpha >0. \end{aligned}\right. \end{aligned}$$

(54)

Let $q=t/(1+t)$. Then we have $\sum _{n=2N}^{\infty }a_n=(1+t)^{-\alpha }q^{2N}$ for $-1<\alpha \le 0$. For $\alpha >0$, one has

$$\begin{aligned} \sum _{n=2N}^{\infty }n^{\alpha }a_n=(1+t)^{-\alpha }q^{2N}(2N)^{\alpha } \sum _{n=0}^{\infty }q^n\Big (1+\frac{n}{2N}\Big )^{\alpha } \le C_{\alpha ,t} 2^{\alpha }(1+t)^{1-\alpha }q^{2N}N^{\alpha }, \end{aligned}$$

where $C_{\alpha ,t} =\sum _{n=0}^{\infty }(n+2)^{\alpha }q^{2Nn}$ is used. With the above equation and (54) yields (42) for $T=1$. Using the following relation

$$\begin{aligned} \big |J^{\alpha }[T,e^{-t\lambda }]- Q_N^{\alpha }[T,e^{-t\lambda }]\big | =T^{-\alpha -1}\big |J^{\alpha }[e^{-(t/T)\lambda }]- Q_N^{\alpha }[e^{-(t/T)\lambda }]\big | \end{aligned}$$

leads to (42) for any $T>0$. The proof is complete. $\square$

1.2 Proof of Theorem 2.

Proof

The following results can be found in [12],

$$\begin{aligned}&{\lambda }_j < \frac{2j+\alpha +3}{2N+\alpha +3} \Big (2j+\alpha +3+\sqrt{(2j+\alpha +3)^2 +0.25-\alpha ^2}\Big ), \end{aligned}$$

(55)

$$\begin{aligned}&{\lambda }_j > \frac{2(J_{\alpha ,j}/2)^2}{2N+\alpha +3},{\quad } J_{\alpha ,j}=\pi (j+3/4+\alpha /2)+O(j^{-1}), \end{aligned}$$

(56)

where (56) holds when j is sufficiently large. For a sufficiently large N, the Laguerre polynomial satisfies (see (7.14) in [34])

$$\begin{aligned} \big |L^{(\alpha )}_N(x)\big | \approx \pi ^{-1/2}(Nx)^{-1/4}e^{x/2}, {\quad }\forall x\ge 0. \end{aligned}$$

(57)

With (55)–(57) and (41), we have the following estimate

$$\begin{aligned} {w}^{(\alpha )}_j\le C_{\alpha }(N+1)^{\alpha } \left( \frac{j+1}{N+1}\right) ^3e^{-{\lambda }_j} \le C(N+1)^{\alpha } e^{-{\lambda }_j}, \end{aligned}$$

(58)

for sufficiently large j, where ${\lambda }_j=\theta _j(j+1)^2/(N+1)$ and $\theta _j$ is bounded and approximately between $\pi ^2/4$ and 4. The proof is completed. $\square$

1.3 Proof of Theorem 3.

Proof

For notational simplicity, we denote

$$\begin{aligned} \widehat{T}_{\ell }=T_{\ell -1}+{\varDelta } T-\tau ,{\quad } \widehat{H}^n_{\ell }(s)=\hat{t}_n-T_{\ell -1}-s. \end{aligned}$$

Next, we investigate how to estimate $N_{\ell }$ in (35), such that the LG quadrature $Q_{N_{\ell }}^{-\alpha }[\widehat{T}_{\ell },e^{-\widehat{H}^n_{\ell }(s)\lambda }]$ to the integral $J^{-\alpha }[\widehat{T}_{\ell },e^{-\widehat{H}^n_{\ell }(s)\lambda }]$ preserves the accuracy up to $O(\epsilon )$ for all $s\in [s_{\ell },s_{\ell -1}]$.

From Theorem 1, we know that the error of $Q_{N_{\ell }}^{-\alpha }[\widehat{T}_{\ell },e^{-\widehat{H}^n_{\ell }(s)\lambda }]$ mainly depends on the following term

$$\begin{aligned} \left( {\widehat{H}^n_{\ell }(s)}/{\widehat{T}_{\ell }}\right) ^{2N} =\left( \frac{\hat{t}_n-s-T_{\ell -1}}{T_{\ell -1}+{\varDelta } T-\tau }\right) ^{2N}, \quad s\in [s_{\ell },s_{\ell -1}]. \end{aligned}$$

Using (34) and $T_{\ell -1}=B^{\ell -1}\tau$ gives

$$\begin{aligned} 0\le \frac{\hat{t}_n-s-T_{\ell -1}}{T_{\ell -1}+{\varDelta } T-\tau }\le \frac{2B-1-B^{1-\ell }}{1+B^{1-\ell }({\varDelta }T/\tau -1)} =\mathcal {T}_{\ell } \le 2B-1,{\quad } \forall \ell \ge 1. \end{aligned}$$

(59)

Using the above inequality and Eq. (42) yields

$$\begin{aligned} \begin{aligned}&\big |J^{-\alpha }[\widehat{T}_{\ell },e^{-\widehat{H}^n_{\ell }(s)\lambda }] -Q_{N_{\ell }}^{-\alpha }[\widehat{T}_{\ell },e^{-\widehat{H}^n_{\ell }(s)\lambda }]\big |\\&\quad \le C_{\alpha }\widehat{T}_{\ell }^{\alpha -1} N^{\alpha }_{\ell }\left( \frac{{\widehat{H}^n_{\ell }(s)}/{\widehat{T}_{\ell }}}{1+{\widehat{H}^n_{\ell }(s)}/{\widehat{T}_{\ell }}}\right) ^{2N_{\ell }} \le C_{\alpha }\widehat{T}_{\ell }^{\alpha -1}N^{\alpha }_{\ell } \left( \frac{\mathcal {T}_{\ell }}{1+\mathcal {T}_{\ell }}\right) ^{2N_{\ell }}. \end{aligned}\end{aligned}$$

(60)

Since the relative error of (60) is independent of $\widehat{T}_{\ell }$, we can let $(\mathcal {T}_{\ell }/(\mathcal {T}_{\ell }+1))^{2N_{\ell }}\le \epsilon$, which yields the minimum $N_{\ell }$ given by (36).

From (44) and (60), we derive that the pointwise error of the truncated quadrature $Q_{N_{\ell },\epsilon _0}^{-\alpha }[\widehat{T}_{\ell },e^{-\widehat{H}^n_{\ell }(s)\lambda }]$ for all $s\in [s_{\ell },s_{\ell -1}]$ is given by

$$\begin{aligned} \begin{aligned} E^{-\alpha ,\ell }_{\epsilon ,\epsilon _0}[e^{-\widehat{H}^n_{\ell }(s)\lambda }] =\,&J^{-\alpha }[\widehat{T}_{\ell },e^{-\widehat{H}^n_{\ell }(s)\lambda }] -Q_{N_{\ell },\epsilon _0}^{-\alpha }[\widehat{T}_{\ell },e^{-\widehat{H}^n_{\ell }(s)\lambda }]\\ =\,&\left( J^{-\alpha }[\widehat{T}_{\ell },e^{-\widehat{H}^n_{\ell }(s)\lambda }] -Q_{N_{\ell }}^{-\alpha }[\widehat{T}_{\ell },e^{-\widehat{H}^n_{\ell }(s)\lambda }]\right) \\&\quad +\left( Q_{N_{\ell }}^{-\alpha }[\widehat{T}_{\ell },e^{-\widehat{H}^n_{\ell }(s)\lambda }] -Q_{N_{\ell },\epsilon _0}^{-\alpha }[\widehat{T}_{\ell },e^{-\widehat{H}^n_{\ell }(s)\lambda }]\right) \\ =\,&O(\epsilon ) + O(\epsilon _0), \end{aligned} \end{aligned}$$

(61)

where $Q_{N_{\ell },\epsilon _0}^{-\alpha }$ is defined by (44) and $N_{\ell }$ is given by (36).

From (35) and (61), we have

$$\begin{aligned} \begin{aligned} \big |H^{\alpha }_{{\varDelta }T}(I^H_{\tau }u,t_n)-{}_FH_{\varDelta T,\tau }^{(\alpha ,n)}u\big | =\,&\Big |\frac{\sin (\alpha \pi )}{\pi }\sum _{\ell =1}^L E^{-\alpha ,\ell }_{\epsilon ,\epsilon _0} [e^{-(\hat{t}_n-T_{\ell -1}-s_{\ell -1})\lambda }y(s_{\ell -1},s_{\ell },\lambda )]\Big |\\ =\,&\Big |\frac{\sin (\alpha \pi )}{\pi }\sum _{\ell =1}^L \int _{s_{\ell }}^{s_{\ell -1}} E^{-\alpha ,\ell }_{\epsilon ,\epsilon _0}[e^{-\widehat{H}^n_{\ell }(s)\lambda }] I_{\tau }^{H}u(s)\,\mathrm{d}s\Big |\\ \le \,&C(\epsilon +\epsilon _0)\int _{0}^{\hat{t}_n}\big |I_{\tau }^{H}u(s)\big |\,\mathrm{d}s\\ \le \,&C\max \{0,t_{n+1}-\varDelta T\} \Vert u\Vert _{\infty }(\epsilon +\epsilon _0). \end{aligned} \end{aligned}$$

(62)

The proof is complete. $\square$