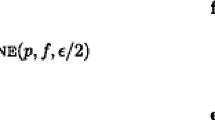Active networks are network architectures with processors that are capable of executing code carried by the packets passing through them. A critical network management concern is the optimization of such networks and tight bounds on their performance serve as useful design benchmarks. A new bound on communication rates is developed that applies to network coding, which is a promising active network application that has processors transmit packets that are general functions, for example a bit-wise XOR, of selected received packets. The bound generalizes an edge-cut bound on routing rates by progressively removing edges from the network graph and checking whether certain strengthened d-separation conditions are satisfied. The bound improves on the cut-set bound and its efficacy is demonstrated by showing that routing is rate-optimal for some commonly cited examples in the networking literature.












Similar content being viewed by others
REFERENCES
S. F. Bush and A. B. Kulkarni, Active Networks and Active Network Management, Kluwer Academic, New York, 2001.
S. F. Bush, Active Virtual Network Management Prediction: Complexity as a Framework for Prediction, Optimization, and Assurance, Available at http://arxiv.org/PS_cache/cs/pdf/0203/0203014.pdf
D. S. Alexander, W. A. Arbaugh, M. W. Hicks, P. Kakkar, A. D. Keromytis, J. T. Moore, C. A. Gunter, S. M. Nettles, and J. M. Smith, The SwitchWare Active Network Architecture, IEEE Network, Vol. 12, No. 3, pp. 27–36, 1998.
K. Calvert, ed. Active Networks Framework, Available at http://www.cc.gatech.edu/projects/canes/papers/arch-1-0.ps.gz
M. Hicks, P. Kakkar, T. Moore, C. Gunter, and S. Nettles, PLAN: A Programmable Language for Active Networks, ACM SIGPLAN Notices, Vol. 34, No. 1, pp. 86–93, 1999.
D. Wetherall, J. Guttag, and D. Tennenhouse, ANTS: Network Services Without the Red Tape, Computer, Vol. 32, No. 4, pp. 42–48, 1999.
L. R. Ford Jr. and D. R. Fulkerson, Flows in Networks, Princeton University Press, Princeton, NJ, 1962.
R. Ahlswede, N. Cai, S.-Y. R. Li, and R. W. Yeung, Network information flow, IEEE Transactions on Information Theory, Vol. 46, No. 4, pp. 1204–1216, 2000.
R. Koetter, Available at http://tesla.csl.uiuc.edu/koetter/NWC/
P. A. Chou, Y. Wu, and K. Jain, Practical network coding, In: Proceedings of the 41st Allerton Conference on Communication, Control and Computing, Monticello, IL, 2003.
T. Ho, M. Médard, J. Shi, D. R. Karger, and M. Effros, On randomized network coding, In: Proceedings of the 41st Allerton Conference on Communication, Control and Computing, Monticello, IL, 2003.
T. Ho, B. Leong, M. Médard, R. Koetter, Y.-H. Chang, and M. Effros, On the utility of network coding in dynamic environments, In: Proceedings of the International Workshop on Wireless Ad-hoc Networks (IWWAN), Oulu, Finland, 2004.
T. Ho, M. Médard, and R. Koetter, An Information-Theoretic View of Network Management, IEEE Transactions on Information Theory, Vol. 51, No. 4, pp. 1295–1312, 2005.
R. Koetter and M. Médard, An Algebraic Approach to Network Coding, IEEE/ACM Transactions on Networking, Vol. 11, No. 5, pp. 782–795, 2003.
Y. Wu. P. A. Chou, and S.-Y. Kung, Minimum-energy multicast in mobile ad hoc networks using network coding, In Proceedings of the Information Theory Workshop 2004, San Antonio, TX, 2004.
Y. Wu, P. A. Chou, Q. Zhang, K. Jain, W. Zhu, and S.-Y. Kung, Network Planning in Wireless Ad Hoc Networks: A Cross-Layer Approach, IEEE Journal on Selected Areas of Communications. Vol. 23, no. 1, pp. 136–150, 2005.
G. B. Dantzig and D. R. Fulkerson, On the max-flow, min-cut theorem of networks, In: H. W. Kuhn (ed.), Linear Inequalities, Annals of Mathematical Studies, Number 38, Princeton University Press, Princeton, NJ, pp. 215–221, 1956.
P. Elias, A. Feinstein, and C. E. Shannon, A Note on the Maximum Flow through a Network, IRE Transactions on Information Theory, Vol. 2, No. 4, pp. 117–119, 1956.
L. R. Ford and D. R. Fulkerson, Maximal Flow through a Network, Canadian Journal of Mathematics, Vol. 8, No. 3, pp. 399–404, 1956.
J. T. Robacker, On Network Theory, The RAND Corporation, Research Memorandum RM-1498, May 26, 1955.
G. Kramer and S. A. Savari, On networks of two-way channels, In: A. Ashikhmin and A. Barg (eds.), Algebraic Coding Theory and Information Theory, DIMACS Workshop, Dec. 15-18, 2003, Rutgers University, Vol. 68: DIMACS Series in Discrete Mathematics and Theoretical Computer Science, American Mathematical Society, Providence, Rhode Island, pp. 133–143, 2005.
J. Pearl, Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference, Morgan Kaufmann, San Mateo. CA, 1988.
G. Kramer, Directed Information for Channels with Feedback, Hartung-Gorre Verlag, Konstanz, 1998, ETH Series in Information Processing, Vol. 11.
T. M. Cover and J. A. Thomas, Elements of information Theory, Wiley, New York, 1991.
S. P. Borade, Network information flow: Limits and achievability, In: Proceedings of the IEEE International Symposium on Information Theory, Lausanne, Switzerland, p. 139, June 30-July 5, 2002.
G. Kramer, Capacity Results for the Discrete Memoryless Network, IEEE Transactions on Information Theory, Vol. 49, No. 1, pp. 4–21, 2003.
A. Schrijver, Combinatorial Optimization, Springer-Verlag, New York, 2003.
T. C. Hu, Multi-commodity Network Flows, Operations Research, Vol. 11, No. 3, pp. 344–360, 1963.
H. Okamura and P. D. Seymour, Multicommodity Flows in Planar Graphs, Journal of Combinatorial Theory, Series B, Vol. 31, No. 1, pp. 75–81, 1981.
N. J. A. Harvey, R. D. Kleinberg, and A. R. Lehman. On the Capacity of Information Networks, IEEE Transactions on Information Theory, in press.
K. Jain, P. A. Chou, V. V. Vazirani, R. Yeung, and G. Yuval, On the Capacity of Multiple Unicast Sessions in Undirected Graphs, IEEE Transactions on Information Theory, in press.
DIMACS Working Group on Network Coding, DIMACS Center, Rutgers University, Piscataway, NJ, Jan. 26–28, 2005, Available at http://dimacs.rutgers.edu/Workshops/NetworkCodingWG.
G. Kramer and S. A. Savari. Progressive d-separating edge set bounds on network coding rates, In: Proceedings of the 2005 IEEE International Symposium on Information Theory, Adelaide, Australia, Sept. 2005.
ACKNOWLEDGMENTS
The authors wish to thank C. Chekuri for stimulating discussions and S. Bush for helpful comments and suggestions. The work of G. Kramer was partially supported by the Board of Trustees of the University of Illinois Subaward No. 04-217 under NSF Grant No. CCR-0325673. Any opinions, findings, conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the University or its Project Director or of the National Science Foundation. The work of S. A. Savari was supported by NSF Grant No. CCF-0430201.
Author information
Authors and Affiliations
Corresponding author
Additional information
Gerhard Kramer is a Member of Technical Staff in the Mathematics of Communications Research Department, Bell Laboratories, Lucent Technologies, Murray Hill, NJ. He is currently serving as a Publications Editor for the IEEE Transactions on Information Theory and has organized several workshops on coding and information theory.
Serap A. Savari is an Associate Professor in the Department of Electrical Engineering and Computer Science at the University of Michigan, Ann Arbor. Her research interests include information theory, data compression, network coding, computing and communication systems. She is currently serving as the Associate Editor for Source Coding for the IEEE Transactions on Information Theory and has been on the program committees of several information theory and data compression conferences.
APPENDIX VALIDITY OF THE PDE BOUND
APPENDIX VALIDITY OF THE PDE BOUND
We prove the validity of the PdE bound described in Sections 5 and 6 for noisy as well as noise-free networks. This section assumes familiarity with advanced concepts in information theory. Recall that we consider the following objects.
-
ɛ d : a set of edges
-
S d: a set of source indices
-
π(.): a one-to-one mapping from \(\{1,\,2, \ldots,|\cal{S}_d |\}\) to S d.
-
a nonempty subset of \(\{\hat W_k^{(i)} :i=1,2, \ldots,D_k\}\) for all \(k \in \cal{S}_d\).
For the last item, recall that Wk is associated with the vertices \((s_k,\,t_k (1),\,t_k (2), \ldots,\,t_k (D_k))\), so we are considering some subset \(\hat{\cal V}_k\) of the vertices t k (i), i=1, 2,舰, D k . We write the corresponding subset of estimates as \(\hat W_k (\hat {\cal V}_k)\).
We continue by noting that, for reliable communication, Fano's inequality [24, p. 39] requires that
We define \(W_\pi ^{k - 1}=[W_{\pi (1)},W_{\pi (2)}, \ldots,W_{\pi (k - 1)} ]\) and bound
where (a) follows because \(I(A;B) \le I(A;BC)\), (b) follows because the messages and noise are statistically independent, and (c) follows by the chain rule for mutual information and because success in step 2) in Section 5 implies that
via fd-separation. Inserting (A.2) into (A.1) and applying the chain rule for mutual information, we find that
We continue by upper bounding the mutual information expression in (A.4) by
where (a) follows by the chain rule for mutual information, (b) and (c) follow by (3.1), (d) follows because conditioning cannot increase entropy, and (e) follows because it is known that (see [24], Ch. 8)
Inserting (A.5) into (A.4) gives (5.1).
Rights and permissions
About this article
Cite this article
Kramer, G., Savari, S.A. Edge-Cut Bounds on Network Coding Rates. J Netw Syst Manage 14, 49–67 (2006). https://doi.org/10.1007/s10922-005-9019-0
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10922-005-9019-0