Experimental Study of the Bottleneck in Fully Developed Turbulence

Abstract

The energy spectrum of incompressible turbulence is known to reveal a pileup of energy at those high wavenumbers where viscous dissipation begins to act. It is called the bottleneck effect (Donzis and Sreenivasan in J Fluid Mech 657:171–188, 2010; Falkovich in Phys Fluids 6:1411–1414, 1994; Frisch et al. in Phys Rev Lett 101:144501, 2008; Kurien et al. in Phys Rev E 69:066313, 2004; Verma and Donzis in Phys A: Math Theor 40:4401–4412, 2007). Based on direct numerical simulations of the incompressible Navier-Stokes equations, results from Donzis and Sreenivasan (657:171–188, 2010) pointed to a power-law decrease of the strength of the bottleneck with increasing intensity of the turbulence, measured by the Taylor micro-scale Reynolds number $R_{\lambda }$. Here we report the first experimental results on the dependence of the amplitude of the bottleneck as a function of $R_{\lambda }$ in a wind-tunnel flow. We used an active grid (Griffin et al. in Control of long-range correlations in turbulence, arXiv:1809.05126, 2019) in the variable density turbulence tunnel (VDTT) (Bodenschatz et al. in Rev Sci Instrum 85:093908, 2014) to reach $R_{\lambda }>5000$, which is unmatched in laboratory flows of decaying turbulence. The VDTT with the active grid permitted us to measure energy spectra from flows of different $R_{\lambda }$, with the small-scale features appearing always at the same frequencies. We relate those spectra recorded to a common reference spectrum, largely eliminating systematic errors which plague hotwire measurements at high frequencies. The data are consistent with a power law for the decrease of the bottleneck strength for the finite range of $R_{\lambda }$ in the experiment.

1 Introduction

Turbulence is omnipresent in natural and technological flows. Its consequences for the associated processes are essential in the fields of astrophysics, geophysics, meteorology, biology, and in many engineering disciplines from chemical engineering, combustion science, heat and mass transfer engineering to aeronautics, marine science and renewable energy research. From the fundamental perspective the mathematical field theory of the incompressible Navier Stokes equation continues to challenge pure and applied mathematicians [1]. In turbulence fluid velocities and accelerations fluctuate greatly and any description can only be statistical in nature. It is believed that at very high turbulence levels at spatial scales smaller than the energy injection scale the turbulence shows universal properties, independent of the particular driving. According to Kolmogorov’s phenomenology from 1941 [2] (abbreviated K41), the universal statistical spatial properties of fully developed turbulence can be captured in three ranges of spatial scales. Kinetic energy is injected into the turbulent fluctuations at the largest scales, whose properties are particular to the driving mechanism. The kinetic energy is transformed into heat at the very smallest scales through viscous dissipation. If the range of spatial scales found in the turbulent structures is large enough, a third range of scales develops, where neither the peculiarities of energy injection, nor viscous dissipation influence the spatial scale-to scale energy transfer. This range is called the inertial range. In this intermediate range statistical properties can be interpreted by the scale-to-scale transfer of kinetic energy only, described by the kinetic energy dissipation range $\varepsilon$(dissipated power per unit mass). The dimensionless quantity used to give the strength of turbulence and thus the size of the inertial range scaling is the Taylor microscale Reynolds number

$$\begin{aligned} R_{\lambda }=\frac{u\lambda }{\nu }. \end{aligned}$$

u is the rms of the velocity fluctuations, $\nu$ is the kinematic viscosity of the fluid, and $\lambda$ is the Taylor microscale, which is a measure for the mean length between two zero-crossings of the velocity fluctuations [3]. $\lambda$ can be thought of as a typical size of an inertial range eddy. In statistically isotropic and homogeneous turbulence $R_{\lambda }$ can be linked to the well-known Reynolds number $\text {Re}=uL/\nu$ based on the large scales L via $R_{\lambda }=\sqrt{15\text {Re}}$ [4]. The integral scale L can be estimated as the integral over the velocity correlation function $L_{11}=\int \langle u(x+r)u(r)\rangle dr$.

In K41 phenomenology for spatially homogeneous and statistically isotropic turbulence the spatial energy spectrum in the inertial range is given by

$$\begin{aligned} E(k)=C_{K}\varepsilon ^{2/3}k^{-5/3}. \end{aligned}$$

(1)

$C_{K}$ is the Kolmogorov constant, k is the wavenumber. In this K41 spectrum the only free parameter is the dissipation rate $\varepsilon$ as indicated above.

Despite its simplicity, Eq. (1) describes the energy spectrum of observed and simulated turbulent flows quite well (see [5] for a compilation and [6] for an experimental study on the $R_{\lambda }$-dependence of the spectral slope). Nevertheless, important deviations are well known. When analyzing the compensated spectrum $E(k)\varepsilon ^{-2/3}k^{5/3}$, deviations from a $k^{-5/3}$ scaling are found. Prominent is an increase in amplitude of the compensated spectrum at the high-wavenumber end of the inertial range. This pileup of energy is commonly called the bottleneck effect [7,8,9,10,11,12]. It has been observed in laboratory flows (e.g. [5, 13,14,15]) and direct numerical simulations (DNS) [16,17,18,19] alike and is typically preceded by a distinct local minimum of the compensated spectrum. The bottleneck peak is very shallow or almost absent in hot-wire measurements of atmospheric boundary layer turbulence at very high $R_{\lambda }>10^{4}$ [20,21,22]. It is generally less pronounced in one-dimensional spectra than in three-dimensional ones [23]. The effect is also present in structure functions and influences the rapidity of the transition between the viscous and inertial ranges in the second-order structure function [19, 24], hints of which can also be found in structure functions of higher orders [25]. The most extensive analysis of the bottleneck effect has been performed by Donzis and Sreenivasan [19] on DNS at $R_{\lambda }$ up to 1000. They found that the bottleneck effect can be characterized as the difference between the bottleneck peak height and the level of the preceding minimum in the compensated spectrum. They conclude that the bottleneck effect weakens as a function of $R_{\lambda }$ and report a scaling of $h \sim R_{\lambda }^{-0.04}$. Furthermore, they find that the peak of the bump occurs around $k\eta \approx 0.13$ in three-dimensional spectra, independent of $R_{\lambda }$. Here $\eta$ is the Kolmogorov length scale, where dissipative effects are expected to dominate.

From a theoretical perspective, various explanations exist for the bottleneck effect. Falkovich [10] showed that a small perturbation to a K41 spectrum in the energy transfer equation leads to a correction of the form $\delta E(k)=E(k)(k/k_{p})^{-4/3}\ln ^{-1}(k_{p}/k)$, where $k_{p}$ is the bottleneck wavenumber. Kurien et al. [9] argued that the time scale of helicity can be comparable to the energy time scale in the inertial range, where the relative helicity is already weak. They propose that the bottleneck effect is a change in the scaling exponent of the energy spectrum from $-5/3$ to $-4/3$. Their DNS supports this claim as they find a corresponding scaling range in the three-dimensional spectrum. The scaling is absent in the one-dimensional versions of their spectra. Frisch et al. [8] studied hyperviscous Navier-Stokes equations (Laplacian of order $\alpha \ge 2$) and attribute the bottleneck effect to an incomplete thermalization of high-wavenumber modes in the spatial spectrum. None of these studies directly incorporates a $R_{\lambda }$-dependence of the bottleneck height. Verma and Donzis [11] study the nonlocal and nonlinear mode-to-mode energy transfer in a shell model of turbulence and find that a significant portion of the energy flux away from a wavenumber shell goes to distant shells. Thus an efficient energy cascade requires a large inertial range. If the inertial range is insufficient, the energy piles up at the dissipative drop-off. As the length of the inertial range is tightly linked to $R_{\lambda }$, this implies a dependence of the bottleneck intensity on the Reynolds number.

In summary, the bottleneck effect has been studied systematically in DNS and various models. Numerical simulations indicate that the effect gets weaker with increasing $R_{\lambda }$, which is also predicted by Verma and Donzis [11] and in agreement with atmospheric measurements at ultra-high $R_{\lambda }$, where it is absent.

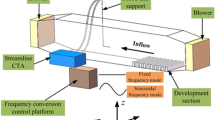
Here we present a detailed analysis of the $R_{\lambda }$-scaling of the bottleneck effect over an unprecedented range of $R_{\lambda }$ in a well controlled laboratory flow. The analysis of the bottleneck effect from experimental data can be demanding as systematic errors can cloud the results. From the perspective of the measuring instrument a small bump in the compensated spectrum is a subtle effect that occurs at rather high frequencies not yet resolvable in PIV or PTV measurements and very difficult to achieve in LDV. We use classical constant temperature hot-wire anemometry (CTA) assuming Taylor frozen flow hypothesis [26] in the Max Planck variable density turbulence tunnel (VDTT) [15]. Even with very well-established hot-wire technology, subtle changes in the energy spectrum at high frequencies can be heavily influenced by amplification or attenuation at such frequencies (see Sect. 2.2 for a review).

In this manuscript we work around those effects and investigate the bottleneck effect from the lowest Reynolds number at which it can be identified ($\sim 200$) up to the highest $R_{\lambda }$ ever measured in a wind tunnel flow.

The paper is organized as follows: first, we present a concise compilation of experimental efforts to reach high $R_{\lambda }$ and describe the variable density turbulence tunnel. We continue with a brief review of challenges posed by constant temperature hot-wire anemometry, especially its frequency responses. In Sect. 3 we introduce the relative spectra that allow us to eliminate instrumentation errors to a large extent. Finally we report the results of our analysis and discuss their relevance for the scaling of the bottleneck effect with $R_{\lambda }$.

2 Experimental Methods

2.1 High $R_{\lambda }$ and the Variable Density Turbulence Tunnel

Kolmogorov’s 1941 predictions of universal scaling in turbulent flows refer to the limit of large $R_{\lambda }$, such that the regimes of energy injection and viscous dissipation are well separated [2]. This condition is cumbersome to achieve practically. A large separation of scales and therefore a large $R_{\lambda }$ is found in atmospheric flows [20,21,22], where control is impossible and stationary conditions are difficult to achieve. Flows of high $R_{\lambda }$ are difficult to achieve in controlled laboratory flows, where all scales can be reliably measured. To reach high $R_{\lambda }$ one can turn two knobs: the size of the energy injection scale L and the dissipation scale $\eta =(\nu ^{3}/\varepsilon )^{1/4}$. In direct numerical simulations (DNS), a compromise between the size of the periodoc box, (limiting L), the spatial and temporal resolution, the convergence time, and the available resources needs to be found [27]. The largest $R_{\lambda }=2340$ achieved in a DNS under these constraints to date has been performed by Ishihara [17]. The limits of computational capabilities in terms of resolution have been recently pointed out by Yeung et al. [27].

In a laboratory experiment the energy injection scale L is limited by the dimensions of the apparatus. Large apparati can be built, e.g. the Modane wind tunnel [28], but are prohibitively expensive to operate, especially considering the many realizations needed for dedicated statistical studies of turbulence. To expand the inertial range the dissipative scales of size $\sim \eta$ can be decreased by lowering the kinematic viscosity $\nu$ of the working fluid demanding a higher resolution of the measurement instrument. Examples for experiments in liquid helium, which has an ultra-low kinematic viscosity, are found for example in Refs. [29,30,31,32]. The authors use liquid helium as working fluid in various flow configurations and have been reported to reach $R_{\lambda }$ up to 10000. The dissipative scales of these flows are so small that they cannot be resolved by current technology.

Our approach to create a large inertial range is to use a closed-loop wind tunnel filled with sulfur-hexaflouride ($\hbox {SF}_{{6}}$) at pressures up to 15 bar [15]—the variable density turbulence tunnel (VDTT). With classical grids it has been shown to create $R_{\lambda }$ up to 1600 and Kolmogorov scales $\sim 10$ µm, making even the smallest spatial scales experimentally accessible [33]. With a specially designed autonomous active grid (see below) it is possible to increase the energy injection scale and thus the inertial range. As $R_{\lambda }\sim (L/\eta )^{2/3}$, the VDTT features two independent handles to change $R_{\lambda }$—pressure and active grid forcing. In combination they create a laboratory flow of $R_{\lambda }$ more than 5000 at scales resolvable with modern thermal anemometry under the limitations described below.

Fig. 1

Several flaps of the active grid. The flow points out of the page. Starting from the top left flap in clockwise direction the flaps are set to $0 {^\circ }$, $45 {^\circ }$, $90 {^\circ }$, and $45 {^\circ }$. The side length of one flap is 11 cm, the black boxes in the flap center are servo motors, the blue rods are the grid support

The autonomous active grid consists of 111 individually controllable flaps of dimensions 11 cm $\times$ 11 cm that rotate around their diagonal. This is different from the Makita-style grids, where the rows and columns of the flaps are mounted rigidly on rotating horizontal and vertical bars [34]. The angle of rotation can be set to any angle between $\pm \,90{^\circ }$ The flow obstruction is smallest (flap parallel to the flow) at $0{^\circ }$. At angles $\pm \,90{^\circ }$ one of the flap sides is facing the incoming flow, while the other side is facing away from the flow. The sign of the angles determines the side that is facing the flow, while the magnitude defines the deviation of the flap from the parallel position. As in a classical grid with rigid grid bars, wakes are formed that interact with each other downstream of the grid to form a turbulent flow field. The flexibility of the grid allows the superposition of larger structures onto those induced by the individual flaps. A detailed account of the autonomous active grid and the algorithm is given in Ref. [35] and briefly summarized here. A snapshot of several flaps of the autonomous active grid is illustrated in Fig. 1.

The algorithm updates the angle of each flap every 0.1s. Each time step starts with a random set of angles and convolves each of those angles with the grid history and a pre-defined kernel. The kernel is always defined by a certain shape (e.g. Gaussian), the spatial and temporal correlations (the number of neighbors and time-steps included in the convolution), and the desired mean absolute angle $\phi _{RMS}$. For the experiments presented here, a ’Long Tail’ kernel has been used, whose description can be found in [35].

Fig. 2

a The correlation volume $V_{\text {corr}}=\sigma _{s}^{2}\sigma _{t}U$ influences the size of the largest flow scales $L=\int C(r) dr$. b The grid Reynolds number defined as $\text {Re}_{\text {Grid}}=\root 3 \of {V_{\text {corr}}}\sin (\phi _{RMS})U/\nu$ determines $R_{\lambda }$. The black line indicates the isotropic relation $\text {Re} = c\cdot \sqrt{R_{\lambda }}$, where c was chosen to fit the data best. c The separation of scales $L/\eta$ as a function of $R_{\lambda }$. The black line indicates a best fit of the K41 prediction of $L/\eta \sim R_{\lambda }^{3/2}$. We attribute the slight deviations from the scaling to the relation between L and $u^3/\varepsilon$, which depends on the large-scale structure of the flow (see Appendix D). The first spectrum of Dataset 1 is not shown in (a) and (b), because $V_{\text {Corr}}$ is not defined for a stationary, open grid

This algorithm leads to dynamically evolving patches of more open and more closed flaps without periodicity, which in turn leads to spatial and temporal correlations of the flow structures. The parameters $\sigma _{s}$ and $\sigma _{t}$ describing the correlation lengths that define the grid behavior are typically linked via the mean flow velocity U to avoid a strongly inhomogeneous flow. The grid correlation lengths define the large-scale flow properties. To link these, we consider the overall fluid volume that passes through a typical correlation patch given by $V_{\text {Corr}}=\sigma _{s}^2\sigma _t U$. The dimensions $L_{\text {Corr}}\approx V_{\text {Corr}}^{1/3}$ are proportional to the largest scales in the flow as demonstrated in Fig. 2a. The sine of the mean flap angle $\phi _{\text {RMS}}$ is proportional to the mean area blocked by a single flap. The larger this blockage is, the stronger are the fluctuations induced by the flaps. The product $\sin (\Phi _{\text {RMS}})U$ is therefore a predictor for the fluctuating velocity component. The knowledge of typical length scales and velocity defined by the active grid naturally leads to the definition of a Reynolds number using the kinematic viscosity $\nu$ of the gas.

$$\begin{aligned} \text {Re}_{\text {Grid}}\sim \frac{\root 3 \of {V_{\text {Corr}}}\sin (\phi _{RMS})U}{\nu }, \end{aligned}$$

Table 1 Properties of all spectra

Figure 2b shows that the a priori quantity $\text {Re}_{\text {Grid}}$ scales with the a posteriori$R_{\lambda }$ with deviations at $\text {Re}_{\text {Grid}}>10^{9}$. Each Dataset has been obtained by increasing $V_{\text {Corr}}$ while keeping the pressure (and therefore $\nu$) constant as indicated in Table 1. We attribute the slight deviations at large $\text {Re}_{\text {Grid}}$ from a power law dependence to the fact that L is approaching half the diameter of the measurement section because the rule-of-thumb $\sigma _s\approx \sigma _t\cdot U$ is relaxed slightly. This is a natural limit for a sensible energy injection in any tunnel. We would like to add the word of caution that when approaching this limit, isotropy and homogeneity cannot be assumed easily anymore, which leads to said deviations from the isotropic relation $R_{\lambda }\sim \text {Re}_{\text {Grid}}^{\zeta }$ with $\zeta \approx 0.5$ (black line in Fig. 2b). This effect can also be observed in Fig. 2c). When approximating $L = \int _0^{\infty } C(r)dr$, deviations from the K41 prediction $L/\eta \sim R_{\lambda }^{3/2}$ appear. The scaling is recovered when calculating $L = C_{\varepsilon } u^3/\varepsilon$ (not shown). We attribute this to differences in $C_{\varepsilon }$ due to the turbulence forcing as discussed e.g. in Refs. [36,37,38,39] and plotted for our experiments in the appendix. From a phenomenological of view, introducing correlations into the flow using the active grid increases $R_{\lambda }$ only up to a certain limit (probably related to the tunnel dimensions). When exceeding this limit, the integral length scale L can no longer be estimated by the correlation length. Nevertheless, these data confirm that the active grid is indeed another ’knob’ to change $R_{\lambda }$ through the largest scales.

2.2 Thermal Anemometry

More than a century after its invention [40], hot-wire anemometry remains the technique of choice to measure the energy spectrum of turbulent velocity fluctuations in a strong mean flow. Constant temperature anemometry is responsive to fluctuations up to very high frequencies. The sensing element’s resistance—and therefore its temperature—is kept constant by a feedback circuit. As long as the feedback circuit is fast enough, the thermal lag of the wire does not attenuate fluctuations faster than the thermal time scale of the wire. This comes at the expense of a more complicated circuitry and frequency response.

The frequency response of CTA circuits has been studied extensively both through theoretical models and experimental testing. Freymuth [41] linearized a circuit with a single feedback amplifier of infinitely flat frequency response and analyzed its response to square and sine waves. He finds that the system can be modeled by a third-order ODE if the circuit responds faster than the wire, and the frequency response is optimal (flat over the entire range of frequencies) when the system response to a step perturbation by a single, slight overshoot (critically damped system). Perry and Morrison [42] investigated more moderate amplifier gains and bridge imbalances in their study yielding similar results. Wood [43] expanded the Perry and Morrison analysis, but considered a single-stage amplifier with a frequency-dependent response. Watmuff [44] further expanded the model with multiple, non-ideal amplifier stages. He showed that at least two amplifier stages are necessary to model the real amplifier properly. This introduces two additional poles to the system and makes the frequency response more complicated. Samie et al. [45] recently studied anemometry with sub-miniature probes in this model and compared it to a real CTA measurement. The results supported the further development of their in-house circuit, such that sub-miniature hot wire probes could be operated successfully on this CTA for the first time.

These theoretical attempts to predict the frequency response of a CTA circuit are accompanied by experimental approaches. Bonnet and de Roquefort [46] heated the wire periodically by a perturbation voltage as well as laser heating to determing the frequency response. Weiss et al. [47] used the aforementioned square wave test and interpreted its power spectrum as a measure for the frequency response curve. Hutchins et al. [48] exploited the well-defined frequency content of pipe flow at different operating pressures to obtain frequency response curves without artificial heating. They were able to create flows of almost identical Reynolds number, but different frequency content and could deduce the frequency-response curves for different circuits and wires. They compared several anemometer circuits and wires and found that the frequency responses are non-constant at frequencies as low as 500 Hz. For the combination of CTA circuit and wire used in the present study, they report an attenuation between 400 Hz and 7 kHz followed by a strong amplification of the signal. We therefore cannot assume a flat frequency response for our measurements and adress these effects below.

The energy spectrum measured by a hot wire is influenced by the effects of finite wire length. Length scales smaller than the sensor’s sensing lengths l will be attenuated, but also larger wavenumbers are influenced. Wyngaard [49] used a Pao model spectrum [50] to investigate this attenuation of small scales. These results were reviewed in Ref. [51] indicating that for $l/\eta =2$, the attenuation of the one-dimensional spectrum is still minimal at $k\eta \sim 0.3$, which was supported by Ashok et al. [52]. Sadeghi et al. [53] used sub-miniature hot wires (NSTAPs) as a benchmark and found that spatial filtering of the energy spectrum is minimal for $l/\eta <3.7$ at $k\eta <0.1$.

In this study we used conventional hot wires of sensing length 450 µm for pressures below 2 bar, as well as nanoscale thermal anemometry probes (NSTAP) of sensing length 30 µm provided by Princeton University with a Dantec Dynamics StreamWare CTA circuit. The NSTAP is a 100 nm thick, 2.5 µm wide, and 30 or 60 µm long free-standing platinum film supported by a silicon structure and soldered to the prongs of a Dantec hot wire. The production process and characteristics are detailed in Refs. [54,55,56,57]. For the conventional hot wire $l/\eta <5$ in all cases and for the NSTAP $l/\eta <3$. Therefore, $\eta$ cannot be fully resolved in all cases. However, the bottleneck effect is typically found around $100\eta$. The aforementioned references show that we can regard the distortions due to finite wire length as minor in this part of the energy spectrum.

To summarize, the spatial resolution of our measurement instruments is sufficient to study the $R_{\lambda }$-dependence of the bottleneck effect. Nevertheless the nonlinear frequency response of the circuitry remains a source of systematic error that is different from random noise occuring at very high frequencies. Here we describe a procedure that takes the response into account and thus removes this systematic measurement error.

3 Relative Spectra

3.1 The Concept

As outlined above, systematic errors influence the energy spectra recorded with a hot-wire anemometer. Formally, this means that the one-dimensional energy spectrum $E_{11}(f)$ is distorted by a frequency-dependent transfer function T(f):

$$\begin{aligned} E_{M}(f)=E_{11}(f)T(f) \end{aligned}$$

T(f) describes the effects of the thermal wire response, which depends on pressure and speed, and the reponse of the constant temperature anemometry circuit. Ideally, T(f) is a constant over the whole range of relevant frequencies, but the evidence detailed above indicates a complex shape of amplification and attenuation of the signal. In this study we do not make any attempt to find T(f). Instead, we control its effects by keeping T(f) the same for several flows at different $R_{\lambda }$.

To ensure that the spectra only differ because of changes in the turbulent fluctuation and not because of the frequency response curve of the anemometer, we need to ensure that the response curve T(f) is unaltered between spectra. We achieve this in two steps. The ambient pressure might influence the heat transfer of the wire and therefore T(f). Furthermore, T(f) is influenced by the CTA tuning (in particular the overheat), and the sensor itself. Therefore, we fix the ambient pressure within a set of spectra (a ’Dataset’) and measure using the same sensor and the same CTA settings.

The second step is to ensure that a given $k\eta$ is influenced by the same part of the frequency response curve T(f). Thus, we need to fix the position of a spectral feature in frequency space. This means that the mean velocity U must be the same within one Dataset. T(f) mainly distorts the small-scale end of the spectrum [41,42,43,44,45, 47, 48, 51], whose location in frequency space at a given U is determined by the kinematic viscosity $\nu$. $\nu$ is fixed within a Dataset because the pressure remains constant.

We can, however, change the energy injection scale and thus $R_{\lambda }$ with the autonomous active grid. This way we can conduct measurements at different $R_{\lambda }$. Ultimately, we can eliminate T(f) by relating each spectrum to a reference spectrum:

$$\begin{aligned} \frac{E_{M}^{i}(f)}{E_{M}^{\text {Ref}}(f)}&=\frac{E_{11}^{i}(f)T^{i}(f)}{E_{11}^{\text {Ref}}(f)T^{\text {Ref}}(f)}\nonumber \\&=\frac{E_{11}^{i}(f)T(f)}{E_{11}^{\text {Ref}}(f)T(f)}=\frac{E_{11}^{i}(kU/2\pi )}{E_{11}^{\text {Ref}}(kU/2\pi )}. \end{aligned}$$

(2)

In the following we call the ratio of a spectra divided by a reference spectrum in the frequncy domain, relative spectrum. We emphasize that the notion of relative spectra is not necessary to investigate $R_{\lambda }$-scaling within one Dataset prepared in the aforementioned way. However, the accessible range of $R_{\lambda }$ by changing only the active grid forcing is limited. Therefore, several of such Datasets with different frequency distortions need to be prepared by changing kinematic viscosity $\nu$ and mean flow speed U to obtain a convincing scaling range. The notion of relative spectra is then required to compare those Datasets.

3.2 Results

We created three sets of spectra that have identical T(f) each. We call these sets ‘Datasets‘. Table 1 shows important parameters for each spectrum. Note that L changes significantly within a given dataset leading to changes in $R_{\lambda }$, while $f_{\eta }=U/\eta$ remains almost constant within the dataset. This indicates that we changed $R_{\lambda }$ only by increasing the large scales, while keeping all small-scale features of the spectrum at the same frequency. For example, in Dataset 2, the peak of the spectral bump always lies at a frequency of $\sim 700$ Hz, whereas the beginning of the inertial range spans a factor of 4 in frequency (2 to 8 Hz). This exemplifies the excellent control over $R_{\lambda }$ permitted by the autonomous active grid as indicated in Fig. 2.

Fig. 3

Reference spectrum at $R_{\lambda }= 1305$ (upper plot) and relative spectra from Dataset 1. The data have been collapsed at $k\eta =0.015$, which we defined as the beginning of the bottleneck region. We identified the peaks in the relative spectra with the bottleneck peak of the absolute spectra. The peak height decreased with increasing $R_{\lambda }$ and different spectra of similar $R_{\lambda }$ result in very similar relative spectra as expected. Furthermore, the slope of the spectrum at $k\eta <0.015$ seems to decrease with $R_{\lambda }$. The shaded areas are a measure of the noise level

Fig. 4

Reference spectrum at $R_{\lambda }=1308$ (upper plot) and relative spectra from Dataset 2. The trends in peak height and slope from Fig. 3 continue

Fig. 5

Reference spectrum at $R_{\lambda }=4247$ (upper plot) and relative spectra from Dataset 3. Unlike in Datasets 1 and 2, the beginning of the bottleneck region around $k\eta =0.015$ is identifiable in the relative spectra as a local extremum

The lower graphs of Figs. 3, 4 and 5 show the spectra from each of the respective datasets divided by the reference spectrum $E_{11}^{\text {Ref}}$. $E_{M}^{\text {Ref}}$ is plotted pre-compensated in the upper graphs of the respective figure. Note that the absolute spectra in the upper graphs are multiplied by an unknown transfer function T(f) accounting for probe effects and therefore can not be used to reliably measure the features of the bottleneck. However, the relative curves are corrected and allow a measurement. The graphs are the result of a smoothing procedure and error estimate detailed in the appendix. In brief, the spectra were smoothed using a 1 / f octave filtering and the error is related to the noise level removed by the smoothing procedure. The spectra have been divided by the reference spectrum in the frequency domain and collapsed at $k\eta =0.015$ afterwards to simplify interpretation.This is the approximate location of the local minimum regularly found in compensated spectra and directly precedes the bottleneck peak in wavenumber space. DNS studies by Donzis and Sreenivasan [19] and Ishihara et al. [17] have shown that the magnitude of the compensated spectrum at $k \eta = 0.015$ is practically independent of $R_{\lambda }$. It is difficult to achieve such a good collapse of compensated spectra in experimental data, because of uncertainties in the measurement of the dissipation rate $\varepsilon$. Donzis and Sreenivasan [19] regard the compensated spectrum around $k \eta = 0.015$ as the true measure of the Kolmogorov constant and build their analysis of the bottleneck effect on the difference between the local minimum and the bottleneck peak. By normalizing the relative spectra at this point we follow their procedure and remove the effects of imperfect estimates of $\varepsilon$. In other words, we define the bottleneck height as the relative departure of the compensated spectrum from its magnitude at $k \eta =0.015$ following the procedure described in Ref. [19]. The remainder of the analysis is carried out on these relative spectra normalized at $k \eta = 0.015$.

While in Dataset 3 the beginning of the bottleneck region around $k\eta =0.015$ is accompanied by a change in the shape of the relative spectra, this point cannot be identified in the relative spectra of Datasets 1 and 2. In the following we concentrate on the bottleneck effect found at $k\eta >0.015$ for the remainder of this section.

The location of the spectral bump forming the bottleneck effect in relative spectra is not obvious. Our data from one-dimensional spectra suggests that the peak occurs between $k \eta = 0.03$ and $k \eta = 0.06$, which is consistent with the findings from DNS, where the peak typically occurs at $k \eta = 0.046$ in the one-dimensional spectra (see e.g. Refs. [19, 17]). However, when considering the background noise, the peak location is not the major source of error. E.g. for $R_{\lambda }=1539$, all points between $0.015<k\eta <0.07$ are within the errorband at $k\eta =0.05$. We therefore define the extremum in the relative spectrum between $0.015<k\eta <0.08$ as the relative height h of the bottleneck effect. This has the additional advantage to be independent of the errors in the estimate of $\eta$. To preclude biases from this definition, we repeat our analysis with different definitions of the relative bottleneck height in Fig. 11 in the appendix.

Finally, the measured bottleneck height cannot depend on which spectrum is chosen as reference. We have calculated the bottleneck height with all possible choices of $E_{11}^{\text {Ref}}$ and found our results to be largely independent of that choice (see Appendix for details).

Figure 6 shows the bottleneck height—defined as above—as a function of $R_{\lambda }/R_{\lambda }^{\text {Ref}}$ within each dataset. The data shows a trend towards smaller peak heights in the relative spectrum with increasing $R_{\lambda }$. The data follows the numerical data we have compiled from various sources [17, 58,59,60]. We have analyzed the data from Buaria et al. [60] at $R_{\lambda }$ up to 1000 ($R_{\lambda }/R_{\lambda }^{\text {Ref}}<1$). The increased small-scale resolution in comparison to [19] seems to have no noticable impact on the bottleneck. Therefore, this data at is practically the same as the one used by Donzis & Sreenivasan [19] for our purposes. The data from $R_{\lambda }=1300$ ($R_{\lambda }/R_{\lambda }^{\text {Ref}}=1)$ was reported in Ref. [58]. The numerical data at $R_{\lambda }/R_{\lambda }^{\text {Ref}}\approx 1.9$, which corresponds to $R_{\lambda }=2340$, is the highest $R_{\lambda }$ reported by Ishihara et al. [17]. The relative spectra of the numerical data were analyzed equivalently to the experimental data and the spectrum at $R_{\lambda }=1300$ was chosen as a reference spectrum. We have used the one-dimensional spectra in our analysis of the numerical data.

When excluding the lowest $R_{\lambda }$, the experimental data is in agreement with the power law of

$$\begin{aligned} h\sim \left( R_{\lambda }/R_{\lambda }^{\text {Ref}}\right) ^{-0.061\pm 0.007}. \end{aligned}$$

The fit was obtained by a bootstrap procedure based on the error bars. It compares well with the findings of Donzis and Sreenivasan [19], who report a bottleneck scaling of $h\sim R_{\lambda }^{-0.04}$. Their analysis similarly defines the bottleneck height as the difference between the height of the compensated spectrum at the bottleneck peak and the local minimum preceding this peak.

The spectrum at $R_{\lambda }=193$ follows the general trend of decreasing peak height with $R_{\lambda }$, but its peak differs substantially from the predictions. The absolute spectrum (not shown) exhibits no signs of a 5 / 3-scaling, and consequently the bottleneck region cannot be clearly separated from the rest of the spectrum. This is substantially different from the other spectra, where the end of the integral range could always be observed in the absolute spectra and we therefore are not surprised that the relative spectrum at $R_{\lambda }=193$ deviates from the remainder of the data. This spectrum has consequently been ignored in our interpretation.

Further, we can change $R_{\lambda }$ only by a factor of 5 through the autonomous active grid. While Dataset 1 and 2 each feature a spectrum at the same $R_{\lambda }$, there is a gap between the highest $R_{\lambda }$ of Dataset 2 (2704) and the lowest of Dataset 3 (3641). To plot h as a function of $R_{\lambda }$ alone, we use the aforementioned power law fit from Fig. 6. Under this assumption we can bridge the gap between the two datasets, because $h_1/h_2 = (R_{\lambda 1}/R_{\lambda 2})^{-0.0061 \pm 0.007}$. Using the final point of Dataset 2 as $R_{\lambda 1} = 2704$ and the corresponding height $h_1$ we can construct $h_2$ using the lowest $R_{\lambda 2} = 3641$ from Dataset 3 to arrive at Fig. 7

Fig. 6

Bottleneck height relative to the corresponding reference spectra for all datasets as a function of $R_{\lambda }/R_{\lambda }^{\text {Ref}}$. The reference spectra collapse at $R_{\lambda }/R_{\lambda }^{\text {Ref}} = 1$ and have a relative bottleneck height of 1 by construction. Numerical simulations from Buaria et al. [60] at $R_{\lambda }$ up to 1000 ($R_{\lambda }/R_{\lambda }^{\text {Ref}}<1$), Buaria et al. [58] ($R_{\lambda }=1$) and Ishihara [17] ($R_{\lambda }>1$ ) are added for reference. The DNS data for $R_{\lambda }<2000$ is practically identical to the data analyzed by Donzis and Sreenivasan [19]. A power law is fitted to the experimental data with the lowest $R_{\lambda }/R_{\lambda }^{\text {Ref}}$ excluded. $(R_{\lambda }/R_{\lambda }^{\text {Ref}})^{-0.061\pm 0.007}$ is a good description of the experimental data over one decade of $R_{\lambda }$ (from 500 to 5000) and agrees with the numerical simulations as well. This power law is used in Fig. 7 to combine Datasets 2 and 3

Fig. 7

We have shifted Dataset 3 from Fig. 6 under the assumption of a power law $\sim \left( R_{\lambda }/R_{\lambda }^{\text {Ref}}\right) ^{\alpha }$ with $\alpha =-\,0.061\pm 0.007$, i.e. the position of Dataset 3 with respect to the other Datasets is constructed artificially from the power law in Fig. 6 to allow us to plot the bottleneck scaling with $R_{\lambda }$ alone, i.e. without dividing by $R_{\lambda }^{\text {Ref}}$. We have no physical justification for this power law and stress that the position of Dataset 3 in this figure is speculative

4 Discussion

In this paper we studied the spectra of a turbulent wind tunnel flow of $R_{\lambda }$ between 193 and 5131. We have used regular hot-wires as well as NSTAPs with a state-of-the-art constant temperature anemometer to record single-point two-time statistics of the turbulent fluctuations, in particular energy spectra. However, such spectra can be heavily influenced by non-ideal frequency responses of the circuit. The frequency response is particularly complicated when operating sub-miniature wires like the NSTAP with a CTA [45, 48]. A constant current anemometer (CCA) might perform better in this respect, because the frequency reponse is limited only by the thermal lag of the wire and no feedback loop is involved. Still, this comes at the expense of a variable wire temperature and -resistance.

In an attempt to interpret CTA data suffering from a non-flat frequency response, we consider energy spectra relative to a reference spectrum. Such an analysis significantly restricts the phenomena that can be observed. The bump in the energy spectrum at the transition from the inertial to the dissipation range can still be identified in the relative spectra as a local extremum beyond $k\eta =0.015.$

To the best of our knowledge, no other wind tunnel achieves $R_{\lambda }>5000$ in a gas. Moreover, we do not know of any other quantitative study of the scaling of the bottleneck effect with $R_{\lambda }$ in a laboratory experiment. We attribute this to the difficulties one faces when interpreting energy spectra from CTA measurements at relatively high frequencies: The spectrum is stronlgy influenced by the CTA circuitry and these influences are hard to quantify or eliminate.

With the aforementioned procedures we are able to extract information about the bottleneck effect from instrument-distorted hot wire spectra. We find indications that the bottleneck effect decreases up to $R_{\lambda }\sim 5000$. We fit a power law of $(R_{\lambda }/R_{\lambda }^{\text {Ref}})^{-\alpha }$ with $\alpha =0.061\pm 0.007$, which is close to the value of $(R_{\lambda })^{-0.04}$ found by Donzis and Sreenivasan [19]. Their numerical results are in general in good agreement with our experimental data, lending support to the experiment and data anlysis procedure. Our data equally supports Verma and Donzis [11], who predict that the bottleneck scales as $h\sim 1-\gamma (1.5\log _{2}(R_{\lambda }))^{2/3}$. Revisiting Fig. 6, the data is not inconsistent with different $R_{\lambda }/R_{\lambda }^{\text {Ref}}$-scalings of the relative bottleneck height in the different datasets. We have therefore calculated the scaling of the individual datasets and found that while Dataset 2 and 3 have almost identical scaling exponents ($-\,0.032\pm 0.012$, and $-\,0.034\pm 0.029$, respectively), Dataset 1 shows a scaling of $-\,0.1528\pm 0.012$. When excluding the two lowest $R_{\lambda }$, the scaling exponent becomes $-\,0.083\pm 0.024$. This points towards different behaviours at low $R_{\lambda }$, probably due to the effects of a not properly developed inertial range, which contaminates the bottleneck scaling. Such a claim is supported by the slopes of the spectra at $0.001< k \eta < 0.015$, which clearly get steeper with increasing $R_{\lambda }$ in Dataset 1, but change very little in Datasets 2 and 3, indicating a properly developed inertial range. Interestingly, this effect cannot be seen in DNS, where the bottleneck scaling of $R_{\lambda }^{-0.04}$ can be found at low Reynolds numbers.

We attempt to plot the relative bottleneck height as a function of $R_{\lambda }$ alone. This requires the assumption that the aforementioned power law holds and can be extrapolated. Such an assumption is highly speculative and the results should be considered as such.

We can not quantify the absolute height of the bottleneck bump. Yet, we can argue that if the relative spectra are still changing with $R_{\lambda }$ in the relevant region, the effect has not completely vanished. We can find a systematic decrease of the peak in the relative spectra for $R_{\lambda }<3000$. The data for $R_{\lambda }>3000$ in Dataset 3 is inconclusive. A small, decreasing trend can be found, consistent with the power law fit. However, the differences in height are so small compared to the error bars that the claim of a constant bottleneck height at $R_{\lambda }>3000$ would also be supported by the data, especially when considering alternative definitions of the bottleneck height in relative spectra as in Fig. 11 found in the appendix. This is not in contradiction to the atmospheric spectra mentioned above, as they have an even higher $R_{\lambda }$. Further, we note that a bottleneck effect might not show up as a peak in a 5 / 3-compensated spectrum, yet might be present when compensating by an intermittency-corrected slope $-(5/3+\beta )$. In this case, the bottleneck effect would still be visible in the relative spectrum. However, the claim that the bottleneck height does not change with $R_{\lambda }$ for $R_{\lambda }>3000$ is not ruled out by the data.

As far as this study is concerned, the data matches the predictions of Verma and Donzis [11]: The bottleneck height decreases with increasing $R_{\lambda }$, but relatively high $R_{\lambda }$ are necessary to make the effect vanish completely. Based on nonlinear and nonlocal shell-to-shell energy transfer Verma and Donzis [11] estimate that the bottleneck is basically absent for $R_{\lambda }>10^{4}$, but acknowledge that this might be an overestimate. While lending support to existing studies of the bottleneck effect, especially [19] and theories that incorporate a $R_{\lambda }$-dependence of the peak height, an investigation of the effect in terms of absolute measurements of spectra seems necessary to confirm these claims experimentally. With subminiature probes of low thermal lag, such a study might be possible with a constant current anemometer, whose frequency response is intriniscally more simple. However, the present study could reliably measure how the bottleneck decreases with increasing $R_\lambda$ for the first time in an laboratory experiment and for $R_\lambda$ much higher than achieved in DNS or other wind tunnel studies.

Appendices

Appendix A: Brief Description of the Wind Tunnel

The VDTT consists of two 11.7 m long straight cylindrical tubes connected by two elbows of center-line radius of 1.75 m. The tunnel was filled with sulfur-hexaflouride (SF6) at pressures between 1.5 and 15 bar for the measurements presented here.

The flow is propelled by a fan rotating at up to 24 Hz creating mean flow speeds of up to 5.5 m/s. It passes the first elbow and enters a heat exchanger, which removes any turbulent energy dissipated into heat and thus keeps the temperature in the tunnel constant. The rectangular cross-section of the heat exchanger is smoothly adapted to the tunnel’s circular geometry by contractions. The vertical slots of the heat exchanger are expected to destroy large-scales structure present in the flow. After the heat exchanger, the flow passes an 80 cm long expansion, which adapts it to the measurement section. While passing this expansion the flow is stabilized and homogenized by three consecutive meshes of ascending spacing. The flow enters a 9 m long measurement section through an 104 cm high active grid, which is directly followed by a 70 cm long expansion to the measurement section’s height of 117 cm. The measurement section is followed by another elbow and enters a second measurement section through another sequence of three meshes before being accelerated again by the fan.

Appendix B: Data Acquisition and Analysis Procedure

The NSTAPs were operated following largely [61] using a Dantec StreamLine 90C10 module within a 90N10 frame. The CTA bridge was set to a 1:1 ratio and the overheat is determined by an external resistor $R_{\text {ext}}$ connected to the system. Typical overheat ratios $R_{\text {ext}}/R_{\text {Probe}}$ were 1.2–1.3, where $R_{\text {Probe}}\sim 100\,\Omega$ denotes the probe cold resistance. The Dantec wires were used in a 1:20 bridge utilizing the internal automatics to set the overheat. The data was acquired in the following procedure: The hot wire frequency response and proper operation was tested on a very basic level using the square wave test built into the Dantec CTA-system. The hot-wire system was calibrated by scanning a range of mean flow speeds set by the fan frequency in the tunnel. We determined the mean flow speed through the differential pressure between a pitot tube and a static pressure probe. The differential pressure was picked up by a Siemens SITRANS differential pressure transfucer/ We chose $\sim$ 20 calibration points spaced by $\sim$ 0.1 m/s. The probe voltage was recorded for 60 s along with the mean pressure difference, a voltage-velocity curve was calculated, and King’s law was fitted to the data. In between calibration points we waited for 45 s for the mean flow to become stationary. The data was recorded with a National Instruments NI PCI-6123 16-bit DAQ-Card at sampling rates of 60 or 200 kHz. Higher sampling rates were used for NSTAP measurements, where the CTA analog low-pass filter was set to 100 kHz. When using standard hot wires, the filter frequency was set to 30 kHz and the data was sampled at 60 kHz. The data was recorded in segments of 6 million voltage samples, each saved to disk in a 16-bit binary format.

We shall briefly outline the initial data analysis procedure used to obtain essential turbulence statistics as well as the power spectrum. Each of the following steps was carried out on each segment and the results were averaged over all files in the end. We used King’s law with parameters obtained from the calibration data to convert the voltages to velocities. Note that the shape of the energy-frequency spectrum is independent of the calibration, which is only required to obtain its absolute value. Because the analog filtering was not sufficient to filter out all noise, we low-pass filtered the data digitally using a butterworth-Filter of order 3 in forward and reverse directions. This introduces edge effects, which we remove by cutting the first and last 60 points of the time series. We then subtract the mean U from the velocity time series to obtain a time series of u. The remaining analysis is performed on this filtered dataset. The power spectra were calculated using MATLB’s fft function, which is based on the FFTW-package . We calculate the correlation function using MATLAB’s xcorr function, which itself relies on the aforementioned fourier transform procedure as well as structure functions of order 1 to 8. Finally, we obtain histograms of velocity and voltage. We use Taylor’s Hypothesis, which assumes that a one-dimensional velocity field can be obtained from a time series by multiplying the time increments by the mean velocity: $\Delta x=\Delta t\cdot U$. The power spectra are normalized using the assumption that $\int E(k)dk=u^{2}$.

We routinely calculate basic turbulence quantities in different ways and check the results for consistency. The quantites $R_{\lambda }$, and $\eta$ depend on the mean energy dissipation rate $\varepsilon$, which we measure using the third-order structure function $S_{3}(r)=\langle (u(x+r)-u(x))^{3}\rangle =4/5(\varepsilon r)$. The last step follows from the Navier-Stokes equations and is also predicted by Kolmogorov’s 1941 theory. In practice we estimate $\varepsilon =\max (5/4\ S_{3}/r)$ and check the result with $\varepsilon =15\nu \int k^{2}E(k)dk$, and $\varepsilon =\max (S_{2}^{3/2}/r)$. The integral length scale is calculated as $L=\int _{0}^{\infty }C(r)dr$, where $C(r)=\langle u(x+r)u(x)\rangle$ is the velocity auto-correlation function. Its error mainly stems from the ambiguous choice of the upper integration limit, which leads to a relative error about 10% in L.

Appendix C: Calculation and Cross-Check of Relative Spectra

To obtain relative spectra, the initial spectrum consisting of 3 million points was downsampled to 50 000 logarithmically spaced datapoints. To remove the noise from these spectra, we have smoothed them using a fractional octave smoothing algorithm. It multiplies the spectrum at each frequency with a Gaussian centered around the current frequency $f_{i}$ with a width of $\sigma _{i}=(f_{i}/n)/\pi$, where n determines the smoothing level. Therefore, the smoothing window is larger for higher frequencies. To estimate the noise level in the spectrum and the associated statistical error, we consider the data within $3\sigma _{i}$ of each frequency. We estimate the standard error as $\delta =\sqrt{\text {Var}/N}$, where N is the number of points considered and $\text {Var}$ denotes their variance. Finally, the compensated spectra are calculated as $\psi (k)=E_{11}(k)k^{5/3}\varepsilon ^{-2/3}$, which can be written as $\psi (f)$ by Taylor’s Hypothesis. Finally, we divide the i-th spectrum in a dataset by the reference spectrum: $\psi _{i}(f)/\psi _{\text {Ref}}(f)$. The result is normalized at $k\eta =0.015$ to remove offsets introduced by uncertainties in $\varepsilon$ and to simplify comparisons.

Fig. 8

The bottleneck height in Dataset 1 with different choices of $E_{11}^{\text {Ref}}$. If the analysis is independent of the choice of reference spectrum, the graphs are parallel in this representation. Note that the reference spectrum always has bottleneck height 1

Fig. 9

Same as Fig. 8 for Dataset 2

An important cross-check of the technique is its independence from the choice of reference spectrum. To this end we have calculated the bottleneck effect according to the analysis outlined above for all possible choices of reference spectra. The results are shown in Figs. 8, 9 and 10. They show the peak height in the relative spectra as a function of $R_{\lambda }/R_{\lambda }^{\text {Ref}}$. $R_{\lambda }/R_{\lambda }^{\text {Ref}}$ has been normalized to the value that was chosen in the main part of the paper to increase the clarity of the figures. If the analysis is independent of the choice of reference spectrum $E_{11}^\text {Ref}$, a different choice $E_{11}'^{\text {Ref}}$, should move the resulting curve by a factor of $E_{11}^{\text {Ref}}/E_{11}^{\text {Ref}}$ upwards and $R_{\lambda }^{\text {Ref}}/R_{\lambda }'^{\text {Ref}}$ to the right. The latter is trivial and has been removed from Figs. 8, 9 and 10 by the additional normalization. Thus, if the spectra are independent of the choice of reference spectrum, the bottleneck curves should be parallel. Figures 8, 9 and 10 show that this is valid in good approximation showing that the analysis is largely independent of the choice of reference spectrum within a dataset. In a similar way, Fig. 11 shows that the qualitative results are largely independent of where the bottleneck effect is measured. The details are found in Sect. 3.2.

Fig. 10

Same as Fig. 8 for Dataset 3

Fig. 11

Bottleneck height as function of $R_{\lambda }/R_{\lambda }^{\text {Ref}}$ with different bottleneck definitions based on the height of the relative spectra at a fixed $k\eta$. The power law is the one found using the initial definition of the bottleneck height in Fig. 6. Upper graph: Bottleneck at $k\eta =0.03$, middle graph at $k\eta =0.04$, lower graph at $k\eta =0.046$ (as predicted by DNS). Datasets 1 and 2 still follow the trend found in the main part. Dataset 3 is not inconsistent with the claim of a constant bottleneck height at $R_{\lambda }>3000$

Appendix D: On the quantity $C_{\varepsilon }=L \varepsilon /u^3$

In Fig. 2c we plot $L/\eta$ as a function of $R_{\lambda }$ and recover to a good approximation the expected scaling of $L/\eta \sim R_{\lambda }^{3/2}$. This scaling is derived from the relation $\varepsilon =C_\varepsilon u^3/L$ and the definitions of $\eta =(\nu ^3/\varepsilon )^{1/4}$ and $\lambda =\sqrt{15\nu u^2/\varepsilon }$. Thus, the scaling depends on the constant $C_\varepsilon$, which is flow-dependent (see e.g. [36,37,38] for a review). We plot this constant as a function of $R_\lambda$ in Fig. 12, where we have used $L=\int C(r) dr$. Between $R_\lambda$ 500 and 2000 the value is approximately constant after being higher at lower $R_\lambda$. This behaviour is qualitatively consistent with the findings reported by Sreenivasan [36]. In general, $C_\varepsilon$ is scattered around 1. We attribute the scatter to the fact that the exact vaue of $C_{\varepsilon }$ depends on the larg-scale flow structure and is thereby influenced by the forcing mechanism. Considering that the active grid forcing is our main means of fine-tuning $R_{\lambda }$, we expect such a scatter in $C_{\varepsilon }$.

Fig. 12

$C_{\varepsilon } = L \varepsilon /u^3$ as a function of $R_{\lambda }$. The data is scattered around $C_{\varepsilon }=1$. We attribute the scatter to the dependence of $C_{\varepsilon }$ on the large scale flow structure, which is our main means of changing $R_{\lambda }$