Alternating event processes during lifetimes: population dynamics and statistical inference

Abstract

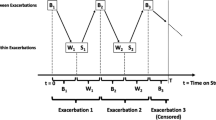
In the literature studying recurrent event data, a large amount of work has been focused on univariate recurrent event processes where the occurrence of each event is treated as a single point in time. There are many applications, however, in which univariate recurrent events are insufficient to characterize the feature of the process because patients experience nontrivial durations associated with each event. This results in an alternating event process where the disease status of a patient alternates between exacerbations and remissions. In this paper, we consider the dynamics of a chronic disease and its associated exacerbation-remission process over two time scales: calendar time and time-since-onset. In particular, over calendar time, we explore population dynamics and the relationship between incidence, prevalence and duration for such alternating event processes. We provide nonparametric estimation techniques for characteristic quantities of the process. In some settings, exacerbation processes are observed from an onset time until death; to account for the relationship between the survival and alternating event processes, nonparametric approaches are developed for estimating exacerbation process over lifetime. By understanding the population dynamics and within-process structure, the paper provide a new and general way to study alternating event processes.

Appendix

The follow assumptions are the regularity conditions:

• (C1) The constant $\tau$ satisfies $P(X\ge \tau )>0$.

• (C2) We assume that the number of switches between exacerbation and remission is bounded.

• (C3) The function $\phi _c(s | y)$ has second order derivative with respect to y, and the density f(y) has second order derivative $f^{(2)}(y)$.

1.1 Proof for Theorem 4.1

We note that $\{D(s):s\in [0,\tau ]\}$ and $\{I(X\ge s):s\in [0,\tau ]\}$ are bounded and of bounded variation, and thus are Donsker. For $s\in [0,\tau ]$, $n^{-1/2}\sum _{i=1}^{n}\{ D_i(s)I(X_i\ge s) - P(D(s) = 1, X\ge s)\}$ and $n^{-1/2}\sum _{i=1}^{n}\{ I(X_i\ge s) - P(X\ge s)\}$ converge to zero-mean Gaussian processes. By applying functional Delta method, we have $\sqrt{n}\{\hat{\phi }(s) - \phi (s) \}$ converges weakly to a zero-mean Gaussian process and

$$\begin{aligned}&\sqrt{n}\{\hat{\phi }(s) - \phi (s) \}\\ =&\frac{1}{P(X\ge s)\sqrt{n}} \sum _{i=1}^n \left\{ I(D_i(s)=1,X_i \ge s) - {P(D(s)=1,X \ge s)}\right\} \\&-\,\frac{P(D(s)=1,X \ge s) }{P(X\ge s)^2\sqrt{n}} \sum _{i=1}^n \left\{ I(X_i \ge s) - P(X\ge s) \right\} + o_p(1)\\&= \frac{1}{\sqrt{n}}\sum _{i=1}^{n}\left\{ \frac{D_i(s)I(X_i\ge s)}{P(X\ge s)} - \frac{\phi (s)I(X_i\ge s)}{P(X\ge s)} \right\} + o_p(1)\\&\equiv \frac{1}{\sqrt{n}}\sum _{i=1}^{n}a_i(s) + o_p(1). \end{aligned}$$

Thus $\sqrt{n}\{\hat{\phi }(s) - \phi (s) \}$ converges weakly to a zero-mean Gaussian process with covariance function $E\{a(s_1)a(s_2)\}$ for $s_1,s_2\in [0,\tau ]$.

1.2 Proof for Theorem 4.2

We first define

$$\begin{aligned} \hat{\mu }(s,y)= & {} n^{-1}\sum _{i=1}^{n}\int _{0}^{\tau } \frac{1}{h}K_{s,y}\left( \frac{y-u}{h}\right) {\hat{S}_C(u)}^{-1} { \Delta _i I(D_i(s)=1)dN^Y_i(u)}, \\ {\mu }(s,y)= & {} \int _{0}^{\tau } \frac{1}{h}K_{s,y}\left( \frac{y-u}{h}\right) {\mu }(s,du), \hat{\lambda }(y)\\= & {} n^{-1}\sum _{i=1}^{n}\int _{0}^{\tau } \frac{1}{h}K_{s,y}\left( \frac{y-u}{h}\right) {\hat{S}_C(u)}^{-1} { \Delta _i dN^Y_i(u)},\\ {\lambda }(y)= & {} \int _{s}^{\tau } \frac{1}{h}K_{s,y}\left( \frac{y-u}{h}\right) F(du). \end{aligned}$$

We further define

$$\begin{aligned} \tilde{\mu }_{i}(s,y)= & {} \int _{0}^{\tau } \frac{1}{h}K_{s,y}\left( \frac{y-u}{h}\right) {{S}_C(u)}^{-1} { \Delta _i I(D_i(s)=1)dN^Y_i(u)},\\ \tilde{\lambda }_{i}(y)= & {} \int _{0}^{\tau } \frac{1}{h}K_{s,y}(\frac{s-u}{h}) {{S}_C(u)}^{-1} { \Delta _i dN^Y_i(u)}. \end{aligned}$$

Note that $E\{\tilde{\mu }_{i}(s,y)\} = \mu (s,y)$ and $E\{\tilde{\lambda }_{i}(y)\} = \lambda (y)$. Let $f^{(2)}$ be the second order derivative of f. With straightforward algebra, we have

$$\begin{aligned} \mu (s,y)&= \phi _c(s | y)f(y)\nonumber \\&\quad + \kappa _{s,y} \left\{ 2\frac{\partial \phi _c(s | y)}{\partial y}f^{(1)}(y)+ \phi _c(s | y)f^{(2)}(y) + \frac{\partial ^2 \phi _c(s | y)}{\partial y^2}f(y) \right\} h^2/2 + o(h^2)\end{aligned}$$

(9)

$$\begin{aligned} \lambda (y)&= f(y) + \kappa _{s,y}f^{(2)}(y)h^2/2 + o(h^2)\nonumber \\ \end{aligned}$$

(10)

$$\begin{aligned} E\{ \tilde{\mu }(s;y) \}^2&= \Vert K_{s,y}\Vert ^2 \phi _c(s | y)f(y)S_C(y)^{-1}h^{-1} {+} o(h^{-1}),\nonumber \\ \end{aligned}$$

(11)

$$\begin{aligned} E\{ \tilde{\lambda }(y)\}^2&= \Vert K_{s,y}\Vert ^2 f(y)S_C(y)^{-1}h^{-1} + o(h^{-1}) \nonumber \\ \end{aligned}$$

(12)

$$\begin{aligned} E\{ \tilde{\mu }(s,y)\tilde{\lambda }(y) \}&= \Vert K_{s,y}\Vert ^2 \phi _c(s | y)f(y)S_C(y)^{-1}h^{-1} + o(h^{-1}). \end{aligned}$$

(13)

For $0<s<y<\tau$, we have

$$\begin{aligned}&(nh)^{1/2}\{ \hat{\phi }_c(s;y) - \mu (s,y)\lambda (y)^{-1}\} \\ =&(nh)^{1/2}{f^{-1}(y)}\{ {\hat{\mu }(s,y)-\mu (s,y)} \} - (nh)^{1/2}\phi _c(s | y){f(y)}^{-1}\{ {\hat{\lambda }(y)-\lambda (y)}\} + o_p(1)\\ =&(nh)^{1/2}{f^{-1}(y)}\left\{ \frac{1}{n}\sum _{i=1}^n \tilde{\mu }_{i}(s,y) -\mu (s,y) \right\} \\&- (nh)^{1/2} \phi _c(s | y){f(y)}^{-1}\left\{ \frac{1}{n}\sum _{i=1}^n \tilde{\lambda }_{i}(y) -\lambda (y) \right\} + o_p(1). \end{aligned}$$

By applying Equations ( 9)–(13), we have

$$\begin{aligned}&\mu (s,y)\lambda (y)^{-1} - \phi _c(s | y)\\&= \frac{1}{2}\kappa _{s,y}h^2\left\{ \frac{\partial ^2\phi _c(s | y)}{\partial y^2} + 2\frac{\partial \phi _c(s | y)}{\partial y}f^{(1)}(y){f^{-1}(y)}\right\} + o(h^2) \end{aligned}$$

and $h\mathrm{Var}\left\{ {f^{-1}(y)}\tilde{\mu }_{i}(s,t) - \phi _c(s | y){f^{-1}(y)} \tilde{\lambda }_{i}(y) \right\}$ is

$$\begin{aligned} \frac{\Vert K_{s,y}\Vert _2^2}{f(y)S_C(y)}\left\{ \phi _c(s | y) - \phi _c(s | y)^2\right\} +o(1). \end{aligned}$$

Then the result of $\hat{\phi }_c(s;y)$ when $0\le s<y\le \tau$ is proved by applying central limit theorem.

1.3 Proof for asymptotic distribution of W

We assume (C1) and (C2) hold. Under the null hypothesis $\mathcal{H}_0$: $\phi _1(s)=\phi _2(s)$, $0\le s\le \tau$, we have

$$\begin{aligned}&(n_1n_2/N)^{1/2}W = (n_2/N)^{1/2}\cdot n_1^{1/2}\int _{0}^{\tau }\{\hat{\phi }_1(s)-\phi _1(s)\}ds\\&- (n_1/N)^{1/2}\cdot n_2^{1/2}\int _{0}^{\tau }\{\hat{\phi }_2(s)-\phi _2(s)\}ds. \end{aligned}$$

For the kth group, define $b_{ki}= \int _0^\tau w(s) a_{ki} (s) ds$, where

$$\begin{aligned} a_{ki} (s)= \frac{I(D_{ki}(s) {=} 1, X_{ki}{\ge } s)}{P(X_{ki}\ge s)} - \frac{P(D_{ki}(s) = 1, X_{ki}\ge s)I(X_{ki}\ge s)}{P(X_{ki}\ge s)^2} , \ \ \ k=1,2. \end{aligned}$$

Then by applying arguments similar to the proof of Theorem 4.1, we have

$$\begin{aligned} (n_1n_2/N)^{1/2}W = n_1^{-1/2}\sqrt{p_2}\sum _{i=1}^{n_1}b_{1i} - n_2^{-1/2}\sqrt{p_1}\sum _{i=1}^{n_2}b_{2i} + o_p(1). \end{aligned}$$

By applying the central limit theorem, we see that the test statistic $(n_1n_2/N)^{1/2}W$ converges in distribution to a normal distribution with zero mean and variance $p_2E( b_{1i}^2)+p_1E( b_{2i}^2)$.