Expectation propagation in linear regression models with spike-and-slab priors

Abstract

An expectation propagation (EP) algorithm is proposed for approximate inference in linear regression models with spike-and-slab priors. This EP method is applied to regression tasks in which the number of training instances is small and the number of dimensions of the feature space is large. The problems analyzed include the reconstruction of genetic networks, the recovery of sparse signals, the prediction of user sentiment from customer-written reviews and the analysis of biscuit dough constituents from NIR spectra. The proposed EP method outperforms in most of these tasks another EP method that ignores correlations in the posterior and a variational Bayes technique for approximate inference. Additionally, the solutions generated by EP are very close to those given by Gibbs sampling, which can be taken as the gold standard but can be much more computationally expensive. In the tasks analyzed, spike-and-slab priors generally outperform other sparsifying priors, such as Laplace, Student’s $t$ and horseshoe priors. The key to the improved predictions with respect to Laplace and Student’s $t$ priors is the superior selective shrinkage capacity of the spike-and-slab prior distribution.

1 Introduction

In many regression problems of practical interest the number of training instances available for induction ($n$) is small and the dimensionality of the data ($d$) is very large. Areas in which these problems arise include the reconstruction of medical images (Seeger et al. 2010), studies of gene expression data (Slonim 2002), the processing of natural language (Sandler et al. 2008) and the modeling of fMRI data (van Gerven et al. 2009). To address these regression tasks, one often assumes a simple multivariate linear model. However, when $d > n$, the calibration of this model is underdetermined because an infinite number of different values for the model parameters can describe the data equally well. In many of these learning tasks, only a subset of the available features are expected to be relevant for prediction. Therefore, the calibration problem can be addressed by assuming that most coefficients in the optimal solution are exactly zero. That is, the vector of model coefficients is assumed to be sparse (Johnstone and Titterington 2009). Different strategies can be used to obtain sparse solutions. For instance, one can include in the target function a penalty term proportional to the $\ell _1$ norm of the vector of coefficients (Tibshirani 1996). In a Bayesian framework, sparsity can be favored by assuming sparsity-enforcing priors on the model coefficients. These types of priors are characterized by density functions that are peaked at zero and also have a large probability mass in a wide range of non-zero values. This structure tends to produce a bi-separation in the coefficients of the linear model: The posterior distribution of most coefficients is strongly peaked at zero; simultaneously, a small subset of coefficients have a large posterior probability of being significantly different from zero (Seeger et al. 2010). The degree of sparsity in the model is given by the fraction of coefficients whose posterior distribution has a large peak at zero. (Ishwaran and Rao 2005) refer to this bi-separation effect induced by sparsity-enforcing priors as selective shrinkage. Ideally, the posterior mean of truly zero coefficients should be shrunk towards zero. At the same time the posterior mean of non-zero coefficients should remain unaffected by the assumed prior. Different sparsity-enforcing priors have been proposed in the machine learning and statistics literature. Some examples are Laplace (Seeger 2008), Student’s $t$ (Tipping 2001), horseshoe (Carvalho et al. 2009) and spike-and-slab (Mitchell and Beauchamp 1988; Geweke 1996; George and McCulloch 1997) priors. The densities of these priors are presented in Table 1. In this table, ${\fancyscript{N}}(\cdot |\mu , \sigma ^2)$ is the density of a Gaussian with mean $\mu$ and variance $\sigma ^2$, $\text {c}^{+}(\cdot |0,1)$ is the density of a positive Cauchy distribution, ${\fancyscript{T}}(\cdot |\nu )$ is a student’s $t$ density with $\nu$ degrees of freedom and $\delta (\cdot )$ is a point probability mass at 0. A description of the hyperparameters of each type of prior is also included in the table. Figure 1 displays plots of the density function of each prior distribution for different hyperparameter values.

Fig. 1

Probability density for Laplace (top left), Student’s $t$ with 5 and 1 degrees of freedom (top middle and top right), horseshoe (bottom left) and spike-and-slab (bottom right) priors. Spike-and-slab priors are a mixture of a broad Gaussian density (the slab) and a point probability mass (the spike), which is displayed by an arrow pointing upwards. The height of this arrow is proportional to the probability mass of the prior at the origin. The horseshoe prior approaches $\infty$ when $x \rightarrow 0$. For each prior distribution, a different color has been used to plot densities whose distance between quantiles 0.1 and 0.9 is equal to $0.75$ (green), $1.75$ (red) and $3$ (blue). In the spike-and-slab prior $p_0$ takes values $0.3$, $0.5$ and $0.8$ and only $v_s$ is tuned. For visualization purposes, the $y$ axis in the two bottom plots has been scaled with a ratio $2.5$ to $1$ (Color figure online)

Table 1 Density functions of sparsity-enforcing priors and hyperparameter descriptions

Spike-and-slab and horseshoe priors have some advantages when compared to Laplace and Student’s $t$ priors. In particular, the first two prior distributions are more effective in enforcing sparsity because they can selectively reduce the magnitude of only a subset of coefficients. The remaining model coefficients are barely affected by these priors. The shrinkage effect induced by Laplace and Student’s $t$ priors is less selective. These types of priors tend to either strongly reduce the magnitude of every coefficient (including coefficients that are actually different from zero and should not be shrunk) or to leave all the model coefficients almost unaffected. The reason for this is that Laplace and Student’s $t$ priors have a single characteristic scale. By contrast, spike-and-slab priors consist of a mixture of two densities with different scales. This allows to discriminate between coefficients that are better modeled by the slab, which are left almost unchanged, and coefficients that are better described by the spike, whose posterior is highly peaked around zero. In terms of their selective shrinkage capacity, spike-and-slab and horseshoe priors behave similarly. However, spike-and-slab priors have additional advantages. Specifically, the degree of sparsity in the linear model can be directly adjusted by modifying the weight of the spike in the mixture. This weight corresponds to the fraction of coefficients that are a priori expected to be zero. Furthermore, spike-and-slab priors can be expressed in terms of a set of latent binary variables that specify whether each coefficient is assigned to the spike or to the slab. The expected value of these latent variables under the posterior distribution yields an estimate of the probabilities that the corresponding model coefficients are actually different from zero. These estimates can be very useful for identifying relevant features. Finally, spike-and-slab priors have a closed-form convolution with the Gaussian distribution while horseshoe priors do not. This is an advantage if we want to use approximate inference methods based on Gaussian approximations.

A disadvantage of spike-and-slab priors is that they make Bayesian inference a difficult and computationally demanding problem. When these priors are used, the posterior distribution cannot be computed exactly when $d$ is large and has to be estimated numerically. Approximate Bayesian inference in linear models with spike-and-slab priors is frequently performed using Markov chain Monte Carlo (MCMC) techniques, which are asymptotically exact. However, in practice, very long Markov chains are often required to obtain accurate approximations of the posterior distribution. The most common implementation of MCMC in linear models with spike-and-slab priors is based on Gibbs sampling¹ (George and McCulloch 1997). However, this method can be computationally very expensive in many practical applications. Another alternative is to use variational Bayes (VB) methods (Attias 1999). An implementation of VB in the linear regression model with spike-and-slab priors is described by Titsias and Lazaro-Gredilla (2012) and Carbonetto and Stephens (2012). The computational cost of Carbonetto’s implementation is only ${\fancyscript{O}}(nd)$. However, the VB approach has some disadvantages. First, this method generates only local approximations to the posterior distribution. This increases the probability of approximating locally one of the many suboptimal modes of the posterior distribution. Second, some empirical studies indicate that VB can be less accurate than other approximate inference methods, such as expectation propagation (Nickisch and Rasmussen 2008).

In this paper, we describe a new expectation propagation (EP) (Minka 2001) algorithm for approximate inference in linear regression models with spike-and-slab priors. The main difference of our EP method with respect to other implementations of EP in linear regression models is that we split the posterior distribution into only three separate factors and then approximate each of them individually. This simplifies considerably our inference algorithm. Other EP methods such as the one described by Seeger (2008) have to approximate a much larger number of factors. This results in more complex EP update operations that require expensive updates / downdates of a Cholesky decomposition. The computational complexity of our EP method and the one described by Seeger (2008) are the same. However, we reduce the multiplicative constant in our method by avoiding having to work with Cholesky factors.

The proposed EP method is compared with other algorithms for approximate inference in linear regression models with spike-and-slab priors, such as Gibbs sampling, VB and an alternative EP method (factorized EP) which does not fully account for correlations in the posterior distribution (Hernández-Lobato et al. 2008). The main advantage of our method with respect to factorized EP is that we take into account correlations in the model coefficients during the execution of EP, while factorized EP does not. Our objective is to achieve improvements both in computational efficiency, with respect to Gibbs sampling, and in predictive accuracy, with respect to VB and to the factorized EP method of Hernández-Lobato et al. (2008). EP has already been shown to be an effective method for approximate inference in a linear model with spike-and-slab priors for the classification of microarray data (Hernández-Lobato et al. 2010). This investigation explores whether these good results can also be obtained when EP is used in sparse linear regression problems. The computational cost of the proposed EP method is ${\fancyscript{O}}(n^2d)$ when $d > n$ . This cost is expected to be smaller than the cost of Gibbs sampling and comparable to the cost of VB in many problems of practical interest. The performance of the proposed EP method is evaluated in regression problems from different application domains. The problems analyzed include the reconstruction of sparse signals (Ji et al. 2008), the prediction of user sentiment (Blitzer et al. 2007), the analysis of biscuit dough constituents from NIR spectra (Osborne et al. 1984; Brown et al. 2001) and the reverse engineering of transcription control networks (Gardner and Faith 2005).

In these problems, the proposed EP method is superior to VB and factorized EP and comparable to Gibbs sampling. The computational costs are similar for VB and for EP. However, EP is orders of magnitude faster than Gibbs sampling. To complete the study, other sparsifying priors, such as Laplace, Student’s $t$ and horseshoe priors, are considered as well. In the tasks analyzed, using the spike-and-slab model and EP for approximate inference yields the best overall results. The improvements in predictive accuracy with respect to the models that assume Laplace and Student’s $t$ priors can be ascribed to the superior selective shrinkage capacity of the spike-and-slab distribution. In these experiments, the differences between spike-and-slab priors and horseshoe priors are fairly small. However, the computational cost of training the models with horseshoe priors using Gibbs sampling is much higher than the cost of the proposed EP method.

The rest of the paper is organized as follows: Sect. 2 analyzes the shrinkage profile of some common sparsity-enforcing priors. Section 3 introduces the linear regression model with spike-and-slab priors (LRMSSP). The EP algorithm for the LRMSSP is described in Sect. 4. The functional form of the approximation used by EP is introduced in Sect. 4.1, the EP update operations in Sect. 4.2 and the EP approximation for the model evidence in Sect. 4.3. Section 5 presents the results of an evaluation of the proposed EP method in different problems: a toy dataset (Sect. 5.1), the recovery of sparse signals (Sect. 5.2), the prediction of user sentiment (Sect. 5.3), the analysis of biscuit dough constituents from NIR spectra (Sect. 5.4) and the reconstruction of transcription networks (Sect. 5.5), Finally, the results and conclusions of this investigation are summarized in Sect. 6.

2 Shrinkage analysis of sparsity-enforcing priors

Most of the sparsity-enforcing priors proposed in the literature can be represented as scale mixtures of Gaussian distributions. Specifically, these priors can be represented as a zero-mean Gaussian with a random variance parameter $\lambda ^2$. The distribution assumed for $\lambda ^2$ defines the resulting family of priors. To evaluate the density of the prior at a given point using this representation, one has to integrate over $\lambda ^2$. However, as suggested by Carvalho et al. (2009), it is possible to analyze the shrinkage profiles of different sparsity-enforcing priors by keeping $\lambda ^2$ explicitly in the formulation. For simplicity, we consider a problem with a single-observation of a target scalar $y$. The distribution of $y$ is assumed to be Gaussian with mean $w$ and unit variance ($y \sim {\fancyscript{N}}(w,1)$). The prior for $w$ is assumed to be a scale mixture of Gaussian distributions

$$\begin{aligned} {\fancyscript{P}}(w) = \int {\fancyscript{N}}(w|0,\lambda ^2) {\fancyscript{P}}(\lambda ^2)\,d\lambda ^2\,. \end{aligned}$$

(1)

Given $\lambda ^2$, the prior for $w$ is Gaussian. In this case, the posterior mean for $w$ can be computed in closed form

$$\begin{aligned} \mathbb {E}[w|y,\lambda ^2] = \frac{\lambda ^2}{1 + \lambda ^2} y = (1 - k)y\,, \end{aligned}$$

where $k = 1 / (1 + \lambda ^2)$, $k \in [0,1]$ is a shrinkage coefficient that can be interpreted as the weight that the posterior mean places at the origin once the target $y$ is observed (Carvalho et al. 2009). For $k = 1$, the posterior mean is shrunk to zero. For $k = 0$, the posterior mean is not regularized at all. Since $k$ is a random variable we can plot its prior distribution, ${\fancyscript{P}}(k)$, for a specific choice of ${\fancyscript{P}}(\lambda ^2)$. The resulting plot represents the shrinkage profile of the prior (1). Ideally, we would like ${\fancyscript{P}}(k)$ to enforce the bi-separation that characterizes sparse models. In sparse models only a few coefficients are significantly different from zero. According to this discussion, the prior ${\fancyscript{P}}(k)$ should have large probability mass in the vicinity of $k=1$, so that most coefficients are shrunk towards zero. At the same time, ${\fancyscript{P}}(k)$ should also be large for values of $k$ close to the origin, so that some of the coefficients are only weakly affected by the prior.

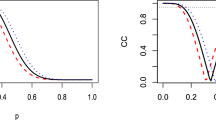
Table 2 displays the expressions of the densities for $\lambda ^2$ corresponding to each of the sparsity-enforcing priors of Table 1. In Table 2, $\text {Exp}(\cdot |\beta )$ is the density of an exponential distribution with survival parameter $\beta$ and $\text {IG}(\cdot |a,b)$ represents the density of an inverse gamma distribution with shape parameter $a$ and scale parameter $b$. The corresponding expressions of the densities for $k$ (not shown) are obtained by performing the change of variable $k = 1 / (1 + \lambda ^2)$. Figure 2 shows plots of these latter densities for different prior distributions and different values of the hyperparameters. For each prior distribution, the hyperparameter values are selected so that the distance between the quantiles 0.1 and 0.9 of the resulting distribution is equal to $0.7$, $3.5$ and $17.5$, respectively. These values correspond to high, medium and low sparsity levels in the posterior distribution. Figure 2 shows that neither the Laplace nor the Student’s $t$ priors with 5 and 1 degrees of freedom simultaneously assign a large probability to values in the vicinity of $k = 1$ and for $k$ close to the origin. This limits the capacity of these priors to enforce sparsity in a selective manner, with the exception of Student’s $t$ priors in which the degrees of freedom approach zero. In this case, ${\fancyscript{P}}(k)$ becomes more and more peaked at $k=0$ and at $k = 1$. However, the Student’s $t$ with zero degrees of freedom is a degenerate distribution that cannot be normalized. In this case, it is not possible to use a fully Bayesian approach. One has to resort to other alternatives such as type-II maximum likelihood techniques (Tipping 2001).

Fig. 2

Plots of prior density of $k$ corresponding to Laplace (top-left), Student’s $t$ with 5 and 1 degrees of freedom (top-middle and top-right), horseshoe (bottom-left) and spike-and-slab (bottom-right) priors. The hyperparameter values are selected so that the distance between the quantiles 0.1 and 0.9 (IQR) of the resulting distribution is equal to $0.7$, $3.5$ and $17.5$. In the spike-and-slab model $p_0$ takes values $0.3$, $0.6$ and $0.9$ and only $v_s$ is tuned. The delta functions are displayed as arrows pointing upwards. The height of the arrows is equal to the probability mass of the delta functions

Table 2 Densities for $\lambda ^2$ corresponding to common sparsity-enforcing priors

In terms of their selective shrinkage capacity, both spike-and-slab and horseshoe priors behave similarly. They yield densities that are peaked at $k = 1$ and at small values of $k$. With spike-and-slab priors, one obtains a positive (non-zero) probability exactly at $k=1$. This means that the posterior distribution of the coefficients corresponding to non-predictive features will tend to concentrate around the origin. On the other extreme (small $k$), horseshoe priors are characterized by very heavy tails. This is reflected in the fact that ${\fancyscript{P}}(k)$ is not bounded at the origin for these priors. Because of this property, horseshoe priors barely reduce the magnitude of those coefficients that are significantly different from zero. A similar effect can be obtained with spike-and-slab priors by increasing the variance of the slab. Therefore, these two distributions produce a selective shrinkage of the posterior mean. An advantage of spike-and-slab priors is that they have a closed-form convolution with the Gaussian distribution. This facilitates the use of approximate inference methods based on Gaussian approximations such as the EP algorithm that is proposed in this paper.

3 Linear regression models with spike-and-slab priors

In this section, we describe the linear regression model with spike-and-slab priors (LRMSSP). Consider the standard linear regression problem in $d$ dimensions

$$\begin{aligned} \mathbf {y} = \mathbf {X} \mathbf {w} + \mathbf {e}\,, \end{aligned}$$

(2)

where $\mathbf {X}=(\mathbf {x}_1,\ldots ,\mathbf {x}_n)^\text {T}$ is an $n\times d$ design matrix, $\mathbf {y} = (y_1, \ldots , y_n)^\text {T}$ is a target vector, $\mathbf {w}=(w_1,\ldots ,w_d)^\text {T}$ is an unknown vector of regression coefficients and $\mathbf {e}$ is an $n$-dimensional vector of independent additive Gaussian noise with diagonal covariance matrix $\sigma _0^2 \mathbf {I}$ ($\mathbf {e} \sim {\fancyscript{N}}(\varvec{0}, \sigma _0^{2} \mathbf {I})$). Given $\mathbf {X}$ and $\mathbf {y}$, the likelihood function for $\mathbf {w}$ is

$$\begin{aligned} {\fancyscript{P}}(\mathbf {y}|\mathbf {w},\mathbf {X}) = \prod _{i=1}^n {\fancyscript{P}}(y_i|\mathbf {w},\mathbf {x}_i) = \prod _{i=1}^n {\fancyscript{N}}(y_i|\mathbf {w}^\text {T} \mathbf {x}_i, \sigma _0^2)\,. \end{aligned}$$

(3)

When $d > n$, this function is not strictly concave and infinitely-many values of $\mathbf {w}$ fit the data equally well. A common approach to identify $\mathbf {w}$ in such an underdetermined scenario is to assume that only a few components of $\mathbf {w}$ are different from zero; that is, $\mathbf {w}$ is assumed to be sparse (Johnstone and Titterington 2009). In a Bayesian approach, the sparsity of $\mathbf {w}$ can be favored by assuming a spike-and-slab prior for the components of this vector (Mitchell and Beauchamp 1988; Geweke 1996; George and McCulloch 1997)

$$\begin{aligned} {\fancyscript{P}}(\mathbf {w} | \mathbf {z}) = \prod _{i=1}^d \left[ z_i {\fancyscript{N}}(w_i|0,v_s) + (1 - z_i) \delta (w_i) \right] \,. \end{aligned}$$

(4)

The slab ${\fancyscript{N}}(\cdot |0,v_s)$, is a zero-mean broad Gaussian whose variance $v_s$ is large. The spike $\delta (\cdot )$, is a Dirac delta function (point probability mass) centered at $0$. The prior is expressed in terms of a vector of binary latent variables $\mathbf {z} = (z_1,\ldots ,z_d)$ such that $z_i=0$ when $w_i = 0$ and $z_i=1$ otherwise. To complete the specification of the prior for $\mathbf {w}$, the distribution of $\mathbf {z}$ is assumed to be a product of Bernoulli terms

$$\begin{aligned} {\fancyscript{P}}(\mathbf {z}) = \prod _{i=1}^d \text {Bern}(z_i|p_0)\,, \end{aligned}$$

(5)

where $p_0$ is the fraction of components of $\mathbf {w}$ that are a priori expected to be different from zero and $\text {Bern}(x|p) = xp+(1-x)(1-p)$, $x \in \{0,1\}$ and $p \in [0,1]$. Note that our parameterization for the prior on $\mathbf {w}$ does not follow the general convention of scaling the prior variance on the regression coefficients by the variance $\sigma _0^2$ of the additive noise.

Given $\mathbf {X}$ and $\mathbf {y}$, the uncertainty about the values of $\mathbf {w}$ and $\mathbf {z}$ that were actually used to generate $\mathbf {y}$ from the design matrix $\mathbf {X}$ according to (2) is given by the posterior distribution ${\fancyscript{P}}(\mathbf {w},\mathbf {z}|\mathbf {X},\mathbf {y})$, which can be computed using Bayes’ theorem

$$\begin{aligned} {\fancyscript{P}}(\mathbf {w},\mathbf {z}|\mathbf {X},\mathbf {y}) = \frac{{\fancyscript{P}}(\mathbf {y}|\mathbf {w},\mathbf {X}) {\fancyscript{P}}(\mathbf {w}|\mathbf {z}){\fancyscript{P}}(\mathbf {z})}{{\fancyscript{P}}(\mathbf {y}|\mathbf {X})}\,, \end{aligned}$$

(6)

where ${\fancyscript{P}}(\mathbf {y}|\mathbf {X})$ is a normalization constant, which is referred to as the model evidence. This normalization constant can be used to perform model selection (MacKay 1992). The central operation in the application of Bayesian methods is the computation of marginalizations or expectations with respect to the posterior distribution. For example, given a new feature vector $\mathbf {x}^\text {new}$, one can compute the probability of the associated target $y^\text {new}$ using

$$\begin{aligned} {\fancyscript{P}}(y^\text {new}|\mathbf {X},\mathbf {y}) = \sum _\mathbf {z} \int {\fancyscript{N}}(y^\text {new}|\mathbf {w}^\text {T} \mathbf {x}^\text {new}, \sigma _0^2) {\fancyscript{P}}(\mathbf {w},\mathbf {z}|\mathbf {X},\mathbf {y})\,d\mathbf {w}\,. \end{aligned}$$

(7)

Additionally, one can marginalize (6) over $w_1,\ldots ,w_d$ and all $z_1,\ldots ,z_d$ except $z_i$ to compute ${\fancyscript{P}}(z_i|\mathbf {X},\mathbf {y})$, the posterior probability that the $i$-th component of $\mathbf {w}$ is different from zero. The probabilities ${\fancyscript{P}}(z_1|\mathbf {X},\mathbf {y}), \ldots ,{\fancyscript{P}}(z_d|\mathbf {X},\mathbf {y})$ can be used to identify the features (columns of $\mathbf {X}$) that are more relevant for predicting the target vector $\mathbf {y}$. Exact Bayesian inference in the LRMSSP involves summing over all the possible configurations for $\mathbf {z}$. When $d$ is large this is infeasible and we have to use approximations. Approximate inference in models with spike-and-slab priors is usually implemented using Markov chain Monte Carlo (MCMC) methods, in particular Gibbs sampling (George and McCulloch 1997). Appendix 1 describes an efficient implementation of this technique for the LRMSSP. The average cost of Gibbs sampling in the LRMSSP is ${\fancyscript{O}}(p_0^2d^3k)$, where $k$ is the number of Gibbs samples drawn from the posterior and often $k > d$ for accurate approximate inference. This large computational cost makes Gibbs sampling infeasible in problems with a high-dimensional feature space and high $p_0$. More efficient alternatives such as variational Bayes (VB) (Attias 1999) have also been proposed for approximate inference in the LRMSSP (Titsias and Lazaro-Gredilla 2012; Carbonetto and Stephens 2012). The cost of Carbonetto and Stephens’ VB method is ${\fancyscript{O}}(nd)$. However, empirical studies show that VB can perform worse than other approximate inference techniques, such as expectation propagation (EP) (Nickisch and Rasmussen 2008). In this work, we propose to use EP as an accurate and efficient alternative to Gibbs sampling and VB. The following section describes the application of EP to the LRMSSP. A software implementation of the proposed method is publicly available at http://jmhl.org.

4 Expectation propagation in the LRMSSP

Expectation propagation (EP) (Minka 2001) is a general deterministic algorithm for approximate Bayesian inference. This method approximates the joint distribution of the model parameters and the observed data by a simpler parametric distribution $Q$, which needs not be normalized. The actual posterior distribution is approximated by the normalized version of $Q$, which we denote by the symbol ${\fancyscript{Q}}$. The form of $Q$ is chosen so that the integrals required to compute expected values, normalization constants and marginal distributions for ${\fancyscript{Q}}$ can be obtained at a very low cost.

For many probabilistic models, the joint distribution of the observed data and the model parameters can be factorized. In the particular case of the LRMSSP, the joint distribution of $\mathbf {w}$, $\mathbf {z}$ and $\mathbf {y}$ given $\mathbf {X}$ can be written as the product of three different factors $f_1$, $f_2$ and $f_3$:

$$\begin{aligned} {\fancyscript{P}}(\mathbf {w}, \mathbf {z}, \mathbf {y}|\mathbf {X}) = \prod _{i=1}^n {\fancyscript{P}}(y_i|\mathbf {w},\mathbf {x}_i){\fancyscript{P}}(\mathbf {w}|\mathbf {z}) {\fancyscript{P}}(\mathbf {z}) = \prod _{i=1}^{3} f_i(\mathbf {w},\mathbf {z}), \end{aligned}$$

(8)

where $f_1(\mathbf {w},\mathbf {z}) = \prod _{i=1}^n {\fancyscript{P}}(y_i|\mathbf {w}, \mathbf {x}_i)$, $f_{2}(\mathbf {w},\mathbf {z}) = {\fancyscript{P}}(\mathbf {w}|\mathbf {z})$ and $f_{3}(\mathbf {w},\mathbf {z}) = {\fancyscript{P}}(\mathbf {z})$. The EP method approximates each exact factor $f_i$ in (8) with a simpler factor $\tilde{f}_i$ so that

$$\begin{aligned} {\fancyscript{P}}(\mathbf {w}, \mathbf {z}, \mathbf {y}|\mathbf {X}) = \prod _{i=1}^{3} f_i(\mathbf {w},\mathbf {z}) \approx \prod _{i=1}^{3} \tilde{f}_i(\mathbf {w},\mathbf {z}) = Q(\mathbf {w},\mathbf {z})\,, \end{aligned}$$

(9)

where all the $\tilde{f}_i$ belong to the same family of exponential distributions, but they need not be normalized. Because exponential distributions are closed under the product operation, $Q$ has the same functional form as $\tilde{f}_1$, $\tilde{f}_2$ and $\tilde{f}_3$. Furthermore, $Q$ can be readily normalized to obtain ${\fancyscript{Q}}$. Marginals and expectations over ${\fancyscript{Q}}$ can be computed analytically because of the simple form of this distribution. Note that we could have chosen to factorize ${\fancyscript{P}}(\mathbf {w}, \mathbf {z}, \mathbf {y}|\mathbf {X})$ into only two factors, by merging the product of $f_2$ and $f_3$ into a single factor. However, the resulting EP method would be equivalent to the one shown here.

The approximate factors $\tilde{f}_1$, $\tilde{f}_2$ and $\tilde{f}_3$ are iteratively refined by EP. Each update operation modifies the parameters of $\tilde{f}_i$ so that the Kullback-Leibler (KL) divergence between the unnormalized distributions $f_i(\mathbf {w},\mathbf {z}) Q^{\setminus i}(\mathbf {w},\mathbf {z})$ and $\tilde{f}_i(\mathbf {w},\mathbf {z}) Q^{\setminus i}(\mathbf {w},\mathbf {z})$ is as small as possible for $i = 1, 2, 3$, where $Q^{\setminus i}(\mathbf {w},\mathbf {z})$ denotes the current approximation to the joint distribution with the $i$-th approximate factor removed

$$\begin{aligned} Q^{\setminus i}(\mathbf {w},\mathbf {z})= \prod _{j\ne i} \tilde{f}_j(\mathbf {w},\mathbf {z}) = \frac{Q(\mathbf {w},\mathbf {z})}{\tilde{f}_i(\mathbf {w},\mathbf {z})}\,. \end{aligned}$$

(10)

The divergence minimized by EP includes a correction term so that it can be applied to unnormalized distributions (Zhu and Rohwer 1995). Specifically, each EP update operation minimizes

$$\begin{aligned} \text {D}_{\text {KL}}(f_iQ^{\setminus i} \Vert \tilde{f}_iQ^{\setminus i}) = \sum _\mathbf {z} \int \left[ f_i Q^{\setminus i}\log \frac{f_iQ^{\setminus i}}{\tilde{f}_i Q^{\setminus i}}+\tilde{f}_i Q^{\setminus i}-f_i Q^{\setminus i}\right] \,d\mathbf {w}\,, \end{aligned}$$

(11)

with respect to the approximate factor $\tilde{f}_i$. The arguments to $f_i Q^{\setminus i}$ and $\tilde{f}_iQ^{\setminus i}$ have been omitted in the right-hand side of (11) to improve the readability of the expression. The complete EP algorithm involves the following steps:

• 1. Initialize all the ${\tilde{f}}_i$ and $Q$ to be uniform (non-informative).

• 2. Repeat until all the $\tilde{f}_i$ have converged:

  • (a) Select a particular factor $\tilde{f}_i$ to be refined. Compute $Q^{\setminus i}$ dividing $Q$ by $\tilde{f}_i$.

  • (b) Update $\tilde{f}_i$ so that $\text {D}_{\text {KL}}(f_iQ^{\setminus i} \Vert \tilde{f}_iQ^{\setminus i})$ is minimized.

  • (c) Construct an updated approximation $Q$ as the product of the new $\tilde{f}_i$ and $Q^{\setminus i}$.

The optimization problem in step (b) is convex and has a single global solution (Bishop 2006). The solution to this optimization problem is found by matching the sufficient statistics between $\tilde{f}_i Q^{\setminus i}$ and $f_i Q^{\setminus i}$ (Minka 2001). Upon convergence ${\fancyscript{Q}}$ (the normalized version of $Q$) is an approximation of the posterior distribution ${\fancyscript{P}}(\mathbf {w},\mathbf {z}|\mathbf {y},\mathbf {X})$. EP is not guaranteed to converge in general. The algorithm may end up oscillating without ever stopping (Minka 2001). This undesirable behavior can be prevented by damping the update operations of EP (Minka and Lafferty 2002). Let $\tilde{f}_i^\text {new}$ denote the minimizer of the Kullback-Leibler divergence (11). Damping consists in using

$$\begin{aligned} \tilde{f}_i^\text {damp} = \left[ \tilde{f}_i^\text {new} \right] ^\epsilon \left[ \tilde{f}_i \right] ^{(1 - \epsilon )}\,, \end{aligned}$$

(12)

instead of $\tilde{f}_i^\text {new}$ in step (b) of the EP algorithm. The quantity $\tilde{f}_i$ represents in (12) the factor before the update. The parameter $\epsilon \in [0,1]$ controls the amount of damping. The original EP update operation (that is, without damping) is recovered in the limit $\epsilon = 1$. For $\epsilon = 0$, the approximate factor $\tilde{f}_i$ is not modified during step (b).

An alternative to damping are convergent versions of EP based on double loop algorithms (Opper and Winther 2005). However, these methods are computationally more expensive and more difficult to implement than the version of EP based on damping. In the experiments described in Sect. 5, our EP method with damping always converged so we did not consider using other convergent alternatives.

The main difference of our EP method with respect to other implementations of EP in linear regression models is that we split the joint distribution (8) into only three separate factors and then approximate each of them individually. This simplifies the implementation of our EP algorithm. Other EP methods such as the one described by Seeger (2008) work by spliting the joint distribution into a much larger number of factors. In that case, the EP update operations are more complex and require to perform expensive rank one updates / downdates of a Cholesky decomposition. The computational complexity of our EP method and the one described by Seeger (2008) are the same. However, we reduce the multiplicative constant in our method by avoiding having to work with Cholesky factors.

4.1 The form of the posterior approximation

In our implementation of EP for the LRMSSP, the posterior ${\fancyscript{P}}(\mathbf {w}, \mathbf {z}|\mathbf {y},\mathbf {X})$ is approximated by the product of $d$ Gaussian and Bernoulli factors. The resulting posterior approximation is a distribution in the exponential family

$$\begin{aligned} {{\fancyscript{Q}}}(\mathbf {w},\mathbf {z}) = \prod _{i=1}^d {\fancyscript{N}}(w_i|m_i,v_i) \text {Bern}(z_i|\sigma (p_i))\,, \end{aligned}$$

(13)

where $\sigma$ is the logistic function

$$\begin{aligned} \sigma (x) = \frac{1}{1 + \exp (-x)} \end{aligned}$$

(14)

and $\mathbf {m}=(m_1,\ldots ,m_d)^\text {T}$, $\mathbf {v}=(v_1,\ldots ,v_d)^\text {T}$ and $\mathbf {p} = (p_1,\ldots ,p_d)^\text {T}$ are free distributional parameters to be determined by the refinement of the approximate factors $\tilde{f}_1$, $\tilde{f}_2$ and $\tilde{f}_3$. The logistic function is used to guarantee the numerical stability of the algorithm, especially when the posterior probability of $z_i = 1$ is very close to 0 or 1 for some value of $i \in \{ 1,\ldots ,d \}$. The role of the logistic function in the EP updates is similar to that of the use of logarithms to avoid numerical underflow errors. This procedure to stabilize numerical computations is particularly effective in the signal reconstruction experiments of Sect. 5.2.

Note that the EP approximation (13) does not include any correlations between the components of $\mathbf {w}$. This might suggest that our implementation of EP assumes independence between the entries of $\mathbf {w}$. However, this is not the case. When we refine the EP approximate factors, we take into account possible posterior correlations in $\mathbf {w}$. Furthermore, once EP has converged, we can easily obtain an approximation to the posterior covariance matrix for $\mathbf {w}$. This is explained at the end of Sect. 4.2.

The approximate factors $\tilde{f}_1$, $\tilde{f}_2$ and $\tilde{f}_3$ in (8) have the same form as (13), except that they need not be normalized

$$\begin{aligned} \tilde{f}_1(\mathbf {w},\mathbf {z})&= \tilde{s}_1 \prod _{i=1}^d \text {exp} \left\{ -\frac{(w_i - \tilde{m}_{1i})^2}{2\tilde{v}_{1i}}\right\} \,,\end{aligned}$$

(15)

$$\begin{aligned} \tilde{f}_2(\mathbf {w},\mathbf {z})&= \tilde{s}_2 \prod _{i=1}^d \text {exp} \left\{ -\frac{(w_i - \tilde{m}_{2i})^2}{2\tilde{v}_{2i}}\right\} \left\{ z_i \sigma (\tilde{p}_{2i}) + (1 - z_i) \sigma (-\tilde{p}_{2i}) \right\} \,,\end{aligned}$$

(16)

$$\begin{aligned} \tilde{f}_3(\mathbf {w},\mathbf {z})&= \tilde{s}_3 \prod _{i=1}^d \left\{ z_i \sigma (\tilde{p}_{3i}) + (1 - z_i) \sigma (-\tilde{p}_{3i}) \right\} \,, \end{aligned}$$

(17)

where $\{ \tilde{\mathbf {m}}_i = (\tilde{m}_{i1},\ldots ,\tilde{m}_{id})^\text {T}, \tilde{\mathbf {v}}_i = (\tilde{v}_{i1},\ldots ,\tilde{v}_{id})^\text {T} \}_{i=1}^2$, $\{ \tilde{\mathbf {p}}_i = (\tilde{p}_{i1},\ldots ,\tilde{p}_{id})^\text {T} \}_{i=2}^{3}$ and $\{ \tilde{s}_i \}_{i=1}^3$ are free parameters to be determined by EP. The normalized version of these factors can be found in Appendix 9. The positive constants $\{ \tilde{s}_i \}_{i=1}^3$ are introduced to guarantee that $\tilde{f}_iQ^{\setminus i}$ and $f_iQ^{\setminus i}$ have the same normalization constant for $i = 1,2,3$. The parameters of (13), $\mathbf {m}$, $\mathbf {v}$ and $\mathbf {p}$, are obtained from $\tilde{\mathbf {m}}_{1}$, $\tilde{\mathbf {m}}_{2}$, $\tilde{\mathbf {v}}_{1}$, $\tilde{\mathbf {v}}_{2}$, $\tilde{\mathbf {p}}_{2}$ and $\tilde{\mathbf {p}}_{3}$ using the product rule for Gaussian and Bernoulli factors (see Appendix 3):

$$\begin{aligned} v_i&= \left[ \tilde{v}_{1i}^{-1} + \tilde{v}_{2i}^{-1} \right] ^{-1}\,, \end{aligned}$$

(18)

$$\begin{aligned} m_i&= \left[ \tilde{m}_{1i}\tilde{v}_{1i}^{-1} + \tilde{m}_{2i}\tilde{v}_{2i}^{-1} \right] v_i \,, \end{aligned}$$

(19)

$$\begin{aligned} p_i&= \tilde{p}_{2i} + \tilde{p}_{3i}\,, \end{aligned}$$

(20)

for $i = 1,\ldots ,d$. The first step of EP is to initialize $\tilde{f}_1$, $\tilde{f}_2$, $\tilde{f}_3$ and ${\fancyscript{Q}}$ to be non-informative $\mathbf {p}=\tilde{\mathbf {p}}_{\left\{ 2,3\right\} }= \mathbf {m}=\tilde{\mathbf {m}}_{\left\{ 1,2\right\} }=(0,\ldots ,0)^\text {T}$ and $\mathbf {v}=\tilde{\mathbf {v}}_{\left\{ 1,2\right\} }=(\infty ,\ldots ,\infty )^\text {T}$. After this, EP iterates over all the approximate factors, updating each $\tilde{f}_i$ so that the divergence $\text {D}_{\text {KL}}(f_iQ^{\setminus i} \Vert \tilde{f}_iQ^{\setminus i})$ is minimized. A cycle of EP consists in the sequential update of all the approximate factors. The algorithm stops when the absolute value of the change in the components of $\mathbf {m}$ and $\mathbf {v}$ between two consecutive cycles is less than a threshold $\delta > 0$. To improve the converge of EP, we use a damping scheme with a parameter $\epsilon$ that is initialized to 1 and then progressively annealed. After each iteration of EP, the value of this parameter is multiplied by a constant $k < 1$. The resulting annealed damping scheme greatly improves the convergence of EP. The values selected for $\delta$ and $k$ are $\delta = 10^{-4}$ and $k = 0.99$. The results obtained are not particularly sensitive to the specific values of these constants, provided that $\delta$ is small enough and that $k$ is close to $1$. In the experiments performed, EP converges most of the times in less than 20 cycles. Exceptionally, EP takes more than 100 iterations to converge, usually when $\sigma _0$ and $p_0$ are very small and very few training instances are available.

4.2 The EP update operations

In this section we describe the EP updates for the minimization of $\text {D}_{\text {KL}}(f_iQ^{\setminus i} \Vert \tilde{f}_iQ^{\setminus i})$ with respect to the parameters of the approximate factor $\tilde{f}_i$, for $i = 1,2,3$. This is a convex optimization problem with a single global optimum. This optimum is obtained by finding the parameters of $\tilde{f}_i$ that make the first and second moments of $\mathbf {w}$ and the first moment of $\mathbf {z}$ for $f_iQ^{\setminus i}$ and for $\tilde{f}_iQ^{\setminus i}$ equal (Minka 2001; Bishop 2006). In the following paragraphs we present the update operations for $\{ \tilde{\mathbf {m}}_i, \tilde{\mathbf {v}}_i \}_{i=1}^2$ and $\{ \tilde{\mathbf {p}}_i \}_{i=2}^{3}$ that result from these moment matching constraints. The update rules for $\{ \tilde{s}_i \}_{i=1}^3$ are described in the next section. The derivation of these operations is given in Appendix 4. For the sake of clarity, we include only the update rules without damping ($\epsilon = 1$). Incorporating the effect of damping in these operations is straightforward. With damping, the natural parameters of the approximate factors become a convex combination of the natural parameters before and after the update without damping

$$\begin{aligned} \left[ \tilde{v}_{ij}^\text {damp} \right] ^{-1}&= \epsilon \left[ \tilde{v}_{ij}^\text {new}\right] ^{-1} + (1 - \epsilon ) \tilde{v}_{ij}^{-1}\,, \end{aligned}$$

(21)

$$\begin{aligned} \tilde{m}_{ij}^\text {damp} \left[ \tilde{v}_{ij}^\text {damp} \right] ^{-1}&= \epsilon \tilde{m}_{ij}^\text {new} \left[ \tilde{v}_{ij}^\text {new} \right] ^{-1} + (1 - \epsilon )\tilde{m}_{ij} \tilde{v}_{ij}^{-1} \,, \end{aligned}$$

(22)

$$\begin{aligned} \tilde{p}_{kj}^\text {damp}&= \epsilon \tilde{p}_{kj}^\text {new} + (1 - \epsilon ) \tilde{p}_{kj}\,, \end{aligned}$$

(23)

where $i = 1, 2$, $k = 2, 3$ and $j = 1,\ldots ,d$. The superscript $new$ denotes the value of the parameter given by the full EP update operation without damping. The superscript $damp$ denotes the parameter value given by the damped update rule. The absence of a superscript refers to the value of the parameter before the EP update. The updates for the parameters $\{ \tilde{s}_i \}_{i=1}^3$ are not damped.

The first approximate factor to be processed by EP is $\tilde{f}_3$. Since the corresponding exact factor $f_3$ has the same functional form as $\tilde{f}_3$, the update for this approximate factor is $\tilde{\mathbf {p}}_3^\text {new} = (\sigma ^{-1}(p_0),\ldots ,\sigma ^{-1}( p_0))^\text {T}$, where $\sigma ^{-1}$ is the logit function

$$\begin{aligned} \sigma ^{-1}(x) = \log \frac{x}{1 - x}\,. \end{aligned}$$

(24)

Because this update rule does not depend on $\tilde{f}_1$ or $\tilde{f}_2$, we only have to update $\tilde{f}_3$ during the first cycle of the EP algorithm.

The second approximate factor to be processed is $\tilde{f}_2$. During the first iteration of the algorithm, the update rule for $\tilde{f}_2$ is $\tilde{\mathbf {v}}_2^\text {new} = (p_0 v_s,\ldots ,p_0v_s)^\text {T}$. In successive cycles, the rule becomes

$$\begin{aligned} \tilde{v}_{2i}^\text {new}&= (a_i^2 - b_i)^{-1} - \tilde{v}_{1i}\,,\end{aligned}$$

(25)

$$\begin{aligned} \tilde{m}_{2i}^\text {new}&= \tilde{m}_{1i} - a_i (\tilde{v}_{2i}^\text {new} + \tilde{v}_{1i})\,,\end{aligned}$$

(26)

$$\begin{aligned} \tilde{p}_{2i}^\text {new}&= \frac{1}{2}\log (\tilde{v}_{1i}) - \frac{1}{2}\log (\tilde{v}_{1i} + v_s) + \frac{1}{2} \tilde{m}_{1i}^2 \left[ \tilde{v}_{1i}^{-1} - (\tilde{v}_{1i}+v_s)^{-1}\right] \,, \end{aligned}$$

(27)

for $i = 1,\ldots ,d$, where $a_i$ and $b_i$ are given by

$$\begin{aligned} a_i&= \sigma (\tilde{p}_{2i}^\text {new} + \tilde{p}_{3i}) \frac{\tilde{m}_{1i}}{\tilde{v}_{1i} + v_s} + \sigma (-\tilde{p}_{2i}^\text {new}-\tilde{p}_{3i}) \frac{\tilde{m}_{1i}}{\tilde{v}_{1i}}\,,\end{aligned}$$

(28)

$$\begin{aligned} b_i&= \sigma (\tilde{p}_{2i}^\text {new} + \tilde{p}_{3i}) \frac{\tilde{m}_{1i}^2 - \tilde{v}_{1i} - v_s}{(\tilde{v}_{1i} + v_s)^{2}} + \sigma (-\tilde{p}_{2i}^\text {new}-\tilde{p}_{3i}) \left[ \tilde{m}_{1i}^2\tilde{v}_{1i}^{-2} - \tilde{v}_{1i}^{-1}\right] \,. \end{aligned}$$

(29)

The update rule (25) may occasionally generate a negative value for some of the variances $\tilde{v}_{21},\ldots ,\tilde{v}_{2d}$. Negative variances in Gaussian approximate factors are common in many EP implementations (Minka 2001; Minka and Lafferty 2002). When this happens, the marginals of $\tilde{f}_2$ with negative variances do not correspond to density functions. Instead, they are correction factors that compensate the errors in the corresponding marginals of $\tilde{f}_1$. However, negative variances in $\tilde{f}_2$ can lead to erratic behavior and slower convergence rates of EP, as indicated by Seeger (2008). Furthermore, when some of the components of $\tilde{\mathbf {v}}_2$ are negative, EP may fail to approximate the model evidence (see the next section). To avoid these problems, whenever (25) generates a negative value for $\tilde{v}_{2i}$, the update rule is modified and the corresponding marginal of $\tilde{f}_{2}$ is refined by minimizing $\text {D}_{\text {KL}}(f_2Q^{\setminus 2} \Vert \tilde{f}_2Q^{\setminus 2})$ under the constraint $\tilde{v}_{2i} \ge 0$. In this case, the update rules for $\tilde{m}_{2i}$ and $\tilde{p}_{2i}$ are still given by (26) and (27), but the optimal value for $\tilde{v}_{2i}$ is now infinite, as demonstrated in Appendix 5. Thus, whenever $(a_i^2 - b_i)^{-1} < \tilde{v}_{1i}$ is satisfied, we simply replace (25) by $\tilde{v}_{2i}^\text {new} = v_\infty$, where $v_\infty$ is a large positive constant. This approach to deal with negative variances is new up to our knowledge.

The last approximate factor to be refined by EP is $\tilde{f}_1$. To refine this factor we have to minimize $\text {D}_{\text {KL}}(f_{1}Q^{\setminus 1}\Vert \tilde{f}_{1}Q^{\setminus 1})$ with respect to $\tilde{f}_{1}$. Since $Q=\tilde{f}_{1}Q^{\setminus 1}$, we have that the update rule for $\tilde{f}_1$ minimizes $\text {D}_{\text {KL}}(f_{1}Q^{\setminus 1}\Vert Q)$ with respect to $Q$. Once we have updated $Q$ by minimizing this objective, we can obtain the new $\tilde{f}_{1}$ by computing the ratio between the new $Q$ and $Q^{\setminus 1}$. If we ignore the constant $\tilde{s}_{1}$, we can perform these operations using normalized distributions. In this case, the update rule consists of two steps. First, the parameters of ${\fancyscript{Q}}$ are determined by minimizing $\text {D}_\text {LK}( {\fancyscript{S}} \Vert {\fancyscript{Q}})$, where ${\fancyscript{S}}$ denotes the normalized product of the exact factor $f_1$ and the approximate factors $\tilde{f}_2$ and $\tilde{f}_3$; then, the parameters of $\tilde{f}_1$ are updated by computing the ratio between ${\fancyscript{Q}}$ and the product of $\tilde{f}_2$ and $\tilde{f}_3$. The rule for updating the parameters of ${\fancyscript{Q}}$ is

$$\begin{aligned} \mathbf {v}^\text {new}&= \text {diag}( \mathbf {V} )\,, \end{aligned}$$

(30)

$$\begin{aligned} \mathbf {m}^\text {new}&= \mathbf {V} \left[ \tilde{\mathbf {V}}_2^{-1} \tilde{\mathbf {m}}_2 + \sigma ^{-2}_0 \mathbf {X}^\text {T} \mathbf {y} \right] \,,\end{aligned}$$

(31)

$$\begin{aligned} \mathbf {p}^\text {new}&= \tilde{\mathbf {p}}_2 + \tilde{\mathbf {p}}_3\,, \end{aligned}$$

(32)

where $\text {diag}(\cdot )$ extracts the diagonal of a square matrix,

$$\begin{aligned} \mathbf {V} = ( \tilde{\mathbf {V}}_2^{-1} + \sigma ^{-2}_0 \mathbf {X}^\text {T} \mathbf {X} )^{-1} \end{aligned}$$

(33)

and $\tilde{\mathbf {V}}_2$ is a diagonal matrix such that $\text {diag}(\tilde{\mathbf {V}}_2)=\tilde{\mathbf {v}}_2$. The calculation of $\text {diag}(\mathbf {V})$ is the bottleneck of the proposed EP method. When $\mathbf {X}^\text {T} \mathbf {X}$ is precomputed and $n \ge d$, the computational cost of performing the inverse of $\tilde{\mathbf {V}}_2^{-1} + \sigma ^{-2}_0 \mathbf {X}^\text {T} \mathbf {X}$ is ${\fancyscript{O}}(d^3)$. However, when $n < d$, the Woodbury formula provides a more efficient computation of $\mathbf {V}$:

$$\begin{aligned} \mathbf {V} = \tilde{\mathbf {V}}_2 - \tilde{\mathbf {V}}_2 \mathbf {X}^\text {T} \left[ \mathbf {I} \sigma ^2_0 + \mathbf {X} \tilde{\mathbf {V}}_2 \mathbf {X}^\text {T} \right] ^{-1} \mathbf {X} \tilde{\mathbf {V}}_2\,. \end{aligned}$$

(34)

With this improvement the time complexity of EP is reduced to ${\fancyscript{O}}(n^2d)$ because it is necessary to compute only $\text {diag}(\mathbf {V})$ and not $\mathbf {V}$ itself. However, the use of the Woodbury formula may lead to numerical instabilities when some of the components of $\tilde{\mathbf {v}}_2$ are very large, as reported by Seeger (2008). This limits the size of the constant $v_\infty$ that is used for the update of $\tilde{v}_{2i}$ when (25) yields a negative result. In our implementation we use $v_\infty = 100$. In practice, the predictive accuracy of the model does not strongly depend on the precise value of $v_\infty$ provided that it is sufficiently large. Once ${\fancyscript{Q}}$ has been refined using (30), (31) and (32), the update for $\tilde{f}_1$ is obtained by computing the ratio between ${\fancyscript{Q}}$ and the product of $\tilde{f}_2$ and $\tilde{f}_3$ (see Appendix 4)

$$\begin{aligned} \tilde{v}_{1i}^\text {new}&= \left[ \left( v_i^\text {new}\right) ^{-1} - \tilde{v}_{2i}^{-1}\right] ^{-1}\,, \end{aligned}$$

(35)

$$\begin{aligned} \tilde{m}_{1i}^\text {new}&= \left[ m_i^\text {new}\left( v_i^\text {new}\right) ^{-1} - \tilde{m}_{2i}\tilde{v}_{2i}^{-1} \right] \tilde{v}_{1i}^\text {new}\,, \end{aligned}$$

(36)

where $i = 1,\ldots ,d$.

Although the approximation (13) does not include any correlations between the components of $\mathbf {w}$, these correlations can be directly estimated once EP has converged. For this, one computes $\mathbf {V}$ using either (33) when $n < d$ or (34) when $n \ge d$. The proposed EP method is in fact taking into account possible correlations among the components of $\mathbf {w}$ when it approximates the posterior marginals of this parameter vector. Such correlations are used, for example, in the computation of (31) for the update of ${\fancyscript{Q}}$. In particular, to obtain (31), we make use of the non-diagonal elements of $\mathbf {V}$. If one is not interested in considering these posterior correlations, a more efficient implementation of EP is obtained by expressing $f_1$ and $\tilde{f}_1$ as a product of $n$ subfactors, one subfactor per data point (Hernández-Lobato et al. 2008). If such a factorization is used, $\tilde{f}_1$ can be updated in $n$ separate steps, one step per subfactor. In this alternative implementation, the computational cost of EP is ${\fancyscript{O}}(nd)$. Appendix 6 provides a detailed description of this faster implementation of EP. However, in this case, the posterior approximation is less accurate because the correlations between the components of $\mathbf {w}$ are ignored. This is shown in the experiments described in Sect. 5.

As mentioned before, the computational cost of our EP method is ${\fancyscript{O}}(n^2d)$. The cost of Gibbs sampling is ${\fancyscript{O}}(p_0^2d^3k)$ (see Appendix 8), where $k$ are the number of samples drawn from the posterior. The cost of the alternative EP method that ignores posterior correlations is ${\fancyscript{O}}(nd)$ (Hernández-Lobato et al. 2008) (see Appendix 6). Gibbs sampling is the preferred approach when $p_0$ is small. For large $p_0$ and large correlations in the posterior distribution, the proposed EP method is the most efficient alternative. Finally, when $p_0$ is large and posterior correlations are small, the EP method described in Appendix 6 should be used. Here, we have ignored the number of iterations $k$ that the Gibbs sampling approach needs to be run to obtain samples from the stationary distribution. When this number is very large, the EP methods would be the preferred option, even if $p_0$ is very small.

4.3 Approximation of the model evidence

An advantage of Bayesian techniques is that they provide a natural framework for model selection (MacKay 2003). In this framework, the alternative models are ranked according to the value of their evidence, which is the normalization constant used to compute the posterior distribution from the joint distribution of the model parameters and the data. In this approach one selects the model with the largest value of this normalization constant. For linear regression problems the model evidence, ${\fancyscript{P}}(\mathbf {y}|\mathbf {X})$, represents the probability that the targets $\mathbf {y}$ are generated from the design matrix $\mathbf {X}$ using (2) when the vector of coefficients $\mathbf {w}$ is randomly sampled from the prior distribution assumed. The main advantage of using the model evidence as a tool for discriminating among different alternatives is that it naturally achieves a balance between rewarding models that provide a good fit to the training data and penalizing their complexity (Bishop 2006).

The exact computation of ${\fancyscript{P}}(\mathbf {y}|\mathbf {X})$ in the LRMSSP is generally infeasible because it involves averaging over the $2^d$ possible configurations of $\mathbf {z}$ and integrating over ${\mathbf w}$. However, EP can also be used to approximate the model evidence using

$$\begin{aligned} {\fancyscript{P}}(\mathbf {y}|\mathbf {X}) \approx \sum _{\mathbf {z}} \int \tilde{f}_1(\mathbf {w},\mathbf {z}) \tilde{f}_2(\mathbf {w},\mathbf {z}) \tilde{f}_3(\mathbf {w},\mathbf {z})\,d\mathbf {w}\,. \end{aligned}$$

(37)

Several studies indicate that the EP approximation of the model evidence can be very accurate in specific cases (Kuss and Rasmussen 2005; Cunningham et al. 2011). The right-hand side of (37) can be computed very efficiently because the approximate factors $\tilde{f}_1$, $\tilde{f}_2$ and $\tilde{f}_3$ have simple exponential forms. However, before evaluating this expression, the parameters $\tilde{s}_1$, $\tilde{s}_2$ and $\tilde{s}_3$ in (15), (16) and (17) need to be calculated. After EP has converged, the value of these parameters is determined by requiring that $\tilde{f}_iQ^{\setminus i}$ and $f_iQ^{\setminus i}$ have the same normalization constant for $i = 1$, $2$ and $3$

$$\begin{aligned} \log \tilde{s}_1 = \,&\frac{1}{2} \mathbf {m}^\text {T} (\tilde{\mathbf {V}}_2^{-1} \tilde{\mathbf {m}}_2 + \sigma ^{-2}_0 \mathbf {X}^\text {T} \mathbf {y}) - \frac{n}{2} \log (2 \pi \sigma _0^2) - \frac{1}{2} \sigma _0^{-2} \mathbf {y}^\text {T} \mathbf {y} - \frac{1}{2} \tilde{\mathbf {m}}_{2}^\text {T} \tilde{\mathbf {V}}_2^{-1} \tilde{\mathbf {m}}_{2}\nonumber \\&- \frac{1}{2} \log \alpha + \frac{1}{2}\sum _{i=1}^d \Bigg \{ \log \left[ 1 + \tilde{v}_{2i}\tilde{v}_{1i}^{-1} \right] + \tilde{m}_{1i}^2\tilde{v}_{1i}^{-1} + \tilde{m}_{2i}^2\tilde{v}_{2i}^{-1} - m_i^2v_i^{-1} \Bigg \} \,,\end{aligned}$$

(38)

$$\begin{aligned} \log \tilde{s}_2 = \,&\sum _{i=1}^d \frac{1}{2} \Bigg \{ 2 \log c_i + \log \left[ 1 + \tilde{v}_{1i} \tilde{v}_{2i}^{-1} \right] + \tilde{m}_{1i}^2\tilde{v}_{1i}^{-1} + \tilde{m}_{2i}^2\tilde{v}_{2i}^{-1} \nonumber \\&- m_i^2v_i^{-1} + 2 \log \left[ \sigma (p_i)\sigma (-\tilde{p}_{3i}) + \sigma (-p_i)\sigma (\tilde{p}_{3i})\right] \nonumber \\&- 2\log \left[ \sigma (\tilde{p}_{3i})\sigma (-\tilde{p}_{3i}) \right] \Bigg \} ,\end{aligned}$$

(39)

$$\begin{aligned} \log \tilde{s}_3 = \,&0\,, \end{aligned}$$

(40)

where $c_i = \sigma (\tilde{p}_{3i}) {\fancyscript{N}}(0|\tilde{m}_{1i},\tilde{v}_{1i} + v) + \sigma (-\tilde{p}_{3i}) {\fancyscript{N}}(0|\tilde{m}_{1i},\tilde{v}_{1i})$, $\alpha = |\mathbf {I} + \sigma _0^{-2} \tilde{\mathbf {V}}_2 \mathbf {X}^\text {T} \mathbf {X}|$ and the logarithms are taken to avoid numerical underflow or overflow errors in the actual implementation of EP. The derivation of these formulas is given in Appendix 4. Sylvester’s determinant theorem provides a more efficient representation for $\alpha$ when $n < d$

$$\begin{aligned} \alpha = | \mathbf {I} + \sigma _0^{-2} \mathbf {X} \tilde{\mathbf {V}}_2 \mathbf {X}^\text {T} |. \end{aligned}$$

(41)

Finally, by taking the logarithm on both sides of (37), $\log {\fancyscript{P}}(\mathbf {y}|\mathbf {X})$ can be approximated as

$$\begin{aligned} \log {\fancyscript{P}}(\mathbf {y}|\mathbf {X}) \approx \,&\log \tilde{s}_1 + \log \tilde{s}_2 + \frac{d}{2} \log (2 \pi ) \nonumber \\&+ \sum _{i=1}^d \frac{1}{2} \left\{ \log v_i + m_i^2v_i^{-1} - \tilde{m}_{1i}^2\tilde{v}_{1i}^{-1} - \tilde{m}_{2i}^2\tilde{v}_{2i}^{-1} \right\} \nonumber \\&+ \sum _{i=1}^d \log \left\{ \sigma (\tilde{p}_{2i}) \sigma (\tilde{p}_{3i}) + \sigma (-\tilde{p}_{2i}) \sigma (-\tilde{p}_{3i}) \right\} \,, \end{aligned}$$

(42)

where $\log \tilde{s}_1$ and $\log \tilde{s}_2$ are given by (38) and (39). The derivation of this formula makes use of the product rules for Gaussian and Bernoulli distributions (see Appendix 3). Note that $\alpha$ can be negative if some of the components of $\tilde{\mathbf {v}}_2$ are negative. In this particular case, $\mathbf {I} + \sigma _0^{-2} \tilde{\mathbf {V}}_2 \mathbf {X}^\text {T} \mathbf {X}$ is not positive definite, $\log \tilde{s}_1$ cannot be evaluated and EP fails to approximate the model evidence. To avoid this, $\tilde{f}_2$ is determined by minimizing $\text {D}_{\text {KL}}(f_2Q^{\setminus 2} \Vert \tilde{f}_2Q^{\setminus 2})$ under the constraint that the components of $\tilde{\mathbf {v}}_2$ be positive, as described in the previous section.

Finally, a common approach in Bayesian methods for selecting the optimal value of the hyperparameters is to maximize the evidence of the model. This procedure is usually referred to as type-II maximum likelihood estimation (Bishop 2006). In the LRMSSP, the hyperparameters are the level of noise in the targets, $\sigma _0$, the variance of the slab, $v_s$, and the prior probability that a coefficient is different from zero, $p_0$. Thus, the values $\sigma _0$, $v_s$ and $p_0$ are determined by maximizing (42).

5 Experiments

The performance of the proposed EP method is evaluated in regression problems from different domains of application using both simulated and real-world data. The problems analyzed include the reconstruction of sparse signals from a reduced number of noisy measurements (Ji et al. 2008), the prediction of user sentiment from customer-written reviews of kitchen appliances and books (Blitzer et al. 2007), the modeling of biscuit dough constituents based on characteristics measured using near infrared (NIR) spectroscopy (Osborne et al. 1984; Brown et al. 2001) and the reverse engineering of transcription networks from gene expression data (Gardner and Faith 2005). These problems have been selected according to the following criteria: First, they all have a high-dimensional feature space and a small number of training instances ($d > n$). Second, only a reduced number of features are expected to be relevant for prediction; therefore, the optimal models should be sparse. Finally, the regression tasks analyzed arise in application domains of interest; namely, the modeling of gene expression data (Slonim 2002), the field of compressive sensing (Donoho 2006), the statistical processing of natural language (Manning and Schütze 2000) and the quantitative analysis of NIR spectra (Osborne et al. 1993).

In these experiments, different inference methods for the linear regression model with spike-and-slab priors are evaluated. The proposed EP method (SS-EP) is compared with Gibbs sampling, variational Bayes and another approximate inference method that is also based on EP, but ignores posterior correlations. Specifically, these include SS-MCMC, which makes Bayesian inference using Gibbs sampling instead of EP. This technique is described in Appendix 1; the variational Bayes method (SS-VB) proposed by Carbonetto and Stephens (2012). Finally, we also consider an alternative EP method which ignores possible correlations in the posterior distribution, which is based on a different factorization of the likelihood (SS-EPF) (Hernández-Lobato et al. 2008). This latter technique is described in Appendix 6.

We also investigate the effect of assuming different sparsity-enforcing priors. These include the sparse linear regression model proposed by Seeger (2008), with Laplace priors and EP for approximate inference (Laplace-EP), a linear model with horseshoe priors and Gibbs sampling (HS-MCMC), which is described in Appendix 2; and, finally, the relevance vector machine (RVM) of Tipping (2001). The RVM is equivalent to assuming Student’s $t$ priors in which the degrees of freedom approach zero. This method employs a type-II maximum likelihood approach for the estimation of the model parameters. An interpretation of this latter method from a variational point of view is given by Wipf et al. (2004). Both Laplace-EP and RVM approximate the posterior using a multivariate Gaussian distribution. The method SS-VB is based on the posterior approximation ${\fancyscript{Q}}^\text {VB}(\mathbf {w},\mathbf {z}) = \prod _{i=1}^d [ z_i p_i^\text {VB}{\fancyscript{N}}(w_i|m_i^\text {VB}, v_i^\text {VB}) + (1 - z_i) (1 - p_i^\text {VB}) \delta (w_i))]$, where $\delta (\cdot )$ is a point probability mass at zero. To select $m_1^\text {VB},\ldots ,m_d^\text {VB}$, $v_1^\text {VB},\ldots ,v_d^\text {VB}$ and $p_1^\text {VB},\ldots ,p_d^\text {VB}$ SS-VB maximizes a lower bound on the model evidence (Carbonetto and Stephens 2012).

The different algorithms are implemented in R (Team 2007) except for RVM and SS-VB. The results for these two methods are obtained using the MATLAB implementation developed by Ji et al. (2008) and the R package made available by Carbonetto and Stephens (2012), respectively. SS-MCMC and HS-MCMC draw 10,000 Gibbs samples from the posterior after a burn-in period of 1000 samples. Preliminary experiments in which more than 10,000 samples are generated produced no significant improvements in predictive accuracy, which indicates that the runs are sufficiently long to produce accurate approximations to the posterior distribution in these models. Besides evaluating the performance of the different methods, we report the estimates of the model evidence given by SS-EP, SS-EPF, Laplace-EP and RVM, and the value of the lower bound for this quantity given by SS-VB. We do not report estimates of the model evidence for SS-MCMC or HS-MCMC. However, such estimates could be computed using thermodynamic integration methods (Calderhead and Girolami 2009). Finally, we also report the training time in seconds for each method.

In the experiments with gene expression data, customer-written reviews and biscuit dough constituents, we tune the hyperparameters of each method to the available training data. For this, in the EP based methods SS-EP, SS-EPF and Laplace-EP, we maximize the EP approximation of the model evidence using the downhill simplex method. Other options could be to do importance sampling using the the EP approximation of the model evidence as importance weights or to sample hyperparameter values over a grid as in the integrated nested Laplace approximation (INLA) (Rue et al. 2009). In SS-MCM and HS-MCMC, we select non-informative priors for the hyperparameters and then sample from their posterior distribution using Gibbs sampling. Finally, in SS-VB and RVM we optimize the lower-bound on the model evidence and the type-II likelihood function, respectively. In the experiments with spike signals we use simulated data. The values of the hyperparameters are in this case determined by taking into account the actual values of the parameters of the generative process for the data.

In SS-MCMC, the Markov chain is initialized to a solution in which the posterior probability is large, so that the Gibbs sampler converges faster to a good solution. To this end, we use a greedy search that starts off by setting $z_1,\ldots ,z_d$ to zero and then activates the component of $\mathbf {z}$ that reduces the mean squared error on the training data the most. This activation step is repeated until $p_0 d$ components of $\mathbf {z}$ are equal to one, where $p_0$ is the hyperparameter value selected by SS-EP. Note that we could have used a random initialization instead, at the cost of having to increase the number of samples generated by the Gibbs sampling approach. In SS-VB, we use an initialization similar to the one used for SS-MCMC.

We first evaluate the performance of the different inference methods for the linear regression model with spike-and-slab priors (SS-EP, SS-MCMC, SS-EPF and SS-VB) on a synthetic toy dataset. This simple toy example illustrates the behavior of each approximation method. After that, we evaluate the performance of the spike-and-slab inference methods (SS-EP, SS-MCMC, SS-EPF and SS-VB) and all the other methods (HS-MCMC, Laplace-EP and RVM) on the remaining problems described above.

5.1 Toy example for spike-and-slab inference methods

We first evaluate the performance of SS-EP, SS-MCMC, SS-EPF and SS-VB on a toy example. This allows us to illustrate the typical behavior of each of these inference methods. We focus on a regression problem in which each $\mathbf {x}_i$ is a two-dimensional vector $(x_{i,1},x_{i,2})^\text {T}$ whose entries are sampled from a two-dimensional multivariate Gaussian distribution with zero mean, unit marginal variances and 0.5 covariance between $x_{i,1}$ and $x_{i,2}$. The true coefficient vector $\mathbf {w}$ is sampled from a spike-and-slab prior distribution (4) in which the probability of sampling each coefficient from the slab is $p_0 = 0.5$ and the slab variance is $v_s = 1$. Given $\mathbf {x}_i$ and $\mathbf {w}$, we sample $y_i$ from a Gaussian with mean $\mathbf {x}_i^\text {T} \mathbf {w}$ and precision $10$. For a direct comparison of the different inference techniques, we fix the hyper-parameters to the optimal values that were used to generate the data. This allows us to avoid discrepancies due to SS-MCMC performing full Bayesian inference on the hyper-parameter values and SS-EP, SS-EPF and SS-VB selecting only the point estimates that maximize an approximation to the model evidence. For each method, we set $p_0 = 0.5$, $\sigma _0^2 = 0.1$ and $v_s = 1$. Note that in the experiments with gene expression data, customer-written reviews and biscuit dough constituents, we tune the hyperparameters of each method to the available training data. In this toy example we use training sets with 2 instances and test sets with 1000 instances. The training/testing process is repeated 100,000 times.

The plots in the top and bottom left of Fig. 3 show the approximation for the posterior of $\mathbf {w}$ generated by SS-EP, SS-EPF and SS-MCMC on a particular case of the toy synthetic data. The posterior distribution generated by SS-MCMC is considered to be the gold standard and it is displayed in each plot in gray colors using the output of a kernel density estimator applied to the samples generated by SS-MCMC. The figure shows that in this case there are two modes in the posterior distribution: one corresponding to solutions in which only $w_1$ is zero and another one corresponding to solutions in which both $w_1$ and $w_2$ are different from zero. We show in blue the Gaussian distribution with the same mean and the same covariance matrix as the samples generated by SS-MCMC. The mean of the Gaussian is shown with an “x” and its covariance matrix is visualized as the ellipse with axes formed by the eigenvectors of the covariance matrix after being scaled by the square root of the corresponding eigenvalues. The Gaussian approximations generated by SS-EP, SS-EPF and SS-VB are shown as discontinuous red ellipses, with an “o” denoting their mean. In SS-EP, the posterior covariances are approximated using (33) once the EP method has converged. The Gaussian approximation generated by SS-EP is very close to a Gaussian with the same mean and covariance matrix as the samples drawn by SS-MCMC. SS-EPF fails to accurately model the posterior covariance since it assumes independence among the entries of $\mathbf {w}$ in the posterior. The approximation generated by SS-VB differs significantly from the one generated by SS-MCMC. SS-VB is stuck in a local solution. This method only approximates the mode in the true posterior for which both $w_1$ and $w_2$ are different from zero and it ignores the mode for which $w_1$ is zero and $w_2$ is not. The plots in the bottom right of Fig. 3 show the marginal posterior activation probabilities for $\mathbf {z}=(z_1,z_2)^\text {T}$ generated by SS-EP, SS-EPF, SS-MCMC and SS-VB on the same instance of the toy synthetic data. The approximation generated by SS-EP is very close to the one generated by SS-MCMC. However, SS-EPF and SS-VB are less accurate approximating the marginal for $z_1$.

Fig. 3

Top and bottom left, posterior approximation for $\mathbf {w}=(w_1,w_2)^\text {T}$ generated by SS-EP, SS-EPF, SS-MCMC and SS-VB on a particular case of the toy synthetic data. See the main text for details. The approximation generated by SS-EP is very close to the Gaussian with the same mean and covariance as the samples generated by SS-MCMC. SS-EPF fails to accurately approximate the posterior covariance since it assumes independence among the entries of $\mathbf {w}$ in the posterior. The approximation generated by SS-VB differs significantly from the one generated by SS-MCMC. SS-VB only approximates one of the modes in the true posterior. In SS-EP, the posterior covariances are approximated using (33) once the EP method has converged. Bottom right, marginal posterior activation probabilities for $\mathbf {z}=(z_1,z_2)^\text {T}$ generated by SS-EP, SS-EPF, SS-MCMC and SS-VB on the same instance of the toy synthetic data. The approximation generated by SS-EP is very close to the one generated by SS-MCMC. SS-EPF and SS-VB are less accurate approximating the marginal for $z_1$

Table 3 shows for each method the average and standard deviation of the test mean squared error (MSE), the model evidence and the training time in seconds. In terms of MSE, the best method is SS-MCMC, closely followed by SS-EP. SS-EPF performs worse than SS-EP and SS-VB obtains the worst results. The gains of SS-MCMC with respect to the other methods are significant at $\alpha = 5\,\%$ according to different paired $t$ tests. The $p$-values obtained are all below $10^{-6}$. Regarding the estimates of $\log {\fancyscript{P}}(\mathbf {y}|\mathbf {X})$, the evidence of SS-EP is larger than the evidence of SS-EPF and SS-VB. Regarding execution times, SS-EP and SS-EPF have similar performance, closely followed by SS-VB. However, SS-MCMC is much more expensive than the other methods.

Table 3 Results of the different methods in the toy dataset

5.2 Reconstruction of sparse signals

The LRMSSP has potential applications also in signal processing and, in particular, in the field of compressive sensing (Candès 2006; Donoho 2006). The objective in compressive sensing is to recover a sparse signal $\mathbf {w}=(w_1,\ldots ,w_d)^\text {T}$ from a limited set of linear measurements $\mathbf {y}=(y_1,\ldots ,y_n)^\text {T}$, where $n < d$. The measurements $\mathbf {y}$ are obtained after projecting the signal $\mathbf {w}$ onto an $n \times d$ measurement matrix $\mathbf {X}$

$$\begin{aligned} \mathbf {y} = \mathbf {X} \mathbf {w} + \mathbf {e}, \end{aligned}$$

(43)

where $\mathbf {e}=(e_1,\ldots ,e_n)^\text {T} \sim {\fancyscript{N}}(\varvec{0}, \sigma _0^{2} \mathbf {I})$ is additive Gaussian noise. Since $\mathbf {w}$ is sparse, it is possible to accurately reconstruct this vector from $\mathbf {y}$ and $\mathbf {X}$ using fewer measurements than the number of degrees of freedom of the signal, which is the limit imposed by the Nyquist sampling theorem to guarantee the reconstruction of general signals. When $\mathbf {w}$ is not sparse, it may be possible to find a $d \times d$ orthonormal matrix $\mathbf {B}$ (for example, a wavelet basis), such that $\tilde{\mathbf {w}}=\mathbf {B}^\text {T} \mathbf {w}$, where $\tilde{\mathbf {w}}$ is sparse or nearly sparse. In this case, the measurement process is performed after projecting the signal onto the columns of $\mathbf {B}$

$$\begin{aligned} \mathbf {y} = \mathbf {X} \mathbf {B}^\text {T} \mathbf {w} + \mathbf {e} = \mathbf {X} \tilde{\mathbf {w}} + \mathbf {e} \end{aligned}$$

(44)

Once an estimate of $\tilde{\mathbf {w}}$ has been obtained from $\mathbf {y}$ and $\mathbf {X}$, $\mathbf {w}$ can be approximated using $\mathbf {w} = \mathbf {B} \tilde{\mathbf {w}}$. Therefore, even if the signal is not sparse, it may still be possible to reconstruct $\mathbf {w}$ with high precision using less than $d$ samples, provided that this vector is compressible in some basis $\mathbf {B}$.

In summary, the problem of recovering a sparse signal from a few compressive measurements is a linear regression problem in which $\mathbf {y}$ is the target vector, $\mathbf {X}$ is the design matrix and the vector of regression coefficients $\mathbf {w}$ (the signal) is assumed to be sparse. Therefore, SS-EP can be used to address this problem. The following experiments evaluate the performance of SS-EP in the recovering of non-uniform and uniform spike signals. These are standard benchmark problems in the field of compressive sensing for the comparison of different algorithms (Ji et al. 2008).

5.2.1 Non-uniform spike signals

In this experiment, 100 signals of length $d = 512$ are generated by randomly selecting 20 non-zero components in each signal vector. The elements in these positions are independently sampled from a standard Gaussian distribution. The remaining components in the signal vectors are zero. In this case it is not necessary to use a basis $\mathbf {B}$ because the signals are already sparse in the original basis. The measurements are performed using a matrix $\mathbf {X}$ whose rows are sampled uniformly from the unit hypersphere. For the reconstruction of the signals, a total of $n = 75$ measurements are used. The noise in the measurement process follows a zero-mean Gaussian distribution with standard deviation $0.005$. The signal reconstruction is given by the posterior mean of $\mathbf {w}$, as approximated by each of the methods analyzed. The hyperparameters in each method are determined in correspondence with the actual signal. In SS-EP, SS-VB and SS-MCMC, $p_0 = 20 / 512$ and $v_s = 1$. In Laplace-EP, the scale parameter is $b = \sqrt{10 / 512}$. This specific value is such that the standard deviations of the Laplace prior and of the signal to be recovered coincide. In HS-MCMC, the scale parameter $\tau$ is selected so that the distance between the $0.01$ and $0.99$ quantiles is the same in the horseshoe prior and in the spike-and-slab prior. In all the methods analyzed, the variance of the noise is $\sigma _0^2 = 0.005^{2}$. Given an estimate $\hat{\mathbf {w}}$ of a signal $\mathbf {w}_0$, the reconstruction error of $\hat{\mathbf {w}}$ is quantified by $||\hat{\mathbf {w}}-\mathbf {w}_0||_2/||\mathbf {w}_0||_2$, where $|| \cdot ||_2$ represents the Euclidean norm.

Table 4 summarizes the results of the experiments with non-uniform spike signals. This table displays the average and the standard deviation of the signal reconstruction error, the logarithm of the model evidence and the time cost in seconds for each method. The best reconstruction performance is obtained by SS-MCMC, followed by SS-EP and SS-EPF. The differences between these methods are not statistically significant. However, the differences between SS-EP and SS-VB, Laplace-EP, HS-MCMC and RVM are significant at the level $\alpha = 5\,\%$ according to different paired $t$ tests. All the resulting $p$-values are below $10^{-4}$. The model evidence is higher for SS-EP than for SS-EPF and Laplace-EP. Furthermore, SS-EP generates estimates of $\log {\fancyscript{P}}(\mathbf {y}|\mathbf {X})$ that are larger than the value of the lower bound given by SS-VB. In this problem RVM obtains the largest estimate of ${\fancyscript{P}}({\mathbf {y}}|\mathbf {X})$. However, the estimates of the evidence given by RVM are too high. The reason for this is that the type-II maximum likelihood approach used by RVM generates a posterior approximation in which many of the model coefficients are exactly zero with probability one. The uncertainty in the actual value of these coefficients is not taken into account by RVM and this method tends to overestimate the value of the evidence. The training time of the EP methods are similar. RVM is slightly faster and SS-VB slightly slower than EP. HS-MCMC and SS-MCMC are the costliest methods: Up to 20,000 and 60,000 times slower than SS-EP, respectively. In this case SS-MCMC is particularly slow because of the specific parallel tempering implementation that prevents the Gibbs sampler from becoming trapped in a suboptimal mode of the posterior distribution. This alternative version of SS-MCMC is described in section “Parallel tempering” of Appendix 1.

Table 4 Results of the different methods in the experiments with non-uniform spike signals

In this problem, the differences between SS-VB and SS-EP have their origin in the propensity of the variational method to become trapped in suboptimal modes of the posterior distribution. This is illustrated by the plots in Fig. 4, which show the signal estimates obtained by these methods in a particular instance of the problem. SS-EP generates a signal estimate which is very accurate and cannot be distinguished in the graph from the original signal (not shown). By contrast, SS-VB produces incorrect spikes that are not present in the original signal. This happens even though we used an annealed version of SS-VB to try to prevent SS-VB from getting trapped in suboptimal modes. This annealed version of SS-VB is described in Appendix 7. The signal estimate generated by RVM also presents similar problems. The reason is that RVM involves an optimization step that often converges to local suboptimal maxima of the type-II likelihood. Laplace-EP has the largest reconstruction error in this problem, as illustrated by the top-right plot in Fig. 4. The Laplace prior produces excessive shrinkage of non-zero coefficients and does not sufficiently reduce the magnitude of the coefficients that should be zero. The reconstruction generated by HS-MCMC is in this case very close to the original signal as well. However, the height of some of the spikes is not correct, especially for the smallest ones. Finally, the signal estimates given by SS-EPF and SS-MCMC (not shown) are very similar to the reconstruction generated by SS-EP.

Fig. 4

Signal reconstructions generated by the different methods on a particular instance of the experiment with non-uniform spike signals. The original signal (not shown) cannot be visually distinguished from the approximation generated by the method SS-EP (top-left plot). The signal estimates given by SS-EPF and SS-MCMC (not shown) are very similar to the reconstruction generated by SS-EP

5.2.2 Uniform spike signals

The uniform spike signals are generated similarly as the non-uniform ones. The only difference is that the non-zero elements of the signals are now sampled at random from the set $\{ -1, 1 \}$. The experimental protocol and the hyperparameters of the different methods are the same as the ones used in the previous set of experiments. However, we now use $100$ measurements for the reconstruction of the signal vectors because the accurate reconstruction of uniform spike signals requires more data.

Table 5 shows the results in the experiments with uniform spike signals. The most accurate reconstruction is provided by SS-MCMC, SS-EP and SS-EPF. The differences between these methods are not statistically significant. However, the differences between SS-EP and all the other techniques are statistically significant at $\alpha = 5\,\%$ according to several paired $t$ tests. The $p$-values obtained are all lower than $10^{-15}$. The ranking of the different methods according to the average estimates of the evidence is RVM, SS-EP, SS-EPF, SS-VB and Laplace-EP from higher to lower values. The average training times of SS-EP, SS-EPF, SS-VB, Laplace-EP and RVM are similar. However, HS-MCMC and SS-MCMC have computational costs that are about 25,000 and 60,000 times larger than the cost of SS-EP, respectively.

Table 5 Results of the different methods in the experiments with uniform spike signals

Figure 5 displays the signal reconstructions generated by the different methods in a particular realization of the problem with uniform spike signals. SS-VB appears to be trapped in some suboptimal mode of the posterior distribution. Similarly, RVM converges to a local maximum of the type-II likelihood, which is suboptimal. By contrast, the signal reconstruction given by SS-EP is very accurate. These results indicate that SS-EP is less affected than SS-VB by the multi-modality of the posterior distribution. The reconstruction given by Laplace-EP is again very poor. This method does not produce an effective selective shrinkage for the different coefficients of the signal vector. The estimation produced by HS-MCMC is very accurate, being almost as good as SS-EP. The differences between SS-EP and HS-MCMC are only in the heights of the predicted spikes. HS-MCMC tends to produce signal reconstructions that slightly over-estimate or underestimate the size of the spikes. This was observed in the experiments with non-uniform spike signals as well. By contrast, the signal reconstructions generated by SS-EP are more accurate. The reason for this is that the spike-and-slab prior applies the same intensity of shrinkage to all the spikes (the shrinkage is given by the slab), while the horseshoe prior may apply different amounts of shrinkage to different spikes, as illustrated by the bottom plots in Fig. 2.

Fig. 5

Signal reconstructions generated by the different methods on a particular instance of the experiment with uniform spike signals. The original signal (not shown) is very similar to the approximation generated by the method SS-EP (top-left plot). The corresponding plots for SS-MCMC and SS-EPF (not shown) cannot be visually distinguished from the one generated by SS-EP

In these experiments, the performances of SS-VB and RVM are markedly worse than in the case with non-uniform spike signals. The reason seems to be that, with uniform spike signals, it is more difficult to avoid suboptimal maxima of the type-II likelihood or suboptimal modes of the posterior distribution.

5.3 Prediction of user sentiment

In this section, we illustrate the effectiveness of the LRMSSP in natural language processing applications (Manning and Schütze 2000). In particular, we consider the problem of sentiment prediction from user-written product reviews. The objective is to predict from the text of a product review the rating assigned by the user to that product. In this work we analyze the sentiment dataset² described by Blitzer et al. (2007). This dataset contains review texts and corresponding rating values taken from www.amazon.com in four different product categories. The range of possible ratings is from 1 to 5 stars. We focus on the categories books and kitchen appliances because these are the hardest and easiest prediction problems, respectively. Each review is represented using a vector of features whose components correspond to the unigrams and bigrams (Manning and Schütze 2000) that appear in at least 100 reviews within the same product category. The feature values are the occurrences of these unigrams and bigrams in the review text. Table 6 contains the total number of instances and features in the resulting datasets.

Table 6 Number of instances and features in the sentiment datasets

The performance of the different methods is evaluated in the problem of predicting the user rating from the vector of features that encodes the text of the product review. For this purpose, 20 random partitions of the data into non-overlapping training and test sets are made. The size of the training set is $n = 500$. This particular size is selected because we are interested in evaluating the results of the LRMSSP when the number of features is larger than the number of training instances (that is, $n < d$). During the training process, the data are normalized so that the instance features and the user ratings have zero mean and unit standard deviation on the training set. The mean squared error (MSE) is then evaluated on the corresponding test set. For training, the rating vector $\mathbf {y}$ is standardized so that it has zero mean and unit standard deviation.

Tables 7 and 8 summarize the results obtained by the different methods in the books and kitchen datasets, respectively. The rows in these tables display the average and the standard deviation of the test MSE, the logarithm of the model evidence and the training time in seconds for each method. In the books dataset, the methods with lowest test MSE are SS-MCMC, SS-EP, SS-EPF and Laplace-EP. The differences in MSE between these techniques are not statistically significant at $\alpha = 5\,\%$ according to different paired $t$ tests. In the kitchen dataset SS-MCMC has the best accuracy. The differences between SS-MCMC and the other approaches are statistically significant at $\alpha = 5\,\%$ according to a paired $t$ test. After SS-MCMC, the highest predictive accuracy is obtained using SS-EP and Laplace-EP. Regarding training times, the fastest method is RVM, followed by SS-EPF and SS-VB. The methods SS-EP, Laplace-EP are a bit slower. The costliest methods are HS-MCMC and SS-MCMC. They are on average 100 times slower than SS-EP. Finally, in both datasets SS-EP obtains the highest evidence.

Table 7 Results in the book dataset

Table 8 Results in the kitchen dataset

Figure 6 is useful to understand the differences of the methods analyzed. This figure shows the posterior means of $\mathbf {w}$ generated by each method on a specific training instance of the kitchen dataset. The plots for the book dataset (not shown) are similar. For SS-EP (top-left plot), the posterior means of most of the model coefficients are shrunk towards zero. Only for a few coefficients are the posterior means significantly different from zero. When a Laplace prior is used, this selective shrinkage process is less effective (top-right plot). The magnitude the coefficients that are close to zero is not significantly reduced. Furthermore, the reduction of the magnitude of non-zero coefficients caused by the Laplace prior tends to be excessive. In contrast, the posterior mean produced by RVM (middle-right plot) includes too many components whose magnitude is significantly different from zero. This leads to overfitting. The posterior means for HS-MCMC and SS-EP are very similar. When SS-VB and SS-EP are compared, it seems that SS-VB excessively reduces the magnitude the coefficients with small posterior means. Finally, the plots for SS-EPF and SS-MCMC (not shown) are very similar to the one generated by SS-EP.

Fig. 6

Posterior mean for the vector $\mathbf {w}$ generated by SS-EP (top-left), Laplace-EP (top-right), HS-MCMC (middle-left), RVM (middle-right) and SS-VB (bottom) on a particular training instance of the kitchen dataset. The corresponding plots for SS-MCMC and SS-EPF (not shown) cannot be visually distinguished from the one generated by SS-EP. Similar patterns are found in the corresponding plots for the book dataset (not shown)

5.4 Biscuit dough data

We also performed experiments with a biscuit dough dataset (Osborne et al. 1984; Brown et al. 2001). The goal in this problem is to predict biscuit dough constituents (fat, sucrose, dry flour, and water) from the spectral characteristics of the samples in the near infrared (NIR). The available features are 700 NIR reflectance points measured from 1,100 to 2,498 nanometers (nm) in steps of 2 nm. The dataset consists of 72 data points. Samples 23 and 44 are considered to be outliers and are thus ignored. The data are randomly partitioned into training and test sets with 47 and 23 instances each, respectively. This process was repeated 50 times and the results averaged over the resulting random partitions. During the training process, the data are normalized so that the different features and the targets have zero mean and unit standard deviation on the training set. The mean squared error (MSE) is then evaluated on the corresponding test set.

Tables 9, 10, 11 and 12 summarize the results obtained by the different methods when predicting the dough constituents fat, sucrose, dry flour and water, respectively. The rows in these tables display the average and the standard deviation of the test MSE, the logarithm of the model evidence and the training time in seconds for each method. In general, the best results are obtained with SS-MCMC, SS-EP, HS-MCMC and Laplace-EP. All of them achieve similar predictive accuracy. In this problem the values determined for the hyperparameters $p_0$, $v_s$ and $\sigma _0^2$ for SS-EPF and SS-VB are suboptimal, which results in poor predictions. To obtain results that are comparable with those of SS-EP and SS-MCMC, we use in SS-EPF and SS-VB the hyperparameter values selected by SS-EP. As illustrated by the results displayed in Tables 9, 10, 11 and 12, even with these values of the hyperparameters SS-EPF and SS-VB perform much worse than SS-EP or SS-MCMC. In this problem most of the available features are highly correlated. The average correlation between features is 0.88. This leads to large correlations between the entries of $\mathbf {w}$ in the posterior, which explains the the poor performance of SS-EPF. By contrast, SS-EPF performs much better in the experiments with sentiment data (Sect. 5.3). The reason is that the correlation between features are much smaller int that case (on average  0.04). RVM also obtains rather poor results in all the cases analyzed. Regarding training time, RVM is the fastest method, followed by SS-EPF. SS-EP, Laplace-EP and SS-VB have all similar costs and SS-MCMC and HS-MCMC are the most expensive methods. Finally, the highest model evidence is obtained by SS-EP and Laplace-EP, while SS-EPF, SS-VB and RVM obtain much lower values.

Table 9 Results in the NIR cookie dataset: target variable fat

Table 10 Results in the NIR cookie dataset: target variable sucrose

Table 11 Results in the NIR cookie dataset: target variable dry flour

Table 12 Results in the NIR cookie dataset: target variable water

Figure 7 shows the posterior mean for $\mathbf {w}$ generated by each method on a specific training instance of the biscuit dough dataset when the target variable is water. The plots for the other target variables (fat, sucrose and dry flour) (not shown) are similar. The posterior means generated by SS-EP, Laplace-EP and HS-MCMC present similar characteristics and include several coefficients which are different from zero. The posterior mean produced by SS-MCMC (not shown) is also very similar. In this dataset, the target vector $\mathbf {y}$ is very noisy and there are not enough data to clearly identify which coefficients should be shrunk to zero. Furthermore, the level of sparsity in this dataset is rather low. SS-EP selects on average the hyperparameter value $p_0 = 0.22$. By contrast, in other cases, such as in the experiments with gene expression data presented in Sect. 5.5, SS-EP selects on average $p_0 = 0.03$. This explains why SS-EP and HS-MCMC do not produce a strong shrinkage of most coefficients and why Laplace-EP performs relatively well, even though this method usually produces solutions in which the posterior means are not strongly shrunk towards zero. From the results of these experiments one concludes that SS-EP can perform very well even in datasets with low sparsity level. An analysis of the plots for RVM and SS-VB in Fig. 7 reveals that these methods generate solutions in which all the coefficients have zero posterior mean. These methods seem to be trapped in some local optima where the whole signal in the target vector $\mathbf {y}$ is assumed to be noise. Finally, SS-EPF seems to produce an excessive shrinkage of the regression coefficients even though in this case it is using the same hyperparameter values as SS-EP. The posterior approximation produced by SS-EPF is in this case much worse than the one generated by SS-EP. The EP method used by SS-EPF does not fully take into account the high correlations present in the posterior distribution.

Fig. 7

Posterior mean for $\mathbf {w}$ generated by SS-EP (top-left), Laplace-EP (top-right), HS-MCMC (middle-left), RVM (middle-right), SS-VB (bottom-left) and SS-EPF (bottom-right) on a particular instance of the biscuit dough dataset when predicting water. The plot for SS-MCMC (not shown) cannot be visually distinguished from the one generated by SS-EP. Similar patterns are found in the corresponding plots for the other targets fat, sucrose and dry flour (not shown)

5.5 Reconstruction of transcription regulatory networks

In this section we analyze the performance of the LRMSSP in the reconstruction of genetic regulatory networks from gene expression data. In these networks each node corresponds to a different gene and each connection represents an interaction between two genes at the transcription level (Alon 2006). The objective is to identify the connections between transcription factors (genes that regulate the expression of other genes) and the genes regulated by them. Bayesian linear models with sparsity enforcing priors are a popular approach for solving this problem since transcription networks are sparsely connected (Steinke et al. 2007). The experiments shown here are particularly useful for evaluating the performance of SS-EP on the estimation of the marginal posterior probabilities for the latent variables $\mathbf {z}$.

Let $\mathbf {X}$ be an $n \times d$ matrix whose columns correspond to different genes and whose rows represent measurements of log-concentration of mRNA obtained under different steady-state conditions. The columns of $\mathbf {X}$ are centered so that they have zero mean. As shown in Appendix 8, if one assumes that the components of $\mathbf {X}$ are contaminated with additive Gaussian noise, $\mathbf {X}$ approximately satisfies

$$\begin{aligned} \mathbf {X} = \mathbf {X} \mathbf {W} + \sigma _0 \mathbf {E} \end{aligned}$$

(45)

In this expression $\mathbf {W}$ is the $d \times d$ matrix of linear regression coefficients that connects the expression level of each gene with that of its transcriptional regulators, $\mathbf {E}$ is a $n \times d$ random matrix whose elements are independent and follow a standard Gaussian distribution and $\sigma _0$ is a positive constant that measures the level of noise in $\mathbf {X}$. The diagonal of $\mathbf {W}$ can be set to zero because any autoregulatory term in (45) can be eliminated using the transformation described in Appendix 8. For the linear model (45), the likelihood of $\mathbf {W}$ given $\mathbf {X}$ and $\sigma _0$ is

$$\begin{aligned} {\fancyscript{P}}(\mathbf {X}|\mathbf {W}) = \prod _{i=1}^n \prod _{j=1}^d {\fancyscript{N}}(x_{ij}|\mathbf {w}_j^\text {T} \mathbf {x}_i, \sigma _0^2)\,, \end{aligned}$$

(46)

where $x_{ij}$ is the element in the $i$-th row and $j$-th column of $\mathbf {X}$, $\mathbf {x}_i$ is the $i$-th column of $\mathbf {X}^\text {T}$ and $\mathbf {w}_j$ is the $j$-th column of $\mathbf {W}$. To complete a Bayesian description for (45), a prior must be specified for $\mathbf {W}$. Note that the value of $\mathbf {W}$ is determined by the connectivity of the network. In particular, the element in the $i$-th row and $j$-th column of $\mathbf {W}$ is non-zero ($w_{ij} \ne 0$) if there is a link from gene $i$ to gene $j$ and $w_{ij} = 0$ otherwise. Therefore, our prior for $\mathbf {W}$ should reflect the expected connectivity of transcription control networks.

Figure 8 shows an example of a realistic transcription control network, generated by the application GeneNetWeaver (Marbach et al. 2009). Most genes in the network have only a few parents. There are also a few hub genes that are connected to a large number of nodes (Thieffry et al. 1998; Barabási and Oltvai 2004). Thus, $\mathbf {W}$ is expected to be sparse. The non-zero elements of $\mathbf {W}$ are clustered on a few rows of $\mathbf {W}$ corresponding to hub genes. The performance of network reconstruction methods can be improved by taking into account this clustering effect (Hernández-Lobato et al. 2010). In the prior used in the present investigation, we assume independence among the components of $\mathbf {W}$. The sparsity assumption can then be captured by a spike-and-slab prior

$$\begin{aligned} {\fancyscript{P}}(\mathbf {W}|\mathbf {Z}) = \prod _{i=1}^d \prod _{j=1}^d \left[ z_{ij} {\fancyscript{N}}(w_{ij}|0,v_s) + (1 - z_{ij}) \delta (w_{ij}) \right] \,, \end{aligned}$$

(47)

where $\mathbf {Z}$ is a $d \times d$ matrix of binary latent variables, $z_{ij} = \{0,1\}$ is the element in the $i$-th row and $j$-th column of $\mathbf {Z}$ and $v_s$ is the prior variance of the components of $\mathbf {W}$ that are different from zero. Note that $z_{ij}=1$ whenever there is an edge in the network from gene $i$ to gene $j$ and $z_{ij} = 0$ otherwise. The prior for $\mathbf {Z}$ is given by a product of Bernoulli terms

$$\begin{aligned} {\fancyscript{P}}(\mathbf {Z}) = \prod _{i=1}^d \prod _{j=1}^d \text {Bern}(z_{ij}|p_{ij})\,, \end{aligned}$$

(48)

where $p_{ij} = p_0$ for $i \ne j$, $p_{ij} = 0$ for $i = j$ to enforce that the diagonal elements of $\mathbf {W}$ be zero and $p_0$ is the expected fraction of regulators of a gene in the network. The posterior distribution for $\mathbf {W}$ and $\mathbf {Z}$ is obtained using Bayes’ theorem

$$\begin{aligned} {\fancyscript{P}}(\mathbf {W},\mathbf {Z}|\mathbf {X}) = \frac{{\fancyscript{P}}(\mathbf {X}|\mathbf {W}) {\fancyscript{P}}(\mathbf {W}|\mathbf {Z}) {\fancyscript{P}}(\mathbf {Z})}{{\fancyscript{P}}(\mathbf {X})} = \prod _{i=1}^d \frac{{\fancyscript{P}}(\mathbf {x}_i|\mathbf {w}_i){\fancyscript{P}}( \mathbf {w}_i|\mathbf {z}_i){\fancyscript{P}}(\mathbf {z}_i)}{{\fancyscript{P}}(\mathbf {x}_i)}\,, \end{aligned}$$

(49)

where $\mathbf {x}_i$, $\mathbf {w}_i$ and $\mathbf {z}_i$ represent the $i$-th columns of $\mathbf {X}$, $\mathbf {W}$ and $\mathbf {Z}$, respectively and the right-most part of (49) reflects the fact that the posterior factorizes in the columns of $\mathbf {W}$ and $\mathbf {Z}$. The $i$-th factor in the right part of (49) ($i = 1,\ldots , d$) is the posterior distribution of a LRMSSP that predicts the expression level of gene $i$ as a function of the expression levels of the other genes in the network. To reconstruct the transcription network, we compute the posterior probability of each possible link. For an edge from gene $i$ to gene $j$, this probability is given by ${\fancyscript{P}}(z_{ij} = 1|\mathbf {X})$, which is computed by marginalizing (49) with respect to $\mathbf {W}$ and all the components of $\mathbf {Z}$ except $z_{ij}$. Once the posterior probability of each possible connection has been computed, a connection from gene $i$ to gene $j$ is predicted whenever ${\fancyscript{P}}(z_{ij} = 1|\mathbf {X}) > \gamma$, where $0 \le \gamma \le 1$ is a pre-specified threshold. In practice, the exact marginalization of (49) is not practicable. Because (49) factorizes into $d$ linear regression problems, the posterior of each of these problems can be approximated using EP. The product of the resulting $d$ partial solutions generates a final approximation of (49), which allows us to compute the posterior probability of each edge very efficiently.

Fig. 8

A transcription regulatory network with 100 nodes. Each node in the network represents a different gene. Edges represent transcriptional interactions between genes. The network has been generated using the application GeneNetWeaver. Hub genes are displayed in the network with a diamond-shape node

We also assess the performance of models based on Laplace, Student’s $t$ and horseshoe priors in the problem of reverse engineering transcription control networks. In these cases, the posterior for $\mathbf {W}$ is also obtained by solving $d$ different regression problems. In each of these problems the log-concentration of mRNA of gene $i$ is expressed as a linear combination of the log-concentration of mRNA of all the other genes plus Gaussian noise, for $i = 1,\ldots ,d$. The global posterior is then given by the product of the $d$ individual posteriors of the surrogate regression problems. However, with these alternative priors, the probability that any component of $\mathbf {W}$ is different from zero is always one. This means that we would always predict a fully connected network, where each gene is connected to all other genes, independently of the value of $\gamma$. To avoid this, we follow Steinke et al. (2007) and approximate the posterior probability of a connection from gene $i$ to gene $j$ by the probability of the event $|w_{ij}| > \delta _e$ under the posterior for $\mathbf {W}$, where $\delta _e$ is a small positive constant. To evaluate this probability, ${\fancyscript{P}}(\mathbf {W}|\mathbf {X})$ is integrated in the set of possible values of $\mathbf {W}$ such that $w_{ij} < -\delta _e$ and $w_{ij} > \delta _e$. This integral does not have an analytic solution. In practice, it is computed using numerical approximation schemes. In the models with Laplace and Student’s $t$ priors, the true posterior is approximated using a multivariate Gaussian. ${\fancyscript{P}}(|w_{ij}| > \delta _e| \mathbf {X})$ is then approximated by integrating the Gaussian marginal for $w_{ij}$ in the intervals $(-\infty ,-\delta _e]$ and $[\delta _e, \infty )$. In the model with horseshoe priors, we draw samples from the exact posterior and approximate ${\fancyscript{P}}(|w_{ij}| > \delta _e| \mathbf {X})$ by the fraction of samples for which $|w_{ij}| > \delta _e$.

5.5.1 DREAM 4 multifactorial sub-challenge

The performance of SS-EP is evaluated in the problem of reverse engineering transcription networks. The experimental protocol is based on the DREAM 4 (2009) multifactorial sub-challenge. The Dialogue for Reverse Engineering Assessments and Methods (DREAM) is an annual conference, in which researchers compare the performance of different methods on a set of network reconstruction tasks (Stolovitzky et al. 2007). The DREAM 4 multifactorial sub-challenge includes 100 steady-state measurements from networks with 100 genes. The levels of expression of all the genes are measured under different perturbed conditions. Each perturbation consists in small random changes in the basal activation of all the genes in the network. The network structures and the gene expression measurements are simulated using the program GeneNetWeaver (Marbach et al. 2009). This program is used to generate 100 networks of size 100 and to sample 100 steady-state measurements from each network. Figure 8 displays one of the networks generated by GeneNetWeaver.

The posterior probability of each edge in each network is approximated using the methods SS-EP, SS-MCMC, SS-EPF, SS-VB, HS-MCMC, Laplace-EP and RVM. The columns of matrix $\mathbf {X}$ are standardized so that they have zero mean and unit standard deviation. The value of $\delta _e$ is set to $0.1$, as recommended by Steinke et al. (2007). The performance of the different approaches is evaluated using the area under the precision recall (PR) and receiver operating characteristics (ROC) curves which are obtained when $\gamma$ is varied from $0$ to $1$ (Davis and Goadrich 2006).

Table 13 displays the results obtained by each method in the experiments with gene expression data. The rows in this table present the average and the standard deviation of the area under the PR and ROC curves, the logarithm of the model evidence and the training time in seconds for each method. In terms of AUC-PR, the best reconstruction is obtained by SS-EP. According to this metric, the improvements of SS-EP with respect to the other techniques are statistically significant at $\alpha = 5\,\%$ based on different paired $t$ tests. The $p$-values obtained are all below $10^{-5}$. When AUC-ROC is used as a performance measure, the differences between the top performing methods are smaller. The best methods are in this case SS-MCMC, HS-MCMC, Laplace-EP and SS-EP. All of them achieve very similar results. Overall, SS-EP is better than SS-EPF and SS-VB. Note that the different rankings of the methods according to AUC-ROC or AUC-PR have their origin in the fact that these performance measures are not monotonically related and algorithms that optimize AUC-ROC do not also optimize AUC-PR and the other way around (Davis and Goadrich 2006). Regarding the estimates of $\log {\fancyscript{P}}(\mathbf {y}|\mathbf {X})$, the evidence of SS-EP is larger than the evidence of SS-EPF and Laplace-EP and larger than the lower-bound given by SS-VB. RVM obtains the highest average evidence. Finally, regarding training times, the fastest methods are SS-VB and RVM. The EP methods SS-EP, SS-EPF and Laplace-EP obtain similar results, while HS-MCMC and SS-MCMC are much slower.

Table 13 Results for each spike-and-slab method in the network reconstruction problem

The superior results of SS-EP over SS-MCMC on AUC-PR could have two explanations: i) the Gibbs sampler would need more iterations to converge to the stationary distribution or ii) with this particular data SS-EP is more robust to model mismatch. The better performance of SS-EP with respect to Laplace-EP and RVM in terms of AUC-PR probably has its origin in the superior selective shrinkage capacity of spike-and-slab priors. The analysis of the approximations of the posterior mean for $\mathbf {W}$ given by the different methods displayed in Fig. 9 supports this claim. In this figure, the $100 \times 100$ matrices are represented as vectors of dimension $10,000$. Each point in the plots represents the posterior mean of a different coefficient. In the plot for SS-EP, most coefficients are strongly shrunk to zero while a few of them take values that are significantly different from zero. By contrast, in the Laplace model this shrinkage effect is less pronounced for small coefficients while the magnitudes of coefficients different from zero are excessively reduced. This result cannot be circumvented by increasing the sparsity level of the Laplace prior; that is, by lowering the value of the hyperparameter $b$, because that would increase the amount of shrinkage in all the model coefficients, including truly non-zero coefficients whose magnitude should not be reduced. The corresponding plot for SS-MCMC (not shown) cannot be visually distinguished from the one generated by SS-EP. The average size of the non-zero coefficients in RVM is similar to the average size of large coefficients in SS-EP. However, RVM includes an excessive number of coefficients whose posterior mean is not close to zero. The insufficient shrinkage for these coefficients makes RVM susceptible to overfitting. The plot for HS-MCMC is very similar to the one produced by SS-EP. When we compare SS-EP with SS-EPF and SS-VB, it seems that SS-EPF and SS-VB produce an excessive shrinkage of small coefficients.

Fig. 9

Approximations of the posterior mean for $\mathbf {W}$ generated by SS-EP (top left), Laplace-EP (top right), HS-MCMC (middle-left), RVM (middle-right), SS-EPF (bottom-left) and SS-VB (bottom-right) for one of the networks generated by GeneNetWeaver. The corresponding plot for SS-MCMC (not shown) cannot be visually distinguished from the one generated by SS-EP

6 Conclusions and discussion

In many regression problems of practical interest $d$, the dimension of the feature vector, is significantly larger than $n$, the number of training instances. In these conditions assuming a sparse linear model can be an effective way to limit the detrimental effects of overfitting (Johnstone and Titterington 2009). In a Bayesian approach, sparsity can be favored by using specific priors such as Laplace (Seeger 2008), Student’s $t$ (Tipping 2001), horseshoe (Carvalho et al. 2009) or spike-and-slab (Mitchell and Beauchamp 1988; Geweke 1996; George and McCulloch 1997) distributions. These priors induce a bi-separation in the posterior between a few coefficients that are significantly different from zero with large probability and a large number of coefficients that have very small posterior means. Ishwaran and Rao (2005) call this bi-separation effect selective shrinkage.

Spike-and-slab priors are generally better at enforcing sparsity than Laplace or Student’s $t$ priors because the two components in the mixture can account for two types of coefficients: The spike captures the prior distribution of coefficients that are exactly zero in the actual model. The slab models the prior of coefficients that are significantly different from zero. By contrast, Laplace and Student’s $t$ priors cannot discriminate between different groups of coefficients (zero versus non-zero coefficients). These priors produce a more uniform reduction of the magnitude of the coefficients and are, in general, less effective than spike-and-slab priors in enforcing sparsity. An exception occurs in the Student’s $t$ distribution when the degrees of freedom approach zero. However, in this case, the Student’s distribution cannot be normalized and a fully Bayesian approach is not possible. Horseshoe priors are similar to spike-and-slab priors in terms of their capacity for selectively shrinking the posterior distribution, but they do not have a closed-form convolution with the Gaussian distribution. This is a disadvantage that renders approximations based on the Gaussian distribution impractical.

Bayesian inference with spike-and-slab priors is a difficult and computationally demanding problem. Approximate Bayesian inference in the linear regression model with spike-and-slab priors (LRMSSP) is usually implemented using Gibbs sampling (George and McCulloch 1997). However, this method has a very high computational cost when $d$ and $p_0$ are very large. Another option is to use variational Bayes (VB) methods (Titsias and Lazaro-Gredilla 2012; Carbonetto and Stephens 2012). However, VB can be less accurate than other alternatives of comparable running time (Nickisch and Rasmussen 2008). We propose to use an expectation propagation (EP) (Minka 2001) algorithm as a more efficient alternative to Gibbs sampling and a more accurate method than VB. The cost of EP in the LRMSSP is ${\fancyscript{O}}(n^2d)$ when the number of training instances $n$ is smaller than $d$. The performance of EP has been evaluated in regression problems from different application fields with $d>n$: the reverse engineering of transcription networks, the reconstruction of sparse signals given a reduced number of linear measurements, the prediction of sentiment from user-written product reviews and the determination of biscuit dough constituents from spectral characteristics. In these tasks, the proposed EP method outperforms VB and an alternative implementation of EP that assumes no correlations in the posterior distribution (Hernández-Lobato et al. 2008). Furthermore, the predictive accuracy achieved is comparable to Gibbs sampling at a much lower computational cost. This good generalization performance is obtained even though the values of the hyperparameters in the proposed method are determined by maximizing the approximation of the model evidence given by EP, while Gibbs sampling performs a full average over the posterior distribution of the hyperparameters.

The superior performance of EP over VB in the problems investigated can be explained by the differences in the form of the KL divergence minimized by these methods. In regression models, the mean of the posterior distribution leads to optimal predictions, in the sense that it minimizes the mean square error. EP usually produces a global fit to the posterior distribution. In contrast, VB approximates the posterior only locally around one of its modes. This is illustrated by the plots shown in Fig. 10. In the multi-modal posterior distributions generated by spike-and-slab priors, the global fit produced by EP is much better at approximating the posterior mean than the local approximations generated by VB. Furthermore, our experiments show that SS-VB often ends up being stuck in suboptimal modes of the posterior distribution with poor predictive properties.

Fig. 10

Comparison of the solutions generated by the minimization of two alternative forms of the KL divergence. The blue contours show a bimodal posterior distribution $p$ generated by a mixture of two Gaussians. The red contours show a single Gaussian distribution $q$ that best approximates $p$ according to the minimization of KL$(q||p)$ (left-plot) or KL$(p||q)$ (right-plot). Variational Bayes minimizes KL$(q||p)$ and produces local approximations to specific modes of the posterior distribution, as illustrated in the left plot. By contrast, EP works by minimizing the reversed KL divergence and produces a global fit to the posterior distribution, as shown in the right plot. In sparse linear regression models, optimal predictive performance in terms of mean square error is given by the mean of the posterior distribution. The mean of $p$ is located between the two modes of the Gaussian components in the mixture. The plots above show that the cost function minimized by EP generates better approximations to the posterior mean in multi-modal posterior distributions, which is the case in linear models with spike-and-slab priors (Color figure online)

The LRMSSP with EP also outperforms other sparse linear regression models that assume Laplace, Student’s $t$ or horseshoe priors. The good overall results of the LRMSSP when compared to models based on Laplace or Student’s $t$ priors are explained by the superior selective shrinkage capacity of spike-and-slab distributions: In the posterior approximation computed by EP, most of the model coefficients are close to zero with large probability. Only for a few coefficients is the posterior probability centered around values that are significantly different from zero. By contrast, Laplace priors produce a more uniform reduction of the magnitude of all coefficients. The consequence is that the shrinkage of the coefficients that should be zero is insufficient. At the same time, the reduction of the size of the coefficients that should be different from zero is too large. The method that assumes Student’s $t$ priors performs rather poorly in all the problems analyzed. The reason is that this method is often stuck in local and suboptimal optima of the type-II likelihood function. In the experiments, the model based on horseshoe priors performs much better than the models based on Laplace or Student’s $t$ priors. In terms of their capacity for selectively shrinking the posterior mean, the performance of models that assume horseshoe priors is comparable to LRMSSP with EP. However, the computational cost of Bayesian inference in the models that assume horseshoe priors, which is carried out using Gibbs sampling, is much larger than the cost of the proposed EP method. Horseshoe priors do not have a closed-form convolution with the Gaussian distribution. This makes the application of EP in models with these types of priors difficult.

A disadvantage of EP is that this method is not guaranteed to converge. In our implementation, different strategies have been used to improve the convergence of EP. In particular, the components of $\tilde{\mathbf {v}}_2$ in (16) are restricted to be positive in the optimization. An annealing process for the damping parameter $\epsilon$ is used to improve the convergence of EP. In all the experiments, the proposed EP method (SS-EP) generally converged in less than 20 iterations. However, in some specific cases, SS-EP might take more than 100 iterations to converge, especially when $\sigma _0$ and $p_0$ are very small and the amount of training data is very small. By contrast, the EP method for the model with Laplace priors (Seeger 2008) exhibits better convergence properties and does not seem to be affected by this drawback. Note that Hernández-Lobato and Hernández-Lobato (2011) describe an alternative implementation of EP in the LRMSSP that is guaranteed to converge. However, the computational cost of this method is much higher than the cost of the EP algorithm described here.

Finally, the proposed EP method could be easily extended to the probit regression setting. For this, we would introduce the vector of auxiliary variables $\mathbf {a}=(a_1,\ldots ,a_n)$, where $a_i = \mathbf {w}^\text {T} \mathbf {x}_i$. The likelihood for $y_i \in {-1,1}$ given $a_i$ is then $p(y_i|a_i)=\varPhi (y_ia_i)$, where $\varPhi$ is the standard Gaussian cumulative distribution function. The probability of $\mathbf {a}$ given $\mathbf {X}$ and $\mathbf {w}$ is then $p(\mathbf {a}|\mathbf {w},\mathbf {X})=\prod _{i=1}^n \delta (a_i - \mathbf {w}^\text {T} \mathbf {x}_i)$, where $\delta (\cdot )$ is a point mass at zero. EP would approximate the likelihood factors $p(y_i|a_i)$ with Gaussian factors as in the Gaussian process classification case (Rasmussen and Williams 2005). The factor $p(\mathbf {a}|\mathbf {w},\mathbf {X})$ can then be approximated in the same way as the likelihood factor $f_1(\mathbf {w},\mathbf {z})$ in the linear regression case.

Appendices

Appendix 1: Gibbs sampling in the LRMSSP

Approximate Bayesian inference in the LRMSSP has been traditionally implemented using Gibbs sampling. This method randomly samples $\mathbf {w}$ and $\mathbf {z}$ from (6). Expectations over the actual posterior are then approximated by expectations over the resulting samples. For the implementation of the Gibbs sampling method, we follow Lee et al. (2003) and sample $\mathbf {z}$ from its marginal distribution after integrating $\mathbf {w}$ out, which speeds up the computations. The central operation in Gibbs sampling is the evaluation of the conditional probability of the event $z_i = 1$ when all the other components of $\mathbf {z}$ stay fixed. This probability can be efficiently computed using the framework described by Tipping and Faul (2003).

First, we introduce some notation. Let $\mathbf {C}_\mathbf {z}$ be an $n \times n$ matrix such that $\mathbf {C}_\mathbf {z} = \sigma _0^2 \mathbf {I} + \mathbf {X} \mathbf {A}_\mathbf {z}^{-1} \mathbf {X}^\text {T}$, where $\mathbf {A}_\mathbf {z}$ is a $d \times d$ diagonal matrix whose $i$-th diagonal element $\alpha _i$ satisfies $\alpha _i = v_s^{-1}$ when $z_i = 1$ and $\alpha _i = \infty$, otherwise. The logarithm of the joint marginal probability of $\mathbf {z}$ and $\mathbf {y}$ is then

$$\begin{aligned} \log {\fancyscript{P}}(\mathbf {z},\mathbf {y}|\mathbf {X}) = -\frac{1}{2} \log |\mathbf {C}_\mathbf {z}| - \frac{1}{2} \mathbf {y}^\text {T} \mathbf {C}^{-1}_\mathbf {z} \mathbf {y} + s_\mathbf {z} \log p_0 + (d - s_\mathbf {z}) \log (1 - p_0) + \text {constant}\,, \end{aligned}$$

(50)

where $s_\mathbf {z}$ is the number of components of $\mathbf {z}$ that are equal to one. Let $\varvec{\varphi }_i$ denote the $i$-th column of $\mathbf {X}$ and let $\varvec{\varSigma }^{-1}_\mathbf {z} = \mathbf {A}_\mathbf {z} + \sigma _0^{-2} \mathbf {X}^\text {T} \mathbf {X}$. Following Tipping and Faul (2003), when $\mathbf {z}$ is updated by switching $z_i$ from one to zero, the corresponding decrement in (50) is

$$\begin{aligned} \log \sqrt{\frac{1}{1 + v_ss_i}} + \frac{q_i^2}{2(v_s^{-1} + s_{i})} + \log \frac{p_0}{1 - p_0}\,, \end{aligned}$$

(51)

where $q_i$ and $s_i$ are given by

$$\begin{aligned} q_i&= \frac{Q_i}{1 - v_sS_i} \,, \quad s_i = \frac{S_i}{1 - v_sS_i} \end{aligned}$$

(52)

and $Q_i$ and $S_i$ are computed using

$$\begin{aligned} Q_i&= \sigma _0^{-2} \varvec{\varphi }_i^\text {T} \mathbf {y} - \sigma _0^{-4} \varvec{\varphi }_i^\text {T} \mathbf {X} \varvec{\varSigma }_\mathbf {z} \mathbf {X}^\text {T} \mathbf {y}\,,\end{aligned}$$

(53)

$$\begin{aligned} S_i&= \sigma _0^{-2} \varvec{\varphi }_i^\text {T} \varvec{\varphi }_i - \sigma _0^{-4} \varvec{\varphi }_i^\text {T} \mathbf {X} \varvec{\varSigma }_\mathbf {z} \mathbf {X}^\text {T} \varvec{\varphi }_i\,, \end{aligned}$$

(54)

where $\mathbf {X}$ and $\varvec{\varSigma }_\mathbf {z}$ involve in (53) and (54) only the features whose corresponding components of $\mathbf {z}$ are one before the update. When $\mathbf {z}$ is updated by switching $z_i$ from zero to one, the resulting increment in (50) is also given by (51). However, $q_i$ and $s_i$ are now fixed as $q_i = Q_i$ and $s_i = S_i$, where $Q_i$ and $S_i$ are obtained using (53) and (54). This allows us to efficiently compute the conditional probability of $z_i$ as a function of $q_i$ and $s_i$ alone

$$\begin{aligned} {\fancyscript{P}}(z_i = 1 | \mathbf {z}_{\setminus i},\mathbf {y},\mathbf {X}) = p_0 \left[ p_0 + (1 - p_0) \exp \left\{ \frac{-q_i^2}{2(v_s^{-1} + s_i)} \right\} \sqrt{1 + v_ss_i}\right] ^{-1}\,, \end{aligned}$$

(55)

where $\mathbf {z}_{\setminus i}$ represents $z_1,\ldots ,z_d$ but with $z_i$ omitted and $q_i$ and $s_i$ are obtained using either the rule $q_i = Q_i$, $s_i = S_i$ or (52), depending on whether $z_i = 1$ is satisfied or not during the computation of $Q_i$ and $S_i$ by (53) and (54). Gibbs sampling generates a sample of $\mathbf {z}$ by randomly iterating through all the components of this vector and drawing a value for each component according to the probability given by (55). The bottleneck of this process is the computation of $\varvec{\varSigma }_\mathbf {z}$ in (53) and (54), which requires ${\fancyscript{O}}(s_\mathbf {z}^2n)$ operations when $s_\mathbf {z} < n$. Nevertheless, Gibbs sampling modifies $\varvec{\varSigma }_\mathbf {z}$ by adding or removing a single feature from this matrix at a time. This allows us to save unnecessary computations by storing $\mathbf {L}_\mathbf {z}$, the Cholesky decomposition of $\varvec{\varSigma }_\mathbf {z}^{-1}$; that is, $\varvec{\varSigma }_\mathbf {z}^{-1} = \mathbf {L}_\mathbf {z} \mathbf {L}_\mathbf {z}^\text {T}$ where $\mathbf {L}_\mathbf {z}$ is a lower triangular matrix. The cost of updating $\mathbf {L}_\mathbf {z}$ after switching on or off a single component of $\mathbf {z}$ is ${\fancyscript{O}}(s_\mathbf {z}^2)$ when efficient methods for modifying matrix factorizations are used (Gill et al. 1974). Once $\mathbf {L}_\mathbf {z}$ is available, we can compute $\varvec{\varSigma }_\mathbf {z}$ in only ${\fancyscript{O}}(s_\mathbf {z}^2)$ operations. After having generated a Gibbs sample for $\mathbf {z}$, we draw a sample of $\mathbf {w}$ conditioning to the current value of $\mathbf {z}$. For this, we set to zero the components of $\mathbf {w}$ whose corresponding $z_1,\ldots ,z_d$ are equal to zero. The other components of $\mathbf {w}$, represented by the $s_\mathbf {z}$-dimensional vector $\mathbf {w}_\mathbf {z}$, are sampled using

$$\begin{aligned} \mathbf {w}_\mathbf {z} = \sigma _0^{-2} \varvec{\varSigma }_\mathbf {z} \mathbf {X} \mathbf {y} + \mathbf {r}^\text {T} \mathbf {L}_\mathbf {z}'\,, \end{aligned}$$

(56)

where $\mathbf {X}$ and $\varvec{\varSigma }_\mathbf {z}$ involve in this formula only those features whose corresponding components of $\mathbf {z}$ are active, $\mathbf {r}$ is an $s_\mathbf {z}$-dimensional random vector whose components follow independent standard Gaussian distributions; that is, $\mathbf {r} \sim {\fancyscript{N}}(\mathbf {0},\mathbf {I})$ and $\mathbf {L}_\mathbf {z}'$ is the Cholesky decomposition of the matrix $\varvec{\varSigma }_\mathbf {z}$ used in this formula. The cost of generating a Gibbs sample of $\mathbf {w}$ is ${\fancyscript{O}}(s_\mathbf {z}^3)$. When $n < d$, the computational complexity of the method is determined by the operations involved in the sampling of $\mathbf {z}$. The expected value of $s_\mathbf {z}$ is $p_0 d$. Hence, generating a total of $k$ samples of $\mathbf {z}$ and $\mathbf {w}$ has a cost equal to ${\fancyscript{O}}(k p_0^2 d^3)$ and often $k \gg d$ for accurate inference.

1.1 Hyper-parameter learning

Learning the hyperparameters $p_0$, $\sigma _0^2$ and $v_s$ is straightforward. For this, we select non-informative conjugate priors and use Gibbs sampling for inference. For $p_0$, we choose the prior ${\fancyscript{P}}(p_0) = \text {Beta}(p_0|a_0,b_0)$, where $a_0 = k \hat{p}_0$, $b_0 = k(1 -\hat{p}_0)$, $\hat{p}_0$ is an initial guess of the true value of $p_0$, $k$ is a concentration parameter specifying the width of ${\fancyscript{P}}(p_0)$ around its mean and $\text {Beta}(\cdot |a_0,b_0)$ denotes a Beta distribution with parameters $a_0$ and $b_0$

$$\begin{aligned} \text {Beta}(x|a,b) = \frac{1}{\text {B}(a,b)}x^{a-1}(1-x)^{b-1}\,, \end{aligned}$$

(57)

where $\text {B}(a,b)$ is the Beta function. The conditional distribution for $p_0$ depends only on $\mathbf {z}$. In particular, we sample $p_0$ from ${\fancyscript{P}}(p_0|\mathbf {z}) =$Beta$(p_0| a_0 + s_\mathbf {z},b_0+d-s_\mathbf {z})$, where $s_\mathbf {z}$ is the number of components of $\mathbf {z}$ that take value one. For $\sigma _0^2$, we choose the prior ${\fancyscript{P}}(\sigma _0^2)=\text {IG}(\sigma _0^2|\alpha _0,\beta _0)$, $\alpha _0 = k/2$, $\beta _0 = k / 2 \hat{\sigma }_0^2$, $\hat{\sigma }_0^2$ is an initial guess for $\sigma _0^2$, $k$ is a concentration parameter specifying the width of ${\fancyscript{P}}(\sigma _0^2)$ around its mean and $\text {IG}(\cdot |\alpha _0,\beta _0)$ denotes an inverse Gamma distribution with parameters $\alpha _0$ and $\beta _0$

$$\begin{aligned} \text {IG}(x|\alpha _0,\beta _0) = \frac{\beta _0^{\alpha _0}}{\varGamma (\alpha _0)} x^{-\alpha _0-1}\exp \left\{ \frac{\beta _0}{x} \right\} \,, \end{aligned}$$

(58)

where $\varGamma$ is the Gamma function. The conditional distribution for $\sigma _0^2$ depends only on $\mathbf {w}$. In particular, we sample $\sigma _0^2$ from ${\fancyscript{P}}(\sigma _0^2|\mathbf {w}) = \text {IG}(\sigma _0^2|\alpha ,\beta )$, where $\alpha =\alpha _0 + n / 2$ and $\beta = 1/2 (\mathbf {y} - \mathbf {X} \mathbf {w})^\text {T} (\mathbf {y} - \mathbf {X} \mathbf {w}) + \beta _0$. For $v_s$, we choose the prior ${\fancyscript{P}}(v_s)=\text {IG}(\sigma _0^2|\alpha _0',\beta _0')$, where $\alpha _0' = k/2$, $\beta _0' = k / 2 \hat{v}_s$, $k$ is a concentration parameter and $\hat{v}_s$ is an initial guess for this hyperparameter. The conditional distribution for $v_s$ depends only on $\mathbf {w}$. In particular, we sample $v_s$ from ${\fancyscript{P}}(v_s|\mathbf {w}) = \text {IG}(v_s|\alpha ',\beta ')$, where $\alpha '=\alpha _0' + s_\mathbf {z} / 2$ and $\beta ' = \sum _{i=1}^d z_i w_i^2 + \beta _0$. Finally, we have to specify the value of $\hat{p}_0$, $\hat{\sigma }_0^2$, $\hat{v}_s$ and $k$. In our case, we have fixed $\hat{p}_0$, $\hat{\sigma }_0^2$ and $\hat{v}_s$ to be the values that maximize the approximation of the evidence returned by the EP method described in Sect. 4. The concentration parameter $k$ is fixed to a low positive integer ($k=3$). This leads to non-informative broad priors.

1.2 Parallel tempering

In the experiments with spike signals from Sect. 5.2, we found that the Gibbs sampling method described above is very often stuck in local and suboptimal modes of the posterior distribution. To avoid this, we use the method parallel tempering (Ferkinghoff-Borg 2002). This technique consists in running several chains in parallel at different temperatures. Chains at higher temperatures have flatter target distributions and are more likely to escape from local and suboptimal modes. Let $\gamma \in [0,1]$ be the inverse temperature parameter of a particular chain. Assuming the hyperparameters $\sigma _0$, $p_0$ and $v_s$ are known, each parallel chain draws samples from

$$\begin{aligned} {\fancyscript{P}}_\gamma (\mathbf {w},\mathbf {z}) \propto {\fancyscript{P}}(\mathbf {y}|\mathbf {w},\mathbf {X})^\gamma {\fancyscript{P}}(\mathbf {w}|\mathbf {z}) {\fancyscript{P}}(\mathbf {z})\,, \end{aligned}$$

(59)

where $\gamma$ determines the temperature of the chain and ${\fancyscript{P}}(\mathbf {y}|\mathbf {w},\mathbf {X})$, ${\fancyscript{P}}(\mathbf {w}|\mathbf {z})$ and ${\fancyscript{P}}(\mathbf {z})$ are given by (3), (4) and (5), respectively. When $\gamma = 1$, the chain generates samples from the original target distribution (6). For values of $\gamma$ lower than 1, the chain gives less weight to the likelihood ${\fancyscript{P}}(\mathbf {y}|\mathbf {w},\mathbf {X})$ and focuses more on the prior ${\fancyscript{P}}(\mathbf {w}|\mathbf {z}) {\fancyscript{P}}(\mathbf {z})$. When $\gamma = 0$, the chain generates samples from the prior. To sample from ${\fancyscript{P}}_\gamma (\mathbf {w},\mathbf {z})$, we simply run the Gibbs sampling method described above with the noise level $\sigma _0^2$ scaled by $\gamma ^{-1}$. That is, instead of using $\sigma _0^2$ as the variance parameter in the Gaussian likelihood ${\fancyscript{P}}(y_i|\mathbf {w},\mathbf {x}_i) = {\fancyscript{N}}(y_i|\mathbf {x}_i \mathbf {w},\sigma _0^2)$, we use $\sigma _0^2 / \gamma$. In the experiments with spike signals, we run a total of 30 chains in parallel for 5000 iterations with temperature parameter $\gamma _i$ for the $i$-th chain given by $\gamma _i = 0.8^{i-1}$, $i = 1,\ldots , 30$. At each iteration, we perform $30$ swap moves, where each of these moves attempts to exchange the states of chains $k$ and $k+1$ and $k$ is sampled uniformly from $\{1,\ldots ,29\}$. Each of these swap moves between chains $k$ and $k+1$ is accepted with probability $\alpha$ given by the Metropolis-Hastings rule

$$\begin{aligned} \alpha = \text {min}\left( 1, \exp \left\{ (\gamma _{k} - \gamma _{k+1}) (\log {\fancyscript{P}}(\mathbf {y}|\mathbf {w}_{k+1},\mathbf {X}) - \log {\fancyscript{P}}(\mathbf {y}|\mathbf {w}_{k},\mathbf {X})) \right\} \right) \,, \end{aligned}$$

(60)

where $\mathbf {w}_k$ and $\mathbf {w}_{k+1}$ are the current states of chains $k$ and $k+1$, respectively. When the move is accepted we generate a new state for all the chains. The new state for each chain is the state of the chain before the swap move was attempted, except for chains $k$ and $k+1$, which have now their previous states swapped. When the move is not accepted, we again generate a new state for all the chains. However, in this case, the new state for each chain is the state of the chain before the swap move was attempted. Finally, we use the samples generated by the first chain ($i= 1$) as samples drawn from the posterior distribution (6), ignoring the first 1000, which are used as burn-in.

Appendix 2: Gibbs sampling in the model with horseshoe prior

The horseshoe prior for $\mathbf {w}$ can be written as

$$\begin{aligned} {\fancyscript{P}}(\mathbf {w}) = \prod _{i=1}^d \int {\fancyscript{N}}(w_i|0,\tau ^2 \lambda _i^2) \text {C}^{+}(\lambda _i|0,1)\,d\lambda _i\,, \end{aligned}$$

where $\text {C}^{+}(\lambda _i|0,1) = 2 \pi ^{-1} (1 + \lambda _i^2)^{-1}$ is a positive Cauchy distribution (Carvalho et al. 2009). Given the likelihood function (3), we can easily compute the logarithm of the joint marginal density of the vector of latent variables $\varvec{\lambda }= (\lambda _1,\ldots ,\lambda _d)^\text {T}$ and the targets $\mathbf {y}$. The resulting formula is similar to (50) in Appendix , namely,

$$\begin{aligned} \log {\fancyscript{P}}(\varvec{\lambda },\mathbf {y}|\mathbf {X}) = -\frac{1}{2} \log |\mathbf {C}_{\varvec{\lambda }}| - \frac{1}{2} \mathbf {y}^\text {T} \mathbf {C}^{-1}_{\varvec{\lambda }} \mathbf {y} + \sum _{i=1}^d \log \text {C}^{+}(\lambda _i|0,1) + \text {constant}\,, \end{aligned}$$

(61)

where $\mathbf {C}_{ \varvec{\lambda }}$ is the $n \times n$ matrix given by $\mathbf {C}_{ \varvec{\lambda }} = \sigma _0^2 \mathbf {I} + \mathbf {X} \mathbf {A}_{\varvec{\lambda }}^{-1} \mathbf {X}^\text {T}$ and $\mathbf {A}_{ \varvec{\lambda }}$ is a $d \times d$ diagonal matrix whose $i$-th diagonal element is equal to $\tau ^{-2} \lambda _i^{-2}$. Following Tipping and Faul (2003) we can obtain the logarithm of the conditional density of $\lambda _i$ when $\mathbf {y}$, $\mathbf {X}$ and all the other components of $\varvec{\lambda }$ are hold fixed:

$$\begin{aligned} \log {\fancyscript{P}}(\lambda _i | \varvec{\lambda }_{-i}, \mathbf {y},\mathbf {X}) = l(\lambda _i) + \log \text {C}^{+}(\lambda _i|0,1) + \text {constant}\,, \end{aligned}$$

(62)

where $\varvec{\lambda }_{-i}$ represents the vector $(\lambda _1,\ldots ,\lambda _d)^\text {T}$ but with $\lambda _i$ omitted, the term $l(\lambda _i)$ is given by the expression

$$\begin{aligned} l(\lambda _i) = \frac{1}{2} \left[ -\log (1 + \lambda _i^2 \tau ^2 s_i) + \frac{q_i^2 \lambda _i^2 \tau ^2}{1 + \lambda _i^2 \tau ^2 s_i} \right] \end{aligned}$$

(63)

and we compute $q_i$ and $s_i$ in this case using

$$\begin{aligned} q_i = \varvec{\varphi }_i^\text {T} \mathbf {C}_{\varvec{\lambda }\setminus \lambda _i}^{-1} \mathbf {y} \quad&s_i&= \varvec{\varphi }_i^\text {T} \mathbf {C}_{\varvec{\lambda }\setminus \lambda _i}^{-1} \varvec{\varphi }_i\,, \end{aligned}$$

where $\varvec{\varphi }_i$ is the $i$-th column of $\mathbf {X}$ and $\mathbf {C}_{\varvec{\lambda }\setminus \lambda _i}$ is obtained by removing the contribution of $\varvec{\varphi }_i$ from $\mathbf {C}_{\varvec{\lambda }}$

$$\begin{aligned} \mathbf {C}_{\varvec{\lambda }\setminus \lambda _i} = \sigma _0^2 \mathbf {I} + \mathbf {X} \mathbf {A}_{\varvec{\lambda }\setminus \lambda _i}^{-1} \mathbf {X}^\text {T}, \end{aligned}$$

(64)

and $\mathbf {A}_{\varvec{\lambda }\setminus \lambda _i}^{-1}$ is equal to $\mathbf {A}_{\varvec{\lambda }}^{-1}$, but with the $i$-th diagonal element equal to zero. We generate a Gibbs sample of $\varvec{\lambda }$ by running randomly through all the components of this vector and generating a value for each $\lambda _i$ according to the density implied by (62). Sampling from such density can be performed using the method proposed by Damien et al. (1999). For this, we first sample an auxiliary latent variable $u$ such that $\exp (u) \sim U[0,\exp (l(\lambda _i))]$, where $l(\lambda _i)$ is given by (63) and second, we sample $\lambda _i$ from $\text {C}^{+}(\lambda _i|0,1)$, but restricted to the set $A_u = \{ \lambda _i : l(\lambda _i) > u \}$. The function $l(\lambda _i)$ has a single global maximum (Faul and Tippin 2001) which is equal to zero when $q_i^2 < s_i$ and to $(q_i^2 - s_i)^{1/2} (s_i^2 \tau ^2)^{-1/2}$ otherwise. Let $\lambda _i^\star$ be the global maximum of $l(\lambda _i)$. Then the set $A_u$ can be identified by finding roots of $l(\lambda _i) - u$ in the intervals $[0,\lambda _i^\star ]$ and $[\lambda _i^\star ,\infty ]$. The costliest operation in this process is the computation of $\mathbf {C}_{\varvec{\lambda }\setminus \lambda _i}^{-1}$ each time that a new $\lambda _i$ has to be sampled. To perform this operation efficiently, we store the Cholesky decompositions of $\mathbf {C}_{\varvec{\lambda }}$ and $\mathbf {C}_{\varvec{\lambda }}^{-1}$ and update these decompositions (Gill et al. 1974) with cost ${\fancyscript{O}}(n^2)$ after a rank-one update of $\mathbf {C}_{\varvec{\lambda }}$ since $\mathbf {C}_{\varvec{\lambda }\setminus \lambda _i} = \mathbf {C}_{\varvec{\lambda }} - \lambda _i^2 \tau ^2 \varvec{\varphi }_i \varvec{\varphi }_i^\text {T}$ and $\mathbf {C}_{\varvec{\lambda }} = \mathbf {C}_{\varvec{\lambda }\setminus \lambda _i} + \lambda _i^2 \tau ^2 \varvec{\varphi }_i \varvec{\varphi }_i^\text {T}$. To avoid numerical errors, the Cholesky decompositions are recomputed from scratch once we have generated ten new Gibbs samples of $\varvec{\lambda }$. Following Scott (2010), the Markov Chain for $\varvec{\lambda }$ is initialized to $\varvec{\lambda }_\text {start} = (1,\ldots ,1)^\text {T}$, a vector whose components are all equal to 1.

Conditioning to $\varvec{\lambda }$, we can sample $\mathbf {w}$ from a Gaussian distribution with covariance matrix $\varvec{\varSigma }_{\varvec{\lambda }} = (\mathbf {A}_{\varvec{\lambda }} + \sigma _0^{-2} \mathbf {X}^\text {T} \mathbf {X})^{-1}$ and mean vector $\sigma _0^{-2} \varvec{\varSigma }_{\varvec{\lambda }} \mathbf {X} \mathbf {y}$. When $d > n$ this can be performed with cost ${\fancyscript{O}}(n^2d)$ using the method described by Seeger (2008) in Appendix B.2. The total cost of Gibbs sampling in the model with horseshoe prior is ${\fancyscript{O}}(kn^2d)$, where $k$ is the number of samples to be generated from the posterior. Often $k \gg d$ for accurate inference.

1.1 Hyper-parameter learning

In this case, the model hyperparameters are $\sigma _0^2$ and $\tau ^2$. We select non-informative conjugate priors and use Gibbs sampling to learn the value of these hyperparameters. We sample $\sigma _0$ in the same way as in Appendix . To sample $\tau ^2$, we choose the prior ${\fancyscript{P}}(\tau ^2)=\text {IG}(\sigma _0^2|\alpha _0,\beta _0)$, where $\alpha _0 = k/2$, $\beta _0 = k / 2 \hat{\tau }^2$, $k$ is a concentration parameter specifying the width of ${\fancyscript{P}}(\tau )$ around its mean and $\hat{\tau }^2$ is an initial guess for $\tau ^2$. The conditional distribution for $\tau ^2$ depends only on $\mathbf {w}$ and $\varvec{\lambda }$. In particular, we sample $\tau ^2$ from ${\fancyscript{P}}(\tau ^2|\mathbf {w},\varvec{\lambda }) = \text {IG}(\tau ^2|\alpha ,\beta )$, where $\alpha =\alpha _0 + d / 2$ and $\beta = \sum _{i=1}^d w_i^2 / \lambda _i^2+ \beta _0$. Finally, we have to specify the values of $\hat{\tau }^2$ and $k$. Let $\hat{p}_0$ and $\hat{v}_s$ be the hyperparameters of the spike-and-slab prior that maximize the approximation of the evidence returned by the EP method from Sect. 4. We select $\hat{\tau }^2$ so that the horseshoe prior with hyperparameter $\hat{\tau }^2$ has the same distance between quantiles $0.05$ and $0.95$ as the spike-and-slab prior with hyperparameters $\hat{p}_0$ and $\hat{v}_s$. The concentration parameter $k$ is fixed to a low positive integer ($k=3$). This leads to a non-informative broad prior.

Appendix 3: Product and quotient rules

We describe the product and quotient rules for Gaussian and Bernoulli distributions, which are useful for the derivation of EP in the LRMSSP. Let ${\fancyscript{N}}(\mathbf {x}|\mathbf {m},\mathbf {V})$ be the density function of a $d$-dimensional Gaussian distribution with mean vector $\mathbf {m}$ and covariance matrix $\mathbf {V}$. The product of two Gaussian densities is another Gaussian density that is no longer normalized:

$$\begin{aligned} {\fancyscript{N}}(\mathbf {x}|\mathbf {m}_1,\mathbf {V}_1) {\fancyscript{N}}(\mathbf {x}|\mathbf {m}_2,\mathbf {V}_2) \propto {\fancyscript{N}}(\mathbf {x}|\mathbf {m}_3,\mathbf {V}_3)\,, \end{aligned}$$

(65)

where $\mathbf {V}_3 = (\mathbf {V}_1^{-1} + \mathbf {V}_2^{-1})^{-1}$, $\mathbf {m}_3 = \mathbf {V}_3(\mathbf {m}_1^\text {T}\mathbf {V}_1^{-1} + \mathbf {m}_2^\text {T}\mathbf {V}_2^{-1})$ and the normalization constant in the right part of (65) is

$$\begin{aligned} (2\pi )^{-d/2} \frac{|\mathbf {V}_3|^{1/2}}{|\mathbf {V}_1|^{1/2} |\mathbf {V}_2|^{1/2}} \exp \left\{ -\frac{1}{2} \left( \mathbf {m}_1^\text {T} \mathbf {V}_1^{-1} \mathbf {m}_1 + \mathbf {m}_2^\text {T} \mathbf {V}_2^{-1} \mathbf {m}_2 - \mathbf {m}_3^\text {T} \mathbf {V}_3^{-1} \mathbf {m}_3 \right) \right\} \,. \end{aligned}$$

(66)

Similarly, the quotient of two Gaussian densities is another Gaussian density, although no longer normalized:

$$\begin{aligned} \frac{{\fancyscript{N}}(\mathbf {x}|\mathbf {m}_1,\mathbf {V}_1)}{{\fancyscript{N}}(\mathbf {x}|\mathbf {m}_2,\mathbf {V}_2)} \propto {\fancyscript{N}}(\mathbf {x}|\mathbf {m}_3,\mathbf {V}_3) \,, \end{aligned}$$

(67)

where $\mathbf {V}_3 = (\mathbf {V}_1^{-1} - \mathbf {V}_2^{-1})^{-1}$, $\mathbf {m}_3=\mathbf {V}^{-3}(\mathbf {m}_1^\text {T}\mathbf {V}_1^{-1} - \mathbf {m}_2^\text {T}\mathbf {V}_2^{-1})$ and the normalization constant in the right part of (67) is in this case

$$\begin{aligned} (2\pi )^{d/2} \frac{|\mathbf {V}_3|^{1/2}|\mathbf {V}_2|^{1/2}}{|\mathbf {V}_1|^{1/2}} \exp \left\{ -\frac{1}{2} \left( \mathbf {m}_1^\text {T} \mathbf {V}_1^{-1} \mathbf {m}_1 - \mathbf {m}_2^\text {T} \mathbf {V}_2^{-1} \mathbf {m}_2 - \mathbf {m}_3^\text {T} \mathbf {V}_3^{-1} \mathbf {m}_3 \right) \right\} \,. \end{aligned}$$

(68)

Let $\text {Bern}(x|\sigma (p)) = x\sigma (p) + (1 - x)(1 - \sigma (p))$ be a Bernoulli distribution, where $x\in \{0,1\}$, $p$ is a real parameter, $\sigma$ is the logistic function (14) and $\sigma (p)$ represents the probability of $x = 1$. The product of two Bernoulli distributions is another Bernoulli distribution, but no longer normalized:

$$\begin{aligned} \text {Bern}(x|\sigma (p_1)) \text {Bern}(x|\sigma (p_2)) \propto \text {Bern}(x|\sigma (p_3))\,, \end{aligned}$$

(69)

where $p_3 = p_1 + p_2$ and the normalization constant in the right part of (69) is $\sigma (p_1)\sigma (p_2) + \sigma (-p_1)\sigma (-p_2)$. The quotient of two Bernoulli distributions is also a Bernoulli distribution which is no longer normalized:

$$\begin{aligned} \frac{\text {Bern}(x|\sigma (p_1))}{\text {Bern}(x|\sigma (p_2))} \propto \text {Bern}(x|\sigma (p_3))\,, \end{aligned}$$

(70)

where $p_3 = p_1 - p_2$ and the normalization constant in the right part of (70) is computed as $\sigma (p_1)/\sigma (p_2) + \sigma (-p_1)/\sigma (-p_2)$.

Appendix 4: Derivation of the EP update operations

In this appendix, we describe the EP update operations for minimizing $\text {D}_{\text {KL}}(f_iQ^{\setminus i} \Vert \tilde{f}_iQ^{\setminus i})$ with respect to $\tilde{f}_i$ for the cases $i = 1, 2$. The update of $\tilde{f}_3$ is not discussed here because it is trivial. To refine $\tilde{f}_1$ and $\tilde{f}_2$ we follow two steps. First, $Q$ is updated so that $\text {KL}(f_i Q^{\setminus i}\Vert Q)$ is minimized and second, $\tilde{f}_i$ is fixed to the ratio between $Q$ and $Q^{\setminus i }$, where $i = 1, 2$. These operations are performed using the normalized versions of $Q$ and $Q^{\setminus i}$: ${\fancyscript{Q}}$ and ${\fancyscript{Q}}^{\setminus i}$, respectively.

1.1 The first approximate factor

To minimize $\text {D}_{\text {KL}}(f_1Q^{\setminus 1} \Vert Q)$, we first compute ${\fancyscript{Q}}^{\setminus 1}$, which has the same functional form as ${\fancyscript{Q}}$ because all the $\tilde{f}_i$ belong to the same family of exponential distributions. The parameters of ${\fancyscript{Q}}^{\setminus 1}$ are obtained from the ratio between $Q$ and $\tilde{f}_1$ (see Appendix ):

$$\begin{aligned} {\fancyscript{Q}}^{\setminus 1}(\mathbf {w},\mathbf {z}) = \prod _{i=1}^d {\fancyscript{N}}(w_i|\tilde{m}_{2i},\tilde{v}_{2i}) \text {Bern}(z_i|\sigma (\tilde{p}_{2i} + \tilde{p}_{3i}))\,. \end{aligned}$$

(71)

The KL divergence is minimized when ${\fancyscript{Q}}$ is modified so that the first and second marginal moments of $\mathbf {w}$ and the first marginal moments of $\mathbf {z}$ are the same under ${\fancyscript{Q}}$ and under $f_1{\fancyscript{Q}}^{\setminus 1}Z^{-1}_1$, where $Z_1$ is the normalization constant of $f_1{\fancyscript{Q}}^{\setminus 1}$. Therefore, the update rule for ${\fancyscript{Q}}$ is given by

$$\begin{aligned} \mathbf {m}^\text {new}&= \mathbb {E}[ \mathbf {w} ]\,,&\mathbf {v}^\text {new}&= \text {diag}(\mathbb {E}[ \mathbf {w} \mathbf {w}^\text {T}] - \mathbb {E}[ \mathbf {w}]\mathbb {E}[ \mathbf {w} ]^\text {T}])\,,&\mathbf {p}^\text {new}&= \sigma ^{-1}(\mathbb {E}[\mathbf {z}])\,, \end{aligned}$$

(72)

where $\text {diag}(\cdot )$ extracts the diagonal of a square matrix, all the expectations are taken with respect to $f_1{\fancyscript{Q}}^{\setminus 1}Z_1^{-1}$ and $\sigma ^{-1}((x_1,\ldots ,x_d)^\text {T}) = (\sigma ^{-1}(x_1),\ldots ,\sigma ^{-1}(x_d))^\text {T}$ where $\sigma ^{-1}$ is the logit function (24). Computing the expectation of $\mathbf {z}$ under $f_1{\fancyscript{Q}}^{\setminus 1}Z^{-1}_1$ is trivial. To compute the first and second moments of $\mathbf {w}$, we note that the likelihood factor $f_1$ has a Gaussian form on $\mathbf {w}$ which is characterized by a precision matrix $\varvec{\Lambda }_ 1$ and a mean vector $\mathbf {m}_1$ such that $\varvec{\Lambda }_1 = \sigma _0^{-2}\mathbf {X}^\text {T}\mathbf {X}$ and $\varvec{\Lambda }_1 \mathbf {m}_1 = \sigma _0^{-2} \mathbf {X}^\text {T} \mathbf {y}$. Because ${\fancyscript{Q}}^{\setminus 1}$ is also Gaussian in $\mathbf {w}$, we can use the product rule for Gaussian distributions (see Appendix ) to obtain the moments of $\mathbf {w}$ with respect to $f_1{\fancyscript{Q}}^{\setminus 1}Z^{-1}_1$. The final update operation for ${\fancyscript{Q}}$ is given by (30), (31) and (32) and the logarithm of the normalization constant of $f_1{\fancyscript{Q}}^{\setminus 1}$ is obtained as

$$\begin{aligned} \log Z_1 = \,&-\frac{n}{2}\log (2 \pi \sigma _0^2) - \frac{1}{2} \log |\mathbf {I} + \sigma _0^{-2} \tilde{\mathbf {V}}_2 \mathbf {X}^\text {T} \mathbf {X}| + \frac{1}{2} \mathbf {m}^\text {T} (\tilde{\mathbf {V}}_2^{-1} \tilde{\mathbf {m}}_2 + \sigma ^{-2}_0 \mathbf {X}^\text {T} \mathbf {y}) \nonumber \\&- \frac{1}{2} \tilde{\mathbf {m}}_2^\text {T} \tilde{\mathbf {V}}_2^{-1} \tilde{\mathbf {m}}_2 - \frac{1}{2} \sigma _0^{-2} \mathbf {y}^\text {T} \mathbf {y} \,, \end{aligned}$$

(73)

where $\mathbf {m}$ is the expectation of $\mathbf {w}$ under ${\fancyscript{Q}}$ after the update of this distribution and $\tilde{\mathbf {V}}_2$ is a $d \times d$ diagonal matrix such that $\text {diag}(\tilde{\mathbf {V}}_2)=\tilde{\mathbf {v}}_2$. Once ${\fancyscript{Q}}$ has been refined, the update rule for $\tilde{f}_1$ is computed as the ratio between ${\fancyscript{Q}}$ and ${\fancyscript{Q}}^{\setminus 1}$, see (35) and (36). Finally, the positive constant $\tilde{s}_1$ in (15) is fixed so that condition

$$\begin{aligned} \tilde{f}_1(\mathbf {w},\mathbf {z}) = Z_1 \frac{{\fancyscript{Q}}(\mathbf {w},\mathbf {z})}{{\fancyscript{Q}}^{\setminus 1}(\mathbf {w},\mathbf {z})} \end{aligned}$$

(74)

is satisfied. This equality is translated into equation (38) for the value of $\log \tilde{s}_1$.

1.2 The second approximate factor

To minimize $\text {D}_{\text {KL}}(f_2Q^{\setminus 2} \Vert Q)$, we first compute ${\fancyscript{Q}}^{\setminus 2}$, whose parameters are obtained from the ratio between $Q$ and $\tilde{f}_2$:

$$\begin{aligned} {\fancyscript{Q}}^{\setminus 2}(\mathbf {w},\mathbf {z}) = \prod _{i=1}^d {\fancyscript{N}}(w_i|\tilde{m}_{1i},\tilde{v}_{1i}) \text {Bern}(z_i|\sigma (\tilde{p}_{3i}))\,. \end{aligned}$$

(75)

The divergence is minimized when ${\fancyscript{Q}}$ is updated so that the marginal moments of $\mathbf {w}$ (first and second moment) and $\mathbf {z}$ (first moment) are the same under ${\fancyscript{Q}}$ and under $f_2{\fancyscript{Q}}^{\setminus 2}Z^{-1}_2$, where $Z_2$ is the normalization constant of $f_2{\fancyscript{Q}}^{\setminus 2}$. Hence, the update rule for the parameters of ${\fancyscript{Q}}$ is given by

$$\begin{aligned} m_i^\text {new}&= \mathbb {E}[w_i]\,,&v_i^\text {new}&= \mathbb {E}[w_i^2] - \mathbb {E}[w_i]^2\,,&p_i^\text {new}&= \sigma ^{-1}(\mathbb {E}[z_i])\,, \end{aligned}$$

(76)

where all the expectations are taken with respect to $f_2{\fancyscript{Q}}^{\setminus 2}Z_2^{-1}$. Because $f_2{\fancyscript{Q}}^{\setminus 2}$ can be factorized in the components of $\mathbf {w}$ and $\mathbf {z}$, $Z_2$ is given by $Z_2 = \prod _{i=1}^d n_i$, the product of the normalization constants of the resulting factors, where

$$\begin{aligned} n_i = \sigma (\tilde{p}_{3i}){\fancyscript{N}}(0|\tilde{m}_{1i},\tilde{v}_{1i} + v_s) + \sigma (-\tilde{p}_{3i}) {\fancyscript{N}}(0|\tilde{m}_{1i},\tilde{v}_{1i}) \end{aligned}$$

(77)

and we have used the property $1 - \sigma (x) = \sigma (-x)$ for any $x \in \mathbb {R}$ of the logistic function. Given $n_i$, we calculate the mean and variance of $w_i$ under $f_2{\fancyscript{Q}}^{\setminus 2}Z^{-1}_2$ very easily. For this, we need only the partial derivatives of $\log n_i$ with respect to $\tilde{m}_{1i}$ and $\tilde{v}_{1i}$ as indicated by formulas (3.18) and (3.19) in the thesis of Minka (2001). Furthermore, the expectation of $z_i$ under $f_2{\fancyscript{Q}}^{\setminus 2}Z^{-1}_2$ is also computed in a straightforward manner. Consequently, we obtain

$$\begin{aligned} \mathbb {E}[w_i]&= \tilde{m}_{1i} + \tilde{v}_{1i} \frac{\partial \log n_i }{\partial \tilde{m}_{1i}}\,,\end{aligned}$$

(78)

$$\begin{aligned} \mathbb {E}[w_i^2] - \mathbb {E}[w_i]^2&= \tilde{v}_{1i} - \tilde{v}_{1i}^2 \left[ \left( \frac{\partial \log n_i}{\partial \tilde{m}_{1i}} \right) ^2 - 2 \frac{\partial \log n_i}{ \partial \tilde{v}_{1i} } \right] \,,\end{aligned}$$

(79)

$$\begin{aligned} \mathbb {E}[z_i]&= \sigma (\tilde{p}_{3i}){\fancyscript{N}}(0|\tilde{m}_{1i},\tilde{v}_{1i} + v_s) n_i^{-1}\,. \end{aligned}$$

(80)

Once ${\fancyscript{Q}}$ has been refined, we obtain the update for $\tilde{f}_2$ by computing the ratio between ${\fancyscript{Q}}$ and ${\fancyscript{Q}}^{\setminus 2}$ (see Appendix ):

$$\begin{aligned} \tilde{v}_{2i}^\text {new}&= \left[ \left( v_i^\text {new}\right) ^{-1} - \tilde{v}_{1i}^{-1}\right] ^{-1}\,,\end{aligned}$$

(81)

$$\begin{aligned} \tilde{m}_{2i}^\text {new}&= \tilde{v}_{2i}^\text {new} \left[ m_i^\text {new} \left( v_i^\text {new}\right) ^{-1} - \tilde{m}_{1i} \tilde{v}_{1i}^{-1}\right] ^{-1}\,,\end{aligned}$$

(82)

$$\begin{aligned} \tilde{p}_{2i}^\text {new}&= p_i^\text {new} - \tilde{p}_{3i}\,, \end{aligned}$$

(83)

After some arithmetic simplifications, these formulas are translated into (25), (26) and (27). Finally, the positive constant $\tilde{s}_2$ in (16) is fixed so that condition

$$\begin{aligned} \tilde{f}_2(\mathbf {w},\mathbf {z}) = Z_2 \frac{{\fancyscript{Q}}(\mathbf {w},\mathbf {z})}{{\fancyscript{Q}}^{\setminus 2}(\mathbf {w},\mathbf {z})} \end{aligned}$$

(84)

is satisfied. This equality is translated into equation (39) for the value of $\log \tilde{s}_2$.

Appendix 5: Constrained minimization of the KL divergence

When $\text {D}_{\text {KL}}(f_2Q^{\setminus 2} \Vert \tilde{f}_2Q^{\setminus 2})$ is minimized with respect to $\tilde{m}_{2i}$, $\tilde{v}_{2i}$ and $\tilde{p}_{2i}$, the optimal value for $\tilde{v}_{2i}$ can be negative. To avoid this situation, we minimize the divergence subject to constraint $\tilde{v}_{2i} \ge 0$. Two different scenarios are possible. In the first one, the optimal unconstrained value for $\tilde{v}_{2i}$ is zero or positive and condition $(a_i^2 - b_i)^{-1} \ge \tilde{v}_{1i}$ is satisfied, where $a_i$ and $b_i$ are given by (28) and (29). The update rules for $\tilde{m}_{2i}$, $\tilde{v}_{2i}$ and $\tilde{p}_{2i}$ are in this case the same as in the unconstrained setting (25), (26) and (27). In the second scenario, the optimal unconstrained value for $\tilde{v}_{2i}$ is negative and condition $(a_i^2 - b_i)^{-1} < \tilde{v}_{1i}$ is satisfied. In this case, the original update operation for $\tilde{v}_{2i}$ needs to be modified. Recall that $\text {D}_{\text {KL}}(f_2Q^{\setminus 2} \Vert \tilde{f}_2Q^{\setminus 2})$ is convex in the natural parameters $\eta _i = \tilde{m}_{2i} \tilde{v}_{2i}^{-1}$ and $\nu _i = \tilde{v}_{2i}^{-1}$. Under this reparameterization, constraint $\tilde{v}_{2i} \ge 0$ is translated into constraint $\nu _i \ge 0$. The optimal constrained value for $\nu _i$ must then lay on the border $\nu _i = 0$ because the optimal unconstrained value for $\nu _i$ is negative in this second scenario and the target function is convex. The update rule for $\tilde{v}_{2i}$ is thus given by $\tilde{v}_{2i} = \infty$. Additionally, the update rule for $\tilde{p}_{2i}$ is still given by (27) because the optimal value for $\tilde{p}_{2i}$ does not depend on $\tilde{m}_{2i}$ or $\tilde{v}_{2i}$. Finally, the optimal value for $\tilde{m}_{2i}$ in the second scenario is again given by (26) since this formula yields the minimizer of $\text {D}_{\text {KL}}(t_2Q^{\setminus 2} \Vert \tilde{t}_2Q^{\setminus 2})$ with respect to $\tilde{m}_{2i}$ when conditioning to the value selected for $\tilde{v}_{2i}$.

Appendix 6: SS-EPF: an EP method with computational cost ${\fancyscript{O}}(nd)$

We describe an implementation of EP for the linear regression model with spike-and-slab priors which has computational cost ${\fancyscript{O}}(nd)$ (Hernández-Lobato et al. 2008). This method has lower computational complexity than the method described in Sect. 4 because it does not directly take into account possible correlations in the posterior distribution. The main difference is that the exact likelihood factor $f_1(\mathbf {w},\mathbf {z}) = \prod _{i=1}^n {\fancyscript{P}}(y_i|\mathbf {w}, \mathbf {x}_i)$ is now decomposed into $n$ factors $f_{1,1},\ldots ,f_{1,n}$ (one per data point) where

$$\begin{aligned} f_{1,i}(\mathbf {w},\mathbf {z}) = {\fancyscript{P}}(y_i|\mathbf {w}, \mathbf {x}_i) = {\fancyscript{N}}(y_i|\mathbf {w}^\text {T} \mathbf {x}_i, \sigma _0^2)\,,\quad i = 1,\ldots ,n\,, \end{aligned}$$

(85)

and each of these $n$ exact factors is then approximated by a different approximate factor $\tilde{f}_{1,i}$ with $i=1,\ldots ,n$. The parametric form of each $\tilde{f}_{1,i}$ is the same as the form of the approximation for the likelihood used in the EP algorithm from Sect. 4 (15). In particular,

$$\begin{aligned} \tilde{f}_{1,i}(\mathbf {w},\mathbf {z}) = \tilde{s}_{1,i} \prod _{j=1}^d \text {exp} \left\{ -\frac{(w_j - \tilde{m}_{1,i,j})^2}{2\tilde{v}_{1,i,j}}\right\} \,,\quad i = 1,\ldots ,n\,, \end{aligned}$$

(86)

where $\left\{ \tilde{\mathbf {m}}_{1,i} = (\tilde{m}_{1,i,1},\ldots ,\tilde{m}_{1,i,d})^\text {T}, \tilde{\mathbf {v}}_{1,i} = (\tilde{v}_{1,i,1},\ldots ,\tilde{v}_{1,i,d})^\text {T}, \tilde{s}_{1,i} \right\} _{i=1}^n$ are free parameters to be determined by EP. The remaining exact factors $f_{2}(\mathbf {w},\mathbf {z}) = {\fancyscript{P}}(\mathbf {w}|\mathbf {z})$ and $f_{3}(\mathbf {w},\mathbf {z}) = {\fancyscript{P}}(\mathbf {z})$ are still approximated by (16) and (17), respectively. The update operations for these two latter approximate factors are the same as the ones described in Sect. 4.2 with the exception that, whenever we need access to the parameters $\tilde{m}_{1,i}$ and $\tilde{v}_{1,i}$ of (15), we now use (18) and (19) to obtain

$$\begin{aligned} \tilde{v}_{1,i}&= \left[ v_i^{-1} - \tilde{v}_{2,i}^{-1} \right] ^{-1}\,,\end{aligned}$$

(87)

$$\begin{aligned} \tilde{m}_{1,i}&= \left[ m_i v_i^{-1} - \tilde{m}_{2,i}\tilde{v}_{2,i}^{-1} \right] \tilde{v}_{1,i}\,, \end{aligned}$$

(88)

where $m_i$ and $v_i$ are mean and variance parameters of the EP posterior approximation (13), which in this case is equal to the normalized product of all the approximate factors $\tilde{f}_{1,1},\ldots ,\tilde{f}_{1,n}$, $\tilde{f}_{2}$ and $\tilde{f}_{3}$, and $\tilde{m}_{2,i}$ and $\tilde{v}_{2,i}$ are mean and variance parameters of the second approximate factor (16). We now describe how to refine the parameters of the new approximate factors $\tilde{f}_{1,1},\ldots ,\tilde{f}_{1,n}$. For the sake of clarity, we include only the update rules without damping. Incorporating the effect of damping in these operations is straightforward. Let

$$\begin{aligned} v_j^{\setminus i}&= \left[ v_j^{-1} - \tilde{v}_{1,i,j}^{-1} \right] ^{-1}\,,\end{aligned}$$

(89)

$$\begin{aligned} m_j^{\setminus i}&= \left[ m_j v_j^{-1} - \tilde{m}_{1,i,j}\tilde{v}_{1,i,j}^{-1} \right] \tilde{v}_j^{\setminus i }\,, \end{aligned}$$

(90)

denote the mean and variance parameters for the $j$-th entry of $\mathbf {w}$ given by the product of all the approximate factors except $\tilde{f}_{1,i}$. Then, the update for the parameters of $\tilde{f}_{1,i}$ is given by

$$\begin{aligned} \tilde{v}_{1,i,j}^\text {new}&= -\beta ^{-1}_{i,j} - v_j^{\setminus i}\,,&\tilde{m}_{1,i,j}^\text {new}&= \frac{\alpha _{i,j} - m_j^{\setminus i} \beta _{i,j}}{1 + \beta _{i,j} v_j^{\setminus i}} \tilde{v}_{1,i,j}^\text {new}\,, \end{aligned}$$

(91)

where $\alpha _{i,j}$ and $\beta _{i,j}$ are defined as

$$\begin{aligned} \alpha _{i,j}&= x_{i,j} \frac{y_i - \sum _{j=1}^d x_{i,j} m_j^{\setminus i}}{ \sigma _0^2 + \sum _{j=1}^d x_{i,j}^2 v_j^{\setminus i} } \,,&\beta _{i,j}&= -\frac{x_{i,j}^2}{\sigma _0^2 + \sum _{j=1}^d x_{i,j}^2 v_j^{\setminus i} }\,, \end{aligned}$$

(92)

for $j = 1,\ldots ,d$. Once we have refined $\tilde{f}_{1,i}$, we update the parameters of the posterior approximation (13) using

$$\begin{aligned} v_j&= \left[ [v_j^{\setminus i}]^{-1} + [\tilde{v}_{1,i,j}^\text {new}]^{-1} \right] ^{-1}\,,\end{aligned}$$

(93)

$$\begin{aligned} m_j&= \left[ m_j^{\setminus i}[v_j^{\setminus i}]^{-1} + \tilde{m}_{1,i,j}^\text {new}[\tilde{v}_{1,i,j}^\text {new}]^{-1} \right] v_j \,. \end{aligned}$$

(94)

Finally, after the EP method has converged, we compute

$$\begin{aligned} \log \tilde{s}_{1,i}&= -\frac{1}{2}\log \left[ 2 \pi + \sum _{j=1}^d x_{i,j}^2 v_j^{\setminus i} + \sigma _0^2 \right] - \frac{1}{2} \left[ \frac{\left( y_i - \sum _{j=1}^d x_{i,j} m_j^{\setminus i} \right) ^2}{ \sum _{j=1}^d x_{i,j}^2 v_j^{\setminus i} + \sigma _0^2 } \right] \nonumber \\&\quad +\frac{1}{2}\sum _{j=1}^d \left\{ \log \left[ 1 + \tilde{v}_{1,i,j}^{-1} v_j^{\setminus i } \right] + [m_j^{\setminus i}]^2 [v_j^{\setminus i }]^{-1} + \tilde{m}_{1,i,j}^2\tilde{v}_{1,i,j}^{-1} - m_i^2 v_i^{-1} \right\} \end{aligned}$$

(95)

and approximate the normalization constant ${\fancyscript{P}}(\mathbf {y}|\mathbf {X})$ as

$$\begin{aligned} {\fancyscript{P}}(\mathbf {y}|\mathbf {X})&\approx \sum _{i=1}^n \log \tilde{s}_{1,i} + \log \tilde{s}_2 + \log \tilde{s}_3 \nonumber \\&\quad +\frac{d}{2} \log (2 \pi ) + \sum _{j=1}^d \frac{1}{2} \left\{ \log v_j + m_j^2v_j^{-1} - \sum _{i=1}^n\tilde{m}_{1,i,j}^2\tilde{v}_{1,i,j}^{-1} - \tilde{m}_{2,j}^2\tilde{v}_{2,j}^{-1} \right\} \nonumber \\&\quad \times \sum _{i=1}^d \log \left\{ \sigma (\tilde{p}_{2i}) \sigma (\tilde{p}_{3i}) + \sigma (-\tilde{p}_{2i}) \sigma (-\tilde{p}_{3i}) \right\} \,. \end{aligned}$$

(96)

Computing the sums $\sum _{j=1}^d x_{i,j} m_j^{\setminus i}$ and $\sum _{j=1}^d x_{i,j}^2 v_j^{\setminus i}$ in (92) has cost ${\fancyscript{O}}(d)$. We have to do this for each of the $n$ approximate factors $\tilde{f}_{1,1},\ldots ,\tilde{f}_{1,n}$. Therefore, the computational cost of this EP algorithm is ${\fancyscript{O}}(nd)$.

The main difference between this alternative EP method and the EP method described in Sect. 4 is that the method from Sect. 4 processes the factor for the likelihood in a single EP update operation. This factor is the only one that introduces correlations in the posterior distribution. Because the method from Sect. 4 refines that factor in a single step, it is able to successfully take into account those correlations when it approximates the posterior distribution. By contrast, the EP method described above splits the likelihood factor $\prod _{i=1}^n {\fancyscript{P}}(y_i|\mathbf {w}, \mathbf {x}_i)$ into $n$ individual factors ${\fancyscript{N}}(y_i|\mathbf {w}^\text {T} \mathbf {x}_i, \sigma _0^2)$, $i = 1,\ldots ,n$, which are individually processed by EP. This makes this method loose track of the correlations induced by the original likelihood.

Appendix 7: Annealed version of SS-VB

In the experiments with spike signals from Sect. 5.2, we found that the standard version of SS-VB is very often stuck in local and suboptimal modes of the posterior distribution. To improve the results of this technique in this dataset, we used an annealed version of SS-VB. In the other datasets, this annealed version did not produce improvements with respect to the original method and consequently, we kept using the original method in those cases.

The annealed version of SS-VB attempts to match a sequence of posterior distributions at different temperatures, starting at high temperatures and then cooling down until the target distribution has the same temperature as the original posterior distribution (6). In this process, the solution to each optimization problem is then used as the initialization to the next optimization problem at a lower temperature. Let $\gamma \in [0,1]$ be the current inverse temperature parameter. Then the new version of SS-VB attempts to match the posterior distribution (6) with the noise level $\sigma _0^2$ scaled by $\gamma ^{-1}$. That is, instead of using $\sigma _0^2$ as the variance parameter in the Gaussian likelihood ${\fancyscript{P}}(y_i|\mathbf {w},\mathbf {x}_i) = {\fancyscript{N}}(y_i|\mathbf {x}_i \mathbf {w},\sigma _0^2)$, we use $\sigma _0^2 / \gamma$. When $\gamma = 1$, we try to match the original posterior distribution (6). For values of $\gamma$ lower than 1, we give less weight to the likelihood ${\fancyscript{P}}(\mathbf {y}|\mathbf {w},\mathbf {X})$ and focus more on the prior ${\fancyscript{P}}(\mathbf {w}|\mathbf {z}) {\fancyscript{P}}(\mathbf {z})$. When $\gamma = 0$, we try to match only the prior. The annealed version of SS-VB solves a total of 30 different optimization problems, with temperature parameter $\gamma _i$ for the $i$-th problem given by $\gamma _i = 0.8^{30-i}$, $i = 1,\ldots , 30$, where the solution to the problem $i$ is used as the initialization to the problem $i+1$. The final output of the annealed version of SS-VB is the solution to the problem $i=30$.

Appendix 8: A linear model for the reconstruction of transcription networks

The LRMSSP can be a useful method for the reconstruction of genetic regulatory networks from gene expression data. Transcription control networks are a specific class of interaction networks in which each node corresponds to a different gene and each connection represents an interaction between two genes at the transcription level (Alon 2006). Specifically, the directed edge $Z\rightarrow Y$ encodes the information that the protein expressed by gene $Z$ has a direct effect on the transcription rate of gene $Y$. Michaelis-Menten interaction kinetics and the Hill equation can be used to characterize this network edge as a differential equation (Alon 2006). Assuming that $Z$ is a transcriptional activator, the equation that describes the regulation kinetics is

$$\begin{aligned} \frac{d \left[ Y\right] }{dt}&= \frac{ V_m \left[ Z \right] ^\alpha }{ \left[ Z \right] ^\alpha + K_A } - \delta \left[ Y\right] . \end{aligned}$$

(97)

When $Z$ is a transcriptional repressor, the evolution of $\left[ Y\right]$ is described by

$$\begin{aligned} \frac{d \left[ Y\right] }{dt}&= \frac{ V_m K_R }{K_R + \left[ Z \right] ^\beta } - \delta \left[ Y\right] \,. \end{aligned}$$

(98)

In these equations, $K_A$ and $K_R$ are activation and repression thresholds, respectively, $\alpha$ and $\beta$ are the Hill coefficients for cooperative binding, $V_m$ is the maximum rate of synthesis, $\left[ \cdot \right]$ stands for ’concentration of mRNA’ and $\delta$ is the rate of degradation of mRNA. The concentration of mRNA $\left[ Z \right]$ is assumed to be a measure of the activity of the protein product of gene $Z$. When the system achieves a steady-state, and assuming that, in this state, the concentrations of mRNA are far from saturation, the relation between the logarithm of the mRNA concentration of $Y$ and the logarithm of the mRNA concentrations of $Z_1,\ldots ,Z_k$ (the parents of $Y$ in the network) is approximately linear (Gardner and Faith 2005)

$$\begin{aligned} \log \left[ Y\right] \approx \sum _{i=1}^k w_i \log \left[ Z_i \right] + \text {constant}\,. \end{aligned}$$

(99)

In this derivation, both activation and repression are assumed to be possible simultaneously. When $Y$ is a self-regulating gene, $\log \left[ Y\right]$ is included in the right part of (99) with associated coefficient $w_{k+1}$. This autoregulatory term can be eliminated by replacing $w_i' = w_i / (1 - w_{k+1})$ for $w_i$, where $i = 1,\ldots ,k$, and setting $w_{k+1}' = 0$. This model can be readily extended to describe the kinetics of all the transcripts present in a biological system. This leads us to the multiple gene model shown in equation (45).

Appendix 9: Normalized approximate factors and posterior approximation

The approximate factors shown in equations (15), (16) and (17) and the approximation $Q$ defined in the right-hand side of equation (9) may not be normalized. This means that when we marginalize out their variables by summing or integrating them out, the result may not be 1. The normalized factors are given by the following expressions:

$$\begin{aligned} \tilde{f}_1^\text {norm}(\mathbf {w},\mathbf {z})&= \prod _{i=1}^d {\fancyscript{N}}(w_i|\tilde{m}_{1i},\tilde{v}_{1i})\,,\end{aligned}$$

(100)

$$\begin{aligned} \tilde{f}_2^\text {norm}(\mathbf {w},\mathbf {z})&= \left[ \prod _{i=1}^d {\fancyscript{N}}(w_i|\tilde{m}_{1i},\tilde{v}_{1i}) \right] \left[ \prod _{i=1}^d \text {Bern}(z_i|\sigma (\tilde{p}_{2i})) \right] \,,\end{aligned}$$

(101)

$$\begin{aligned} \tilde{f}_3^\text {norm}(\mathbf {w},\mathbf {z})&= \prod _{i=1}^d \text {Bern}(z_i|\sigma (\tilde{p}_{3i}))\,. \end{aligned}$$

(102)

Note that the parameters (means, variances and activation probabilities) of these normalized factors and the un-normalized ones shown in (15), (16) and (17) are the same. The normalized $Q$ is given in (13).