Three-Dimensional Structural Geological Modeling Using Graph Neural Networks

Abstract

Three-dimensional structural geomodels are increasingly being used for a wide variety of scientific and societal purposes. Most advanced methods for generating these models are implicit approaches, but they suffer limitations in the types of interpolation constraints permitted, which can lead to poor modeling in structurally complex settings. A geometric deep learning approach, using graph neural networks, is presented in this paper as an alternative to classical implicit interpolation that is driven by a learning through training paradigm. The graph neural network approach consists of a developed architecture utilizing unstructured meshes as graphs on which coupled implicit and discrete geological unit modeling is performed, with the latter treated as a classification problem. The architecture generates three-dimensional structural models constrained by scattered point data, sampling geological units and interfaces as well as planar and linear orientations. The modeling capacity of the architecture for representing geological structures is demonstrated from its application on two diverse case studies. The benefits of the approach are (1) its ability to provide an expressive framework for incorporating interpolation constraints using loss functions and (2) its capacity to deal with both continuous and discrete properties simultaneously. Furthermore, a framework is established for future research for which additional geological constraints can be integrated into the modeling process.

1 Introduction

Three-dimensional structural geological models provide a means of improving our understanding of the subsurface useful for various earth science applications (Wellmann and Caumon 2018). Models are typically generated from various observations, such as field measurements, borehole logs, and horizon boundaries, using various mathematical modeling methods. Currently, implicit-based modeling approaches are the most widely used method for producing such models due to their fast, automatic, and reproducible characteristics. Implicit approaches can be split into meshless (Lajaunie et al. 1997; Hillier et al. 2014) and discrete (Frank et al. 2007; Caumon et al. 2013) categories, where the latter requires a mesh for computation. These approaches implicitly define relevant geological interfaces as iso-surfaces of a volumetric scalar field, interpolated from point data sampled over a region of interest. Scalar field interpolants can be constrained by various types of point data including positions of geological interfaces, as well as planar (e.g., strata, foliation) and linear (e.g., fold axis) orientations. In addition, incorporation of discontinuous features such as faults (Calcagno et al. 2008) and constraints associated with polyphase deformation (Laurent et al. 2016) enables the modeling of more complex geological structures.

Notwithstanding the benefits of existing implicit-based geomodeling approaches, there are some scenarios—usually structurally complex terrains—in which these approaches can fail to produce geologically valid models given sparse or heterogeneously sampled data and available geological knowledge. Corresponding implicit models typically exhibit erroneous topological features inconsistent with the known geological history and spatial relationships between relevant geological structures (e.g., stratigraphy, faults, unconformities). This issue can be attributed to limitations in the types of data and knowledge constraints that implicit interpolants can incorporate. All types of data and knowledge are incorporated as a set of linear constraints written in terms of a continuous scalar field. Although there have been ways developed to incorporate geological knowledge by combining multiple interpolated scalar fields (Calcagno et al. 2008; Laurent et al. 2016), there still exist fundamental limitations on the types of information that can constrain these implicit interpolants. For example, constraints such as non-orthogonal angular relationships, Gaussian curvature, or topological constraints (e.g., number of connect components or holes, spatial relationships) cannot be incorporated.

Recently, new approaches using Bayesian inference (de la Varga and Wellmann 2016; Grose et al. 2019) have emerged for considering a priori knowledge and data uncertainty that current implicit mathematical models cannot incorporate. It is important to note that these Bayesian approaches still depend on the underlying implicit interpolants as forward models by varying their parameterization and input data using probability density and likelihood functions. The range of models (e.g., model space) is therefore limited to those models that can be generated with a specific interpolation structure. Hence, in some geological settings, the Bayesian inference approach of model parameter and data distribution sampling may not be sufficient to sample a geological valid model. It is therefore important to improve geological interpolation using all available data and knowledge so that geologically valid models are guaranteed. This would also benefit Bayesian inference approaches.

In this paper, we introduce a new three-dimensional structural geological modeling approach that generates structural models using graph neural networks (GNNs) (Bronstein et al. 2017; Hamilton et al. 2017a; Wu et al. 2020) from the same types of structural data used in existing implicit approaches. GNNs are a relatively new type of deep learning approach for graph structure data that propagates information through a graph’s connectivity structure. Compared to traditional convolutional neural networks (CNNs), GNNs do not have a regular neighborhood structure and permit complex structural information and relationships, opening new opportunities for enhancing the modeling capacity for three-dimensional structural geological applications. In recent years, there has been substantial growth in the use of GNNs for a wide range of applications including recommender systems (e.g., streaming services, e-commerce, social networks) (Ying et al. 2018), chemistry (e.g., molecular modeling) (Duvenaud et al. 2015), citation networks (Kipf and Welling 2016a, b), computer programming (Allamanis et al. 2017), and geometric deep learning (e.g., three-dimensional vision, manifold learning) (Qi et al. 2017; Monti et al. 2017)—each of which can express corresponding data in graph form. Here, the graphs represent tetrahedral meshes. Each sampled data point is collocated with a distinct vertex in the resultant mesh. Additionally, a mesh can be optimized to adaptively vary tetrahedron volumes to accommodate heterogeneous point sampling, reducing overall data storage while also supplying higher resolution where needed.

Our proposed GNN architecture makes scalar field predictions generated by deep learning methodologies using typical implicit point data (e.g., interface points associated with multiple distinct geological interfaces, and linear/planar orientations). Scalar field predictions are constrained by scalar values encoding the stratigraphic sequence of sampled interfaces as well as new angular constraints for orientation observations. The new angular constraints permit any orientation relationship with the gradient of the scalar field to be considered. These constraints can be used for the usual normal and tangent data, but also permit non-orthogonal angular relationships useful for bedding-cleavage relationships. If geological rock unit observations are available, scalar field predictions can be used as input to a coupled GNN, leveraging the structural features of the scalar field to generate geological unit predictions. The coupled GNN treats geological units as discrete data and is formulated as a classification problem. By comparison, current implicit approaches use inequality constraints (Dubrule and Kostov 1986; Frank et al. 2007; Hillier et al. 2014) on continuous scalar values to express discrete data, requiring the use of computationally expensive optimization methods to find a solution. Interpolation constraints are incorporated in the presented approach using loss functions that measure the error between the GNN’s predictions and the available constraints. Loss functions provide a flexible framework for incorporating geological interpolation constraints, since the only requirement is that the error is measurable. Moreover, solving a large linear system of equations with prescribed mathematical conditions (e.g., positive definiteness) is avoided. In addition, the proposed GNN architecture provides a promising foundation for directly incorporating into the modeling knowledge constraints expressible as a graph (e.g., topology, and other knowledge graphs).

The remainder of this paper is organized as follows. Section 2 describes the GNN architecture and its associated methodology used to generate constrained three-dimensional structural geological models. Section 3 includes two case studies in which the proposed GNN architecture is applied to demonstrate its structural geological modeling performance. Section 4 discusses the modeling characteristics of the GNN approach and its capacities for three-dimensional geological modeling, along with useful empirical observations. Conclusions are given in the last section.

2 GNN Architecture and Methodology

2.1 Definitions and Notations

Notations and formal definitions are given for the graphs used throughout this paper.

First, the notations for scalar, vector, and matrix quantities are as follows: lowercase, bold lowercase, and bold uppercase characters, respectively.

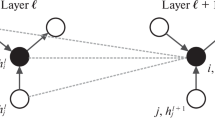
Graphs are represented by $G=(V,E)$, where $V$ is the set of nodes (vertices) and $E$ is the set of edges (Fig. 1). The set $V$ contains $N$ nodes ${v}_{i}\in V$ and an edge ${e}_{ij}=({v}_{i},{v}_{j})\in E$ connecting from ${v}_{i}$ to ${v}_{j}.$ An edge, ${e}_{ij}$, can be associated with a weight ${w}_{ij}$ for weighted graphs and ${w}_{ij}=1$ for unweighted graphs. The direct neighborhood of node $v$, also known as the one-hop neighborhood, is defined as $\mathcal{N}\left(v\right)=\left\{u\in V|(u,v)\in E\right\}$. The global connectivity structure of a graph can be represented by an adjacency matrix ${\varvec{A}}\in {\mathbb{R}}^{N\times N}$, where ${A}_{ij}={w}_{ij}$ if ${e}_{ij}\in E$ and ${A}_{ij}=0$ if ${e}_{ij}\notin E$. Graphs can be categorized as either directed or undirected. As the name implies, directed graphs have directions associated with the edges. In contrast, all edges in undirected graphs are bidirectional—information can go in both directions. Graphs in our work are undirected and have associated node features ${\varvec{X}}\in {\mathbb{R}}^{N\times d}$ with each node ${{\varvec{x}}}_{v}\in {\mathbb{R}}^{d}$ containing relevant data associated with the node.

Fig. 1

Simple undirected graph with an associated adjacency matrix ${\varvec{A}}$ and node feature matrix ${\varvec{X}}$

2.2 GNNs

GNNs are deep learning models using graph structured data for various learning tasks such as regression, classification, and link prediction performed in an end-to-end manner. There are four kinds of GNNs: recurrent (Scarselli et al. 2008), convolutional (Kipf and Welling 2016a; Gilmer et al. 2017; Hamilton et al. 2017b), graph autoencoders (Kipf and Welling 2016b), and spatial–temporal (Yan et al. 2018). GNNs generate embeddings ${\varvec{h}}$ which are low-dimensional vectors that encode high-level representations of various graph elements such as nodes and edges, as well as graph themselves, encapsulating topological structure and other relevant associated property information in a compressed form. Embeddings are used to make predictions for relevant learning task(s), and the information (e.g., their meaning) encoded within them is task-dependent. During the training process, the network learns how to encode better embeddings that capture domain-specific meaning and latent data characteristics. Furthermore, embeddings are encoded such that similar things are positioned closer together within the continuous embedding space. This provides a means for measuring errors during training that can be minimized, producing higher-quality embeddings. The higher the quality of the embeddings, the more accurate the resultant predictions.

The proposed GNN architecture used for three-dimensional structural geological modeling is illustrated in Fig. 2. Spatial-based convolutional GNNs are used to generate graph node embeddings by stacking multiple neural network layers, each of which computes a convolution at every graph node $v$. Node embeddings ${{\varvec{h}}}_{v}$ are initialized to node features ${{\varvec{x}}}_{v}$ and used as input to the network’s first layer. Spatial context is provided to the GNN by setting each graph node’s features ${{\varvec{x}}}_{v}$ to the normalized spatial coordinates of the node positioned in three-dimensional space ${{\varvec{x}}}_{v}=({\widehat{x}}_{v},{\widehat{y}}_{v},{\widehat{z}}_{v})$. Each normalized Cartesian coordinate is computed by centering the data on $\mathbf {0}$ and rescaling each coordinate by the maximum coordinate range. For example, the normalized $x$-coordinate is computed as

Fig. 2

Proposed GNN architecture for three-dimensional structural geological modeling composed of two GNN modules which generate scalar field predictions and rock unit predictions, respectively. Green arrows indicate GNN input and red arrows GNN output. Training data (bottom) are associated which each module. Iso-contours (dashed curves) represent interfaces between stratigraphic layers

$${\widehat{x}}_{v}=\frac{\left({x}_{v}-{x}_{c}\right)}{{\max}\left({x}_{\max}-{x}_{\min},{y}_{\max}-{y}_{\min},{z}_{\max}-{z}_{\min}\right)/2},$$

(1)

where ${x}_{v}$ is the un-normalized $x$-coordinate of the mesh node, and ${x}_{c}$ is the computed center of the $x$-coordinates (e.g., ${x}_{c}=\left({x}_{\max}+{x}_{\min}\right)/2$). Each normalized coordinate is scaled by the same factor to ensure isometric scaling. The scale factor is divided by 2 to place the maximum coordinate range between $\left[-1, 1\right]$. Feature normalization is a common preprocessing requirement for machine learning algorithms. This is particularly important when using geospatial data, where coordinate values can be extremely large and their variation over a region of interest is small.

The GNN input consists of (1) a graph representing a volumetric unstructured mesh constrained by scattered structural field point data; (2) a node feature matrix ${\varvec{X}}$ containing normalized spatial coordinates of the nodes; and (3) training data associated with subsets of graph nodes collocated with geological data. There are two separate GNN modules that generate different coupled aspects of the three-dimensional model and are associated with different learning tasks. The first GNN module (Scalar Field GNN) generates scalar field predictions for every graph node, creating an implicit model incorporating structural features sampled by structural field observations. The second GNN module (Rock Unit GNN), uses the predictions from the first module and leverages the structural continuity of the predicted scalar field as input (e.g., inputted node features) to make predictions about geological rock units. It is important to note that the Rock Unit GNN can also influence the implicit modeling of the Scalar field GNN. In addition, each GNN module can also be used on its own if the necessary data for the other module is unavailable.

2.3 Spatial Convolutions

Convolutions play a critical role in any convolution neural network by extracting localized information relevant to a learning task via the application of learnable filter weights ${\varvec{W}}$ throughout a domain. In GNNs, there are two types of convolutions: spectral and spatial. Spectral approaches define filters from a graph signal perspective requiring eigendecomposition on the graph’s Laplacian, whereas spatial approaches define them from a node’s local neighborhood. Empirically, we have found that spatial-based convolutions yielded far superior modeling as compared to spectral-based convolutions. However, these findings are not surprising given that three-dimensional modeling is driven by spatial interpolation. Furthermore, embedding spaces generated by spectral convolutions are likely to be disconnected from the corresponding physical space in which they are created. We consider two spatial convolutions ${\left({\varvec{W}}\star {\varvec{h}}\right)}_{v}$ of a graph node $v$ suitable for three-dimensional structural geological modeling applications. The first and simpler convolution inspired by GraphSAGE (Hamilton et al. 2017b) is a weighted average of transformed neighbor embeddings

$${\left({\varvec{W}}\star {\varvec{h}}\right)}_{v}=\frac{\sum_{u\in {\mathcal{N}}_{v}}{w}_{uv}\left({{\varvec{h}}}_{u}{\varvec{W}}+{\varvec{b}}\right)}{\sum_{u\in {\mathcal{N}}_{v}}{w}_{uv}},$$

(2)

where ${\varvec{W}}\in {\mathbb{R}}^{{d}_{in}\times {d}_{{out}}}$ and ${\varvec{b}}\in {\mathbb{R}}^{{1\times d}_{{out}}}$ are respectively learnable matrices and vectors used to linearly transform neighbor embeddings ${{\varvec{h}}}_{u}\in {\mathbb{R}}^{{1\times d}_{in}}$ with dimension ${d}_{in}$ into dimension ${d}_{{out}}$. The edge weights ${w}_{uv}$ for this convolution are leveraged to incorporate additional geometric information (e.g., neighbor distances, tetrahedron volume) of the tetrahedral mesh into the graph structure. The geometry-dependent edge weights derived from discrete Laplacian operators (Alexa et al. 2020) are computed from

$${w}_{ij}=\frac{1}{6}\sum_{ijkl}{l}_{kl}\cot{\theta }_{kl}.$$

(3)

Here the sum is taken over all tetrahedra containing edge ${e}_{ij}$, ${l}_{kl}$ is the length of the edge ${e}_{kl}$ belonging to tetrahedron indexed by $ijkl$, and ${\theta }_{kl}$ is the dihedral angle between the two faces of the tetrahedron containing ${e}_{kl}$ (Fig. 3).

Fig. 3

Geometric quantities used to compute graph edge weights

The second convolution uses a Gaussian mixture model (GMM) (Monti et al. 2017) composed of $K$ parameterized Gaussian kernels

$${\left({\varvec{W}}\star {\varvec{h}}\right)}_{v}={{\varvec{h}}}_{v}{{\varvec{W}}}_{{node}}+{\varvec{b}}+\frac{1}{\left|{\mathcal{N}}_{v}\right|}\sum_{u\in {\mathcal{N}}_{v}}{\frac{1}{K}\sum_{k=1}^{K}{w}_{uv}^{k}\left({{\varvec{p}}}_{uv}\right){{\varvec{h}}}_{u}}{{\varvec{W}}}_{neigh}^{k}, {w}_{uv}^{k}\left({{\varvec{p}}}_{uv}\right)=\exp\left(-\frac{1}{2}{\left({{\varvec{p}}}_{uv}-{{\varvec{\mu}}}_{k}\right)}^{T}{\Sigma }_{k}^{-1}\left({{\varvec{p}}}_{uv}-{{\varvec{\mu}}}_{k}\right)\right),$$

(4)

where $({{\varvec{W}}}_{{node}},{{\varvec{W}}}_{neigh}^{k})\in {\mathbb{R}}^{{d}_{in}\times {d}_{{out}}}$ and ${\varvec{b}}\in {\mathbb{R}}^{{1\times d}_{{out}}}$ are learnable matrices and vectors to linearly transform the node $v$ and their neighbor $u\in {\mathcal{N}}_{v}$ embeddings $({{\varvec{h}}}_{v},{{\varvec{h}}}_{u})\in {\mathbb{R}}^{1\times {d}_{in}}$ into dimension ${d}_{{out}}$. GMM-based convolutions associate each edge connecting two nodes $u$ and $v$ with $K$ weights depending on the edge’s pseudo-coordinate ${{\varvec{p}}}_{uv}\in {\mathbb{R}}^{d}$, and learnable $d\times 1$ vector ${\mu }_{k}$ and $d\times d$ matrix ${\Sigma }_{k}^{-1}$ corresponding to the mean and covariance, respectively, of a Gaussian kernel. Note that our implementations of GMM-based convolutions do not restrict the covariance ${\Sigma }_{k}$ to have diagonal form (Monti et al. 2017)—to ensure the learnable covariance matrix is positive definite, we simply use ${\Sigma }_{k}^{\prime}={\Sigma }_{k}{\Sigma }_{k}^{T}$. Here we use the pseudo-coordinates ${{\varvec{p}}}_{uv}=\left({\widehat{x}}_{u}-{\widehat{x}}_{v},{\widehat{y}}_{u}-{\widehat{y}}_{v},{\widehat{z}}_{u}-{\widehat{z}}_{v}\right)$; however, this vectorial variable can also be leveraged for other geometrical information that can be associated to the edge.

2.4 Node Embedding and Prediction

As previously mentioned, GNNs generate embeddings ${\varvec{h}}$ that encode useful high-level representations which in turn are used to make predictions relevant to specific learning tasks. Our GNN architecture generates node embeddings with dimension ${d}_{{embed}}$ which are used to make scalar field predictions as well as rock unit predictions if those data observations are available. The node embedding and prediction generation algorithm given by Algorithm 1 represents the forward propagation (e.g., feed-forward) stage of the neural network having $D$ convolutional layers. As a result of recursive application of $D$ spatial convolutions, every graph node $v$ aggregates information up to its $D$-hop neighborhood (Fig. 4) and increases the receptive field surrounding the node. Therefore, as the network’s depth $D$ is increased, more global information can be encoded into the node’s embedding. The network’s final layer transforms embeddings into predictions for relevant learning tasks with the prescribed dimensionality ${d}_{{pred}}$. For graph node classification tasks, for example, the final layer outputs a vector for each graph node with a dimensionality equal to the total number of possible classes, with each vector element denoting the probability of a specific class. Dimensionalities of both embeddings and predictions are controlled through the linear transformation’s output dimension ${d}_{{out}}$ performed by the spatial convolutions (Eqs. 2, 4). For embeddings, ${d}_{{out}}={d}_{{embed}}$, while for predictions, ${d}_{{out}}={d}_{{pred}}$.

Fig. 4

Neighborhood aggregation of target node (red) in a two-layer GNN neural network

2.5 Training

Training the neural network involves optimizing associated network variables such that prediction accuracy is maximized. Since there are very few data observations in comparison to the number of nodes in our graphs, we utilize GNNs primarily in a semi-supervised context where only errors on graph nodes associated with data observations are computed via loss functions. However, when anisotropy information is available to describe directions of structural continuity, local errors in modeled orientation can be efficiently computed on all graph nodes—useful for both global and local anisotropy modeling. At every iteration of the learning algorithm, errors are minimized through the process of backpropagation where neural network variables are updated. As iterations increase, node embeddings encode more and more useful high-level information suitable for the learning objective, thereby maximizing prediction accuracy. Depending on the type of network prediction (e.g., continuous variable, discrete classes) and learning objective, loss functions will vary (Sects. 2.6 and 2.7). The resulting loss is simply the sum of the individual loss functions for corresponding available data constraints.

2.6 Scalar Field GNN

Scalar field predictions ${z}_{v}^{{\rm scalar}}$ are generated by the Scalar Field GNN module for every graph node and are constrained by data points that sample interfaces between stratigraphic layers and structural orientation observations. Interface points sampling $H$ horizons indexed by $\left\{1,\cdots ,H\right\}$ are associated with iso-values $f$ encoding the stratigraphic order such that

$${f}_{1}>\cdots >{f}_{H},$$

(5)

where ${f}_{1}$ and ${f}_{H}$ are the youngest and oldest, respectively. In implicit modeling, these iso-values define two-dimensional manifold surfaces embedded within a volumetric scalar field $s\left({\varvec{x}}\right)$ and are obtained by iso-surface extraction methods (Treece et al. 1999). The subset of graph nodes $v$ collocated with the set of sampled interface points $I$ are given the scalar field constraint

$$I=\left\{v\in V|{s}_{v}={f}_{v}\right\}.$$

(6)

The associated loss function for sample interface points measures the squared difference between the network’s predictions ${z}_{v}^{{\rm scalar}}$ and the scalar field constraints ${s}_{v}$ and sums them

$${\mathcal{L}}_{{\rm interface}}=\sum_{v\in I}^{\left|I\right|}{\left({z}_{v}^{{\rm scalar}}-{s}_{v}\right)}^{2}.$$

(7)

The loss function associated with orientation constraints measures, at a node, the angle between the gradient of the scalar field and an orientation observation for the set of graph nodes $O$ associated with those observations. To measure these angles, the gradient of the predicted scalar field at these graph nodes must first be estimated. To do so, we utilize the first-order Taylor series approximation of the scalar field using the one-hop neighborhood surrounding a given graph node and perform a least square fit of directional derivatives (Correa et al. 2009) on the predicted scalar field

$${{\varvec{P}}}_{v}^{T}{{\varvec{P}}}_{v}\nabla {z}_{v}^{{\rm scalar}}={{\varvec{P}}}_{v}^{T}{{\varvec{S}}}_{v},$$

(8)

where $\nabla {z}_{v}^{{\rm scalar}}=\left(\partial {z}_{v}^{{\rm scalar}}/\partial x,\partial {z}_{v}^{{\rm scalar}}/\partial y,\partial {z}_{v}^{{\rm scalar}}/\partial z\right)$ is the estimated gradient of the scalar field at node $v$, and matrices ${{\varvec{P}}}_{v}$ and ${{\varvec{S}}}_{v}$ are defined by

$$\begin{array}{cc}\begin{array}{c}{{\varvec{P}}}_{v}=\left[\begin{array}{ccc}{\widehat{x}}_{u}-{\widehat{x}}_{v}& {\widehat{y}}_{u}-{\widehat{y}}_{v}& {\widehat{z}}_{u}-{\widehat{z}}_{v}\\ \vdots & \vdots & \vdots \end{array}\right]\\ {{\varvec{S}}}_{v}=\left[\begin{array}{c}{z}_{u}^{{\rm scalar}}-{z}_{v}^{{\rm scalar}}\\ \vdots \end{array}\right]\end{array},& \forall u\in {\mathcal{N}}_{v}\end{array},$$

(9)

where $\widehat{x, }\widehat{y}, \widehat{z}$ are the normalized spatial coordinates of a given node. The estimated angle between the predicted scalar field gradient at node $v$ and a collocated orientation vector ${\boldsymbol{\alpha }}_{v}$

$$cos{\theta }_{v}^{pred}=\frac{{\boldsymbol{\alpha }}_{v}\bullet \nabla {z}_{v}^{{\rm scalar}}}{\Vert {\boldsymbol{\alpha }}_{v}\Vert \Vert \nabla {z}_{v}^{{\rm scalar}}\Vert }$$

(10)

is used to measure the angular error compared with the observed angular constraint ${\theta }_{v}^{obs}$. In general, for any angular constraint ${\theta }_{v}^{obs}$, the loss function

$${\mathcal{L}}_{\rm Orientation}=\sum_{v\in O}^{\left|O\right|}\left|cos{\theta }_{v}^{obs}-cos{\theta }_{v}^{pred}\right|$$

(11)

can be used. For normal data (e.g., ${{\varvec{n}}}_{v}$) ${\theta }_{v}^{obs}=0^\circ$, the resulting loss function

$${\mathcal{L}}_{{\rm normal}}=\sum_{v\in O}^{\left|O\right|}1-\frac{{{\varvec{n}}}_{v}\bullet \nabla {z}_{v}^{{\rm scalar}}}{\Vert {{\varvec{n}}}_{v}\Vert \Vert \nabla {z}_{v}^{{\rm scalar}}\Vert }$$

(12)

can be used, and for tangent data (e.g., ${{\varvec{t}}}_{v}$) ${\theta }_{v}^{obs}=90^\circ$,

$${\mathcal{L}}_{{\rm tangent}}=\sum_{v\in O}^{\left|O\right|}\left|\frac{{{\varvec{t}}}_{v}\bullet \nabla {z}_{v}^{{\rm scalar}}}{\Vert {{\varvec{t}}}_{v}\Vert \Vert \nabla {z}_{v}^{{\rm scalar}}\Vert }\right|.$$

(13)

It is important to note that for modeling multiple geological interfaces simultaneously, the polarity normal data ${{\varvec{n}}}_{v}$ is required to be consistent with the younging direction (e.g., direction of younger stratigraphy). Tangent data ${{\varvec{t}}}_{v}$ can be used to describe foliation data where planar polarity has no geological meaning as well as for anisotropic characteristics of structural features such as local plunge vectors (Hillier et al. 2014). For foliation data, a dip vector and strike vector are used as tangent constraints to describe the planar orientation. Meanwhile, for local or global anisotropy, a tangent vector is used to describe the direction of the plunge axis—the loss function is independent of the polarity of the vector due to the absolute value.

2.7 Rock Unit GNN

Our GNN architecture can also incorporate rock unit observations commonly available from drill core and outcrop datasets. This is particularly advantageous for geological datasets absent of interface observations and where there is an abundance of rock unit observations. Since rock units are discrete properties this GNN module is associated with a classification learning task. Given a set rock unit observations $R$ containing a total of ${N}_{{\rm classes}}$ possible classes collocated with a subset of graph nodes, each rock unit observation is assigned a one-hot vector ${{\varvec{y}}}_{v}$ indicating the class to which it belongs. One-hot vectors are vectors whose elements are all zero except for a single element which is given a value of 1. For example, for a dataset containing ${N}_{{\rm classes}}=3$, one-hot vectors corresponding to classes $a$, $b$, $c$ are respectively

$${{\varvec{y}}}_{v}^{a}=\left({1,0},0\right),$$

(14)

$${{\varvec{y}}}_{v}^{b}=\left({0,1},0\right),$$

$${{\varvec{y}}}_{v}^{c}=\left({0,0},1\right).$$

The loss function associated with these data is the cross-entropy loss

$${\mathcal{L}}_{{\rm RockUnit}}=-\sum_{v\in R}\left({{\varvec{y}}}_{v}\bullet log\left({{\varvec{y}}}_{v}^{pred}\right)\right),$$

(15)

where ${{\varvec{y}}}_{v}^{pred}$ is the predicted class probabilities obtained from

$${y}_{{v}_{i}}^{pred}=Softmax\left( {z}_{{v}_{i}}^{{\rm unit}}\right)=\frac{{e}^{{z}_{{v}_{i}}^{{\rm unit}}}}{\sum_{j}{e}^{{z}_{{v}_{j}}^{{\rm unit}}}},$$

(16)

where ${z}_{{v}_{i}}^{{\rm unit}}$ is the $i$-th element of vector ${{\varvec{z}}}_{v}^{{\rm unit}}$, which is the output of the rock unit GNN module. The softmax function is routinely used in machine learning to normalize network outputs to a probability distribution over the number of classes ${N}_{{\rm classes}}$.

3 Case Studies

Three-dimensional structural geological modeling results from the proposed GNN architecture are presented here for a synthetic and a real-world case study to demonstrate proof of concept. Results for both case studies were obtained using a desktop PC with an Intel Core i9-9980XE CPU and a single NVIDIA RTX 2080 Ti GPU. Each case study consists of scattered structural observations sampling stratigraphic interfaces and bedding (S0—e.g., normal data), with one case study (synthetic) having rock unit observations. Locations of structural observations are used to generate constrained tetrahedral meshes generated by TetGen (Hang 2015), with each data point being collocated with a distinct mesh vertex. Each mesh is converted into a graph structure dataset $G=(V,E)$ encoding all relevant data used as input into the GNN architecture, including the following:

• Node features ${{\varvec{x}}}_{v}=({\widehat{x}}_{v},{\widehat{y}}_{v},{\widehat{z}}_{v})$ of normalized spatial coordinates.

• A node $v$ collocated with a structural observation can have the following attached data:

  • o Iso-value ${f}_{v}$ encoding stratigraphic order. Iso-values normalized to $\left[-1, 1\right]$ range.

  • o Normal vector ${{\varvec{n}}}_{v}$ describing bedding orientation with polarity specifying younging direction.

  • o One-hot vector ${{\varvec{y}}}_{v}$ indicating geological unit class.

• Edges ${e}_{ij}$ are associated with geometry-dependent weights ${w}_{ij}$ (Eq. 3).

The learnable variables of the GNN architecture are initialized using Xavier initialization (Glorot and Bengio 2010). In addition, both case studies use AdamW (Loshchilov and Hutter 2017) as the optimizer to update network parameters using GNN model parameters summarized in Table 1.

Table 1 GNN model parameter values for the architecture with prelu being the parametric rectified linear activation function

3.1 Synthetic Example

The first case study is of a conformally folded stratigraphic layered volume where folds are cylindrical (Fig. 5a). Constraint data composed of 67 interface points and 50 planar orientations are randomly sampled from synthetic interface surfaces. In addition, 44 rock unit observations sampling six distinct rock units from simulated drill-hole data are used as constraints for the GNN architecture. A tetrahedral mesh (Fig. 5b) containing 239,784 tetrahedrons generated from these point constraints was converted into a graph-structured dataset and used as the architecture’s input. Coupled implicit and geological unit modeling results after 300 epochs of training using weighted mean convolution (Eq. 2) are presented in Fig. 5c, d, respectively. Note that “epoch” is the term to indicate one complete feed-forward pass (Algorithm 1) and one backpropagation pass of all training nodes. Average computational time for each epoch was approximately 0.05 s. Model performance as measured by loss functions for each constraint type and the average nearest distance between synthetic and modeled surfaces is tabulated in Table 2. The fact that this distance is $\overline{\Delta d}=1.564$ m and that the average stratigraphic thickness is 15 m between interfaces clearly indicates that the proposed GNN architecture is beneficial for three-dimensional structural geological modeling. By visual comparison, the GNN is nearly identical to the synthetic model (Fig. 5e). It even maintains the cylindricity of the fold even though no global plunge information has been used to constrain the model.

Fig. 5

Three-dimensional structural geological modeling results using weighted mean spatial convolution on a synthetic conformally folded (cylindrically) stratigraphic layered model. a Point data constraints including interface (spheres), normal orientation (white arrows), and rock unit observations (triangles) sampled throughout the volume, b tetrahedral mesh constrained by point data constraints illustrating constraints are collocated with mesh vertices (inset), c implicit scalar field and d rock unit predictions outputted by corresponding GNN modules after 300 epochs of training, e comparison of synthetic (white) and modeled (red) surfaces viewed along the global plunge axis

Table 2 Model performance metrics after 300 epochs of learning algorithm on synthetic case study

3.2 Real-World Dataset

The second case study utilizes a real-world dataset from the Purcell Anticlinorium in the east Kootenay region of Southeastern British Columbia (de Kemp et al. 2016). A subset of the large regional-scale dataset is taken surrounding the Sullivan mine area where a world-class sedimentary exhalative deposit (SEDEX) is located along with several deep drill holes sampling several stratigraphic interfaces. Field observations taken from outcrops sampling these interfaces, as well as bedding orientation (S0), are also available. In total, the dataset contains 103 interface points sampling six distinct interfaces and 187 bedding observations as shown in Fig. 6a. Point constraints are heterogeneously sampled with dense drill-hole sampling in a small portion of the model and a strong horizontal sampling bias (e.g., small variance in elevation) for the outcrop observations—typical of geological survey and mineral exploration datasets. Furthermore, bedding observations exhibit large local variations sampling multiple scales not necessarily important to the scale of the region of interest in the model. These orientation data were used to fit a Kent distribution (Kent 1982) and clearly indicate the presence of a folded structure. The fitted distribution ($\kappa =8, \beta =4$) has strong ellipticity ($e=2\beta /\kappa =1$) suggesting a more cylindrically folded structure.

Fig. 6

Structural modeling results using GMM spatial convolutions. a Heterogeneously distributed point constraints accompanied by fitted Kent distribution (right) of the bedding orientation, b predicted scalar field outputted by GNN—red rectangular regions indicate cross sections shown in e and f, c and d iso-surfaces extracted from mesh from two viewing perspectives—large red arrow indicates global plunge direction determined from orientation analysis

The resulting model presented in Fig. 6b was obtained using GMM spatial convolutions (Eq. 4) with one kernel (e.g., $K=1$) for each layer of the Scalar Field GNN module after 150 epochs of training. The average computational time for each epoch was approximately 0.12 s using a mesh containing 555,396 tetrahedrons. Iso-surfaces extracted from the scalar field model for the six stratigraphic interfaces are shown in Fig. 6c, d from two viewing perspectives. Both cross sections (Fig. 6e, f) highlight the GNN’s fitting characteristics on nearby structural geological data. For this dataset, the GNN was trained for only 150 epochs to avoid overtraining—also known as early stopping. With more training the GNN will attempt to transition from capturing the global features of the model to minimizing the errors associated to large localized structural variations (typical of real-world noisy datasets). If there are structural contradictions or hard-to-reconcile features with the given data, as with this dataset, more training can negatively impact the resulting model. This will occur in later phases of training when loss function values begin to fluctuate significantly from epoch to epoch. Table 3 summarizes the resulting model performance metrics on this dataset.

Table 3 Model performance metrics after 150 epochs of training on real-world dataset

4 Discussion

The presented case studies show that the GNN architecture can generate three-dimensional structural geological models constrained by point data sampling geological units, stratigraphic interfaces, and planar structural orientation. The first case study demonstrates that the architecture can perform both implicit and geological unit modeling that is effective in producing a model that is nearly identical to the synthetic model. In addition, the coupled scalar field and geological unit GNN modules of the architecture highlight the ability of the GNN to cope with continuous and discrete properties simultaneously. Furthermore, its capacity to capture global anisotropy of the fold without being provided this information from orientation analysis is notable. In the second case study, we show that the architecture can produce a geologically reasonable structural model given noisy and hard-to-reconcile real-world data, and provides promise for general application for constrained three-dimensional structural geological modeling. The developed architecture is a new way to model geological structures and is, to the best of the authors’ knowledge, the first deep learning approach to geological implicit modeling.

The proposed GNN approach opens new opportunities for enhancing three-dimensional structural geological modeling. This is provided by the approach’s expressive framework for incorporating interpolation constraints using loss functions and the ability to consider both continuous and discrete properties. Loss functions provide an intuitive mechanism for constraining resulting models by computing errors between the GNN’s predictions and constraints, which does not require solving large systems of equations. Any model property (e.g., interfaces, orientation, rock units) derived from GNN’s predictions representing a structural model can be compared with data or model constraints using loss functions. Discrete properties, like rock units, can be handled by GNNs by treating them as a classification problem. Resulting GNN predictions of these properties are expressed as a vector containing continuous class probabilities in a range between 0 and 1. The class of a node is simply determined by the vector element with the largest probability. Alternatively, rock unit observations can also be expressed as inequality constraints (Kervadec et al. 2019) using scalar field values like previous implicit approaches not requiring convex optimization methods. However, treating them as a classification problem can be advantageous because it provides the lithostratigraphic model directly from which additional model metrics can be potentially derived (e.g., area, volume, thickness, spatial relationships between classes) for other model-based constraints. Furthermore, treating discrete properties this way permits integration of other discrete geological properties that cannot be represented as continuous scalar values.

Although not demonstrated here, GNNs have been shown to be massively scalable by application to graphs containing billions of nodes for web-scale recommender systems (Ying et al. 2018). This is made possible by partitioning a graph into batches of sampled sub-graphs (Hamilton et al. 2017b) describing k-hop neighborhoods which can be distributed across cloud computing infrastructure for training and inference. This is a promising direction for massive-scale three-dimensional geological modeling.

One modeling assumption is imposed by the presented GNN approach. This assumption, also known as inductive bias, asserts that nearby information is more useful than distant information for making geologically related predictions. This bias is provided by the graph’s structure, which for the presented approach is a tetrahedral mesh. Since predictions on graph nodes are derived from recursion aggregation of neighboring node embeddings, and these neighboring nodes are spatially close, local information has a greater influence on these predictions than distant information. For geological applications, this inductive bias is strongly supported and originates from Tobler’s first law of geography, which states that closer things are more related to each other than things that are further away (Tobler 1970). Furthermore, this law is the foundation for spatial interpolation methods such as kriging.

One potential limitation of the presented GNN approach are challenges with reproducibility—an aspect of all deep learning methods. Since the network’s learnable parameters are initialized randomly, rerunning the algorithm under the same conditions will not yield the exact same geological model. Normally, resultant models are quite similar, with small shifts in modeled geological surfaces. However, in some circumstances the differences can be large if (1) the modeling capacity of the GNN model is not sufficient (e.g., too few learnable parameters) or (2) a diverse set of plausible structural geological solutions exist given the supplied constraints. In these circumstances, there are many local minima in the neural network’s solution space. In contrast, existing implicit approaches achieve perfect reproducibility because they are deterministic methods that return the global minimum solution obtained from a linear system of equations or convex optimization problem. However, since three-dimensional geological modeling applications suffer from limited data compared to the volumes they aim to resolve, there is an infinite set of plausible geological models given the sampled data. Therefore, because the GNN can generate a family of solutions given the same modeling parameters, it provides a means for exploring a larger set of plausible geological structures (Jessell et al. 2010). Challenges with reproducibility of geological models obtained from GNNs could be addressed by fully characterizing the space of solutions as well as generating model uncertainty through Bayesian deep learning techniques on graphs (Ryu et al. 2019).

Modeling assumptions imposed by existing implicit approaches can in some circumstances negatively impact the resultant structural models. All existing implicit interpolants impose explicit smoothness criteria to obtain a unique interpolation. For meshless methods, this is the minimum norm interpolant criterion that corresponds to the smoothest possible interpolation given the chosen kernel function. On the other hand, for discrete methods, this is the constant scalar gradient criterion between neighboring tetrahedra. Both smoothness criteria can lead to poor geological modeling of highly variant structures due to the compromising influence of local variations on the geological reasonableness (de Kemp et al. 2017) of the model. An example of this behavior is shown in Fig. 7, in which critical points (vanishing derivatives) within the scalar field create topological features (Ni et al. 2004) in the modeled interface which are not geologically reasonable. Although, this issue can be mitigated to varying degrees of success by approximating solutions (e.g., nugget effect, regression smoothing) instead of exact interpolation. For GNNs, these explicit smoothness criteria are not imposed. Instead, smoothness of resulting predictions is implicitly driven by the recursive spatial convolutions of node embeddings and loss functions associated with various constraints. Spatial convolutions in GNNs can be viewed as a generalization of kernel functions in classical implicit interpolation (Gong et al. 2020) whose parameterization is optimized through training on given constraints. In addition to the smoothness criterion, existing implicit approaches also impose assumptions on normal orientation data—useful for modeling overturned structures—quantifying planar orientation as well as direction (polarity) of younger stratigraphy. Existing approaches use a scalar gradient constraint equal to a normal vector whose norm (e.g., vector magnitude) is arbitrarily chosen, typically as a unit normal. The magnitude of the gradient controls the scalar field’s rate of change in the direction of the normal. Moreover, all gradient constraints are associated with the same norm value that consequently restricts modeling especially in highly deformed settings where stratigraphic thicknesses typically vary. The angular constraints used in the proposed GNN architecture provides the desired orientational control on modeled geometries unaffected and unrestricted by the arbitrarily chosen norm.

Fig. 7

Example of a radial basis function (RBF) interpolation yielding a geologically unreasonable model of an interface (black curve) using interface (blue) and normal constraints (red) sampling a highly variable structure. For reference, a geologically reasonable interpretation is shown (dotted white curve)

In addition, the presented GNN approach for three-dimensional geological modeling can also be used as a framework for incorporating additional forms of geological knowledge. Since edges of a graph can be used to represent any form of relation between two objects, they can be exploited for incorporating topological relationships between various geological entities like stratigraphy, unconformities, intrusions, and faults. Since these interlinked entities can be represented as a graph (Thiele et al. 2016), we see potential in leveraging GNNs for incorporating these graph-based constraints into the modeling process. The concept of using edges to model relations is one of our motivations for using GNNs over existing implicit approaches.

Experience with GNN modeling has led to some practical observations regarding the effect of GNN model parameterization, including the types of graph convolution, edge weights, embedding dimension, regularization, and network depth. The effect of changing the type of convolution, edge weights, and embedding dimension on representing an overturned fold can be found in the “Appendix”. In order to represent geological structures, the network requires sufficient modeling capacity, with complex structures requiring more modeling capacity than simpler structures. Increasing the network’s modeling capacity can be achieved by using a spatial convolution that has sufficient parameters as well as increasing the embedding dimension. Using a GMM convolution (Eq. 4), the modeling capacity can be improved by simply increasing the number of Gaussian kernels $K$ used. It should be noted that we tested other graph-based convolutions (Fey et al. 2018; Verma et al. 2018; Thekumparampil et al. 2018) using the PyTorch Geometric library (Fey and Lenssen 2019), and preliminary results indicate that they are useful for three-dimensional structural geological modeling. More work, beyond the scope of this paper, would be required to fully assess their general use for geological modeling. The use of edge weights, either geometrically derived or dynamically learned by the network via GMM convolutions, consistently produces better representations of geological structures. For regularization, various methods can be used to avoid overfitting GNN models given noisy or structurally contradictory data, including early stopping (as per the second case study) as well as L1 and L2 vector space norm regularization of network parameters and dropout (Srivastava et al. 2014). With respect to network depth, we found no significant improvement in geological modeling when increased beyond three layers, which is attributed to a bottlenecking issue in current GNNs (Alon and Yahav 2020). This issue results from information loss during successive spatial convolutions, each of which compresses information into fixed-size embedding vectors. As network depth is increased, the amount of information that needs to be compressed grows exponentially, resulting in diminishing returns in prediction accuracy.

5 Conclusions

A GNN-based deep learning approach to three-dimensional structural geological modeling has been presented. The approach can generate both structural scalar fields for implicit modeling and geological unit modeling constrained by typical scattered implicit point data and geological unit observations. Two case studies demonstrate the GNN architecture’s modeling performance in representing three-dimensional geological structures using two diverse datasets. The case studies highlight the GNN’s capability to constrain orientation using angular constraints, to handle continuous and discrete properties simultaneously, and to produce reasonable models using noisy real-world data. The approach provides an expressive framework for incorporating interpolation constraints using loss functions, enabling new opportunities for three-dimensional structural geological modeling.

Appendix: The Effect of GNN Model Parameters on Resulting Three-Dimensional Geological Models

To demonstrate the effect of using different model parameters within the presented graph neural network architecture, eight three-dimensional structural geological models are produced of a synthetic overturned fold (Fig. 

Fig. 8

Effect of important GNN parameters on three-dimensional structural geological modeling of a synthetic overturned folded structure (grey) using sampled interface (blue) and normal constraints (green). Investigated parameters include graph convolution type, edge weight type, and node embedding dimension. Refer to Table 4 for details on parameters used for each subfigure. Each sub-figure contains two views: (left) along fold axis (right) perpendicular to fold axis

8) using parameterization summarized in Table

Table 4 Modeling parameters used for each of the subfigures in Fig. 8 and associated error metrics ${\mathcal{L}}_{{\rm interface}}$ and ${\mathcal{L}}_{{\rm normal}}$ from each modeling result

4. Each structural model was produced after 150 epochs of training using a network depth of 3. Results show that GMM convolutions (Fig. 8f–i) better reproduce the overturned fold as compared to mean-based convolutions (Fig. 8b–e) due to increased modeling capacity and the ability to dynamically learn optimal edge weights for modeling. When no edge weights are used (Fig. 8c), the resulting iso-surfaces are not as smooth as when the geometrically derived weights are used (Fig. 8b). In both cases, the use of a low embedding dimension (Fig. 8d, h) results in a modeled structure that is far from optimal, with notable creases throughout. On the other hand, when a high embedding dimension (Fig. 8e, i) is used, the resultant modeled structure is much smoother. Because of an increase in learnable parameters when using a high embedding dimension, 150 epochs of training is insufficient to minimize the errors on the interface constraints when using a mean-based convolution (Fig. 8e). Interestingly, this is not the case for GMM-based convolution (Fig. 8i).