Abstract
Geometric Continuum Mechanics ( GCM) is a new formulation of Continuum Mechanics ( CM) based on the requirement of Geometric Naturality ( GN). According to GN, in introducing basic notions, governing principles and constitutive relations, the sole geometric entities of space-time to be involved are the metric field and the motion along the trajectory. The additional requirement that the theory should be applicable to bodies of any dimensionality, leads to the formulation of the Geometric Paradigm ( GP) stating that push-pull transformations are the natural comparison tools for material fields. This basic rule implies that rates of material tensors are Lie-derivatives and not derivatives by parallel transport. The impact of the GP on the present state of affairs in CM is decisive in resolving questions still debated in literature and in clarifying theoretical and computational issues. As a consequence, the notion of Material Frame Indifference ( MFI) is corrected to the new Constitutive Frame Invariance ( CFI) and reasons are adduced for the rejection of chain decompositions of finite elasto-plastic strains. Geometrically consistent notions of Rate Elasticity ( RE) and Rate Elasto-Visco-Plasticity ( REVP) are formulated and consistent relevant computational methods are designed.






Similar content being viewed by others
Notes
In differential geometry these are respectively denoted by low and high asterisks ∗;∗ [51]. This standard notation leads however to consider too many similar stars in the geometric sky, i.e. push, pull, duality, Hodge operator.
The time-function
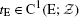 is assumed to be a projection, i.e. surjective with a surjective tangent map.
is assumed to be a projection, i.e. surjective with a surjective tangent map.An immersion is a injective map whose tangent map is injective too.
The introduction of the geometric notions of connection and parallel transport can be avoided by restricting oneself to transport by translation in Euclid space.
The proof is due to Fréchet, von Neumann, Jordan, see [59]. Validity of parallelogram identity is an assumption stronger than the one of validity of Pythagoras’ theorem.
For bodies of maximal dimension, the VPP is a proved theorem [27].
The Whitney product of tensor bundles with projection \(\boldsymbol{\pi}_{\mathbb{M},\mathbb{N}}\in \mathrm{C}^{1}(\mathbb{N};\mathbb{M}) \) and \(\boldsymbol{\pi}_{\mathbb{M},\mathbb{H}}\in \mathrm{C}^{1}(\mathbb{H};\mathbb{M}) \) over the same base manifold \(\mathbb{M}\), is the product bundle fulfilling the condition \(\mathbb{N}\times_{\mathbb{M}}\mathbb{H}:=\{(\mathbf{n},\mathbf{h})\in \mathbb{N}\times \mathbb{H}\mid \boldsymbol{\pi}_{\mathbb{M},\mathbb{N}}(\mathbf{n})= \boldsymbol{\pi}_{\mathbb{M},\mathbb{H}}(\mathbf{h})\}\) [27].
References
Ambrosi D et al. (2011) Perspectives on biological growth and remodeling. J Mech Phys Solids 59:863–888
Argyris JH (1966) Continua discontinua. In: Proc conf matrix methods struct mech AFFDL-TR-66-80, Oct. 26–28, 1965, Wright-Patterson AFB Ohio
Barretta R (2012) On the relative position of twist and shear centres in the orthotropic and fiberwise homogeneous Saint-Venant beam theory. Int J Solids Struct 49:3038–3046
Barretta R (2013) On Cesàro-Volterra method in orthotropic Saint-Venant beam. J Elast 112(2):233–253. doi:10.1007/s10659-013-9432-7
Barretta R (2013) On stress function in Saint-Venant beams. Meccanica. doi:10.1007/s11012-013-9747-2
Barretta R, Barretta A (2010) Shear stresses in elastic beams: an intrinsic approach. Eur J Mech A, Solids 29:400–409
Barretta R (2013) Analogies between Kirchhoff plates and Saint-Venant beams under torsion. Acta Mech. doi:10.1007/s00707-013-0912-4
Belytschko T, Liu WK, Moran B (2000) Nonlinear finite elements for continua and structures. Wiley, New York
Bernstein B (1960) Hypo-elasticity and elasticity. Arch Ration Mech Anal 6:90–104
Cowin CS (1996) Strain or deformation rate dependent finite growth in soft tissues. J Biomech 29:647–649
Crisfield MA (1991) Non-linear finite element analysis of solids and structures, vol. 1: Essentials. Wiley, London
Crisfield MA (1996) Non-linear finite element analysis of solids and structures, vol. 2: Advanced topics. Wiley, London
De Cicco S, Diaco M (2002) A theory of thermoelastic materials with voids without energy dissipation. J Therm Stresses 25(5):493–503
Epstein M (2010) The geometrical language of continuum mechanics. Cambridge University Press, Cambridge
Euler L (1761) Principia motus fluidorum. Novi Comm Acad Sci Petrop 6:271–311
Gurtin ME (1981) An introduction to continuum mechanics. Academic Press, San Diego
Humphrey JD (2003) Continuum biomechanics of soft biological tissues. Proc R Soc Lond A 459:3–46
Lee EH (1969) Elastic-plastic deformations at finite strains. J Appl Mech 36(1):1–6
Lubarda V (2004) Constitutive theories based on the multiplicative decomposition deformation gradient: thermoelasticity, elastoplasticity, and biomechanics. Appl Mech Rev 57(2):95–108
Lubliner J (1990) Plasticity theory. McMillan, New York
Marsden JE, Hughes TJR (1983) Mathematical foundations of elasticity. Prentice Hall, Redwood City
Noll W (1958) A mathematical theory of the mechanical behavior of continuous media. Arch Ration Mech Anal 2:197–226
Oden JT (2006) Finite elements of nonlinear continua. McGraw-Hill, New York. Dover, New York (1972)
Ogden RW (1997) Non-linear elastic deformations. Dover, New York
Ogden RW (2001) Elements of the theory of finite elasticity. In: Fu YB, Ogden RW (eds) Nonlinear elasticity: theory and applications. Cambridge University Press, Cambridge, pp 1–47
Pinsky PM, Ortiz M, Pister KS (1983) Numerical integration of rate constitutive equations in finite deformation analysis. Comput Methods Appl Mech Eng 40:137–158
Romano G (2007) Continuum mechanics on manifolds. Lecture notes, University of Naples Federico II, Naples, Italy, pp 1–695. http://wpage.unina.it/romano
Romano G (2011) On the geometric approach to non-linear continuum mechanics. In: General lecture, XX Congress AIMETA, Bologna, Italy, 13 September. http://wpage.unina.it/romano
Romano G, Barretta R (2011) Covariant hypo-elasticity. Eur J Mech A, Solids 30(6):1012–1023
Romano G, Barretta R (2013) On Euler’s stretching formula in continuum mechanics. Acta Mech 224:211–230
Romano G, Barretta R (2013) Geometric constitutive theory and frame invariance. Int J Non-Linear Mech 51:75–86
Romano G, Marotti de Sciarra F, Diaco M (1998) Hybrid variational principles for non-smooth structural problems. In: Proceedings of the international conference on nonlinear mechanics, ICNM, pp 353–359
Romano G, Rosati L, Diaco M (1999) Well-posedness of mixed formulations in elasticity. Z Angew Math Mech 79(7):435–454
Romano G, Marotti de Sciarra F, Diaco M (2001) Well-posedness and numerical performances of the strain gap method. Int J Numer Methods Eng 51(1):103–126
Romano G, Barretta R, Sellitto C (2005) On the evaluation of the elastoplastic tangent stiffness. In: Owen DRJ, Oñate E, Suarez B (eds) Computational plasticity—fundamentals and applications, part 2. CIMNE, Barcelona, pp 1118–1121
Romano G, Diaco M, Barretta R (2006) On the theory of material inhomogeneities. Mech Res Commun 33(6):758–763
Romano G, Barretta R, Diaco M (2007) Conservation laws for multiphase fracturing materials. In: Carpinteri A, Gambarova P, Ferro G, Plizzari G (eds) Proceedings of the 6th international conference on fracture mechanics of concrete and concrete structures—fracture mechanics of concrete and concrete structures, vol 1. Taylor & Francis, London, pp 411–418
Romano G, Sellitto C, Barretta R (2007) Nonlinear shell theory: a duality approach. J Mech Mater Struct 2(7):1207–1230
Romano G, Barretta R, Barretta A (2009) On Maupertuis principle in dynamics. Rep Math Phys 63(3):331–346
Romano G, Barretta R, Diaco M (2009) On the general form of the law of dynamics. Int J Non-Linear Mech 44(6):689–695
Romano G, Barretta R, Diaco M (2009) On continuum dynamics. J Math Phys 50:102903
Romano G, Barretta R, Diaco M (2010) Algorithmic tangent stiffness in elastoplasticity and elastoviscoplasticity: a geometric insight. Mech Res Commun 37(3):289–292
Romano G, Diaco M, Barretta R (2010) Variational formulation of the first principle of continuum thermodynamics. Contin Mech Thermodyn 22(3):177–187
Romano G, Barretta A, Barretta R (2012) On torsion and shear of Saint-Venant beams. Eur J Mech A, Solids 35:47–60
Segev R (2013) Notes on metric independent analysis of classical fields. Math Methods Appl Sci 36:497–566
Segev R, Rodnay G (1999) Cauchy theorem on manifold. J Elast 56(2):129–144
Šilhavý M (1997) Mechanics and thermodynamics of continuous media. Springer, Berlin
Simó JC (1988) A framework for finite strain elastoplasticity based on maximum plastic dissipation and the multiplicative decomposition: continuum formulation. Comput Methods Appl Mech Eng 66:199–219
Simó JC, Ortiz M (1985) A unified approach to finite deformation elastoplastic analysis based on the use of hyperelastic constitutive equations. Comput Methods Appl Mech Eng 49:221–245
Simó JC, Pister KS (1984) Remarks on rate constitutive equations for finite deformation problems: computational implications. Comput Methods Appl Mech Eng 46:201–215
Spivak M (2005) A comprehensive introduction to differential geometry, vols. I–V, 3rd edn. Publish or Perish, Houston
Truesdell C (1955) Hypo-elasticity. J Ration Mech Anal 4(83–133):1019–1020
Truesdell C (1977/1991) A first course in rational continuum mechanics. Academic Press, New York
Truesdell C, Noll W (1965) The non-linear field theories of mechanics. Handbuch der physik, vol III/3. Springer, Berlin, pp 1–602
Truesdell C, Toupin RA (1960) The classical field theories. Handbuch der physik, vol III/1. Springer, Berlin, pp 226–793
Villaggio P (1997) Mathematical models for elastic structures. Cambridge University Press, Cambridge
Villaggio P (2013) Crisis of mechanics literature? Meccanica. doi:10.1007/s11012-013-9722-y
Yavari A, Ozakin A (2008) Covariance in linearized elasticity. Z Angew Math Phys 59:1081–1110
Yosida K (1980) Functional analysis. Springer, New York
Acknowledgements
The geometric formulation of CM has been the subject of a general lecture delivered by the first author at the AIMETA XX Congress, in Bologna, Italy, on Sept. 13, 2011. The kind invitation of the president of AIMETA and of the president of the local organizing committee is gratefully acknowledged. Useful hints and precious comments by an anonymous reviewer are also gratefully acknowledged.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Romano, G., Barretta, R. & Diaco, M. Geometric continuum mechanics. Meccanica 49, 111–133 (2014). https://doi.org/10.1007/s11012-013-9777-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11012-013-9777-9





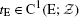 is assumed to be a projection, i.e. surjective with a surjective tangent map.
is assumed to be a projection, i.e. surjective with a surjective tangent map. in which the change of constitutive operator due to the change of observer is not taken into account [
in which the change of constitutive operator due to the change of observer is not taken into account [