A mixed modal-differential quadrature method for free and forced vibration of beams in contact with fluid

Abstract

A simple and accurate mixed modal-differential quadrature formulation is proposed to study the dynamic behavior of beams in contact with fluid. Both free and forced vibration problems are considered. The proposed mixed methodology uses the modal technique for the structural domain while it applies the differential quadrature method (DQM) to the fluid domain. Thus, the governing partial differential equations of the beam and fluid are reduced to a set of ordinary differential equations in time. In the case of forced vibration, the Newmark time integration scheme is employed to solve the resulting system of ordinary differential equations. The proposed formulation, in general, combines the simplicity of the modal method and high accuracy and efficiency of the DQM. Its application is shown by solving some beam-fluid interaction problems. Comparisons with analytical solutions show that the present method is very accurate and reliable. To demonstrate its efficiency, the test problems are also solved using the finite element method (FEM). It is found that the proposed method can produce better accuracy than the FEM using less computational time. The technique presented in this investigation is general and can be used to solve various fluid-structure interaction problems.

Appendices

Appendix A: Explicit analytical solution for natural frequencies of simply supported beams in contact with a bounded incompressible fluid with Dirichlet boundary conditions

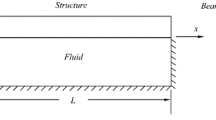
Consider the beam-fluid system shown in Fig. 1. If we ignore the compressibility of the fluid, the non-dimensional governing differential equations for free vibration of the beam-fluid system can be expressed as

$$\begin{aligned} &\frac{\partial^{4} w}{\partial X^{4}} + \alpha\frac{\partial^{2} w}{ \partial t^{2}} = -\beta p ( X, Z =0, t ) \end{aligned}$$

(73)

$$\begin{aligned} & \frac{\partial^{2} p}{\partial X^{2}} + \gamma^{2} \frac{\partial ^{2} p}{ \partial Z^{2}} =0 \end{aligned}$$

(74)

where

$$ \begin{aligned}[c] &X= \frac{x}{L},\qquad Z= \frac{z}{H},\qquad\alpha= \frac{\rho_{s} A L^{4}}{EI},\\ &\beta= \frac{b L^{4}}{EI},\qquad\gamma= \frac{L}{ H} \end{aligned} $$

(75)

The boundary conditions of the fluid domain are given in Eqs. (3) and (4). For free vibration of the beam-fluid system in the nth mode, the normal mode functions are given by [43, 44]

$$ \begin{aligned}[c] &w_{n} ( X ) = W_{n} \sin n\pi X,\\ & p_{n} ( X,Z ) = P_{n} \sin n\pi X \sinh n\pi\vartheta( 1-Z ),\\ & \quad \vartheta= \frac{1}{\gamma} = \frac{H}{L} \end{aligned} $$

(76)

where W _n and P _n are constants. Applying the natural boundary condition at beam-fluid interface (see Eq. (3)), one has

$$ P_{n} = \frac{- \rho_{f} H W_{n}}{n\pi\vartheta\cosh n\pi \vartheta} \omega_{n}^{2} $$

(77)

where ω _n is the nth natural frequency of the beam-fluid system. Now, substituting Eqs. (76) and (77) into Eq. (73) gives

$$ \omega_{n}^{2} = \frac{n^{4} \pi^{4}}{\alpha+ \frac{\rho_{f} H\beta\gamma}{n\pi} \tanh n\pi\vartheta} $$

(78)

Introducing dimensionless frequency parameter $\varOmega_{n}^{2} = \omega_{n}^{2} \frac{\rho_{s} A L^{4}}{EI}$, Eq. (78) can be rewritten as

$$ \varOmega_{n}^{2} = \frac{n^{4} \pi^{4}}{1+ \frac{\lambda}{n\pi} \tanh n\pi\vartheta},\quad\lambda= \frac{\rho_{f} L}{\rho_{s} h} $$

(79)

where h is beam thickness. It can be seen that the dimensionless frequency parameter depends only on values of dimensionless variables λ and ϑ. Besides, when λ→0 or ϑ→0, the wet natural frequencies (given in Eq. (79)) approach to the dry natural frequencies ($\varOmega_{n}^{2} =n^{4} \pi^{4}$).

Appendix B: General implicit analytical solution for free and forced vibration of beams in contact with a bounded fluid

Consider the beam-fluid system shown in Fig. 1. The governing equations for forced vibration of the beam-fluid system is given in Eqs. (1) and (2). The beam and fluid responses are assumed to be

$$ \begin{aligned}[c] &w ( x, t ) = \sum_{j =1}^{N} d_{j} ( t ) \psi_{j} ( x )\\ &p ( x,z,t ) = \sum _{i=1}^{n} \sum_{j=1}^{m} p_{ij} ( t ) \varphi _{i} ( x ) \theta_{j} (z) \end{aligned} $$

(80)

where ψ _j (x) are beam eigenfunctions, φ _i (x) and θ _j (z) are fluid mode shapes. The hydrodynamic pressure can also be described by the following single-series expansion

$$ p ( x,z,t ) = \sum_{j=1}^{nm} P_{j} ( t ) \varLambda_{j} ( x,z ) $$

(81)

where Λ _j (x,z) can be obtained from tensor product of the one-dimensional mode shapes φ _i (x) and θ _j (z) as follows

$$\begin{aligned} & \begin{bmatrix} \varLambda_{1} ( x,z ) & \varLambda_{2} ( x,z )&\dots& \varLambda_{m} ( x,z )\\ \varLambda_{m+1} ( x,z ) & \varLambda_{m+2} ( x,z )&\dots& \varLambda_{2m} ( x,z )\\ \vdots& \vdots&\ddots& \vdots\\ \varLambda_{ ( n - 1 ) m+1} ( x,z ) & \varLambda_{ ( n - 1 ) m+2} ( x,z ) &\dots& \varLambda_{nm} ( x,z ) \end{bmatrix} \\ &\quad = \left\{ \begin{matrix} \varphi _{1} ( x )\\ \varphi _{2} ( x )\\ \vdots\\ \varphi _{n} ( x ) \end{matrix} \right\} \left\{ \begin{matrix} \theta_{1} (z) & \theta_{2} (z) & \cdots & \theta_{m} (z) \end{matrix} \right \} \end{aligned}$$

(82)

Substituting Eqs. (80) and (81) into Eqs. (1) and (2) and using the weak formulation [41, 45], we obtain

$$\begin{aligned} & \begin{bmatrix} [ \boldsymbol{M}^{\boldsymbol{f}} ]_{nm\times nm} & [ \boldsymbol{M}^{*} ]_{nm\times N}\\ [ \boldsymbol{0} ]_{N\times nm} & [ \boldsymbol{M}^{s} ]_{N\times N} \end{bmatrix} \left\{ \begin{matrix} \{\ddot{ \boldsymbol{p} }\}_{nm\times1}\\ \{\ddot{ \boldsymbol{d} }\}_{N\times1} \end{matrix} \right\} \\ &\qquad + \begin{bmatrix} [ \boldsymbol{K}^{f} ]_{nm\times nm} & [ \boldsymbol{0} ]_{nm\times N}\\ [ \boldsymbol{K}^{*} ]_{N\times nm} & [ \boldsymbol{K}^{s} ]_{N\times N} \end{bmatrix} \left\{ \begin{matrix} \{ \boldsymbol{p} \}_{nm\times1}\\ \{ \boldsymbol{d} \}_{N\times1} \end{matrix} \right\} \\ &\quad = \left\{ \begin{matrix} \{ \boldsymbol{0} \}_{nm\times1}\\ \{ \boldsymbol{f}^{s} \}_{N\times1} \end{matrix} \right\} \end{aligned}$$

(83)

where [M ^s], [K ^s], and {f ^s} are defined in Eqs. (37)–(39), and

$$\begin{aligned} & \begin{aligned}[c] &K_{ij}^{*} =b \int_{0}^{L} \psi_{i} \varLambda_{j} ( x,0 ) dx,\\ &\quad i=1,2,\dots,N,\ j=1,2,\dots,nm,\\ &\bigl[ \boldsymbol{M}^{*} \bigr] = \frac{\rho_{f}}{b} \bigl[ \boldsymbol{K}^{*} \bigr]^{T} \end{aligned} \end{aligned}$$

(84)

$$\begin{aligned} & \begin{aligned}[c] &K_{ij}^{f} = \int_{0}^{H} \int_{0}^{L} \biggl( \frac{\partial\varLambda_{i}}{ \partial x} \frac{\partial\varLambda_{j}}{\partial x} + \frac{\partial \varLambda_{i}}{\partial y} \frac{\partial\varLambda_{j}}{\partial y} \biggr) dxdz,\\ & M_{ij}^{f} = \frac{1}{c^{2}} \int_{0}^{H} \int_{0}^{L} \varLambda_{i} \varLambda_{j} dxdz,\quad i,j=1,2,\dots,nm \end{aligned} \end{aligned}$$

(85)

For free vibration, we take {p}={P}e ^iωt and {d}={D}e ^iωt. Thus Eq. (83) becomes

$$ \begin{bmatrix} [ \boldsymbol{K}^{f} ] & [ \boldsymbol{0} ]\\ [ \boldsymbol{K}^{*} ] & [ \boldsymbol{K}^{s} ] \end{bmatrix} \left\{ \begin{matrix} \{ \boldsymbol{P} \}\\ \{ \boldsymbol{D} \} \end{matrix} \right\} = \omega^{2} \begin{bmatrix} [ \boldsymbol{M}^{\boldsymbol{f}} ] & [ \boldsymbol{M}^{*} ]\\ [ \boldsymbol{0} ] & [ \boldsymbol{M}^{s} ] \end{bmatrix} \left\{ \begin{matrix} \{ \boldsymbol{P} \}\\ \{ \boldsymbol{D} \} \end{matrix} \right\} $$

(86)

which can be solved for the eigenvalues ω. Since exact eigenfunctions are employed, the above eigenvalue problem gives exact natural frequencies for beams in contact with bounded fluids. For the case of forced vibration analysis, the above procedure is semi-analytic since the time derivatives should only be approximated. The fluid eigenfunctions for Dirichlet boundary conditions are given in Eq. (76). For the case of Neumann-type boundary conditions, they are

$$ \begin{aligned}[c] &\varphi _{i} ( x ) = \cos\frac{i\pi}{L} x,\\ & \theta_{i} ( z ) = \cosh\frac{i\pi H}{L} \biggl( 1- \frac{z}{H} \biggr) \end{aligned} $$

(87)