Skip to main content
SpringerLink
Log in

Benchmark solution for free vibration of thick open cylindrical shells on Pasternak foundation with general boundary conditions

  • Published:
Meccanica Aims and scope Submit manuscript

Abstract

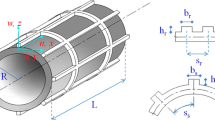
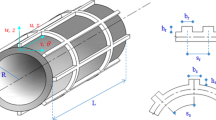
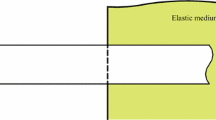
In the present article, a new three-dimensional exact solution for free vibration of thick open cylindrical shells on Pasternak foundation with general boundary conditions is presented. The three-dimensional elasticity theory is employed to formulate the theoretical model. The admissible functions of the thick shells are described as a combination of a three-dimensional (3-D) Fourier cosine series and auxiliary functions. Compared with the traditional Fourier series, the improved Fourier series can eliminate all the relevant discontinuities of the displacements and their derivatives at the edges regardless of boundary conditions. The excellent accuracy and reliability of the current solutions are demonstrated by numerical examples and comparison of the present results with those available in the literature and obtained by using ABAQUS which is based on the finite element method. Numerous new results for thick open cylindrical shells on Pasternak foundation with elastic boundary conditions are presented. In addition, comprehensive studies on the effects of the elastic restraint parameters, geometric parameters and elastic foundation coefficients are also reported.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

References

  1. Tornabene F (2011) Free vibrations of anisotropic doubly-curved shells and panels of revolution with a free-form meridian resting on Winkler–Pasternak elastic foundations. Compos Struct 94(1):186–206

    Article  Google Scholar 

  2. Tornabene F et al (2015) Numerical and exact models for free vibration analysis of cylindrical and spherical shell panels. Compos B Eng 81:231–250

    Article  Google Scholar 

  3. Tornabene F, Ceruti A (2013) Free-form laminated doubly-curved shells and panels of revolution resting on Winkler–Pasternak elastic foundations: a 2-D GDQ solution for static and free vibration analysis. World J Mech 3(01):1

    Article  Google Scholar 

  4. Tornabene F et al (2014) Winkler–Pasternak foundation effect on the static and dynamic analyses of laminated doubly-curved and degenerate shells and panels. Compos B Eng 57:269–296

    Article  Google Scholar 

  5. Tornabene F, Reddy J (2013) FGM and laminated doubly-curved and degenerate shells resting on nonlinear elastic foundations: a GDQ solution for static analysis with a posteriori stress and strain recovery. J Indian Inst Sci 93(4):635–688

    MathSciNet  Google Scholar 

  6. Sofiyev A (2010) The buckling of FGM truncated conical shells subjected to axial compressive load and resting on Winkler–Pasternak foundations. Int J Press Vessels Pip 87(12):753–761

    Article  Google Scholar 

  7. Sofiyev A (2010) Buckling analysis of FGM circular shells under combined loads and resting on the Pasternak type elastic foundation. Mech Res Commun 37(6):539–544

    Article  MATH  Google Scholar 

  8. Sofiyev A, Kuruoglu N (2013) Torsional vibration and buckling of the cylindrical shell with functionally graded coatings surrounded by an elastic medium. Compos B Eng 45(1):1133–1142

    Article  Google Scholar 

  9. Shah AG et al (2010) Vibrations of functionally graded cylindrical shells based on elastic foundations. Acta Mech 211(3–4):293–307

    Article  MATH  Google Scholar 

  10. Tj HG et al (2006) Free vibration characteristics of cylindrical shells partially buried in elastic foundations. J Sound Vib 290(3):785–793

    Article  ADS  Google Scholar 

  11. Shen H-S (2012) Nonlinear vibration of shear deformable FGM cylindrical shells surrounded by an elastic medium. Compos Struct 94(3):1144–1154

    Article  Google Scholar 

  12. Shen H-S, Yang J, Kitipornchai S (2010) Postbuckling of internal pressure loaded FGM cylindrical shells surrounded by an elastic medium. Eur J Mech A Solids 29(3):448–460

    Article  Google Scholar 

  13. Bakhtiari-Nejad F, Bideleh SMM (2012) Nonlinear free vibration analysis of prestressed circular cylindrical shells on the Winkler/Pasternak foundation. Thin Walled Struct 53:26–39

    Article  Google Scholar 

  14. Golovko K, Lugovoi P, Meish V (2007) Solution of axisymmetric dynamic problems for cylindrical shells on an elastic foundation. Int Appl Mech 43(12):1390–1395

    Article  Google Scholar 

  15. Malekzadeh P et al (2008) Three-dimensional free vibration analysis of thick cylindrical shells resting on two-parameter elastic supports. J Sound Vib 313(3):655–675

    Article  ADS  Google Scholar 

  16. Najafov A, Sofiyev A, Kuruoglu N (2013) Torsional vibration and stability of functionally graded orthotropic cylindrical shells on elastic foundations. Meccanica 48(4):829–840

    Article  MathSciNet  MATH  Google Scholar 

  17. Gunawan H et al (2005) Finite element analysis of cylindrical shells partially buried in elastic foundations. Comput Struct 83(21):1730–1741

    Article  Google Scholar 

  18. Farid M, Zahedinejad P, Malekzadeh P (2010) Three-dimensional temperature dependent free vibration analysis of functionally graded material curved panels resting on two-parameter elastic foundation using a hybrid semi-analytic, differential quadrature method. Mater Des 31(1):2–13

    Article  Google Scholar 

  19. Paliwal D, Kanagasabapathy H, Gupta K (1995) The large deflection of an orthotropic cylindrical shell on a Pasternak foundation. Compos Struct 31(1):31–37

    Article  Google Scholar 

  20. Paliwal D, Pandey R (2001) Free vibrations of an orthotropic thin cylindrical shell on a Pasternak foundation. AIAA J 39(11):2188–2191

    Article  ADS  Google Scholar 

  21. Paliwal D, Pandey RK, Nath T (1996) Free vibrations of circular cylindrical shell on Winkler and Pasternak foundations. Int J Press Vessels Pip 69(1):79–89

    Article  Google Scholar 

  22. Paliwal D, Singh S (1999) Free vibrations of orthotropic cylindrical shell on elastic foundation. AIAA J 37(9):1135–1139

    Article  ADS  Google Scholar 

  23. Ye T et al (2014) Three-dimensional free vibration analysis of thick cylindrical shells with general end conditions and resting on elastic foundations. Int J Mech Sci 84:120–137

    Article  Google Scholar 

  24. Suzuki K, Leissa A (1986) Exact solutions for the free vibrations of open cylindrical shells with circumferentially varying curvature and thickness. J Sound Vib 107(1):1–15

    Article  ADS  MATH  Google Scholar 

  25. Mizusawa T (1988) Application of spline strip method to analyse vibration of open cylindrical shells. Int J Numer Methods Eng 26(3):663–676

    Article  MATH  Google Scholar 

  26. Aragh BS, Hedayati H (2012) Static response and free vibration of two-dimensional functionally graded metal/ceramic open cylindrical shells under various boundary conditions. Acta Mech 223(2):309–330

    Article  MathSciNet  MATH  Google Scholar 

  27. Ohga M, Takao H, Shigematsu T (1995) Natural frequencies and modes of open cylindrical shells with a circumferential thickness taper. J Sound Vib 183(1):143–156

    Article  ADS  MATH  Google Scholar 

  28. Zhang L, Xiang Y (2006) Vibration of open circular cylindrical shells with intermediate ring supports. Int J Solids Struct 43(13):3705–3722

    Article  MATH  Google Scholar 

  29. Zhang L, Xiang Y (2006) Vibration of open cylindrical shells with stepped thickness variations. J Eng Mech 132(7):780–784

    Article  Google Scholar 

  30. Ribeiro P (2009) On the influence of membrane inertia and shear deformation on the geometrically non-linear vibrations of open, cylindrical, laminated clamped shells. Compos Sci Technol 69(2):176–185

    Article  MathSciNet  Google Scholar 

  31. Kandasamy S, Singh AV (2006) Free vibration analysis of skewed open circular cylindrical shells. J Sound Vib 290(3):1100–1118

    Article  ADS  Google Scholar 

  32. Kandasamy S, Singh AV (2006) Transient vibration analysis of open circular cylindrical shells. J Vib Acoust 128(3):366–374

    Article  Google Scholar 

  33. Jiarang F, Hongyu S (1997) Exact solution for laminated continuous open cylindrical shells. Appl Math Mech 18(11):1073–1086

    Article  MATH  Google Scholar 

  34. Yu S, Cleghorn W, Fenton R (1995) On the accurate analysis of free vibration of open circular cylindrical shells. J Sound Vib 188(3):315–336

    Article  ADS  MATH  Google Scholar 

  35. Abbas LK, Lei M, Rui X (2009) Natural vibrations of open-variable thickness circular cylindrical shells in high temperature field. J Aerosp Eng 23(3):205–212

    Article  Google Scholar 

  36. Ye T et al (2014) A unified formulation for vibration analysis of open shells with arbitrary boundary conditions. Int J Mech Sci 81:42–59

    Article  Google Scholar 

  37. Ye T et al (2014) A unified Chebyshev–Ritz formulation for vibration analysis of composite laminated deep open shells with arbitrary boundary conditions. Arch Appl Mech 84(4):441–471

    Article  MATH  Google Scholar 

  38. Abramovich H, Zarutskii V (2008) Stability of open circular cylindrical shells reinforced with longitudinal ribs. Int Appl Mech 44(12):1389–1396

    Article  MathSciNet  MATH  Google Scholar 

  39. Padovan J, Koplik B (1970) Vibrations of closed and open sandwich cylindrical shells using refined theory. J Acoust Soc Am 47(3B):862–869

    Article  ADS  Google Scholar 

  40. Fan S, Luah M (1995) Free vibration analysis of arbitrary thin shell structures by using spline finite element. J Sound Vib 179(5):763–776

    Article  ADS  Google Scholar 

  41. Zhang X, Liu G, Lam K (2001) Frequency analysis of cylindrical panels using a wave propagation approach. Appl Acoust 62(5):527–543

    Article  Google Scholar 

  42. Bardell N, Dunsdon J, Langley R (1997) On the free vibration of completely free, open, cylindrically curved isotropic shell panels. J Sound Vib 207(5):647–669

    Article  ADS  Google Scholar 

  43. Lim C, Liew K, Kitipornchai S (1998) Vibration of open cylindrical shells: a three-dimensional elasticity approach. J Acoust Soc Am 104(3):1436–1443

    Article  ADS  Google Scholar 

  44. Brischetto S (2013) Exact elasticity solution for natural frequencies of functionally graded simply-supported structures. CMES. Comput Model Eng Sci 95(5):391–430

    MathSciNet  Google Scholar 

  45. Brischetto S (2014) Three-dimensional exact free vibration analysis of spherical, cylindrical, and flat one-layered panels. Shock Vib 2014:1–29

    Article  Google Scholar 

  46. Brischetto S, Torre R (2014) Exact 3D solutions and finite element 2D models for free vibration analysis of plates and cylinders. Curved Layer Struct 1(1):59–92

    Google Scholar 

  47. Kulikov G et al (2016) Exact geometry solid-shell element based on a sampling surfaces technique for 3D stress analysis of doubly-curved composite shells. Curved Layer Struct 3(1):1–16

    ADS  MathSciNet  Google Scholar 

  48. Li WL (2000) Free vibrations of beams with general boundary conditions. J Sound Vib 237(4):709–725

    Article  ADS  Google Scholar 

  49. Li WL (2002) Comparison of Fourier sine and cosine series expansions for beams with arbitrary boundary conditions. J Sound Vib 255(1):185–194

    Article  ADS  Google Scholar 

Download references

Acknowledgments

The authors would like to thank the anonymous reviewers for their very valuable comments. The authors also gratefully acknowledge the financial support from the National Natural Science Foundation of China (No. 51209052).

Author information

Authors and Affiliations

  1. College of Mechanical and Electrical Engineering, Harbin Engineering University, Harbin, 150001, People’s Republic of China

    Qingshan Wang, Dongyan Shi & Fazl e Ahad

  2. College of Shipbuilding Engineering, Harbin Engineering University, Harbin, 150001, People’s Republic of China

    Fuzhen Pang

Authors
  1. Qingshan Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Dongyan Shi
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Fuzhen Pang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Fazl e Ahad
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Qingshan Wang.

Appendix 1: Detailed expressions of the matrices M, K and G

Appendix 1: Detailed expressions of the matrices M, K and G

$${\mathbf{K}} = \left[ {\begin{array}{*{20}c} {{\mathbf{K}}_{uu} } & {{\mathbf{K}}_{uv} } & {{\mathbf{K}}_{uw} } \\ {{\mathbf{K}}_{uv}^{T} } & {{\mathbf{K}}_{vv} } & {{\mathbf{K}}_{vw} } \\ {{\mathbf{K}}_{uw}^{T} } & {{\mathbf{K}}_{vw}^{T} } & {{\mathbf{K}}_{ww} } \\ \end{array} } \right],{\mathbf{M}} = \left[ {\begin{array}{*{20}c} {{\mathbf{M}}_{uu} } & {\mathbf{0}} & {\mathbf{0}} \\ {\mathbf{0}} & {{\mathbf{M}}_{vv} } & {\mathbf{0}} \\ {\mathbf{0}} & {\mathbf{0}} & {{\mathbf{M}}_{ww} } \\ \end{array} } \right],{\mathbf{G}} = \left[ {\begin{array}{*{20}c} {{\mathbf{G}}_{u} } \\ {{\mathbf{G}}_{v} } \\ {{\mathbf{G}}_{w} } \\ \end{array} } \right]$$
(18)
$$\begin{aligned} {\mathbf{K}}_{uu} = \iiint {\left\{ {\left( {\chi + 2\varUpsilon } \right)r\frac{{\partial {\mathbf{U}}^{T} }}{\partial x}\frac{{\partial {\mathbf{U}}}}{\partial x} + \varUpsilon r\frac{{\partial {\mathbf{U}}^{T} }}{\partial r}\frac{{\partial {\mathbf{U}}}}{\partial r} + \frac{\varUpsilon }{r}\frac{{\partial {\mathbf{U}}^{T} }}{\partial \theta }\frac{{\partial {\mathbf{U}}}}{\partial \theta }} \right\}dV} \hfill \\ + \iint {\left\{ {k_{x0}^{u} {\mathbf{U}}^{T} {\mathbf{U}}} \right\}_{|x = 0} dS_{0} } + \iint {\left\{ {k_{xL}^{u} {\mathbf{U}}^{T} {\mathbf{U}}} \right\}_{|x = L} dS_{1} } \hfill \\ + \iint {\left\{ {k_{\theta 0}^{u} {\mathbf{U}}^{T} {\mathbf{U}}} \right\}_{|\theta = 0} dS_{2} } + \iint {\left\{ {k_{\theta 1}^{u} {\mathbf{U}}^{T} {\mathbf{U}}} \right\}_{|\theta = \phi } dS_{3} } \hfill \\ \iint {\left\{ {K_{w} {\mathbf{W}}^{T} {\mathbf{W}} + K_{s} \frac{{\partial {\mathbf{W}}^{T} }}{\partial r}\frac{{\partial {\mathbf{W}}}}{\partial r} + \frac{{K_{s} }}{{r^{2} }}\frac{{\partial {\mathbf{W}}^{T} }}{\partial \theta }\frac{{\partial {\mathbf{W}}}}{\partial \theta }} \right\}_{|z = 0} dS_{4} } \hfill \\ \end{aligned}$$
(19)
$${\mathbf{K}}_{uv} = \iiint {\left\{ {\chi \left( {\frac{{\partial {\mathbf{V}}^{T} }}{\partial \theta }\frac{{\partial {\mathbf{U}}}}{\partial x} + \frac{{\partial {\mathbf{V}}}}{\partial \theta }\frac{{\partial {\mathbf{U}}^{T} }}{\partial x}} \right) + \varUpsilon \left( {\frac{{\partial {\mathbf{V}}^{T} }}{\partial x}\frac{{\partial {\mathbf{U}}}}{\partial \theta } + \frac{{\partial {\mathbf{V}}}}{\partial x}\frac{{\partial {\mathbf{U}}^{T} }}{\partial \theta }} \right)} \right\}dV}$$
(20)
$${\mathbf{K}}_{uw} = \iiint {\left\{ \begin{aligned} &\chi r\left( {\frac{{\partial {\mathbf{W}}^{T} }}{\partial r}\frac{{\partial {\mathbf{U}}}}{\partial x} + \frac{{\partial {\mathbf{W}}}}{\partial r}\frac{{\partial {\mathbf{U}}^{T} }}{\partial x}} \right) + \chi \left( {{\mathbf{W}}^{T} \frac{{\partial {\mathbf{U}}}}{\partial x} + {\mathbf{W}}\frac{{\partial {\mathbf{U}}^{T} }}{\partial x}} \right) \hfill \\ &+ \varUpsilon \left( {\frac{{\partial {\mathbf{W}}^{T} }}{\partial x}\frac{{\partial {\mathbf{U}}}}{\partial r} + \frac{{\partial {\mathbf{W}}}}{\partial x}\frac{{\partial {\mathbf{U}}^{T} }}{\partial r}} \right) \end{aligned} \right\}dV}$$
(21)
$$\begin{aligned} {\mathbf{K}}_{vv} & = \iiint {\left\{ {\frac{{\left( {\chi + 2\varUpsilon } \right)}}{r}\frac{{\partial {\mathbf{V}}^{T} }}{\partial \theta }\frac{{\partial {\mathbf{V}}}}{\partial \theta } + \varUpsilon r\left( {\frac{{\partial {\mathbf{V}}}}{\partial r} - \frac{{\mathbf{V}}}{r}} \right)\left( {\frac{{\partial {\mathbf{V}}^{T} }}{\partial r} - \frac{{{\mathbf{V}}^{T} }}{r}} \right) + \varUpsilon \frac{{\partial {\mathbf{V}}^{T} }}{\partial x}\frac{{\partial {\mathbf{V}}}}{\partial x}} \right\}dV} \\ & \quad + \iint {\left\{ {k_{x0}^{v} {\mathbf{V}}^{T} {\mathbf{V}}} \right\}_{|x = 0} dS_{0} } + \iint {\left\{ {k_{xL}^{v} {\mathbf{V}}^{T} {\mathbf{V}}} \right\}_{|x = L} dS_{1} } \\ & \quad + \iint {\left\{ {k_{\theta 0}^{v} {\mathbf{V}}^{T} {\mathbf{V}}} \right\}_{|\theta = 0} dS_{2} } + \iint {\left\{ {k_{\theta 1}^{v} {\mathbf{V}}^{T} {\mathbf{V}}} \right\}_{|\theta = \phi } dS_{3} } \\ \end{aligned}$$
(22)
$${\mathbf{K}}_{vw} = \iiint {\left\{ \begin{aligned} &\left( {\chi + 2\varUpsilon } \right)\frac{1}{r}\left( {{\mathbf{W}}^{T} \frac{{\partial {\mathbf{V}}}}{\partial \theta } + {\mathbf{W}}\frac{{\partial {\mathbf{V}}^{T} }}{\partial \theta }} \right) + \chi \left( {\frac{{\partial {\mathbf{W}}^{T} }}{\partial r}\frac{{\partial {\mathbf{V}}}}{\partial \theta } + \frac{{\partial {\mathbf{W}}}}{\partial r}\frac{{\partial {\mathbf{V}}^{T} }}{\partial \theta }} \right) \hfill \\ &+ \varUpsilon \left\{ {\frac{{\partial {\mathbf{W}}^{T} }}{\partial \theta }\left( {\frac{{\partial {\mathbf{V}}}}{\partial r} - \frac{{\mathbf{V}}}{r}} \right) + \frac{{\partial {\mathbf{W}}}}{\partial \theta }\left( {\frac{{\partial {\mathbf{V}}^{T} }}{\partial r} - \frac{{{\mathbf{V}}^{T} }}{r}} \right)} \right\} \hfill \\ \end{aligned} \right\}dV}$$
(23)
$$\begin{aligned} {\mathbf{K}}_{ww} & = \iiint {\left\{ \begin{aligned} \left( {\chi + 2\varUpsilon } \right)r\frac{{\partial {\mathbf{W}}^{T} }}{\partial r}\frac{{\partial {\mathbf{W}}}}{\partial r} + \left( {\chi + 2\varUpsilon } \right)\frac{1}{r}{\mathbf{W}}^{T} {\mathbf{W}} + \varUpsilon \frac{1}{r}\frac{{\partial {\mathbf{W}}^{T} }}{\partial \theta }\frac{{\partial {\mathbf{W}}}}{\partial \theta } + \varUpsilon r\frac{{\partial {\mathbf{W}}^{T} }}{\partial x}\frac{{\partial {\mathbf{W}}}}{\partial x} + \chi \left( {\frac{{\partial {\mathbf{W}}^{T} }}{\partial r}{\mathbf{W}} + \frac{{\partial {\mathbf{W}}}}{\partial r}{\mathbf{W}}^{T} } \right) \hfill \\ \end{aligned} \right\}dV} \\ & \quad + \iint {\left\{ {k_{x0}^{w} {\mathbf{W}}^{T} {\mathbf{W}}} \right\}_{|x = 0} dS_{0} } + \iint {\left\{ {k_{xL}^{w} {\mathbf{W}}^{T} {\mathbf{W}}} \right\}_{|x = L} dS_{1} } + \iint {\left\{ {k_{\theta 0}^{w} {\mathbf{W}}^{T} {\mathbf{W}}} \right\}_{|\theta = 0} dS_{2} } \\ & \quad + \iint {\left\{ {k_{\theta 1}^{w} {\mathbf{W}}^{T} {\mathbf{W}}} \right\}_{|\theta = \phi } dS_{3} } + \iint {\left\{ {K_{w} {\mathbf{W}}^{T} {\mathbf{W}} + K_{s} \frac{{\partial {\mathbf{W}}^{T} }}{\partial x}\frac{{\partial {\mathbf{W}}}}{\partial x} + K_{s} \frac{1}{{r^{2} }}\frac{{\partial {\mathbf{W}}^{T} }}{\partial \theta }\frac{{\partial {\mathbf{W}}}}{\partial \theta }} \right\}_{{|r = R_{1} }} R_{1} dS_{4} } \\ \end{aligned}$$
(24)
$${\mathbf{M}}_{uu} = \iiint {\left\{ {\rho r{\mathbf{U}}^{T} {\mathbf{U}}} \right\}dV};{\mathbf{M}}_{vv} = \iiint {\left\{ {\rho r{\mathbf{V}}^{T} {\mathbf{V}}} \right\}dV};{\mathbf{M}}_{ww} = \iiint {\left\{ {\rho r{\mathbf{W}}^{T} {\mathbf{W}}} \right\}dV}$$
(25)
$${\mathbf{G}}_{u} = \left\{ \begin{aligned} A_{000} , \ldots ,A_{mnq} , \ldots ,A_{MNQ} , \ldots ,a_{00}^{1} , \ldots ,a_{MN}^{1} ,a_{00}^{2} , \ldots ,a_{MN}^{2} \hfill \\ ,a_{00}^{3} , \ldots ,a_{MQ}^{3} ,a_{00}^{4} , \ldots ,a_{MQ}^{4} ,a_{00}^{5} , \ldots ,a_{NQ}^{5} ,a_{00}^{6} , \ldots ,a_{NQ}^{6} \hfill \\ \end{aligned} \right\}e^{j\omega t}$$
(26)
$${\mathbf{G}}_{v} = \left\{ \begin{aligned} B_{000} , \ldots ,B_{mnq} , \ldots ,B_{MNQ} , \ldots ,b_{00}^{1} , \ldots ,b_{MN}^{1} ,b_{00}^{2} , \ldots ,b_{MN}^{2} \hfill \\ ,b_{00}^{3} , \ldots ,b_{MQ}^{3} ,b_{00}^{4} , \ldots ,b_{MQ}^{4} ,b_{00}^{5} , \ldots ,b_{NQ}^{5} ,b_{00}^{6} , \ldots ,b_{NQ}^{6} \hfill \\ \end{aligned} \right\}e^{j\omega t}$$
(27)
$${\mathbf{G}}_{w} = \left\{ \begin{aligned} C_{000} , \ldots ,C_{mnq} , \ldots ,C_{MNQ} , \ldots ,c_{00}^{1} , \ldots ,c_{MN}^{1} ,c_{00}^{2} , \ldots ,c_{MN}^{2} \hfill \\ ,c_{00}^{3} , \ldots ,c_{MQ}^{3} ,c_{00}^{4} , \ldots ,c_{MQ}^{4} ,c_{00}^{5} , \ldots ,c_{NQ}^{5} ,c_{00}^{6} , \ldots ,c_{NQ}^{6} \hfill \\ \end{aligned} \right\}e^{j\omega t}$$
(28)

where

$${\mathbf{U}} = \left\{ \begin{aligned} &\cos \lambda_{L0} x, \ldots ,\cos \lambda_{L0} x\cos \lambda_{\phi n} \theta \cos \lambda_{hq} r, \ldots ,\cos \lambda_{LM} x\cos \lambda_{\phi N} \theta \cos \lambda_{hQ} r, \hfill \\ &\zeta_{r}^{1} \left( r \right), \ldots ,\zeta_{r}^{1} \left( r \right)\cos \lambda_{L0} x\cos \lambda_{\phi n} \theta , \ldots ,\zeta_{z}^{1} \left( z \right)\cos \lambda_{LM} x\cos \lambda_{\phi N} \theta , \hfill \\ &\zeta_{\theta }^{2} \left( \theta \right), \ldots ,\zeta_{\theta }^{2} \left( \theta \right)\cos \lambda_{L0} x\cos \lambda_{hq} r, \ldots ,\zeta_{\theta }^{2} \left( \theta \right)\cos \lambda_{LM} x\cos \lambda_{hQ} r, \hfill \\ &\zeta_{x}^{2} \left( x \right), \ldots ,\zeta_{x}^{2} \left( z \right)os\lambda_{\phi n} \theta \cos \lambda_{hq} r, \ldots ,\zeta_{z}^{2} \left( z \right)\cos \lambda_{\phi N} \theta \cos \lambda_{hQ} r \hfill \\ \end{aligned} \right\}$$
(29)
$${\mathbf{V}} = {\mathbf{W = U}}$$
(30)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wang, Q., Shi, D., Pang, F. et al. Benchmark solution for free vibration of thick open cylindrical shells on Pasternak foundation with general boundary conditions. Meccanica 52, 457–482 (2017). https://doi.org/10.1007/s11012-016-0406-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11012-016-0406-2

Keywords

Search

Navigation