Families of Asymmetric Periodic Orbits in the Restricted Three-body Problem

Abstract

This paper studies the asymmetric solutions of the restricted planar problem of three bodies, two of which are finite, moving in circular orbits around their center of masses, while the third is infinitesimal. We explore, numerically, the families of asymmetric simple-periodic orbits which bifurcate from the basic families of symmetric periodic solutions f, g, h, i, l and m, as well as the asymmetric ones associated with the families c, a and b which emanate from the collinear equilibrium points L ₁, L ₂ and L ₃ correspondingly. The evolution of these asymmetric families covering the entire range of the mass parameter of the problem is presented. We found that some symmetric families have only one bifurcating asymmetric family, others have infinity number of asymmetric families associated with them and others have not branching asymmetric families at all, as the mass parameter varies. The network of the symmetric families and the branching asymmetric families from them when the primaries are equal, when the left primary body is three times bigger than the right one and for the Earth–Moon case, is presented. Minimum and maximum values of the mass parameter of the series of critical symmetric periodic orbits are given. In order to avoid the singularity due to binary collisions between the third body and one of the primaries, we regularize the equations of motion of the problem using the Levi-Civita transformations.

1 Introduction

The study, the determination and the calculation of families of symmetric periodic orbits in the restricted three-body problem is the popular subject of decades researchers while hundreds papers about them have been written. On the contrary, only few papers have dealt with families of asymmetric periodic solutions of the problem (e.g. Kristiansson 1933; Strömgren 1935; Message 1958, 1959; Bartlett 1964; Danby 1967; Deprit et al. 1967; Markellos 1974, 1977, 1978; Taylor 1983a, 1983b; Zagouras et al. 1996; Hènon 2005 etc). A systematic exploration of the families of asymmetric periodic orbits is not as simple as in the case of symmetric ones, because now two initial values must be simultaneously adjusted instead of one. The initial condition space of planar asymmetric periodic orbits is three dimensional while that of symmetric ones which is two dimensional.

The main goal of the present work is the determination of families of asymmetric periodic orbits associated with the families of symmetric simple-periodic orbits throughout the entire range of the mass parameter of the restricted three-body problem. When we mention asymmetric periodic orbit we mean the periodic solution of the problem which is non-symmetric with respect to the horizontal x-axis. The asymmetric families were found consist of asymmetric periodic orbits which are non-symmetric with respect to the horizontal x-axis or with no symmetry at all.

The method we use has been developed by Hénon (1965, 2005). We find the horizontal stability indices a _h and b _h of known symmetric periodic orbits and we check if a _h  = 1 and b _h  = 0 at the same time. In this case the symmetric periodic orbit is a critical orbit, and a family of planar asymmetric periodic orbits bifurcates from it. Once an asymmetric orbit has been found then we calculate the whole one-parameter family to which that orbit belongs. In this way we can calculate the network of the asymmetric families which bifurcate from the symmetric families.

We have, numerically, explored the families of asymmetric simple-periodic (two intersections with x-axis) orbits which bifurcate from the basic symmetric families (Strömgren 1935) f, g, h, i, l and m, as well as the asymmetric ones associated with the families c, a and b which emanate from the collinear equilibrium points L ₁, L ₂ and L ₃ correspondingly. For these nine symmetric families we study the existence and the determination of their critical symmetric periodic solutions with a _h  = 1 and b _h  = 0 for the entire range of the mass parameter μ. Then we calculate the bifurcating asymmetric families of these critical points for three cases: when the primary bodies are equal (μ = 0.5), when the left primary is three times bigger than the right one (μ = 0.25) and finally for the Earth–Moon case (μ = 0.012141).

The equations of motion of the infinitesimal mass m ₃, of the planar, circular restricted problem of three bodies, in the usual dimensionless rectangular rotating coordinate system are written as (Szebehely 1967),

$$ \ddot{x}-2\dot{y}=\frac{\partial \Omega}{\partial x}, \quad \ddot{y}+2\dot{x}=\frac{\partial \Omega}{\partial y}, $$

(1)

where dots denote time derivatives while the gravitational potential Ω in synodic coordinates is defined as

$$ \Omega=\frac{1}{2}(x^2+y^2)+\frac{1-\mu}{r_1}+\frac{\mu}{r_2}, $$

(2)

where

$$ r_1^2=(x+\mu)^2+y^2, \quad r_2^2=(x+\mu-1)^2+y^2 $$

(3)

and μ is the mass parameter of the problem. The primaries m ₁ and m ₂ have masses 1−μ and μ, and coordinates (−μ, 0), (1−μ, 0) correspondingly.

The energy (Jacobi) integral of this problem, is given by the expression

$$ \dot{x}^2+\dot{y}^2=2\Omega-C, $$

(4)

where C is the Jacobi constant.

Due to the large number of calculated periodic orbits and the often fact that the third body collides with the two primaries, we regularize the equations of motion (Szebehely 1967) using the Levi-Civita (1906) transformations. The Levi-Civita regularization is a local regularization and therefore we eliminate the two singularities of the problem (for each primary body) separately.

2 Case of Equal Primaries μ = 0.5

In this section we present the network of the planar symmetric simple-periodic orbits of the classical restricted three-body problem as it has illustrated by Papadakis (1996) when the masses of the primary bodies are equal (μ = 0.5, Copenhagen problem). By symmetric simple-periodic orbits we mean the solutions which have two perpendicular intersections with the horizontal x-axis.

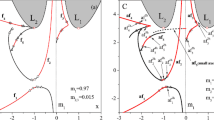
In this case, there are 22 families which are classified in three groups. The first group consists of pairs of families which are symmetric to each other with respect to the origin (namely the family pairs are: i-g, h-f, a-b, s-t, u-v, w-x and y-z), the second one contains families with periodic orbits which have the y-axis as an axis of symmetry (namely the families of this group are: c, m, l, k and r) and the third group has families with the following property: for each periodic orbit of the family with Jacobian constant C, there is a symmetric, with respect to the y-axis, periodic orbit which corresponds to the same value of the Jacobian constant C (namely the families of the third group are: j, n and o). In Fig. 1 we present the network of the symmetric families of the problem (simple-periodic solutions) and we distinguish the families a, b and c which emanate from the collinear equilibrium points as well as the six basic families f, g, h, i, l and m where we are going to study. Families a and b consist of retrograde symmetric periodic orbits around the equilibrium points L ₂ and L ₃ correspondingly, family f has periodic orbits which are retrograde around the second body m ₂, family h has retrograde orbits around the first body m ₁, family i has direct orbits around m ₁ and family g consists of direct orbits around m ₂. As we have already mentioned all these families belong to the first group and therefore for a given periodic orbit of one family, one obtains the symmetric to it periodic orbit of its pair family by replacing x, y and μ by −x, −y and 1−μ. So, for instance, family a changes into family b and vice versa. We will use this property in order to determine these coupled-families.

Fig. 1

The network of the families of symmetric (black lines) and asymmetric (blue lines) periodic orbits of the restricted three-body problem with equal primaries. Small circles denote the positions of the critical symmetric periodic orbits (a _h  = 1, b _h  = 0)

Family c consists of symmetric periodic orbits which are retrograde orbits around the inner collinear equilibrium point L ₁, and families l and m have periodic orbits which are retrograde solutions around the two primaries m ₁ and m ₂. Properties, initial conditions, evolution, etc. of the above mentioned 22 families in the case of equal masses (μ = 0.5) or not (μ ≠ 0.5) in the gravitational and in the photogravitational restricted three-body problem are given, in detail, by Hénon (1965), Papadakis (1996) etc.

Although we have calculated asymmetric solutions from several symmetric families of the problem, the main goal of this work is the determination of the asymmetric families which bifurcate from the nine basic symmetric families and to study their evolution as the parameter of mass varies.

We remark that in Fig. 1, as well as in all the Figures in this paper, only those parts of the family characteristics are presented which represent simple-periodic orbits. The family characteristics continue with other parts corresponding to higher-multiplicity orbits which evolve after collisions with one of the primaries, but these parts are not considered in this paper.

In Fig. 1 with small circles we denote the positions of the critical symmetric periodic orbits (a _h  = 1, b _h  = 0) from which families of non-symmetric periodic orbits bifurcate for μ = 0.5, while the dotted vertical lines denote the positions of the primary bodies. The predictor-corrector procedure for the determination of asymmetric periodic solutions (and the continuation of a family) of a dynamical system of two degrees of freedom, as our problem, is given in detail by Markellos and Halioulias (1977). All calculations reported here were performed using the variable step R-K 8th-order direct integration and settings the allowable energy variation ΔC = |C _start − C _end| < 10⁻¹² and $|{{\mathbf{x}}}_0-{{\mathbf{x}}}_T| < 10^{-8}$ (initial and final conditions at t = 0 and t = T).

2.1 Families of the Equilibrium Points

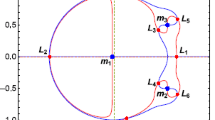
In this subsection we present the network of the symmetric and asymmetric families around the collinear equilibrium points L _i , i = 1,...,3. In the left frame of Fig. 2 the 8 families of symmetric simple-periodic orbits (i.e. the families c, i, x, r, o, s, y and n) which exist around the inner collinear equilibrium point L ₁, are illustrated. In the middle frame we zoom in the area A of the left frame while in the right frame we enlarge the area B of the middle frame. In all these frames we present the characteristic curves (blue lines) of families of asymmetric simple-periodic orbits which bifurcate from critical symmetric periodic orbits (small circles) of the above symmetric families. Although we will focus our attention in the family c and their asymmetric families bifurcate from it, we note here that the characteristic curve of the only asymmetric family which bifurcates from family c for μ = 0.5, and all the asymmetric families bifurcating from the other families which we present in Fig. 2, spiral around points in the (x ₀, C) plane which have ordinate $C=C_{L_{(4,5)}}.$

Fig. 2

The network of the symmetric and asymmetric families near the equilibrium points L ₁ (left). Zooming in area A (middle) and B (right)

The characteristic curves of the asymmetric families near the other two collinear equilibrium points L ₂ and L ₃ have the same property as we see in Fig. 3.

Fig. 3

The network of the symmetric and asymmetric families near the equilibrium points L ₂ (left) and L ₃ (right)

We note that the characteristic curves of the families of symmetric periodic orbits specify the initial conditions of the periodic orbits namely ${\mathbf{x}}_{{\mathbf{0}}}=\{x_0, y_0=0, \dot{x}_0=0, \dot{y}_0(C)\}.$ Contrary, the characteristic curves of the families of asymmetric periodic orbits in the (x ₀, C) plane do not define the complete set of the initial conditions of the orbits since they do not provide any information about the values of the vertical or the horizontal component of the velocity of the third body. For comparison reasons, between symmetric and asymmetric families, we use the same presentation on the (x ₀, C) plane. We also note that in all figures, we plot the characteristic curves of the families of asymmetric periodic orbits which correspond to $\dot{x}_0 > 0.$ In Fig. 4 we present characteristic curves of the two families: the family a of the symmetric periodic orbits which emanate from the collinear point L ₂ as well as the family of asymmetric periodic orbits which bifurcate from it. In the third frame of this Figure the stability diagram of these two families using the isoenergetic stability horizontal parameters a _h and b _h for the symmetric family and the index S _h  = (a _h  + d _h )/2 for the asymmetric one (Hénon 1965a, 1973), is illustrated. The first periodic orbits of the asymmetric family are stable since −1 ≤ S _h  ≤ 1.

Fig. 4

Characteristic curve of the asymmetric family which bifurcates from the symmetric family a (left). C versus T from the symmetric family a and the asymmetric family (middle). The stability diagram of the symmetric family a (solid lines) and of the asymmetric family (dashed line) (right)

In the next Figure three members of this asymmetric family are plotted. The first periodic orbit is the critical one from which the asymmetric family starts. The second one is a typical asymmetric periodic orbit of the family while the last is one of the termination orbits of the family. The family terminates with a homoclinic asymptotic orbit on the triangular equilibrium point L ₅ (Fig. 5). All the asymmetric periodic orbits of this family are non-symmetric and with respect to the y-axis. If we calculate the family when the initial velocity $\dot{x}_0 < 0,$ then the family terminates with homoclinic asymptotic orbit on the symmetric triangular equilibrium point L ₄. As we have already mentioned, family b is symmetric to family a and therefore we find the critical symmetric periodic orbit of family b by the corresponding critical orbit of family a by replacing x ₀ = −x _T/2 (the Jacobi constant C is the same). The family of asymmetric periodic orbits which bifurcate from family b has orbits which are symmetric, with respect to y-axis, to the asymmetric periodic orbits of family a and it is not presented here. In Figs. 6 and 7 we present the symmetric family c, which emanate from the inner collinear equilibrium point L ₁, as well as the family of asymmetric periodic orbits which bifurcates from it. The asymmetric family has its first periodic orbits stable, from one side has termination orbits which are homoclinic asymptotic orbits at L ₅ (third frame of Fig. 7), and from the other side $(\dot{x}_0 < 0)$ the family terminates at L ₄. All the asymmetric periodic orbits of this family are symmetric with respect to the y-axis. This asymmetric family was described at first by Strömgren (1930) who published some limiting members from this “class of pear-shaped orbits" and were asymptotic at L ₄, later Danby (1967) gave the evolution of this family from the critical symmetric periodic orbit of “Strömgren’s class c" up to the asymptotic orbit at L ₄.

Fig. 5

The critical symmetric periodic orbit of family a (left) and a typical member of the family of asymmetric periodic orbits which bifurcate from family a (middle). The “end" of the asymmetric family is a homoclinic asymptotic orbit on L ₅ (right)

Fig. 6

Characteristic curve of the asymmetric family which bifurcates from the symmetric family c (left). C versus T from the symmetric family c and the asymmetric family (middle). The stability diagram of the symmetric family c (solid lines) and of the asymmetric family (dashed line) (right)

2.2 The Basic Families f, g, h, i, l and m

Families f, h and m, for μ = 0.5, have not critical simple-symmetric periodic orbits of type a _h  = 1 and b _h  = 0 hence there are no intersections with another family of asymmetric periodic orbits.

Family i (and its symmetric g) has one critical symmetric orbit and one family of asymmetric periodic orbits bifurcates from it. In Figs. 2 (first frame) and 3 (left frame) we plot the characteristic curves (blue lines) of the asymmetric families i and g correspondingly. Both characteristics spiral around points in the (x ₀, C) plane which have ordinate $C=C_{L_{4(5)}}.$ The asymmetric family i begins with stable periodic orbits as we see from its stability diagram in Fig. 8 (left frame). The critical bifurcating symmetric periodic orbit (middle frame) and the termination asymptotic orbit to L ₅ (right frame) of the asymmetric family, are plotted. All the asymmetric periodic orbits of this family (and its symmetric g) are non-symmetric with respect to both x and y-axis.

Symmetric family l and its bifurcating families of asymmetric periodic orbits, is the most popular subject concerning the asymmetric solutions of the restricted three-body problem in the bibliography.

Excluding the asymmetric Trojan type of orbits, the first family of asymmetric simple periodic orbits was determined by Kristiansson (1933) for the case of equal masses of the primaries. It was an asymmetric family which bifurcates from the symmetric family l at a point of bifurcation called l ₂ by Hénon (1965). Strömgren in 1935 found, among others asymmetric-asymptotic orbits, the terminating orbit of this asymmetric family and Bartlett (1964) added to this list several asymmetric orbits. Message (1959, 1970) determined the same asymmetric family in the Sun-Jupiter case and Markellos (1978) did the same for μ = 0.45, while Taylor (1983) described the evolution of the family as the mass parameter varies. A second family of asymmetric periodic orbits bifurcating from the point l ₃ (Hénon, 1973) of the family l of symmetric orbits was determined numerically by Markellos et al. (1978) for μ = 0.45.

Family l has a different property with respect to the previous eight presented symmetric families. The characteristic curve of this family in the (x ₀, C) plane, spirals in to a point which has ordinate $C=C_{L_{4(5)}}$ (Left frame-Fig. 9). In the next two frames of the same Fig. 9, which are enlargements of the first frame, we see the evolution of the characteristic curve. As the curve spirals in toward the limit, the oscillations of C become smaller in amplitude.

Fig. 7

The critical symmetric periodic orbit of family c (left) and a typical member of the family of asymmetric periodic orbits which bifurcate from family c (middle). The “end" of the asymmetric family is a homoclinic asymptotic orbit on L ₅ (right)

Fig. 8

Left: The stability diagram of the symmetric family i (solid lines) and of the asymmetric family (dashed line). Middle: The critical symmetric periodic orbit of family i. Right: The termination homoclinic asymptotic orbit of the family of asymmetric periodic orbits

We calculated the stability parameters of the family l and we found the symmetric periodic orbits with a _h  = 1 and b _h  = 0. From the first four bifurcation points we determined numerically the families of asymmetric periodic orbits which bifurcate from them. In Fig. 9 the first four asymmetric families (blue lines) are presented. The characteristic curves of these families spiral around points which have ordinate $C=C_{L_{4(5)}}.$ In every loop of the characteristic curve of the symmetric family l, a new bifurcating family of asymmetric periodic orbits exist. The family l possesses, theoretically, infinity number of bifurcation-critical points and therefore infinity families of asymmetric periodic orbits bifurcate from them.

In the left frame of Fig. 10 we illustrate the characteristic curves of the first four asymmetric families of family l in the $(x, \dot{x})$ plane. The inside windows of this frame are enlargement areas of the characteristic curves of the third and fourth asymmetric family. Projection of the family l of symmetric periodic orbits and the branching of the four families of asymmetric periodic orbits in the (C, T) plane are shown (Fig. 10—middle). In the last frame of Fig. 10 we plot the stability parameters a _h and b _h versus C of the symmetric family l as well as the stability curve S _h of the first bifurcating asymmetric family (dotted line). The first asymmetric periodic orbits of this family are stable. Similarly the rest of the three families of asymmetric periodic orbits have their first periodic orbits stable. The small circles which are labeled by the numbers 1,...,4 indicate the first four critical symmetric periodic orbits of family l.

In the first row of Fig. 11 we present the first four critical symmetric periodic orbits of family l while in the second row we plot the “termination" orbits (orbits which approximate the asymptotic orbits) of the four asymmetric families correspondingly. In the last frame of the second row the two inside windows which are enlargements of the area near the triangular equilibrium points, are presented.

Fig. 9

The symmetric family l and the first four asymmetric families which bifurcate from it. Left: The first and the second families of asymmetric periodic orbits. Center: Zoom in the area of the second and the third asymmetric families. Right: Zoom in the area of the third and the fourth asymmetric families

Fig. 10

Characteristic curves of the first four asymmetric families which bifurcate from the symmetric family l (left). C versus T from the symmetric family l and the first four asymmetric families (middle). The stability diagram of the symmetric family l (solid lines) and of the first asymmetric family (dashed line) (right)

From the present results we see that all the determined four families of asymmetric periodic orbits terminate from one side, with a homoclinic asymptotic orbit at L ₄ or L ₅ alternatively. From the other side ($\dot{x} < 0,$) due to the symmetrical property of the solutions (Szebehely 1967), these families terminate again with homoclinic asymptotic orbits at L ₅ or L ₄ (alternatively). So we ascertain, numerically, for the specific family the conjecture of Markellos et al. (1978) that, infinite number of families of asymmetric simple-periodic orbits branching from the symmetric family l and terminate with homoclinic asymptotic orbits at the equilateral Lagrangian points L ₄ (from one side) and L ₅ (from another side).

3 Series of Critical Periodic Orbits

In this subsection we explore how the bifurcating asymmetric families from the nine symmetric families of periodic solutions evolve with the mass parameter. So we need to know how the critical symmetric periodic orbits with a _h  = 1 and b _h  = 0 change as μ varies. We shall call the set of initial conditions and other quantities describing a critical orbit for a range of values of μ, a bifurcation series or a series of critical orbits.

The families f, h and m have not critical symmetric periodic orbits, of the above type, and therefore there are not bifurcating asymmetric families from them throughout the range of the mass parameter.

The other six families have critical orbits for various values of μ and asymmetric families, when the primary bodies are not equal, bifurcate from the corresponding symmetric families a, b, c, l, i and g of the problem. So, for these six families, we computed numerous critical periodic orbits with a _h  = 1 and b _h  = 0 for the entire range of μ in order to trace the series accurately and densely. In Fig. 12 we illustrate the characteristic curves of these series of critical periodic orbits where x ₀ is the initial condition (t = 0, y = 0) (solid lines) and x ₁ the position of the particle on the x-axis at the period t = T/2 (dashed lines).

Fig. 11

First Row: Four critical symmetric periodic orbits of family l from which four families of asymmetric periodic orbits bifurcate. Second row: The “termination" orbits of these four families are homoclinic asymmetric asymptotic orbits to L ₄ or L ₅

We have plotted the characteristic curves only in the range μ ∈ [0, 0.5] since we can obtain the curves for μ ∈ [0.5, 1] as follows: The curves of the family a (corresponding the family b) for μ ≥ 0.5 are obtained from the curves of the family b (corresponding the family a) for μ ≤ 0.5 by substituting μ = 1−μ, x ₀ = −x ₁ and x ₁ = −x ₀. Similarly working we obtain the series of the critical periodic orbits of the families i and g for μ ≥ 0.5. The curves of the family c for μ ≥ 0.5 are obtained from the same family c for μ ≤ 0.5 by substituting μ = 1−μ, x ₀ = −x ₁ and x ₁ = −x ₀. Similarly we work for the family l.

From the first bifurcation point of family l we obtain the only series of critical periodic orbits which exists in the entire range of μ (solid and dashed black lines in the fourth frame of Fig. 12).

In the fourth frame of Fig. 12 we present the characteristic curves of the three first series of critical periodic orbits of the family l. We note here that the second series l ₂ starts at μ = 0.5 and has a minimum at μ = 0.0737 and then it comes back at μ = 0.5 on the third series of critical periodic orbits l ₃. Similarly, the third series goes up to a minimum μ = 0.1058 and then it comes back on the fourth series (at μ = 0.5) and so on.

In two small windows inside the forth frame of Fig. 12, we present details of the characteristic curves around the areas A and B where the minima, with respect to μ, of the series l ₂ and l ₃ occur.

In Table 1 we give the corresponding minimum and maximum values of the mass parameter for each series of critical periodic orbits. We note here that in this Table we give the range of μ in which families g and i have infinite number of bifurcating asymmetric families g _k and i _k ,  k = 1,...,∞ correspondingly.

Table 1 Minimum and maximum of the mass parameter μ of the series of critical symmetric periodic orbits

4 Cases of Non-equal Primaries

In this subsection we study the evolution of the families of asymmetric periodic orbits when the primary bodies of the problem are not equal. Two cases are examined. In the first case we consider that the left primary body is three times bigger than the right one (μ = 0.25) and then we study the Earth–Moon case where μ = 0.012141.

4.1 Case of μ = 0.25

Five families, of the families we study, have critical symmetric periodic orbits for μ = 0.5. Namely, the families a, b and c which emanate from the collinear equilibrium points, have one critical symmetric periodic orbit with a _h  = 1 and b _h  = 0 and therefore one family of asymmetric periodic orbits bifurcates from each such point. Family l, as in the Copenhagen problem (μ = 0.5), keeps to contain infinite number of critical periodic orbits and thus there exist infinite number of families of asymmetric simple periodic orbits branching from this family. The difference, with respect to the case when μ = 0.5, is that now family g has infinite number of families of asymmetric simple periodic orbits which bifurcate from it. In the right frame of Fig. 13, where we zoom in the area of family g, we observe that now (for μ = 0.25), the characteristic curve of this family, in the (x, C) plane, spirals asymptotically around point which has ordinate $C=C_{L_{4(5)}}.$ This means that for every new loop of the characteristic curve, a new critical symmetric periodic orbit exists and therefore a new asymmetric family bifurcates from this point.

Fig. 12

Series of the critical periodic orbits of families a, b, c, l, i and g for varying μ. The dotted lines named by m ₁ and m ₂ represent the positions of the primary bodies

In the first row of Fig. 14 we plot the critical symmetric periodic orbits of families a, b, c, l (one of the infinite) and g (one of the infinite) while in the second row of the same figure we present the corresponding “termination" orbits of the bifurcating families of asymmetric periodic orbits of these five families. All the calculated asymmetric periodic orbits of these families are unstable except the first few orbits, for each family, near the bifurcating point.

Fig. 13

Left: The network of the symmetric and asymmetric families of the restricted three-body problem with unequal primaries (μ = 0.25). Right: Zooming areas near the family g

4.2 Earth–Moon Case (μ = 0.012141)

In the Earth–Moon case the network of the symmetric and asymmetric families is quite different with respect to the two previous cases. Only two families, of the nine symmetric families we study, have critical periodic orbits. Namely, the families a, c, h, f, m, i and g have not asymmetric families which bifurcate from them. Only the families b and l have branching asymmetric families. Family b has one critical symmetric periodic orbit and therefore one bifurcating asymmetric family. In contrast of the previous examined cases, family l has not any more infinite number of asymmetric bifurcating families. Now, in the Earth–Moon case, family l has one critical periodic orbit and thus only one asymmetric family bifurcates from it.

In Fig. 15 we present the network of the families of symmetric simple-periodic orbits (black solid lines) as well as the characteristic curves of the two families of asymmetric periodic orbits which bifurcate from the families b and l correspondingly (blue solid lines). In the left frame of Fig. 16 we present the evolution of the family of asymmetric periodic orbits which bifurcates from the family b. The black periodic orbit is the critical symmetric one and the rest colored orbits are typical members of the asymmetric family. The asymmetric family terminates on the triangular equilibrium point L ₅. As we have already mentioned about the symmetry property of the solutions of the problem, there is the symmetric part, with respect to the synodical axis, of this asymmetric family which terminates on the other triangular equilibrium point L ₄. The initial conditions corresponding to a symmetric orbit are ${{\mathbf{x}}}=(x_0,y_0=0,\dot{x}_0=0,\dot{y}_0),$ but when the orbit is not symmetric (with respect to the synodical line x) then the initial conditions are ${{\mathbf{x}}}=(x_0,y_0=0,\dot{x}_0,\dot{y}_0)$ i.e. we have three free variables. So for the numerical determination of one periodic orbit we need the intersection points of the orbit with the x-axis. From the left frame of Fig. 16 we observe that there are asymmetric periodic orbits of the family which do not intersect the synodical axis any more. In the search for symmetric periodic orbits, the numerical integration of the equations of motion only need to proceed for half the period because of the symmetry property of the solutions. For asymmetric orbits, however, numerical integration continues until the orbit is closed again and the periodicity conditions are established at the end of the period. Therefore, for asymmetric periodic orbits the x-axis does not offer any special advantage and any other line in the plane (x,y) can be used instead. So, for the computation of asymmetric periodic orbits which do not intersect the synodical line we use the horizontal line that passes through the equilateral equilibrium point L ₅.

Fig. 14

First row: Critical symmetric periodic orbits of families a, b, c, l and g for μ = 0.25. Second row: The corresponding “termination" orbits of the bifurcating asymmetric families of the above families

The blue solid line in Fig. 15 presents the characteristic curve of the asymmetric family which bifurcates from family b. This stops at the point where the last asymmetric periodic orbit intersects the synodical line. The blue dotted line presents the characteristic curve of the same asymmetric family with initial conditions on the horizontal line that passes through the equilibrium point L ₅.

The family of asymmetric periodic orbits which bifurcates from the symmetric family b consists of stable solutions as we see from the stability diagram of the family (dashed line) in the right frame of Fig. 16.

This calculated asymmetric family is the known short-period family emanating from the Lagrangian equilibrium point L ₅ and terminates on a symmetrical periodic orbit belonging to the family b, which family b emanates from the collinear equilibrium point L ₃ (Deprit et al. 1967). The critical symmetric simple-periodic orbit of family b is the orbit where the branches of the short-period family of L ₄ and L ₅ meet the branch of L ₃. Family l, as we have already mentioned, has only one bifurcating asymmetric family. This occurs because the characteristic curve of the symmetric family l, in the (x,C) plane, does not spiral at any point (Fig. 15). In the first row of Fig. 17 we present the evolution of the family of asymmetric periodic orbits. The asymmetric family consists of simple periodic orbits (blue solid characteristic curve) and then has orbits with four intersections with x-axis (blue dashed line). The family terminates on a symmetrical periodic orbit which belongs to a family of symmetric periodic orbits with multiplicity 2 (two intersections with x-axis at the half period).

Fig. 15

The network of the symmetric and asymmetric families in the Earth–Moon case (μ = 0.012141)

In the second frame of Fig. 17 we have plotted a member of the family of asymmetric simple periodic orbits which has the horizontal stability parameter S _h  = −1. This means that this critical orbit represents bifurcation of the asymmetric family with another family of asymmetric double-periodic orbits (Hénon 1965a). We found several critical asymmetric periodic orbits with S _h  = −1, of the calculated asymmetric families in the present work, but this time as an example, we have calculated this new asymmetric family and we present its characteristic curve in the (x, C) plane (red closed line in Fig. 15) and in $(x, \dot{x})$ plane (red closed curve in the frame of second row of Fig. 17). Typical members of this family of asymmetric double-periodic orbits we plot in the second row of Fig. 17. Initial conditions and other quantities describing all the critical symmetric simple-periodic orbits (a _h  = 1 and b _h  = 0), which are presented in the figures of this paper, are given in Table 2.

Table 2 Critical symmetric simple-periodic orbits (a _h  = 1, b _h  = 0)

Initial conditions, energy, period and stability of random members, corresponding to the families of asymmetric periodic solutions plotted in Figs. 2, 13 (right frame, inside window) and 17 (second row), are listed in Table 3. In all these asymmetric orbits we have

Fig. 16

Left: The evolution of the family of asymmetric periodic orbits in the Earth–Moon case (μ = 0.012141) which bifurcates from family b. Right: The stability diagram of the family b of the symmetric periodic orbits (solid lines) and the stability diagram of the bifurcating asymmetric family (dashed line)

$\dot{y}_0 > 0.$

Table 3 Initial conditions, energy, period and stability of random samples of asymmetric periodic solutions presented in this paper

5 Comments

We have studied the families of asymmetric periodic orbits which bifurcate from the basic symmetric families of the restricted three-body problem. Namely, we calculated the bifurcating asymmetric families from the symmetric families c, a and b, which emanate from the collinear equilibrium points L _i , i = 1,2,3 correspondingly, as well as from the six basic symmetric families l, m, h, f, i and g, of the problem. We have examined the evolution of these asymmetric families as the mass parameter μ of the problem varies. In order to avoid the singularity due to binary collisions between the third body and one of the primaries, we regularize the equations of motion of the problem using the Levi-Civita transformations.

From our results we conclude:

• 1. Families m, h and f have not critical symmetric periodic orbits of type a _h  = 1 and b _h  = 0 and therefore there are not bifurcating families of asymmetric simple-periodic orbits from these families for the entire range of μ.

• 2. Families a, b and c have bifurcating asymmetric families for the majority of values of the mass parameter but not for every value of μ (Table 1). For the values of μ, where asymmetric families exist, each of the families a and b always has one bifurcating asymmetric family.

• 3. Family c in the range of μ ∈ [0.0668, 0.5] has families of asymmetric simple-periodic orbits bifurcate from it. Namely, for each value of μ ∈ (0.1479, 0.5) family c has one bifurcating asymmetric family while for each value of μ ∈ (0.0668, 0.1479) has two bifurcating asymmetric families. Substituting μ = 1−μ we obtain the corresponding intervals of the mass parameter μ for μ > 0.5.

• 4. Family l is the only family which has at least one bifurcating asymmetric family for the entire range of the mass parameter. For the majority of values of μ (Table 1), family l has infinite number of asymmetric families which bifurcate from it. Namely, as we observe from the fourth frame of Fig. 12 and the minima and maxima values of μ as they are given in Table 1, family l has one asymmetric family for each value of μ in the interval 0 ≤ μ < 0.0737, two asymmetric families for μ = 0.0737, three asymmetric families for each value of μ when 0.0737 < μ < 0.1058 and four asymmetric families for μ = 0.1058. For μ > 0.1058 family l has more (but finite number) asymmetric families (zoom area A in the fourth frame of Fig. 12) up to the value μ = 0.122. For μ ∈ [0.123, 0.5] the characteristic curves, in the (x, C) plane, of the family l spiral around points which have ordinate $C=C_{L_{4(5)}}$ and infinite number of bifurcating asymmetric families exist. For μ > 0.5 we have the symmetric situation (μ = 1−μ).

• 5. Family g in the interval μ ∈ [0.0651, 0.6442] has asymmetric families as follows: one asymmetric family for each value of μ ∈[0.0651, 0.12], infinite number of asymmetric families for each value of μ ∈ [0.1205, 0.4805] and one asymmetric family for each value of μ ∈ [0.481, 0.6442] (fifth frame of Fig. 12 and Table 1). Substituting μ = 1−μ we obtain the corresponding intervals of the mass parameter for the symmetric family i.

• 6. All the families of asymmetric simple-periodic orbits we found which bifurcate from the basic simple-symmetric families under consideration, terminate from one side at the Lagrangian point L ₄ and from the other at L ₅. The terminating orbits are homoclinic asymptotic orbits to one or to the other equilibrium point.

• 7. The asymmetric families we found mainly consist of periodic solutions which are strongly unstable except in a small vicinity near the bifurcation critical periodic orbits (index −1 < S _h  < 1 in Figs. 4, 6, 8 and 10). The only family which consist of stable asymmetric periodic solutions entirely, is the bifurcating asymmetric family from the symmetric family b in the Earth–Moon case (right frame of Fig. 16).

• 8. When the primary bodies are equal (μ = 0.5), the asymmetry families a, b, i and g consists of periodic orbits without any symmetry (Figs. 5 and 8) whilst the asymmetry families c and l have periodic orbits which are symmetric with respect to the vertical y-axis (Figs. 7 and 11). For μ ≠ 0.5 all the periodic orbits of the asymmetry families we found are without any symmetry (Figs. 14, 16 and 17).

Fig. 17

First row: The evolution of the family of asymmetric periodic orbits which bifurcates from the symmetric family l in the Earth–Moon case (μ = 0.012141). Second row: First frame: Characteristic curves of two bifurcating families of asymmetric periodic orbits. Rest frames: The evolution of the family of asymmetric double-periodic orbits which bifurcates from the family of asymmetric simple-periodic orbits. The red periodic orbit is the critical bifurcation orbit of the two families of asymmetric solutions