On the Fractional Order Model of Viscoelasticity

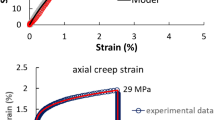
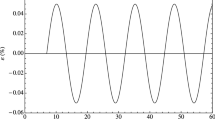
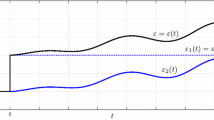
Abstract

Fractional order models of viscoelasticity have proven to be very useful for modeling of polymers. Time domain responses as stress relaxation and creep as well as frequency domain responses are well represented. The drawback of fractional order models is that the fractional order operators are difficult to handle numerically. This is in particular true for fractional derivative operators. Here we propose a formulation based on internal variables of stress kind. The corresponding rate equations then involves a fractional integral which means that they can be identified as Volterra integral equations of the second kind. The kernel of a fractional integral is integrable and positive definite. By using this, we show that a unique solution exists to the rate equation. A motivation for using fractional operators in viscoelasticity is that a whole spectrum of damping mechanisms can be included in a single internal variable. This is further motivated here. By a suitable choice of material parameters for the classical viscoelastic model, we observe both numerically and analytically that the classical model with a large number of internal variables (each representing a specific damping mechanism) converges to the fractional order model with a single internal variable. Finally, we show that the fractional order viscoelastic model satisfies the Clausius–Duhem inequality (CDI).