Skip to main content
SpringerLink
Log in

Dynamic stability and bifurcation of a nonlinear in-extensional rotating shaft with internal damping

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

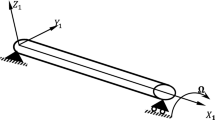
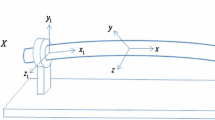
In this paper, stability and bifurcations in a simply supported rotating shaft are studied. The shaft is modeled as an in-extensional spinning beam with large amplitude, which includes the effects of nonlinear curvature and inertia. To include the internal damping, it is assumed that the shaft is made of a viscoelastic material. In addition, the torsional stiffness and external damping of the shaft are considered. To find the boundaries of stability, the linearized shaft model is used. The bifurcations considered here are Hopf and double zero eigenvalues. Using center manifold theory and the method of normal form, analytical expressions are obtained, which describe the behavior of the rotating shaft in the neighborhood of the bifurcations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  1. Bolotin, V.V.: Dynamic Stability of Elastic Systems. Holden-Day, San Francisco (1964)

    MATH  Google Scholar 

  2. Yamamoto, T., Ishida, Y., Ikeda, T.: Super-summed-and-differential harmonic oscillations in a symmetrical rotating shaft system. Bull. JSME 28, 679–686 (1985)

    Article  Google Scholar 

  3. Kurnik, W.: Bifurcating self-excited vibrations of a horizontally rotating viscoelastic shaft. Ing.-Arch. 57, 467–476 (1987)

    Article  MATH  Google Scholar 

  4. Shaw, J., Shaw, S.W.: Instabilities and bifurcations in a rotating shaft. J. Sound Vib. 132, 227–244 (1989)

    Article  MATH  Google Scholar 

  5. Shaw, J., Shaw, S.W.: Non-linear resonance of an unbalanced rotating shaft with internal damping. J. Sound Vib. 147, 435–451 (1991)

    Article  Google Scholar 

  6. Chang, C.O., Cheng, J.W.: Non-linear dynamics and instability of a rotating shaft-disk system. J. Sound Vib. 160, 433–454 (1993)

    Article  MATH  Google Scholar 

  7. Ishida, Y., Yamamoto, T.: Forced oscillations of a rotating shaft with nonlinear spring characteristics and internal damping (1/2 order subharmonic oscillations and entrainment). Nonlinear Dyn. 4, 413–431 (1993)

    Article  Google Scholar 

  8. Noah, S., Sundararajan, P.: Significance of considering nonlinear effects in predicting the dynamic behavior of rotating machinery. J. Vib. Control 1, 431–458 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  9. Ishida, Y., Nagasaka, I., Inoue, T., Lee, S.: Forced oscillations of a vertical continuous rotor with geometric nonlinearity. Nonlinear Dyn. 11, 107–120 (1996)

    Article  Google Scholar 

  10. Kurnik, W.: Stability and bifurcation analysis of a nonlinear transversally loaded rotating shaft. Nonlinear Dyn. 5, 39–52 (1994)

    Google Scholar 

  11. Cveticanin, L.: Large in-plane motion of a rotor. J. Vib. Acoust. 120, 267–271 (1998)

    Article  Google Scholar 

  12. Ji, Z., Zu, J.W.: Method of multiple scales for vibration analysis of rotor-shaft systems with non-linear bearing pedestal model. J. Sound Vib. 218, 293–305 (1998)

    Article  Google Scholar 

  13. Luczko, J.: A geometrically non-linear model of rotating shafts with internal resonance and self-excited vibration. J. Sound Vib. 255, 433–456 (2002)

    Article  Google Scholar 

  14. Shabaneh, N., Zu, J.W.: Nonlinear dynamic analysis of a rotor shaft system with viscoelastically supported bearings. J. Sound Vib. 125, 290–298 (2003)

    Google Scholar 

  15. Ji, J.C., Leung, A.Y.T.: Non-linear oscillations of a rotor-magnetic bearing system under superharmonic resonance conditions. Int. J. Non-Linear Mech. 38, 829–835 (2003)

    Article  MATH  Google Scholar 

  16. Ishida, Y., Inoue, T.: Internal resonance phenomena of the Jeffcott Rotor with nonlinear spring characteristics. J. Vib. Acoust. 126, 476–484 (2004)

    Article  Google Scholar 

  17. Viana Serra Villa, C., Sinou, J.J., Thouverez, F.: The invariant manifold approach applied to nonlinear dynamics of a rotor-bearing system. Eur. J. Mech. A, Solids 24, 676–689 (2005)

    Article  MATH  Google Scholar 

  18. Cveticanin, L.: Free vibration of a Jeffcott rotor with pure cubic nonlinear elastic property of the shaft. Mech. Mach. Theory 40, 1330–1344 (2005)

    Article  MATH  Google Scholar 

  19. Wang, J.S., Wang, C.C.: Nonlinear dynamic and bifurcation analysis of short aerodynamic journal bearings. Tribol. Int. 38, 740–748 (2005)

    Article  Google Scholar 

  20. Dimentberg, M.F.: Vibration of a rotating shaft with randomly varying internal damping. J. Sound Vib. 285, 759–765 (2005)

    Article  Google Scholar 

  21. Shahghli, M., Khadem, S.E.: Stability analysis of a nonlinear rotating asymmetrical shaft near the resonances. Nonlinear Dyn. 70, 1311–1325 (2012)

    Article  Google Scholar 

  22. Wang, C.-C., Wang, C.-C.: Bifurcation and nonlinear dynamic analysis of noncircular aerodynamic journal bearing system. Nonlinear Dynamics 72, 477–489 (2013)

    Article  MathSciNet  Google Scholar 

  23. Han, Q., Chu, F.: Parametric instability of a Jeffcott rotor with rotationally asymmetric inertia and transverse crack. Nonlinear Dyn. (2013). doi:10.1007/s11071-013-0835-6

    Google Scholar 

  24. Hosseini, S.A.A., Khadem, S.E.: Free vibrations analysis of a rotating shaft with nonlinearities in curvature and inertia. Mech. Mach. Theory 44, 272–288 (2009)

    Article  MATH  Google Scholar 

  25. Hosseini, S.A.A., Khadem, S.E.: Combination resonances in a rotating shaft. Mech. Mach. Theory 44, 1535–1547 (2009)

    Article  MATH  Google Scholar 

  26. Khadem, S.E., Shahgholi, M., Hosseini, S.A.A.: Primary resonances of a nonlinear in-extensional rotating shaft. Mech. Mach. Theory 45, 1067–1081 (2010)

    Article  MATH  Google Scholar 

  27. Khadem, S.E., Shahgholi, M., Hosseini, S.A.A.: Two-mode combination resonances of an in-extensional rotating shaft with large amplitude. Nonlinear Dyn. 65, 217–233 (2011)

    Article  MathSciNet  Google Scholar 

  28. Crespo da Silva, M.R.M., Glynn, C.C.: Nonlinear flexural-flexural-torsional dynamics of inextensional beams. I. Equations of motion. J. Struct. Mech. 6, 437–448 (1978)

    Article  Google Scholar 

  29. Nayfeh, A.H., Pai, P.F.: Linear and Nonlinear Structural Mechanics. Wiley-Interscience, New York (2004)

    Book  MATH  Google Scholar 

  30. Chandiramani, N.K., Librescu, L., Aboudi, J.: The theory of orthotropic viscoelastic shear deformable composite flat panel and their dynamic stability. Int. J. Solids Struct. 25, 465–482 (1989)

    Article  MATH  Google Scholar 

  31. Ehrich, F.F.: Shaft whirl induced by rotor internal damping. J. Appl. Mech. 31, 279–282 (1964)

    Article  MATH  Google Scholar 

  32. Wiggins, S.: Introduction to Applied Nonlinear Dynamical Systems and Chaos. Springer, New York (1990)

    Book  MATH  Google Scholar 

  33. Nayfeh, A.H.: Method of Normal Forms. Wiley-Interscience, New York (1993)

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Kharazmi University, Mofatteh Avenue, P.O. Box 15719-14911, Tehran, Iran

    S. A. A. Hosseini

Authors
  1. S. A. A. Hosseini
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to S. A. A. Hosseini.

Appendices

Appendix A

Parameters ω, Λ j (j=1–4), Δ j (j=1–8) and Θ j (j=1,2) presented in Sect. 4 are defined as

$$\begin{aligned} &{\omega = \mu _{e}/\bigl(n^{2}\pi ^{2}\mu _{i}\bigr)} \\&{\varLambda _{1} = 2n^{6}\pi ^{6}\mu _{i}/\vartheta} \\&{\varLambda _{2} = n^{8}\pi ^{8}\mu _{i}^{2}\bigl(\mu _{e} + n^{4}\pi ^{4}\mu _{i}\bigr) \bigl(\mu _{e}^{2} + 2n^{4}\pi ^{4}\mu _{i}\mu _{e}}\\&{\hphantom{\varLambda _{2} =} {} - 12n^{4}\pi ^{4} + n^{8}\pi ^{8}\mu _{i}^{2}\bigr)\big/\vartheta^{3}} \\&{\varLambda _{3} = \bigl(\mu _{e}^{2} + n^{4}\pi ^{4}\mu _{e}\mu _{i} + 4n^{4}\pi ^{4}\bigr)/\vartheta} \\&{\varLambda _{4} = 2n^{10}\pi ^{10}\mu _{i}^{2}\bigl(3\mu _{e}^{2} + 6n^{4}\pi ^{4}\mu _{e}\mu _{i} + 3n^{8}\pi ^{8}\mu _{i}^{2}}\\&{\hphantom{\varLambda _{4} =} {} - 4n^{4}\pi ^{4}\bigr)\big/\vartheta ^{3}} \\&{\Delta _{1} = - \bigl[2n^{2}\pi ^{2} \bigl(n^{2}\pi ^{2}/3 - 3/8\bigr)\mu _{e}^{2} \bigl(\mu _{e} + n^{4}\pi ^{4}\mu _{i} \bigr)}\\&{\hphantom{\Delta _{1} =} {} + n^{10}\pi ^{10}\mu _{i}^{2}\bigl(5 \mu _{e} + 2n^{4}\pi ^{4}\mu _{i}\bigr) \bigr]\big/\bigl(2n^{4}\pi ^{4}\mu _{i}^{2} \vartheta \bigr)} \\&{\Delta _{2} = \bigl[7n^{6}\pi ^{6}\mu _{e}\mu _{i}^{2}\bigl(\mu _{e} + n^{4}\pi ^{4}\mu _{i}\bigr)}\\&{\hphantom{\Delta _{2} =} {} + 8 \bigl(n^{2}\pi ^{2}\bigl(n^{2}\pi ^{2}/3 - 3/8\bigr)\mu _{e}^{2} + n^{10}\pi ^{10}\mu _{i}^{2}\bigr)\bigr]}\\&{\hphantom{\Delta _{2} =} {}\big/\bigl(4n^{2}\pi ^{2} \mu _{i}^{2}\vartheta \bigr)} \\&{\Delta _{3} = - \bigl[2\varGamma \mu _{e}^{2} \bigl(\mu _{e} + n^{4}\pi ^{4}\mu _{i} \bigr) + \mu _{i}^{2}n^{10}\pi ^{10}\bigl( - 3\mu _{e}}\\&{\hphantom{\Delta _{3} =} {} + 2n^{4}\pi ^{4}\mu _{i}\bigr) \bigr]\big/\bigl(2n^{4}\pi ^{4}\mu _{i}^{2} \vartheta \bigr)} \\&{\Delta _{4} = - \bigl[n^{6}\pi ^{6}\mu _{e}\mu _{i}^{2}\bigl(\mu _{e} + n^{4}\pi ^{4}\mu _{i}\bigr)}\\&{\hphantom{\Delta _{4} =} {} - 8\bigl(\varGamma \mu _{e}^{2} + n^{10}\pi ^{10}\mu _{i}^{2}\bigr)\bigr]\big/\bigl(4n^{2}\pi ^{2} \mu _{i}^{2}\vartheta \bigr)} \\&{\Delta _{5} = \bigl[3n^{6}\pi ^{6}\mu _{e}\mu _{i}^{2}\bigl(\mu _{e} + n^{4}\pi ^{4}\mu _{i}\bigr)}\\&{\hphantom{\Delta _{5} =} {} - 8\bigl(\varGamma \mu _{e}^{2} + n^{10}\pi ^{10}\mu _{i}^{2}\bigr)\bigr]\big/\bigl(4n^{2}\pi ^{2} \mu _{i}^{2}\vartheta \bigr)} \\&{\Delta _{6} = - \bigl[2\varGamma \mu _{e}^{2} \bigl(\mu _{e} + n^{4}\pi ^{4}\mu _{i} \bigr) + n^{10}\pi ^{10}\mu _{i}^{2}\bigl( - 5\mu _{e}}\\&{\hphantom{\Delta _{6} =} {} + 2n^{4}\pi ^{4}\mu _{i}\bigr) \bigr]\big/\bigl(2n^{4}\pi ^{4}\mu _{i}^{2} \vartheta \bigr)} \\&{\Delta _{5} = - \bigl[5n^{6}\pi ^{6}\mu _{e}\mu _{i}^{2}\bigl(\mu _{e} + n^{4}\pi ^{4}\mu _{i}\bigr)}\\&{\hphantom{\Delta _{5} =} {} + 8\bigl(\varGamma \mu _{e}^{2} + n^{10}\pi ^{10}\mu _{i}^{2}\bigr)\bigr]\big/\bigl(4n^{2}\pi ^{2} \mu _{i}^{2}\vartheta \bigr)} \\&{\Delta _{8} = - \bigl[2\varGamma \mu _{e}^{2} \bigl(\mu _{e} + n^{4}\pi ^{4}\mu _{i} \bigr) }\\&{\hphantom{\Delta _{8} =} {}+ n^{10}\pi ^{10}\mu _{i}^{2}\bigl(3 \mu _{e} + 2n^{4}\pi ^{4}\mu _{i}\bigr) \bigr]\big/\bigl(2n^{4}\pi ^{4}\mu _{i}^{2} \vartheta \bigr)} \\&{\varTheta _{1} = \varGamma \mu _{e}\bigl(\mu _{e} + n^{4}\pi ^{4}\mu _{i}\bigr)\big/ \bigl(n^{2}\pi ^{2}\mu _{i}\vartheta \bigr)} \\&{\varTheta _{2} = - 2\varGamma \mu _{e}n^{2} \pi ^{2}\big/\bigl(n^{2}\pi ^{2}\mu _{i} \vartheta \bigr)} \end{aligned}$$

where

$$\vartheta = \mu _{e}^{2} + 2n^{4}\pi ^{4}\mu _{e}\mu _{i} + n^{8}\pi ^{8}\mu _{i}^{2} + 4n^{4}\pi^{4} $$

Appendix B

Parameter Ψ j (j=1–7) presented in Sect. 4 is defined as

$$\begin{aligned} &{\varPsi _{1} = 1/2(\varTheta _{2} + i\varTheta _{1})} \\&{\varPsi _{2} = 1/8\bigl[( - \Delta _{7} + \Delta _{2} + \Delta _{5} - \Delta _{4})i + \Delta _{1} - \Delta _{3}}\\&{\hphantom{\varPsi _{2} =} {} - \Delta _{6} + \Delta _{8}\bigr]} \\&{\varPsi _{3} = 1/8\bigl[( - 3\Delta _{2} + 3\Delta _{5} + \Delta _{7} - \Delta _{4})i + \Delta _{3} + 3\Delta _{6}}\\&{\hphantom{\varPsi _{3} =} {} + 3\Delta _{1} + \Delta _{8}\bigr]} \\&{\varPsi _{4} = 1/8\bigl[(3\Delta _{2} + 3\Delta _{5} + \Delta _{7} + \Delta _{4})i + \Delta _{3} - 3\Delta _{6}}\\&{\hphantom{\varPsi _{4} =} {} + 3\Delta _{1} - \Delta _{8}\bigr]} \\&{\varPsi _{5} = 8\bigl(\varOmega _{1} + \varLambda _{3}\varepsilon + \varLambda _{4}\varepsilon ^{2} \bigr)} \\&{\varPsi _{6} = 8\bigl(\varLambda _{1}\varepsilon + \varLambda _{2}\varepsilon ^{2}\bigr)} \\&{\varPsi _{7} = 1/8\bigl[( - \Delta _{7} - \Delta _{2} + \Delta _{5} + \Delta _{4})i + \Delta _{1} - \Delta _{3}}\\&{\hphantom{\varPsi _{7} =} {} + \Delta _{6} - \Delta _{8}\bigr]} \end{aligned}$$

Rights and permissions

Reprints and permissions

About this article

Cite this article

Hosseini, S.A.A. Dynamic stability and bifurcation of a nonlinear in-extensional rotating shaft with internal damping. Nonlinear Dyn 74, 345–358 (2013). https://doi.org/10.1007/s11071-013-0974-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-013-0974-9

Keywords

Search

Navigation