Nonlinear vibration of rotating pre-deformed blade with thermal gradient

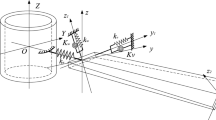
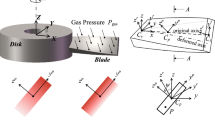
Abstract

In this paper, the nonlinear dynamic behavior is investigated for a rotating pre-deformed pre-twisted blade subjected to harmonic gas pressure. The pre-deformation curve produced by thermal gradient is derived. A novel nonlinear vibration system is established by considering the influence of pre-deformation. The combination of the Lagrange principle and the assumed modes method is utilized to obtain the motion equations, and then the equations are transformed into a dimensionless form through introducing a set of dimensionless parameters. For the purpose of ensuring high precision in determination of the internal resonance condition, the equations of motion are discretized by adequate trial functions. An eigenvalue analysis is conducted on the corresponding linear system to obtain the natural frequencies and examine the possibility of the 2:1 internal resonance. The method of multiple scales is developed to solve the resulting multi-degree-of-freedom nonlinear ordinary differential equations. A numerical integration by means of Runge–Kutta is performed to establish the validity of the derived formulations. The evolution of frequency response curves with the rotating speed is observed. The influences of the thermal gradient, gas pressure and damping coefficient on the resonant dynamics of the system are investigated in detail. For the purpose of comparison, another distribution profile of pre-deformation, which is frequently used in previous literature, is also examined. It could be found that not only the amplitude but also the distribution of the initial deflection could influence the steady-state nonlinear response of the pre-deformed blade. A series of interesting nonlinear dynamic phenomena are discovered from the results.

Appendix

The matrices and their components in Eq. (22) are derived as:

$$\begin{aligned} {{\varvec{M}}}= & {} \left[ {{\begin{array}{cc} {\left[ {{\varvec{M}}}^{{{\varvec{22}}}} \right] _{{n_{2} \times n_{2}}} }&{} \quad 0 \\ 0&{}\quad {\left[ {{\varvec{M}}}^{{{\varvec{33}}}} \right] _{{n_{3} \times n_{3}}} } \\ \end{array} }} \right] \end{aligned}$$

(51)

$$\begin{aligned} {{\varvec{C}}}= & {} \left[ {{\begin{array}{cc} {\left[ {{\varvec{C}}}^{{{\varvec{22}}}} \right] _{{n_{2} \times n_{2}}} }&{}\quad 0\\ 0&{}\quad {\left[ {{{\varvec{C}}}}^{{{\varvec{33}}}} \right] _{{n_{3} \times n_{3}}}} \\ \end{array} }} \right] \end{aligned}$$

(52)

$$\begin{aligned} {{\varvec{K}}}= & {} \left[ {{\begin{array}{cc} {\left[ {{{\varvec{K}}}^{22}} \right] _{{n_{2} \times n_{2}}} }&{}\quad {\left[ {{{\varvec{K}}}^{23}} \right] _{{n_{2} \times n_{3}}} } \\ {\left[ {{{\varvec{K}}}^{32}} \right] _{{n_{3} \times n_{2}} }}&{}\quad {\left[ {{{\varvec{K}}}^{33}} \right] _{{n_{3} \times n_{3}}}} \\ \end{array} }} \right] \end{aligned}$$

(53)

$$\begin{aligned} {{\varvec{q}}}= & {} \left( {q_{21} ,\ldots ,q_{{2n_{2}}} ,q_{31} ,\ldots ,q_{{3n_{3}}} } \right) ^\mathrm{T} \end{aligned}$$

(54)

$$\begin{aligned} {{\varvec{Q}}}= & {} \left( {\left[ {{{\varvec{Q}}}^{2}} \right] _{{n_{2} \times 1}}^\mathrm{T} ,\left[ {{{\varvec{Q}}}^{3}} \right] _{{n_{3} \times 1}}^\mathrm{T}} \right) ^{\mathrm{T}} \end{aligned}$$

(55)

whose components are:

$$\begin{aligned}&M_{ij}^{22} =\int _{0}^{1} {\phi _{2i} \phi _{2j} \hbox {d}x} , \quad M_{ij}^{33} =\int _{0}^{1} {\phi _{3i} \phi _{3j} \hbox {d}x} \end{aligned}$$

(56)

$$\begin{aligned}&C_{ij}^{22} =c_{d}\int _0^1 {\phi _{2i} \phi _{2j} \hbox {d}x} , \quad C_{ij}^{33} =c_{d} \int _{0}^{1} {\phi _{3i} \phi _{3j} \hbox {d}x}\nonumber \\ \end{aligned}$$

(57)

$$\begin{aligned} K_{ij}^{22}= & {} \int _{0}^{1} {J_{3} {\phi }''_{2i} {\phi }''_{2j} \hbox {d}x} +\eta ^{2}\int _{0}^{1} {{u}'_{20} {u}'_{20} {\phi }'_{2i} {\phi }'_{2j} \hbox {d}x} \nonumber \\&-\,\gamma ^{2}\int _0^1 {\phi _{2i} \phi _{2j} \hbox {d}x}\nonumber \\&+\,\frac{1}{2}\gamma ^{2}\int _0^1 {{\phi }'_{2i} {\phi }'_{2j} \left( {1-x^{2}+2\delta -2\delta x} \right) \hbox {d}x}\nonumber \\ \end{aligned}$$

(58)

$$\begin{aligned}&K_{ij}^{23} =\int _0^1 {J_{23} {\phi }''_{2i} {\phi }''_{3j} \hbox {d}x} +\eta ^{2}\int _0^1 {{u}'_{20} {u}'_{30} {\phi }'_{2i} {\phi }'_{3j} \hbox {d}x}\nonumber \\ \end{aligned}$$

(59)

$$\begin{aligned} K_{ij}^{32}= & {} \int _{0}^{1} {J_{23} {\phi }''_{3i} {\phi }''_{2j} \hbox {d}x} +\eta ^{2}\int _0^1 {{u}'_{20} {u}'_{30} {\phi }'_{3i} {\phi }'_{2j} \hbox {d}x} \nonumber \\\end{aligned}$$

(60)

$$\begin{aligned} K_{ij}^{33}= & {} \int _{0}^{1} {J_2 {\phi }''_{3i} {\phi }''_{3j} \hbox {d}x} +\eta ^{2}\int _0^1 {{u}'_{30} {u}'_{30} {\phi }'_{3i} {\phi }'_{3j} \hbox {d}x} \nonumber \\&+\,\frac{1}{2}\gamma ^{2}\int _0^1 {{\phi }'_{3i} {\phi }'_{3j} \left( {1-x^{2}+2\delta -2\delta x} \right) \hbox {d}x}\nonumber \\ \end{aligned}$$

(61)

$$\begin{aligned} Q_{i}^{2}= & {} \int _{0}^{1} {\phi _{2i} P_{gas} \sin \left( {\varTheta x+\varPsi } \right) \hbox {d}x} \cos \left( {\omega t} \right) \nonumber \\&-\,\eta ^{2}\left[ \frac{3}{2}\sum _{j=1}^{{n_{2}}} {\sum _{k=1}^{{n_{2}}} {\left( {\int _{0}^{1} {{u}'_{20} {\phi }'_{2i} {\phi }'_{2j} {\phi }'_{2k} \hbox {d}x} } \right) q_{2j} q_{2k}} }\right. \nonumber \\&+\,\frac{1}{2}\sum _{j=1}^{n_3 } {\sum _{k=1}^{{n_{3}}} {\left( {\int _{0}^{1} {{u}'_{20} {\phi }'_{2i} {\phi }'_{3j} {\phi }'_{3k} \hbox {d}x} } \right) q_{3j} q_{3k}} }\nonumber \\&+\,\sum _{j=1}^{{n_{2}}} {\sum _{k=1}^{{n_{3}}} {\left( {\int _{0}^{1} {{u}'_{30} {\phi }'_{2i} {\phi }'_{2j} {\phi }'_{3k} \hbox {d}x} } \right) q_{2j} q_{3k} } } \nonumber \\&+\,\frac{1}{2}\sum _{j=1}^{n_2 } {\sum _{k=1}^{{n_{2}}} {\sum _{l=1}^{{n_{2}}} {\left( {\int _{0}^{1} {{\phi }'_{2i} {\phi }'_{2j} {\phi }'_{2k} {\phi }'_{2l} \hbox {d}x} } \right) q_{2j} q_{2k} q_{2l} } } } \nonumber \\&\left. +\,\frac{1}{2}\sum _{j=1}^{{n_{2}}} {\sum _{k=1}^{{n_{3}}} {\sum _{l=1}^{{n_{3}}} {\left( {\int _{0}^{1} {{\phi }'_{2i} {\phi }'_{2j} {\phi }'_{3k} {\phi }'_{3l} \hbox {d}x} } \right) q_{2j} q_{3k} q_{3l} } } } \right] ,\nonumber \\&\qquad i=1,2,\ldots , n_{2} \end{aligned}$$

(62)

$$\begin{aligned} Q_{i}^{3}= & {} -\int _0^1 {\phi _{3i} P_{gas} \cos \left( {\varTheta x+\varPsi } \right) \hbox {d}x} \cos \left( {\omega t} \right) \nonumber \\&-\,\eta ^{2}\left[ \frac{1}{2}\sum _{j=1}^{{n_{2}}} {\sum _{k=1}^{{n_{2}}} {\left( {\int _{0}^{1} {{u}'_{30} {\phi }'_{3i} {\phi }'_{2j} {\phi }'_{2k} \hbox {d}x} } \right) q_{2j} q_{2k} } } \right. \nonumber \\&+\,\frac{3}{2}\sum _{j=1}^{{n_{3}}} {\sum _{k=1}^{{n_{3}}} {\left( {\int _{0}^{1} {{u}'_{30} {\phi }'_{3i} {\phi }'_{3j} {\phi }'_{3k} \hbox {d}x} } \right) q_{3j} q_{3k}}}\nonumber \\&+\,\sum _{j=1}^{{n_{2}}} {\sum _{k=1}^{{n_{3}}} {\left( {\int _{0}^{1} {{u}'_{20} {\phi }'_{3i} {\phi }'_{2j} {\phi }'_{3k} \hbox {d}x}}\right) q_{2j} q_{3k} } } \nonumber \\&+\,\frac{1}{2}\sum _{j=1}^{{n_{3}}} {\sum _{k=1}^{{n_{3}}} {\sum _{l=1}^{{n_{3}}} {\left( {\int _{0}^{1} {{\phi }'_{3i} {\phi }'_{3j} {\phi }'_{3k} {\phi }'_{3l} \hbox {d}x} } \right) q_{3j} q_{3k} q_{3l}} } } \nonumber \\&\left. +\,\frac{1}{2}\sum _{j=1}^{{n_{2}}} {\sum _{k=1}^{{n_{2}}} {\sum _{l=1}^{{n_{3}}} {\left( {\int _{0}^{1} {{\phi }'_{3i} {\phi }'_{2j} {\phi }'_{2k} {\phi }'_{3l} \hbox {d}x} } \right) q_{2j} q_{2k} q_{3l}} } } \right] ,\nonumber \\&\qquad i=1,2,\ldots ,n_{3} \end{aligned}$$

(63)

The coefficients in Eq.(25) are written as followings.

$$\begin{aligned} f_{2i}= & {} \int _0^1 {\phi _{2i} P_{gas} \sin \left( {\varTheta x+\varPsi } \right) \hbox {d}x} ,f_{3i}\nonumber \\= & {} -\int _{0}^{1} {\phi _{3i} P_{gas} \cos \left( {\varTheta x+\varPsi } \right) \hbox {d}x} \end{aligned}$$

(64)

$$\begin{aligned} \alpha _{ij}^{21}= & {} -c_d \int _{0}^{1} {\phi _{2i} \phi _{2j} \hbox {d}x} ,\alpha _{ij}^{31} =-c_{d} \int _{0}^{1} {\phi _{3i} \phi _{3j} \hbox {d}x} \nonumber \\\end{aligned}$$

(65)

$$\begin{aligned} \alpha _{ijk}^{22}= & {} -\frac{3}{2}\eta ^{2}\int _{0}^{1} {{u}'_{20} {\phi }'_{2i} {\phi }'_{2j} {\phi }'_{2k} \hbox {d}x} ,\alpha _{ijk}^{32}\nonumber \\= & {} -\frac{1}{2}\eta ^{2}\int _{0}^{1} {{u}'_{30} {\phi }'_{3i} {\phi }'_{2j} {\phi }'_{2k} \hbox {d}x} \end{aligned}$$

(66)

$$\begin{aligned} \alpha _{ijk}^{23}= & {} -\frac{3}{2}\eta ^{2}\int _{0}^{1} {{u}'_{20} {\phi }'_{2i} {\phi }'_{3j} {\phi }'_{3k} \hbox {d}x} ,\alpha _{ijk}^{33}\nonumber \\= & {} -\frac{1}{2}\eta ^{2}\int _{0}^{1} {{u}'_{30} {\phi }'_{3i} {\phi }'_{3j} {\phi }'_{3k} \hbox {d}x} \end{aligned}$$

(67)

$$\begin{aligned} \alpha _{ijk}^{24}= & {} -\eta ^{2}\int _{0}^{1} {{u}'_{30} {\phi }'_{2i} {\phi }'_{2j} {\phi }'_{3k} \hbox {d}x} ,\alpha _{ijk}^{34}\nonumber \\= & {} -\eta ^{2}\int _{0}^{1} {{u}'_{20} {\phi }'_{3i} {\phi }'_{2j} {\phi }'_{3k} \hbox {d}x} \end{aligned}$$

(68)

The coefficients in Eqs. (34)–(36) are listed as following formulation.

For 1 $\le s \le n_{2}$,

$$\begin{aligned} \beta _{10s}= & {} -\sum _{j=1}^{{n_{2}}} {2i\omega _1 M_{sj}^{22} p_{12j}} \end{aligned}$$

(69)

$$\begin{aligned} \beta _{11s}= & {} \sum _{j=1}^{{n_{2}}} {i\omega _1 \alpha _{sj}^{21} p_{12j}} \end{aligned}$$

(70)

$$\begin{aligned} \beta _{12s}= & {} \sum _{j=1}^{{n_{2}}} {\sum _{k=1}^{{n_{2}}} {2\alpha _{sjk}^{22} \bar{{p}}_{12j} p_{22k} } } +\sum _{j=1}^{{n_{3}}} {\sum _{k=1}^{{n_{3}}} {2\alpha _{sjk}^{23} \bar{{p}}_{13j} p_{23k}}}\nonumber \\&+\sum _{j=1}^{{n_{2}}} {\sum _{k=1}^{{n_{3}}} {\alpha _{sjk}^{24} \left( {\bar{{p}}_{12j} p_{23k} +p_{22j} \bar{{p}}_{13k} } \right) } } \end{aligned}$$

(71)

$$\begin{aligned} \beta _{13s}= & {} \frac{f_{2s} }{2} \end{aligned}$$

(72)

$$\begin{aligned} \beta _{20s}= & {} -\sum _{j=1}^{{n_{2}}} {2i\omega _{2} M_{sj}^{22} p_{22j}} \end{aligned}$$

(73)

$$\begin{aligned} \beta _{21s}= & {} \sum _{j=1}^{{n_{2}}} {i\omega _2 \alpha _{sj}^{21} p_{22j}} \end{aligned}$$

(74)

$$\begin{aligned} \beta _{22s}= & {} \sum _{j=1}^{{n_{2}}} {\sum _{k=1}^{{n_{2}}} {\alpha _{sjk}^{22} p_{12j} p_{12k} } } +\sum _{j=1}^{{n_{3}}} {\sum _{k=1}^{{n_{3}}} {\alpha _{sjk}^{23} p_{13j} p_{13k}}}\nonumber \\&+\sum _{j=1}^{{n_{2}}} {\sum _{k=1}^{{n_{3}}} {\alpha _{sjk}^{24} p_{12j} p_{13k}}} \end{aligned}$$

(75)

$$\begin{aligned} \beta _{30s}= & {} -\sum _{j=1}^{{n_{2}}} {2i\omega _3 M_{sj}^{22} p_{32j}} \end{aligned}$$

(76)

$$\begin{aligned} \beta _{31s}= & {} \sum _{j=1}^{{n_{2}}} {i\omega _{3} \alpha _{sj}^{21} p_{32j}} \end{aligned}$$

(77)

For $n_{2}+1 \le s \le \quad n_{2} + n_{3}$, assume that ${s}'=s-n_2$, then

$$\begin{aligned} \beta _{10s}= & {} -\sum _{j=1}^{{n_{3}}} {2i\omega _1 M_{{s}'j}^{33} p_{13j}} \end{aligned}$$

(78)

$$\begin{aligned} \beta _{11s}= & {} \sum _{j=1}^{{n_{3}}} {i\omega _1 \alpha _{{s}'j}^{31} p_{13j}} \end{aligned}$$

(79)

$$\begin{aligned} \beta _{12s}= & {} \sum _{j=1}^{{n_{2}}} {\sum _{k=1}^{{n_{2}}} {2\alpha _{{s}'jk}^{32} \bar{{p}}_{12j} p_{22k} } }\nonumber \\&+\sum _{j=1}^{{n_{3}}} {\sum _{k=1}^{{n_{3}}} {2\alpha _{{s}'jk}^{33} \bar{{p}}_{13j} p_{23k}}} \nonumber \\&+\sum _{j=1}^{{n_{2}}} {\sum _{k=1}^{{n_{3}}} {\alpha _{{s}'jk}^{34} \left( {\bar{{p}}_{12j} p_{23k} +p_{22j} \bar{{p}}_{13k} } \right) } } \end{aligned}$$

(80)

$$\begin{aligned} \beta _{13s}= & {} \frac{f_{3{s}'} }{2} \end{aligned}$$

(81)

$$\begin{aligned} \beta _{20s}= & {} -\sum _{j=1}^{{n_{3}}} {2i\omega _{2} M_{{s}'j}^{33} p_{23j}} \end{aligned}$$

(82)

$$\begin{aligned} \beta _{21s}= & {} \sum _{j=1}^{{n_3}} {i\omega _{2} \alpha _{{s}'j}^{31} p_{23j}} \end{aligned}$$

(83)

$$\begin{aligned} \beta _{22s}= & {} \sum _{j=1}^{{n_{2}}} {\sum _{k=1}^{{n_{2}}} {\alpha _{{s}'jk}^{32} p_{12j} p_{12k}}} +\sum _{j=1}^{{n_{3}}} {\sum _{k=1}^{{n_{3}}} {\alpha _{{s}'jk}^{33} p_{13j} p_{13k}}}\nonumber \\&+\sum _{j=1}^{{n_{2}}} {\sum _{k=1}^{{n_{3}}} {\alpha _{{s}'jk}^{34} p_{12j} p_{13k}}} \end{aligned}$$

(84)

$$\begin{aligned} \beta _{30s}= & {} -\sum _{j=1}^{{n_{3}}} {2i\omega _3 M_{{s}'j}^{33} p_{33j}} \end{aligned}$$

(85)

$$\begin{aligned} \beta _{31s}= & {} \sum _{j=1}^{{n_{3}}} {i\omega _{3} \alpha _{{s}'j}^{31} p_{33j}} \end{aligned}$$

(86)

In Eqs. (69)–(86), the notation $p_{r2j}$ (r = 1, 2, 3; $j= 1, 2,{\ldots }$, $n_{2})$ represents the $j^{\mathrm{th}}$ component in the $r^{\mathrm{th}}$ mode vector of the chrodwise vibration, and $p_{r3j}$ ($r = 1, 2, 3; j = 1, 2, \ldots ,n_{3})$ represents that of the flapwise vibration.