Skip to main content
SpringerLink
Log in

Global dynamics of an autoparametric beam structure

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

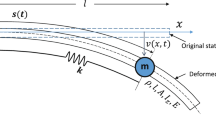
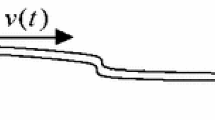
Global dynamics of an autoparametric beam structure derived from a flexible L-shaped beam subjected to base excitation with one-to-two internal resonance and principal resonance are investigated. Hamilton’s principle is employed to obtain the nonlinear partial differential governing equations of the multi-beam structure. A linear theoretical analysis is implemented to derive the modal functions, and the orthogonality conditions are established. The analytical modal functions obtained are then adopted to truncate the partial differential governing equations into a set of coupled nonlinear ordinary differential equations via the Galerkin’s procedure. The method of multiple scales is applied to yield a set of autonomous equations of the first-order approximations to the response of the dynamical system. The Energy-Phase method is used to study the global bifurcation and multi-pulse chaotic dynamics of such autoparametric system. The present analysis indicates that the chaotic dynamics results from the existence of Šilnikov’s type of homoclinic orbits and the parameter set for which the system may exhibit chaotic motions in the sense of Smale horseshoes are predicted analytically. Numerical simulations are performed to validate the theoretical results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  1. Schmidt, G., Tondl, A.: Non-Linear Vibrations. Cambridge University Press, Cambridge (1986)

    Book  MATH  Google Scholar 

  2. Nurre, G.S., Ryan, R.S., Scofield, H.N., Sims, J.L.: Dynamics and control of large space structures. J. Guid. Control Dyn. 7, 514–526 (1984)

    Article  MATH  Google Scholar 

  3. Hu, H.Y., Tian, Q., Zhang, W., Jin, D.P., Song, Y.P.: Nonlinear dynamics and control of large deployable space structures composed of trusses and meshes. Adv. Mech. 43, 390–414 (2013)

    Google Scholar 

  4. Banerjee, B., Bajaj, A.K.: Amplitude modulated chaos in two-degree-of-freedom systems with quadratic nonlinearities. Acta Mech. 124, 131–154 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  5. Haddow, A.G., Barr, A.D.S., Mook, D.T.: Theoretical and experimental study of modal interaction in a two-degree-of-freedom structure. J. Sound Vib. 97, 451–473 (1984)

    Article  MathSciNet  Google Scholar 

  6. Nayfeh, A.H.: Introd. Pert. Tech. Wiley-Interscience, New York (1981)

    Google Scholar 

  7. Bux, S.L., Roberts, J.W.: Non-linear vibratory interactions in systems of coupled beams. J. Sound Vib. 104, 497–520 (1986)

    Article  Google Scholar 

  8. Ashworth, R.P.: The resonances of structures with quadratic inertial non-linearity under direct and parametric harmonic excitation. J. Sound Vib. 118, 47–68 (1987)

    Article  MathSciNet  MATH  Google Scholar 

  9. Nayfeh, A.H., Zavodney, L.D.: Experimental observation of amplitude and phase modulated responses of two internally coupled oscillators to a harmonic excitation. J. Appl. Mech. 55, 706–710 (1988)

    Article  Google Scholar 

  10. Nayfeh, A.H., Balachandran, B., Colbert, M.A., Nayfeh, M.A.: An experimental investigation of complicated responses of a two-degree-of-freedom structure. J. Appl. Mech. 56, 960–967 (1989)

    Article  MathSciNet  Google Scholar 

  11. Nayfeh, A.H., Balachandran, B.: Experimental investigation of resonantly forced oscillations of a two-degree-of-freedom structure. Int. J. Non-Linear Mech. 25, 199–209 (1990)

    Article  Google Scholar 

  12. Nayfeh, T.A., Nayfeh, A.H., Mook, D.T.: A theoretical and experimental investigation of a three-degree-of-freedom structure. Nonlinear Dynamics. 6, 353–374 (1994)

    Article  Google Scholar 

  13. da Sliva Crespo, M.R.M.: A reduced-order analytical model for the nonlinear dynamics of a class of flexible multi-beam structures. Int. J. Solids Struct. 35, 3299–3315 (1998)

    Article  MATH  Google Scholar 

  14. Apiwattanalunggarn, P., Shaw, S.W., Pierre, C.: Component mode synthesis using nonlinear normal modes. Nonlinear Dynamics 41, 17–46 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  15. Hurty, W.C.: Dynamic analysis of structural systems using component modes. AIAA J. 3, 678–685 (1965)

    Article  Google Scholar 

  16. Craig, R.R., Bampton, M.C.C.: Coupling of substructures for dynamic analysis. AIAA J. 6, 1313–1319 (1968)

    Article  MATH  Google Scholar 

  17. Wang, F.X., Bajaj, A.K.: Nonlinear normal modes in multi-mode models of an inertial coupled elastic structure. Nonlinear Dynamics 47, 25–47 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  18. Warminski, J., Cartmell, M.P., Bochenski, M., Ivanov, I.: Analytical and experimental investigations of an autoparametric beam structure. J. Sound Vib. 315, 486–508 (2008)

    Article  Google Scholar 

  19. Georgiades, F., Warminski, J., Cartmell, M.P.: Towards linear modal analysis for an L-shaped beam: Equation of motion. Mech. Res. Commun. 47, 50–60 (2013)

    Article  Google Scholar 

  20. Georgiades, F., Warminski, J., Cartmell, M.P.: Linear modal analysis of L-shaped beam structures. Mech. Syst. Signal Process. 38, 312–332 (2013)

    Article  Google Scholar 

  21. Melnikov, V.K.: On the stability of the center for time periodic perturbation. Trans. Moscow Math. Soc. 12, 1–57 (1963)

    MathSciNet  Google Scholar 

  22. Arnold, V.I.: Instability of dynamical systems with several degrees of freedom. Sov. Math. 5, 581–585 (1964)

    Google Scholar 

  23. Wiggins, S.: Global Bifurcations and Chaos: Analytical Methods. Springer-Verlag, New York (1988)

    Book  MATH  Google Scholar 

  24. Haller, G., Wiggins, S.: N-pulse homoclinic orbits in perturbations of resonant Hamiltonian systems. Arch. Ration. Mech. Anal. 130, 25–101 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  25. Haller, G.: Universal homoclinic bifurcations and chaos near double resonances. J. Stat. Phys. 86, 1011–1051 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  26. Haller, G.: Chaos Near Resonances. Springer-Verlag, New York (1999)

    Book  MATH  Google Scholar 

  27. Malhotra, N., Sri Namachchivaya, N., McDonald, R.J.: Multi-pulse orbits in the motion of flexible spinning discs. J. Nonlinear Sci. 12, 1–26 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  28. Yu, W.Q., Chen, F.Q.: Global bifurcations and chaos in externally excited cyclic system. Commun. Nonlinear Sci. Numer. Simul. 15, 4007–4019 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  29. Li, S.B., Zhang, W., Yao, M.H.: Using energy-phase method to study global bifurcations and Shilnikov type multipulse chaotic dynamics for a nonlinear vibration absorber. Int. J. Bifurc. Chaos 22, 1250001 (2012)

    Article  MATH  Google Scholar 

  30. Yu, T.J., Zhou, S., Zhang, W., Yang, X.D.: Multi-pulse chaotic dynamics of an unbalanced Jeffcott rotor with gravity effect. Nonlinear Dyn. 87, 647–664 (2017)

  31. Yu, T.J., Zhou, S., Yang, X.D., Zhang, W.: Homoclinic orbits and chaos of a supercritical composite panel with free-layer damping treatment in subsonic flow. Compos. Struct. 159, 288–298 (2017)

    Article  Google Scholar 

  32. Zhou, S., Yu, T. J., Yang, X. D., Zhang, W.: Global dynamics of pipes conveying pulsating fluid in the supercritical regime. Int. J. App. Mech. 9(2) (2017)

  33. Suleman, A., Modi, V.J., Venkayya, V.B.: Structural modeling issues in flexible systems. AIAA J. 33, 919–923 (1995)

    Article  MATH  Google Scholar 

  34. Nayfeh, A.H., Pai, P.F.: Linear and Nonlinear Structural Mechanics. Wiley-VCH, Germany (2004)

    Book  MATH  Google Scholar 

  35. Reddy, J.N.: Mechanics of Laminated Composite Plates and Shells: Theory and Analysis (2\(^{nd}\) edition). CRC Press LLC, Florida (2004)

    Google Scholar 

  36. Meirovitch, L.: Analytical Methods in Vibration. The Macmillan Co., New York (1967)

    MATH  Google Scholar 

  37. Asmar, N.H.: Partial Differential Equations and Boundary Value Problems with Fourier Series (2\(^{nd}\) edition). Pearson Education Inc., London (2004)

    Google Scholar 

Download references

Acknowledgements

This research is supported by National Natural Science Foundation of China (NNSFC) through Grant Nos. 11290150, 11290152, 11290154, 11322214 and 11427801, the Funding Project for Academic Human Resources Development in Institutions of Higher Learning under the Jurisdiction of Beijing Municipality (PHRIHLB).

Author information

Authors and Affiliations

  1. Beijing Key Laboratory of Nonlinear Vibrations and Strength of Mechanical Structures, College of Mechanical Engineering, Beijing University of Technology, Beijing, 100124, P. R. China

    Tian-Jun Yu, Wei Zhang & Xiao-Dong Yang

Authors
  1. Tian-Jun Yu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Wei Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Xiao-Dong Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Wei Zhang.

Appendix

Appendix

The coefficients of two-degree-of-freedom equations of motions are expressed as follows

$$\begin{aligned} \mu _1= & {} \frac{\mu K_{11} }{2M_{11} },\quad \omega _1^2 = \frac{K_{11} }{M_{11} },\quad p_{11} = \frac{P_{11} }{M_{11} },\\ p_{12}= & {} \frac{P_{12} }{M_{11} },\quad g_{11} = \frac{G_{11} }{M_{11} },\quad g_{12} = \frac{G_{12} }{M_{11} },\\ g_{22}= & {} \frac{G_{22} }{M_{11} },s_{11} = \frac{S_{11} }{M_{11} },\quad s_{12} = \frac{S_{12} }{M_{11} },\\ s_{21}= & {} \frac{S_{21} }{M_{11} },\quad s_{22} = \frac{S_{22} }{M_{11} }, \quad e_{11} = \frac{E_{11} }{M_{11} }\\ M_{11}= & {} \int _0^1 {\left( {S_{\eta _{11} } } \right) } ^{2}\hbox {d}\xi _1 +\alpha ^{3}\beta \int _0^1 {\left( {S_{\eta _{21} } } \right) } ^{2}\hbox {d}\xi _2\\&+\,\alpha \beta \left( {S_{\eta _{11} } \left( 1 \right) } \right) ^{2},\\ K_{11}= & {} \int _0^1 {\left( {{S}''_{\eta _{11} } } \right) } ^{2}\hbox {d}\xi _1 +\frac{\gamma }{\alpha }\int _0^1 {\left( {{S}''_{\eta _{21} } } \right) } ^{2}\hbox {d}\xi _2\\ P_{11}= & {} \alpha ^{2}\beta \left[ \int _0^1 {S_{\eta _{21} } \left( {-{S}'_{\eta _{21} } } \right) } \hbox {d}\xi _2\right. \\&\left. + \,\int _0^1 {\left( {1-\xi _2 } \right) S_{\eta _{21} } {S}''_{\eta _{21} } } \hbox {d}\xi _2 \right] \\ P_{12}= & {} \alpha ^{2}\beta \left[ \int _0^1 {S_{\eta _{21} } \left( {-{S}'_{\eta _{22} } } \right) } \hbox {d}\xi _2 \right. \\&\left. + \,\int _0^1 {\left( {1-\xi _2 } \right) S_{\eta _{21} } {S}''_{\eta _{22} } } \hbox {d}\xi _2 \right] \\ G_{11}= & {} \alpha ^{2}\beta \int _0^1 {S_{\eta _{21} } } \int _0^1 {\left( {{S}'_{\eta _{11} } } \right) } ^{2}\hbox {d}\xi _1 \hbox {d}\xi _2 ,\\ G_{12}= & {} 2\alpha ^{2}\beta \int _0^1 {S_{\eta _{21} } } \int _0^1 {S}'_{\eta _{11} } {S}'_{\eta _{12} } \hbox {d}\xi _1 \hbox {d}\xi _2\\ G_{22}= & {} \alpha ^{2}\beta \int _0^1 {S_{\eta _{21} } } \int _0^1 {\left( {{S}'_{\eta _{12} } } \right) } ^{2}\hbox {d}\xi _1 \hbox {d}\xi _2\\ S_{11}= & {} -\alpha ^{2}\beta \left[ \int _0^1 S_{\eta _{21} } \hbox {d}\xi _2 \int _0^1 {S_{\eta _{11} } {S}''_{\eta _{11} } } \hbox {d}\xi _1\right. \\&+ \,\frac{1}{2} {S}'_{\eta _{11} } \left( 1 \right) \int _0^1 {S_{\eta _{11} } {S}''_{\eta _{11} } } \hbox {d}\xi _1 +S_{\eta _{11} } \left( 1 \right) \end{aligned}$$
$$\begin{aligned}&\left. \int _0^1 {S_{\eta _{21} } {S}'_{\eta _{21} } } \hbox {d}\xi _2 \right] \\&- \, S_{\eta _{11} } \left( 1 \right) \int _0^1 \left( {1-\xi _2 } \right) S_{\eta _{21}} {S}''_{\eta _{21} } \hbox {d}\xi _2 \\&-\,\int _0^1 {S_{\eta _{21} } } \int _0^1 {\left( {{S}'_{\eta _{11} } } \right) } ^{2}\hbox {d}\xi _1 \hbox {d}\xi _2\\ S_{12}= & {} -\alpha ^{2}\beta \left[ \int _0^1 S_{\eta _{21} } \hbox {d}\xi _2 \int _0^1 {S_{\eta _{11} } {S}''_{\eta _{12} } } \hbox {d}\xi _1 \right. \\&+ \,\frac{1}{2} {S}'_{\eta _{11} } \left( 1 \right) \int _0^1 {S_{\eta _{11} } {S}''_{\eta _{12} } } \hbox {d}\xi _1 +S_{\eta _{11} } \left( 1 \right) \\&\left. \times \int _0^1 {S_{\eta _{21} } {S}'_{\eta _{22} } } \hbox {d}\xi _2 \right] \\&- \, S_{\eta _{11} } \left( 1 \right) \int _0^1 {\left( {1-\xi _2 } \right) S_{\eta _{21} } {S}''_{\eta _{22} } } \hbox {d}\xi _2\\&-\,\int _0^1 {S_{\eta _{21} } } \int _0^1 {{S}'_{\eta _{11} } {S}'_{\eta _{12} } } \hbox {d}\xi _1 \hbox {d}\xi _2\\ S_{21}= & {} -\alpha ^{2}\beta \left[ \int _0^1 S_{\eta _{22} } \hbox {d}\xi _2 \int _0^1 {S_{\eta _{11} } {S}''_{\eta _{11} } } \hbox {d}\xi _1 \right. \\&+ \,\frac{1}{2} {S}'_{\eta _{12} } \left( 1 \right) \int _0^1 {S_{\eta _{11} } {S}''_{\eta _{11} } } \hbox {d}\xi _1 +S_{\eta _{12} } \left( 1 \right) \\&\left. \times \int _0^1 {S_{\eta _{21} } {S}'_{\eta _{21} } } \hbox {d}\xi _2 \right] \\&- \, S_{\eta _{12} } \left( 1 \right) \int _0^1 {\left( {1-\xi _2 } \right) S_{\eta _{21} } {S}''_{\eta _{21} } } \hbox {d}\xi _2 \\&-\,\int _0^1 {S_{\eta _{21} } } \int _0^1 {{S}'_{\eta _{11} } {S}'_{\eta _{12} } } \hbox {d}\xi _1 \hbox {d}\xi _2\\ S_{22}= & {} -\alpha ^{2}\beta \left[ \int _0^1 S_{\eta _{22} } \hbox {d}\xi _2 \int _0^1 {S_{\eta _{11} } {S}''_{\eta _{12} } } \hbox {d}\xi _1\right. \\&+ \,\frac{1}{2} {S}'_{\eta _{12} } \left( 1 \right) \int _0^1 {S_{\eta _{11} } {S}''_{\eta _{12} } } \hbox {d}\xi _1\\&\left. + \, S_{\eta _{12} } \left( 1 \right) \int _0^1 {S_{\eta _{21} } {S}'_{\eta _{22} } } \hbox {d}\xi _2 \right] \\&- \, S_{\eta _{12} } \left( 1 \right) \int _0^1 {\left( {1-\xi _2 } \right) S_{\eta _{21} } {S}''_{\eta _{22} } } \hbox {d}\xi _2\\&-\,\int _0^1 {S_{\eta _{21} } } \int _0^1 {\left( {{S}'_{\eta _{12} } } \right) } ^{2}\hbox {d}\xi _1 \hbox {d}\xi _2\\ E_{11}= & {} \int _0^1 {S_{\eta _{11} } } \hbox {d}\xi _1\mu _2 = \frac{\mu K_{22} }{2M_{22} },\\ \omega _2^2= & {} \frac{K_{22} }{M_{22} }, \quad p_{21} = \frac{P_{21} }{M_{22} },p_{22} = \frac{P_{22} }{M_{22} },\\ \bar{{g}}_{11}= & {} \frac{\bar{{G}}_{11} }{M_{22} },\quad \bar{{g}}_{12} = \frac{\bar{{G}}_{12} }{M_{22} } \end{aligned}$$
$$\begin{aligned} \bar{{g}}_{22}= & {} \frac{\bar{{G}}_{22} }{M_{22} },\quad \bar{{s}}_{11} = \frac{\bar{{S}}_{11} }{M_{22} },\quad \bar{{s}}_{12} = \frac{\bar{{S}}_{12} }{M_{22} },\\ \bar{{s}}_{21}= & {} \frac{\bar{{S}}_{21} }{M_{22} },\bar{{s}}_{22} = \frac{\bar{{S}}_{22} }{M_{22} },e_{12} = \,\frac{E_{12} }{M_{22} }\\ M_{22}= & {} \int _0^1 {\left( {S_{\eta _{12} } } \right) } ^{2}\hbox {d}\xi _1 +\,\alpha ^{3}\beta \int _0^1 {\left( {S_{\eta _{22} } } \right) } ^{2}\hbox {d}\xi _2 \\&+\,\alpha \beta \left( {S_{\eta _{12} } \left( 1 \right) } \right) ^{2},\\ K_{22}= & {} \int _0^1 {\left( {{S}''_{\eta _{12} } } \right) } ^{2}\hbox {d}\xi _1 +\,\frac{\gamma }{\alpha }\int _0^1 {\left( {{S}''_{\eta _{22} } } \right) } ^{2}\hbox {d}\xi _2\\ P_{21}= & {} \alpha ^{2}\beta \left[ \int _0^1 {S_{\eta _{22} } \left( {-{S}'_{\eta _{21} } } \right) } \hbox {d}\xi _2 \right. \\&\left. +\int _0^1 {\left( {1-\xi _2 } \right) S_{\eta _{22} } {S}''_{\eta _{21} } } \hbox {d}\xi _2 \right] \\ P_{22}= & {} \alpha ^{2}\beta \left[ \int _0^1 {S_{\eta _{22} } \left( {-{S}'_{\eta _{22} } } \right) } \hbox {d}\xi _2\right. \\&\left. +\int _0^1 {\left( {1-\xi _2 } \right) S_{\eta _{22} } {S}''_{\eta _{22} } } \hbox {d}\xi _2 \right] \\ \bar{{G}}_{11}= & {} \alpha ^{2}\beta \int _0^1 {S_{\eta _{22} } } \int _0^1 {\left( {{S}'_{\eta _{11} } } \right) } ^{2}\hbox {d}\xi _1 \hbox {d}\xi _2 ,\\ \bar{{G}}_{12}= & {} \alpha ^{2}\beta \left[ \int _0^1 {S_{\eta _{22} } } \int _0^1 {S}'_{\eta _{11} } {S}'_{\eta _{12} } \hbox {d}\xi _1 \hbox {d}\xi _2 \right. \\&\left. + \,\int _0^1 {{S}'_{\eta _{22} } } \int _0^1 {S}'_{\eta _{11} } {S}'_{\eta _{12} } \hbox {d}\xi _1 \hbox {d}\xi _2 \right] \\ \bar{{G}}_{22}= & {} \alpha ^{2}\beta \int _0^1 {S_{\eta _{22} } } \int _0^1 {\left( {{S}'_{\eta _{12} } } \right) } ^{2}\hbox {d}\xi _1 \hbox {d}\xi _2\\ \bar{{S}}_{11}= & {} -\alpha ^{2}\beta \left[ \int _0^1 S_{\eta _{21} } \hbox {d}\xi _2 \int _0^1 {S_{\eta _{12} } {S}''_{\eta _{11} } } \hbox {d}\xi _1\right. \\&+\,\frac{1}{2} {S}'_{\eta _{11} } \left( 1 \right) \int _0^1 {S_{\eta _{12} } {S}''_{\eta _{11} } } \hbox {d}\xi _1\\&\left. + \, S_{\eta _{11} } \left( 1 \right) \int _0^1 {S_{\eta _{22} } {S}'_{\eta _{21} } } \hbox {d}\xi _2 \right] \\&- \, S_{\eta _{11} } \left( 1 \right) \int _0^1 {\left( {1-\xi _2 } \right) S_{\eta _{22} } {S}''_{\eta _{22} } } \hbox {d}\xi _2 \\&- \, \int _0^1 {S_{\eta _{22} } } \int _0^1 {\left( {{S}'_{\eta _{11} } } \right) } ^{2}\hbox {d}\xi _1 \hbox {d}\xi _2\\ \bar{{S}}_{12}= & {} -\alpha ^{2}\beta \left[ \int _0^1 S_{\eta _{21} } \hbox {d}\xi _2 \int _0^1 {S_{\eta _{12} } {S}''_{\eta _{12} } } \hbox {d}\xi _1\right. \\&\left. + \,\frac{1}{2} {S}'_{\eta _{11} } \left( 1 \right) \int _0^1 {S_{\eta _{12} } {S}''_{\eta _{12} } } \hbox {d}\xi _1 +S_{\eta _{11} } \left( 1 \right) \right. \\&\left. \times \int _0^1 S_{\eta _{22} } {S}'_{\eta _{22} } \hbox {d}\xi _2 \right] \end{aligned}$$
$$\begin{aligned}&- \, S_{\eta _{11} } \left( 1 \right) \int _0^1 {\left( {1-\xi _2 } \right) S_{\eta _{22} } {S}''_{\eta _{22} } } \hbox {d}\xi _2 \\&- \, \int _0^1 {S_{\eta _{22} } } \int _0^1 {{S}'_{\eta _{11} } {S}'_{\eta _{12} } } \hbox {d}\xi _1 \hbox {d}\xi _2\\ \bar{{S}}_{21}= & {} -\alpha ^{2}\beta \left[ \int _0^1 S_{\eta _{22} } \hbox {d}\xi _2 \int _0^1 {S_{\eta _{12} } {S}''_{\eta _{11} } } \hbox {d}\xi _1 \right. \\&\left. + \,\frac{1}{2} {S}'_{\eta _{12} } \left( 1 \right) \int _0^1 {S_{\eta _{12} } {S}''_{\eta _{11} } } \hbox {d}\xi _1 +S_{\eta _{12} } \left( 1 \right) \right. \\&\times \left. \int _0^1 {S_{\eta _{22} } {S}'_{\eta _{21} } } \hbox {d}\xi _2 \right] \\&- \, S_{\eta _{12} } \left( 1 \right) \int _0^1 {\left( {1-\xi _2 } \right) S_{\eta _{22} } {S}''_{\eta _{21} } } \hbox {d}\xi _2\\&- \, \int _0^1 {S_{\eta _{22} } } \int _0^1 {{S}'_{\eta _{11} } {S}'_{\eta _{12} } } \hbox {d}\xi _1 \hbox {d}\xi _2\\ \bar{{S}}_{22}= & {} -\alpha ^{2}\beta \left[ \int _0^1 S_{\eta _{22} } \hbox {d}\xi _2 \int _0^1 {S_{\eta _{12} } {S}''_{\eta _{12} } } \hbox {d}\xi _1 \right. \\&\left. + \,\frac{1}{2} {S}'_{\eta _{12} } \left( 1 \right) \int _0^1 {S_{\eta _{12} } {S}''_{\eta _{12} } } \hbox {d}\xi _1 +S_{\eta _{12} } \left( 1 \right) \right. \\&\times \left. \int _0^1 {S_{\eta _{22} } {S}'_{\eta _{22} } } \hbox {d}\xi _2 \right] \\&- \, S_{\eta _{12} } \left( 1 \right) \int _0^1 {\left( {1-\xi _2 } \right) S_{\eta _{22} } {S}''_{\eta _{22} } } \hbox {d}\xi _2 \\&- \, \int _0^1 {S_{\eta _{22} } } \int _0^1 {\left( {{S}'_{\eta _{12} } } \right) } ^{2}\hbox {d}\xi _1 \hbox {d}\xi _2\\ E_{12}= & {} \int _0^1 {S_{\eta _{12} } } \hbox {d}\xi _1 \end{aligned}$$

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yu, TJ., Zhang, W. & Yang, XD. Global dynamics of an autoparametric beam structure. Nonlinear Dyn 88, 1329–1343 (2017). https://doi.org/10.1007/s11071-016-3313-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-016-3313-0

Keywords

Search

Navigation