Skip to main content
SpringerLink
Log in

Deformation rogue wave to the (2+1)-dimensional KdV equation

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

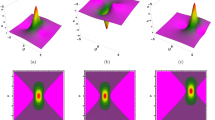
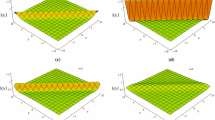
Deformation rogue wave as exact solution of the (2+1)-dimensional Korteweg–de Vries (KdV) equation is obtained via the bilinear method. It is localized in both time and space and is derived by the interaction between lump soliton and a pair of resonance stripe solitons. In contrast to the general method to get the rogue wave, we mainly combine the positive quadratic function and the hyperbolic cosine function, and then the lump soliton can be evolved rogue wave. Under the small perturbation of parameter, rich dynamic phenomena are depicted both theoretically and graphically so as to understand the property of (2+1)-dimensional KdV equation deeply. In general terms, these deformations mainly have three types: two rogue waves, one rogue wave or no rogue wave.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

References

  1. Draper, L.: Freak ocean waves. Weather 21, 2–4 (1966)

    Article  Google Scholar 

  2. Kjeldsen, S.P.: Dangerous wave groups. Nor. Marit. Res. 12, 4–16 (1984)

    Google Scholar 

  3. Walker, D.A.G., Taylor, P.H., Taylor, R.E.: The shape of large surface waves on the open sea and the Draupner new year wave. Appl. Ocean Res. 26, 73–83 (2004)

    Article  Google Scholar 

  4. Stenflo, L., Marklund, M.: Rogue waves in the atmosphere. J. Plasma Phys. 76, 293–295 (2009)

    Article  Google Scholar 

  5. Bludov, Y.V., Konotop, V.V., Akhmediev, N.: Matter rogue waves. Phys. Rev. A 80, 033610 (2009)

    Article  Google Scholar 

  6. Chabchoub, A., Hoffmann, N.P., Akhmediev, N.: Rogue wave observation in a water wave tank. Phys. Rev. Lett. 106, 204502 (2011)

    Article  Google Scholar 

  7. Ablowitz, M.J., Horikis, T.P.: Interacting nonlinear wave envelopes and rogue wave formation in deep water. Phys. Fluids 27, 012107 (2015)

    Article  MATH  Google Scholar 

  8. Didenkulova, I., Pelinovsky, E.: On shallow water rogue wave formation in strongly inhomogeneous channels. J. Phys. A Math. Theor. 49, 194001 (2016)

    Article  MATH  MathSciNet  Google Scholar 

  9. Babanin, A.V., Rogers, W.E.: Generation and limiters of rogue waves. Int. J. Ocean Clim. Syst. 5, 39–50 (2014)

    Article  Google Scholar 

  10. Xia, H., Maimbourg, T., Punzmann, H., Shats, M.: Oscillon dynamics and rogue wave generation in Faraday surface ripples. Phys. Rev. Lett. 109, 114502 (2012)

    Article  Google Scholar 

  11. Walczak, P., Randoux, S., Suret, P.: Optical rogue waves in integrable turbulence. Phys. Rev. Lett. 114, 143903 (2015)

    Article  MathSciNet  Google Scholar 

  12. Solli, D.R., Ropers, C., Koonath, P., Jalali, B.: Optical rogue waves. Nature 450, 1054–1058 (2007)

    Article  Google Scholar 

  13. Schober, C.M.: Rogue waves and the Benjamin–Feir instability. World Sci. Ser. Non linear Sci. Ser. B 12, 194–213 (2015)

    MATH  MathSciNet  Google Scholar 

  14. Ruban, V.P.: Nonlinear stage of the Benjamin–Feir instability: three-dimensional coherent structures and rogue waves. Phys. Rev. Lett. 99, 044502 (2007)

    Article  Google Scholar 

  15. Peregrine, D.H.: Water waves, nonlinear schr\(\ddot{o}\)dinger equations and their solutions. J. Aust. Math. Soc. Ser. B 25, 16–43 (1983)

  16. Zhao, L.C., Guo, B.L., Ling, L.M.: High-order rogue wave solutions for the coupled nonlinear schr\(\ddot{o}\)dinger equations-II. J. Math. Phys. 57, 043508 (2016)

  17. Ankiewicz, A.: Soliton, rational, and periodic solutions for the infinite hierarchy of defocusing nonlinear schr\(\ddot{o}\)dinger equations. Phys. Rev. E 94, 012205 (2016)

    Article  Google Scholar 

  18. Akhmediev, N., Soto-Crespo, J.M., Ankiewicz, A.: Extreme waves that appear from nowhere: on the nature of rogue waves. Phys. Lett. A 373, 2137–2145 (2009)

    Article  MATH  MathSciNet  Google Scholar 

  19. Huang, X.: Rational solitary wave and rogue wave solutions in coupled defocusing Hirota equation. Phys. Lett. A 380, 2136–2141 (2016)

    Article  MATH  MathSciNet  Google Scholar 

  20. Chen, S.H.: Twisted rogue-wave pairs in the Sasa-Satsuma equation. Phys. Rev. E 88, 023202 (2013)

    Article  Google Scholar 

  21. Chen, J.C., Chen, Y., Feng, B.F., Maruno, K.I.: Rational solutions to two-and onedimensional multicomponent Yajima-Oikawa systems. Phys. Lett. A 379, 1510–1519 (2015)

    Article  MATH  MathSciNet  Google Scholar 

  22. Zhang, X.E., Chen, Y., Tang, X.Y.: Rogue wave and a pair of resonance stripe solitons to a reduced generalized (3+1)-dimensional KP equation. arXiv:1610.09507 (2016)

  23. Wen, X.Y., Yan, Z.Y.: Higher-order rational solitons and rogue-like wave solutions of the (2+1)-dimensional nonlinear fluid mechanics equations. Commun. Nonlinear Sci. Numer. Simul. 43, 311–329 (2017)

    Article  MathSciNet  Google Scholar 

  24. Boiti, M., Leon, J.J.-P., Manna, M., Pempinelli, F.: On the spectral transform of a Korteweg-de Vries equation in two spatial dimensions. Inverse Probl. 2, 271–279 (1986)

    Article  MATH  MathSciNet  Google Scholar 

  25. Estevez, P.G., Leble, S.: A wave equation in 2+1: painleve analysis and solutions. Inverse Probl. 11, 925–937 (1995)

    Article  MATH  MathSciNet  Google Scholar 

  26. Lou, S.Y.: Generalized dromion solutions of the (2+1)-dimensional kdv equation. J. Phys. A Math. Theor. 28, 7227–7232 (1995)

    MATH  MathSciNet  Google Scholar 

  27. Tang, X.Y., Lou, S.Y., Zhang, Y.: Localized excitations in (2+1)-dimensional systems. Phys. Rev. E 66, 046601 (2002)

    Article  MathSciNet  Google Scholar 

  28. Lin, J., Wu, F.M.: Fission and fusion of localized coherent structures for a (2+1)-dimensional KdV equation. Chaos Solitons Fractals 19, 189–193 (2004)

    Article  MATH  Google Scholar 

  29. Kumar, C.S., Radha, R., Lakshmanan, M.: Trilinearization and localized coherent structures and periodic solutions for the (2+1)-dimensional kdv and nnv equations. J. Phys. A Math. Theor. 39, 942–955 (2009)

    MATH  Google Scholar 

  30. Radha, R., Lakshmanan, M.: Singularity analysis and localized coherent structures in (2+1)-dimensional generalized Korteweg-de Vries equations. J. Math. Phys. 35, 4746–4756 (1994)

    Article  MATH  MathSciNet  Google Scholar 

  31. Fan, E.G.: Quasi-periodic waves and an asymptotic property for the asymmetrical Nizhniknovikov-Veselov equation. J. Phys. A Math. Theor. 42, 095206 (2009)

    Article  MATH  Google Scholar 

  32. Wang, C.J.: Spatiotemporal deformation of lump solution to (2+1)-dimensional KdV equation. Nonlinear Dyn. 84, 697–702 (2016)

    Article  MathSciNet  Google Scholar 

  33. Wazwaz, A.M.: Single and multiple-soliton solutions for the (2+1)-dimensional KdV equation. Appl. Math. Comput. 204, 20–26 (2008)

    MATH  MathSciNet  Google Scholar 

Download references

Acknowledgements

We would like to express our sincere thanks to S. Y. Lou, W. X. Ma, E. G. Fan, Z. Y. Yan, X. Y. Tang, J. C. Chen, X. Wang and other members of our discussion group for their valuable comments.

Author information

Authors and Affiliations

  1. Shanghai Key Laboratory of Trustworthy Computing, East China Normal University, Shanghai, 200062, China

    Xiaoen Zhang & Yong Chen

Authors
  1. Xiaoen Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yong Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yong Chen.

Additional information

The project is supported by the Global Change Research Program of China (No. 2015CB953904), National Natural Science Foundation of China (Nos. 11275072, 11435005, 11675054) and Shanghai Collaborative Innovation Center of Trustworthy Software for Internet of Things (No. ZF1213).

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhang, X., Chen, Y. Deformation rogue wave to the (2+1)-dimensional KdV equation. Nonlinear Dyn 90, 755–763 (2017). https://doi.org/10.1007/s11071-017-3757-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-017-3757-x

Keywords

Search

Navigation