Dynamics of 1-dof and 2-dof energy sink with geometrically nonlinear damping: application to vibration suppression

Abstract

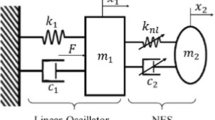
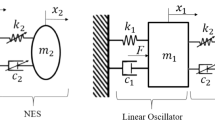
Nonlinear energy sink (NES) refers to a lightweight nonlinear device that is attached to a primary linear or weakly nonlinear system for passive energy localization into itself. In this paper, the dynamics of 1-dof and 2-dof NES with geometrically nonlinear damping is investigated. For 1-dof NES, an analytical treatment for the bifurcations is developed by presenting a slow/fast decomposition leading to slow flows, where a truncation damping and failure frequency are reported. Existence of strongly modulated response (SMR) is also determined. The procedures are then partly paralleled to the investigation of 2-dof NES for the bifurcation analysis, with particular attention paid to the effect of mass distribution between the NES. To study the frequency response for 2-dof NES, the periodic solutions and their stability are obtained by incremental harmonic balance method and Floquet theory, respectively. Poincare map and energy spectrum are specially introduced for numerical analysis of the systems in the neighborhood of resonance frequency, which in turn are used to compare the efficiency of the NESs to the application of vibration suppression. It is demonstrated that a 2-dof NES can generate extra SMR by adjusting its mass distribution and hence to a great extent reduces the undesired periodic responses and provides with a more effective vibration absorber.

Appendix A: Realization of geometrically nonlinear damping

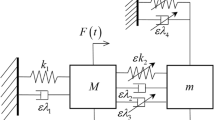
This appendix is devoted to the realization of geometrically nonlinear damping, and one may also refer to Ref. [42,43,44] for its main ideas. The trick here is to use two linear dampers described in Fig. 32, and the dampers are aligned horizontally with one end pinned and the other free to translate vertically a distance x.

Fig. 32

Realization of geometrically nonlinear damping by means of two linear dampers

Let the displacement along each damper be $\delta$, and then, the force in each damper can be computed as

$$\begin{aligned} {F_i} = c\dot{\delta } ,\;\;\;i = 1,2 \end{aligned}$$

(A.1)

one thus have the total vertical force

$$\begin{aligned} F = 2c\dot{\delta } \sin \theta \end{aligned}$$

(A.2)

from geometry, one has the following relationship

$$\begin{aligned} \delta = \sqrt{{l^2} + {x^2}} - l,\;\;\;\;\sin \theta = \frac{x}{{\sqrt{{l^2} + {x^2}} }} \end{aligned}$$

(A.3)

and hence, the time derivative of $\delta$ is

$$\begin{aligned} \dot{\delta } = \frac{{x\dot{x}}}{{\sqrt{{l^2} + {x^2}} }} = \dot{x}\sin \theta \end{aligned}$$

(A.4)

Substituting Eqs. (A.3) and (A.4) into Eq. (A.2) leads to

$$\begin{aligned} F = 2c\dot{x}{\sin ^2}\theta \end{aligned}$$

(A.5)

assuming small angles

$$\begin{aligned} \sin \theta \approx \theta \approx \tan \theta = \frac{x}{l} \end{aligned}$$

(A.6)

one finally have the equation for total force

$$\begin{aligned} F = \frac{{2c}}{{{l^2}}}{x^2}\dot{x} \propto {x^2}\dot{x} \end{aligned}$$

(A.7)

Thus, we have the nonlinear damping. The validity of the small angle approximation can be preserved by selecting a suitably long distance l in the physical setting.