General high-order rogue waves to nonlinear Schrödinger–Boussinesq equation with the dynamical analysis

Abstract

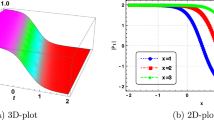
General high-order rogue waves of the nonlinear Schrödinger–Boussinesq equation are obtained by the KP-hierarchy reduction theory, and the N-order rogue waves are expressed with the determinants, whose entries are all algebraic forms, which is shown in the theorem. It is found that the fundamental first-order rogue waves can be classified into three patterns: four-petal state, dark state, bright state by choosing different values of parameter $\alpha$. An interesting phenomenon is discovered as the evolution of the parameter $\alpha$: the rogue wave changes from four-petal state to dark state, whereafter bright state, which are consistent with the change in the corresponding critical points to the function of two variables. Furthermore, the dynamical property of second-order and third-order rogue waves is plotted, which can be regarded as the nonlinear superposition of the fundamental first-order rogue waves.

Appendix A

In this appendix, we will give the proof to the lemma in Sect. 3 with the KP reduction theory. The detail is as follows:

Proof

Based on the solution of the bilinear KP-hierarchy (4), let us bring in the functions with the following form

$$\begin{aligned} \hat{m}^{(n)}= & {} \frac{1}{p+q}\left( -\frac{p-a}{q+a}\right) ^ne^{\gamma +\hat{\gamma }},~~ \hat{\phi }^{(n)}\nonumber \\= & {} (p-a)^ne^{\gamma },~~ \hat{\psi }^{(n)} =\left( \frac{-1}{q+a}\right) ^ne^{\hat{\gamma }}, \end{aligned}$$

(32)

where

$$\begin{aligned} \gamma= & {} \frac{1}{p-a}x_{-1}+px_1+p^2x_2+p^3x_3,\\ \hat{\gamma }= & {} \frac{1}{q+a}+qx_1-q^2x_2+q^3x_3, \end{aligned}$$

in addition, these functions should be satisfied the differential form

$$\begin{aligned} \partial _{x_1}\hat{m}^{(n)}= & {} \hat{\phi }^{(n)}\hat{\psi }^{(n)},\\ \partial _{x_2}\hat{m}^{(n)}= & {} \left( \partial _{x_1}\hat{\phi }^{(n)}\right) \hat{\psi }^{(n)}-\hat{\phi }^{(n)}\left( \partial _{x_1}\hat{\psi }^{(n)}\right) ,\\ \partial _{x_3}\hat{m}^{(n)}= & {} \left( \partial _{x_1}^2\hat{\phi }^{(n)}\right) \hat{\psi }^{(n)}-\left( \partial _{x_1}\hat{\phi }^{(n)}\right) \hat{\psi }^{(n)}\\&\quad +\,\hat{\phi }^{(n)}\left( \partial _{x_1}^2\hat{\psi }^{(n)}\right) ,\\ \partial _{x_{-1}}\hat{m}^{(n)}= & {} -\,\hat{\phi }^{(n-1)}\hat{\psi }^{(n+1)},\\ \hat{m}^{(n+1)}= & {} \hat{m}^{(n)}+\hat{\phi }^{(n)}\hat{\psi }^{(n+1)},\\ \partial _{x_2}\hat{\phi }^{(n)}= & {} \partial _{x_1}^2\hat{\phi }^{(n)},\\ \partial _{x_3}\hat{\phi }^{(n)}= & {} \partial _{x_1}^3\hat{\phi }^{(n)},\\ \hat{\phi }^{(n+1)}= & {} (\partial _{x_1}-a)\hat{\phi }^{(n)},\\ \partial _{x_2}\hat{\psi }^{(n)}= & {} -\partial _{x_1}^2\hat{\psi }^{(n)},\\ \partial _{x_3}\hat{\psi }^{(n)}= & {} \partial _{x_1}^3\hat{\psi }^{(n)},\\ \hat{\psi }^{(n-1)}= & {} -(\partial _{x_1}+a)\hat{\psi }^{(n)}. \end{aligned}$$

Then introduce a new entries of the matrix composed by two differential operators:

$$\begin{aligned} \hat{m}_{ij}^{(\mu \nu n)}= & {} A_{i}^{(\mu )}B_{j}^{(\nu )}\hat{m}^{(n)}, \hat{\phi }_i^{(\mu n)}=A_{i}^{(\mu )}\hat{\phi }^{(n)}, \hat{\psi }_j^{(\nu n)}\\= & {} B_{j}^{(\nu )}\hat{\psi }^{(n)}. \end{aligned}$$

It is clear that the operators $A_i^{\mu }, B_{j}^{\nu }$ can commute with the differential operator $\partial _{x_1}, \partial _{x_{-1}}, \partial _{x_2}, \partial _{x_3}$, so these functions are suit for the bilinear KP-hierarchy (3). Furthermore, for an arbitrary $(i_1, i_2, \ldots i_N;$ $\mu _1, \mu _2, \ldots , \mu _N, j_1, j_2, \ldots , j_N, \nu _1, \nu _2, \ldots , \nu _N)$, the corresponding determinant

$$\begin{aligned} \hat{\tau _n}=\text{ det }\left( \hat{m}_{i_k,j_l}^{(\mu _k, \nu _l,n)}\right) \end{aligned}$$

is satisfied the bilinear KP-hierarchy, especially, when $\hat{\tau }_n=\underset{1\le i,j\le N}{\text{ det }}\left( \hat{m}_{2i-1,2j-1}^{N-i,N-j,n}\right)$, it is also the solution. Based on the Leibniz rule, one can get

$$\begin{aligned} \begin{aligned}&\left[ (p-a)\partial _p\right] ^m\left( p^3+\frac{p}{4}-\frac{1}{8(p-a)}\right) \\&\quad =\sum _{l=0}^{m}\left( \begin{array}{cc} m\\ l \end{array} \right) \left[ 3^l(p{-}a)^3{+}3a2^l(p{-}a)^2\right. \\&\qquad \left. +\,(3a^2{+}\frac{1}{4})(p{-}a){+}({-}1)^{l{+}1}\frac{1}{8(p{-}a)}\right] \\&\qquad \left[ (p{-}a)\partial _p\right] ^{m{-}l}+\left( a^3+\frac{1}{4}a\right) [(p-a)\partial _p]^m, \end{aligned} \end{aligned}$$

(33)

and

$$\begin{aligned} \begin{aligned}&\left[ (q+a)\partial _q\right] ^m\left( q^3+\frac{q}{4}-\frac{1}{8(q+a)}\right) \\&\quad =\sum _{l=0}^{m}\left( \begin{array}{cc} m\\ l \end{array} \right) \left[ 3^l(q{+}a)^3{-}3a2^l(q{+}a)^2\right. \\&\qquad \left. +\,(3a^2{+}\frac{1}{4})(q{+}a){+}({-}1)^{l{+}1}\frac{1}{8(q{+}a)}\right] \\&\qquad \left[ (q{+}a)\partial _q\right] ^{m{-}l}-\left( a^3+\frac{1}{4}a\right) [(q+a)\partial _q]^m. \end{aligned} \end{aligned}$$

(34)

Hence, one can obtain the commutator operation

$$\begin{aligned} \begin{aligned}&\left[ A_k^{(\mu )}, p^3+\frac{p}{4}-\frac{1}{8(p-a)}\right] \\&=\sum _{j=0}^{k}\frac{a_j^{(\mu )}}{(k-j)!} \left[ \left( (p-a)\partial _p\right) ^{k-j}, p^3 +\frac{p}{4}-\frac{1}{8(p-a)} \right] \\&=\sum _{j=0}^{k-1}\sum _{l=1}^{k{-}j}\frac{a_j^{(\mu )}\left[ 3^l(p{-}a)^3{+}3a2^l(p{-}a)^2{+}(\frac{12a^2{+}1}{4})(p{-}a){+}\frac{({-}1)^{l{+}1}}{8(p{-}a)}\right] \left[ (p{-}a)\partial _p\right] ^{k{-}j{-}l}}{l!(k{-}j{-}l)!}\\ \end{aligned} \end{aligned}$$

(35)

where $\left[ ,\right]$ devotes the commutator given by $\left[ X,Y\right] =XY-YX$.

Suppose $\theta$ is the solution of the quadratic dispersion equation

$$\begin{aligned}&3\left( \theta -a\right) ^3+6a\left( \theta -a\right) ^2+\left( 3a^2+\frac{1}{4}\right) (\theta -a)\nonumber \\&\quad +\frac{1}{8(\theta -a)}=0, \end{aligned}$$

(36)

then the commutator operation equals to zero when $k=0, 1$,

$$\begin{aligned} \left[ A_k^{(\mu )}, p^3+\frac{p}{4}-\frac{1}{8(p-a)}\right] \Bigg |_{p=\theta }=0. \end{aligned}$$

(37)

When $k\ge 2$:

$$\begin{aligned} \begin{aligned}&\left[ A_k^{(\mu )}, p^3+\frac{p}{4}-\frac{1}{8(p-a)}\right] \\&\quad =\sum _{j=0}^{k-2}\sum _{l=2}^{k{-}j}\frac{a_j^{(\mu )}\left[ 3^l(p{-}a)^3{+}3a2^l(p{-}a)^2{+}\left( \frac{12a^2{+}1}{4}\right) (p{-}a){+}\frac{({-}1)^{l{+}1}}{8(p{-}a)}\right] \left[ (p{-}a)\partial _p\right] ^{k{-}j{-}l}}{l!(k{-}j{-}l)!}\Bigg |_{p=\theta }\\&\quad =\sum _{j=0}^{k-2}\sum _{\tilde{l}=0}^{k{-}j{-}2}\frac{a_j^\mu \left[ 3^{\tilde{l}+2}(p{-}a)^3{+}3a2^{\tilde{l}+2}(p{-}a)^2{+}\left( \frac{12a^2{+}1}{4}\right) (p{-}a){+}\frac{({-}1)^{\tilde{l}{+}1}}{8(p{-}a)}\right] \left[ (p{-}a)\partial _p\right] ^{k{-}j{-}\tilde{l}{-}2}}{(\tilde{l}{+2})!(k{-}j{-}\tilde{l}{-}2)!}\Bigg |_{p=\theta }\\&\quad =\sum _{\hat{j}=0}^{k-2}\left( \sum _{\hat{l}=0}^{\hat{j}}\frac{3^{\hat{l}+2}(p{-}a)^3{+}3a2^{\hat{l}+2}(p{-}a)^2{+}\left( \frac{12a^2{+}1}{4}\right) (p{-}a){+}\frac{({-}1)^{\hat{l}{+}1}}{8(p{-}a)}}{(\hat{l}+2)!}a_{\hat{j}-\hat{l}}^{(\mu )}\right) \frac{\left( (p-a)\partial _p\right) ^{k-2-\hat{j}}}{(k-2-\hat{j})!}\Bigg |_{p=\theta }\\&\quad =\sum _{\hat{j}=0}^{k-2}a_{\hat{j}}^{(\mu +1)}\frac{\left( (p-a)\partial _p\right) ^{k-2-\hat{j}}}{(k-2-\hat{j})!}\bigg |_{p=\theta } =A_{k-2}^{(\mu +1)}\big |_{p=\theta }. \end{aligned} \end{aligned}$$

(38)

Thus, there exists a recurrence relation between the two differential operators

$$\begin{aligned} \left[ A_{k}^{(\mu )}, p^3+\frac{p}{4}-\frac{1}{8(p-a)}\right] \bigg |_{p=\theta }=A_{k-2}^{(\mu +1)}\bigg |_{p=\theta }, \end{aligned}$$

spontaneously, when $k<0$, this operator $A_{k}^{(\mu )}=0$.

Similarly, it is obviously that the differential operator $B_{l}^{(\nu )}$ also satisfies

$$\begin{aligned} \left[ B_{l}^{\nu },q^3+\frac{q}{4}-\frac{1}{8(q+a)}\right] =B_{l-2}^{(\nu +1)}\big |_{q=\theta ^*} \end{aligned}$$

when $l>0$, and when $l<0$, we define $B_{l}^{(\nu )}=0.$

Under the above two recurrence equation, the following derivative relation can be derived as:

$$\begin{aligned} \begin{aligned}&\left( \partial _{x_3}+\frac{1}{4}\partial _{x_1}-\frac{1}{8}\partial _{x_{-1}}\right) \hat{m}_{kl}^{(\mu \nu n)}\bigg |_{p=\theta , q=\theta ^*}\\&\quad =\left( A_{k}^{(\mu )}B_{l}^{(\nu )}\left( p^3+q^3+\frac{1}{4}(p+q)\right. \right. \\&\qquad \left. \left. -\frac{1}{8}\left( \frac{1}{p-a}+\frac{1}{q+a}\right) \right) \hat{m}^{(n)}\right) \Bigg |_{p=\theta ,q=\theta ^*}\\&\quad =\left( A_{k}^{(\mu )}\left( p^3{+}\frac{p}{4}{-}\frac{1}{8(p{-}a)}\right) \right. \\&\qquad \left. B_{l}^{(\nu )}\hat{m}^{(n)}\right) \Bigg |_{p=\theta ,q=\theta ^*}\\&\qquad {+}\left( A_{k}^{(\mu )}B_{l}^{(\nu )}\left( q^3{+}\frac{q}{4}{-}\frac{1}{8(q{+}a)}\right) \right. \\&\qquad \left. \hat{m}^{(n)}\right) \Bigg |_{p=\theta ,q=\theta ^*}\\&\quad =\left( \left( \left( (p^3{+}\frac{p}{4}{-}\frac{1}{8(p{-}a)})A_{k}^{(\mu )}\right) \right. \right. \\&\qquad \left. \left. {+}A_{k-2}^{(\mu +1)}\right) B_{l}^{(\nu )}\hat{m}^{(n)}\right) \Bigg |_{p=\theta ,q=\theta ^*}\\&\qquad {+}\left( A_{k}^{(\mu )}\left( \left( \left( q^3{+}\frac{q}{4}{-}\frac{1}{8(q{+}a)}\right) B_{l}^{(\nu )}\right) \hat{m}^{(n)}\right) \right. \\&\qquad \left. +B_{l-2}^{\nu +1}\right) \Bigg |_{p=\theta ,q=\theta ^*}\\&\quad =\left( p^3{+}\frac{p}{4}{-}\frac{1}{8(p{-}a)}\right) \hat{m}_{kl}^{(\mu \nu n)}\Bigg |_{p=\theta , q=\theta ^*}\\&\qquad +\hat{m}_{k-2,l}^{(\mu +1,\nu ,n)}\Bigg |_{p=\theta ,q=\theta ^*}\\&\qquad +\left( q^3{+}\frac{q}{4}{-}\frac{1}{8(q{+}a)}\right) \hat{m}^{(\mu \nu n)}_{kl}\Bigg |_{p=\theta ,q=\theta ^*}\\&\qquad +\hat{m}_{k,l-2}^{(\mu ,\nu +1,n)}\Bigg |_{p=\theta ,q=\theta ^*}. \end{aligned} \end{aligned}$$

(39)

Once more, based on the above relation, the differential form of a special determinant rewritten as

$$\begin{aligned} \hat{\hat{\tau }}_n=\underset{1\le i,j\le N}{\text{ det }}\left( \hat{m}_{2i-1,2j-1}^{N-i,N-j,n}\big |_{p=\theta ,q=\theta ^*}\right) \end{aligned}$$

(40)

can be worked out as

$$\begin{aligned} \begin{aligned}&\left( \partial _{x_3}+\frac{1}{4}\partial _{x_1}-\frac{1}{8}\partial _{x_{-1}}\right) \hat{\hat{\tau }}_n\\&\quad =\sum _{i=1}^{N}\sum _{j=1}^{N}\triangle _{ij}\left( \partial _{x_3}+\frac{1}{4}\partial _{x_1}-\frac{1}{8}\partial _{x_{-1}}\right) \\&\qquad \left( \hat{m}_{2i-1,2j-1}^{N-1,N-j,n}\Bigg |_{p=\theta ,q=\theta ^*}\right) \\&\quad =\sum _{i=1}^{N}\sum _{j=1}^{N}\triangle _{ij}\bigg [\left( p^3{+}\frac{p}{4}{-}\frac{1}{8(p{-}a)}\right) \\&\qquad \hat{m}_{2i-1,2j-1}^{(N-i,N-j n)}\bigg |_{p=\theta , q=\theta ^*}\\&\qquad +\hat{m}_{2i-3,2j-1}^{(N-i+1,N-j,n)}\bigg |_{p=\theta ,q=\theta ^*}\\&\qquad +\left( q^3{+}\frac{q}{4}{-}\frac{1}{8(q{+}a)}\right) \hat{m}^{(N-i,N-j n)}_{2i-1,2j-1}\Bigg |_{p=\theta ,q=\theta ^*}\\&\qquad +\hat{m}_{2i-1,2j-3}^{(N-i,N-j+1,n)}\bigg |_{p=\theta ,q=\theta ^*}\bigg ]\\&\quad =\left( p^3{+}\frac{p}{4}{-}\frac{1}{8(p{-}a)}\right) N\hat{\hat{\tau }}_n\bigg |_{p=\theta ,q=\theta ^*}\\&\qquad +\sum _{i=1}^{N}\sum _{j=1}^{N}\triangle _{ij}\hat{m}_{2i-3,2j-1}^{(N-i+1,N-j,n)}\bigg |_{p=\theta ,q=\theta ^*}\\&\qquad +\left( q^3{+}\frac{q}{4}{-}\frac{1}{8(q{+}a)}\right) N\hat{\hat{\tau }}_n\bigg |_{p=\theta ,q=\theta ^*}\\&\qquad +\sum _{i=1}^{N}\sum _{j=1}^{N}\triangle _{ij}\hat{m}_{2i-1,2j-3}^{(N-i,N-j+1,n)}\bigg |_{p=\theta ,q=\theta ^*}, \end{aligned} \end{aligned}$$

(41)

where $\triangle _{ij}$ is the (i, j)-cofactor of the matrix $\left( \hat{m}_{2i-1,2j-1}^{N-i,N-j,n}\right)$. It is obvious that $\sum _{i=1}^{N}\sum _{j=1}^{N}\triangle _{ij}\hat{m}_{2i-3,2j-1}^{(N-i+1,N-j,n)}\big |_{p=\theta ,q=\theta ^*}=0$ for $\triangle _{ij}$ is the (i, j)-cofactor of the matrix $\left( \hat{m}_{2i-1,2j-1}^{N-i,N-j,n}\right)$ but not the $\left( \hat{m}_{2i-3,2j-1}^{N-i+1,N-j,n}\right)$. Similarly, $\sum _{i=1}^{N}\sum _{j=1}^{N}\triangle _{ij}\hat{m}_{2i-1,2j-3}^{(N{-}i,N{-}j{+}1,n)}\big |_{p=\theta ,q=\theta ^*}=0.$ Therefore, Eq. (41) will be changed into

$$\begin{aligned} \begin{aligned}&\left( \partial _{x_3}+\frac{1}{4}\partial _{x_1}-\frac{1}{8}\partial _{x_{-1}}\right) \hat{\hat{\tau }}_n\\&\quad =\left( p^3{+}\frac{p}{4}{-}\frac{1}{8(p{-}a)}+q^3{+}\frac{q}{4}{-}\frac{1}{8(q{+}a)}\right) N\hat{\hat{\tau }}_n. \end{aligned} \end{aligned}$$

(42)

Due to $\hat{\hat{\tau }}_n$ is a special case of $\hat{\tau }_n$, so $\hat{\hat{\tau }}_n$ is the solution to the ($1+1$)-dimensional bilinear equation:

$$\begin{aligned} \begin{aligned}&\left( D^{2}_{x_1}+2aD_{x_1}-D_{x_2}\right) \hat{\hat{\tau }}_{n+1}\cdot \hat{\hat{\tau }}_{n}=0,\\&\left( D_{x_1}^2+D_{x_1}^4+3D_{x_2}^2-1\right) \hat{\hat{\tau }}_{n}\cdot \hat{\hat{\tau }}_{n}+\hat{\hat{\tau }}_{n+1}\cdot \hat{\hat{\tau }}_{n-1}=0. \end{aligned} \end{aligned}$$

(43)

Under reduction Eq. (42), these variables $x_{-1}, x_{3}$ in $\hat{\hat{\tau }}_n$ will become dummy. Thus, the matrix entries $\hat{m}_{2N-i,2N-j}^{(N-i,N-j,n)}$ reduce to $m^{(N-i,N-j,n)}_{2N-i,2N-j}$, $\tau _n$ in Eq. (11) satisfy Eq. (6), and the proof is completed. $\square$