Dynamic evolution of a primary resonance MEMS resonator under prebuckling pattern

Abstract

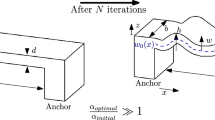
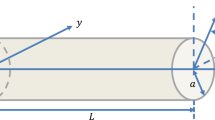
This paper analytically investigates the dynamic evolution of the primary frequency response of a prebuckling microbeam-based resonator with $\hbox {Z}_{2}$ symmetry. A doubly clamped straight microbeam actuated by two symmetric stationary electrodes is simplified as a time-varying capacitor model for qualitative analysis purpose. Nonlinearities induced by the midplane stretching of the microbeam and the electrostatic force are considered. During solution procedure, electrostatic force holds its original form without any Taylor series expansion, and only one assumption with a small ratio of AC to DC voltage is introduced. The average equation, frequency response, backbone curve and stability condition are determined, respectively, based on the method of multiple scales combined with homotopy concept. Results demonstrate for the first time that the frequency response includes two types of branches, namely low- energy branch and high-energy branch. As the increase ion AC excitation amplitude, both branches close to each other along the backbone curve until they intersect. Further analyses are then performed to investigate the details of the backbone curve and the frequency response equation. Analytical formulas to determine the hardening and softening switches of the frequency response and the intersection condition of the low- and high-energy branches are both deduced and examined in depth. Primary frequency response properties in pull-in and secondary pull-in case are classified and depicted through theoretical predictions via the method of multiple scales and then verified through numerical results via the finite difference method combined with Floquet theory. Finally, a specific case study based on equivalent lumped parameters via Galerkin method is presented. Excellent agreements between theoretical predictions and simulation results illustrate the effectiveness of the whole analyses.

Appendix

1.1 Appendix A

The derivation of the secular term via the method of multiple scales combined with the residue theorem can be described as follows.

We denote the right side of Eq. (10) as

$$\begin{aligned} \Theta =\Theta _1 +\Theta _2 +\Theta _3 \end{aligned}$$

(A.1)

where

$$\begin{aligned} \Theta _1= & {} -2D_0 D_1 x_0 +\omega ^{2}x_0 -x_0 -\mu D_0 x_0 -\alpha x_0^3 \nonumber \\ \end{aligned}$$

(A.2)

$$\begin{aligned} \Theta _2= & {} \gamma \left[ {\frac{1}{(1-x_0 )^{2}}-\frac{1}{(1+x_0 )^{2}}} \right] \end{aligned}$$

(A.3)

$$\begin{aligned} \Theta _3= & {} \frac{2\gamma \rho }{(1-x_0 )^{2}}\sin (\omega T_0 ) \end{aligned}$$

(A.4)

The secular term in Eq. (A.1) can be calculated through the following average process

$$\begin{aligned} \int _0^{2\pi } {\Theta \exp (-\hbox {i}\varphi )\mathrm{d}\varphi }= & {} \int _0^{2\pi } {(\Theta _1 +\Theta _2 +\Theta _3 )\exp (-\hbox {i}\varphi )\mathrm{d}\varphi } \nonumber \\= & {} \int _0^{2\pi } {\Theta _1 \exp (-\hbox {i}\varphi )\mathrm{d}\varphi } \nonumber \\&+\,\int _0^{2\pi } {\Theta _2 \exp (-\hbox {i}\varphi )\mathrm{d}\varphi } \nonumber \\&+\,\int _0^{2\pi } {\Theta _3 \exp (-\hbox {i}\varphi )\mathrm{d}\varphi } \nonumber \\= & {} 0 \end{aligned}$$

(A.5)

where $\varphi =\omega T_0 +\beta (T_1 )$.

We can easily derive the integration of the first term in Eq. (A.5) as

$$\begin{aligned} \int _0^{2\pi } {\Theta _1 \exp (-\hbox {i}\varphi )\mathrm{d}\varphi }= & {} -A\pi -\frac{3}{4}A^{3}\pi \alpha -\hbox {i}A\pi \mu \omega \nonumber \\&+\,A\pi \omega ^{2}-2\hbox {i}\pi \omega \frac{\mathrm{d}A}{\mathrm{d}T_1 }\nonumber \\&+\,2A\pi \omega \frac{\mathrm{d}\beta }{\mathrm{d}T_1 } \end{aligned}$$

(A.6)

The integration of the next two terms in Eq. (A.5) can be solved based on residue theorem. One can introduce the following variable

$$\begin{aligned} z=\mathrm{e}^{\mathrm{i}\varphi } \end{aligned}$$

(A.7)

The trigonometric functions $\sin \varphi$ and $\cos \varphi$ can be written as

$$\begin{aligned} \sin \varphi =\frac{1}{2\hbox {i}}\left( {z-\frac{1}{z}} \right) , \quad \cos \varphi =\frac{1}{2}\left( {z+\frac{1}{z}} \right) \end{aligned}$$

(A.8)

Then, the integration of the second term in Eq. (A.5) can be rewritten as

$$\begin{aligned}&\int _0^{2\pi } {\Theta _2 \exp (-\hbox {i}\varphi )\mathrm{d}\varphi } \nonumber \\&\quad =\int _{\left| z \right| =1} {-\frac{32\hbox {i}Az(1+z^{2})\gamma }{(A-2z+Az^{2})^{2}(A+2z+Az^{2})^{2}}\mathrm{d}z}\nonumber \\ \end{aligned}$$

(A.9)

Applying the residue theorem, one can obtain

$$\begin{aligned} \int _0^{2\pi } {\Theta _2 \exp (-\hbox {i}\varphi )\mathrm{d}\varphi } =\frac{4\pi \gamma A}{(1-A^{2})^{3/2}} \end{aligned}$$

(A.10)

Similarly, one can derive the third integration in Eq. (A.5) as follows

$$\begin{aligned}&\int _0^{2\pi } {\Theta _3 \exp (-\hbox {i}\varphi )\mathrm{d}\varphi } \nonumber \\&\quad =\frac{4\hbox {i}\pi \gamma \rho [(1-A^{2})^{1/2}-1]\cos \beta }{A^{2}(1-A^{2})^{1/2}}\nonumber \\&\qquad -\,\frac{4\pi \gamma \rho [(1-A^{2})^{3/2}-1\hbox {+}2A^{2}]\sin \beta }{A^{2}(1-A^{2})^{3/2}} \end{aligned}$$

(A.11)

Finally, the secular term can be expressed as

$$\begin{aligned}&-\,A\pi -\frac{3}{4}A^{3}\pi \alpha -\hbox {i}A\pi \mu \omega +A\pi \omega ^{2}\nonumber \\&\quad -\,2\hbox {i}\pi \omega \frac{\mathrm{d}A}{\mathrm{d}T_1 }+2A\pi \omega \frac{\mathrm{d}\beta }{\mathrm{d}T_1 }+\frac{4\pi \gamma A}{(1-A^{2})^{3/2}} \nonumber \\&\quad +\,\frac{4\hbox {i}\pi \gamma \rho [(1-A^{2})^{1/2}-1]\cos \beta }{A^{2}(1-A^{2})^{1/2}}\nonumber \\&\quad -\,\frac{4\pi \gamma \rho [(1-A^{2})^{3/2}-1 + 2A^{2}]\sin \beta }{A^{2}(1-A^{2})^{3/2}}=0\nonumber \\ \end{aligned}$$

(A.12)

Separating the imaginary and real parts can derive the average equation Eq. (12).

1.2 Appendix B

The coefficients in Eq. (15) are as follows

$$\begin{aligned} J_{11}= & {} -\frac{\mu }{2}+\frac{2\gamma \rho [2-3A^{2}-2(1-A^{2})^{3/2}]\cos \beta }{\omega A^{3}(1-A^{2})^{3/2}}\nonumber \\ \end{aligned}$$

(B.1)

$$\begin{aligned} J_{12}= & {} \frac{2\gamma \rho [1-(1-A^{2})^{1/2}]\sin \beta }{\omega A^{2}(1-A^{2})^{1/2}} \end{aligned}$$

(B.2)

$$\begin{aligned} J_{21}= & {} \frac{3\alpha A}{4\omega }-\frac{6\gamma A}{\omega (1-A^{2})^{5/2}}\nonumber \\&+\,\frac{2\gamma \rho [8A^{4}-8A^{2}+3-3(1-A^{2})^{5/2}]}{\omega A^{4}(1-A^{2})^{5/2}}\sin \beta \nonumber \\ \end{aligned}$$

(B.3)

$$\begin{aligned} J_{22}= & {} \frac{2\gamma \rho [(1-A^{2})^{3/2}+(2A^{2}-1)]}{\omega A^{3}(1-A^{2})^{3/2}}\cos \beta \end{aligned}$$

(B.4)

The coefficients in Eq. (16) are as follows

$$\begin{aligned} \mathfrak {R}_1= & {} \frac{\mu ^{2}[2(1-2A^{2})(1-A^{2})^{1/2}-3A^{2}(A^{2}-1)-1]}{4(1-A^{2})^{2}}\nonumber \\ \end{aligned}$$

(B.5)

$$\begin{aligned} \mathfrak {R}_2= & {} \frac{3\alpha A^{2}}{8\omega }+\frac{1-\omega ^{2}}{2\omega }-\frac{2\gamma }{\omega (1-A^{2})^{3/2}}\nonumber \\ \end{aligned}$$

(B.6)

$$\begin{aligned} \mathfrak {R}_3= & {} \frac{[1-(1-A^{2})^{1/2}][8A^{4}-8A^{2}+3-3(1-A^{2})^{5/2}]}{[(1-A^{2})^{3/2}-(1-2A^{2})]^{2}}\nonumber \\ \end{aligned}$$

(B.7)

$$\begin{aligned} \mathfrak {R}_4= & {} \frac{A^{2}[3\alpha (1-A^{2})^{5/2}-24\gamma ][1-(1-A^{2})^{1/2}]}{4\omega (1-A^{2})^{3}[1-(1-2A^{2})(1-A^{2})^{{-3}/2}]} \end{aligned}$$

(B.8)