Subcritical Hopf and saddle-node bifurcations in hunting motion caused by cubic and quintic nonlinearities: experimental identification of nonlinearities in a roller rig

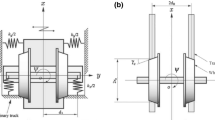
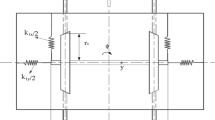
Abstract

Railway vehicles suffer from hunting motion, even when traveling below the critical speed obtained by linear analysis, due to the nonlinear characteristics of the wheel system. Nonlinear characteristics in Hopf bifurcations can be characterized as subcritical or supercritical, depending on whether the cubic nonlinearity is softening or hardening, respectively. In a system with softening cubic nonlinearity, third-order nonlinear analysis cannot detect nontrivial stable steady-state oscillations because they are affected by quintic nonlinearity. Therefore, in such a system, it is necessary to apply fifth-order nonlinear analysis to a system model in which quintic nonlinearity is taken into account. In this study, we investigated the cubic and quintic nonlinear phenomena in hunting motion with a roller rig that is widely used for hunting motion research. Previous experimental studies using a roller rig were restricted to the linear stability and the cubic nonlinear stability. We clarified that roller rig experiments can observe the hysteresis phenomenon and the existence of subcritical Hopf and saddle-node bifurcations, indicating that not only the cubic but also the quintic nonlinearity of the wheel system plays an important role. In addition, we obtained the normal form governing the nonlinear dynamics. We developed an experimental identification method to obtain the coefficients of the normal form. The validity of our method was confirmed by comparing the bifurcation diagrams obtained from the experimental time history and the normal form whose coefficients were experimentally identified using the proposed method.

Appendices

Appendix A: Hysteresis width depending on the amount of surface roughness or disturbance

Disturbances created from surface roughness can change the linear and nonlinear critical speeds, that is, the width of the hysteresis region, as follows. Figure 11 is a schematic bifurcation diagram. In the hysteresis region, the unstable steady-state amplitude is the threshold determining whether the amplitude grows up to the stable nontrivial steady-state amplitude or decreases to the zero amplitude. Therefore, when the disturbance is small, as in Fig. 11a, where the disturbance is denoted by short thick arrows, the linear and nonlinear critical speeds, ${v_\mathrm{c}}$ and ${v_\mathrm{n}}$, are approximately equal to those theoretically obtained values under the assumption of an infinitely small disturbance. At these critical speeds, the amplitude grows or decreases along the thin arrow.

In contrast, under a large disturbance, as in Fig. 11b, where the disturbance is denoted by long thick arrows, the linear and nonlinear critical speeds decrease and increase, respectively. Therefore, the threshold becomes narrower than it is for a small disturbance. As one application of these nonlinear characteristics, measurement of the width of threshold can prove an identical method for determining the amount of disturbance.

Fig. 11

Hysteresis width depending on the amount of surface roughness, that is, disturbance, in the roller rig. ${\varDelta v_\mathrm{cr}}$ indicates the hysteresis width under different disturbance, where ${\varDelta v_{\text {cr-a}}>\varDelta v_{\text {cr-b}}}$. The solid and dashed curves denote the stable and unstable steady-state amplitudes, respectively

Appendix B: Eigenvalues of the equation of motion

Matrix $\varvec{A}$ consists of the coefficients of the linear terms, and vector ${\varvec{N}(\varvec{x},\epsilon )}$ includes the cubic and quintic nonlinear terms and the detuning term denoted by the second term of Eq. (5). At the linear critical speed (${\epsilon =0}$), the four eigenvalues of the matrix $\varvec{A}$ include a pair of pure imaginary eigenvalues as

$$\begin{aligned} \pm \, i\omega =\pm \, i\sqrt{\frac{d_{11}k_{22}+d_{22}k_{11}}{d_{11}+d_{22}}}, \end{aligned}$$

(B-1)

and one complex conjugate pair of eigenvalues with a negative real part as

$$\begin{aligned} \lambda _R\pm \, i\lambda _I=-\frac{1}{2}C\pm \,\frac{1}{2}i\sqrt{4D-C^2}, \end{aligned}$$

(B-2)

where

$$\begin{aligned} C&=\frac{d_{11}+d_{22}}{v_\mathrm{c}^*},\nonumber \\ D&=\frac{d_{11}d_{22}}{v_\mathrm{c}^{*2}}+\frac{k_{11}d_{11}+k_{22}d_{22}}{d_{11}+d_{22}}. \end{aligned}$$

(B-3)

Appendix C: Reduction in nonlinear terms of the equation of r

We obtain the equation governing ${\eta }$ under the consideration of different orders from Eq. (21). The linear part (${O(\epsilon ^{1/2})}$) of Eq. (21) is obtained as:

$$\begin{aligned} \dot{\eta }=i\omega \eta , \end{aligned}$$

(C-1)

and the cubic part (${O(\epsilon ^{3/2})}$) of Eq. (21) is obtained as

$$\begin{aligned} \dot{\eta }&=i\omega q+\hat{N}_1(O(\eta ^3))+\frac{\partial q}{\partial \eta }(-i\omega \eta )+\frac{\partial q}{\partial \bar{\eta }}(i\omega \bar{\eta })\nonumber \\&=D_1\epsilon \eta +(D_2+2i\omega \varGamma _2)\epsilon \bar{\eta } +(D_3-2i\omega \varGamma _3)\eta ^3\nonumber \\&\quad +\,D_4\eta ^2\bar{\eta }+(D_5+2i\omega \varGamma _5) \eta \bar{\eta }^2+(D_6+4i\omega \varGamma _6)\bar{\eta }^3. \end{aligned}$$

(C-2)

To reduce the number of nonlinear terms in the equation, we consider

$$\begin{aligned}&(D_2+2i\omega \varGamma _2)\epsilon \bar{\eta }=0, (D_3-2i\omega \varGamma _3)\eta ^3=0,\nonumber \\&(D_5+2i\omega \varGamma _5)\eta \bar{\eta }^2=0, (D_6+4i\omega \varGamma _6)\bar{\eta }^3=0. \end{aligned}$$

(C-3)

Therefore, the cubic nonlinear coefficients of Eq. (20) are selected as

$$\begin{aligned} \varGamma _2=-\frac{D_2}{2i\omega }, \varGamma _3=\frac{D_3}{2i\omega }, \varGamma _5=-\frac{D_5}{2i\omega }, \varGamma _6=-\frac{D_6}{4i\omega }, \end{aligned}$$

(C-4)

and we select ${\varGamma _1}$, ${\varGamma _4}$ as

$$\begin{aligned} \varGamma _1=0, \varGamma _4=0. \end{aligned}$$

(C-5)

Then, Eq. (C-2) is simplified as follows:

$$\begin{aligned} \dot{\eta }=D_1\varepsilon \eta +D_4\eta ^2\bar{\eta }. \end{aligned}$$

(C-6)

The quintic part (${O(\epsilon ^{5/2})}$) of Eq. (21) is obtained as follows:

$$\begin{aligned} \dot{\eta }&=i\omega q-(i\omega \eta +D_1\epsilon \eta +D_4\eta ^2\bar{\eta }) \frac{\partial q}{\partial \eta }\nonumber \\&\quad +\,(-i\omega \bar{\eta }+\bar{D}_1\epsilon \bar{\eta }+\bar{D}_4\eta \bar{\eta }^2) \frac{\partial q}{\partial \bar{\eta }}+\hat{N}_1(O(\eta ^5))\nonumber \\&=(D_7+D_2\bar{\varGamma }_2)\epsilon ^2\eta +(2i\omega \varGamma _8+D_8+D_1\varGamma _2-\bar{D}_1\varGamma _2)\epsilon ^2\bar{\eta }\nonumber \\&\quad +\,(-2i\omega \varGamma _9+D_9-2D_1\varGamma _3+D_2\bar{\varGamma }_6+D_4\bar{\varGamma }_2)\epsilon \eta ^3\nonumber \\&\quad +\,(D_{10}+D_2\bar{\varGamma }_5+3D_3\varGamma _2+2D_5\bar{\varGamma }_2)\epsilon \eta ^2\bar{\eta }\nonumber \\&\quad +\,(2i\omega \varGamma _{11}+D_{11}-2\bar{D}_1\varGamma _5-\bar{D}_4\varGamma _2+2D_4\varGamma _2+3D_6\bar{\varGamma }_2)\nonumber \\&\qquad \epsilon \eta \bar{\eta }^2\nonumber \\&\quad +\,(4i\omega \varGamma _{12}+D_{12}-3\bar{D}_1\varGamma _6+D_1\varGamma _6+D_2\bar{\varGamma }_3)\epsilon \bar{\eta }^3\nonumber \\&\quad +\,(-4i\omega \varGamma _{13}+D_{13}+3D_3\varGamma _3+D_4\bar{\varGamma }_6)\eta ^5\nonumber \\&\quad +\,(-2i\omega \varGamma _{14}+D_{14}-D_4\varGamma _3+D_4\bar{\varGamma }_5+2D_5\bar{\varGamma }_6)\eta ^4\bar{\eta }\nonumber \\&\quad +\,(D_{15}+3D_3\varGamma _5-D_5\bar{\varGamma }_6+2D_5\bar{\varGamma }_5+3D_6\bar{\varGamma }_6)\eta ^3\bar{\eta }^2\nonumber \\&\quad +\,(2i\omega \varGamma _{16}+D_{16}+D_4\varGamma _5-2\bar{D}_4\varGamma +3D_3\varGamma _6+D_4\bar{\varGamma }_3\nonumber \\&\quad +\,D_5\bar{\varGamma }_5+2D_5\varGamma _5+3D_6\bar{\varGamma }_5)\eta ^2\bar{\eta }^3\nonumber \\&\quad +\,(4i\omega \varGamma _{17}+D_{17}-3\bar{D}_4\varGamma _6+2D_4\varGamma _6+2D_5\bar{\varGamma }_3)\eta \bar{\eta }^4\nonumber \\&\quad +\,(6i\omega \varGamma _{18}+D_{18}+D_5\bar{\varGamma }_3+3D_6\bar{\varGamma }_3)\bar{\eta }^5. \end{aligned}$$

(C-7)

We consider that

$$\begin{aligned}&(2i\omega \varGamma _8+D_8+D_1\varGamma _2-\bar{D}_1\varGamma _2)\epsilon ^2\bar{\eta }=0,\nonumber \\&\qquad (-2i\omega \varGamma _9+D_9-2D_1\varGamma _3+D_2\bar{\varGamma }_6+D_4\bar{\varGamma }_2)\epsilon \eta ^3=0,\nonumber \\&\qquad (2i\omega \varGamma _{11}+D_{11}-2\bar{D}_1\varGamma _5-\bar{D}_4\varGamma _2+2D_4\varGamma _2+3D_6\bar{\varGamma }_2)\nonumber \\&\qquad \quad \epsilon \eta \bar{\eta }^2=0,\nonumber \\&\qquad (4i\omega \varGamma _{12}+D_{12}-3\bar{D}_1\varGamma _6+D_1\varGamma _6+D_2\bar{\varGamma }_3)\epsilon \bar{\eta }^3=0,\nonumber \\&\qquad (-4i\omega \varGamma _{13}+D_{13}+3D_3\varGamma _3+D_4\bar{\varGamma }_6)\eta ^5=0,\nonumber \\&\qquad (-2i\omega \varGamma _{14}+D_{14}-D_4\varGamma _3+D_4\bar{\varGamma }_5+2D_5\bar{\varGamma }_6)\eta ^4\bar{\eta }=0,\nonumber \\&\qquad (2i\omega \varGamma _{16}+D_{16}+D_4\varGamma _5-2\bar{D}_4\varGamma +3D_3\varGamma _6+D_4\bar{\varGamma }_3\nonumber \\&\quad \quad +\,D_5\bar{\varGamma }_5+2D_5\varGamma _5+3D_6\bar{\varGamma }_5)\eta ^2\bar{\eta }^3=0,\nonumber \\&\qquad (4i\omega \varGamma _{17}+D_{17}-3\bar{D}_4\varGamma _6+2D_4\varGamma _6+2D_5\bar{\varGamma }_3)\eta \bar{\eta }^4=0,\nonumber \\&\qquad (6i\omega \varGamma _{18}+D_{18}+D_5\bar{\varGamma }_3+3D_6\bar{\varGamma }_3)\bar{\eta }^5=0. \end{aligned}$$

(C-8)

Therefore, the quintic nonlinear coefficients of Eq. (20) are selected as

$$\begin{aligned} \varGamma _8&=-\,(D_8+D_1\varGamma _2-\bar{D}_1\varGamma _2)/(2i\omega ),\nonumber \\ \varGamma _9&=(D_9-2D_1\varGamma _3+D_2\bar{\varGamma }_6+D_4\bar{\varGamma }_2)/(2i\omega ),\nonumber \\ \varGamma _{11}&=-\,(D_{11}-2\bar{D}_1\varGamma _5-\bar{D}_4\varGamma _2+2D_4\varGamma _2+3D_6\bar{\varGamma }_2)/(2i\omega ),\nonumber \\ \varGamma _{12}&=-\,(D_{12}-3\bar{D}_1\varGamma _6+D_1\varGamma _6+D_2\bar{\varGamma }_3)/(4i\omega ),\nonumber \\ \varGamma _{13}&=(D_{13}+3D_3\varGamma _3+D_4\bar{\varGamma }_6)/(4i\omega ),\nonumber \\ \varGamma _{14}&=(D_{14}-D_4\varGamma _3+D_4\bar{\varGamma }_5+2D_5\bar{\varGamma }_6)/(2i\omega ),\nonumber \\ \varGamma _{16}&=-\,(D_{16}+D_4\varGamma _5-2\bar{D}_4\varGamma +3D_3\varGamma _6+D_4\bar{\varGamma }_3\nonumber \\&\quad +\,D_5\bar{\varGamma }_5+2D_5\varGamma _5+3D_6\bar{\varGamma }_5)/(2i\omega ),\nonumber \\ \varGamma _{17}&=-\,(D_{17}-3\bar{D}_4\varGamma _6+2D_4\varGamma _6+2D_5\bar{\varGamma }_3)/(4i\omega ),\nonumber \\ \varGamma _{18}&=-\,(D_{18}+D_5\bar{\varGamma }_3+3D_6\bar{\varGamma }_3)/(6i\omega ). \end{aligned}$$

(C-9)

Then, we select ${\varGamma _7}$, ${\varGamma _{10}}$, and ${\varGamma _{15}}$ as

$$\begin{aligned} \varGamma _7=0, \varGamma _{10}=0,\varGamma _{15}=0. \end{aligned}$$

(C-10)

Finally, Eq. (C-7) is simplified:

$$\begin{aligned} \dot{\eta }=\varGamma _7'\varepsilon ^2\eta +\varGamma _{10}' \varepsilon \eta ^2\bar{\eta }+\varGamma _{15}'\eta ^3\bar{\eta }^2, \end{aligned}$$

(C-11)

where

$$\begin{aligned} \varGamma _7'&=D_7+D_2\bar{\varGamma }_2,~\varGamma _{10}'=D_{10}+D_2\bar{\varGamma }_5+3D_3\varGamma _2+2D_5\bar{\varGamma }_2,\nonumber \\ \varGamma _{15}'&=D_{15}+3D_3\varGamma _5+D_5\bar{\varGamma }_6+2D_5\bar{\varGamma }_5+3D_6\bar{\varGamma }_6. \end{aligned}$$

(C-12)

Therefore, the equation of ${\eta }$ in consideration of quintic nonlinearity (${O(\epsilon ^{5/2})}$) can be obtained as follows:

$$\begin{aligned} \dot{\eta }&=i\omega \eta +D_1\varepsilon \eta +D_4\eta ^2\bar{\eta }\nonumber \\&\quad +\,\varGamma _7'\varepsilon ^2\eta +\varGamma _{10}'\varepsilon \eta ^2\bar{\eta } +\varGamma _{15}'\eta ^3\bar{\eta }^2. \end{aligned}$$

(C-13)