Skip to main content
SpringerLink
Log in

Lie symmetry reductions and group invariant solutions of (2 + 1)-dimensional modified Veronese web equation

  • Original paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

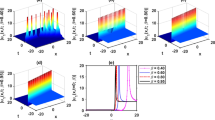
The Lie symmetry method is successfully applied to compute group invariant solutions for (2 + 1)-dimensional modified Veronese web equation. The purpose of this present article is to study the modified Veronese web (mVw) equation and to obtain its infinitesimals, commutation table of Lie algebra, symmetry reductions and closed form analytical solutions. The obtained results are explicitly in the form of the functions \(f_1(y),f_2(t),f_3(x)\) and \(f_4(x)\) and hold numerous solitary wave solutions that are more helpful to describe dynamical phenomena through their evolution profile. The solutions are analysed physically via numerical simulation. Consequently, elastic behaviour multisolitons, line soliton, doubly soliton, parabolic wave profile, nonlinear behaviour of wave profile and elastic interaction soliton profile of solutions are demonstrated in the analysis and discussion section to make this study more praiseworthy.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

References

  1. Qiu, J., Sun, K., Wang, T., Gao, H.: Observer-based fuzzy adaptive event-triggered control for pure-feedback nonlinear systems with prescribed performance. IEEE Trans. Fuzzy Syst. (2019). https://doi.org/10.1109/TFUZZ.2019.2895560

    Google Scholar 

  2. Sun, K., Mou, S., Qiu, J., Wang, T., Gao, H.: Adaptive fuzzy control for non-triangular structural stochastic switched nonlinear systems with full state constraints. IEEE Trans. Fuzzy Syst. (2018). https://doi.org/10.1109/TFUZZ.2018.2883374

    Google Scholar 

  3. Wazwaz, A.M.: Two new integrable fourth-order nonlinear equations: multiple soliton solutions and multiple complex soliton solutions. Nonlinear Dyn. 94, 2655–2663 (2018)

    Google Scholar 

  4. Xu, G.Q., Wazwaz, A.M.: Characteristics of integrability, bidirectional solitons and localized solutions for a (3 + 1)-dimensional generalized breaking soliton equation. Nonlinear Dyn. https://doi.org/10.1007/s11071-019-04899-6

    Google Scholar 

  5. Wazwaz, A.M., Kaur, L.: New integrable Boussinesq equations of distinct dimensions with diverse variety of soliton solutions. Nonlinear Dyn. 97, 83–94 (2019)

    Google Scholar 

  6. Ferapontov, E.V., Moss, J.: Linearly degenerate PDEs and quadratic line complexes. Commun. Anal. Geom. 23(1), 91–127 (2015)

    MATH  Google Scholar 

  7. Zakharevich, I.: Nonlinear wave equation, nonlinear Riemann problem, and the twistor transform of Veronese webs arXiv:math-ph/0006001 (2000)

  8. Dunajski, M., Krynski, W.: Einstein–Weyl geometry, dispersionless Hirota equation and Veronese webs. Math. Proc. Camb. Philos. Soc. 157, 139–150 (2014)

    MathSciNet  MATH  Google Scholar 

  9. Krasil’shchik, I.S., Morozov, O.I., Vojcak, P.: Nonlocal symmetries, conservation laws and recursion operators of the Veronese web equation. arXiv:1902.09341v1 [nlin.SI] (2019)

    MathSciNet  MATH  Google Scholar 

  10. Lelito, A., Morozov, O.I.: Three component nonlocal conservation laws for Lax-integrable 3D partial differential equations. J. Geom. Phys. 131, 89–100 (2018)

    MathSciNet  MATH  Google Scholar 

  11. Boris, K., Andriy, P.: Veronese webs and nonlinear PDEs. J. Geom. Phys. 115, 45–60 (2017). https://doi.org/10.1016/j.geomphys.2016.08.008

    MathSciNet  MATH  Google Scholar 

  12. Marvan, M.: Differential Geometry and applications. In: Proceedings Conference, Brno, pp. 393–402 (1995)

  13. Baran, H., Krasil’shchik, I.S., Morozov, O.I., Vojcak, P.: Nonlocal symmetries of integrable linearly degenerate equations: a comparative study. Theor. Math. Phys. 196, 1089–1110 (2018)

    MathSciNet  MATH  Google Scholar 

  14. Baran, H., Krasil’shchik, I.S., Morozov, O.I., Vojcak, P.: Symmetry reductions and exact solutions of Lax integrable 3-dimensional systems. J. Nonlinear Math. Phys. 21, 643–671 (2014)

    MathSciNet  MATH  Google Scholar 

  15. Baran, H., Krasil’shchik, I.S., Morozov, O.I., Vojcak, P.: Integrability properties of some equations obtained by symmetry reductions. J. Nonlinear Math. Phys. 22, 210–232 (2015)

    MathSciNet  MATH  Google Scholar 

  16. Baran, H., Krasil’shchik, I.S., Morozov, O.I., Vojcak, P.: Coverings over Lax integrable equations and their nonlocal symmetries. Theor. Math. Phys. 188, 1273–1295 (2016)

    MATH  Google Scholar 

  17. Manakov, S.V., Santini, P.M.: Inverse scattering problem for vector fields and the Cauchy problem for the heavenly equation. Phys. Lett. A. 359, 613–619 (2006)

    MathSciNet  MATH  Google Scholar 

  18. Manakov, S.V., Santini, P.M.: Integrable dispersionless PDEs arising as commutation condition of pairs of vector fields. J. Phys. Conf. Ser. 482, 012029 (2014). https://doi.org/10.1088/1742-6596/482/1/012029

    Google Scholar 

  19. Rogers, C., Schief, W.K.: Backlund and Darboux Transformations: Geometry and Modern Applications in Soliton Theory, vol. 30. Cambridge University Press, Cambridge (2002)

    MATH  Google Scholar 

  20. Sahoo, S., Garai, G., Saha, S.R.: Lie symmetry analysis for similarity reduction and exact solutions of modified KdV–Zakharov–Kuznetsov equation. Nonlinear Dyn. 87(3), 1995–2000 (2017)

    MathSciNet  MATH  Google Scholar 

  21. Wazwaz, A.M.: The tan h method: solitons and periodic solutions for the Dodd-Bullough-Mikhailov and the Tzitzeica–Dodd–Bullough equations. Chaos Solitons Fractals 25(1), 55–63 (2005)

    MathSciNet  MATH  Google Scholar 

  22. Bluman, W.G., Cole, D.J.: Similarity methods for differential equations. Appl. Math. Sci. (1974). https://doi.org/10.1007/978-1-4612-6394-4

    MATH  Google Scholar 

  23. Bluman, G.W., Kumei, S.: Symmetries and Differential Equations. Springer, Berlin (1989)

    MATH  Google Scholar 

  24. Olver, P.J.: Applications of Lie Groups to Differential Equations, vol. 107. Springer, Berlin (1993)

    MATH  Google Scholar 

  25. Abdelrahman, M.A.E., Sohaly, M.A.: Solitary waves for the nonlinear Schrodinger problem with the probability distribution function in the stochastic input case. Eur. Phys. J. Plus. 132, 339 (2017)

    Google Scholar 

  26. Yang, X.F., Deng, Z.C., Wei, Y.: A Riccati-Bernoulli sub-ODE method for nonlinear partial differential equations and its application. Adv. Differ. Equ. 2015, 117 (2015)

    MathSciNet  MATH  Google Scholar 

  27. Mingliang, W.: Solitary wave solutions for variant Boussinesq equations. Phys. Lett. A 199, 169–172 (1995)

    MathSciNet  Google Scholar 

  28. Clarkson, P.A., Kruskal, M.D.: New similarity reductions of the Boussinesq equation. J. Math. Phys. 30(10), 2201–2213 (1989)

    MathSciNet  MATH  Google Scholar 

  29. Lie, S.: On integration of a class of linear partial differential equations by means of definite integrals. CRC Handb. Lie Group Anal. Differ. Equ. 2, 328–368 (1881)

    MATH  Google Scholar 

  30. Kumar, S., Kumar, D.: Lie symmetry analysis, complex and singular solutions of (2 + 1)-dimensional combined MCBS-nMCBS equation. Int. J. Dyn. Control. 7, 496–509 (2019)

    MathSciNet  Google Scholar 

  31. Kumar, S., Kumar, D.: 2019 Solitary wave solutions of (3 + 1)-dimensional extended Zakharov–Kuznetsov equation by Lie symmetry approach. Comput. Math. Appl. 77, 2096–2113 (2019)

    MathSciNet  Google Scholar 

  32. Kumar, S., Kumar, D.: Group invariant solutions of (3 + 1)-dimensional generalized B-type Kadomstsev Petviashvili equation using optimal system of Lie subalgebra. Phys. Scr. 94, 065204 (2019)

    Google Scholar 

  33. Kumar, S., Pratibha, Gupta, Y.K.: Invariant Solutions of Einstein Field equation for non-conformally flat fluid spheres of embedding class one. Int. J. Mod. Phys. A 25, 3993–4000 (2010)

    MATH  Google Scholar 

  34. Kumar, M., Kumar, R., Kumar, A.: On similarity solutions of Zabolotskaya–Khokhlov equation. Comput. Math. Appl. 68(4), 454–463 (2014)

    MathSciNet  MATH  Google Scholar 

  35. Kumar, M., Tiwari, A.K.: Some group invariant solution of potential Kadomtsev–Petviashvili equaton by using Lie symmetry approach. Nonlinear Dyn. 92, 781–792 (2018)

    MATH  Google Scholar 

  36. Kumar, M., Tanwar, D.V., Kumar, R.: On Lie symmetry and soliton solution of (2 + 1)-dimensional Bogoyavlenskii equation. Nonlinear Dyn. 94, 2547–2561 (2018)

    Google Scholar 

  37. Kumar, S., Gupta, Y.K.: Generalized invariant solutions for spherical symmetric non-conformally flat fluid distributions of embedding class one. Int. J. Theor. Phys. 53, 2041–2050 (2014)

    MATH  Google Scholar 

  38. Jadaun, V., Kumar, S.: Lie symmetry analysis and invariant solutions of (3 + 1)-dimensional Calogero–Bogoyavlenskii–Schiff equation. Nonlinear Dyn. 93, 349–360 (2018)

    MATH  Google Scholar 

  39. Kumar, S., Wazwaz, A.M., Kumar, D., Kumar, A.: Group invariant solutions of (2 + 1)-dimensional rdDym equation using optimal system of Lie subalgebra. Phys. Scr. (2019). https://doi.org/10.1088/1402-4896/ab2d65

    Google Scholar 

  40. Kaur, L., Gupta, R.K.: Kawahara equation and modified Kawahara equation with time dependent coefficients: symmetry analysis and generalized (\(\frac{G^{\prime }}{G}\)) expansion method. Math. Methods Appl. Sci. 36, 584–600 (2013)

    MathSciNet  MATH  Google Scholar 

  41. Kaur, L., Wazwaz, A.M.: Painleve analysis and invariant solutions of generalized fifth-order nonlinear integrable equation. Nonlinear Dyn. 94(4), 2469–2477 (2018)

    MATH  Google Scholar 

  42. Kaur, L., Wazwaz, A.M.: Similarity solutions of field equations with an electromagnetic stress tensor as source. Rom. Rep. Phys 70(114), 1–12 (2018)

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Faculty of Mathematical Sciences, University of Delhi, Delhi, 110007, India

    Sachin Kumar

  2. Department of Mathematics, Sri Venkateswara College, University of Delhi, Delhi, 110021, India

    Amit Kumar

Authors
  1. Sachin Kumar
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Amit Kumar
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Sachin Kumar.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Ethical approval

The authors declare that they have adhered to the ethical standards of research execution.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kumar, S., Kumar, A. Lie symmetry reductions and group invariant solutions of (2 + 1)-dimensional modified Veronese web equation. Nonlinear Dyn 98, 1891–1903 (2019). https://doi.org/10.1007/s11071-019-05294-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-019-05294-x

Keywords

Search

Navigation