Abstract
We present an enhanced version of the parametric nonlinear reduced-order model for shape imperfections in structural dynamics we studied in a previous work. In this model, the total displacement is split between the one due to the presence of a shape defect and the one due to the motion of the structure. This allows to expand the two fields independently using different bases. The defected geometry is described by some user-defined displacement fields which can be embedded in the strain formulation. This way, a polynomial function of both the defect field and actual displacement field provides the nonlinear internal elastic forces. The latter can be thus expressed using tensors, and owning the reduction in size of the model given by a Galerkin projection, high simulation speedups can be achieved. We show that the adopted deformation framework, exploiting Neumann expansion in the definition of the strains, leads to better accuracy as compared to the previous work. Two numerical examples of a clamped beam and a MEMS gyroscope finally demonstrate the benefits of the method in terms of speed and increased accuracy.
Similar content being viewed by others
1 Introduction
The finite element (FE) method has long been a fundamental analysis and design tool in many areas of science and engineering. In structural mechanics, it is almost mandatory to use FE models to investigate the behavior of complex systems, which often have many geometric details that would be difficult to handle with alternative approaches, such as lumped parameter or analytical models [1]. However, large FE simulations would often require considerable computational resources and time, so in some cases designers may prefer to perform real experiments rather than numerical ones. On the one hand, this need for fast and affordable FE simulations has given rise to numerical techniques to improve computational efficiency: Domain decomposition and substructuring [2, 3] and FE Tearing and Interconnecting (FETI, [4]) are just a few examples. On the other hand, model-order reduction methods have emerged, consisting in the construction of a reduced-order model (ROM), whose number of degrees of freedom (dofs) is much smaller than that of the reference full-order model (FOM). The use of linear ROMs also in industrial contexts is nowadays well established as the theory underlying them. Guyan reduction [5] and modal analysis [6] are two well-known examples in mechanical statics and dynamics, respectively, where FOM’s static deformations and vibration modes (VMs, also known as eigenmodes or natural modes of the linear system) are used to construct a reduced basis (RB) that projects the governing equations onto a lower-dimensional subspace. Linear ROMs were also successfully coupled with substructuring techniques in the Craig–Bampton and Rubin methods [7, 8], which are available in many commercial software.
For nonlinear FE studies, many solutions have been proposed over the last decades, but none of them seems to have prevailed over the others, as each of them offers certain advantages, requires certain costs and/or targets specific problems. Overall, however, the literature is mature enough to provide the analyst with many different options in several practical applications, ranging from bolted joints [9], gears [10], contacts [11, 12], friction [13] and viscoplasticity [14] to flexible multi-body dynamics with geometric nonlinearities [15] and substructuring [16].
Nonlinear ROMs can be classified according to (i) whether they are RB-projection based or not, (ii) whether they are data- or model-driven and (iii) their (non-)intrusiveness. In the following, we consider mostly projection approaches, as the one adopted in this work; alternatively, one could resort to different strategies, such as normal form theory or spectral submanifolds. The most recent contributions in this sense include [17] and [18,19,20]. In (ii), for data-driven ROMs we usually refer to ROMs constructed using previous FOM simulation data (or experimental data, [21]), as opposed to model-driven methods that rely on some intrinsic properties of the model itself for ROM construction, such as modal approaches [22,23,24,25]. As for intrusiveness, we usually denote a ROM as non-intrusive [26] if it can be used with routines and solvers of commercial FE software and, conversely, as intrusive a method requiring dedicated routines. Specifically, intrusive methods require access and manipulation to element-level quantities, as, for instance, nonlinear generalized forces and Jacobians. Other distinctions can be made in terms of the types of nonlinearities that a given model can handle and the way nonlinear functions are evaluated [27]. All these differences ultimately affect the two phases that all ROMs have in common: the offline phase, in which the ROM is constructed, and the online phase, in which the simulation responses are retrieved. As the main goal of ROMs is to reduce computational effort and time, a key aspect to keep in mind when choosing a method is the overhead cost to pay in the offline phase; in the case of data-driven methods, this cost can be as high as the cost associated with the solution of the FOM [11]. Generally speaking then, data-driven methods (usually based on Proper Orthogonal Decomposition, or POD, strategies [28]) are used in scenarios where the high cost associated with the data generation can be amortized: typically, this is the case of multi-query analysis. In this sense, although not as versatile and generally applicable as data-driven POD-based approaches, model-driven strategies in structural dynamics are desirable, for no FOM simulation is required a priori. Rayleigh–Ritz procedures [29], dual modes [26] and modal derivatives (MDs) [30,31,32] are some popular examples.
One way to mitigate the offline overhead costs of all the aforementioned methods, but especially the data-driven ones, is to resort to (nonlinear) parametric ROMs, (NL-)pROMs. Also in this context, the literature on linear systems is quite well developed and consolidated. An extensive survey and comparison of these methods can be found in [33]. The reduction of nonlinear parametric partial differential equations (PDEs) is instead still an active research topic, which has attracted increasing interest in various disciplines over the years. Interestingly, the vast majority of nonlinear parametric model-order reduction methods is data-driven, POD-based. Some recent examples include non-intrusive interpolation methods for evaluating nonlinear functions with hypersurfaces [34, 35] and use of Gaussian Processes and machine learning for error evaluation and refinement of the pROM [36] or interpolation on the Grassmann manifold via tangent spaces [37]. Alternatively, many of these methods approximate the nonlinear function using hyper-reduction methods as the discrete empirical interpolation method (DEIM) [38, 39] to speed up the evaluation, and in this sense, online basis selection and adaptive algorithms were studied [40, 41]. However, as mentioned above, POD (and DEIM) needs a number of FOM simulations to construct the ROM. For this reason, [42] implemented a multi-fidelity strategy in which the parametric dependence was reconstructed using a large number of low-fidelity models and a minimal number of high-fidelity evaluations. Other approaches exploit machine learning to construct an input–output relationship, with convolutional neural networks [43] and autoencoders [44], which require the training of a network, again, using preexisting data. Note that most of the above methods lead to pROMs that are only evaluated in the online phase, i.e., no simulation is actually performedFootnote 1, but the solutions at the known parameter locations are “interpolated” to obtain the result.
Although model-driven NL-pROMs seem to be less popular, they offer the undeniable advantage of being simulation-free, thus considerably cutting down the offline costs. Interesting recent examples are loosely based on the extension of methods for linear systems, such as the nonlinear moment matching (NLMM) scheme [45,46,47]. In Ref. [48], a nonparametric ROM is constructed with NLMM and DEIM for each parameter instance sampled from the parameter space. These models are then “adjusted” onto a common subspace where they are interpolated to produce the pROM. This strategy, however, requires the solution of a set of nonlinear algebraic equations on the FOM at different time instances, for different signal generators, and at each point on the parameter grid. For large systems, the computational effort could still be significant, although lower than that of POD methods.
In this paper, we propose a NL-pROM for geometric nonlinearities and parametrized shape defects to study the behavior of imperfect structures. This is motivated by the fact that as it is observed in many engineering applications, even small imperfections can significantly change characteristics and performances of a system, as, for instance, in the case of MEMS devices [49, 50] and mistuning of gas turbine blades [13]. Other ROMs have already been developed in this sense [51, 52], but limited to localized defects. Regarding geometric nonlinearities, we recall that in the case of continuum finite elements with linear elastic constitutive law and total Lagrangian formulation, as in our study, the nonlinear elastic forces are a polynomials which can be represented using tensors, so that qualitativelyFootnote 2 the FOM governing equations writeFootnote 3

where M, \(\mathbf{C} _d \in {\mathbb {R}}^{n \times n}\) are the mass and damping matrices, \(\mathbf{u} ^F, \,{\dot{\mathbf{u }}}^F, \,{\ddot{\mathbf{u }}}^F \in {\mathbb {R}}^n\) are the displacement, velocity and acceleration vectors, and \(\mathbf{f} _{\mathrm{ext}}(t)\in {\mathbb {R}}^n\) is an external forcing, being n the FOM number of dofs.  ,
,  and
and  are the stiffness tensors for the linear, quadratic and cubic elastic internal forces.
are the stiffness tensors for the linear, quadratic and cubic elastic internal forces.
Conceptually, the method retraces the one we presented in [53], but it is based on a different deformation scheme (of which our earlier work resulted to be a sub-case). An overview of the individual steps of the method is shown in Fig. 1. The user defines as input data the nominal structure (in terms of geometry, material properties and FE mesh) and a number m of displacement fields representing the shape defects, which are intended as small deviations from the nominal geometry (Fig. 1a). These can be known analytically, from experimental measurements or previous simulations, and finally, they can be discretized with displacement field vectors \(\mathbf{U} _i\) and collected in a matrix \(\mathbf{U} =[\mathbf{U} _1,\ldots ,\mathbf{U} _m]\). Each defect can then be leveraged in amplitude by the parameter vector \(\varvec{\xi }=[\xi _1, \ldots ,\xi _m]^T\) (Fig. 1b) so that the final defected geometry represented by the model is given by the global defect displacement field \(\mathbf{u} _d=\mathbf{U} \varvec{\xi }\), i.e., a linear superposition of the selected defects (Fig. 1c). With this information about the nominal structure and shape defects, we assemble the RB using a modal approach with VMs, MDs and defect sensitivities (DSs). We then construct the reduced stiffness tensors, once and for all, projecting the element-level tensors with the selected RB (Fig. 1d). In this way, linear, quadratic and cubic elastic forces can be evaluated directly with respect to the reduced coordinates and shape defect magnitudes without switching between the full- and reduced-order space when evaluating the nonlinear function. Our strategy can then be classified as model-driven (simulation-free). Finally, in the online phase, the simulation is performed with the reduced governing equations (Fig. 1e). Notice that the model is used to run a simulation, not to evaluate a solution as in interpolation-like techniques: As such, different forcing terms and also different analysis types (e.g., transient, frequency response) are possible. All of this is possible thanks to the modified definition of the Green–Lagrange strain tensor we use. Specifically, our strain tensor embeds two subsequent transformations: (i) the one from nominal to defected geometry (which, at the end, will be parametrized) and (ii) the one from the defected configuration to the deformed/final one. The deformation produced by the latter is the one we measure, so no strain/stresses are introduced by the presence of the defect in (i); however, the deformation of (ii) will depend on (i). The formulation we obtain, however, contains rational terms which cannot be used for a tensorial representation (which can describe polynomials only). Given the assumed small entity of the shape defects, we advocate the use of a Neumann expansion to approximate the Green–Lagrange tensor, obtaining again a polynomial form. Applying standard FE procedures, we finally get to the expression of the reduced elastic internal forces, which will parametrically depend on the defect amplitudes \(\varvec{\xi }\). In this framework, we show that the model in [53] (whose deformation formulation was based on [54]) corresponds to a lower-order Neumann expansion with integrals evaluated on the nominal volume, and that the higher-order approximation we propose here leads to better accuracy and to a larger applicability range.
The work is organized as follows: The modified strain formulation is given in Sect. 2 and approximated using Neumann expansion in Sect. 3. In Sect. 4, the FE discretization is developed and then used in Sect. 5 to construct the reduced-order stiffness tensors. The choice and computation of the RB is described in Sect. 6. Finally, numerical studies in Sects. 7 and 8 demonstrate the effectiveness of the proposed approach on a 2D FE clamped beam and on a MEMS gyroscope and computational times are discussed.
2 Strain formulation: a two-step deformation approach
Strategies to represent the motion of imperfect structures by splitting the total displacement into a constant part, representing a geometrical imperfection, and a variable part, representing the actual displacement, are not new and have been successfully used in many analytical studies with applications to beams and plates [54,55,56]. In Ref. [55], a shallow shell model is obtained from the von Karman plate model by introducing an additional out-of-plane displacement field directly in the definition of the strains and neglecting higher-order terms; in [54], a similar strategy was used for imperfect beams, where the cancellation of h.o.t. was justified by removing the contribution of the deformations artificially produced by the introduction of the defect. In both cases, the imperfection was taken as a natural mode of the system. In Ref. [56], such limitation was removed and plates were studied expanding the defect using an arbitrary number of natural modes. Using a different approach, the authors introduce the imperfection directly in the governing equations, adding external forces to restore static equilibrium and, finally, enforcing stresses to zero (as the defected configuration is stress-free). In this work, we follow an alternative approach, based on a two-step deformation scheme, which applies to solid mechanics in general.
Scheme for the considered deformation setting. A nominal structure, of coordinates \(\mathbf{x} _0\), undergoes a deformation described by the transformation map \({\mathcal {F}}_1\). The structure is now in the deformed configuration (coordinates \(\mathbf{x} _d\)). A second transformation \({\mathcal {F}}_2\) and the displacement \(\mathbf{u} \) describe the deformation from the defected configuration to the final one
Let us consider the scheme depicted in Fig. 2. A nominal body of coordinates \(\mathbf{x} _0=\{x_0,\,y_0,\,z_0\}\) undergoes a first deformation described by the map \({\mathcal {F}}_1\), which brings the body in a new configuration with coordinates \(\mathbf{x} _d=\{x_d,\,y_d,\,z_d\}={\mathcal {F}}_1(\mathbf{x} _0)\). The displacement corresponding to this operation is \(\mathbf{u} _d=\{u_d,\,v_d,\,w_d\}=\mathbf{x} _d-\mathbf{x} _0\). We will refer to this second configuration as the defected configuration. As it will be detailed later, in our method \(\mathbf{u} _d\) will be a user-defined displacement field representing a small shape defect which, superimposed to the nominal geometry, defines the configuration with respect to which we measure deformation. There is no a priori restriction for the choice of the shape of the field \(\mathbf{u} _d\) (which can also change the location of the boundaries)Footnote 4, as long as no topological changes are introduced (e.g., holes). Let us now consider a second deformation, described by the map \({\mathcal {F}}_2\), from the defected configuration to the final one, with coordinates \(\mathbf{x} (t)=\{x(t),\,y(t),\,z(t)\}={\mathcal {F}}_2(\mathbf{x} _d,t)\). We will refer to the latter as to the deformed or final configuration, whose displacement is given by \(\mathbf{u} =\{u,\,v,\,w\}=\mathbf{x} -\mathbf{x} _d\).
Considering the infinitesimal line segment \(\text {d}{} \mathbf{x} _0\) in the nominal geometry, we can define the line segments d\(\mathbf{x} _d\) and d\(\mathbf{x} \) in the defected and deformed configurations as
where the deformation gradients \(\mathbf{F} _1\) and \(\mathbf{F} _2\) are given by
and where \(\mathbf{D} _d\) and \(\mathbf{D} _2\) are the displacement derivative matrices of the first and second transformations, respectively. Using the chain rule, we can also define
so that \(\mathbf{D} _2=\mathbf{D} \mathbf{F} _1^{-1}\) can be referred to the nominal coordinates.
Using Eqs. (2)–(4), the stretch between deformed and defected configurations writes
Measuring the deformation with respect to the defected configuration, the second-order strain tensor \(\mathbf{E} _2\) is defined as
which, rearranged, leads to
Looking at Eqs. (5) and (7), it can be easily verified that \(\mathbf{E} _2\) correctly satisfies the minimum requirements for a strain measure to vanish under a rigid body translation (\(\mathbf{F} _2=\mathbf{I} \)) and/or rotation (\(\mathbf{F} _2^T\mathbf{F} _2 = \mathbf{R} ^T\mathbf{R} =\mathbf{I} \), \(\mathbf{R} \) being an orthonormal rotation matrix), for any \(\mathbf{F} _1\). Equation (7) is indeed an exact expression for the strains from defected to final configuration. Notice, however, that in this form, all the quantities are computed with respect to the nominal coordinates \(\mathbf{x} _0\).
3 Strain approximations
The introduced strain measure, being referred to the nominal geometry only, paves the way for the pre-computation of the stiffness tensors, as it will be shown in the following sections. However, as mentioned in the introduction, a tensorial formulation can be applied only when the internal forces display a polynomial dependence on the displacements, which in the present case include both \(\mathbf{u} _d\) and \(\mathbf{u} \). The inverse of the deformation gradient \(\mathbf{F} _1\) in Eq. (7) entails a rational dependence on \(\mathbf{u} _d\) and therefore needs some attention. Let us consider the following known result: Neumann expansion If \(\mathbf{P} \) is a square matrix and the Neumann series \(\sum _{n=0}^{+\infty } \mathbf{P} ^n\) is convergent, we have that
A spectral normFootnote 5\(\varepsilon =\left\Vert \mathbf{P} \right\Vert _2<1\) is a sufficient condition for the convergence of the Neumann series. Moreover, it can be shown [57] that truncating the sum to order N the norm error \(\delta _N\) is bounded as
Letting \(\mathbf{P} =-\mathbf{D} _d\), we can expand \(\mathbf{F} _1^{-1}\) using the Neumann series as
The series, under the assumption of small defects (i.e., \(\left\Vert \mathbf{D} _d\right\Vert _2 \ll 1\)), is guaranteed to converge. Moreover, we can truncate the sum in Eq. (10) to \(N=1\), obtaining:
which, solving the product, can be rewritten as:

where we stroke out terms that cancel each other. Finally, neglecting the terms \({\mathcal {O}}(\mathbf{D} _d^2)\), i.e., assuming that the first transformation \({\mathcal {F}}_1\) is linear, Eq. (12) reduces to:
The modified Green–Lagrange strain tensor \(\mathbf{E} _{2,N1}\) is a polynomial function of the derivatives of the displacement fields \(\mathbf{u} \) and \(\mathbf{u} _d\) and can be thus used to compute a ROM using tensors. Notice that defect-induced strains are not present when there is no deformation, that is \(\mathbf{E} _{2,N1}=\mathbf{0} \) (being proportional to \(\mathbf{D} \)) when \(\mathbf{u} =\mathbf{0} \).
Remark 1
(on Budiansky approximation). The strain formulation in [54], used by Budiansky to study buckling in the presence of defects, was obtained by subtracting the strain that a defect would produce on the nominal structure from the strain of the deformed structure measured with respect to the nominal configuration. It can be shown that truncating the Neumann series to the zeroth order (i.e., setting \(N=0\), so that \(\mathbf{F} _1^{-1}=\mathbf{I} \)) and using Eqs. (7) and (10), the strain writes:
which is the same strain tensor we adopted in [53] following Budiansky’s approximation.
4 Finite element formulation
In this and the next section, we derive in detail the FE formulation leading to the parametrized reduced internal elastic forces (Eqs. (27) and (28a)), which are used in the following numerical tests. We start deriving the elastic internal forces (at element level) for the FE discretization of the full-order model based on the strain as defined in Eq. (13). We remark that this full model represents just an approximation of the reference full-order model FOM\(_d\) (where the defect is embedded directly in the mesh by shifting the position of the nodes). Although not offering any direct advantage over FOM\(_d\), this full model will allow us to compute the parametric ROM, as it will be explained in Sect. 5.
First, it is convenient to switch to Voigt notation, exploiting the symmetry of \(\mathbf{E} _{2,N1}\). Let \(\varvec{\theta }=\{u_{,x}\,u_{,y}\,u_{,z}\,v_{,x}\,v_{,y}\,v_{,z}\,w_{,x}\,w_{,y}\,w_{,z}\}^T\) be the vectorized form of \(\mathbf{D} \) and, similarly, \(\varvec{\theta }_d\) the vectorized form of \(\mathbf{D} _d\).Footnote 6 Calling \(\mathbf{u} ^e \in {\mathbb {R}}^{n_e}\) and \(\mathbf{u} _d^e \in {\mathbb {R}}^{n_e}\) the nodal displacement and defect vectors, respectively, of a continuum finite element with \(n_e\) dofs and \(\mathbf{G} \in {\mathbb {R}}^{9 \times n_e}\) the shape function derivatives matrix, the displacement derivative vectors can be written as functions of the displacements:
Equation (13) rewrites:
where \((\bullet )_\text {v}\) denotes Voigt notation and
such that
Exploiting the property by which \(\mathbf{A} _1(\varvec{\theta })\delta \varvec{\theta }=\mathbf{A} _1(\delta \varvec{\theta })\varvec{\theta }\), the virtual variation of the strain in Eq. (15) writes
where \(\mathbf{B} \) is the strain–displacement matrix and where we dropped the explicit dependencies on \(\varvec{\theta }_d\) and \(\varvec{\theta }\) to ease the notation. The virtual work of internal forces on one element is given by
where \(\mathbf{S} _{\text {v}}=\mathbf{C} \mathbf{E} _{\text {v}}\) is the Piola–Kirchhoff stress in Voigt notation, being \(\mathbf{C} \) the linear elastic constitutive matrix, and where \(V_d^e\) is the volume of the element in the defected configuration. The expression for the element internal forces \(\mathbf{f} _{\mathrm{int}}^{\,e}\) follows from the virtual work:
The global internal force vector \(\mathbf{f} _{\mathrm{int}}\) can be then obtained assembling the element-level \(\mathbf{f} _{\mathrm{int}}^{\,e}\) using standard FE procedures. Finally, the tangent stiffness matrix can be computed as usual taking the virtual variation of the internal forces (see “Appendix B”). Equations (15) and (19) can be used to perform tests and/or simulations of the full model and to compare the results to the corresponding FOM-d in order to assess the quality of the approximation before the reduction of the model. In the next section, the DpROM derived from this formulation is presented.
4.1 Element-level tensors
Equation (19) in full can be written as
In the present form, the displacement vectors \(\mathbf{u} ^e\) and \(\mathbf{u} _d^e\) are encapsulated in the expressions of \(\mathbf{A} _1\), \(\mathbf{A} _2\) and \(\mathbf{A} _3\). As our aim is to compute the stiffness coefficients of the elastic forces, we need to make them explicit in Eq. (20). We can write:
where \(\mathbf{L _1},\mathbf{L} _2 \in {\mathbb {R}}^{6 \times 9 \times 9}\) and \(\mathbf{L} _3 \in {\mathbb {R}}^{6 \times 9 \times 9 \times 9}\) are constant sparse matrices (see “Appendix A”).
We can separate the contributions in Eq. (20) as
where \(\mathbf{f} _1^{\,e}\), \(\mathbf{f} _2^{\,e}\) and \(\mathbf{f} _3^{\,e}\) are the linear, quadratic and cubic terms in the displacement \(\mathbf{u} ^e\), respectively. These can be recast in tensorial form as



where



The element-level tensors in Eq. (24) are named using the left-subscript to denote their dimension with a number and with a letter to specify if the tensor does not multiply the defect vector \(\mathbf{u} _d\) (letter “n”), if it multiplies \(\mathbf{u} _d\) once (letter “d”) or twice (letters “dd”). In particular, a tensor denoted by the letter “n” corresponds to the tensor computed for the nominal geometry. For instance,  is the third-order tensor multiplying \(\mathbf{u} _d\) once and
is the third-order tensor multiplying \(\mathbf{u} _d\) once and  is the nominal second-order tensor. Finally, we remark once more that these are element-level tensors that, in theory, could be assembled to form the FOM tensors. In practice, however, FOM tensors would require a prohibitive amount of memory and are never computed.
is the nominal second-order tensor. Finally, we remark once more that these are element-level tensors that, in theory, could be assembled to form the FOM tensors. In practice, however, FOM tensors would require a prohibitive amount of memory and are never computed.
5 DpROM formulation
5.1 Reduced tensors and internal forces
We now derive the reduced internal forces and tensors via Galerkin projection. Let \(\mathbf{V} \in {\mathbb {R}}^{n \times m}\) be the RB for \(\mathbf{u} ^F \in {\mathbb {R}}^n\), with \(m \ll n\) vectors (or modes), and let \(\mathbf{U} \in {\mathbb {R}}^{n \times m_d}\) be a basis of \(m_d\) user-defined defect shapes, collected column-wise, for \(\mathbf{u} _d^F \in {\mathbb {R}}^n\). The selection for the modes in \(\mathbf{V} \) will be discussed in Sect. 6. We have then that \(\mathbf{u} ^F \approx \mathbf{V} \varvec{\eta }\), \(\mathbf{u} _d^F= \mathbf{U} \varvec{\xi }\) and, referring to element-level quantities, we can reduce \(\mathbf{u} ^e\) and \(\mathbf{u} _d^e\) as:
being \(\mathbf{V} ^e\) and \(\mathbf{U} ^e\) the partitions of \(\mathbf{V} \) and \(\mathbf{U} \) pertaining to the element and \(\varvec{\eta }\) and \(\varvec{\xi }\) the reduced coordinates.
Plugging Eqs. (21) and (25) into Eq. (22), we can directly identify the reduced-order tensor coefficients for \(\varvec{\eta }\) and \(\varvec{\xi }\) (and their combinations). Defining the projections of shape function derivative matrix \(\mathbf{G} \) over the two basis as \(\varvec{\varGamma }=\mathbf{G} \mathbf{V} ^e\) and \(\varvec{\Upsilon }=\mathbf{G} \mathbf{U} ^e\), using Einstein’s notation we obtain:









where, for convenience, tensor dimensions of size m are denoted by capital letter subscripts and dimensions of size \(m_d\) by underlined capital letter ones. So, for example,  .
.
The global reduced tensors of the full structure can then be computed directly summing up the element contributions as

where  is one of the element-level tensors in Eq. (26a26b26c26d),
is one of the element-level tensors in Eq. (26a26b26c26d),  is the assembled tensor for the FOM, and \(N_{el}\) is the total number of elements. Notice that this procedure is highly parallelizable, as
is the assembled tensor for the FOM, and \(N_{el}\) is the total number of elements. Notice that this procedure is highly parallelizable, as  can be computed separately and summed up in the end. Reduced (global) internal forces \(\mathbf{f} _{\mathrm{int},r}\) can therefore be defined as
can be computed separately and summed up in the end. Reduced (global) internal forces \(\mathbf{f} _{\mathrm{int},r}\) can therefore be defined as

where



while the reduced tangent stiffness matrix  can be written simply as
can be written simply as

Upon inspection of Eq. (27), it can be seen that elastic internal forces are cubic in \(\varvec{\eta }\) and quadratic in \(\varvec{\xi }\), thus producing quintic terms in \((\varvec{\eta }, \varvec{\xi })\).
Remark 2
(on tensor computation). Equations (26a26b26c26d) give directly the stiffness tensors in reduced form, and this is in general highly desirable as their integration over the element volume takes multiple evaluations (e.g., through Gauss quadrature). Since the computational complexity highly depends on the number of dofs of the tensor, it is preferable to integrate directly the reduced ones as long as the number of reduced coordinates m is lower than the number of element’s dofs \(n_e\) (e.g., \(n_e=60\) for a serendipity hexahedron with quadratic shape functions). In case \(m>n_e\), it is computationally more efficient to compute the element tensors first (using Eqs (26a26b26c26d) and replacing both \(\varvec{\varGamma }\) and \(\varvec{\Upsilon }\) with \(\mathbf{G} \)) for Gauss integration and then project the element tensors using \(\mathbf{V} \) and \(\mathbf{U} \) accordingly. A similar reasoning can be done for \(m_d\), but under the very likely hypothesis that \(m_d \ll n_e\), it results almost always convenient to adopt the reduced form.
5.2 Volume integration
The tensors in Eqs. (27)–(28a) must be computed over the defected volume \(V_d\). As such, the model cannot be profitably used, as for each new instance of the parameter vector \(\varvec{\xi }\), the volume \(V_d\) would change and a new integration would be required. This way, one would need to compute a new ROM for each parameter realization, which is in direct contrast to the very idea of pROM. To circumvent this problem, one can adopt the following approximation.
Let  be the generic expression of an element tensor to be integrated over the volume \(V_d^e\). We can compute the global reduced tensor
be the generic expression of an element tensor to be integrated over the volume \(V_d^e\). We can compute the global reduced tensor  as:
as:

where \(N_{el}\) is the total number of elements. The determinant of \(\mathbf{F} _1\) can now be approximated retaining only first-order terms. To the purpose of illustration, let us consider the following 2D example where the global defect is given by the linear superposition of two shape defects, that is:
where we denote with \(\mathbf{f} ^{\,(i)}=[f_u^{(i)},\,f_v^{(i)}]^T\) the vector of the functions describing the i-th shape defect for the x-displacement \(u_d\) and the y-displacement \(v_d\), respectively. We can approximate the determinant of \(\mathbf{F} _1\) as
where we neglected higher-order terms, consistently with the assumption of small defects (already introduced for the Neumann expansion of the strains). Generalizing this result for \(m_d\) defects, we can write
so that Eq. (30) can be approximated as:

where


 is the tensor evaluated on the nominal volume and
is the tensor evaluated on the nominal volume and  is the contribution of the i-th defect, which can be computed again once and for all offline, referring to the nominal volume. The additional computational burden to compute
is the contribution of the i-th defect, which can be computed again once and for all offline, referring to the nominal volume. The additional computational burden to compute  grows less than linearly with the number of defects, since in a quadrature integration scheme we can use the
grows less than linearly with the number of defects, since in a quadrature integration scheme we can use the  evaluated at integration points for both Eq. (34). The additional computations therefore involve only scalar by tensor multiplications and tensor sums, so that most of the added computational time is merely due to memory access management. Notice that one could also compute all the additional tensors needed to describe det(\(\mathbf{F} _1\)) with no approximation (even though this is in most cases unnecessary, for h.o.t. do not improve accuracy significantly). However, the first-order approximation we presented has the advantage to introduce only one new term for every additional defect.
evaluated at integration points for both Eq. (34). The additional computations therefore involve only scalar by tensor multiplications and tensor sums, so that most of the added computational time is merely due to memory access management. Notice that one could also compute all the additional tensors needed to describe det(\(\mathbf{F} _1\)) with no approximation (even though this is in most cases unnecessary, for h.o.t. do not improve accuracy significantly). However, the first-order approximation we presented has the advantage to introduce only one new term for every additional defect.
Remark 3
(on computational efficiency). The corrective terms \(\mathbf{Q} ^{\prime \prime }_i\) in Eq. (33) are null for an isochoric transformation between nominal and defected domains (det(\(\mathbf{F} _1\))=1). In practice, one can set up a procedure to avoid the computation of these terms to speed up the construction of the reduced tensors.
Remark 4
(on Budiansky approximation). According to the framework presented in [54] and used in [53], integration can only be carried out on the nominal volume \(V_0\). This constitutes an additional approximation on top of the lower-order expansion discussed in Remark 1. As it will be later shown in Sect. 8, when the imposed defect does not represent an (almost) isochoric transformation and/or is not sufficiently small, integration over \(V_0\) is a too coarse approximation and yields large errors.
5.3 Equations of motion
Finally, the equations of motion for the parametric reduced-order system write:
where \(\mathbf{M} _r = \mathbf{V} ^T \mathbf{M} _d \mathbf{V} \) and \(\mathbf{C} _r = \mathbf{V} ^T \mathbf{C} _d \mathbf{V} \) are the reduced mass and damping matrices and \(\mathbf{f} _{\mathrm{ext},r}(t)=\mathbf{V} ^T \mathbf{f} _{\mathrm{ext}}(t)\) the reduced external forces acting on the system. Notice that since mass and damping matrices must be integrated over \(V_d\), new matrices must be computed for each new parameter realization. However, being these matrices constant during the analysis, this additional cost is negligible.
5.4 Truncated version
Before concluding this section, we present a lighter version of the proposed model, with the aim to alleviate the offline computational burden. Considering Eq. (13), we can make the further assumption that \({\mathcal {O}}(\mathbf{D} _d\mathbf{D} ^2)\) terms can be neglected, obtaining
All the subsequent equations are consequently modified by putting \(\mathbf{A} _3=\mathbf{0} \) and \(\mathbf{L} _3=\mathbf{0} \), resulting in the fact that the tensors in Eq. (26a26b26c26d) can be simplified. In particular, the last two terms in  (Eq. (26e26f26g26h26i)) and the entire
(Eq. (26e26f26g26h26i)) and the entire  ,
,  and
and  tensors are null. In this sense, the reduced elastic internal forces in Eq. (27) are “truncated.” As fifth- and sixth-order tensors are the most expensive to construct, neglecting them greatly reduces offline costs. As it will be shown in Sect. 8, this further approximation, although empirical, does not appreciably deteriorate the quality of the results.
tensors are null. In this sense, the reduced elastic internal forces in Eq. (27) are “truncated.” As fifth- and sixth-order tensors are the most expensive to construct, neglecting them greatly reduces offline costs. As it will be shown in Sect. 8, this further approximation, although empirical, does not appreciably deteriorate the quality of the results.
5.5 Models and nomenclature
In Sects. 7 and 8, we study two numerical examples using different levels of approximation for our defect parametric ROM, DpROM. Specifically, we use the zeroth-order Neumann expansion for the strains (Eq. (14)), the first-order one (Eq. (13)) and its truncated version, discussed in the previous section. The three variations will also be tested in the case of integration over \(V_d\) and over \(V_0\) (which is a further approximation). The acronyms to denote each model are shown in Table 1, where, for convenience, information about the RB of each model (discussed in the next section) is also reported. Finally, notice that the model we presented in [53] corresponds to DpROM-0\(_n\).
6 Reduction basis
To construct the system described so far, it is necessary to select the bases \(\mathbf{V} \) and \(\mathbf{U} \). The latter is simply a collection of user-defined displacement vectors, each representing one specific defect, so that the final defected shape is given by a linear superposition (see Eq. (25b)). The (properly said) RB is \(\mathbf{V} \), whose choice may not be trivial, as it must correctly represent the system response over a range of parameters without the possibility to be changed (since a change would require to recompute the stiffness tensors). As previously done in [53], our choice is to use a modal-based approach including VMs, MDs and defect sensitivities (DSs) [58] in the RB, as this solution offers a way to construct a basis in a direct way, that is without convoluted basis selection strategies, the need of computing all (or an excessively high number of) eigenvectors or the need for previously computed simulations. We remark, however, that, in principle, one could use also other RBs, as long as they are valid over the parameter space.
Let us consider the following eigenvalue problem
where \(\mathbf{K} _t=\mathbf{K} _t(\mathbf{u} ,\mathbf{u} _d)\) is the tangent stiffness matrix, M the mass matrix, \(\omega _i\) the i-th eigenfrequency and \(\varvec{\varPhi }_i\) the corresponding eigenvector. Static modal derivatives \(\varvec{\theta }_{ij}\) (MDs) are computed neglecting the mass term, by taking the derivative of Eq. (37) with respect to \(\eta _j\) and evaluating the resulting expression at equilibrium (i.e., \(\eta _j=0\)) and for \(\varvec{\xi }=\mathbf{0} \):
being \(\mathbf{K} _0=\mathbf{K} _t\left( \mathbf{0} ,\mathbf{0} \right) \). Retaining \(m_\varPhi \) VMs in the basis \(\mathbf{V} \), \(m_\varPhi (m_\varPhi +1)/2\) MDs can be computed.
Defect sensitivities (DSs) \(\varvec{\Xi }_{i,j}\) can be obtained following a similar procedure, differentiating each VM \(\varvec{\varPhi }_i\) with respect to each defect amplitude \(\xi _j\):
A total of \(m_d m_\varPhi \) DSs can be computed this way, being \(m_d\) the number of defects in \(\mathbf{U} \). Expressions for the tangent stiffness derivatives are given in “Appendix B.”
Remark 5
(on higher derivatives). Given the increased accuracy of the model, larger defect magnitudes can be considered as compared to [53]. To fully exploit the increased applicability range, a richer RB might be necessary, reason why we here introduce second defect sensitivities (DS2s) and MDs sensitivities (MDSs). Let us take the derivative of Eq. (38) with respect to the k-th defect amplitude \(\xi _k\). We define the MDS \(\varvec{\theta }_{ij,k}\) as:
Notice that \(\varvec{\theta }_{ij,k} \ne \varvec{\theta }_{ji,k}\). In the same manner, the second defect sensitivities (DS2s) with respect to \(\xi _k\) write:
It is evident that the blind inclusion of DS2s and/or MDSs in the RB would add an unacceptable number of unknowns, especially when considering MDSs. Depending on the type of the analysis (linear/nonlinear), on the kind of the defect (i.e., affecting the linear or the nonlinear dynamics) and on the entity of the defect itself (large/small), one can decide whether to include some vectors or not. Pre-selection strategies to reduce the basis size, as the one presented in [59] and [32], are beyond the scopes of this work and are not treated hereafter.
7 Numerical tests-I
We consider now a FE model of an aluminum beam, of length \(l_x=2\) m, thickness \(t_y=50\,\) mm and width \(w_z=0.2\) m, clamped at both ends. We use a 2D plain strain model, with a mesh of 80 quadrilateral elements with quadratic shape functions (630 dofs). A Rayleigh damping matrix \(\mathbf{C} _d=\alpha \mathbf{M} _d + \beta \mathbf{K} _0\) is introduced by imposing a quality factor \(Q_1=Q_2=100\) on the first and second modes of the linear system (\(\alpha =3.1,\,\beta =6.3\cdot 10^{-6}\)). A nodal load F is applied to the mid-span of the beam (with \(F=1\) kN and \(F=4\) kN for the forced responses). A single shape defect defined as the vertical translation of the nodes \(v_d(x,\xi ) = \xi t_y \sin ( \pi /l_x x)\) is imposed, deforming the nominal geometry of the straight beam into a shallow arch. Notice that this kind of defect represents an isochoric transformation, therefore integration over the nominal volume \(V_0\) is used for this example (see Sect. 5.2).
Again, refer to Table 1 for the acronyms used for the models of this and the next numerical study. For \(\xi = \{0,\,0.25,\,0.5,\,0.75,\,1\}\), backbones and frequency responses (FR) are computed for ROM\(_d\), DpROM-1\(_n\) and DpROM-0\(_n\), constructed using 5 VMs, 15 MDs and 5 DSs (only for DpROMs), i.e.,
for a total of 25 RB modes (i.e., \(m_\varPhi =5\) VMs, \(m_\varPhi (m_\varPhi +1)/2=15\) MDs and \(m_d m_\varPhi = 5\) DSs, being \(\mathbf{U} \in {\mathbb {R}}^{n \times m_d}\) and \(m_d=1\)).
Remark 6
(on basis choice). Reduction with MDs was historically introduced as an extension of time-domain linear modal analysis to the field of (mild) geometric nonlinearities [30]. As such, the selection criterion is frequency-based, meaning that modes are chosen accordingly to the spectral content of the forcing. Usually, vibration modes are retained up to 3-5 times the highest frequency of interest, as a rule of thumb. All the MDs related to the retained VMs are then included (as well as all the DSs for the DpROMs). Also, notice that MDs, loosely speaking, represent the second-order Taylor expansion of the solution [30, 32] and results are thus expected to deteriorate for high amplitudes of the response. In the present case, being our analysis restricted to the first mode, we include all the vibration modes up to the fifth, being \(\omega _{05}/\omega _{01} \approx 9\). This is a rather conservative choice which allows us to study the parametric variations of the model with relative comfort and up to relatively large levels of vibrations. Indeed, it could be shown that retaining VMs up to the third (\(\omega _{03}/\omega _{01} \approx 3.7\)) is already sufficient to retrieve a good accuracy, showing slight departure at larger amplitudes. (With reference to the results in Fig. 3, FOM and ROM backbones start departing for normalized amplitudes greater than 0.8, ultimately leading to a 1Hz difference at an amplitude of 1.2.) Interestingly, the aforementioned empiric rules used to select VMs find theoretical confirmation in [17, 60], where it is argued that a slow–fast decomposition assumption has to be made for the MD-based quadratic manifold approach to work, indicating a threshold ratio of 4 between the linear eigenfrequencies (i.e., \(\omega _p/\omega _s \ge 4\), \(p \ne s\)). However, to the best of the authors’ knowledge, there is no guarantee that this limit remains valid also in the MD-based linear manifold approach used in this work (i.e., where MDs are appended to the RB and additional independent reduced coordinates are introduced).
a Model-I: Nominal mesh and defected mesh with \(\xi =1\) (and a \(\times \)5 scale factor). b Frequency responses and backbone curves for different defect amplitudes \(\xi \) using the harmonic balance method (7 harmonics) for: ROM\(_d\) (
 ), DpROM-1\(_n\) (
), DpROM-1\(_n\) (
 ), DpROM-0\(_n\) (
), DpROM-0\(_n\) (
 , only backbones). Backbones have been computed also for the FOM\(_d\) (
, only backbones). Backbones have been computed also for the FOM\(_d\) (
 ) using the shooting method for validation. The vertical displacement of the mid-span of the beam is shown (first harmonic coefficient of the Fourier series, normalized over the beam thickness \(t_y\)). For each plot, the detuning parameter is \(\sigma =f-f_{01,d}\), being f [Hz] the forcing frequency and \(f_{01,d}\) [Hz] the first eigenfrequency of the FOM\(_d\) (corresponding to the selected \(\xi \)). The bottom-right figure collects the backbone curves for comparison. (Color figure online)
) using the shooting method for validation. The vertical displacement of the mid-span of the beam is shown (first harmonic coefficient of the Fourier series, normalized over the beam thickness \(t_y\)). For each plot, the detuning parameter is \(\sigma =f-f_{01,d}\), being f [Hz] the forcing frequency and \(f_{01,d}\) [Hz] the first eigenfrequency of the FOM\(_d\) (corresponding to the selected \(\xi \)). The bottom-right figure collects the backbone curves for comparison. (Color figure online)
The harmonic balance (HB) method was used (with 7 harmonics) using the NLvib MATLAB tool [61] (slightly modified to adapt the direct use of tensors) and our in-house MATLAB FE code. To validate the results of the ROMs, the shooting method is used to find the backbones of the corresponding FOM-d. Results are shown in Fig. 3. Computations were carried out in MATLAB 2020a on a local machine equipped with an Intel(R) Xeon(R) Silver 4214 CPU @2.20 GHz and 256 GB RAM @2666 MHz. Tensors were built in a Julia subroutine, called by the main MATLAB code, which uses the TensorOperations package [62] for the tensor contraction. At present, the tensor construction is implemented serially, therefore leaving space for possible future speedups exploiting parallel computing, as mentioned earlier. We remark once more that tensors in Eq. (28a) are evaluated offline before performing HB/shooting: Online evaluations use only the second-, third- and fourth-order reduced stiffness tensors for both ROM\(_d\) and the DpROMs.
As it can be observed, the shift from hardening to softening behavior is well captured by all the models, with a minor loss of accuracy of the DpROMs as \(\xi \) increases. In particular, DpROM-0\(_n\) shows a significant frequency offset of the first linear eigenfrequency which remains constant throughout the backbone curve. (The same happens for the FRs, but we omitted to plot them for the sake of figures clarity.) The main goal of the present test was to assess the accuracy of the method verifying the results against the FOM and over a range of frequencies. However, computational times are collected in Table 2 for completeness. Run times for the shooting method with the (Dp)ROMs are included for comparison. These figures, however, must be taken just as an indication, first because of the difference between FOM and ROMs in terms of convergence during continuation (ROMs are less likely to incur into numerical artifacts) and, second, because speed and convergence of this kind of analysis are highly sensitive to several parameters and finding the best combination by trial-and-error usually leads to sub-optimal performances. Last but not least, the size of the FOM in this case is too low to really appreciate the savings in terms of ROM construction.
8 Numerical tests-II
8.1 MEMS gyroscope
The last example we present is a prototype MEMS mono-axial gyroscope, shown in Fig. 4a. The device consists in a mass suspended by four S-shaped springs, connected to the ground on the bottom of the anchors. It is a monolithic piece, produced via deep reactive-ion etching (DRIE), a process which removes material from a plane silicon wafer to obtain the final geometry. The etching procedure is the main cause of production shape defects of MEMS devices, as it will be detailed later. In operative conditions, the mass is kept in motion by comb finger electrodes at the natural frequency of the drive mode (i.e., a mode featuring motion mainly in the x-direction), so that in the presence of an external angular rate \(\varOmega \) (along the y-axis), a vertical displacement \(w_{\mathrm{sense}}\) arises due to Coriolis effect along the z-axis (sense). The latter is then converted into an electrical signal through the parallel plate electrode placed on the ground below the mass, providing the measure for the angular rate. In general, a defect or a combination of them may create a coupling between the x- and z-axes so that the drive motion generates an additional out-of-plane displacement which superimposes to the Coriolis displacement to be measured. This is usually referred to as quadrature error since, being proportional to the drive displacement, it is in phase quadrature with the Coriolis signal, proportional to the drive velocity. Though it is possible to tell apart the two contributions, this is highly undesirable as it requires dedicated, over-sized electronics to accommodate the larger displacements. Ultimately, this results in higher power consumption.
8.2 FE model, defects and simulation details
The FE model is shown in Fig. 4b and describes in detail the geometry and mesh of the device, counting 14,920 quadratic hexahedral elements for a total of 261,495 dofs. For the present study, we selected two typical defects occurring in the production of MEMS devices, namely the wall angle (shown in Fig. 5a) and a restriction of the cross section of the beams (Fig. 5b). The first is generated by the fact that the plasma beam of the DRIE process might be not perfectly perpendicular to the working plane, while the second one typically comes from an overexposure to the chemical attacks (over-etching). In the spirit of our method, we can describe the global defects as the superposition of these two displacement fields (see Eq. (25b)), letting \(\mathbf{U} = [\mathbf{U} _1,\,\mathbf{U} _2]\) with the associated amplitude parameter vector \(\varvec{\xi }=[\xi _1,\,\xi _2]^T\). The wall angle shape defect \(\mathbf{U} _1=[\mathbf{u} _{d1},\,\mathbf{v} _{d1},\,\mathbf{w} _{d1}]^T\) is given by
and \(v_{d1}=w_{d1}=0\). The tapering of the beams \(\mathbf{U} _2=[\mathbf{u} _{d2},\,\mathbf{v} _{d2},\,\mathbf{w} _{d2}]^T\) is defined as
where
and \(u_{d2}=w_{d2}=0\). \(L_b\) and \(W_b\) are the length and the width of the beam, \(x_{\mathrm{off}}\) is an offset depending on the location of each beam, and \(y_{\mathrm{mid}}\) is the y-coordinate corresponding to the middle line of each beam. To ease the interpretation of the amplitude parameters, in the following \(\xi _1\) is reported in degrees to represent the physical wall angle coming from the product \(\xi _1 \tan (\alpha _y)\) in Eq. (43), while \(\xi _2\) is reported as a percentage of the beam thickness.
a First defect shape, \(\mathbf{U} _1\): constant wall angle \(\alpha _y\) (only one beam is shown). The colormap indicates x-displacement. b Second defect shape, \(\mathbf{U} _2\): tapering of the suspension beams, 3D and top views. (Only one beam is shown.) The colormap indicates y-displacement (absolute value). (Color figure online)
We compute the FR of the MEMS gyroscope using the NLvib MATLAB tool and our in-house MATLAB FE code. We used a reduction basis with 3 VMs, the corresponding 6 MDs and 3 DSs per defect (only for the DpROMs). More details about the RB are given in “Appendix C.” \(H=5\) harmonics were selected for the HB method (with \(N_s=3H+1\) time samples per period, the minimum number of samples by which no sampling error is introduced in the harmonics up to the H-th order when considering polynomial nonlinearities up to the third order [63], as in our case). Given the size of the model, we take as reference the results of ROM\(_d\), as it would be prohibitively time and memory consuming to compute the frequency response for FOM\(_d\). Apart from the practical issues, we justify this choice considering on the one side the good results obtained for lower-dimensional models (as the one presented in the previous section), and on the other side considering that, ultimately, our DpROMs will be at best as good as ROM-d, which is not parametric and not approximated in its formulation.
The frequency response was obtained forcing the system in the center of the suspended mass with a nodal load directed along the x-direction, with amplitude \(F=0.4 \, \upmu \)N, and using a Rayleigh damping matrix with \(\alpha =105\) and \(\beta =0\). Figure 6 reports the FRs around the first eigenfrequency of the system for the x-displacement u (drive direction) and the z-displacement w (sense direction) for all the combinations of \(\xi _1=\{0^{\circ },\,0.5^{\circ },\,1^{\circ }\}\) and \(\xi _2=\{0\%,\, 0.5\%,\, 1\%,\, 1.5\%,\, 2\% \}\). For the present study, all the DpROM versions reported in Table 1 are tested and compared.
Frequency responses and backbone curves for different defect amplitudes \(\xi _1\) (shown in degrees) and \(\xi _2\) (reported as percentage of the beam width) using the harmonic balance method (5 harmonics) for: ROM\(_d\) (
 ), DpROM-0\(_n\) (
), DpROM-0\(_n\) (
 ), DpROM-1t\(_n\) (
), DpROM-1t\(_n\) (
 ), DpROM-1\(_n\) (
), DpROM-1\(_n\) (
 ), DpROM-0\(_d\) (
), DpROM-0\(_d\) (
 ), DpROM-1t\(_d\) (
), DpROM-1t\(_d\) (
 ) and DpROM-1\(_d\) (
) and DpROM-1\(_d\) (
 ). The displacements u and w of the center of the mass are shown (first harmonic coefficient of the Fourier series). For each plot, the percent detuning parameter \(\sigma =(f-f_{01,d})/f_{01,d} \times 100\) is referred to the corresponding FOM\(_d\) first eigenfrequency \(f_{01,d}\). (Color figure online)
). The displacements u and w of the center of the mass are shown (first harmonic coefficient of the Fourier series). For each plot, the percent detuning parameter \(\sigma =(f-f_{01,d})/f_{01,d} \times 100\) is referred to the corresponding FOM\(_d\) first eigenfrequency \(f_{01,d}\). (Color figure online)
8.3 Results
With reference of Fig. 6, considering first the effect of the wall angle defect only, it is apparent how DpROM-0\(_n\) performances quickly degrade as soon as the parameter \(\xi _1\) is increased. This can be seen both in the error on the linear eigenfrequency and especially in the overestimated w-response, approximately one order of magnitude higher than the reference. This may be due to the fact that the S-shaped beams are specifically designed to minimize the cross-coupling between the drive (x-) and sense (z-) axes created by the wall angle, so that the w-response is so small (2 orders of magnitude lower than the u-response) that it cannot be accurately captured by DpROM-0\(_n\). The same observations can be made for DpROM-0\(_d\), as the wall angle defect by itself represents an isochoric transformation. The responses of all the other tested DpROMs show instead a perfect match with the reference when \(\xi _2=0\%\).
If the tapering defect only is considered (i.e., with \(\xi _1=0^{\circ }\)), we observe that DpROM-(0/1t/1)\(_n\) have similar responses, with an error on the eigenfrequency that translates the whole response by an approximately constant \(\varDelta f\). This error is expected, as the tapering is a volume-changing defect and integration over \(V_0\) is thus a too coarse approximation. Moreover, the volume changed by this defect affects the suspension beams dimensions, to which the eigenfrequencies of the system are very sensitive. If on the one hand DpROM-0\(_d\) still presents relevant errors, on the other hand DpROM-1t\(_d\) and DpROM-1\(_d\) show very accurate results in the full range of the tested \(\xi _2\).
For the remaining cases, the trends observed for the parameters \(\xi _1\) and \(\xi _2\) individually mix. Notice that looking at some results (e.g., u-response for \(\xi _1 = 1^{\circ }\), \(\xi _2=0.5\%\)), it may seem that DpROM-0\(_n\) gives better results than DpROM-1\(_n\). This is, however, just a coincidence, as for DpROM-0\(_n\) the first defect shifts the first eigenfrequency to lower frequencies while the second defect to higher frequencies, so that the two errors in this case cancel out. Indeed, when the volume correction is used in DpROM-0\(_d\), only the first effect is observed, and the frequencies are shifted to the left.
In Fig. 7, we also show the transient response of the forced node for ROM\(_d\) and DpROMs\(_d\) (case with \(\xi _1 = 1^{\circ }\), \(\xi _2=0.5\%\)). Each model is forced at its own first resonance frequency \(f_0\) (as it is usually the case for MEMS gyroscopes) with a harmonic forcing, taking 100 samples per period and for a time span equal to 10 times T\(_0=1/f_0\), with \(F=50\,\upmu \)N. The integration was carried out in MATLAB with our in-house code, using a Newmark integration scheme. Looking at the responses along the three axes, we observe that the three DpROMs yield correct results but for DpROM-0\(_d\) along the sense z-direction (w component). Also, considering the z-response, we can see that DpROM-1\(_n\) is slightly better DpROM-1t\(_n\), fact that was not very visible in the FRs.
8.4 Computational times
Table 3 reports the average time for the FR analyses and for the construction of the different models. To compare in terms of time ROM\(_d\) and the DpROMs, it is convenient to consider the variable costs (T\(_{\mathrm{var}}\)), i.e., the ones that have to be sustained for each new parameter realization, and the overhead costs (T\(_{\mathrm{oh}}\)), i.e., the ones sustained once and for all independently from the number of realizations. In the case of ROM\(_d\), we have that \(\text {T}_{\mathrm{var}}=\text {T}_{\mathrm{constr}}+\text {T}_{\mathrm{sim}}\), being \(\text {T}_{\mathrm{constr}}\) the time to construct the model (i.e., RB and tensors computation) and \(\text {T}_{\mathrm{sim}}\) the time for one simulation, while T\(_{\mathrm{oh}}=0\). For ROM\(_d\) indeed, there are no common overhead costs, but a new model must be constructed for each new realization of the parameters. In the case of DpROMs instead, we have that \(\text {T}_{\mathrm{var}}^{p}=\text {T}_{\mathrm{sim}}^p\) and \(\text {T}_{\mathrm{oh}}^p=\text {T}_{\mathrm{const}r}^p\). (We use the superscript “p” to distinguish the parametric models from ROM\(_d\).) For the parametric models, we have in fact to pay upfront the cost of model construction, which is generally more expensive than the one for ROM\(_d\), but thereafter only the simulation cost must be sustained for each new case. The first trivial conclusion is then that there exist a number \({\bar{N}}\) of parameter realizations above which DpROMs become convenient, that is:
For \({\bar{N}}\) to be positive and finite, it follows that
From Eq. (46), it can be seen how the convenience of the parametric model over the nonparametric one depends on the relative weight between the simulation and construction times of the latter and the simulation time of the former, as it can be observed in Table 3 looking at the different speedupsFootnote 7 for the FR and transient analyses.
That said, it is clearly difficult to draw general and definitive conclusions on the benefits of the two solutions, ROM\(_d\) and DpROMs, time-wise. In the experience of the authors, transient analysis offers the best gains, as simulation speed is very high, grows almost linearly with the simulation time span and is less sensitive to the number of dofs than other kind of analysis, as the ones requiring continuation methods. When continuation is required, one could potentially find greater benefits in using a model with a low number of dofs, so that ROM\(_d\) could actually become the best choice. We remark, however, that for ROM\(_d\), we have to take into account also the construction cost as a variable cost, and that for large FE models, the sole computation of structural eigenmodes can already take several minutes, making this cost very high.
9 Conclusions
We presented a ROM for geometric nonlinearities that can parametrically describe a shape imperfection with respect to the nominal (blueprint) design, named for brevity DpROM. The imperfection is given by the superposition of user-defined defect shapes, whose amplitudes are parameters of the model and can be changed without reconstructing the model itself. This result has been made possible thanks to a polynomial representation of the internal forces resulting from a two-step deformation process (which brings the nominal geometry into the defected one and then into the deformed one) and from the approximation of the strains obtained by a Neumann expansion. The latter allowed to eliminate rational expressions under the hypothesis of small defects, so that the elastic internal forces are written as simple polynomials both with respect to the displacement field representing the defect and with respect to the actual displacement field. Using a Galerkin projection and a modal-based approach for selecting the RB, the reduced internal forces have been recast in tensorial form, where the linear, quadratic and cubic stiffness tensors are found to be functions of a parameter vector collecting the amplitudes of the defects imposed on the structure. Within this framework, we tested different versions of the DpROM for different degrees of approximation. In particular, we have shown that the model we had previously developed using Budiansky’s approach corresponds to the zeroth-order expansion of our model, integrated over the nominal volume \(V_0\) (i.e., DpROM-0\(_n\)). Finally, in the numerical studies we showed that the higher-order approximation DpROM-1\(_n\) effectively leads to more accurate results and that for volume-changing defects, a large improvement can be achieved by approximating the tensor integral over the real volume of the defective geometry (DpROM-(0/1)\(_d\)). The truncated version DpROM-1t\(_{n/d}\) was also presented, which has almost the same accuracy as its complete counterpart, but without the need to construct tensors with dimensionality higher than four. The computational costs were then critically discussed, taking into account different types of analysis. In particular, we showed that in transient studies, we can usually expect very high speedups from the parametric models. In the case of FR analysis, which we used to assess the quality of the solutions over a range of frequencies as an alternative to multiple time analyses, the gains will be more contained. In this context, to reduce the dofs of both the parametric and nonparametric ROMs and make FR analysis faster and thus closer to transient analysis in terms of time and speedups, we think that an a priori selection of the RB vectors and hyper-reduction strategies would actually be very beneficial, and they can constitute the spur for future investigation.
Code availability
The MATLAB FE code and the Julia routines used in this work can be made available upon request to the authors.
Notes
By simulation, we refer to the solution of a set of equations describing a system in any kind of analysis setting (e.g., in time or frequency domain).
Due to memory limitations, third- and fourth-order stiffness tensors cannot be computed for the FOM, but they can be constructed in reduced form directly operating at element level [27].
\(\otimes \) denotes the outer product, and : and denote the double and triple contraction operations. Using Einstein notation, we have that \(\mathbf{X} =\mathbf{x} \otimes \mathbf{x} \otimes \mathbf{x} \) (being \(\mathbf{x} \) a vector) corresponds to \(X_{IJK}=x_Ix_Jx_K\), \(\mathbf{a} =\mathbf{B} :\mathbf{C} \) (being B and C a 3- and a 2-dimensional matrix, respectively) to \(a_I=B_{Iij}C_{ij}\) and, similarly,
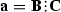 to \(a_I=B_{Iijk}C_{ijk}\) (where B and C are now 4- and 3-dimensional, respectively).
to \(a_I=B_{Iijk}C_{ijk}\) (where B and C are now 4- and 3-dimensional, respectively).\({\mathcal {F}}_1(\mathbf{x} _0)\) can be thought as a transformation corresponding to a static analysis with imposed forces and/or boundary displacements.
The spectral norm of a matrix \(\mathbf{A} \) is defined as the square root of the largest singular value of \(\mathbf{A} ^*\mathbf{A} \), being \(\mathbf{A} ^*\) the conjugate transpose of \(\mathbf{A} \), that is: \( \left\Vert \mathbf{A} \right\Vert _2 = \sqrt{ \lambda _{max}(\mathbf{A} ^*\mathbf{A} )} \)
For the derivatives of the displacement components, we use the notation \(u_{,x}=\frac{\partial u}{\partial x_0}\) and \(u_{d,x}=\frac{\partial u_d}{\partial x_0}\) (similar definition for v, w and the other spatial coordinates).
Speedups are computed considering the variable costs only, with respect to ROM\(_d\).
References
Belytschko, T., Liu, W.K., Moran, B., Elkhodary, K.: Nonlinear Finite Elements for Continua and Structures. Wiley, Hoboken (2013)
Toselli, A., Widlund, O.B.: Domain Decomposition Methods—Algorithms and Theory. Springer Series in Computational Mathematics, vol. 34. Springer, Berlin (2005)
Klerk, D.D., Rixen, D.J., Voormeeren, S.N.: General framework for dynamic substructuring: history, review and classification of techniques. AIAA J. 46(5), 1169–1181 (2008). https://doi.org/10.2514/1.33274.
Farhat, C., Roux, F.X.: A method of finite element tearing and interconnecting and its parallel solution algorithm. Int. J. Numer. Methods Eng. 32(6), 1205–1227 (1991). https://doi.org/10.1002/nme.1620320604.
Guyan, R.J.: Reduction of stiffness and mass matrices. AIAA J. 3(2), 380–380 (1965). https://doi.org/10.2514/3.2874.
He, J., Fu, Z.F.: Modal Analysis. Elsevier, Amsterdam (2001). https://doi.org/10.1016/B978-0-7506-5079-3.X5000-1
Craig, R., Bampton, M.: Coupling of substructures for dynamic analyses. AIAA J. 6(7), 1313–1319 (1968)
Rubin, S.: Improved component-mode representation for structural dynamic analysis. AIAA J. 13(8), 995–1006 (1975). https://doi.org/10.2514/3.60497.
Pichler, F., Witteveen, W., Fischer, P.: Reduced-order modeling of preloaded bolted structures in multibody systems by the use of trial vector derivatives. J. Comput. Nonlinear Dyn. 12(5), 051032 (2017). https://doi.org/10.1115/1.4036989.
Blockmans, B., Tamarozzi, T., Naets, F., Desmet, W.: A nonlinear parametric model reduction method for efficient gear contact simulations. Int. J. Numer. Methods Eng. 102(5), 1162–1191 (2015). https://doi.org/10.1002/nme.4831.
Balajewicz, M., Amsallem, D., Farhat, C.: Projection-based model reduction for contact problems. Int. J. Numer. Methods Eng. 106, 644–663 (2015). https://doi.org/10.1002/nme.
Géradin, M., Rixen, D.J.: A ‘nodeless’ dual superelement formulation for structural and multibody dynamics application to reduction of contact problems. Int. J. Numer. Methods Eng. 106(10), 773–798 (2016). https://doi.org/10.1002/nme.5136.
Mehrdad Pourkiaee, S., Zucca, S.: A reduced order model for nonlinear dynamics of mistuned bladed disks with shroud friction contacts. J. Eng. Gas Turbines Power 141(1), 1–13 (2019). https://doi.org/10.1115/1.4041653
Ghavamian, F., Tiso, P., Simone, A.: POD-DEIM model order reduction for strain softening viscoplasticity. Comput. Methods Appl. Mech. Eng. 317, 458–479 (2017). https://doi.org/10.1016/j.cma.2016.11.025.
Wu, L., Tiso, P., Tatsis, K., Chatzi, E., van Keulen, F.: A modal derivatives enhanced Rubin substructuring method for geometrically nonlinear multibody systems. Multibody Syst. Dyn. 45(1), 57–85 (2019). https://doi.org/10.1007/s11044-018-09644-2.
Wu, L., Tiso, P., van Keulen, F.: Interface reduction with multilevel Craig–Bampton substructuring for component mode synthesis. AIAA J. (2018). https://doi.org/10.2514/1.J056196
Vizzaccaro, A., Salles, L., Touzé, C.: Comparison of nonlinear mappings for reduced-order modelling of vibrating structures: normal form theory and quadratic manifold method with modal derivatives. Nonlinear Dyn. (2020). https://doi.org/10.1007/s11071-020-05813-1.
Jain, S., Tiso, P., Haller, G.: Exact nonlinear model reduction for a von Kármán beam: slow-fast decomposition and spectral submanifolds. J. Sound Vib. 423, 195–211 (2018). https://doi.org/10.1016/j.jsv.2018.01.049
Ponsioen, S., Jain, S., Haller, G.: Model reduction to spectral submanifolds and forced-response calculation in high-dimensional mechanical systems. J. Sound Vib. 488, 115640 (2020). https://doi.org/10.1016/j.jsv.2020.115640
Jain, S., Haller, G.: How to compute invariant manifolds and their reduced dynamics in high-dimensional finite-element models? pp. 1–40 (2021). http://arxiv.org/abs/2103.10264
Perez, R., Bartram, G., Beberniss, T., Wiebe, R., Spottswood, S.M.: Calibration of aero-structural reduced order models using full-field experimental measurements. Mech. Syst. Signal Process. 86, 49–65 (2017). https://doi.org/10.1016/j.ymssp.2016.04.013
Touzé, C., Vidrascu, M., Chapelle, D.: Direct finite element computation of non-linear modal coupling coefficients for reduced-order shell models. Comput. Mech. 54(2), 567–580 (2014). https://doi.org/10.1007/s00466-014-1006-4
Hollkamp, J.J., Gordon, R.W.: Reduced-order models for nonlinear response prediction: implicit condensation and expansion. J. Sound Vib. 318(4–5), 1139–1153 (2008). https://doi.org/10.1016/j.jsv.2008.04.035
Kuether, R.J., Deaner, B.J., Hollkamp, J.J., Allen, M.S.: Evaluation of geometrically nonlinear reduced-order models with nonlinear normal modes. AIAA J. 52(11), 3273–3285 (2015). https://doi.org/10.2514/1.J053838
Amabili, M.: Reduced-order models for nonlinear vibrations, based on natural modes: the case of the circular cylindrical shell. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 371(1993), 20120474 (2013). https://doi.org/10.1098/rsta.2012.0474.
Mignolet, M.P., Przekop, A., Rizzi, S.A., Spottswood, S.M.: A review of indirect/non-intrusive reduced order modeling of nonlinear geometric structures. J. Sound Vib. 332(10), 2437–2460 (2013). https://doi.org/10.1016/j.jsv.2012.10.017.
Jain, S.: Model Order Reduction for Non-linear Structural Dynamics (2015). http://resolver.tudelft.nl/uuid:cb1d7058-2cfa-439a-bb2f-22a6b0e5bb2a
Lu, K., Jin, Y., Chen, Y., Yang, Y., Hou, L., Zhang, Z., Li, Z., Fu, C.: Review for order reduction based on proper orthogonal decomposition and outlooks of applications in mechanical systems. Mech. Syst. Signal Process. 123, 264–297 (2019). https://doi.org/10.1016/j.ymssp.2019.01.018.
Noor, A.K., Peterst, J.M.: Reduced basis technique for nonlinear analysis of structures. AIAA J. 18(4), 455–462 (1980). https://doi.org/10.2514/3.50778.
Idelsohn, S.R., Cardona, A.: A reduction method for nonlinear structural dynamic analysis. Comput. Methods Appl. Mech. Eng. 49(3), 253–279 (1985). https://doi.org/10.1016/0045-7825(85)90125-2.
Sombroek, C.S., Tiso, P., Renson, L., Kerschen, G.: Numerical computation of nonlinear normal modes in a modal derivative subspace. Comput. Struct. 195, 34–46 (2018). https://doi.org/10.1016/j.compstruc.2017.08.016.
Jain, S., Tiso, P., Rutzmoser, J.B., Rixen, D.J.: A quadratic manifold for model order reduction of nonlinear structural dynamics. Comput. Struct. 188, 80–94 (2017). https://doi.org/10.1016/j.compstruc.2017.04.005.
Baur, U., Benner, P., Haasdonk, B., Himpe, C., Maier, I., Mario Ohlberger, M., Dynamik Komplexer, F.: Comparison of methods for parametric model order reduction of instationary problems (2017). http://www.mpi-magdeburg.mpg.de/preprints/
Xiao, D., Fang, F., Buchan, A.G., Pain, C.C., Navon, I.M., Muggeridge, A.: Non-intrusive reduced order modelling of the Navier–Stokes equations. Comput. Methods Appl. Mech. Eng. 293, 522–541 (2015). https://doi.org/10.1016/j.cma.2015.05.015.
Xiao, D., Fang, F., Pain, C.C., Navon, I.M.: A parameterized non-intrusive reduced order model and error analysis for general time-dependent nonlinear partial differential equations and its applications. Comput. Methods Appl. Mech. Eng. 317, 868–889 (2017). https://doi.org/10.1016/j.cma.2016.12.033.
Xiao, D.: Error estimation of the parametric non-intrusive reduced order model using machine learning. Comput. Methods Appl. Mech. Eng. 355, 513–534 (2019). https://doi.org/10.1016/j.cma.2019.06.018.
Zimmermann, R.: Manifold interpolation and model reduction, pp. 1–36 (2019). http://arxiv.org/abs/1902.06502
Barrault, M., Maday, Y., Nguyen, N.C., Patera, A.T.: An ‘empirical interpolation’ method: application to efficient reduced-basis discretization of partial differential equations. C.R. Math. 339(9), 667–672 (2004). https://doi.org/10.1016/j.crma.2004.08.006.
Chaturantabut, S., Sorensen, D.C.: Nonlinear model reduction via discrete empirical interpolation. SIAM J. Sci. Comput. 32(5), 2737–2764 (2010). https://doi.org/10.1137/090766498.
Phalippou, P., Bouabdallah, S., Breitkopf, P., Villon, P., Zarroug, M.: ‘On-the-fly’ snapshots selection for proper orthogonal decomposition with application to nonlinear dynamics. Comput. Methods Appl. Mech. Eng. 367, 113120 (2020). https://doi.org/10.1016/j.cma.2020.113120.
Cho, H., Shin, S.J., Kim, H., Cho, M.: Enhanced model-order reduction approach via online adaptation for parametrized nonlinear structural problems. Comput. Mech. 65(2), 331–353 (2020). https://doi.org/10.1007/s00466-019-01771-7.
Kast, M., Guo, M., Hesthaven, J.S.: A non-intrusive multifidelity method for the reduced order modeling of nonlinear problems. Comput. Methods Appl. Mech. Eng. 364, 112947 (2020). https://doi.org/10.1016/j.cma.2020.112947.
Hesthaven, J.S., Ubbiali, S.: Non-intrusive reduced order modeling of nonlinear problems using neural networks. J. Comput. Phys. 363, 55–78 (2018). https://doi.org/10.1016/j.jcp.2018.02.037.
Maulik, R., Lusch, B., Balaprakash, P.: Reduced-order modeling of advection-dominated systems with recurrent neural networks and convolutional autoencoders. arXiv (2020)
Astolfi, A.: Model reduction by moment matching for nonlinear systems. In: 2008 47th IEEE Conference on Decision and Control, vol. 2015-Febru, pp. 4873–4878. IEEE (2008). https://doi.org/10.1109/CDC.2008.4738791. http://ieeexplore.ieee.org/document/7039956/
Astolfi, A.: Model reduction by moment matching for linear and nonlinear systems. IEEE Trans. Autom. Control 55(10), 2321–2336 (2010). https://doi.org/10.1109/TAC.2010.2046044.
Ionescu, T.C., Astolfi, A.: Nonlinear moment matching-based model order reduction. IEEE Trans. Autom. Control 61(10), 2837–2847 (2016). https://doi.org/10.1109/TAC.2015.2502187
Rafiq, D., Bazaz, M.A.: A framework for parametric reduction in large-scale nonlinear dynamical systems. Nonlinear Dyn. 102(3), 1897–1908 (2020). https://doi.org/10.1007/s11071-020-05970-3.
Acar, C., Shkel, A.: MEMS Vibratory Gyroscopes. Springer, Berlin (2008)
Izadi, M., Braghin, F., Giannini, D., Milani, D., Resta, F., Brunetto, M.F., Falorni, L.G., Gattere, G., Guerinoni, L., Valzasina, C.: A comprehensive model of beams’ anisoelasticity in MEMS gyroscopes, with focus on the effect of axial non-vertical etching. In: 5th IEEE International Symposium on Inertial Sensors and Systems, INERTIAL 2018 - Proceedings pp. 1–4 (2018). https://doi.org/10.1109/ISISS.2018.8358126
Wang, X.Q., Phlipot, G.P., Perez, R.A., Mignolet, M.P.: Locally enhanced reduced order modeling for the nonlinear geometric response of structures with defects. Int. J. Non-Linear Mech. 101, 1–7 (2018). https://doi.org/10.1016/j.ijnonlinmec.2018.01.007
Wang, X.Q., O’Hara, P.J., Mignolet, M.P., Hollkamp, J.J.: Reduced order modeling with local enrichment for the nonlinear geometric response of a cracked panel. AIAA J. 57(1), 421–436 (2018). https://doi.org/10.2514/1.j057358
Marconi, J., Tiso, P., Braghin, F.: A nonlinear reduced order model with parametrized shape defects. Comput. Methods Appl. Mech. Eng. 360, 112785 (2020). https://doi.org/10.1016/j.cma.2019.112785
Budiansky, B.: Dynamic buckling of elastic structures: criteria and estimates. In: Proceedings of an International Conference Held at Northwestern University, Evanston, Illinois. Pergamon Press Ltd (1967). https://doi.org/10.1016/B978-1-4831-9821-7.50010-7
Amabili, M.: Theory and experiments for large-amplitude vibrations of rectangular plates with geometric imperfections. J. Sound Vib. 291(3–5), 539–565 (2006). https://doi.org/10.1016/j.jsv.2005.06.007
Camier, C., Touzé, C., Thomas, O.: Non-linear vibrations of imperfect free-edge circular plates and shells. Eur. J. Mech. A/Solids 28(3), 500–515 (2009). https://doi.org/10.1016/j.euromechsol.2008.11.005.
Wang, X., Cen, S., Li, C.: Generalized neumann expansion and its application in stochastic finite element methods. Math. Probl. Eng. (2013). https://doi.org/10.1155/2013/325025
Hay, A., Borggaard, J., Akhtar, I., Pelletier, D.: Reduced-order models for parameter dependent geometries based on shape sensitivity analysis. J. Comput. Phys. 229(4), 1327–1352 (2010). https://doi.org/10.1016/j.jcp.2009.10.033.
Tiso, P.: Optimal second order reduction basis selection for nonlinear transient analysis. In: Proceedings of the 29th IMAC A Conference on Structural Dynamics 2011, vol. 3, pp. 27–39 (2011). https://doi.org/10.1007/978-1-4419-9299-4_3
Shen, Y., Vizzaccaro, A., Kesmia, N., Yu, T., Salles, L., Thomas, O., Touzé, C.: Comparison of reduction methods for finite element geometrically nonlinear beam structures. Vibration 4(1), 175–204 (2021). https://doi.org/10.3390/vibration4010014
Krack, M., Gross, J.: Harmonic Balance for Nonlinear Vibration Problems. Springer: Berlin (2019). https://doi.org/10.1007/978-3-030-14023-6
Jutho, G., Lyon, S., Protter, M., Leo, M.P., Garrison, J., Otto, F., Saba, E., Iouchtchenko, D., Privett, A., Morley, A.: Jutho/tensoroperations.jl: v1.1.0 (2019). https://doi.org/10.5281/zenodo.3245497
Woiwode, L., Balaji, N.N., Kappauf, J., Tubita, F., Guillot, L., Vergez, C., Cochelin, B., Grolet, A., Krack, M.: Comparison of two algorithms for harmonic balance and path continuation. Mech. Syst. Signal Process. 136, 106503 (2020). https://doi.org/10.1016/j.ymssp.2019.106503.
Acknowledgements
The authors want to express their gratitude to the AMS R&D division at STMicroelectronics, Cornaredo (IT), for their support in this work.
Funding
Open Access funding provided by ETH Zurich.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
A. Localization matrices L \(_1\), L \(_2\) and L \(_3\)
We report in Tables 4 and 5 the expressions for the matrices \(\mathbf{L} _1\), \(\mathbf{L} _2\) and \(\mathbf{L} _3\) defined in Eq. 21, for the plane-strain/stress continuum problem (2D case) and the three-dimensional continuum problem (3D case). In the tables, name subscripts are moved to superscripts to avoid confusion with the indexes (e.g., \(L_{ijk}^{(1)}\) is a component of L\(_1\)).
B Tangent stiffness matrix derivatives
The virtual variation wrt \(\mathbf{u} \) of the internal elastic forces as defined in Eq. (20) writes
Recalling that \(\mathbf{A} _1\delta \varvec{\theta }=\delta \mathbf{A} _1\varvec{\theta }\), we can write
being
The second term on the right-hand side of Eq. (48) can be rewritten to put in evidence the displacement virtual variation \(\delta \mathbf{u} \) as
where Einstein notation was used for convenience. The tangent stiffness matrix therefore writes:
where
Substituting \(\mathbf{u} =\varvec{\varPhi }_i\eta _i\) and \(\mathbf{u} _d = \mathbf{U} _j\xi _j\) in Eq. (51), taking the derivative wrt either \(\eta _i\) and/or \(\xi _j\) and evaluating the resulting expressions at equilibrium and with zero defect amplitudes, as required by Eqs. (38)–(41), we can write the derivatives of \(\mathbf{K} _t\) as:
where recalling that \(\eta _i\) and \(\xi _j\) are scalars, we used \(\mathbf{A} _1(\mathbf{G} \varvec{\varPhi }_i\eta _i) = \mathbf{A _1}_i \eta _i\) and \(\mathbf{A} _2(\mathbf{G} \mathbf{U} _j\xi _j) = \mathbf{A _2}_j \xi _j\) (same for \(\mathbf{A} _3\)) to avoid a cumbersome notation, and where \(\cdot _{ij}\) denotes the contraction of the i-th dimension of the first term with the j-th dimension of the second term.
C RB for Model-II
Also for Model–II, the RB selection criterion described in Remark 6 is adopted and eigenmodes up to 3 times the first eigenfrequency are retained. The reduction basis is thus formed as:
that is, 3 VMs and all their corresponding MDs and DSs are included. Figure 8 shows the mode shapes. Apart from VMs, the interpretation of these vectors is in general not trivial. One can, for instance, recognize in \(\varvec{\theta }_{33}\) a necessary element to correctly represent the rotation happening in mode \(\varvec{\varPhi }_3\) and in \(\varvec{\theta }_{11}\) the stretching of the suspension beams required to capture their nonlinear behavior. To better inspect the contribution of DSs, we plotted \(\varvec{\Xi }_{i,k}^{\bot }\), i.e., \(\varvec{\Xi }_{i,k}\) orthogonalized with respect to \(\varvec{\varPhi }_i\) (via Gram–Schmidt). \(\varvec{\Xi }_{1,1}^{\bot }\) is particularly significant as it represents the out-of-plane motion of the structure induced on the first VM (x-polarized) by the presence of the wall angle defect, which is responsible for the gyroscope quadrature error. Similarly, it can be observed how \(\varvec{\Xi }_{2,1}^{\bot }\) represents an in-plane motion associated with the second VM (z-polarized) due to the wall angle defect. The contributions of \(\varvec{\Xi }_{i,2}^{\bot }\) are instead local and restricted to the suspension beams, as it can be expected given the local nature of the tapering.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Marconi, J., Tiso, P., Quadrelli, D.E. et al. A higher-order parametric nonlinear reduced-order model for imperfect structures using Neumann expansion. Nonlinear Dyn 104, 3039–3063 (2021). https://doi.org/10.1007/s11071-021-06496-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11071-021-06496-y


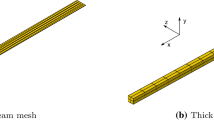








 ), DpROM-0
), DpROM-0 ), DpROM-1t
), DpROM-1t ) and DpROM-1
) and DpROM-1 ). The forcing is harmonic with period T
). The forcing is harmonic with period T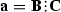 to
to 