1 Introduction

Optical methods for distance measurement include many schemes, most of which are based on lasers (Berkovic and Shafir 2012; Donati 2004). Telemeters are indeed one of the most successful applications of this device, since 1970, just after its invention.

Among different options, time-of-flight telemeters (Donati 2004) are based on the measurement of the time required by the laser radiation to cover the round trip distance to a target. Both pulsed and sine-wave time-of-flight telemeters require proper design and processing to tackle the ambiguity problem in distance measurement. Moreover, pulsed telemeters require fast laser power switching, fast electronic circuits and possibly the implementation of gating and optimum filtering techniques to get high resolution. Even though the basic principles of pulsed telemeters are well-known, recent contributions can be found in the literature, especially on electronic detection and processing (Kurti 2018; Norgia et al. 2016).

Telemeters based on optical injection have been also designed: in these schemes, the laser power is modulated by the optical power reflected or diffused back by a target (Donati 1978, 2004; Donati et al. 1995; Norgia et al. 2017). Optical injection has been proposed also for other applications, including chaos generation and chaotic cryptography (Donati and Mirasso 2002). Optical chaos also provides a means to measure a distance (Mecozzi et al. 2009).

In the last 2 decades, semiconductor ring lasers have been developed. The most typical application of this device is the laser gyroscope (Taguchi et al. 1999; Numai 2000), but others have been proposed including, for example, an optical flip-flop (Trita et al. 2014) and an optical clock (Li et al. 2016).

A mathematical model for the ring laser has been derived (Numai 2000), and different regimes have been theoretically predicted and experimentally observed (Sorel et al. 2002a; b), including bistability (or, strictly speaking, quasi-unidirectional regime) between the two clockwise, counter-clockwise (CW/CCW) modes. Also, optical feedback effects have been studied (Friart et al. 2017), as well as methods to reduce the laser sensitivity to feedback (Khoder et al. 2018; Lenstra and van Schaijk 2019; Van Schaijk et al. 2018), or to select the operating wavelength and mode (Khoder et al. 2016; Verschaffelt and Khoder 2018). Chaos generation in a ring laser (Li et al. 2018) has been also investigated, and even an application to decision making in artificial intelligence (Homma et al. 2019) has been proposed.

However, to our knowledge, the application of a ring laser to telemetry has not yet been considered.

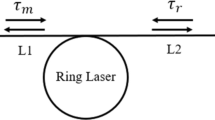
In this paper, we propose a telemeter, shown in Fig. 1, which makes use of a semiconductor ring laser in the bistable regime, and is based on an operating principle similar to that presented in (Trita et al. 2014) and (Li et al. 2016). In our scheme, laser switching between CW and CCW modes is not determined by injection of external radiation pulses, but it is self-generated by the laser.

Fig. 1
figure 1

Scheme of the semiconductor ring-laser telemeter (M1–M2: mirrors)

Full size image

Suppose that at a given time the laser is in the CW regime. The radiation emitted from one ring-laser end (right end in Fig. 1) is reflected back by the target and after a round trip time, which depends on the laser-target distance, it re-enters the laser cavity in opposite direction and, for proper operating conditions, switches the laser to CCW. The laser emission from the other output (left end in Fig. 1) is directed toward a nearer (and fixed) local mirror along a short optical path to switch the laser back to CW, so that the operation can start again, producing a periodic variation of the power direction inside the cavity, which can be detected, for example, by a photodiode positioned behind the local (partial) mirror. Since the first round trip time depends on the laser-target distance, while the second is constant, the laser-target distance can be measured from the oscillation period.

This telemeter, which combines time-of-flight and optical injection, has a very simple scheme, since, in addition to the laser, it only requires mirrors and collimation or focusing optics. Also electronic driving and processing are straightforward, since no pulser is needed, and one has only to measure the period or frequency of the detected optical output. Finally, this telemeter is not affected by the ambiguity problem.

In the following, this scheme is numerically evaluated. Numerical models have been proposed by different authors for the ring laser with and without feedback (Sorel et al. 2002a; b; Friart et al. 2017; Khoder et al. 2016; Li et al. 2018; Van Schaijk et al. 2018; Verschaffelt and Khoder 2018). In the following, we start from the work by Numai (2000), which contains a detailed derivation of what, to our knowledge, is the first model proposed in the literature for the ring laser.

Adding optical feedback, we obtain two equation sets, which describe our telemeter with different levels of accuracy.

2 Numerical models

We start from the model by Numai including gain saturation, and neglecting spontaneous emission (Eqs. 16, 17, 18 in Numai 2000):

$$\frac{{dS_{1} }}{dt} = [G - \beta S_{1} - \theta S_{2} ]S_{1} - \frac{{S_{1} }}{{\tau_{ph} }} + \frac{{\eta_{2} }}{{\tau_{in} }}S_{2} (t - \tau_{r} )$$
(1)
$$\frac{{dS_{2} }}{dt} = [G - \beta S_{2} - \theta S_{1} ]S_{2} - \frac{{S_{2} }}{{\tau_{ph} }} + \frac{{\eta_{1} }}{{\tau_{in} }}S_{1} (t - \tau_{m} )$$
(2)
$$\frac{dN}{dt} = \frac{J}{ed} - [G - \beta S_{1} - \theta S_{2} ]S_{1} - [G - \beta S_{2} - \theta S_{1} ]S_{2} - \frac{N}{{\tau_{n} }}$$
(3)

where G = G0(N − N0).

In these equations, S1, S2 are CW and CCW photon densities, N is the carrier concentration, J is the current density, gain G has been linearized and G0 is the modal gain coefficient, β and θ are the (assumed symmetrical) saturation coefficients, and e is the electron charge. Other symbols are listed in Table 1.

Table 1 System parameters
Full size table

Since the original model does not include optical injection, we have added the two last terms of Eqs. (1) and (2), where η1, η2, account for the total attenuations from the laser to each mirror and back, τin is the time of flight in the laser cavity, and τr, τm are the round trip times from the laser to the local reflector and to the measuring mirror, respectively. These two terms are the same that are usually added in the Lang-Kobayashi model (Lang and Kobayashi 1980) of the standard semiconductor laser, to take into account back-reflection from a remote mirror, as required to study, for example, chaotic dynamics (Donati and Mirasso 2002). Photon density S can be converted into optical power P (a more directly measurable quantity), by P = kS, where:

$$k = hv\upsilon_{g} S_{b}$$
(4)

h being the Plank constant, v = c/λ the optical frequency (c light speed in vacuum), while vg and Sb are defined in Table 1.

In the following, we will refer to this model as the three-equation model.

This model can be simplified, in view of numerical integration, by the reasonable assumption that the dynamics of N can be considered slow enough, with respect to photon dynamics, to be safely neglected. Thus, we set dN/dt = 0 in Eq. (3), so that the gain G0(N − N0) is constant, as a first approximation.

Normalizing time t to the photon lifetime τph, and expressing the dynamics in terms of power instead of photon density, we finally get a new model of a very simple form:

$$\frac{{dP_{1} }}{dt} = [\mu (1 - sP_{1} - cP_{2} ) - 1]P_{1} + \eta_{2}^{{\prime }} P_{2} (t - \tau_{r}^{{\prime }} )$$
(5)
$$\frac{{dP_{2} }}{dt} = [\mu (1 - sP_{2} - cP_{1} ) - 1]P_{2} + \eta_{1}^{{\prime }} P_{1} (t - \tau_{m}^{{\prime }} )$$
(6)

where the new parameters are related to those of the previous model by:

$$\begin{array}{*{20}l} {\mu = G_{0} (N - N_{0} )\tau_{ph} } \hfill \\ {s = \beta \tau_{ph} /\mu k^{{\prime }} } \hfill \\ {c = \theta \tau_{ph} /\mu k^{{\prime }} } \hfill \\ {\eta_{2}^{{\prime }} = \eta_{1} \tau_{ph} /\tau_{in} } \hfill \\ {\eta_{2}^{{\prime }} = \eta_{2} \tau_{ph} /\tau_{in} } \hfill \\ \end{array}$$

and \(\tau_{r}^{{\prime }}\), \(\tau_{m}^{{\prime }}\), k′ are the normalized values of τr, τm, k.

In the following, we will refer to Eqs. (5, 6) as the two-equation model.

3 Numerical results

First, the more accurate and complete three-equation model has been used to demonstrate the operating principle of the telemeter and to explore its linearity. We have assumed for most parameters (Table 1) the same values as in Numai (2000), while β, θ have been optimized for a 1 mW laser.

To start, we have found a convenient working point, for which a robust bistable regime takes place. Power time series of the CW and CCW laser modes are shown in Fig. 2, for η1 = η2 = η = 0.3, I = JSa= 5.3 mA, giving stable and clear oscillation signals (local arm: 100 μm, target distance: 20 cm).

Fig. 2
figure 2

Sample of power time series for CW and CCW modes (three-equation model, local arm: 100 μm, target distance: 20 cm)

Full size image

Then, we have numerically tested the telemeter for different distances of both the local and the remote mirror, assuming we work in the air (speed of light c). A remarkably linear behavior has been found, as shown in Fig. 3, where a plot of oscillation period vs. target distance is drawn, for the same parameters of Fig. 2, and for a short range round-trip target distance (up to 1 m).

Fig. 3
figure 3

Linearity plot of the telemeter simulated by the three-equation model (local arm: 100 μm)

Full size image

From Fig. 3, the period is approximately T = 2m, i.e., twice the laser-target round trip time. For a large target distance with respect to the local mirror distance (τm ≫ τr), this was expected, since 2τm is the time required for the laser radiation to completely fill and and then leave the measuring arm, i.e., between two commutations. Linearity has been confirmed sweeping the target round trip distance from 10 cm up to 32 m, and for different values of β, θ, η, provided that I is optimized to take the laser in the bistable regime. The local mirror distance has been tested from 10 cm down to 10 μm, since a short local arm is preferable, especially in view of a Photonic Integrated Circuit (PIC) implementation. In our simulations, we have added noise sources, i.e., Langevin noise (Ju et al. 2004) and shot noise (not shown in the equations).

Then we have tested the two-equation model finding that, in spite of its simple form, it provides essentially the same predictions. From Eqs. (5, 6), in bistable operation, without feedback (η’1 = η’2 = η’ = 0), either P1 or P2 must be zero. Assuming P1 = 0, dP2/dt = 0 (stationary conditions), we get:

$$P_{20} = (\mu - 1)/(s\mu )$$

from which μ > 1 is the condition for the laser to work.

Since we are investigating the oscillation period as a function of distance, and we are not concerned with amplitude, we can normalize the output power to P20, and select small numbers for parameters μ = 2, η’1 = η’2 = 0.3, s = 0.005, c = 0.03, to speed up numerical simulations. A sample of power time series is shown in Fig. 4, for the same target distance as in Fig. 2. Time on the horizontal axis has been de-normalized, to allow for a comparison: it is found that, in spite of some minor differences in the waveform shape, the period is exactly the same.

Fig. 4
figure 4

Sample of power time series for CW and CCW modes (two-equation model, local arm: 100 μm, target distance: 20 cm)

Full size image

Finally, Fig. 5 shows the linearity plot for a local arm length of 10 μm, and a round trip distance up to 32 m, where again the horizontal axis has been rescaled to the same units as in Fig. 3.

Fig. 5
figure 5

Linearity plot of the telemeter simulated by the two-equation model (local arm: 10 μm)

Full size image

One may observe that the two-equation model, whose main advantage lies in its simplicity, could have been directly written from the word description of the working principle of the telemeter. In fact, Eqs. (5, 6) simply state that each counter-rotating mode is characterized by a gain, which is reduced by a direct and a cross saturation effect, and that each mode receives delayed optical feedback from one mirror.

However, we would like to point out the importance of having validated this model by comparison with the more accurate and theoretically sound three-equation model. Since the results we found are consistent for all distances we tested, we can be confident that the two-equation model is suitable to simulate the ring laser at least to this specific purpose, and that its predictions are also reliable.

From the three equation model, we also found that the laser cannot work in the bistable regime if we substantially modify its parameter values with respect to those shown in Table 1 (τn, τph, β, θ). This means that the laser should be designed or optimized for this specific application, even though a more accurate model (describing technological details of the device) should be employed to better investigate this point.

Even if the laser is in the bistability regime, the system may be unsuitable to work as a telemeter. For example, in Fig. 6 we show a case where the laser, after a transient, fails to periodically switch between CW and CCW regimes. This may happen, for example, on some ranges of supply current, or for too large attenuation (parameter η) or for low values of parameters β, θ.

Fig. 6
figure 6

Sample of power time series for CW and CCW modes when bistability switching fails (three-equation model)

Full size image

This confirms that to practically make the telemeter, suitable system design is required. However, the scheme is robust in the sense that (at least with the rate equation models) the desired operating regime is found for a relatively large parameter range around the optimal settings. Since, in addition, this regime has been experimentally observed by different authors (e.g., Sorel et al. 2002; Li et al. 2016), we are confident that our scheme can be successfully implemented.

In simulations, we assumed a 1 mW laser, which is a typical output power for both a semiconductor ring laser and a short range telemeter. Our scheme has been tested up to a round-trip distance of 32 m, but there is no fundamental limitation in the model preventing it from measuring longer distances.

In a practical implementation, a maximum operating distance is expected due to available power and beam attenuation, and depending on focusing or collimating optics. However, large distances and/or attenuations can be managed, in principle, using a device having an adequate power.

Also, with a real device, some discrepancy with respect to the ideal T = 2τm response may be expected due to the details of laser switching dynamics.

In Li et al. (2016), the typical experimental switching time is of the order of 1.5 ns, and it may change by 0.7–0.001%, depending on the feedback level. This fluctuation would directly affect the telemeter accuracy on a single round trip. Similarly, the accuracy of a typical pulsed time-of-flight telemeter is limited, on a single round trip, by the fluctuation of the detector response time.

Since in our scheme we measure a frequency instead of a single time flight, a mean over different response times is inherently performed, and the effect of fluctuations in the laser regime and in the refractive index along the path is reduced. In a typical time-of-flight telemeter the same result is obtained by taking the mean over many single measurements.

The proposed scheme can be also used to measure the distance between two targets, by allowing both reflectors to move. In this case, an output signal can be conveniently obtained by including a short passive guide section just outside the ring laser, along one arm, to detect the traveling power, or measuring the voltage drop across the laser as in Numai (2000).

4 Conclusions

In this paper we have numerically demonstrated a time-of-flight telemeter based on a properly designed ring laser. This scheme has a very simple optical arrangement, requiring only collimation or focalization of the laser and the alignment of the target, and measures distance without ambiguity. The laser power supply is a simple d.c. current source, and electronic processing only consists in photodetection and amplification of the laser emission, and in measuring the period of the square wave output signal. Two different mathematical models have been proposed, and the linearity has been evaluated from 10 cm up to 32 m of round-trip distance, for a 1 mW laser.