Abstract
Systems dominated by heterogeneity over a multiplicity of scales, like porous media, still challenge our modeling efforts. The presence of disparate length- and time-scales that control dynamical processes in porous media hinders not only models predictive capabilities, but also their computational efficiency. Macrosopic models, i.e., averaged representations of pore-scale processes, are computationally efficient alternatives to microscale models in the study of transport phenomena in porous media at the system, field or device scale (i.e., at a scale much larger than a characteristic pore size). We present an overview of common upscaling methods used to formally derive macroscale equations from pore-scale (mass, momentum and energy) conservation laws. This review includes the volume averaging method, mixture theory, thermodynamically constrained averaging, homogenization, and renormalization group techniques. We apply these methods to a number of specific problems ranging from food processing to human bronchial system, and from diffusion to multiphase flow, to demonstrate the methods generality and flexibility in handling different applications. The primary intent of such an overview is not to provide a thorough review of all currently available upscaling techniques, nor a complete mathematical treatment of the ones presented, but rather a primer on some of the tools available for upscaling, the basic principles they are based upon, and their specific advantages and drawbacks, so to guide the reader in the choice of the most appropriate method for particular applications and of the most relevant technical literature.













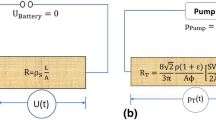
Adapted from (Arunachalam et al. 2015)


Similar content being viewed by others
References
Achanta, S., Cushman, J.H., Okos, M.R.: On multicomponent, multiphase thermomechanics with interfaces. Int. J. Eng. Sci. 32(11), 1717–1738 (1994)
Achanta, S., Okos, M., Cushman, J., Kessler, D.: Moisture transport in shrinking gels during saturated drying. AICHE J. 43(8), 2112–2122 (1997)
Acharya, R.C., der Zee, S.E.A.T.M.V., Leijnse, A.: Transport modeling of nonlinearly adsorbing solutes in physically heterogeneous pore networks. Water Resour. Res. 41(W02), 020 (2005). https://doi.org/10.1029/2004WR003500
Adler, P.M.: Porous Media: Geometry and Transports. Butterworth-Heinemann, Oxford (1992)
Alam, T., Takhar, P.S.: Microstructural characterization of fried potato discs using x-ray micro computed tomography. J. Food Sci. 81(3), E651–E664 (2016)
Alexander, F.J., Garcia, A.L., Tartakovsky, D.M.: Algorithm refinement for stochastic partial differential equations: 1. Linear diffusion. J. Comput. Phys. 182, 47–66 (2002)
Alexander, F.J., Garcia, A.L., Tartakovsky, D.M.: Algorithm refinement for stochastic partial differential equations: II. Correlated systems. J. Comput. Phys. 207(2), 769–787 (2005)
Anderson, T.B., Jackson, R.: Fluid mechanical description of fluidized beds. Equations of motion. Ind. Eng. Chem. Fundam. 6(4), 527–539 (1967)
Andrade Jr., J., Costa, U., Almeida, M., Makse, H., Stanley, H.: Inertial effects on fluid flow through disordered porous media. Phys. Rev. Lett. 82, 5249–5252 (1998)
Aris, R.: On the dispersion of a solute in a fluid flowing through a tube. Proc. R. Soc A Math. Phys. Eng. Sci. 235(1200), 67–77 (1956)
Arunachalam, H., Onori, S., Battiato, I.: On veracity of macroscopic Lithium-ion battery models. J. Electrochem. Soc. 162(9), A1–A12 (2015)
Arunachalam, H., Korneev, S., Battiato, I., Onori, S.: Multiscale modeling approach to determine effective lithium-ion transport properties. In: 2017 American Control Conference, Seattle (2017). https://doi.org/10.23919/ACC.2017.7962936
Astarita, G., Sarti, G.: A class of mathematical models for sorption of swelling solvents in glassy polymers. Polym. Eng. Sci. 18, 388–395 (1978)
Auriault, J.L.: On the domain of validity of Brinkman’s equation. Transp. Porous Med. 79, 215–223 (2009)
Auriault, J.L., Adler, P.M.: Taylor dispersion in porous media: analysis by multiple scale expansions. Adv. Water Resour. 4(18), 217–226 (1995)
Auriault, J.L., Geindreau, C., Boutin, C.: Filtration law in porous media with poor separation of scales. Transp. Porous Med. 60, 89–108 (2005)
Bakhvalov, N., Panasenko, G.: Homogenisation: Averaging Processes in Periodic Media. Kluwer Academic Publishers, Dordrecht (1989)
Bansal, H., Takhar, P.S., Maneerote, J.: Modeling multiscale transport mechanisms, phase changes and thermomechanics during frying. Food Res. Int. 62, 709–717 (2014)
Bansal, H., Takhar, P.S., Alvarado, C.Z., Thompson, L.D.: Transport mechanisms and quality changes in chicken nuggets during frying-hybrid mixture theory based multiscale modeling and experimental verification. J. Food Sci. 80(12), E2759–E2773 (2015)
Barry, D.A., Prommer, H., Miller, C.T., Engesgaard, P., Brun, A., Zheng, C.: Modelling the fate of oxidisable organic contaminants in groundwater. Adv. Water Resour. 25(8–12), 945–983 (2002)
Bassingthwaighte, J.B., Liebovitch, L.S., West, B.J.: Fractal Physiology. Springer, Berlin (2013)
Battiato, I.: Multiscale models of flow and transport, chap 29. In: Cushman, J.H., Tartakovsky, D.M. (eds.) Handbook of Groundwater Engineering. CRC Press, Boca Raton (2016)
Battiato, I., Rubol, S.: Single-parameter model of vegetated aquatic flows. Water Resour. Res. 50(8), 6358–6369 (2014)
Battiato, I., Tartakovsky, D.M.: Applicability regimes for macroscopic models of reactive transport in porous media. J. Contam. Hydrol. 120–121, 18–26 (2011)
Battiato, I., Tartakovsky, D.M., Tartakovsky, A.M., Scheibe, T.: On breakdown of macroscopic models of mixing-controlled heterogeneous reactions in porous media. Adv. Water Resour. 32, 1664–1673 (2009)
Battiato, I., Bandaru, P.R., Tartakovsky, D.M.: Elastic response of carbon nanotube forests to aerodynamic stresses. Phys. Rev. Lett. 105(144), 504 (2010). https://doi.org/10.1103/PhysRevLett.105.144504
Battiato, I., Tartakovsky, D.M., Tartakovsky, A.M., Scheibe, T.D.: Hybrid models of reactive transport in porous and fractured media. Adv. Water Resour. 34(9), 1140–1150 (2011). https://doi.org/10.1016/j.advwatres.2011.01.012
Battiato, I., Tartakovsky, D.M., Cabrales, P., Intaglietta, M.: Role of glycocalyx in attenuation of shear stress on endothelial cells: from in vivo experiments to microfluidic circuits. In: IEEE Transactios on Biomedical Circuits and Systems Conference, Catania (2017)
Baveye, P., Sposito, G.: The operational significance of the continuum hypothesis in the theory of water movement through soils and aquifers. Water Resour. Res. 20(5), 521–530 (1984)
Bear, J.: Modeling Phenomena of Flow and Transport in Porous Media. Springer, Cham (2018)
Bedford, A., Ingram, J.D.: A continuum theory of fluid saturated porous media. J. Appl. Mech. Trans. ASME 38(1), 1–7 (1971). https://doi.org/10.1115/1.3408744
Bennethum, L.S., Cushman, J.H.: Multiscale, hybrid mixture theory for swelling systems.1. Balance laws. Int. J. Eng. Sci. 34(2), 125–145 (1996a)
Bennethum, L.S., Cushman, J.H.: Multiscale, hybrid mixture theory for swelling systems. 2: Constitutive theory. Int. J. Eng. Sci. 34(2), 147–169 (1996b)
Bennethum, L., Murad, M., Cushman, J.: Macroscale thermodynamics and the chemical potential for swelling porous media. Transp. Porous Med. 39(2), 187–225 (2000)
Berkowitz, B., Scher, H.: Theory of anomalous chemical transport in random fracture networks. Phys. Rev. E 57(5), 5858–5869 (1998)
Bhattad, P., Willson, C.S., Thompson, K.E.: Effect of network structure on characterization and flow modeling using x-ray micro-tomography images of granular and fibrous porous media. Transp. Porous Med. 90(2), 363–391 (2011)
Blunt, M.J.: Multiphase Flow in Permeable Media. Cambridge University Press, Cambridge (2017)
Boso, F., Battiato, I.: Homogenizability conditions of multicomponent reactive transport processes. Adv. Water Resour. 62, 254–265 (2013)
Bouchaud, J.P., Georges, A.: Anomalous diffusion in disordered media: statistical mechanisms, models and physical applications. Phys. Rep. 195(4–5), 127–293 (1990)
Bowen, R.: Theory of Mixtures, vol. 3. Academic Press, New York (1976)
Brenner, H.: Transport Processes in Porous Media. McGraw-Hill, New York (1987)
Brinkman, H.C.: A calculation of the viscous force exerted by a flowing fluid on a dense swarm of particles. Appl. Sci. Res. A1, 27–34 (1949)
Bruna, M., Chapman, S.J.: Diffusion in spatially varying porous media. SIAM J. Appl. Math. 75(4), 1648–1674 (2015)
Celia, M.A., Hassanizadeh, S.M., Dahle, H.K.: Inclusion of dynamic capillary pressure in unsaturated flow simulators. In: EOS Transactions, American Geophysical Union Fall Meeting, American Geophysical Union, San Francisco, vol. 82(47), H12F–02 (2001)
Chen, L.Y., Goldenfeld, N., Oono, Y.: Renormalization-group theory for the modified porous-medium equation. Phys. Rev. A 44(10), 6544 (1991). https://doi.org/10.1103/PhysRevA.44.6544
Christakos, G., Hristopulos, D.T.: Stochastic radon operators in porous media hydrodynamics. Q. Appl. Math. LV(1), 89–112 (1997)
Christakos, G., Hristopulos, D., Miller, C.: Stochastic diagrammatic analysis of groundwater flow in heterogeneous soils. Water Resour. Res. 31(7), 1687–1703 (1995)
Christensen, R.: Theory of Viscoelasticity. Academic Press, New York (1982)
Ciucci, F., Lai, W.: Derivation of micro/macro lithium battery models from homogenization. Transp. Porous Med. 88(2), 249–270 (2011). https://doi.org/10.1007/s11242-011-9738-5
Crochet, M.J., Naghdi, P.M.: On constitutive equations for flow of fluid through an elastic solid. Int. J. Eng. Sci. 4(4), 383–401 (1966)
Cushman, J.H.: Proofs of the volume averaging theorems for multiphase flow. Adv. Water Resour. 5(4), 248–253 (1982)
Cushman, J.H.: Multiphase transport equations: I-general equation for macroscopic statistical, local space-time homogeneity1. Transp. Theory Stat. Phys. 12(1), 35–71 (1983)
Cushman, J.H.: On unifying the concepts of scale, instrumentation, and stochastics in the development of multiphase transport theory. Water Resour. Res. 20(11), 1668–1676 (1984)
Cushman, J.H. (ed.): Dynamics of Fluids in Hierarchical Porous Media. Academic Press, San Diego (1990)
Cushman, J.H.: The Physics of Fluids in Hierarchical Porous Media: Angstroms to Miles. Kluwer Academic Publishers, Dordrecht (1997)
Cushman, J.H., O’Malley, D.: Fickian dispersion is anomalous. J. Hydrol. 531, 161–167 (2015). https://doi.org/10.1016/j.jhydrol.2015.06.036
Cushman, J.H., Bennethum, L.S., Hu, B.X.: A primer on upscaling tools for porous media. Adv. Water Resour. 25(8–12), 1043–1067 (2002)
Darcy, H.: Les fontaines publiques de la Ville de Dijon: exposition et application des principes à suivre et des formules à employer dans les questions de distribution d’eau, vol Paris. V. Dalmont (1856)
Davit, Y., Quintard, M.: Technical notes on volume averaging in porous media I: how to choose a spatial averaging operator for periodic and quasiperiodic structures. Transp. Porous Med. 119(3), 555–584 (2017)
Davit, Y., Bell, C.G., Byrne, H.M., Chapman, L.A.C., Kimpton, L.S., Lang, G.E., Leonard, K.H.L., Oliver, J.M., Pearson, N.C., Shipley, R.J., Waters, S.L., Whiteley, J.P., Wood, B.D., Quintard, M.: Homogenization via formal multiscale asymptotics and volume averaging: How do the two techniques compare? Adv. Water Resour. 62, 178–206 (2013)
de Marsily, G.: Quantitative Hydrogeology. Academic Press, San Diego (1986)
Deck, C., Ni, C., Vecchio, K.S., Bandaru, P.: The response of carbon nanotube ensembles to fluid flow: applications to mechanical property measurements and diagnostics. J. Appl. Phys. 106(074), 304 (2009)
Dit-u dompo, S., Takhar, P.S.: Hybrid mixture theory based modeling of transport mechanisms and expansion-thermomechanics of starch during extrusion. Am. Inst. Chem. Eng. J. (AIChEJ) 61(12), 4517–4532 (2015)
Doyle, M., Newman, J.: The use of mathematical modeling in the design of lithium/polymer battery systems. Electrochim Acta 40(13–14), 2191–2196 (1995). https://doi.org/10.1016/0013-4686(95)00162-8
Doyle, M., Fuller, T.F., Newman, J.: Modeling of galvanostatic charge and discharge of the lithium/polymer/insertion cell. J. Electrochem. Soc. 140(6), 1526–1533 (1993). https://doi.org/10.1149/1.2221597
Dummit, D.S., Foote, R.M.: Abstract Algebra, vol. 3. Wiley, New York (2004)
Durlofsky, L., Brady, J.: Analysis of the brinkman equation as a model for flow in porous media. Phys. Fluids 30(11), 3329–3341 (1987). https://doi.org/10.1063/1.866465
Durlovsky, L., Brady, J.F.: Analysis of the brinkman equation as a model for flow in porous media. Phys. Fluids 30(11), 3329–3341 (2009)
Ehlers, W., Bluhm, J.: Porous Media: Theory, Experiments and Numerical Applications. Springer, Berlin (2002)
Einstein, A.: Über die von der molekularkinetischen theorie der wärme geforderte bewegung von in ruhenden flüssigkeiten suspendierten teilchen. Ann. Phys. 4(17), 549 (1905)
Einstein, A.: Investigations on the Theory of the Brownian Movement. Dover Publications, Mineola (1956)
Eringen, A.C.: Mechanics of Continua. R. E. Krieger Pub. Co., Huntington (1980)
Farassat, F.: Discontinuities in aerodynamics and aeroacoustics: the concept and applications of generalized derivatives. J. Sound Vib. 55(2), 165–193 (1977)
Finden, E.: A homogenized thermal model for lithium ion batteries. Master’s thesis, Norwegian University of Life Sciences (2012)
Forchheimer, P.: Wasserbewegung durch boden. Z. Ver. Deutsch. Ing. 45, 1782–1788 (1901)
Freeze, R.A., Cherry, J.A.: Groundwater, vol 7632, 604. Prentice-Hall Inc., Englewood Cliffs (1979)
Fulks, W., Guenther, R., Roetman, E.: Equations of motion and continuity for fluid flow in a porous medium. Bewegungs- und Kontinuitätsleichungen von Flüssigkeitsströmungen in einem porösen medium. Acta Mech. 12(1/2), 121 (1971)
Gell-Mann, M., Low, F.E.: Quantum electrodynamics at small distances. Phys. Rev. 95(5), 1300 (1954). https://doi.org/10.1103/PhysRev.95.1300
Giorgi, T.: Derivation of the forchheimer law via matched asymptotic expansions. Transp. Porous Med. 29, 191–206 (1997)
Golfier, F., Wood, B.D., Orgogozo, L., Quintard, M., Buès, M.: Biofilms in porous media: development of macroscopic transport equations via volume averaging with closure for local mass equilibrium conditions. Adv. Water Resour. 32(3), 463–485 (2009)
Goyeau, B., Benihaddadene, T., Gobin, D., Quintard, M.: Averaged momentum equation for flow through a nonhomogeneous porous structure. Transp. Porous Med. 28, 19–50 (1997)
Gray, W.G., Lee, P.: On the theorems for local volume averaging of multiphase systems. Int. J. Multiph. Flow 3(4), 333–340 (1977)
Gray, W.G., Miller, C.T.: Thermodynamically constrained averaging theory approach for modeling flow and transport phenomena in porous medium systems: 1. Motivation and overview. Adv. Water Resour. 28(2), 161–180 (2005)
Gray, W.G., Miller, C.T.: Thermodynamically constrained averaging theory approach for modeling flow and transport phenomena in porous medium systems: 3. Single-fluid-phase flow. Adv. Water Resour. 29(11), 1745–1765 (2006). https://doi.org/10.1016/j.advwatres.2006.03.010
Gray, W.G., Miller, C.T.: Thermodynamically constrained averaging theory approach for heat transport in single-fluid-phase porous medium systems. J. Heat Transf. 131(10), 101,002 (2009a). https://doi.org/10.1115/1.3160539
Gray, W.G., Miller, C.T.: Thermodynamically constrained averaging theory approach for modeling flow and transport phenomena in porous medium systems: 5. Single-fluid-phase transport. Adv. Water Resour. 32(5), 681–711 (2009b). https://doi.org/10.1016/j.advwatres.2008.10.013
Gray, W.G., Miller, C.T.: Thermodynamically constrained averaging theory approach for modeling flow and transport phenomena in porous medium systems: 7. Single-phase megascale flow models. Adv. Water Resour. 32(8), 1121–1142 (2009c). https://doi.org/10.1016/j.advwatres.2009.05.010
Gray, W.G., Miller, C.T.: Thermodynamically constrained averaging theory approach for modeling flow and transport phenomena in porous medium systems: 8. Interface and common curve dynamics. Adv. Water Resour. 33(12), 1427–1443 (2010). https://doi.org/10.1016/j.advwatres.2010.01.010
Gray, W.G., Miller, C.T.: TCAT analysis of capillary pressure in non-equilibrium, two-fluid-phase, porous medium systems. Adv. Water Resour. 34(6), 770–778 (2011). https://doi.org/10.1016/j.advwatres.2011.04.001
Gray, W.G., Miller, C.T.: A generalization of averaging theorems for porous medium analysis. Adv. Water Resour. 62, 227–237 (2013). https://doi.org/10.1016/j.advwatres.2013.06.006
Gray, W.G., Miller, C.T.: Introduction to the Thermodynamically Constrained Averaging Theory for Porous Medium Systems. Springer, Switzerland (2014). https://doi.org/10.1007/978-3-319-04010-3
Gray, W.G., Miller, C.T., Schrefler, B.A.: Averaging theory for description of environmental problems: What have we learned? Adv. Water Resour. 51, 123–138 (2013). https://doi.org/10.1016/j.advwatres.2011.12.005
Gray, W.G., Dye, A.L., McClure, J.E., Pyrak-Nolte, L.J., Miller, C.T.: On the dynamics and kinematics of two-fluid-phase flow in porous media. Water Resour. Res. 51(7), 5365–5381 (2015). https://doi.org/10.1002/2015wr016921
Green, A.E., Steel, T.R.: Constitutive equations for interacting continua. Int. J. Eng. Sci. 4(4), 483–500 (1966)
Grmela, M.: Why GENERIC. J Non-Newton Fluid 165, 980–986 (2010)
Grmela, M., Grazzini, G., Lucia, U., Yahia, L.: Multiscale mesoscopic entropy of driven macroscopic systems. Entropy 15(11), 5053–5064 (2013)
Groot, J.: State-of-health estimation of li-ion batteries: cycle life test methods. PhD thesis, Chalmers University of Technology (2012)
Hassanizadeh, S., Gray, W.: High velocity flow in porous media. Transp. Porous Med. 2, 521–531 (1987)
Hassanizadeh, S.M., Gray, W.G.: General conservation equations for multiphase systems: 1. Averaging procedure. Adv. Water Resour. 2, 131–144 (1979a)
Hassanizadeh, S.M., Gray, W.G.: General conservation equations for multiphase systems: 2. Mass, momenta, energy, and entropy equations. Adv. Water Resour. 2, 191–208 (1979b)
Hollister, S.J., Kikuchi, N.: Homogenization theory and digital imaging: a basis for studying the mechanics and design principles of bone tissue. Biotechnol. Bioeng. 43, 586–596 (1994)
Hornung, U.: Homogenization and Porous Media. Springer, New York (1997)
Howes, F.A., Whitaker, S.: The spatial averaging theorem revisited. Chem. Eng. Sci. 40(8), 1387–1392 (1985)
Hristopulos, D., Christakos, G.: Diagrammatic theory of nonlocal effective hydraulic conductivity. Stoch. Hydrol. Hydraul. 11(5), 369–395 (1997)
Hristopulos, D., Christakos, G.: Renormalization group analysis of permeability upscaling. Stoch. Environ. Res. Risk Assess. 13(1–2), 131–161 (1999). https://doi.org/10.1007/s004770050036
Hristopulos, D.T.: Renormalization group methods in subsurface hydrology: overview and applications in hydraulic conductivity upscaling. Adv. Water Resour. 26(12), 1279–1308 (2003). https://doi.org/10.1016/S0309-1708(03)00103-9
Hu, R., Oskay, C.: Spatial–temporal nonlocal homogenization model for transient anti-plane shear wave propagation in periodic viscoelastic composites. Comput. Methods Appl. Mech. Eng. 342, 1–31 (2018)
Hu, R., Oskay, C.: Multiscale nonlocal effective medium model for in-plane elastic wave dispersion and attenuation in periodic composites. J. Mech. Phys. Solids 124, 220–243 (2019)
Hubbert, M.K.: Darcy’s law and the field equations of the flow of underground fluids. Hydrol. Sci. J 2(1), 23–59 (1957)
Hui, T., Oskay, C.: A nonlocal homogenization model for wave dispersion in dissipative composite materials. Int. J. Solids Struct. 50(1), 38–48 (2013)
Jackson, A., Rybak, I., Helmig, R., Gray, W., Miller, C.: Thermodynamically constrained averaging theory approach for modeling flow and transport phenomena in porous medium systems: 9. Transition region models. Adv. Water Resour. 42, 71–90 (2012). https://doi.org/10.1016/j.advwatres.2012.01.006
Jackson, A.S., Miller, C.T., Gray, W.G.: Thermodynamically constrained averaging theory approach for modeling flow and transport phenomena in porous medium systems: 6. Two-fluid-phase flow. Adv. Water Resour. 32(6), 779–795 (2009). https://doi.org/10.1016/j.advwatres.2008.11.010
Jones, D.S.: The Theory of Generalized Functions. Cambridge University Press, Cambridge (1982)
Kanwal, R.P.: Generalized Functions Theory and Technique: Theory and Technique. Academic Press, New York (1983)
Karlin, S.: A First Course in Stochastic Processes. Academic press, New York (2014)
Kechagia, P.E., Tsimpanogiannis, I.N., Yortsos, Y.C., Lichtner, P.C.: On the upscaling of reaction-transport processes in porous media with fast or finite kinetics. Chem. Eng. Sci. 57(13), 2565–2577 (2002). https://doi.org/10.1016/S0009-2509(02)00124-0
Kim, D.J., Caruthers, J.M., Peppas, N.A.: Viscoelastic properties of dodecane polystyrene systems. Polymer 34(17), 3638–3647 (1993)
King, P.: The use of renormalization for calculating effective permeability. Transp. Porous Med. 4(1), 37–58 (1989)
Klika, V.: A guide through available mixture theories for applications. Crit. Rev. Solid State Mater. Sci. 39(2), 154–174 (2014)
Klika, V., Krause, A.: Beyond Onsager–Casimir relations: shared dependence of phenomenological coefficients on state variables. J. Phys. Chem. Lett. 9, 7021–7025 (2018)
Klika, V., Pavelka, M., Benziger, J.: Functional constraints on phenomenological coefficients. Phys. Rev. E 95(022), 125 (2017)
Korneev, S., Battiato, I.: Sequential homogenization of reactive transport in porous media. Multiscale Model. Simul. 14(4), 1301–1318 (2016)
Korneev, S.V., Yang, X., Zachara, J.M., Scheibe, T.D., Battiato, I.: Downscaling-based segmentation for unresolved images of highly heterogeneous granular porous samples. Water Resour. Res. 54, 2871–2891 (2018). https://doi.org/10.1002/2018WR022886
Kreutzer, M.T., Kapteijn, F., Moulijn, J.A.: Shouldn’t catalysts shape up?: structured reactors in general and gas-liquid monolith reactors in particular. Catal. Today 111(1–2), 111–118 (2006)
Lai, W.M., Hou, J.S., Mow, V.C.: A triphasic theory for the swelling and deformation behaviors of articular cartilage. J. Biomech. Eng. 113(3), 245–258 (1991)
Lalam, S., Sandhu, J., Takhar, P.S., Thompson, L., Alvarado, C.: Experimental study on transport mechanisms during deep fat frying of chicken nuggets. LWT-Food Sci. Technol. 50(1), 110–119 (2013)
Lasseux, D., Valdés-Parada, F.J.: On the developments of darcy’s law to include inertial and slip effects. C. R. Méc. 345(9), 660–669 (2017)
Lasseux, D., Parada, F.J.V., Porter, M.L.: An improved macroscale model for gas slip flow in porous media. J. Fluid Mech. 805, 118–146 (2016)
Leemput, P., Vandekerckhove, C., Vanroose, W., Roose, D.: Accuracy of hybrid lattice Boltzmann/finite difference schemes for reaction diffusion systems. Multiscale Model. Simul. 6(3), 838–857 (2007)
Lévy, T.: Fluid flow through an array of fixed particles. Int. J. Eng. Sci. 21, 11–23 (1983)
Li, H., Pan, C., Miller, C.T.: Pore-scale investigation of viscous coupling effects for two-phase flow in porous media. Phys. Rev. E 72(2), 026705 (2005)
Ling, B., Tartakovsky, A.M., Battiato, I.: Dispersion controlled by permeable surfaces: surface properties and scaling. J. Fluid Mech. 801, 13–42 (2016)
Ling, B., Oostrom, M., Tartakovsky, A.M., Battiato, I.: Hydrodynamic dispersion in thin channels with micro-structured porous walls. Phys. Fluids 30, 076601 (2018). (Accepted)
Malley, D.O., Karra, S., Currier, R.P., Makedonska, N., Hyman, J.D., Viswanathan, H.S.: Where does water go during hydraulic fracturing? Groundwater 54(4), 488–497 (2016)
Marle, C.: Ecoulements monophasiques en milieu poreux. Rev. Inst. Francais du Petrole 22(10), 1471–1509 (1967)
Marle, C.: On macroscopic equations governing multiphase flow with diffusion and chemical reactions in porous media. Int. J. Eng. Sci. 20(5), 643–662 (1982a)
Marle, C.M.: On macroscopic equations governing multiphase flow with diffusion and chemical reactions in porous media. Int. J. Eng. Sci. 20(5), 643–662 (1982b)
Marušić-Paloka, E., Mikelic, A.: The derivation of a non-linear filtration law including the inertia effects via homogenization. Nonlinear Anal. Theory Methods Appl. 42, 97–137 (2000)
Marušić-Paloka, E., Piatnitski, A.: Homogenization of a nonlinear convection–diffusion equation with rapidly oscillating coefficients and strong convection. J. Lond. Math. Soc. 2(72), 391–409 (2005)
McClure, J.E., Armstrong, R.T., Berrill, M.A., Schlüeter, S., Berg, S., Gray, W.G., Miller, C.T.: A geometric state function for two-fluid flow in porous media. Phys. Rev. Fluids 3, 084306 (2018). https://doi.org/10.1103/PhysRevFluids.3.084306
Mikelic, A., Devigne, V., Van Duijn, C.J.: Rigorous upscaling of the reactive flow through a pore, under dominant Peclet and Damköhler numbers. SIAM J. Math. Anal. 38(4), 1262–1287 (2006)
Miller, C.T., Gray, W.G.: Thermodynamically constrained averaging theory approach for modeling flow and transport phenomena in porous medium systems: 2. Foundation. Adv. Water Resour. 28(2), 181–202 (2005)
Miller, C.T., Gray, W.G.: Thermodynamically constrained averaging theory approach for modeling flow and transport phenomena in porous medium systems: 4. Species transport fundamentals. Adv. Water Resour. 31(3), 577–597 (2008). https://doi.org/10.1016/j.advwatres.2007.11.004
Miller, C.T., Christakos, G., Imhoff, P.T., McBride, J.F., Pedit, J.A., Trangenstein, J.A.: Multiphase flow and transport modeling in heterogeneous porous media: challenges and approaches. Adv. Water Resour. 21(2), 77–120 (1998)
Miller, C.T., Valdés-Parada, F.J., Wood, B.D.: A pedagogical approach to the thermodynamically constrained averaging theory. Transp. Porous Med. 119(3), 585–609 (2017). https://doi.org/10.1007/s11242-017-0900-6
Miller, C.T., Gray, W.G., Kees, C.E.: Thermodynamically constrained averaging theory: principles, model hierarchies, and deviation kinetic energy extensions. Entropy 20(4), 253 (2018a). https://doi.org/10.3390/e20040253
Miller, C.T., Valdés-Parada, F.J., Ostvar, S., Wood, B.D.: A priori parameter estimation for the thermodynamically constrained averaging theory: species transport in a saturated porous medium. Transp. Porous Med. 122(3), 611–632 (2018b). https://doi.org/10.1007/s11242-018-1010-9
Mls, J.: On the existence of the derivative of the volume average. Transp. Porous Med. 2(6), 615–621 (1987)
Montroll, E.W., Scher, H.: Random walks on lattices. IV. Continuous time random walks and influence of adsorbing boundaries. J. Stat. Phys. 9(2), 101–135 (1973)
Morse, J.W., Arvidson, R.S.: The dissolution kinetics of major sedimentary carbonate minerals. Earth Sci. Rev. 58, 51–84 (2002)
Neuman, S.P.: Theoretical derivation of Darcy’s law. Acta Mecanica 25, 153–170 (1977)
Neuman, S.P., Tartakovsky, D.M.: Perspective on theories of anomalous transport in heterogeneous media. Adv. Water Resour. 32(5), 670–680 (2009)
Newman, J., Tiedemann, W.: Porous-electrode theory with battery applications. AIChE J. 21(1), 25–41 (1975). https://doi.org/10.1002/aic.690210103
Nitsche, L.C., Brenner, H.: Eulerian kinematics of flow through spatially periodic models of porous media. Arch. Ration. Mech. Anal. 107(3), 225–295 (1989)
O’Malley, D., Cushman, J.H.: A renormalization group classification of nonstationary and/or infinite second moment diffusive processes. J. Stat. Phys. 146(5), 989–1000 (2012a). https://doi.org/10.1007/s10955-012-0448-3
O’Malley, D., Cushman, J.H.: Two-scale renormalization-group classification of diffusive processes. Phys. Rev. E 86(1), 011126 (2012b). https://doi.org/10.1103/PhysRevE.86.011126
Oztop, M., Bansal, H., Takhar, P., McCarthy, M.J., McCarthy, K.L.: Using multi-slice-multi-echo images with NMR relaxometry to assess water and fat distribution in coated chicken nuggets. LWT Food Sci. Technol. 55(2), 690–694 (2014)
Pangarkar, K., Schildhauer, T.J., van Ommen, J.R., Nijenhuis, J., Kapteijn, F., Moulijn, J.A.: Structured packings for multiphase catalytic reactors. Ind. Eng. Chem. Res. 47(10), 3720–3751 (2008)
Peszynska, M., Lu, Q., Wheeler, M.: Coupling different numerical coupling different numerical algorithms for two phase fluid flow. In: Mathematics of Finite Elements and Applications X. Elsevier, pp. 205–214 (2000)
Peter, M.A.: Homogenization in domains with evolving microstructure. C. R. Méc. 335, 357–362 (2007)
Peter, M.A.: Coupled reaction–diffusion processes inducing an evolution of the microstructure: analysis and homogenization. Nonlinear Anal. Theory Methods Appl. 70(2), 806 (2009)
Picchi, U.A.B.N.D.: Modelling of core-annular and plug flows of newtonian/non-newtonian shear-thinning fluids in pipes and capillary tubes. Int. J. Multiph. Flow 103, 43–60 (2018)
Pinson, M.B., Bazant, M.Z.: Theory of SEI formation in rechargeable batteries: capacity fade, accelerated aging and lifetime prediction. J. Electrochem. Soc. 160(2), A243–A250 (2013). https://doi.org/10.1149/2.044302jes
Ploehn, H.J., Ramadass, P., White, R.E.: Solvent diffusion model for aging of lithium-ion battery cells. J. Electrochem. Soc. 151(3), A456–A462 (2004). https://doi.org/10.1149/1.1644601
Quintard, M., Whitaker, S.: Transport in ordered and disordered porous media ii: generalized volume averaging. Transp. Porous Med. 14(2), 179–206 (1994a)
Quintard, M., Whitaker, S.: Transport in ordered and disordered porous media iii: closure and comparison between theory and experiment. Transp. Porous Med. 15(1), 31–49 (1994b)
Quintard, M., Whitaker, S.: Transport in ordered and disordered porous media iv: computer generated porous media for three-dimensional systems. Transp. Porous Med. 15(1), 51–70 (1994c)
Quintard, M., Whitaker, S.: Transport in ordered and disordered porous media v: geometrical results for two-dimensional systems. Transp. Porous Med. 15(2), 183–196 (1994d)
Rajagopal, K.R., Tao, L.: Mechanics of Mixtures. Series on Advances in Mathematics for Applied Sciences. World Scientific, Singapore (1995)
Rubol, S., Battiato, I., de Barros, F.P.J.: Vertical dispersion in vegetated shear flows. Water Resour. Res. 52, 8066–8080 (2016). https://doi.org/10.1002/2016WR018907
Rubol, S., Ling, B., Battiato, I.: Universal scaling-law for flow resistance over canopies with complex morphology. Sci. Rep. 8, 4430 (2018). https://doi.org/10.1038/s41598-018-22346-1
Rybak, I.V., Gray, W.G., Miller, C.T.: Modeling two-fluid-phase flow and species transport in porous media. J. Hydrol. 521, 565–581 (2015). https://doi.org/10.1016/j.jhydrol.2014.11.051
Salvadori, A., Bosco, E., Grazioli, D.: A computational homogenization approach for Li-ion battery cells: part 1—formulation. J. Mech. Phys. Solids 65, 114–137 (2014). https://doi.org/10.1016/j.jmps.2013.08.010
Sanchez-Palencia, E.E.: Solutions périodiques par rapport aux variables d’espaces et applications. C. R. Acad. Sci. Paris Sér. A-B 271(A), 1129–1132 (1970)
Scher, H., Montroll, E.W.: Anomalous transit time dispersion in amorphous solids. Phys. Rev. B 12(6), 2455–2477 (1975)
Schreyer-Bennethum, L.: Theory of flow and deformation of swelling porous materials at the macroscale. Comput. Geotech. 34(4), 267–278 (2007)
Schwartz, L.: Théorie des Distributions. Hermann, Paris (1966)
Sciumé, G., Shelton, S.E., Gray, W.G., Miller, C.T., Hussain, F., Ferrari, M., Decuzzi, P., Schrefler, B.A.: Tumor growth modeling from the perspective of multiphase porous media mechanics. Mol. Cell. Biomech. 202(1), 1–20 (2012)
Sciumé, G., Shelton, S., Gray, W.G., Miller, C.T., Hussain, F., Ferrari, M., Decuzzi, P., Schrefler, B.A.: A multiphase model for three-dimensional tumor growth. New J. Phys. 15, 015005 (2013). https://doi.org/10.1088/1367-2630/15/1/015005
Semenenko, M.G.: Application effective medium approximation approach for economic researching. Phys. A Stat. Mech. Appl. 329(1–2), 264–272 (2003)
Shapiro, M., Brenner, H.: Taylor dispersion of chemically reactive species: irreversible first-order reactions in bulk and on boundaries. Chem. Eng. Sci. 41(6), 1417–1433 (1986)
Shapiro, M., Brenner, M.: Dispersion of a chemically reactive solute in a spatially periodic model of a porous medium. Chem. Eng. Sci. 43(3), 551–571 (1988). https://doi.org/10.1016/0009-2509(88)87016-7
Shapiro, M., Fedou, R., Thovert, J., Adler, P.M.: Coupled transport and dispersion of multicomponent reactive solutes in rectilinear flows. Chem. Eng. Sci. 51(22), 5017–5041 (1996). https://doi.org/10.1016/0009-2509(96)00269-2
Shilov, G.E.: Generalized Functions and Partial Differential Equations. Gordon and Breach, London (1968)
Singh, P.P., Cushman, J.H., Bennethum, L.S., Maier, D.: Thermomechanics of swelling biopolymeric systems. Transp. Porous Med. 53(1), 1–24 (2003a)
Singh, P.P., Cushman, J.H., Maier, D.: Multiscale fluid transport theory for swelling biopolymers. Chem. Eng. Sci. 58(11), 2409–2419 (2003b)
Singh, P.P., Cushman, J.H., Maier, D.: Three scale thermomechanical theory for swelling biopolymeric systems. Chem. Eng. Sci. 58(17), 4017–4035 (2003c)
Singh, P.P., Maier, D., Cushman, J.H., Haghighi, K., Corvalan, C.: Effect of viscoelastic relaxation on moisture transport in foods. Part i: solution of general transport equation. J. Math. Biol. 49(1), 1–19 (2004)
Slattery, J.C.: Flow of viscoelastic fluids through porous media. AIChE J. 13(6), 1066–1071 (1967)
Slattery, J.C.: Advanced Transport Phenomena. Cambridge University Press, Cambridge (1999)
Smith, A.J., Burns, A.C., Zhao, X., Xiong, D., Dahn, J.R.: A high precision coulometry study of the SEI growth in Li/graphite cells. J. Electrochem. Soc. 158(5), A447–A452 (2011). https://doi.org/10.1149/1.3557892
Song, H., Litchfield, J., Morris, H.D.: Three-dimensional microscopic MRI of maize kernels during drying. J. Agric. Eng. Res. 53, 51–69 (1992)
Spagnolo, S.: Sulla convergenza di soluzioni di equazioni paraboliche ed ellittiche. Ann. Scuola. Norm. Sup. Pisa. 3(22), 571–597 (1968)
Sun, T.Y., Mehmani, Y., Balhoff, M.T.: Hybrid multiscale modeling through direct numerical substitution of pore-scale models into near-well reservoir simulators. Energy Fuels 26, 5828–5836 (2012)
Takhar, P.S.: Hybrid mixture theory based moisture transport and stress development in corn kernels during drying: coupled fluid transport and stress equations. J. Food Eng. 105(4), 663–670 (2011)
Takhar, P.S.: Unsaturated fluid transport in swelling poroviscoelastic biopolymers. Chem. Eng. Sci. 109, 98–110 (2014)
Takhar, P.S., Maier, D.E., Campanella, O., Chen, G.: Hybrid mixture theory based moisture transport and stress development in corn kernels during drying: validation and simulation results. J. Food Eng. 106, 275–282 (2011)
Tartakovsky, D.M., Dentz, M.: Diffusion in porous media: phenomena and mechanisms. Transp. Porous Med. 1–23, (2019). https://doi.org/10.1007/s11242-019-01262-6
Tartakovsky, D.M., Neuman, S.P.: Transient flow in bounded randomly heterogeneous domains. 1. Exact conditional moment equations and recursive approximation. Water Resour. Res. 34(1), 1–12 (1998)
Tartakovsky, D.M., SP, S.P.N., Lu, Z.: Conditional stochastic averaging of steady state unsaturated flow by means of kirchoff transformation. Water Resour. Res. 35(3), 731–745 (1999)
Tartakovsky, A.M., Meakin, P., Scheibe, T.D., West, R.M.E.: Simulation of reactive transport and precipitation with smoothed particle hydrodynamics. J. Comput. Phys. 222, 654–672 (2007)
Taverniers, S., Alexander, F.J., Tartakovsky, D.M.: Noise propagation in hybrid models of nonlinear systems: the ginzburg-landau equation. J. Comput. Phys. 262, 313–324 (2014)
Taylor, G.I.: Dispersion of soluble matter in solvent flowing slowly through a tube. Proc. R. Soc. A 219(1137), 186–203 (1953)
Thomas, K.E., Newman, J.: Thermal modeling of porous insertion electrodes. J. Electrochem. Soc. 150(2), A176–A192 (2003). https://doi.org/10.1149/1.1531194
Thomas, N.L., Windle, A.H.: A deformation model for case-ii diffusion. Polymer 21(6), 613–619 (1980)
Thomas, N.L., Windle, A.H.: A theory of case-ii diffusion. Polymer 23(4), 529–542 (1982)
Um, W., Serne, R.J., Yabusaki, S.B., Owen, A.T.: Enhanced radionuclide immobilization and flow path modifications by dissolution and secondary precipitates. J. Environ. Qual. 34, 1404–1414 (2005)
Valdés-Parada, F.J., Alvarez-Ramírez, J.: A volume averaging approach for asymmetric diffusion in porous media. J. Chem. Phys. 134(20), 204709 (2011)
Valdés-Parada, F.J., Romero-Paredes, H., Espinosa Paredes, G.: Numerical simulation of a tubular solar reactor for methane cracking. Int. J. Hydrogen Energy 36(5), 3354–3363 (2011)
Valdés-Parada, F.J., Varela, J.R., Alvarez-Ramirez, J.: Francisco j. valdés-parada and juan r. varela and josé alvarez-ramirez. Phys. A Stat. Mech. Appl. 391(3), 606–615 (2012)
Vervloet, D., Kapteijn, F., Nijenhuis, J., van Ommen, J.R.: Process intensification of tubular reactors: considerations on catalyst hold-up of structured packings. Catal. Today 216, 111–116 (2013)
Veverka, V.: Theorem for the local volume average of a gradient revised. Chem. Eng. Sci. 36(5), 833–838 (1981)
Weibel, E.R.: The pathway for oxygen: structure and function in the mammalian respiratory system. Harvard University Press, Cambridge (1984)
Whitaker, S.: Diffusion and dispersion in porous media. AIChE J. 13(3), 420–427 (1967)
Whitaker, S.: Simultaneous heat, mass, and momentum transfer in porous media: a theory of drying. Adv. Heat Transf. 13, 119–203 (1977)
Whitaker, S.: A simple geometrical derivation of the spatial averaging theorem. Chem. Eng. Educ. 19(1), 18–21 (1985)
Whitaker, S.: Flow in porous media I: a theoretical derivation of darcy’s law. Transp. Porous Med. 1(1), 3–25 (1986). https://doi.org/10.1007/BF01036523
Whitaker, S.: The forchheimer equation: a theoretical development. Transp. Porous Med. 25, 27–61 (1996)
Whitaker, S.: The method of volume averaging, vol. 13. Springer, Berlin (1999)
Wilson, K.G.: The renormalization group and critical phenomena. Rev. Mod. Phys. 55(3), 583 (1983). https://doi.org/10.1103/RevModPhys.55.583
Wilson, K.G., Kogut, J.: The renormalization group and the \(\epsilon \) expansion. Phys. Rep. 12(2), 75–199 (1974). https://doi.org/10.1016/0370-1573(74)90023-4
Wojciechowski, K.J.: (2011) Analysis and numerical solution of nonlinear volterra partial integrodifferential equations modeling swelling porous materials. Thesis
Wojciechowski, K.J., Chen, J., Schreyer-Bennethum, L., Sandberg, K.: Well-posedness and numerical solution of a nonlinear volterra partial integro-differential equation modeling a swelling porous material. J. Porous Med. 17(9), 763–784 (2014)
Wood, B.D.: Review of upscaling methods for describing unsaturated flow. Tech. Rep. 13325, Pacific Northwest National Lab., Richland (2000)
Wood, S.N.: Generalized Additive Models. An Introduction with R. Chapman & Hall/CRC, Boca Raton (2006)
Wood, B.D.: The role of scaling laws in upscaling. Adv. Water Resour. 32(5), 723–736 (2009)
Wood, B.D., Valdés-Parada, F.J.: Volume averaging: local and nonlocal closures using a green’s function approach. Adv. Water Resour. 51, 139–167 (2013)
Wood, B.D., Quintard, M., Whitaker, S.: Calculation of effective diffusivities for biofilms and tissues. Biotechnol. Bioeng. 77(5), 495–516 (2002)
Wood, B., Apte, S., Liburdy, J., Ziazi, R., He, X., Finn, J., Patil, V.: A comparison of measured and modeled velocity fields for a laminar flow in a porous medium. Adv. Water Resour. 85, 45–63 (2015)
Wood, B.D., He, B., Apte, S.V.: (2020) Modeling turbulent flows in porous media. Ann. Rev. Fluid Mech. 52. (in production)
Xing, H., Takhar, P., Helms, G., He, B.: Nmr imaging of continuous and intermittent drying of pasta. J. Food Eng. 78, 61–68 (2007)
Yakhot, V., Orszag, S.A.: Renormalization group analysis of turbulence. I. Basic theory. J. Sci. Comput. 1(1), 3–51 (1986). https://doi.org/10.1007/BF01061452
Youzefzadeh, M., Battiato, I.: Nonintrusive hybrid models of reactive transport in fractured media: an immersed boundary method approach. J. Comput. Phys. 244, 320–338 (2017)
Zhang, X., Tartakovsky, D.M.: Effective ion diffusion in charged nanoporous materials. J. Electrochem. Soc. 164(4), E53–E61 (2017a)
Zhang, X., Tartakovsky, D.M.: Optimal design of nanoporous materials for electrochemical devices. Appl. Phys. Lett. 110(14), 143,103 (2017b)
Zhao, Y., Takhar, P.: Freezing of foods: mathematical and experimental aspects. Food. Eng. Rev. (2017). https://doi.org/10.1007/s12393-016-9157-z:1-28
Acknowledgements
The work of IB was fully supported by the Department of Energy under the Early Career Award DE-SC0014227953 “Multiscale dynamics of reactive fronts in the subsurface.” The work of DO was supported by the Laboratory Directed Research and Development program of Los Alamos National Laboratory under Project Number 20180481ER. The work of CTM was supported by Army Research Office Grant W911NF-14-1-02877 and National Science Foundation Grants 1619767 and 1604314. The work of PST was supported by the National Science Foundation award 0756762, and USDA-NIFA awards 2009- 35503-05279 and 2003- 3550-13963/TEXR-2006-03846. BDW was supported in part by NSF award EAR 1521441.
Author information
Authors and Affiliations
Contributions
The authors are listed in alphabetical order. IB led the effort, conceptualized the analysis, organized the entire manuscript, reviewed the homogenization method and integrated all the contributions by the other co-authors; DO reviewed renormalization group theory; CTM and FJV-P provided the overview on the thermodynamically constrained averaging theory; PST reviewed hybrid mixture theory; BDW and PTF-V provided the overview of the volume averaging method. All authors have reviewed and provided feedbacks on the manuscript structure and content.
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix: Notation
Appendix: Notation
1.1 Hybrid Mixture Theory
1.2 Latin Symbols
- \(A^{\alpha _{j}}\) :
-
Helmholtz free energy of the jth component in the \(\alpha \) phase [J/kg]
- \(A^{\alpha }\) :
-
Total Helmholtz free energy of the \(\alpha \) phase computed in volume V (=\(A_{I}^{\alpha } M^{\alpha }\)) [J/kg]
- \(A_{I}^{\alpha }\) :
-
Inner part of the Helmholtz free energy of the \(\alpha \) phase [J/kg]
- \(B_c\) :
-
Viscoelastic parameter [m\(^ 3\) s/kg]
- \(b^{\alpha _{j}}\) :
-
External entropy source for the jth component in the \(\alpha \) phase [J/(kg s K)]
- \(b^{\alpha }\) :
-
External entropy source for the \(\alpha \) phase [J/(kg s K)]
- \(C^{\alpha _{j}}\) :
-
Mass concentration of the jth component in the \(\alpha \) phase \((=\rho ^{\alpha _{j}}/\rho ^{\alpha })\) [dimensionless]
- D :
-
Coefficient of diffusivity [m\(^2\)/s]
- \(d_{kl}^{\alpha }\) :
-
Rate of deformation tensor of the \(\alpha \) phase [s\(^{-1}\)]
- \({}^{\beta } {\hat{e}}^{\alpha _{j}}\) :
-
Net mass transfer from the phase \(\beta \) to the jth component in the \(\alpha \) phase [kg/(m\(^3\) s)]
- \({}^{\beta } {\hat{e}}^{\alpha }\) :
-
Net mass transfer from the phase \(\beta \) to the phase \(\alpha \) [kg/(m\(^3\) s)]
- \(E^{\alpha _{j}}\) :
-
Internal energy of the jth component in the \(\alpha \) phase [J/kg]
- \(E^{\alpha }\) :
-
Internal energy of the \(\alpha \) phase [J/kg]
- \({\hat{E}}^{\alpha _{j}}\) :
-
energy gained by the jth component from other components in the same phase [J/(m\(^3\)s)]
- \(E_{MM}^{s}\) :
-
Trace of Lagrangian strain tensor of the solid phase [dimensionless]
- \(g_{l}^{\alpha _{j}}\) :
-
Gravitational force on the jth component in the \(\alpha \) phase [m\(^2\)/s]
- \(g_{l}^{\alpha }\) :
-
Gravitational force on the \(\alpha \) phase [m\(^2\)/s]
- \(G^{w}\) :
-
Gibbs free energy [J/kg]
- G(t):
-
Stress relaxation function for the viscoelastic biopolymers [Pa]
- \(G_i\) :
-
With i from 0 to N, relaxation parameters for the Generalized Maxwell model [Pa]
- \(h^{\alpha _{j}}\) :
-
Net external energy source for the jth component in the \(\alpha \) phase [J/(kg s)]
- \(h^{\alpha }\) :
-
Net external energy source for the \(\alpha \) phase [J/(kg s)]
- \({\hat{i}}_{l}^{\alpha _{j}}\) :
-
Momentum transfer to the jth component due to interaction with other components in the same phase [N/m\(^3\)]
- \(p^{\alpha }\) :
-
Thermodynamic pressure in the \(\alpha \) phase [Pa]
- p :
-
Total thermodynamic pressure for the particle (solid+liquid) [Pa]
- \(\mathrm{P}^{\alpha }\) :
-
Classical pressure of the \(\alpha \) phase [Pa]
- \(q_{l}^{\alpha _{j}}\) :
-
Heat flux vector for the jth component in the \(\alpha \) phase [J/(m\(^2\) s)]
- \(q_{l}^{\alpha }\) :
-
Heat flux vector for the \(\alpha \) phase [J/(m\(^2\) s)]
- \(q_{l}\) :
-
Total heat flux vector for the particle (solid+liquid) [J/(m\(^2\) s)]
- \({}^{\beta } {\hat{Q}}^{\alpha _{j}}\) :
-
Net heat gained by the jth component in the phase \(\alpha \) from the phase \(\beta \) [J/(m\(^3\) s)]
- \({}^{\beta } {\hat{Q}}^{\alpha }\) :
-
Net heat gained by the phase \(\alpha \) from the phase \(\beta \) [J/(m\(^3\) s)]
- \({\hat{r}}^{\alpha _{j}}\) :
-
Mass production of the jth component in phase \(\alpha \) due to chemical reactions within the phase [kg/(m\(^3\) s)]
- \(S^\alpha \) :
-
Degree of saturation for the \(\alpha \) phase [dimensionless]
- \(\hbox {REV}\) :
-
Representative elementary volume
- t :
-
Time [s]
- \(t_{kl}^{\alpha _{j}}\) :
-
Stress tensor of the jth component in the phase \(\alpha \) [Pa]
- \(t_{kl}^{\alpha }\) :
-
Stress tensor of the phase \(\alpha \) [Pa]
- \(t_{kl}\) :
-
Total stress tensor of the particle (solid+liquid) [Pa]
- \(T^{\alpha _{j}}\) :
-
Temperature of the jth component in the phase \(\alpha \) [K]
- T :
-
Temperature [K]
- \({}^{\beta } {\hat{T}}_{l} ^{\alpha _{j}}\) :
-
Momentum transfer to the jth component in the phase \(\alpha \) due to mechanical interactions with the phase \(\beta \) [N/\(m^3\)]
- \({}^{\beta }{\hat{T}}_{l}^{\alpha }\) :
-
Momentum transfer to the phase \(\alpha \) due to mechanical interactions with the phase \(\beta \) [N/m\(^3\)]
- \(u_{k}^{\alpha _{j}}\) :
-
Diffusion velocity of the jth component in the phase \(\alpha \) [m/s]
- \(v_{l}^{\alpha _{j}}\) :
-
Velocity of the jth component in the phase \(\alpha \) [m/s]
- \(v_{l}^{\alpha }\) :
-
Velocity of the \(\alpha \) phase [m/s]
- \(x_{k}^{\alpha }\) :
-
Eulerian coordinate in the \(\alpha \) phase [m]
- \(X_{K}^{\alpha }\) :
-
Lagrangian coordinate in the phase \(\alpha \) [m]
1.3 Greek Symbols
- \(\delta _{kl}\) :
-
Kronecker delta function in Eulerian coordinates
- \(\delta _{KL}\) :
-
Kronecker delta function in Lagrangian coordinates
- \(\varepsilon ^{\alpha }\) :
-
Volume fraction of the phase \(\alpha \) [dimensionless]
- \(\eta ^{\alpha _{j}}\) :
-
Entropy of the jth component in the \(\alpha \) phase [J/(kg K)]
- \(\eta ^{\alpha }\) :
-
Entropy of the \(\alpha \) phase [J/(kg K)]
- \({\hat{\eta }}^{\alpha _{j}}\) :
-
Entropy gained by the jth component in a phase by interaction with other components in the same phase [J/(m\(^3\)s K)]
- \(K^\alpha \) :
-
Permeability of the porous matrix for phase \(\alpha \) [m\(^2\)]
- \(\varLambda ^{\alpha _{j}}\) :
-
Net entropy production for the jth component in the \(\alpha \) phase [J/(m\(^3\) s K)]
- \(\varLambda ^{\alpha }\) :
-
Net entropy production in the \(\alpha \) phase [J/(m\(^3\) s K)]
- \(\varLambda \) :
-
Net entropy production in the system at mesoscale [J/(m\(^3\) s K)]
- \(\lambda _i\) :
-
Relaxation time for ith element of generalized Maxwell model [s]
- \({\mathcal {M}}\) :
-
Memory function in the generalized Darcy’s law for biopolymers [m\(^5\)/(kg s)]
- \(\rho ^{\alpha _{j}}\) :
-
Density of the jth component in the \(\alpha \) phase [kg/m\(^3\)]
- \(\rho ^{\alpha }\) :
-
Density of the \(\alpha \) phase [kg/m\(^3\)]
- \(\phi _{l}^{\alpha _{j}}\) :
-
Entropy flux vector for the jth component in the \(\alpha \) phase [J/(m\(^2\) s K)]
- \(\phi _{l}^{\alpha }\) :
-
Entropy flux vector for the \(\alpha \) phase [J/(m\(^2\) s K)]
- \({}^{\beta } {\hat{\phi }}^{\alpha _{j}}\) :
-
Entropy transfer to the jth component in the \(\alpha \) phase from the \(\beta \) phase [J/(m\(^3\) s K)]
- \({}^{\beta } {\hat{\phi }}^{\alpha }\) :
-
Entropy transfer to the \(\alpha \) phase from the \(\beta \) phase [J/(m\(^3\) s K)]
1.4 Subscripts
- \(k,\; l\) :
-
Coordinate indices
1.5 Superscripts
- \(\mathrm{s}\) :
-
Solid phase
- \(\mathrm{w}\) :
-
Water (or liquid) phase
- \(\mathrm{f}\) :
-
Fluid phase
- \(\alpha ,\; \beta \) :
-
General representation of phases
- j :
-
A given component of species
1.6 Special Symbols
- \(\dfrac{D^{\alpha _{j}}}{Dt}\) :
-
Material derivative of a function with respect to velocity of jth component in the \(\alpha \) phase [s\(^{-1}\)]
- \(\dfrac{D^{\alpha }}{Dt}\) :
-
Material derivative of a function with respect to velocity of the \(\alpha \) phase [s\(^{-1}\)]
- \(v_{l}^{\alpha ,s}\) :
-
Velocity of the \(\alpha \) phase relative to the solid phase (=\(v_{l}^{\alpha }-v_{l}^{s} \)) [m/s]
1.7 Thermodynamically Constrained Averaging Theory
1.8 Roman Letters
- \({{\hat{c}}}^{wn}\) :
-
Capillary pressure relaxation rate coefficient
- \(\varvec{\mathsf {d}}\) :
-
Rate of strain tensor
- F :
-
A generalized additive function
- \(\varvec{\mathsf {G}}\) :
-
Geometric orientation tensor
- \({\varvec{\mathrm g}}\) :
-
Gravitational acceleration vector
- \({\varvec{\mathsf {I}}}\) :
-
Identity tensor
- \({{\mathscr {I}}}_{\mathrm {c}{{\alpha }}}^+\) :
-
Index set of entities connected to the \({{\alpha }}\) entity that are of a higher dimension than the \({{\alpha }}\) entity
- \({{{\mathscr {I}}_{\mathrm{f}}}}\) :
-
Index set of fluid phases
- \(J_w^{wn}\) :
-
Mean curvature of the wn interface
- \(K_{E}\) :
-
Kinetic energy term due to velocity fluctuations
- \({{\hat{k}}}_1^{wn}\) :
-
Interfacial area relaxation coefficient
- \({{\varvec{\mathrm n}}_{{{\alpha }}}}\) :
-
Outward unit normal vector from entity \({{\alpha }}\)
- p :
-
Fluid pressure
- \({{\hat{R}}}\) :
-
Resistance coefficient
- \({\overset{{{{\alpha }}}\rightarrow {{{\kappa }}}}{{\varvec{\mathrm T}}}}\) :
-
Transfer rate of momentum from the \({{\alpha }}\) to the \({{\kappa }}\) entity
- \(\varvec{\mathsf {t}}\) :
-
Stress tensor
- \(\varvec{\mathsf {t}}_s^*\) :
-
Solid-phase stress tensor corresponding to the action of a common curve on the solid phase
- t :
-
time
- \({\mathscr {U}}\) :
-
Set of unknowns
- \({\varvec{\mathrm v}}\) :
-
Velocity
- \({\varvec{\mathrm w}}^{wn}\) :
-
Velocity of the fluid-fluid interface
1.9 Greek Letters
- \(\gamma \) :
-
Interfacial or curvilinear tension
- \({\epsilon }\) :
-
Porosity
- \({{{\epsilon }^{{\overline{\overline{{{\alpha }}}}}}}}\) :
-
Specific entity measure of the \({{\alpha }}\) entity (volume fraction, specific interfacial area)
- \({\theta }\) :
-
Temperature
- \({{{\kappa }}^{\,{\overline{\overline{{wns}}}}}_{G}}\) :
-
Geodesic curvature of the common curve
- \({{{\kappa }}^{\,{\overline{\overline{{wns}}}}}_{N}}\) :
-
Normal curvature of the common curve
- \({\varLambda }\) :
-
Entropy density production rate
- \(\mu \) :
-
Chemical potential
- \(\rho \) :
-
Mass density
- \({\chi }^{{\overline{\overline{n}}}}\) :
-
Euler characteristic of the non-wetting phase
- \(\chi _s\) :
-
Wetted fraction of the solid phase
- \({\varphi }^{{\overline{\overline{{ws},{wn}}}}}\) :
-
Contact angle between the \({ws}\) and \({wn}\) interfaces
- \(\psi \) :
-
body force potential per unit mass (e.g., gravitational potential)
- \({{\varOmega }_{}}\) :
-
Spatial domain
1.10 Subscripts and Superscripts
- \(\mathrm {eq}\) :
-
An equilibrium state
- n :
-
Index that indicates a non-wetting phase
- ns :
-
Index that indicates the non-wetting–solid phase interface
- s :
-
Index that indicates a solid phase
- w :
-
Entity index corresponding to the wetting phase
- wn :
-
Index that indicates the wetting–non-wetting phase interface
- wns :
-
Index that denotes the common curve
- ws :
-
Entity index corresponding to the wetting–solid interface
- \({{\alpha }}\) :
-
General entity index qualifier
- \({{\kappa }}\) :
-
General entity index qualifier
1.11 Other Mathematical Symbols
- \(\overline{\ }\) :
-
Above a superscript refers to a density weighted macroscale average
- \(\overline{\overline{\ }}\) :
-
Above a superscript refers to a uniquely defined macroscale average
- \(\mathrm {D}^{}_{{}}/\mathrm {D}t\) :
-
Material derivative
1.12 Abbreviations
- \(\hbox {EI}\) :
-
Entropy inequality
- \(\hbox {REV}\) :
-
Representative elementary volume
- \(\hbox {TCAT}\) :
-
Thermodynamically constrained averaging theory
1.13 Homogenization Theory
- \({\mathcal {B}}\) :
-
Pore space domain in the unit cell Y
- \(|{\mathcal {B}}|\) :
-
Volume of \({\mathcal {B}}\) [L\(^3\)]
- \({\mathcal {B}}^\varepsilon \) :
-
Pore space domain in the porous medium \(\varOmega \)
- \(c_\varepsilon \) :
-
Dimensionless pore-scale aqueous concentration of species C [–]
- \({{\hat{c}}}_\varepsilon \) :
-
Pore-scale aqueous concentration of species C [mol L\(^{-3}\)]
- \(\langle c_\varepsilon \rangle \) :
-
Average of \(c_\varepsilon \) over the unit cell Y
- \(\langle c_\varepsilon \rangle _{{\mathcal {B}}}\) :
-
Average of \(c_\varepsilon \) over the pore volume \({\mathcal {B}}\)
- \(\langle c_\varepsilon \rangle _\varGamma \) :
-
Average of the quantity \(c_\varepsilon \) over the solid-liquid interface \(\varGamma \)
- \({{\overline{c}}}\) :
-
\(:=\root n \of {k_d/k}\), threshold aqueous concentration of species C [mol L\(^{-3}\)]
- \({{\overline{c}}}^n\) :
-
\(:=\) solubility product of species C
- \({\mathbf {D}}\) :
-
dimensionless molecular diffusion coefficient defined by (119) [–]
- \({\mathcal {D}}\) :
-
Molecular diffusion coefficient [L\(^2~\)T\(^{-1}\)]
- \({\mathcal {D}}_0\) :
-
Characteristic value of \({\mathcal {D}}\), [L\(^2\) T\(^{-1}\)]
- \({\mathbf {D}}^*\) :
-
Dimensionless dispersion tensor defined by (137)
- Da :
-
\(:={{\hat{t}}}_{\mathrm d}/{{\hat{t}}}_{\mathrm {r}}\), Damköhler number defined by (121)
- \({\mathcal {G}}\) :
-
Solid matrix domain in the unit cell Y
- k :
-
Reaction rate of the forward heterogeneous reaction \(C \rightarrow S\)
- \(k_{c}\) :
-
reaction rate of the backward homogeneous reaction \(A+B \leftarrow C\).
- \(k_{d}\) :
-
Reaction rate of the backward heterogeneous reaction \(C \leftarrow S\)
- \({\mathbf {k}}\) :
-
Closure variable defined by (??)
- \({\mathbf {K}}\) :
-
\(:=\langle {\mathbf {k}}({\mathbf {y}})\rangle \), permeability tensor
- \({\mathcal {K}}^\star \) :
-
Effective reaction rate constant defined by (??)
- \(\ell \) :
-
Characteristic length of the periodic unit cell Y
- L :
-
Characteristic length of macroscopic porous medium domain \(\varOmega \)
- n :
-
Heterogeneous reaction order, [-]
- \({{\hat{p}}}\) :
-
Fluid dynamic pressure, [ML\(^{-1}\)T\(^{-2}\)]
- Pe :
-
Péclet number defined by (121)
- t :
-
\(:={{\hat{t}}}/{{\hat{t}}}_{\mathrm d}\), dimensionless time [–]
- \({{\hat{t}}}_{\mathrm a}\) :
-
Advection timescale [T]
- \({{\hat{t}}}_{\mathrm d}\) :
-
Diffusion timescale [T]
- \({{\hat{t}}}_{\mathrm {rj}}\) :
-
\(j=\{1,2,3\}\), reaction timescales [T]
- U :
-
Characteristic velocity associated with \(\hat{{\mathbf {v}}}_\varepsilon \) [TL\(^{-1}\)]
- \({\mathbf {v}}_\varepsilon \) :
-
Dimensionless pore-scale fluid velocity [–]
- \(\hat{{\mathbf {v}}}_\varepsilon \) :
-
Pore-scale fluid velocity [T L\(^{-1}\)]
- \({\mathbf {x}}\) :
-
Spatial coordinate of the pore space \({\mathcal {B}}_\varepsilon \)
- \({\mathbf {y}}\) :
-
Spatial coordinate of the unit cell Y
- Y :
-
Spatially periodic unit cell
- |Y|:
-
Volume of the spatially periodic unit cell [L\(^3\)]
- \(\alpha \) :
-
Coefficient for the definition of \(Pe = \varepsilon ^{-\alpha }\)
- \(\beta \) :
-
Coefficient for the definition of \(Da = \varepsilon ^\beta \)
- \(\varepsilon \) :
-
\(:= \ell / L \), scale separation coefficient [–]
- \(\hat{\phi }\) :
-
Unit cell porosity [–]
- \(\varGamma \) :
-
Solid–liquid interface in the unit cell Y
- \(\varGamma ^\varepsilon \) :
-
Solid–liquid interface in the porous medium \(\varOmega \)
- \(\mu \) :
-
Fluid dynamic viscosity [M L\(^{-1}\) T\(^{-1}\)]
- \(\varOmega \) :
-
Porous medium domain
- \(\psi \) :
-
General dimensionless pore-scale function
- \(\psi _m\) :
-
Y-periodic terms of order m for the multiple-scale expansion of \(\psi \)
- \(\psi _\varepsilon \) :
-
\(\psi \) defined in \({\mathcal {B}}_{\varepsilon }\)
- \({\hat{\psi }}_\varepsilon \) :
-
Dimensional value of \(\psi \) in \({\mathcal {B}}_{\varepsilon }\)
Rights and permissions
About this article
Cite this article
Battiato, I., Ferrero V, P.T., O’ Malley, D. et al. Theory and Applications of Macroscale Models in Porous Media. Transp Porous Med 130, 5–76 (2019). https://doi.org/10.1007/s11242-019-01282-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11242-019-01282-2