Skip to main content
SpringerLink
Log in

Performance of Subcarrier Intensity Modulated FSO Systems over Gamma–Gamma Turbulence Channels with Pointing Errors

  • Published:
Wireless Personal Communications Aims and scope Submit manuscript

Abstract

In this paper, we consider a free-space optical communication system using subcarrier intensity modulation (SIM) with general-order rectangular quadrature amplitude modulation (QAM) and operating over Gamma–Gamma turbulence channels subjected to pointing errors. We derive novel, exact closed-form expression for the average symbol error probability of the considered system in terms of the Fox H function. Using the derived analytical results, we investigate the combined effects of turbulence-induced fading and misalignment-induced fading on the performance of the SIM-QAM FOS communication system. Numerical and computer simulation results are presented in order to verify the accuracy of the proposed mathematical analysis.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

Notes

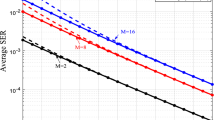
  1. Our results indicate excellent agreement for higher order QAM modulations, but are excluded due to space constraints.

References

  1. Ghassemlooy, Z., Popoola, W., & Rajbhandari, S. (2013). Optical wireless communications. System and channel modelling with MATLAB. Boca Raton, FL: CRC Press, Taylor & Francis Group.

    Google Scholar 

  2. Li, E. J., Liu, J. Q., & Taylor, D. P. (2007). Optical communication using subcarrier PSK intensity modulation through atmospheric turbulence channels. IEEE Transactions on Communications, 55(8), 1598–1606.

    Article  Google Scholar 

  3. Popoola, W. O., Ghassemlooy, Z., Allen, J. I. H., Leitgeb, E., & Gao, S. (2008). Free-space optical communication employing subcarrier modulation and spatial diversity in atmospheric turbulence channel. IET Opto Electronics, 2(1), 16–23.

    Article  Google Scholar 

  4. Popoola, W. O., & Ghassemlooy, Z. (2009). BPSK subcarrier modulated free-space optical communications in atmospheric turbulence. Journal of Lightwave Technology, 27(8), 967–973.

    Article  Google Scholar 

  5. Samimi, H., & Azmi, P. (2010). Subcarrier ıntensity modulated free-space optical communications in K-distributed turbulence channels. Journal of Optical Communications and Networking, 2(8), 625–632.

    Article  Google Scholar 

  6. Samimi, H. (2012). Optical communication using subcarrier intensity modulation through generalized turbulence channels. IEEE/OSA Journal of Optical Communications and Networking, 4(5), 378–381.

    Article  Google Scholar 

  7. Peppas, K. P., & Datsikas, C. K. (2010). Average symbol error probability of general-order rectangular quadrature amplitude modulation of optical wireless communication systems over atmospheric turbulence channels. IEEE/OSA Journal of Optical Communications and Networking, 2, 102–110.

    Article  Google Scholar 

  8. Zoheb Hassan, Md, Song, X., & Cheng, J. (2012). Subcarrier ıntensity modulated wireless optical communications with rectangular QAM. Journal of Optical Communications and Networking, 4(6), 522–532.

    Article  Google Scholar 

  9. Farid, A. A., & Hranilovic, S. (2007). Outage capacity optimization for free-space optical links with pointing errors. Journal of Lightwave Technology, 25(7), 1702–1710.

    Article  Google Scholar 

  10. Song, X., Yang, F., & Cheng, J. (2013). Subcarrier ıntensity modulated optical wireless communications in atmospheric turbulence with pointing errors. IEEE/OSA Journal of Optical Communications and Networking, 5(4), 349–357.

    Article  Google Scholar 

  11. Kilbas, A., & Saigo, M. (2004). H-transforms: Theory and applications (Analytical method and special function) (1st ed.). Boca Raton: CRC Press.

    Book  MATH  Google Scholar 

  12. Zhu, X., & Kahn, J. M. (2002). Free-space optical communication through atmospheric turbulence channels. IEEE Transactions on Communications, 50(8), 1293–1300.

    Article  Google Scholar 

  13. Gradshteyn, I. S., & Ryzhik, I. M. (2000). Table of integrals, series, and products (6th ed.). New York: Academic.

    MATH  Google Scholar 

  14. I. Wolfram Research. (2010). Mathematica edition: Version 8.0. Champaign, IL: Wolfram Research Inc.

    Google Scholar 

  15. Sandalidis, H. G., Tsiftsis, T. A., & Karagiannidis, G. K. (2009). Optical wireless communications with heterodyne detection over turbulence channels with pointing errors. Journal of Lightwave Technology, 27(20), 4440–4445.

    Article  Google Scholar 

  16. Mittal, P., & Gupta, K. (1972). An integral involving generalized function of two variables (pp. 117–123). Bengaluru: Indian Academy of Sciences.

    MATH  Google Scholar 

  17. Peppas, K. (2012). A new formula for the average bit error probability of dual-hop amplify-and-forward relaying systems over generalized shadowed fading channels. IEEE Wireless Communications Letters, 1(2), 85–88.

    Article  Google Scholar 

  18. Yi, X., Liu, Z., & Yue, P. (2013). Formula for the average bit error rate of free-space optical systems with dual-branch equal-gain combining over gamma–gamma turbulence channels. Optics Letters, 38(2), 208–210.

    Article  Google Scholar 

  19. Yilmaz, F., & Alouini, M.-S. (2009). Product of the powers of generalized Nakagami-m variates and performance of cascaded fading channels. In Proceedings of IEEE global communications conference (GLOBECOM 2009), Honolulu, Hawaii, USA, November 30–December 4.

Download references

Author information

Authors and Affiliations

  1. Communications Technology Department, ICT Research Institute, P. O. Box 14155-3961, Tehran, Iran

    Hossein Samimi

Authors
  1. Hossein Samimi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Hossein Samimi.

Appendices

Appendix 1: Derivation of Closed-Form Solution for \({\mathcal{M}}\left( {\alpha ,\beta ,\bar{\mu },\xi } \right)\)

In this Appendix, we present the derivation of an exact closed-for expression for the integral \({\mathcal{M}}\left( {\alpha ,\beta ,\bar{\mu },\xi } \right) = \mathop \int \limits_{0}^{\infty } Q\left( {\xi \sqrt \mu } \right)f_{\mu } \left( \mu \right)d\mu\). First note that we can write Gaussian Q function in terms of the complementary error function \({\text{erfc}}\left( \cdot \right)\) as Q \(\left( x \right) = 1/2{\text{erfc}}\left( {x/\sqrt 2 } \right)\) Furthermore, the erfc(.) function can be written in terms of the Meijer G function as \({\text{erfc}}\left( z \right) = 1/\sqrt {\pi } G_{1, 2}^{2, 0} \left( {\left. {z^{2} } \right|_{1/2 , 0}^{ 1} } \right)\) [13]. Finally, using [13, Eq. (6.2.8)], we can write the Meijer G function in terms of the desired Fox H function yielding

$$Q\left( x \right) = \frac{1}{2\sqrt \pi } H_{1, 2}^{2, 0} \left( {\left. {\begin{array}{l} {} \\ {\frac{{x^{2} }}{2}} \\ {} \\ \end{array} } \right|\begin{array}{l} {\left( {1,1} \right)} \\ {\left( {\frac{1}{2},1} \right) , \left( {0,1} \right) } \\ \end{array}_{{}}^{{}} } \right)$$
(8)

Using (8) and (3), \({\mathcal{M}}\left( {\alpha ,\beta ,\bar{\mu },\xi } \right)\) can be described as

$$\begin{aligned} {\mathcal{M}}\left( {\alpha ,\beta ,\bar{\mu },\xi } \right) &= \frac{{\upalpha \upbeta g^{2} }}{{4\varGamma \left(\upalpha \right)\varGamma \left(\upbeta \right)\sqrt {\pi \bar{\mu }} }} \times \mathop \int \limits_{0}^{\infty } \mu^{{ - \frac{1}{2}}} H_{1, 2}^{2, 0} \left( {\left. {\begin{array}{*{20}c} {} \\ {\frac{{\xi^{2} \mu }}{2}} \\ {} \\ \end{array} } \right|\begin{array}{*{20}c} {\left( {1,1} \right)} \\ {\left( {\frac{1}{2},1} \right) , \left( {0,1} \right) } \\ \end{array}_{{}}^{{}} } \right)\\& \quad \times H_{1, 3}^{3, 0} \left( {\left. {\begin{array}{*{20}c} {} \\ {\upalpha \upbeta \sqrt {\frac{\mu }{{\bar{\mu }}}} } \\ {} \\ \end{array} } \right|\begin{array}{*{20}c} {\left( {g^{2} ,1} \right)} \\ {\left( {g^{2} - 1,1} \right) , \left( {\upalpha - 1,1} \right) , \left( {\upbeta - 1,1} \right)} \\ \end{array}_{{}}^{{}} } \right)d\mu \\ \end{aligned}$$
(9)

Using the integral identity [13, Eq. (2.8.4)], \({\mathcal{M}}\left( {\alpha ,\beta ,\bar{\mu },\xi } \right)\) can be derived in closed-form as

$$\begin{aligned} {\mathcal{M}}\left( {\alpha ,\beta ,\bar{\mu },\xi } \right) = \frac{{\upalpha \upbeta g^{2} }}{{2\varGamma \left(\upalpha \right)\varGamma \left(\upbeta \right)\xi \sqrt {2\pi \bar{\mu }} }} \hfill \\ \times H_{3, 4}^{3, 2} \left( {\left. {\begin{array}{*{20}c} {} \\ {\frac{{\upalpha \upbeta }}{\xi }\sqrt {\frac{2}{{\bar{\mu }}}} } \\ {} \\ \end{array} } \right|\begin{array}{*{20}c} {\left( {0,\frac{1}{2}} \right) , \left( {\frac{1}{2},\frac{1}{2}} \right) , \left( {g^{2} ,1} \right)} \\ {\left( {g^{2} - 1,1} \right) , \left( {\upalpha - 1,1} \right) , \left( {\upbeta - 1,1} \right) , \left( { - \frac{1}{2},\frac{1}{2}} \right)} \\ \end{array}_{{}}^{{}} } \right) \hfill \\ \end{aligned}$$
(10)

Appendix 2: Derivation of Closed-Form Solution for \({\mathcal{F}}\left( {\alpha ,\beta ,\bar{\mu },\xi ,\rho } \right)\)

In this Appendix, we present the derivation of an exact closed-for expression for the integral\({\mathcal{F}}\left( {\alpha ,\beta ,\bar{\mu },\xi ,\rho } \right) = \mathop \int \limits_{0}^{\infty } Q\left( {\xi \sqrt \mu } \right)Q\left( {\rho \sqrt \mu } \right)f_{\mu } \left( \mu \right)d\mu\). Using (8) and (3),\({\mathcal{F}}\left( {\alpha ,\beta ,\bar{\mu },\xi ,\rho } \right)\) can be written as

$$\begin{aligned} {\mathcal{F}}\left( {\alpha ,\beta ,\bar{\mu },A_{I} ,A_{Q} } \right) = \frac{{\upalpha \upbeta g^{2} }}{{8\pi\Gamma \left(\upalpha \right)\Gamma \left(\upbeta \right)\sqrt {\bar{\mu }} }} \hfill \\ \times \mathop \int \limits_{0}^{\infty } \mu^{{ - \frac{1}{2}}} H_{1, 2}^{2, 0} \left( {\left. {\begin{array}{*{20}c} {} \\ {\frac{{\xi^{2} \mu }}{2}} \\ {} \\ \end{array} } \right|\begin{array}{*{20}c} {\left( {1,1} \right)} \\ {\left( {\frac{1}{2},1} \right) , \left( {0,1} \right) } \\ \end{array}_{{}}^{{}} } \right) H_{1, 2}^{2, 0} \left( {\left. {\begin{array}{*{20}c} {} \\ {\frac{{\rho^{2} \mu }}{2}} \\ {} \\ \end{array} } \right|\begin{array}{*{20}c} {\left( {1,1} \right)} \\ {\left( {\frac{1}{2},1} \right) , \left( {0,1} \right) } \\ \end{array}_{{}}^{{}} } \right) \hfill \\ H_{1, 3}^{3, 0} \left( {\left. {\begin{array}{*{20}c} {} \\ {\upalpha \upbeta \sqrt {\frac{\mu }{{\bar{\mu }}}} } \\ {} \\ \end{array} } \right|\begin{array}{*{20}c} {\left( {g^{2} ,1} \right)} \\ {\left( {g^{2} - 1,1} \right) , \left( {\upalpha - 1,1} \right) , \left( {\upbeta - 1,1} \right)} \\ \end{array}_{{}}^{{}} } \right)d\mu \hfill \\ \end{aligned}$$
(11)

Using the identity [16, Eq. (2.3)], \({\mathcal{F}}\left( {\alpha ,\beta ,\bar{\mu },A_{I} ,A_{Q} } \right)\) can be obtained in terms of the bivariate Fox H function as

$${\mathcal{F}}\left( {\alpha ,\beta ,\bar{\mu },A_{I} ,A_{Q} } \right) = \frac{{\upalpha \upbeta g^{2} }}{{4\pi\Gamma \left(\upalpha \right)\Gamma \left(\upbeta \right)\xi \sqrt {2\bar{\mu }} }} \times H\left( {\left. {\left. {\begin{array}{*{20}c} {\left( {\begin{array}{*{20}c} 0 & 2 \\ 1 & 2 \\ \end{array} } \right)} \\ {} \\ {\left( {\begin{array}{*{20}c} 2 & { 0} \\ 1 & 2 \\ \end{array} } \right)} \\ {} \\ {\left( {\begin{array}{*{20}c} 3 & 0 \\ 1 & 3 \\ \end{array} } \right)} \\ {} \\ \end{array} } \right|\begin{array}{*{20}c} {\left( {0;1,\frac{1}{2}} \right) , \left( {\frac{1}{2};1,\frac{1}{2}} \right) } \\ {\left( { - 1;1,\frac{1}{2}} \right)} \\ {\left( {1,1} \right)} \\ {\left( {\frac{1}{2},1} \right) , \left( {0,1} \right)} \\ {\begin{array}{*{20}c} {\left( {g^{2} ,1} \right)} \\ {\left( {g^{2} - 1,1} \right) , \left( {\upalpha - 1,1} \right) , \left( {\upbeta - 1,1} \right)} \\ \end{array} } \\ \end{array} } \right|\frac{{\rho^{2} }}{{\xi^{2} }} ,\frac{{\upalpha \upbeta }}{\xi }\sqrt {\bar{\mu }} } \right)$$
(12)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Samimi, H. Performance of Subcarrier Intensity Modulated FSO Systems over Gamma–Gamma Turbulence Channels with Pointing Errors. Wireless Pers Commun 95, 1407–1416 (2017). https://doi.org/10.1007/s11277-016-3854-z

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11277-016-3854-z

Keywords

Search

Navigation