Secrecy Outage Performance Analysis of DF Cognitive Relay Network With Co-channel Interference

Abstract

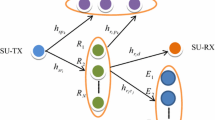
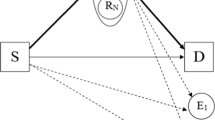
In this paper, we investigate the secrecy outage performance of the decode-and-forward cognitive relay network with the existence of the co-channel interference, where all nodes are equipped with single antenna and all channels experience Rayleigh fading channels, which are also independent non-identical distribution (i.n.i.d). We also consider the multiple user selection scheme and the single eavesdropper, which could wiretap the information at each hop. There is no evidence of the direct links from the source to the destinations because of the bad conditions. To evaluate the system secrecy performance, we derive the closed form expressions of the secrecy outage probabilities, and the Monte Carlo simulations are also presented to validate the accuracy of the theoretical analysis.

Appendices

Appendices

1.1 Appendix 1: Proof of Corollary 1

According to $Z_1 = \frac{{Id_{nD}^{ - \alpha }}}{{\left( {\rho - 1} \right) {N_{{0_D}}}}}{\left| {{h_{nD}}} \right| ^2} - \frac{{\rho Id_{nE}^{ - \alpha }}}{{\left( {\rho - 1} \right) {N_{{0_E}}}}}{\left| {{h_{nE}}} \right| ^2}$, the CDF of $Z_1$ can be expressed as

$$\begin{aligned} {F_{Z_1}}\left( z \right)&= \Pr \left( {Z_1< z} \right) \nonumber \\&= \!\Pr \! \left( \! {\frac{{{{\left| {{h_{SR}}} \right| }^2}}}{{1\! +\! \sum \nolimits _{i = 1}^{{L_R}} {{{\left| {{h_{Ri}}} \right| }^2}} }}\! <\! \frac{{\left( {\rho \! -\! 1} \right) \!{N_{0R}}}}{I}z \!+\! \frac{{\rho {N_{0R}}}}{{{N_{0E}}}}{{\left| {{h_{SE}}} \right| }^2}}\! \right) \nonumber \\&= \int _0^\infty {{F_{X_1}}\left( {\frac{{\left( {\rho - 1} \right) {N_{0R}}}}{I}z + \frac{{\rho {N_{0R}}}}{{{N_{0E}}}}y} \right) {f_{Y_1}}\left( y \right) dy}, \end{aligned}$$

(24)

where $X_1 = \frac{{{{\left| {{h_{SR}}} \right| }^2}}}{{1 + \sum \nolimits _{i = 1}^{{L_R}} {{{\left| {{h_{Ri}}} \right| }^2}} }}$ and $Y_1 = {\left| {{h_{SE}}} \right| ^2}$. The CDF of $X_1$ is ${F_{X_1}}\left( x \right) = 1 - \exp \left( { - \frac{1}{{{\beta _1}}}x} \right) {\left( {\frac{{{\beta _1}}}{{{\lambda _R}x + {\beta _1}}}} \right) ^{{L_R}}}$, and the PDF of $Y_1$ is ${f_{Y_1}}\left( y \right) = \frac{1}{{{\varepsilon _1}}}\exp \left( { - \frac{1}{{{\varepsilon _1}}}y} \right)$. By substituting ${F_{X_1}}\left( x \right)$ and ${f_{Y_1}}\left( y \right)$ into (24), ${F_{Z_1}}\left( z \right)$ can be referenced in Corollary1.

1.2 Appendix 2: Proof of Corollary 2

To solve the integration in (11), we should simplify the Gamma function first according to [18, eq. (8.352.5)],

$$\begin{aligned} \Gamma \left( {1 \!-\! {L_R},{T_3}{T_4}t \!+\! {T_3}{\beta _1}} \right)&= \! -\! \underbrace{\frac{{{{\left( {\! -\! 1} \right) }^{{L_R} + 1}}}}{{\left( {{L_R}\! -\! 1} \right) !}}Ei\left( {\! - \!\left( {{T_3}{T_4}t\! +\! {T_3}{\beta _1}} \right) } \right) }_{{B_1}} \nonumber \\&\quad - \underbrace{\frac{{{{\left( { - 1} \right) }^{{L_R} + 1}}}}{{\left( {{L_R} - 1} \right) !}}\sum \limits _{m = 0}^{{L_R} - 2} {\frac{{{{\left( { - 1} \right) }^m}m!\exp \left( { - \left( {{T_3}{T_4}t + {T_3}{\beta _1}} \right) } \right) }}{{{{\left( {{T_3}{T_4}t + {T_3}{\beta _1}} \right) }^{m + 1}}}}} }_{{B_2}} \nonumber \\&= - {B_1} - {B_2}. \end{aligned}$$

(25)

Next, we can rewrite ${P_1}$ as

$$\begin{aligned} {P_1}&= \underbrace{\int _{\frac{I}{{{P_{\max }}}}}^\infty {\frac{1}{{{\alpha _1}}}\exp \left( { - \frac{1}{{{\alpha _1}}}t} \right) } dt}_{{I_1}}\nonumber \\&\quad + \underbrace{\int _{\frac{I}{{{P_{\max }}}}}^\infty {{T_1}{B_1}\frac{1}{{{\alpha _1}}}\exp \left( {\left( {{T_2} - \frac{1}{{{\alpha _1}}}} \right) t} \right) } dt}_{{I_2}}\nonumber \\&\quad + \underbrace{\int _{\frac{I}{{{P_{\max }}}}}^\infty {{T_1}{B_2}\frac{1}{{{\alpha _1}}}\exp \left( {\left( {{T_2} - \frac{1}{{{\alpha _1}}}} \right) t} \right) } dt}_{{I_3}}\nonumber \\&= {I_1} + {I_2} + {I_3}. \end{aligned}$$

(26)

${I_1}$ can be easily derived as

$$\begin{aligned} {I_1} = \exp \left( { - \frac{I}{{{\alpha _1}{P_{\max }}}}} \right) . \end{aligned}$$

(27)

${I_2}$ can be rewritten as

$$\begin{aligned} {I_2}&= \frac{{{T_1}{{\left( { - 1} \right) }^{{L_R} + 1}}}}{{{\alpha _1}\left( {{L_R} - 1} \right) !}}\exp \left( { - \left( {\frac{1}{{{\alpha _1}}} - {T_2}} \right) \frac{I}{{{P_{\max }}}}} \right) \nonumber \\&\quad \times \!\! \underbrace{\int _0^\infty \!\!\! {\exp \left( {\! -\! \left( {\frac{1}{{{\alpha _1}}}\! -\! {T_2}} \right) \!s} \!\right) } Ei\left( { \!-\! {T_3}{T_4}s\! -\! \left( {{T_3}{T_4}{P_{\max }}\! +\! {T_3}{\beta _1}} \right) } \right) ds}_P. \end{aligned}$$

(28)

To obtain the integration P, we should deal with the form of integration $H=\int _0^\infty {\exp \left( { - ax} \right) Ei\left( { - bx - c} \right) dx}$ first, and we will detailedly illustrate the process. After further derivation, H can be rewritten as

$$\begin{aligned} H&= \frac{1}{b}\exp \left( {\frac{{ac}}{b}} \right) \int _c^\infty {Ei\left( { - t} \right) \exp \left( {\frac{{ - a}}{b}t} \right) } dt\nonumber \\&=\frac{1}{b}\exp \left( {\frac{{ac}}{b}} \right) \left( {\underbrace{\int _0^\infty {Ei\left( { - t} \right) \exp \left( {\frac{{ - a}}{b}t} \right) } dt}_{{H_1}}} \right. \nonumber \\&\quad \left. {- \underbrace{\int _0^c {Ei\left( { - t} \right) \exp \left( {\frac{{ - a}}{b}t} \right) } dt}_{{H_2}}} \right) . \end{aligned}$$

(29)

According to [18, eq. (6.224.1)], we can derive

$$\begin{aligned} {H_1} = - \frac{b}{a}\ln \left( {1 + \frac{a}{b}} \right) . \end{aligned}$$

(30)

In addition, ${H_2}$ can be rewritten as

$$\begin{aligned} {H_2} = \int _0^\infty {\theta \left( {c - t} \right) Ei\left( { - t} \right) \exp \left( { - \frac{a}{b}t} \right) } dt, \end{aligned}$$

(31)

where ${\theta \left( {t} \right) }$ is the unit step function. According to [17, eq. (3.4.1.9)], we can derive

$$\begin{aligned} {H_2} = \frac{b}{a}\left[ {Ei\left( { \!- c\! -\! \frac{{ac}}{b}} \right) \! - \exp \left( { \!- \frac{{ac}}{b}} \right) Ei\left( { - c} \right) \! + \ln \left( {1 \!+ \frac{a}{b}} \right) } \right] . \end{aligned}$$

(32)

Thus, we can obtain the final result H by combining (30) and (31)

$$\begin{aligned} H&=\int _0^\infty {\exp \left( { - ax} \right) Ei\left( { - bx - c} \right) dx}\nonumber \\&= - \frac{1}{a}\left[ {\exp \left( {\frac{{ac}}{b}} \right) Ei\left( { - c - \frac{{ac}}{b}} \right) + Ei\left( { - c} \right) } \right] . \end{aligned}$$

(33)

Thus, according to (33), we can easily obtain the ${I_2}$

$$\begin{aligned} {I_2}&= \frac{{{T_1}{{\left( { - 1} \right) }^{{L_R} + 1}}}}{{{\alpha _1}\left( {{L_R} - 1} \right) !}}\exp \left( { - \left( {\frac{1}{{{\alpha _1}}} - {T_2}} \right) \frac{I}{{{P_{\max }}}}} \right) \nonumber \\&\quad \times \frac{1}{{{a_1}}}\left[ { - \exp \left( {\frac{{{a_1}{c_1}}}{{{b_1}}}} \right) Ei\left( { - {c_1} - \frac{{{a_1}{c_1}}}{{{b_1}}}} \right) + Ei\left( { - {c_1}} \right) } \right] , \end{aligned}$$

(34)

where the details of ${a_1}$, ${b_1}$ and ${c_1}$ can be referenced the Corollary 2.

Next, ${I_3}$ can be expressed as

$$\begin{aligned} {I_3}&= \underbrace{\sum \nolimits _{m = 0}^{{L_R} - 2} {\frac{{{T_1}{{\left( { - 1} \right) }^{{L_R} + 1}}}}{{{\alpha _1}\left( {{L_R} - 1} \right) !}}{{\left( { - 1} \right) }^m}} m!}_{{G_1}}\nonumber \\&\quad \!\times \!\int _{\frac{I}{{{P_{\max }}}}}^\infty \!\! {\exp \left( {\! -\! \left( {\frac{1}{{{\alpha _1}}}\! -\! {T_2}} \right) t} \right) } \frac{{\exp \left( {\! -\! \left( {{T_3}{T_4}t + {T_3}{\beta _1}} \right) } \right) }}{{{{\left( {{T_3}{T_4}t + {T_3}{\beta _1}} \right) }^{m + 1}}}}dt, \end{aligned}$$

(35)

we can simplify the integration by letting $s = {T_3}{T_3}t + {T_3}{\beta _1}$, after further derivation, and ${I_3}$ can be rewritten

$$\begin{aligned} {I_3}&= \underbrace{{G_1}\exp \left( {\left( {\frac{1}{{{\alpha _1}}} - {T_2}} \right) \frac{{{\beta _1}}}{{{T_4}}}} \right) \frac{1}{{{T_3}{T_4}}}}_{{G_2}}\nonumber \\&\quad \times \int _{{T_3}{T_4}\frac{I}{{{P_{\max }}}} + {T_3}{\beta _1}}^\infty \! {\frac{{\exp \left( { - \left( {\frac{1}{{{\alpha _1}{T_3}{T_4}}} - \frac{{{T_2}}}{{{T_3}{T_4}}} + 1} \right) s} \right) }}{{{s^{m + 1}}}}} ds. \end{aligned}$$

(36)

Once more, we should let $y = \frac{1}{{{\alpha _1}{T_3}{T_4}}} - \frac{{{T_2}}}{{{T_3}{T_4}}} + 1$ to calculate the integration. Now, ${I_3}$ is

$$\begin{aligned} {I_3}&= \underbrace{{G_2}{{\left( {\frac{1}{{{\alpha _1}{T_3}{T_4}}} - \frac{{{T_2}}}{{{T_3}{T_4}}} + 1} \right) }^m}}_{{G_3}}\nonumber \\&\quad \times \int _{\left( {\frac{1}{{{\alpha _1}{T_3}{T_4}}} - \frac{{{T_2}}}{{{T_3}{T_4}}} + 1} \right) \left( {{T_3}{T_4}\frac{I}{{{P_{\max }}}} + {T_3}{\beta _1}} \right) }^\infty {\frac{{\exp \left( { - y} \right) }}{{{y^{m + 1}}}}} dy. \end{aligned}$$

(37)

According to $\Gamma \left( {\alpha ,x} \right) = \int _x^\infty {{e^{ - t}}{t^{\alpha - 1}}dt}$ [18, eq. (8.350.2)], we can derive the closed form of ${I_3}$

$$\begin{aligned} {I_3} = {G_3}\times \Gamma \left( { \!- m,\left( {\frac{1}{{{\alpha _1}{T_3}{T_4}}} \!-\! \frac{{{T_2}}}{{{T_3}{T_4}}}\! +\! 1} \right) \!\!\left( {\frac{{{T_3}{T_4}I}}{{{P_{\max }}}}\! +\! {T_3}{\beta _1}} \right) }\! \right) . \end{aligned}$$

(38)

Thus, combining the results of ${I_1}$, ${I_2}$ and ${I_3}$, $P_1$ is shown in (13).