Skip to main content
SpringerLink
Log in

A conservative numerical method for the fractional nonlinear Schrödinger equation in two dimensions

  • Articles
  • Published:
Science China Mathematics Aims and scope Submit manuscript

Abstract

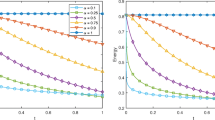
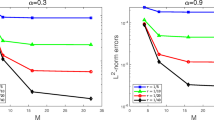
This paper proposes and analyzes an efficient finite difference scheme for the two-dimensional nonlinear Schrödinger (NLS) equation involving fractional Laplacian. The scheme is based on a weighted and shifted Grünwald-Letnikov difference (WSGD) operator for the spatial fractional Laplacian. We prove that the proposed method preserves the mass and energy conservation laws in semi-discrete formulations. By introducing the differentiation matrices, the semi-discrete fractional nonlinear Schrödinger (FNLS) equation can be rewritten as a system of nonlinear ordinary differential equations (ODEs) in matrices formulations. Two kinds of time discretization methods are proposed for the semi-discrete formulation. One is based on the Crank-Nicolson (CN) method which can be proved to preserve the fully discrete mass and energy conservation. The other one is the compact implicit integration factor (cIIF) method which demands much less computational effort. It can be shown that the cIIF scheme can approximate CN scheme with the error O(τ2). Finally numerical results are presented to demonstrate the method’s conservation, accuracy, efficiency and the capability of capturing blow-up.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Aboelenen T. A high-order nodal discontinuous Galerkin method for nonlinear fractional Schrödinger type equations. Commun Nonlinear Sci Numer Simul, 2018, 54: 428–452

    Article  MathSciNet  Google Scholar 

  2. Bhrawy A H, Abdelkawy M A. A fully spectral collocation approximation for multi-dimensional fractional Schrödinger equations. J Comput Phys, 2015, 294: 462–483

    Article  MathSciNet  Google Scholar 

  3. Boulenger T, Himmelsbach D, Lenzmann E. Blowup for fractional NLS. J Funct Anal, 2016, 271: 2569–2603

    Article  MathSciNet  Google Scholar 

  4. Çelik C, Duman M. Crank-Nicolson method for the fractional diffusion equation with the Riesz fractional derivative. J Comput Phys, 2012, 231: 1743–1750

    Article  MathSciNet  Google Scholar 

  5. Chang Q, Jia E, Sun W. Difference schemes for solving the generalized nonlinear Schrödinger equation. J Comput Phys, 1999, 148: 397–415

    Article  MathSciNet  Google Scholar 

  6. Dehghan M, Taleei A. A compact split-step finite difference method for solving the nonlinear Schrödinger equations with constant and variable coefficients. Comput Phys Comm, 2010, 181: 43–51

    Article  MathSciNet  Google Scholar 

  7. Duan B, Zheng Z, Cao W. Finite element method for a kind of two-dimensional space-fractional diffusion equation with its implementation. Amer J Comput Math, 2015, 5: 135

    Article  Google Scholar 

  8. Duo S, Zhang Y. Mass-conservative Fourier spectral methods for solving the fractional nonlinear Schrödinger equation. Comput Math Appl, 2016, 71: 2257–2271

    Article  MathSciNet  Google Scholar 

  9. Fröhlich J, Jonsson B L G, Lenzmann E. Boson stars as solitary waves. Comm Math Phys, 2007, 274: 1–30

    Article  MathSciNet  Google Scholar 

  10. Gong Y, Wang Q, Wang Y, et al. A conservative Fourier pseudo-spectral method for the nonlinear Schrödinger equation. J Comput Phys, 2017, 328: 354–370

    Article  MathSciNet  Google Scholar 

  11. Hou T, Tang T, Yang J. Numerical analysis of fully discretized Crank-Nicolson scheme for fractional-in-space Allen-Cahn equations. J Sci Comput, 2017, 72: 1214–1231

    Article  MathSciNet  Google Scholar 

  12. Ionescu A D, Pusateri F. Nonlinear fractional Schrödinger equations in one dimension. J Funct Anal, 2014, 266: 139–176

    Article  MathSciNet  Google Scholar 

  13. Ji C C, Sun Z Z. A high-order compact finite difference scheme for the fractional sub-diffusion equation. J Sci Comput, 2015, 64: 959–985

    Article  MathSciNet  Google Scholar 

  14. Khaliq A Q M, Liang X, Furati K M. A fourth-order implicit-explicit scheme for the space fractional nonlinear Schrödinger equations. Numer Algorithms, 2017, 75: 147–172

    Article  MathSciNet  Google Scholar 

  15. Kirkpatrick K, Lenzmann E, Staffilani G. On the continuum limit for discrete NLS with long-range lattice interactions. Comm Math Phys, 2013, 317: 563–591

    Article  MathSciNet  Google Scholar 

  16. Klein C, Sparber C, Markowich P. Numerical study of fractional nonlinear Schrödinger equations. Proc Math Phys Eng Sci, 2014, 470: 20140364

    Article  MathSciNet  Google Scholar 

  17. Laskin N. Fractional quantum mechanics. Phys Rev E, 2000, 62: 3135–3145

    Article  Google Scholar 

  18. Laskin N. Fractional Schrödinger equation. Phys Rev E, 2002, 66: 056108

    Article  MathSciNet  Google Scholar 

  19. Lenzmann E. Well-posedness for semi-relativistic Hartree equations of critical type. Math Phys Anal Geom, 2007, 10: 43–64

    Article  MathSciNet  Google Scholar 

  20. Li M, Huang C, Wang P. Galerkin finite element method for nonlinear fractional Schrödinger equations. Numer Algorithms, 2017, 74: 499–525

    Article  MathSciNet  Google Scholar 

  21. Liang X, Khaliq A Q M, Bhatt H, et al. The locally extrapolated exponential splitting scheme for multi-dimensional nonlinear space-fractional Schrödinger equations. Numer Algorithms, 2017, 76: 939–958

    Article  MathSciNet  Google Scholar 

  22. Magin R L, Abdullah O, Baleanu D, et al. Anomalous diffusion expressed through fractional order differential operators in the Bloch-Torrey equation. J Magnet Reson, 2008, 190: 255–270

    Article  Google Scholar 

  23. Meerschaert M M, Tadjeran C. Finite difference approximations for fractional advection-dispersion flow equations. J Comput Appl Math, 2004, 172: 65–77

    Article  MathSciNet  Google Scholar 

  24. Merle F, Tsutsumi Y. L 2 concentration of blow-up solutions for the nonlinear Schrödinger equation with critical power nonlinearity. J Differential Equations, 1990, 84: 205–214

    Article  MathSciNet  Google Scholar 

  25. Moler C, Loan C V. Nineteen dubious ways to compute the exponential of a matrix, twenty-five years later. SIAM Rev, 2003 45: 3–49

    Article  MathSciNet  Google Scholar 

  26. Nie Q, Wan F Y M, Zhang Y, et al. Compact integration factor methods in high spatial dimensions. J Comput Phys, 2008, 227: 5238–5255

    Article  MathSciNet  Google Scholar 

  27. Nie Q, Zhang Y, Zhao R. Efficient semi-implicit schemes for stiff systems. J Comput Phys, 2006, 214: 521–537

    Article  MathSciNet  Google Scholar 

  28. Obrecht C. Remarks on the full dispersion Davey-Stewartson systems. Commun Pure Appl Anal, 2015, 14: 1547–1561

    Article  MathSciNet  Google Scholar 

  29. Ortigueira M D. Riesz potential operators and inverses via fractional centred derivatives. Int J Math Math Sci, 2006, 2006: 1–12

    Article  MathSciNet  Google Scholar 

  30. Tian W, Zhou H, Deng W. A class of second order difference approximations for solving space fractional diffusion equations. Math Comput, 2015, 84: 1703–1727

    Article  MathSciNet  Google Scholar 

  31. Wang D, Zhang L, Nie Q. Array-representation integration factor method for high-dimensional systems. J Comput Phys, 2014, 258: 585–600

    Article  MathSciNet  Google Scholar 

  32. Wang P, Huang C. An energy conservative difference scheme for the nonlinear fractional Schrödinger equations. J Comput Phys, 2015, 293: 238–251

    Article  MathSciNet  Google Scholar 

  33. Wang P, Huang C. Split-step alternating direction implicit difference scheme for the fractional Schrödinger equation in two dimensions. Comput Math Appl, 2016, 71: 1114–1128

    Article  MathSciNet  Google Scholar 

  34. Xu Y, Shu C. Local discontinuous Galerkin methods for nonlinear Schrödinger equations. J Comput Phys, 2005, 205: 72–97

    Article  MathSciNet  Google Scholar 

  35. Yang Q, Liu F, Turner I. Numerical methods for fractional partial differential equations with Riesz space fractional derivatives. Appl Math Model, 2010, 34: 200–218

    Article  MathSciNet  Google Scholar 

  36. Yang Q, Turner I, Liu F, et al. Novel numerical methods for solving the time-space fractional diffusion equation in two dimensions. SIAM J Sci Comput, 2011, 33: 1159–1180

    Article  MathSciNet  Google Scholar 

  37. Yang Z. A class of linearized energy-conserved finite difference schemes for nonlinear space-fractional Schrödinger equations. Int J Comput Math, 2016, 93: 609–626

    Article  MathSciNet  Google Scholar 

  38. Zhang R, Yu X, Li M, et al. A conservative local discontinuous Galerkin method for the solution of nonlinear Schrödinger equation in two dimensions. Sci China Math, 2017, 60: 2515–2530

    Article  MathSciNet  Google Scholar 

  39. Zhang R, Zhu J, Yu X, et al. A conservative spectral collocation method for the nonlinear Schrödinger equation in two dimensions. Appl Math Comput, 2017, 310: 194–203

    MathSciNet  MATH  Google Scholar 

  40. Zhao X, Sun Z, Hao Z. A fourth-order compact ADI scheme for two-dimensional nonlinear space fractional Schrödinger equation. SIAM J Sci Comput, 2014, 36: 2865–2886

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

This work was supported by National Natural Science Foundation of China (Grant Nos. 61573008 and 61703290), the Foundation of LCP (Grant No. 6142A0502020717) and National Science Foundation of USA (Grant No. DMS-1620108).

Author information

Authors and Affiliations

  1. School of Mathematics and Systematic Sciences, Shenyang Normal University, Shenyang, 110034, China

    Rongpei Zhang & Yi Zhang

  2. Department of Applied and Computational Mathematics and Statistics, University of Notre Dame, Notre Dame, IN, 46556, USA

    Yong-Tao Zhang

  3. College of Mathematics and Systems Science, Shandong University of Science and Technology, Qingdao, 266590, China

    Zhen Wang

  4. College of Mathematics and Statistics, Shenzhen University, Shenzhen, 518060, China

    Bo Chen

Authors
  1. Rongpei Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yong-Tao Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Zhen Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Bo Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Yi Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Rongpei Zhang.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhang, R., Zhang, YT., Wang, Z. et al. A conservative numerical method for the fractional nonlinear Schrödinger equation in two dimensions. Sci. China Math. 62, 1997–2014 (2019). https://doi.org/10.1007/s11425-018-9388-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11425-018-9388-9

Keywords

MSC(2010)

Search

Navigation